Thermal Characteristics of the Main Structural Schemes of AC Power Cables Based on High-Temperature Superconductors

Abstract

High-temperature superconducting cables (HTS cables) cooled with liquid nitrogen are an alternative to traditional cables. The amount of heat supplied from the HTS cable to the cryoagent, as well as the choice of the optimal cryoagent circulation scheme and the option of cooling the superconducting line as a whole, depends on the internal structure of the cable. The paper presents a theoretical model describing the transfer of heat flow through the cylindrical layers of the cable. Analytical equations are obtained that determine the specific linear heat flow to cables of various types: with three separate shielded phases contained in separate cryostats with a common return cryogenic pipeline, with three shielded phases in separate cryostats with the organization of a reverse flow of the cryoagent inside the cryostats, and with three shielded phases located in one cryostat, as well as in a triaxial cable with different cryoagent circulation schemes. For all types of cables, the ratios between the total linear heat fluxes through the thermal insulation of the cryostat and the heat fluxes from the cable have been determined depending on the mass flow rate of liquid nitrogen. Also, a comparative analysis of the relationship between specific heat fluxes, temperatures of the cryoagent after cooling, and hydraulic resistances per unit length of cables has been carried out. The proposed technique makes it possible to evaluate the thermal–hydraulic parameters of the considered cable structures and to choose the most appropriate technical solution.

In many cases in which it is necessary to reduce losses in the transmission of electrical-energy superconducting cables based on high-temperature superconductors (HTS cables) become an effective means of power supply in comparison with traditional power cables, especially in conditions of limited space for placing the power line. The increased current density in three-phase ac HTS cables allows a high power flow at low voltages allowing power generators to be connected directly to consumers. The amount of heat coming to the cable cryoagent from the environment through the thermal insulation of the cable cryostat, as well as due to internal heat release caused by electromagnetic losses in the cable, is the most important factor determining the efficiency and reliability of the cable. Minimizing the heat inputs reduces the energy cost in the cryogenic installation to dissipate this heat.

There are several types of HTS cables characterized by different design schemes of the phase arrangement and different configurations of the direction of cryogen movement inside the cable, which should lead to changes in the temperature distribution in the cable, as well as to changes in the total heat flux per unit length of the cable. The criteria for comparing cables vary and in many cases are contradictory. For example, when reducing the diameter of the inner channel of the cable, it is possible (with the same radial dimensions of the superconductor system, designed for a certain current and voltage) to reduce the outer diameter of the cryostat. In this case, the material capacity is reduced, as are the heat flow from the environment and, consequently, the load on the cryogenic unit; however, hydraulic losses and load on the circulating pump are increased. Increasing the mass flow allows the temperature inside and at the cable outlet to be reduced, but requires one to increase the pressure in the circulation circuit.

When developing a cable of a certain type designed to work in a real electrical network, it is necessary to carry out a rather complex thermohydraulic analysis including numerical computer-simulation methods. For preliminary evaluation of characteristics of different cable types, it is convenient to use approximate analytical methods allowing the influence of various factors on the efficiency of their work to be revealed.

VARIANTS OF HTS CABLE CRYOSTATS

There are several variants for cooling HTS cables: the cable is integrated into the cycle of the cryogenic installation (in which case the superconductor is cooled by the working body of the installation itself, circulating in the cable with the main compressor), the heat is removed by cryogenic machines, or the heat of phase transition of a third-party cryoagent is used for its compensation. In the two latter cases, cooling of the HTS cable in a circular circuit (Fig. 1) is usually performed by supercooled liquid nitrogen in a single-phase state at a temperature of 67–68 K, which is pumped through the cable using a circulating cryogenic pump in which the cryogen temperature in the forward and reverse flows increases due to the heat inflow from the environment through the external surface of the cable cryostat and from internal heat sources inside the cable due to electromagnetic losses. The temperature of the cryoagent decreases in the cryogenic unit where the absorbed heat is removed.

Fig. 1.

Schematic diagram of superconductor cable cooling: (1) cryopump, (2) subcooler, (3) generator of cold (cryogenic installation), (4) superconductor cable, (5) channel of forward flow of cryogen in the cable, and (6) channel of return flow.

Power required for cable cooling $N = {{N}_{{\text{k}}}} + {{N}_{{{\text{add}}}}}$, where ${{N}_{{\text{k}}}} = {{Q}_{{\text{k}}}}{\text{/}}\varepsilon$ is the power required by the cryogenic installation for compensation of heat flows to the cable cryogen Q_k, $\varepsilon = {{\varepsilon }_{{{\text{id}}}}}{{\eta }_{{\text{t}}}}$ is the cooling coefficient of the cryogenic installation, ε_id is the cooling coefficient of the ideal cooler, and η_t is the thermodynamic efficiency of the installation. It can be determined that power for heat removal N_k constitutes the main share in the total balance, in which additional power N_add is the sum of the power required for running the circulation and vacuum pumps, which maintain vacuum in thermal insulation of the cable cryostat, as well as for cooling of cryogenic current leads, which introduce and remove energy from the cable if they have their own cooling system [1].

The table shows cooling schemes for three-phase power cables distributed according to the signs of cryogen flow inside the cable in forward and reverse flows. Also shown are conventional images of alternating layers (at half the phase diameter) involved in the transfer of heat from the environment to the cryogen.

Table 1.   Classification of methods of cryogen circulation in a cable

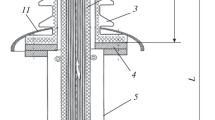
The scheme of cryogen movement is determined by the type of HTS cable, the main structural components of which are shown in Fig. 2: each phase is in its own cryostat (in this case, the return of cryogen to the cryogenic unit can be performed either inside each phase cryostat or in a separate cryogenic pipeline where flows are collected after cooling); all phases are located in one common cryostat; superconductor ribbons of each phase separated by electric insulation are concentrically wound on one another. In all cases, it is assumed that the current-carrying superconductor is shielded.

Fig. 2.

Types of the HTS cables: (a) type I, cable phases are in separate cryostats (one phase is shown); (b) type II, cable phases are in separate cryostats with return flow inside the cryostat (one phase is shown); (c) type III, phases are placed in a common cryostat; and (d) type IV, triaxial cable. (1) Conductive HTS tapes, (2) shield (in type IV cable, it is a neutral conductor), (3) electrical insulation, (4) cryoagent, and (5) cryostat.

The temperature field in the cable varies depending on the number and sequence of layers with different geometric characteristics having different thermal conductivity (thermal insulation of the cryostat, superconductor, electrical insulation) along the cable radius. Changing the flow rate and direction of cryogen flow in the cooling channels should also lead to changes in the distribution of heat flow and temperature in the radial layers and along the cable axis. Designations of schemes of cryogen flow in different types of cables are shown in the table (the names of the layers with different shading are shown in Fig. 3).

Fig. 3.

Location of numbered layers along the cable radius: (a) cross section of a shielded cable phase cooled according to type I, (b) pipeline with cryogen return flow, (c) cross section of a phase cooled according to type II and (A) cryoagent, (B) phase (copper layers + HTS tapes), (C) electrical insulation. (D) shield (HTS tapes + copper layers), and (E) cryostat thermal insulation. 1, …, 10 is numbering of layers, r is layer radius, T_amb is temperature of the environment surrounding the cryostat, ${{\bar {T}}_{{\text{f}}}}{\text{ and }}{{\bar {T}}_{{{\text{rtrn}}}}}$ are average temperatures of the cryogen in the forward and return flows, and (${{\left( {{{q}_{1}}} \right)}_{{r1}}},~{{\left( {{{q}_{5}}} \right)}_{{r1}}},{{\left( {{{q}_{6}}} \right)}_{{r1}}},~{{\left( {{{q}_{{10}}}} \right)}_{{r7}}}$ are the linear densities of heat flows to the cryogen.

In cooling scheme I, each phase has a separate cryostat. The cryoagent passes inside the structure of the superconductor–electrical insulation–superconductor shield, and the liquid nitrogen is returned to the cryogenic unit via a separate cryogenic pipeline. In existing designs, the cable cryostat usually consists of thin-walled corrugated metal shells, which form the inner wall of the cryostat and the outer casing (not shown in the figures). The flexible inner sheath of the cable serves as a channel for the cryoagent, as well as the base (the former core) for winding the current-carrying superconducting ribbons and electrical insulation, in addition to serving the copper ribbons as a stabilizer.

In configuration II/1, each phase is also housed in its own cryostat, however, unlike type I, the cryoagent returns in an annular space surrounding the cooled superconducting structure. Cooling method II/2 may be applied where the direct flow runs in an annular section and the return flow proceeds in an internal channel.

In cooling method III/1, all three phases are in a common cryostat. The forward flow passes inside the superconducting structure of each of the three phases surrounded by a return flow of liquid nitrogen flowing in the interphase space. In the III/2 system, the forward and reverse flows have opposite directions of motion.

In a type IV cooled triaxial HTS cable, the ribbons of the three superconducting phases are concentrically wound onto each other through electrical insulation and enclosed by a copper neutral conductor. Liquid nitrogen flows in the inner channel and along the outer surface of the neutral conductor.

In the IV/1 system, the forward flow is along the inner channel and the reverse flow is along the outer channel. In the IV/2 cooling system, the flow directions are reversed. When the central channel of the core (the former) is plugged, the forward and reverse flows of liquid nitrogen can flow separately [2]. The forward flow then passes in the outer annulus of the cryostat and returns in a separate pipe (similar to scheme I), or the flows may reverse their direction, with the forward flow routed through the cryogenic pipeline returning through the cable to the cryogenic unit.

THEORETICAL MODEL

One of the tasks of the theoretical study is to study the influence of the mass flow rate of liquid nitrogen on the total linear heat flux in cables of different designs. To compare the obtained results, it is necessary to bring the geometries of the layers as close as possible to each other, assuming that the diameters of the inner channels (d₁ = 2r₁) in different types of cables are equal. We assume that the heat flow passes in the radial direction through a multilayered cylindrical wall with perfect thermal contact between the layers (i.e., the temperatures of the contacting layers are equal) and with a constant heat transfer coefficient in each layer. We consider a one-dimensional problem of heat transfer from the surface of the external casing of the cryostat (the temperature of which is assumed equal to ambient temperature T_amb) to the average temperature of the cryogen the temperature difference of which between the inlet and outlet of the cooling channel is ${{T}_{{{\text{out}}}}} - {{T}_{{{\text{in}}}}} = \frac{{{{{\left( q \right)}}_{{r = {{r}_{{{{N}_{2}}}}}}}}L}}{{G{{c}_{P}}}}$. Here, L, m, is the cable length; ${{\left( q \right)}_{{r = {{r}_{{{{N}_{2}}}}}}}}$, W/m, is the linear density of heat flux approaching the layer with radial coordinate ${{r}_{{{{N}_{2}}}}}$ in which liquid nitrogen flows with the mass flow of G, kg/s; and c_p, J/(kg K), is the heat capacity of nitrogen.

For the cooling options to be comparable with each other, we consider the conditional design of the superconducting part of the cable (conductive core–electrical insulation–screen) assuming equal thicknesses of layers with equal coefficients of effective thermal conductivity of the superconductor δ_sc and λ_sc and electrical insulation δ_{e_ins} and λ_{e_ins} along the direction of heat-flow distribution. Thermal conductivity coefficients of the screen-vacuum thermal insulation λ_{t_ins} and its thickness δ_{t_ins} are also assumed constant. The geometric dimensions of the layers are tied to the diameter of the central channel through which the cryoagent flows.

As an example, Fig. 3 shows the arrangement of the numbered layers along the radius of the cable, the design of which corresponds to the type I cooling. Let us denote the radius of the inner channel as r₁; then, the outer radii will be as follows: conductive core r₂ = r₁ + δ_sc, electrical insulation r₃ = r₁ + δ_sc + δ_{e_ins}, and so on. In cooling scheme II, the thickness of the cryoagent layer surrounding the superconducting screen is determined based on the condition that the cross-sectional areas of the annular space and the inner channel are equal.

The heat transfer in the cable occurs through a multilayer cylindrical wall consisting of i = 1, 2, …, n infinitely long cylindrical layers with certain thermophysical properties. There is internal heat generation in the conductive layers containing a superconductor. We assume constant coefficient of thermal conductivity of the layer material λ_i and a uniform distribution of internal heat sources q_v, W/m³. In the stationary mode, temperature T_i(r) and specific heat flux q_i(r) in each cable layer can be found after solving the system of differential equations known from the theory of heat transfer:

$$\frac{{{{d}^{2}}{{T}_{i}}}}{{d{{r}^{2}}}} + \frac{1}{r}\frac{{d{{T}_{i}}}}{{dr}} + \frac{{{{q}_{\nu }}}}{{{\lambda }}} = 0;~$$

(1)

$${{T}_{i}} = {{C}_{i}}{\kern 1pt} \ln {\kern 1pt} r + {{C}_{{i + 1}}} - \frac{{{{q}_{{{\nu }}}}{{r}^{2}}}}{{4{{\lambda }_{i}}}};$$

(2)

$$~{{q}_{i}} = \pi \left( {2{{\lambda }_{i}}{{C}_{i}} - {{r}^{2}}{{q}_{\nu }}} \right).$$

(3)

In the layers (electrical insulation, cryostat thermal insulation) where there is practically no internal heat generation, q_ν = 0 and Eq. (1) takes the form

$$\frac{{{{d}^{2}}{{T}_{i}}}}{{d{{r}^{2}}}} + \frac{1}{r}\frac{{d{{T}_{i}}}}{{dr}} = 0.$$

(4)

The solution of Eq. (4) for each layer determines the change in temperature and heat flux in it:

$${{T}_{i}} = {{C}_{i}}{\kern 1pt} \ln {\kern 1pt} r + {{C}_{{i + 1}}};$$

(5)

$${{q}_{i}} = 2\pi {{\lambda }_{i}}{{C}_{i}}.$$

(6)

The integration constants present in Eqs. (2), (3), (5), and (6) are determined from a system of equations establishing the heat transfer or temperature conditions at the boundary surfaces of the layers. These equations are supplemented by equations defining the coupling conditions for temperatures and heat fluxes at adjacent layers.

COMPARISON OF THE EFFICIENCIES OF CABLE COOLING SCHEMES

Let us first consider cooling system I in which the return flow flows in a separate conduit and compare other cooling systems with it. Integration constants in Eqs. (2), (3), (5), and (6) are found based on the conditions of equality of temperature and heat flow in the contiguous layers and the boundary conditions $~{{({{T}_{1}})}_{{r1}}} = {{\bar {T}}_{{{\text{I}},{\text{f}}}}}$, $~{{({{T}_{4}})}_{{r5}}} = {{T}_{{{\text{amb}}}}}$ in the forward flow (Fig. 3a) and $~{{({{T}_{5}})}_{{r1}}} = {{\bar {T}}_{{{\text{I,amb}}}}},~~{{({{T}_{5}})}_{{r5}}} = {{T}_{{{\text{amb}}}}}$ in the reverse flow (Fig. 3b). The obtained solution makes it possible to establish, at a given cryoagent flow rate, the temperature distribution in the layers and the heat flux to liquid nitrogen where the linear heat flux density is

$$\begin{gathered} {{q}_{{{\text{I}},{\text{f}}}}} = ~{{\left( {{{q}_{1}}} \right)}_{{r1}}} = 2{{\lambda }_{{{\text{t}_{-}\text{ins}}}}}\left( {{{T}_{{{\text{amb}}~}}} - {{{\bar {T}}}_{{{\text{I}},{\text{f}}}}}} \right) \\ + \,\,\ln \frac{{{{r}_{5}}}}{{{{r}_{{4~}}}}}\left[ {{{q}_{{\nu 1}}}\left( {r_{2}^{2} - r_{1}^{2}} \right) + {{q}_{{\nu 2}}}\left( {r_{4}^{2} - r_{3}^{2}} \right)} \right] \\ \times \,\,\left( {\frac{{\pi {{c}_{P}}G}}{{{{c}_{P}}G{\kern 1pt} \ln {\kern 1pt} \frac{{{{r}_{5}}}}{{{{r}_{4}}}} + \pi L{{\lambda }_{{{\text{t}_{-}\text{ins}}}}}}}} \right). \\ \end{gathered} $$

(7)

Here, q_ν1 and q_ν2 are the densities of volumetric heat release in the phase and in the screen and G is the flow rate of the cryoagent passing in the cooling channel. Volumetric heat-release densities can be expressed in terms of the heat fluxes referred to unit length of the cable q_L:

$${{q}_{{\nu 1}}} = {{q}_{{L1}}}{\text{/}}\pi \left( {r_{2}^{2} - r_{1}^{2}} \right),\,\,\,\,{{q}_{{\nu 2}}} = {{q}_{{L2}}}{\text{/}}\pi \left( {r_{4}^{2} - r_{3}^{2}} \right).$$

(8)

At the average temperature of the return flow of cryoagent in the channel of radius r₁ (Fig. 3b), the specific heat flux is

$$~{{q}_{{{\text{I}},{\text{rtrn}}}}} = {{\left( {{{q}_{5}}} \right)}_{{r1}}} = \frac{{2\pi {{\lambda }_{{{\text{t}_{-}\text{ins}}}}}\left( {{{T}_{{{\text{amb}}~}}} - {{{\text{T}}}_{{{\text{I}},{\text{in}}{\text{.rtrn}}}}}} \right)}}{{\ln \frac{{{{r}_{6}}}}{{{{r}_{1}}}}~\,\, + \,\,~\frac{{\pi L{{\lambda }_{{{\text{t}_{-}\text{ins}}}}}}}{{nG{{c}_{P}}}}}},$$

(9)

where r₆ = r₁ + δ_{t_ins}, δ_{t_ins} is the thickness of thermal insulation; T_I.in.rtrn is the temperature of the cryoagent at the return-flow inlet after cooling the phases; and n = 3 is the number of phases. The temperature at the outlet of the cryogenic pipeline of the return flow in the cooling scheme I is

$$~{{T}_{{{\text{I}}{\text{.out}}{\text{.rtrn}}}}} = {{T}_{{{\text{I}}{\text{.in}}{\text{.f}}}}} + \frac{L}{{{{c}_{P}}G}}\left( {{{q}_{{{\text{I}},{\text{f}}}}} + \frac{{{{q}_{{{\text{I}},{\text{rtrn}}}}}}}{n}} \right),$$

(10)

where T_I.in.f is the temperature at the inlet of the direct cable duct (assumed to be 68 K).

Net specific heat flux per unit length in direct and return flows q₁ = nq_I.f + q_I.rtrn.

Unlike the type I cables, in the type II–IV cables, there is a layer of liquid nitrogen between the phases and the cryostatic shell (cryostat), which shields the superconductors of the phase within which the cryoagent flows. If we adopt a model in which the heat from electromagnetic disturbances is removed by the cryoagent flowing in the internal channel of the phase and the heat passing through the cryostat insulation is taken by the liquid nitrogen flowing in the annular channels (type II and IV) or in the space between the phases (type III), then the solution of Eqs. (2), (3), (5), and (6) is found from the assumption that there is no heat flow at the outer boundary of the superconducting system; e.g., for cable II, ${{\left( {d{{T}_{8}}{\text{/}}dr} \right)}_{{{{r}_{4}}}}}$ = 0 (Fig. 3c). Then, in the II/1 cooling scheme, the total linear heat in-flux is

$${{q}_{{{\text{II}}/1}}} = n\left[ {{{q}_{{L1}}} + {{q}_{{L2}}} + \frac{{2\pi {{\lambda }_{{{\text{t}_{-}\text{ins}}}}}\left( {{{T}_{{{\text{amb}}}}} - {{{\bar {T}}}_{{{\text{II}}/1,{\text{rtrn}}}}}} \right)}}{{\ln \frac{{{{r}_{8}}}}{{{{r}_{7}}}}}}} \right].$$

(11)

When a direct flow of nitrogen with a temperature of 68 K enters the external cooling circuit and returns into the cable, the direction of cryogen flow is reversed, with the specific linear heat flow satisfying the condition q_II/2 ≈ q_II/1, as seen in Fig. 4, which shows the relationship between the heat flows at different cooling methods referenced to linear heat flow q_I. The slight increase in the flow q_II/2 as compared to q_II/1 is explained by a decrease in the average temperature of the cryoagent in the external channel. The calculated model does not take into account the influence of heat introduced from the supporting elements, which fix the phases relative to the cryostat shell, as we are not considering a real cable design in which the distribution of heat flow in the forward and reverse flows may be different. For all types of cooling, directing the forward flow to the external channel directly after the cryostat leads to a slight increase in the heat flow, especially when the flow rate of cooling nitrogen is reduced.

Fig. 4.

Correlation between linear heat fluxes q*/q_I in various cooling schemes depending on mass flow of liquid nitrogen G: (1) $q{\kern 1pt} * = {{q}_{{{\text{II}}/1}}}$; (2) $q{\kern 1pt} * = {{q}_{{{\text{II}}/2}}}$; (3) $q{\kern 1pt} * = {{q}_{{{\text{III}}/1}}}$; (4) $q{\kern 1pt} * = {{q}_{{{\text{III}}/2}}}$; (5) $q{\kern 1pt} * = {{q}_{{{\text{IV}}/1}}};$ (6) $q{\kern 1pt} * = {{q}_{{{\text{IV}}/2}}}$.

Figure 4 shows the relations between the heat fluxes at the same values of volumetric heat densities in the layers with a superconductor q_ν = 1.5 × 10³ W/m³. Values of thermal conductivity coefficients of thermal insulation λ_{t_ins} = 5 × 10^–4 W/(m K), electrical insulation λ_{e_ins} = 0.25 W/(m K), and transverse thermal conductivity of the superconductor λ_sc = 15 W/(m K) are not related to particular materials, are taken from the data of [3–5], and are assumed to be the same for all versions of cables. Specific heat capacity of liquid nitrogen c_p = 2 × 10³ J/(kg K). Since the relative characteristics of different cooling schemes are considered, the errors in the calculation are leveled.

Of course, the graphs in Fig. 4 do not reflect the entire variety of possible design variants of superconductor cables, as they only determine the trend in the variations of the heat flux in cables that are similar in terms of geometric dimensions and carry equal currents, since the diameter of the cryostat shell and the volumetric heat dissipation in the superconductor affect the total heat flux.

A comparison between the different cooling methods shows that the linear heat in-flux in cable III is approximately 20% smaller than that in cables I and II. The heat flux to the cryogen is inversely proportional to the value $\ln \frac{{r + {{\delta }_{{{\text{t}_{-}\text{ins}}}}}}}{r},$ where r is the inner radius of the cylindrical channel where the liquid nitrogen passes; and δ_{t_ins} is the thickness of the thermal insulation. The specific heat flow in different cable designs is determined by the number of channels for the passage of the cryogen to which the heat from the environment comes and their geometric dimensions. The minimum radius of a cylinder R in which it is possible to place a certain number of smaller cylinders is defined in [6]. In the “three in one” cable (type III), the ratio between the radii of the cryostat cylindrical bath and the phases (without technological gaps) is $\frac{R}{r} = 1 + \frac{2}{3}\sqrt 3$.

Despite the larger diameter of the type III cryostat and, therefore, the greater heat input to the return flow compared to cable I, the total heat in-flux in the III/1 cooling scheme is smaller because more heat is delivered to the individual forward flow cryostats of each phase in cable I. The ${{q}_{{{\text{III}}/1}}}{\text{/}}{{q}_{{\text{I}}}}$ ratio decreases even more as the current decreases. In the absence of current, the heat flux will depend mainly on the radii of the cooling channels and the thickness of the cryostats' thermal insulation:

$$\begin{gathered} \frac{{{{q}_{{{\text{III}}/1}}}}}{{{{q}_{{\text{I}}}}}} = \left[ {{\text{ln}}\left( {1 + \frac{{{{\delta }_{{{\text{t}_{-}\text{ins}}}}}}}{{{{r}_{{{\text{III}},{\text{amb}}}}}}}} \right)_{{_{{_{{_{{}}^{{}}}}^{{}}}}^{{_{{}}^{{}}}}}}^{{_{{_{{_{{}}^{{}}}}^{{}}}}^{{_{{_{{}}^{{}}}}^{{}}}}}}} \right. \\ \times \,\,{{\left. {\left( {\frac{n}{{\ln \left( {1 + \frac{{{{\delta }_{{{\text{t}_{-}\text{ins}}}}}}}{{{{r}_{{{\text{I}},{\text{f}}}}}}}} \right)}} + \frac{1}{{\ln \left( {1 + \frac{{{{\delta }_{{{\text{t}_{-}\text{ins}}}}}}}{{{{r}_{{{\text{I}},{\text{amb}}}}}}}} \right)}}} \right)} \right]}^{{ - 1}}}, \\ \end{gathered} $$

(12)

where r_I.f = r₁ + δ_sc is the inner radius of the phase cryostat shells, r₁ is the inner channel radius, δ_sc is the thickness of the superconductor current-carrying system, r_I.sh = r₁ is the radius of the return cryogenic pipeline, and r_III.sh = $\left( {{{r}_{1}} + {{\delta }_{{{\text{sc}}}}}} \right)\left( {1 + \frac{2}{3}\sqrt 3 } \right)$ is the outer radius of the cylindrical bath of cryostat III.

The outer diameter of a type IV triaxial cable depends on width of the outer ring channel ${{\Delta }_{{{{N}_{2}}}}}$, which is difficult to relate to radius of the inner channel r₁ for purposes of making a comparison of this type of cable with others. However, if the criterion for comparison of cables IV and III is the equality of return-flow hydraulic resistances, then width ${{\Delta }_{{{{N}_{2}}}}}$ can be calculated. In this case, with the same dimensions of internal channels r₁, the same thicknesses δ_sc and δ_{t_ins}, and equality of internal heat dissipation in the layers, the smallest heat flow will go to cable IV. As ${{\Delta }_{{{{N}_{2}}}}}$ decreases, the heat flux to the cable will decrease and the hydraulic resistance will increase.

The flow rate of the cryoagent is important for providing reliability to the superconducting cable. Figure 5 shows the change in temperature difference between the temperature at the cable inlet and outlet after passing through the forward and reverse cooling branches. If the flow rate of liquid nitrogen is more than 0.3 kg/s, its temperature at the given geometrical and physical parameters and the initial temperature of 68 K does not exceed 72–74 K. At small flow rates (less than 0.2 kg/s), the temperature around the superconductor rises by more than 6–10 K (depending on the cable type), which narrows the margin relative to the allowed operating temperature range of the superconductor.

Fig. 5.

Dependence of cryogen temperature increase ΔT on its flow rate G after passing through the direct and reverse cooling channels of cables of different types: (1) $\Delta {{T}_{{\text{I}}}};$ (2) $\Delta {{T}_{{{\text{II}}}}};$ (3) $\Delta {{T}_{{{\text{III}}}}};$ (4) $\Delta {{T}_{{{\text{IV}}}}}$. The index indicates cable type.

Concentric arrangement of phases in a cable of type IV makes the design of this cable more compact, however, the pressure drop in the central channel of cable IV $\left( {\Delta {{P}_{{{\text{IV}},{{r}_{1}}}}}} \right)$ in comparison, for example, with the channel of a separate phase in cable I ($\Delta {{P}_{{{\text{I}},{{r}_{1}}}}})~$ will be approximately nine times greater at equal diameters ($\Delta {{P}_{{{\text{IV}},{{r}_{1}}}}}{\text{/}}\Delta {{P}_{{{\text{I}},{{r}_{1}}}}} \approx {{n}^{2}}$). The total hydraulic resistances in the forward and return channels of cables of types I and IV have similar values. Figure 6 shows the linear pressure loss in different cables depending on the mass flow rate of the flowing liquid nitrogen (at the accepted geometrical dimensions of the cooling channels) calculated by the Darcy–Weisbach equation at the same hydraulic friction coefficients. The smallest pressure loss corresponds to a type III cable.

Fig. 6.

Hydraulic resistance per unit length of cables of different types ($p = \Delta P{\text{/}}L$; (1) ${{p}_{{\text{I}}}};$ (2) ${{p}_{{{\text{II}}}}};$ (3) ${{p}_{{{\text{III}}}}}$; (4) ${{p}_{{{\text{IV}}}}}$. The index indicates cable type.

Increasing the mass flow decreases the maximum temperature inside the cable but increases the hydraulic resistance, which must be overcome by increasing the pressure inside the cable. The maximum pressure is limited by the allowable mechanical characteristics of the superconductor or cable sheath. The minimum pressure should not be less than the saturation pressure at the highest temperature of the cryogen at the outlet of the return flow to prevent the emergence of a two-phase flow.

It should be noted that the thermohydraulic characteristics of HTS cables are only a part of their important features. If, for example, the task of reducing the number of HTS ribbons in a cable is considered, this goal is the easiest to achieve in a triaxial cable in which the total vector of magnetic fields from differently directed currents in the coaxially located phases is very small, which does not allow shielding each phase, as in other types of cables. For geometrical reasons, a type IV cable is more compact than a type III cable. In a type IV cable, it is also more convenient to install the superconductor system by pulling it inside the cryostat; however, on the other hand, in an emergency situation, such as a short circuit, all phases can be disconnected at the same time. If one of the main characteristics of a cable is high reliability, then layers of copper are added to each phase to prevent the superconductor from overheating in abnormal situations. It is also possible to fill the formers with copper to shunt the current in the event of a short circuit. Additional copper layers are most advantageous inside the cable, since there is practically no alternating magnetic field there and, therefore, no eddy currents are induced. However, in this case, there are limitations associated with the flow of liquid nitrogen in the central channel.

CONCLUSIONS

Comparative analysis of thermohydraulic characteristics (specific linear heat flux, cryogen outlet temperature, and hydraulic resistance) showed that the smaller total heat flux goes to the triaxial cable, while the largest goes to the cable in which the phases are in separate cryostats. A small value of hydraulic resistance and a small rise in cryogen temperature are typical for the cable in which the phases are located in one cryostat.