To transmit high-power electricity from the site of its generation at the power plant to the step-up transformer substation, the throughput of a cable line under conditions of limited space needs to be increased. The technical characteristics of the second-generation HTSC conductors (HTSC-2s) made possible practical use of superconductivity for the transmission and distribution of electricity. The possibility of increasing the load current in oil- or gas-filled power cables is limited by the allowable heating temperature of the conductive cable conductors. Therefore, to transmit substantial power of several hundred megawatts, it is necessary to have several parallel power lines with a current density that does not allow them to be excessively heated. HTSC cables cooled with liquid nitrogen have a higher current density, low active power losses, and environmental friendliness, due to the absence of insulating oils or fluorinated gases, than do conventional power cables.

The necessary devices for a superconducting cable are current leads (sometimes called terminations). The current in a current lead is determined by the generator voltage and the transmitted power. A relatively low generator voltage when transmitting large energy flows eliminates many problems associated with the design and reliability of high-voltage electrical insulation but requires a substantial increase in the current (up to tens of kiloamperes) [1], which leads to problems associated with the injection of high currents.

COOLING METHODS FOR CURRENT LEADS

Depending on the level of heat load and the frequency of operation, cryogenic supply systems with a liquid cryoagent or cryogenic gas machines (cryogenerators) are used to cool the cable. Supercooled liquid nitrogen pumped by centrifugal pumps is widely used to cool HTSC cables. A decrease in the nitrogen temperature to a temperature lower than the equilibrium temperature corresponding to the pumping pressure occurs in a reservoir—a subcooler—in which the vapor space above a liquid nitrogen mirror is pumped out by vacuum pumps up to a pressure of about 15 kPa (64 K) [2].

The cable through which the three-phase current flows assumes the presence of six current leads (one current lead at the input and output of each phase). The cooling system of current leads can be part of an overall cable cooling system; otherwise, the current leads are cooled autonomously. There are several ways to cool current leads: using cryogenerators, which compensate for the heat released in the current lead, or by cold vapors of nitrogen or other heat exchange gas with high heat capacity cooled to nitrogen temperature, e.g., gaseous helium. Let us consider a cooling method in which the current lead is cooled by cold nitrogen gas.

DETERMINATION OF THE GEOMETRIC DIMENSIONS OF THE CURRENT LEAD

The schematic diagram of a high-current, high-voltage current lead is shown in Fig. 1. The current lead, which is cooled by liquid nitrogen evaporated from the cryostat, consists of current-carrying element (CCE) 1 covered with electrical insulation of bushing 2, which contains the conductors. The current lead is located on support insulator 3 located on flange 4 of the neck of cryostat 5. Gaseous nitrogen 6 comes out through branch pipe 7. The current lead is connected to the current source by bus 8 and connected to the superconducting cable by coupling 9.

Fig. 1.
figure 1

Schematics of the current lead of a superconductor cable: (1) current-carrying element, (2) bushing, (3) support insulator, (4) flange, (5) cryostat neck, (6) gaseous cryoagent, (7) branch pipe for outlet of gaseous cryoagent, (8) bus, (9) coupling, and (10, 11) shields to equalize electric field intensities.

Full size image

Total length of the current lead L is determined by the distance between the busbar and coupling. This length is a length of the cryostat throat and height of the support insulator h. The diameter of a current lead depends on the quantitative characteristics: the cross-sectional area of a fuel element and the thickness of electrical insulation, which are determined based on the current required for energy transfer and the generator voltage. The support insulator of a current lead is in direct contact with the external environment; therefore, the insulator should work reliably under conditions of wet weather and contamination of the insulator surface. When designing an insulator, the technical parameters should comply with the standards that govern the climatic performance of products. To calculate the length of a current lead in accordance with rules and regulations, it is required to classify the reference insulator designed for a certain voltage and determine the operating conditions: the category of placement (outdoors or indoors) and climatic characteristics (minimum and maximum temperature and relative humidity).

For an insulator with a known placement category, which is placed in a certain climatic zone, a certain leakage distance along the external insulation should be provided depending on the selected degree of pollution. In regulatory requirements, the leakage distance is understood as the smallest distance along the insulator surface between metal parts under different potential. The leakage distance is determined according to four levels of contamination, from light to very severe. At an average degree of contamination, specific leakage distance λleak should be at least 2.0 cm/kV.

Due to the uneven deposition of contaminants on the surface of external insulation and geometric dimensions of the insulation, the length of surface overlap can be less than the geometric leakage distance; therefore, the concept of effective leakage distance λef is also introduced in the regulatory requirements. When choosing the dimensions of external insulation, leakage distance of the insulator Li is determined by the equation

$${{L}_{{\text{i}}}} = {{\lambda }_{{{\text{ef}}}}}Uk,$$

where U is the highest operating phase-to-phase voltage and k is the efficiency factor. For example, with an average degree of contamination and a rated voltage up to 35 kV, λef should be at least 2.35 cm/kV. Coefficient k is assigned depending on the ratio of geometric leakage distance to height of the insulating structure h. If Li/h ≤ 2.5, k = 1. Insulator height h is determined after designating the overhang and the spacing of edges and drawing of the insulator profile, so that the length of the obtained profile is not less than leakage distance Li.

POWER LOSS IN AN AC CURRENT LEAD

If each current lead at the input/output of a superconducting power cable is connected with the generator phase, the effective current in the current lead is determined based on the total power of the entire three-phase system Pt and phase-to-phase (linear) voltage Ul, I = \(\frac{{{{P}_{{\text{t}}}}}}{{\sqrt 3 }}{{U}_{{\text{l}}}}\). At a rated phase-to-phase voltage of the generator from 21 to 27 kV and a transmitted power of 400–500 MV A, the effective current will be 9–14 kA. Due to the reactive component, only some of the total electrical energy can be converted into its other types. The current at which the required energy can be transferred can be determined based on active (useful) power Pа and power factor cos φ, I = \({{{{P}_{{\text{t}}}}} \mathord{\left/ {\vphantom {{{{P}_{{\text{t}}}}} {\sqrt 3 {{U}_{{\text{l}}}}\cos {\kern 1pt} \varphi }}} \right. \kern-0em} {\sqrt 3 {{U}_{{\text{l}}}}\cos {\kern 1pt} \varphi }}\). The lower the reactance, the less the current that is required to transfer a certain active power.

Unlike dc current leads, the distribution of alternating current over the conductor cross section will be ununiform due to the surface effect: the current density in the center of the conductor will be less than on the conductor surface. The displacement of current to the periphery (skin effect) decreases the current-carrying section, leads to an increase in the active resistance, heating of current-carrying elements, and to an increase in the energy losses. In the current-carrying element with a larger diameter, the nonuniformity a current density over the section will be greater than in the element with a smaller diameter, and most of the cross-sectional area of ​​the conductor will not be used for the passage of current. Therefore, the current-carrying element of the ac current lead should consist of separate conductors, the thickness of which should be comparable with the current penetration depth from the conductor surface to the center, depending on the magnetic permeability and resistivity of the material. For pure technical copper, the skin layer thickness will be 9 mm at room temperature and 3 mm at liquid nitrogen temperature. In the current lead split into separate conductors, the thickness of which is not higher than that of a skin layer, the losses will be minimum.

The total conductivity of the electric circuit of ac current leads is Y = \({{\left( {{{G}^{2}} + {{B}^{2}}} \right)}^{{\frac{1}{2}}}}\), where G and B are the equivalent active and reactive (inductive) conductivities. The inductance of a current lead depends on the cross-sectional shape of the individual current-carrying elements and their position inside the current lead casing.

The range of materials from which the structure of the current-carrying system of a current lead can be made is diverse. Parallel connected current-carrying elements can be made of a package of tapes, tubes, rods, wires, and braids, and the braids can be placed parallel or concentrically to each other. Sheets, e.g., perforated or rolled ones, can also be used. In general, the design should satisfy contradictory requirements due to the physical processes that occur in the current lead and take into account various factors, such as the induction and mutual induction of conductors, heat transfer in them, heat exchange with a cooling cryoagent, the hydraulic resistance of cooling channels, the dielectric strength of insulation, thermal shrinkage of dissimilar materials leading to mechanical loads, and contact resistance when connecting the current lead to the cable superconductor.

Some of the total power is converted into heat. Irreversible energy losses occur in the current lead due to the release of heat in current-carrying elements, as well as energy losses in metal shells, where closed circuits of eddy currents can form. Energy is also expended to polarize the molecules of the dielectric material of electrical insulation.

Insulation thickness Δin is determined on the basis of allowable (calculated) electric field strength Ecal, which should be part of the experimentally obtained strength at breakdown of the used insulation Ebr = Ecalk, where k is the safety factor, k = 3–5. If the potential of a flange on which the current lead is based is uniform and equal to zero and the potential of the insulated casing of a current lead, which contains the package of current-carrying elements (cores), is equal to phase voltage Uph, minimum insulation thickness Δin,min can be calculated according to an equation known in high-voltage technology,

$${{\Delta }_{{{\text{in,min}}}}} = {{r}_{{{\text{in}}}}}\left[ {\exp \left( {\frac{{{{U}_{{{\text{ph}}}}}}}{{{{r}_{{{\text{in}}}}}}}{{E}_{{{\text{cal}}}}}} \right) - 1} \right],$$
(1)

where rin is the inner radius of insulation.

When determining the working thickness of the insulation, instead of phase voltage, in Eq. (1), calculated voltage Ucal > Uph can be used according to the regulatory requirements that determine the test voltage based on the category of location of a current lead, class of its voltage, and insulation life time. Thus, the margin for dielectric strength of the insulation is established either by an increase in the calculated voltage relative to the nominal one or by a decrease in the allowable voltage.

Dielectric losses in electrical insulation are determined by the current frequency, the calculated voltage, the tangent of the dielectric loss angle, and the insulator capacitance.

The release of heat in the electrical insulation of current leads due to short insulation length (compared to the total cable length) is small. The main energy losses are losses for heating the current-carrying elements of a current lead. The total power spent on heating in the resistive sections of all phase current leads is

$${{P}_{{{\text{CL}}}}} = {{r}_{{{\text{in}}}}}\frac{{6{{I}^{2}}L\int\limits_{{{T}_{0}}}^{{{T}_{L}}} {\rho (T)dt} }}{{S({{T}_{L}} - {{T}_{0}})}},$$

where S is the total cross-sectional area of current-carrying elements, L is the length of a current lead, ρ is the specific resistance of material of current leads, and T0 and TL are the temperatures of the lower and upper ends of a current lead.

CALCULATION OF THE SPECIFIC RESISTANCE OF MATERIAL OF THE CURRENT-CARRYING ELEMENT

To carry out calculations related to the determination of the performance characteristics of current leads, it is necessary to know the temperature dependence of specific resistance and thermal conductivity of material of the current-carrying element. The form of functions ρ(T) and λ(T) is affected by the presence of impurities in the composition of the used conductive metal; i.e., it is determined by the ratio of residual resistance (sometimes denoted as RRR): the ratio of resistivity at room temperature (or at 0°C) to resistivity at liquid helium temperature, which is taken as residual resistance ρ4.2K ≈ ρ0.

According to Matthiessen’s rule,

$$\rho (T) = {{\rho }_{0}} + C{{\left( {\frac{T}{\theta }} \right)}^{5}}\int\limits_0^{\frac{\theta }{T}} {\frac{{{{x}^{5}}dx}}{{{\text{s}}{{{\text{h}}}^{2}}\left( {\frac{x}{2}} \right)}}} ,$$
(2)

where ρ0 is the residual resistance and the second term is the temperature dependence of resistance of an ideal pure metal ρi (T), which is represented by the modified Bloch–Gruneisen equation. In Eq. (2), x is a dimensionless variable, θ is the characteristic Debye temperature, C = 1.0565\(\rho _{i}^{\theta }\) is the constant characterizing metal properties, and \(\rho _{i}^{\theta }\) is the specific ideal resistance at temperature θ.

To calculate by Eq. (2), it is necessary to know temperature θ and ideal copper resistance \(\rho _{i}^{\theta }\) at this temperature. The characteristic Debye temperature is characterized by a wide spread in values. For copper, e.g., θ = 310–345 K, since the temperatures ​​are obtained either experimentally by comparing the Debye equation with the experimental data on specific volumetric thermal capacity or theoretically at T → 0 (larger value of θ relates to this case). Theoretically, it is impossible to unambiguously select a constant value of θ that would satisfy Eq. (2) in the entire range of temperature T, since the characteristic temperature θ is constant only at temperatures above room temperature, where the Dulong and Petit empirical law about the constant value of specific volumetric thermal capacity of materials is observed. For further calculations, let us take θ = 315 K.

Let us determine \(\rho _{i}^{\theta }\) from the equation

$$\rho _{i}^{\theta } = 0.946\frac{{\rho _{i}^{{{{T}_{{{\text{r}}{\text{.r}}}}}}}}}{{{{{\left( {\frac{T}{\theta }} \right)}}^{5}}\int\limits_0^{\frac{\theta }{{{{T}_{{{\text{r}}{\text{.r}}}}}}}} {\frac{{{{x}^{5}}dx}}{{{\text{s}}{{{\text{h}}}^{2}}\left( {\frac{x}{2}} \right)}}} }}.$$
(3)

The value of \(\rho _{i}^{{{{T}_{{{\text{r}}{\text{.r}}}}}}}\) presented here can be obtained from experimental data. For example, it was obtained for a commercial copper sample [3]: \(\rho _{i}^{{{{T}_{{{\text{r}}{\text{.r}}}}}}}\) = ρ295K – ρ4.2K = (1.725—0.0206) ×10–8 Ω m = 1.704 × 10–8 Ω m.

There are a wide range of metals (with different chemical purity and heat treatment) that can be used as current-carrying elements; therefore, the determination of the temperature dependence of resistivity and thermal conductivity can be carried out only by means of calculations and estimation. Otherwise, it is necessary to know experimental dependences ρ(T) and λ(T) of the metal that will be specifically used in the manufacture of current-carrying elements.

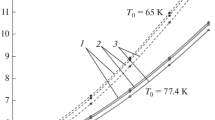
Based on Eqs. (2) and (3), let us consider temperature dependence of the specific resistance ρ(T) of copper with differing purity in the range of temperatures from 63.15 K (the triple point of nitrogen) to 500 K. By assuming ρ295 K/ρ0 = 20, 50, and 100, we can determine from Eq. (3) the value of \(\rho _{i}^{\theta }\) for copper with differing purity when ρ295K = 17.2 nΩ m. The obtained dependences ρ(T) are shown in Fig. 2. According to Eq. (4), the mean values ​​of specific resistance \(\bar {\rho }\) can be calculated for certain temperature ranges T2–T1

$$\bar {\rho } = 0\frac{{\left[ {{{\rho }_{0}} + {{{\left( {\frac{T}{{{{T}_{{{\text{r}}{\text{.r}}}}}}}} \right)}}^{5}}\rho _{i}^{{{{T}_{{{\text{r}}{\text{.r}}}}}}}\frac{{\int\limits_0^{\frac{\theta }{T}} {\frac{{{{x}^{5}}}}{{{\text{s}}{{{\text{h}}}^{2}}\left( {\frac{x}{2}} \right)}}} }}{{\int\limits_0^{\frac{\theta }{{{{T}_{{{\text{r}}{\text{.r}}}}}}}} {\frac{{{{x}^{5}}}}{{{\text{s}}{{{\text{h}}}^{2}}\left( {\frac{x}{2}} \right)}}} }}} \right]dT}}{{{{T}_{2}} - {{T}_{1}}}}.$$
(4)
Fig. 2.
figure 2

Temperature dependence of specific resistance ρ of copper with different residual resistance ρ0, ρ(295 K) = 15.2 nΩ m; TTP is the temperature of the triple point of nitrogen.

Full size image

As is known from the theoretical and experimental data, at temperatures above 40–50 K, due to the predominance of the effect of thermal vibrations of a lattice on the resistance, the values of ρ ​​for copper with different purities converge with an increase in the temperature. When comparing dependences ρ(T) for copper with different ρ0 at T ≥ θ, dependence ρ(T) for copper with a lower RRR should be considered as the upper limit.

CALCULATIONS OF THERMAL CONDUCTIVITY

At high (T ≥ θ) and low (T ≤ θ/20) temperatures, the thermal conductivity coefficient can be determined using the Wiedemann–Franz–Lorentz (WFL) law: λTρT = LT. Here, λT and ρT are the thermal conductivity and specific resistance at a certain temperature T and L is the Lorentz number, which has a constant value L0 = 2.45 × W Ω K–2 in this temperature range. In the intermediate zone, the WFL law is not fulfilled and the Lorentz number is affected by the temperature.

Heat transfer in solids is a complex physical process that can hardly be described mathematically. The transfer of thermal energy is close in nature to the transfer of electric charges; however, the mechanism of thermal conductivity is much more complex than that of electrical conductivity [4]. An approximate form of function λ(T) can be determined by analogy with Matthiessen’s rule after the additive addition of the thermal resistance associated with lattice defects in the metal Wl = 1/λl and the ideal thermal resistance caused by thermal vibrations Wi = 1/λl : λ−−1(T) = Wl(T) + Wi(T) [5], where

$${{W}_{i}}(T) = {{W}_{\infty }}2{{\left( {\frac{T}{\theta }} \right)}^{2}}\int\limits_0^{\frac{\theta }{T}} {\frac{{{{x}^{3}}dx}}{{\left( {{{e}^{x}} - 1} \right)\left( {1 - {{e}^{{ - x}}}} \right)}}.} $$
(5)

In Eq. (5), the heat resistance at high temperature, where the WFL law is observed, will be expressed by \({{W}_{\infty }} \approx \frac{1}{{{{\lambda }_{{{\text{r}}{\text{.r}}}}}}} \approx \frac{{{{L}_{0}}{{T}_{{{\text{r}}{\text{.r}}}}}}}{{{{\rho }_{{295{\text{K}}}}}}}\). If the thermal resistance caused by lattice deformations is written as \({{W}_{{\text{l}}}} \approx {{{{L}_{0}}T} \mathord{\left/ {\vphantom {{{{L}_{0}}T} {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}}\), mean integral thermal conductivity \(\bar {\lambda }\) (function λ(T), Fig. 3) will be equal to

$$\bar {\lambda } = \frac{{\int\limits_{{{T}_{1}}}^{{{T}_{2}}} {{{{\left[ {\frac{{{{\rho }_{0}}}}{{{{L}_{0}}T}} + \frac{{{{\rho }_{{295\,\,{\text{K}}}}}}}{{2{{L}_{0}}{{T}_{{{\text{r}}{\text{.r}}}}}}}{{{\left( {\frac{T}{\theta }} \right)}}^{2}}\int\limits_0^{\frac{\theta }{T}} {\frac{{{{x}^{3}}dx}}{{{\text{s}}{{{\text{h}}}^{2}}\left( {\frac{x}{2}} \right)}}} } \right]}}^{{ - 1}}}} }}{{\left( {{{T}_{2}} - {{T}_{1}}} \right)}}.$$
(6)
Fig. 3.
figure 3

Temperature dependence of thermal conductivity coefficient λ for copper with different purity.

Full size image