Multiwavelength Generation of Stokes Radiation Components with a Small Wavelength Spacing under Stimulated Raman Scattering in a SrMoO₄ Crystal

Abstract

Theoretical and experimental studies were conducted on providing conditions for the generation of multiple radiation components with a small wavelength spacing in a crystalline synchronously pumped SRS laser with combined frequency shift on high-frequency and low-frequency vibrational modes of an SRS-active crystal. A theoretical analysis has shown an important role of four-wave parametric Raman interactions on the low-frequency vibrational mode of the crystal provided the conditions of coherence and of nonlinear phase capture of such interactions are satisfied. For the first time, SRS generation was carried out at five closely spaced wavelengths of 1194, 1242, 1294, 1336, and 1396 nm in a SrMoO₄ crystal under synchronous pumping by a high intensity picosecond YAlO₃:Nd³⁺ laser at a wavelength of 1079 nm satisfying the condition of nonlinear phase capture.

1 INTRODUCTION

Multiwavelength radiation sources with a small wavelength spacing are becoming increasingly popular nowadays due to the advancement of microelectronics, optical communications, physics, chemistry, and biomedicine. Their main application today is spectrum multiplexing of optical communication channels. The key areas of research worldwide are the creation of such emitters based on semiconductor [1] and fiber-optic [2] quantum electronics. However, we have to use solid-state laser sources in laser impact tasks to overcome the problem of optical breakdown of the active medium. Multiwavelength generation can be carried out in solid-state quantum electronics by stimulated Raman scattering (SRS) in crystals (see, e.g., [3]), but the SRS-based laser frequency conversion is usually accompanied by a large frequency shift on the most intense high-frequency vibrational mode of a crystal. The participation of second low-frequency vibrational modes can reduce the wavelength spacing between generated SRS radiation components. This multiwavelength generation with a small wavelength spacing was carried out for the first time in a BaWO₄ crystal based on nanosecond SRS with combined frequency shift simultaneously on the high-frequency and low-frequency vibrational modes [4]. The generation was achieved at four wavelengths (554, 564, 575, and 583 nm) in the visible spectral range using second-harmonic pumping of a neodymium laser with a wavelength of 527 nm. Similar operations were performed later using SRS on two vibrational modes of KGd(WO₄)₂ [5], GdVO₄ [6], and YVO₄ [7] crystals. A series of operations has been performed recently with synchronously pumped SRS on combined vibrational modes in various crystals under pumping with a wavelength of 1063 nm [8–10] to achieve multiwavelength generation in the near-infrared range, which is more relevant for telecommunication applications. The use of transient SRS regime under synchronous picosecond pumping was shown to increase the efficiency of multiwavelength SRS generation on combined vibrational modes. For instance, SRS generation was implemented in [8] using a SrWO₄ crystal at four closely spaced wavelengths of 1178, 1227, 1279, and 1321 nm for different combinations of high-frequency and low-frequency shifts. This was due to the fact that the generation efficiency under the transient SRS regime depends on the integral Raman cross section, which has close values for the first (symmetric stretching) and second (symmetric bending) vibrational modes in tetragonal crystals because the second (less intense) mode is spectrally broad.

This paper is devoted to the search for conditions of the efficient SRS generation of a large number of spectrally multiplexed Stokes radiation components on combined vibrational modes. A theoretical study indicating the important role of four-wave parametric Raman interactions on the low-frequency vibrational mode of an SRS-active crystal has been carried out. SRS generation at five closely spaced wavelengths (1194, 1242, 1294, 1336, and 1396 nm) in a SrMoO₄ crystal under high-intensity synchronous pumping by a picosecond YAlO₃:Nd³⁺ laser with a wavelength of 1079 nm has been experimentally realized for the first time.

2 THEORY

The interaction of radiation with two vibrational modes of an SRS-active crystal can be described as follows:

$$\frac{{{{\partial }^{2}}E}}{{\partial {{z}^{2}}}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}(\varepsilon E)}}{{\partial {{t}^{2}}}} = \frac{{4\pi }}{{{{c}^{2}}}}{{N}_{1}}\frac{{\partial \alpha }}{{\partial {{Q}_{1}}}}\frac{{{{\partial }^{2}}({{Q}_{1}}E)}}{{\partial {{t}^{2}}}} + \frac{{4\pi }}{{{{c}^{2}}}}{{N}_{2}}\frac{{\partial \alpha }}{{\partial {{Q}_{2}}}}\frac{{{{\partial }^{2}}({{Q}_{2}}E)}}{{\partial {{t}^{2}}}},$$

(1)

$$\frac{{{{\partial }^{2}}{{Q}_{1}}}}{{\partial {{t}^{2}}}} + \frac{2}{{{{\tau }_{1}}}}\frac{{\partial {{Q}_{1}}}}{{\partial t}} + \Omega _{1}^{2}{{Q}_{1}} = \frac{1}{{2{{m}_{1}}}}\frac{{\partial \alpha }}{{\partial {{Q}_{1}}}}{{E}^{2}},$$

(2)

$$\frac{{{{\partial }^{2}}{{Q}_{2}}}}{{\partial {{t}^{2}}}} + \frac{2}{{{{\tau }_{2}}}}\frac{{\partial {{Q}_{2}}}}{{\partial t}} + \Omega _{2}^{2}{{Q}_{2}} = \frac{1}{{2{{m}_{2}}}}\frac{{\partial \alpha }}{{\partial {{Q}_{2}}}}{{E}^{2}},$$

(3)

where Q₁ and Q₂ are the amplitudes of the first and second vibrations, respectively (e.g., the first vibration is the symmetric stretching mode of internal vibrations of the anionic group of a scheelite-like crystal and the second vibration is the symmetric bending mode of internal vibrations of the same anionic group); Ω_1,2 = $2\pi {{{v}}_{{1,2}}}c$ is the central cyclic frequency of the first and second vibrational modes (Ω₁ > Ω₂); ${{{v}}_{{1,2}}}$ and τ_1,2 is the wave number and dephasing time of the first and second vibrational modes; m_1,2 and N_1,2 is the effective mass and concentration of vibrating particles participating in the first and second vibrations; $\partial \alpha {\text{/}}\partial {{Q}_{{1,2}}}$ is the medium polarizability variation under the action of the first and second vibrations; с is the light speed in vacuum. The model (1)–(3) differs from the classical SRS model [11] by the presence of an additional constitutive equation (3) for the forced vibration of the crystal on the second vibrational mode and of an additional (last) summand in the wave equation (1) to account for this additional vibration.

We assume that the SRS-active crystal is placed in an optical resonator with a high quality factor for the spectral region containing not only the first Stokes component of SRS radiation with high-frequency shift (Ω₁), but also the next two (second and third) Stokes components with an additional low-frequency shift (Ω₂). Let the index p denote the pump wave with frequency ω_p and wavelength λ_p; index S denote the first SRS radiation Stokes component with high-frequency shift (the frequency ω_S = ω_p − Ω₁, wavelength λ_S = ${{(\lambda _{{\text{p}}}^{{ - 1}} - {{{v}}_{1}})}^{{ - 1}}}$); index Ss denote the second Stokes component with an additional low-frequency shift (the frequency ω_Ss = ω_S – Ω₂, wavelength λ_Ss = ${{(\lambda _{{\text{S}}}^{{ - 1}} - {{{v}}_{2}})}^{{ - 1}}}$); index Sss denote the third Stokes component with another additional low-frequency shift (the frequency ω_Sss = ω_Ss − Ω₂, wavelength λ_Sss = ${{(\lambda _{{{\text{Ss}}}}^{{ - 1}} - {{{v}}_{2}})}^{{ - 1}}}$). Then the light field and the amplitudes of medium vibrations in the approximation of slowly varying amplitudes can be written as

$$\begin{gathered} E = \frac{1}{2}{{E}_{{\text{p}}}}{\text{exp(i}}{{\omega }_{{\text{p}}}}t - {\text{i}}{{k}_{{\text{p}}}}z{\text{)}} + \frac{1}{2}{{E}_{{\text{S}}}}{\text{exp(i}}{{\omega }_{{\text{S}}}}t - {\text{i}}{{k}_{{\text{S}}}}z{\text{)}} \\ + \frac{1}{2}{{E}_{{{\text{Ss}}}}}{\text{exp(i}}{{\omega }_{{{\text{Ss}}}}}t - {\text{i}}{{k}_{{{\text{Ss}}}}}z{\text{)}} + \frac{1}{2}{{E}_{{{\text{Sss}}}}}{\text{exp(i}}{{\omega }_{{{\text{Sss}}}}}t - {\text{i}}{{k}_{{{\text{Sss}}}}}z{\text{)}} + {\text{c}}{\text{.c}}{\text{.,}} \\ \end{gathered} $$

(4)

$${{Q}_{1}} = \frac{1}{2}{{q}_{1}}{\text{exp[i}}{{\Omega }_{1}}t - {\text{i}}({{k}_{{\text{P}}}} - {{k}_{{\text{S}}}})z{\text{]}} + {\text{c}}{\text{.c}}.,$$

(5)

$${{Q}_{2}} = \frac{1}{2}{{q}_{2}}{\text{exp[i}}{{\Omega }_{2}}t - {\text{i}}({{k}_{{\text{S}}}} - {{k}_{{{\text{Ss}}}}})z{\text{]}} + {\text{c}}{\text{.c}}.,$$

(6)

where E_j, ω_j, and k_j are a slowly varying amplitude, frequency, and the wave number for each radiation component (j = p, S, Ss, Sss); q₁ and q₂ are the slowly varying amplitudes of the first and second medium vibration. The substitution of the expressions (4) to (6) into the wave equation (1) yields the following system of shortened wave equations for each presented radiation component:

$$\begin{gathered} \frac{{\partial {{E}_{{\text{p}}}}}}{{\partial z}} + \frac{1}{{{{u}_{{\text{p}}}}}}\frac{{\partial {{E}_{{\text{p}}}}}}{{\partial t}} = - \,{\text{i}}\frac{{\pi {{\omega }_{{\text{p}}}}}}{{{{n}_{{\text{p}}}}c}}{{N}_{1}}\frac{{\partial \alpha }}{{\partial {{Q}_{1}}}}{{E}_{{\text{S}}}}{{q}_{1}} - \frac{\beta }{2}{{E}_{{\text{p}}}}, \\ \frac{{\partial {{E}_{{\text{S}}}}}}{{\partial z}} + \frac{1}{{{{u}_{{\text{S}}}}}}\frac{{\partial {{E}_{{\text{S}}}}}}{{\partial t}} = - \,{\text{i}}\frac{{\pi {{\omega }_{{\text{S}}}}}}{{{{n}_{{\text{S}}}}c}}{{N}_{1}}\frac{{\partial \alpha }}{{\partial {{Q}_{1}}}}{{E}_{{\text{p}}}}q_{1}^{ * } - \,{\text{i}}\frac{{\pi {{\omega }_{{\text{S}}}}}}{{{{n}_{{\text{S}}}}c}}{{N}_{2}}\frac{{\partial \alpha }}{{\partial {{Q}_{2}}}}{{E}_{{{\text{Ss}}}}}{{q}_{2}} - \frac{\beta }{2}{{E}_{{\text{S}}}}, \\ \frac{{\partial {{E}_{{{\text{Ss}}}}}}}{{\partial z}} + \frac{1}{{{{u}_{{{\text{Ss}}}}}}}\frac{{\partial {{E}_{{{\text{Ss}}}}}}}{{\partial t}} = - \,{\text{i}}\frac{{\pi {{\omega }_{{{\text{Ss}}}}}}}{{{{n}_{{{\text{Ss}}}}}c}}{{N}_{2}}\frac{{\partial \alpha }}{{\partial {{Q}_{2}}}}{{E}_{{\text{S}}}}q_{2}^{ * } - \,{\text{i}}\frac{{\pi {{\omega }_{{{\text{Ss}}}}}}}{{{{n}_{{{\text{Ss}}}}}c}}{{N}_{2}}\frac{{\partial \alpha }}{{\partial {{Q}_{2}}}}{{E}_{{{\text{Sss}}}}}{{q}_{2}}{\text{exp(}} - {\text{i}}\Delta {{k}_{2}}z{\text{)}} - \frac{\beta }{2}{{E}_{{{\text{Ss}}}}}, \\ \frac{{\partial {{E}_{{{\text{Sss}}}}}}}{{\partial z}} + \frac{1}{{{{u}_{{{\text{Sss}}}}}}}\frac{{\partial {{E}_{{{\text{Sss}}}}}}}{{\partial t}} = - \,{\text{i}}\frac{{\pi {{\omega }_{{{\text{Sss}}}}}}}{{{{n}_{{{\text{Sss}}}}}c}}{{N}_{2}}\frac{{\partial \alpha }}{{\partial {{Q}_{2}}}}{{E}_{{{\text{Ss}}}}}q_{2}^{ * }{\text{exp(i}}\Delta {{k}_{2}}z{\text{)}} - \frac{\beta }{2}{{E}_{{{\text{Sss}}}}}, \\ \end{gathered} $$

(7)

where u_j is the group velocity of the jth radiation component; n_j is the refractive index of the jth radiation component; Δk₂ = k_S + k_Sss – 2k_Ss is the wave mismatch of the parametric four-wave coupling of the SRS radiation components with a low-frequency relative shift. The last summand describing linear losses in the medium with the harmful loss factor β was formally introduced into the equations of (7). The substitution of (4) to (6) into the material equations (2) and (3) yields shortened material equations of the first and second vibrations of the SRS-active crystal:

$$\begin{gathered} \frac{{\partial {{q}_{1}}}}{{\partial t}} + \frac{1}{{{{\tau }_{1}}}}{{q}_{1}} = - \,{\text{i}}\frac{1}{{4{{m}_{1}}{{\Omega }_{1}}}}\frac{{\partial \alpha }}{{\partial {{Q}_{1}}}}{{E}_{{\text{p}}}}E_{{\text{S}}}^{ * }, \\ \frac{{\partial {{q}_{2}}}}{{\partial t}} + \frac{1}{{{{\tau }_{2}}}}{{q}_{2}} = - \,{\text{i}}\frac{1}{{4{{m}_{2}}{{\Omega }_{2}}}}\frac{{\partial \alpha }}{{\partial {{Q}_{2}}}}[{{E}_{{\text{S}}}}E_{{{\text{Ss}}}}^{ * } + {{E}_{{{\text{Ss}}}}}E_{{{\text{Sss}}}}^{ * }{\text{exp(i}}\Delta {{k}_{2}}z{\text{)}}]. \\ \end{gathered} $$

(8)

We find the following expressions in steady-state approximation $(\partial {{q}_{{1,\,2}}}{\kern 1pt} /{\kern 1pt} \partial t = 0)$ for the steady-state SRS gain of SRS radiation Stokes components on the first and second vibrational modes (in terms of radiation intensity):

$$\begin{gathered} {{g}_{1}} = \frac{{4{{\pi }^{2}}{{\omega }_{{\text{S}}}}{{N}_{1}}{{\tau }_{1}}}}{{{{m}_{1}}{{\Omega }_{1}}{{c}^{2}}{{n}_{{\text{S}}}}{{n}_{{\text{p}}}}}}{{\left( {\frac{{\partial \alpha }}{{\partial {{\Omega }_{1}}}}} \right)}^{2}}, \\ {{g}_{2}} = \frac{{4{{\pi }^{2}}{{\omega }_{{{\text{Ss}}}}}{{N}_{2}}{{\tau }_{2}}}}{{{{m}_{2}}{{\Omega }_{2}}{{c}^{2}}{{n}_{{{\text{Ss}}}}}{{n}_{{\text{S}}}}}}{{\left( {\frac{{\partial \alpha }}{{\partial {{\Omega }_{2}}}}} \right)}^{2}}, \\ \end{gathered} $$

(9)

which are experimentally measurable characteristics.

We write the system of equations (7), (8) through the experimentally measured characteristics. For this purpose, we introduce modified vibration amplitudes similarly as it was done in [12]:

$$\begin{gathered} {{{\bar {q}}}_{1}} = {{q}_{1}}\frac{{{{m}_{1}}{{\Omega }_{1}}{{c}^{2}}{{n}_{{\text{p}}}}{{n}_{{\text{S}}}}}}{{4{{\omega }_{{\text{S}}}}\partial \alpha {\text{/}}\partial {{Q}_{1}}}}, \\ {{{\bar {q}}}_{2}} = {{q}_{2}}\frac{{{{m}_{2}}{{\Omega }_{2}}{{c}^{2}}{{n}_{{\text{S}}}}{{n}_{{{\text{Ss}}}}}{{n}_{{{\text{Sss}}}}}}}{{4{{\omega }_{{{\text{Ss}}}}}\partial \alpha {\text{/}}\partial {{Q}_{2}}}}. \\ \end{gathered} $$

(10)

Then we get the final model. The system of wave equations:

$$\begin{gathered} \frac{{\partial {{E}_{{\text{p}}}}}}{{\partial z}} + \frac{1}{{{{u}_{{\text{p}}}}}}\frac{{\partial {{E}_{{\text{p}}}}}}{{\partial t}} = - \,{\text{i}}{{g}_{1}}\Delta {{{v}}_{1}}\frac{{{{\omega }_{{\text{p}}}}}}{{{{n}_{{\text{p}}}}}}{{E}_{{\text{S}}}}{{{\bar {q}}}_{1}} - \frac{\beta }{2}{{E}_{{\text{p}}}}, \\ \frac{{\partial {{E}_{{\text{S}}}}}}{{\partial z}} + \frac{1}{{{{u}_{{\text{S}}}}}}\frac{{\partial {{E}_{{\text{S}}}}}}{{\partial t}} = - \,{\text{i}}{{g}_{1}}\Delta {{{v}}_{1}}\frac{{{{\omega }_{{\text{S}}}}}}{{{{n}_{{\text{S}}}}}}{{E}_{{\text{p}}}}\bar {q}_{1}^{ * } - {\text{i}}{{g}_{2}}\Delta {{{v}}_{2}}\frac{{{{\omega }_{{\text{S}}}}}}{{{{n}_{{\text{S}}}}{{n}_{{{\text{Sss}}}}}}}{{E}_{{{\text{Ss}}}}}{{{\bar {q}}}_{2}} - \frac{\beta }{2}{{E}_{{\text{S}}}}, \\ \frac{{\partial {{E}_{{{\text{Ss}}}}}}}{{\partial z}} + \frac{1}{{{{u}_{{{\text{Ss}}}}}}}\frac{{\partial {{E}_{{{\text{Ss}}}}}}}{{\partial t}} = - \,{\text{i}}{{g}_{2}}\Delta {{{v}}_{2}}\frac{{{{\omega }_{{{\text{Ss}}}}}}}{{{{n}_{{{\text{Ss}}}}}{{n}_{{{\text{Sss}}}}}}}{{E}_{{\text{S}}}}\bar {q}_{2}^{ * } - {\text{i}}{{g}_{2}}\Delta {{{\text{v}}}_{2}}\frac{{{{\omega }_{{{\text{Ss}}}}}}}{{{{n}_{{{\text{Ss}}}}}{{n}_{{{\text{Sss}}}}}}}{{E}_{{{\text{Sss}}}}}{{{\bar {q}}}_{2}}{\text{exp(}} - {\text{i}}\Delta {{k}_{2}}z{\text{)}} - \frac{\beta }{2}{{E}_{{{\text{Ss}}}}}, \\ \frac{{\partial {{E}_{{{\text{Sss}}}}}}}{{\partial z}} + \frac{1}{{{{u}_{{{\text{Sss}}}}}}}\frac{{\partial {{E}_{{{\text{Sss}}}}}}}{{\partial t}} = - \,{\text{i}}{{g}_{2}}\Delta {{{v}}_{2}}\frac{{{{\omega }_{{{\text{Sss}}}}}}}{{n_{{{\text{Sss}}}}^{{\text{2}}}}}{{E}_{{{\text{Ss}}}}}\bar {q}_{2}^{ * }{\text{exp(i}}\Delta {{k}_{2}}z{\text{)}} - \frac{\beta }{2}{{E}_{{{\text{Sss}}}}}, \\ \end{gathered} $$

(11)

where $\Delta {{{v}}_{{1,2}}}$ = 1/(πcτ_1,2) is the line widths of the first and second vibrational modes, respectively (in cm^–1). The system of constitutive equations is:

$$\begin{gathered} \frac{{\partial {{{\bar {q}}}_{1}}}}{{\partial t}} + \frac{1}{{{{\tau }_{1}}}}{{{\bar {q}}}_{1}} = - \,{\text{i}}\frac{{{{c}^{2}}{{n}_{{\text{p}}}}{{n}_{{\text{S}}}}}}{{16{{\omega }_{{\text{S}}}}}}{{E}_{{\text{p}}}}E_{{\text{S}}}^{ * }, \\ \frac{{\partial {{{\bar {q}}}_{2}}}}{{\partial t}} + \frac{1}{{{{\tau }_{2}}}}{{{\bar {q}}}_{2}} = - \,{\text{i}}\frac{{{{c}^{2}}{{n}_{{\text{S}}}}{{n}_{{{\text{Ss}}}}}{{n}_{{{\text{Sss}}}}}}}{{16{{\omega }_{{{\text{Ss}}}}}}}[{{E}_{{\text{S}}}}E_{{{\text{Ss}}}}^{ * } + {{E}_{{{\text{Ss}}}}}E_{{{\text{Sss}}}}^{ * }{\text{exp(i}}\Delta {{k}_{2}}z{\text{)}}]. \\ \end{gathered} $$

(12)

An analysis of the system of equations (11), (12) has shown that according to (9) the SRS gain is determined by the coefficient g_1,2; therefore, the second vibrational mode loses competition to the first mode because g₂ < g₁. In the essentially transient mode, when the second summand on the left side of the equations (12) can be neglected, the SRS gain on both vibrational modes depends on the characteristic parameter ${{g}_{{1,2}}}\Delta {{{v}}_{{1,2}}}$, so it is necessary to select a crystal for SRS on combined vibrational modes, for which ${{g}_{2}}\Delta {{{v}}_{2}}$ is close to ${{g}_{1}}\Delta {{{v}}_{1}}$ (in other words, the integral cross sections for the first and second vibrational modes are about equal).

Tetragonal crystals, in particular scheelite-like crystals for which ${{g}_{2}}\Delta {{{v}}_{2}}$ ≈ ${{g}_{1}}\Delta {{{v}}_{1}}$ due to $\Delta {{{v}}_{2}}$ > $\Delta {{{v}}_{1}}$, are suitable for this problem [8, 13]. We chose the SrMoO₄ crystal as the test object because it has the broadest line of the second vibrational mode with a relatively high SRS gain coefficient among scheelite-like crystals [8]. We have the following characteristics for SrMoO₄ under the action of pumping by radiation polarized perpendicular to the crystal’s optical axis: ${{{v}}_{1}}$ = 888 cm^–1, $\Delta {{{v}}_{1}}$ = 2.6 cm^–1 and g₁ = 5. 6 cm/GW for λ_p ≈ 1.06 µm [14]; ${{{v}}_{2}}$ = 327 cm^–1, $\Delta {{{v}}_{2}}$ = 10.5 cm^–1, and g₂ ≈ g₁J₂/J₁ = 1.17 cm/GW (J_1,2 are the intensities of the first and second vibrational modes in the Raman spectrum) for λ_p ≈ 1.06 μm [8]. The values of the characteristic parameters for the first and second vibrational modes are close: ${{g}_{1}}\Delta {{{v}}_{1}}$ = 14 GW^–1 and ${{g}_{2}}\Delta {{{v}}_{2}}$ = 12.3 GW^–1. This should provide the transient SRS with combined frequency shift. Another reason for the crystal selection is the well-known data on the refractive index dispersion of the SrMoO₄ crystal throughout its region of transparency [15]. This made it possible to calculate the wave mismatch of the partially degenerate four-wave parametric interaction processes on the first and second vibrational modes [11]:

$$\Delta {{k}_{{1,2}}} = {{k}_{{{\text{p}},{\text{S}}}}} + {{k}_{{{\text{Ss,Sss}}}}} - 2{{k}_{{{\text{S,Ss}}}}} = ({{n}_{{{\text{p,S}}}}} + {{n}_{{{\text{Ss,Sss}}}}} - 2{{n}_{{{\text{S,Ss}}}}})2\pi \lambda _{{{\text{S,Ss}}}}^{{ - 1}} + ({{n}_{{{\text{p,S}}}}} - {{n}_{{{\text{Ss,Sss}}}}})2\pi {{{v}}_{{1,2}}}.$$

(13)

For λ_p = 1079 nm, it has a relatively low Δk₂ = 4.4 cm^–1 on the second vibrational mode compared to Δk₁ = 34.9 cm^–1 on the first vibrational mode owing to ${{{v}}_{2}}$ < ${{{v}}_{1}}$. That is why the four-wave interaction of the SRS radiation components with the low-frequency relative shift is accounted for in model (11), (12), but the high-frequency relative shift is disregarded.

3 NUMERICAL MODELING

We assumed in numerical modeling that the SRS-active crystal was placed in a ring resonator whose length is equal to the pump pulse repetition period in order to carry out synchronous single-pass pumping by a series of ultrashort pulses. Therefore, the numerical calculation of the system of equations (11), (12) describing the single-pass SRS was made repeatedly so that corresponding output parameters of the previous calculation of the amplitudes of the SRS radiation component were taken as input values of the amplitudes in each subsequent calculation of single-pass SRS. The dephasing time (τ_1,2) was believed to be significantly shorter than the pump pulse repetition period and thus the vibrational amplitudes were supposed to be equal to zero at the start of each calculation that followed. So, the pump pulse repetition period had no effect in the calculations on the simulated SRS process. In order to save computational time, the pump pulse repetition period was chosen as short as possible being equal to three times the duration of the Gaussian pump pulse. The duration of Gaussian pump pulses was set to be 43 ps at level 1/e (36 ps at half-maximum). The output parameters of each calculation also took into account useful loss of the resonator having an output mirror with reflection coefficients R_S = 99%, R_Ss = 96%, and R_Sss = 92% at wavelengths λ_S = 1194 nm, λ_Ss = 1242 nm, and λ_Sss = 1294 nm under pumping at a wavelength λ_p = 1079 nm. The harmful loss factor β was set to be 0.005 cm^–1. The resonator was chosen to be highly adequate for the first Stokes component (λ_S) in the interest of stimulating the SRS stage with an additional low-frequency shift. The model does not take into account the generation of the second Stokes component with high-frequency shift under the assumption of low quality factor of the resonator at its wavelength (λ_Ss = (${{\lambda }_{{\text{S}}}}^{{ - 1}} - {{{v}}_{1}}$)^—1 = 1335 nm). The intensity of the radiation components was defined as I_j = |E_j|²cn_j/8π.

Figure 1 shows the results of calculating SRS processes for a SrMoO₄ crystal 3 cm long under synchronous pumping by a series of picosecond pulses with peak intensities of 0.15 (Fig. 1a), 0.9 (Fig. 1b), and 4.9 GW/cm² (Fig. 1c).

Fig. 1.

The results of calculating SRS processes for a 3 cm long SrMoO₄ crystal under synchronous pumping by a series of pulses with peak intensities of 0.15 (a), 0.9 (b), and 4.9 GW/cm² (c) (the blue curves indicate pump radiation (I_p), the green curves indicate the first Stokes component (I_S), the orange curves indicate the second Stokes component (I_Ss), and the red curves indicate the third Stokes component (I_Sss); the green, orange and red arrows indicating the generation thresholds of the first, second and third Stokes components, respectively).

It can be seen from Fig. 1 that with a low pump intensity of 0.15 GW/cm² (Fig. 1a) the generation threshold of the first SRS radiation Stokes component with high-frequency shift (green line) can be reached at a pump pulse number of 33. The generation thresholds of the second and third SRS radiation Stokes components with additional low-frequency shifts (orange and red lines) are reached at pump pulse numbers of 54 and 57, respectively. This is a cascade mode of SRS conversion with suppressed Raman-parametric coupling due to violation of its coherence condition (Δk₂L < π).

Higher pump intensity up to 0.9 GW/cm² (Fig. 1b) reduces the threshold values of the pump pulse number to 6, 12, and 13 for the first, second, and third Stokes components of SRS radiation, respectively. It is important that the generation threshold of the third Stokes component approaches the generation threshold of the second Stokes component. Consequently, the influence of parametric Raman four-wave coupling is enhanced, which can be explained by nonlinear phase capture of interacting waves [16].

A further increase in the pump intensity up to 4.9 GW/cm² (Fig. 1c) at which the generation threshold of the first Stokes component is reached already under the action of the first pulse leads not only to a decrease in the generation thresholds, but also to their equalization for higher (second and third) Stokes components of SRS radiation, which ensures simultaneous generation of several Stokes components with a low-frequency relative shift.

In terms of theory [16–18], the effect of nonlinear phase capture of the parametric Raman interaction occurs when the following condition is satisfied:

$$\frac{{\Delta k}}{{g{{I}_{{\text{p}}}}}} < 1,$$

(14)

where Δk is the wave mismatch of the parametric four-wave interaction; g is the SRS gain coefficient; I_p is the pump radiation intensity of the parametric Raman interaction. Then it is possible to introduce a critical pump intensity of the parametric Raman interaction which, if exceeded, ensures nonlinear capture of the phases of this interaction on the first or second vibrational mode:

$${{I}_{{{\text{cr}}1,2}}} = \frac{{\Delta {{k}_{{1,2}}}}}{{{{g}_{{1,2}}}}}.$$

(15)

So the interaction on the first vibrational mode of the SrMoO₄ crystal (Δk₁ = 34.9 cm^–1, g₁ = 5.6 cm/GW) requires a very high pump intensity, I_p > I_cr1 = 6.2 GW/cm²; however, for the parametric Raman interaction on the second vibrational mode of SrMoO₄ (Δk₂ = 4.4 cm^–1, g₂ = 1.17 cm/GW), the critical intensity decreases to I_cr2 = 3.7 GW/cm².

Our process of synchronously pumped SRS with combined frequency shift can be represented as the first stage of conversion by means of SRS with high-frequency shift and the second stage of parametric Raman conversion with low-frequency shift. Then the role of the pump radiation of the four-wave interaction is played at a separate second conversion stage by the first Stokes component with wavelength λ_S that has a parametric Raman coupling with the second (λ_Ss) and third (λ_Sss) components. The condition of nonlinear phase capture of such parametric Raman interaction is written as I_Stokes > I_cr2 where I_Stokes = I_S/(1 – R_S) is the intraresonator intensity of the first Stokes component and I_S is its output intensity.

The calculation showed (see Fig. 1) that the output intensity of the first Stokes component at the generation threshold of this component was I_S = 0.02, 0.05, and 0.13 GW/cm² for pump intensities I_p = 0.15, 0.9, and 4.9 GW/cm², respectively. And the intraresonator intensity of the first Stokes component was I_Stokes = 0.5I_cr2, 1.3I_cr2, and 3.5I_cr2, respectively (Δk = 4.4 cm^–1, g₂ = 1.17 cm/GW, and R_S = 0. 99).

Thus, in the first case with I_p = 0.15 GW/cm² (Fig. 1a), the condition I_Stokes > I_cr2 is not fulfilled, the intermediate case I_p = 0.9 GW/cm² (Fig. 1b) is approximately at the limit of fulfillment of this condition, and the higher pump intensity I_p = 4.9 GW/cm² (Fig. 1c) fully supports the fulfillment of this condition. Therefore, it can be assumed that we can be guided by a simpler condition I_p > I_cr2 = 3.7 GW/cm² in order to ensure completely the effect of nonlinear phase capture.

Figure 2 displays calculated dependences of the output pulse intensity of the third Stokes component (I_Sss) normalized to the input pump intensity (I_p) on the length of the SRS-active crystal (L) for the pump pulse with the indicated number at I_pL = 0.45 GW/cm (Fig. 2a) and I_pL = 5.7 GW/cm (Fig. 2b).

Fig. 2.

The calculated dependences of the output pulse intensity of the third Stokes component (I_Sss) normalized to the input pump intensity (I_p) on the SrMoO₄ crystal length for a pump pulse with the indicated number at I_pL = 0.45 (a) and 5.7 GW/cm (b).

Figure 2a demonstrates the case of low-intensity pumping whereby the condition of nonlinear phase capture I_Stokes > I_cr2 is not satisfied except for the shortest crystal length (L = 0.5 cm, I_p = 0.9 GW/cm²) for which I_Stokes = 1.3I_cr2. The generation of the third Stokes component is shown for three numbers (56, 57, and 58) of the pump pulse which overcome the generation threshold of the second Stokes component. It should be noted that Fig. 1a corresponds to Fig. 2a for L = 3 cm. The generation threshold of the second Stokes component is reached at the 54th pump pulse (see the orange arrow in Fig. 1a), and the same is observed irrespective of the crystal length for a constant value of I_pL.

In Fig. 2a, there is a characteristic dependence of the generation intensity reduction when the condition of nonlinear interaction coherence is violated [19], Δk₂L < π being the effective generation of the third Stokes component at L < 1.5 cm. It can be concluded that in the case of low-intensity pumping where the condition of nonlinear phase capture I_Stokes > I_cr2 is violated it is necessary to reduce the length of the SRS-active crystal for multiwavelength generation of Stokes components with low-frequency shift. It agrees with earlier experiments on SRS generation in an SrWO₄ crystal under synchronous picosecond pumping with low intensity up to 0.4 GW/cm² [8, 20]. The long SrWO₄ crystal (L = 3.6 cm) [20] produced the generation of only the first (λ_S) and second (λ_Ss) Stokes components while in a short SrWO₄ crystal (L = 1.4 cm) under similar experimental conditions [8], an additional third (λ_Sss) Stokes component with combined frequency shift was generated due to the maintenance of the coherence condition.

Figure 2b shows the case of high-intensity pumping that fulfills the condition of nonlinear phase capture I_Stokes > I_cr2 except for the longest crystals (L > 5.5 cm, I_p < 1 GW/cm²). The generation of the third Stokes component is shown for three numbers (8, 9, and 10) of the pump pulse where the generation threshold of the second Stokes component is overcome. It can be seen that the reduction of generation efficiency with crystal length is observed only at the 8th pump pulse, but at the next (9th and 10th) pump pulses the dependence even starts to increase slowly, which demonstrates the nonlinear phase capture of the parametric Raman interaction. It can be concluded that it is advantageous to increase the crystal length for the multiwavelength generation of the SRS radiation Stokes components with low-frequency shift under high-intensity pumping that supports the fulfillment of the condition of nonlinear phase capture.

4 AN EXPERIMENTAL STUDY AT HIGH-INTENSITY PUMPING

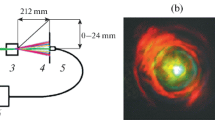
We have performed an experiment on SRS in a long (7 cm) SrMoO₄ crystal under the action of high-intensity synchronous picosecond pumping that satisfied the condition that nonlinear phase capture (I_p > I_cr2 = 3.7 GW/cm²) should be fully achieved. The optical scheme of the experiment is presented in Fig. 3.

Fig. 3.

The optical scheme of the laser system and the photograph (bottom) of the spatial distribution of Stokes SRS components after the decomposition of the output SRS radiation into spectrum by a diffraction grating: (1) focusing mirror; (2) SRS active element; (3–6) resonator mirrors.

The radiation from the YA1O₃: Nd³⁺pump laser was focused by the concave mirror 1 into the SRS-active element 2 placed in an external zigzag optical resonator consisting of two concave (3 and 4) and two flat (5 and 6) mirrors. The output SRS radiation was decomposed into a spectrum using a diffraction grating (600/mm) and sent to a recording system.

A high-power oscillator-amplifier laser system based on YAlO₃:Nd³⁺ crystals with a wavelength λ_p = 1079 nm was used as a pump laser generating in the passive mode locking regime trains of 56 laser pulses with a duration of individual pulses τ_p = 64 ps and their repetition period of 8 ns. The energy of the laser pulse train was 18 mJ, which corresponded to the energy of individual pulses E_p = 320 μJ [21]. The pump laser was isolated from the SRS laser by means of a Faraday isolator (not shown in Fig. 3). The use of a concave mirror 1 with a radius of curvature of 240 cm made it possible to focus the pump radiation beam into a focal spot with the minimum beam radius r_p = 290 µm (at level 1/e²) and Gaussian transverse distribution of radiation intensity, which yielded a high pump radiation intensity I_p = 2W_p/$({{\tau }_{{\text{p}}}}\pi r_{{\text{p}}}^{2})$ = 3.8 GW/cm² exceeding I_cr2.

An SrMoO₄ crystal of length L = 7 cm with antireflection coatings on plane-parallel end faces was used as the active element of the SRS laser. The crystal was grown by the Czochralski method at the Research Center for Laser Materials and Technologies, General Physics Institute of the Russian Academy of Sciences. The optical axis of the crystal was directed perpendicular to the direction of laser radiation propagation and oriented along the polarization direction of the pump radiation in order to excite not only the first (${{{v}}_{1}}$ = 888 cm^–1) but also the second (${{{v}}_{2}}$ = 327 cm^–1) vibrational mode of the SrMoO₄ crystal [8].

The length of the SRS laser resonator was precisely adjusted (the mirror 6 was installed on a micrometer table) to synchronize the resonator round trip time with the pump pulse repetition period (8 ns). The end plane mirror 5 was highly reflective at SRS radiation wavelengths from 1194 to 1396 nm (R_1192-1396 > 99%). Concave mirrors 3 and 4 (radius of curvature 100 cm) were transparent at the pump wavelength (transmittance T₁₀₇₉ = 97.1%) and had the following of reflection coefficient distribution over wavelengths of SRS radiation: R₁₁₉₄ = 99.3%, R₁₂₄₂ = 99.2%, R₁₂₉₄ = 92.9%, R₁₃₃₆ = 7.0%, and R₁₃₉₆ = 15.3%. The output plane mirror 6 had the following distribution of reflection coefficients over the SRS radiation wavelengths: R₁₁₉₄ = 99.2%, R₁₂₄₂ = 98.5%, R₁₂₉₄ = 86.6%, R₁₃₃₆ = 24.2%, and R₁₃₉₆ = 48.0%. The resonator configuration was calculated in the ReZonator software tool [22] to match the size of the fundamental transverse mode of the first Stokes component of the SRS radiation with the pump beam focal radius (r_p = 290 µm) at the resonator round trip time synchronized with the pump pulse repetition period (8 ns).

It should be noted that we observed in the experiment a larger number of generated components of SRS radiation than in the theory discussed above: not only the calculated wavelengths λ_S = 1194 nm, λ_Ss = 1242 nm, and λ_Sss = 1294 nm, but also λ_SS = ${{(\lambda _{{\text{S}}}^{{ - 1}} - {{{v}}_{1}})}^{{ - 1}}}$ = 1336 nm and λ_SSs = ${{(\lambda _{{{\text{SS}}}}^{{ - 1}} - {{{v}}_{2}})}^{{ - 1}}}$ = 1396 nm. The wavelengths of all five generated SRS radiation components recorded by OceanOptics HR2000 spectrometer (200–1100 nm, resolution 2 nm) after frequency doubling with lithium iodate crystal corresponded to the above calculated values. The radiation linewidths did not exceed the resolution of the spectrometer. Figure 4 demonstrates this measurement result.

Fig. 4.

Spectrum of the generated SRS radiation.

The beam profiles of each of the five separated SRS radiation components were also recorded (see Fig. 3, photo below). The beam profiles were close to Gaussian, which indicates high spatial quality of the generated SRS radiation owing to matching the size of the fundamental transverse mode of SRS radiation with the pump beam radius.

Figure 5 shows the dependence of the pulse train energy of the total output SRS radiation on the SRS laser resonator length detuning for the energy of the laser pulse train equal to 18 mJ. It can be seen that the detuning curve is relatively wide (ΔL_1/2 = 16 mm at half-maximum) and symmetric, which is characteristic of the case of high-intensity synchronous picosecond pumping [21, 23] in contrast to the narrow (ΔL_1/2 < 1 mm) and asymmetric detuning curves obtained with low-intensity synchronous picosecond pumping [8–10, 24]. The maximum train energy of the total output SRS radiation at the best pump synchronization was 1.3 ± 0.1 mJ (output energy instability of 8%) at a pump pulse train energy of 18 ± 1 mJ (input energy instability 5%), which corresponded to an SRS conversion efficiency of about 7%. The output energy was distributed over the SRS components as follows: 9% to λ_S = 1194 nm, 62% to λ_Ss = 1242 nm, 17% to λ_Sss = 1294 nm, 8% to λ_SS = 1336 nm, and 4% to λ_SSs = 1396 nm.

Fig. 5.

The dependency of the total output SRS pulse train energy on the SRS laser resonator length detuning.

Figure 6 shows oscillograms of all components of the generated radiation. The oscillograms were obtained using four LFD-2F avalanche photodiodes connected to a four-channel Tektronix TDS7404B (4 GHz) oscilloscope with two consecutive measurements first for the components with wavelengths λ_p, λ_S, λ_Sss, and λ_SSs and then for the components with wavelengths λ_p, λ_Ss, and λ_SS to be further combined. It can be seen from Fig. 6 that the generation of the first Stokes component (λ_S = 1194 nm) with high-frequency shift ${{{v}}_{1}}$ occurred without a time delay relative to the pump pulse train (λ_p = 1079 nm), i.e., it was carried out practically in one pass of the SRS crystal due to high-intensity pumping. The second Stokes component (λ_SS = 1336 nm) with a doubled high-frequency shift $2{{{v}}_{1}}$ was also generated without delay. The resonator mirrors for this component had low reflection coefficients (R₁₃₃₆ = 7.0% for concave mirrors 3 and 4 and 24.2% for output mirror 6), so its generation was also done in one pass.

Fig. 6.

Oscillograms of frequency components of the generated radiation.

However, the generation of the second Stokes component with combined frequency shift $({{{v}}_{1}}~ + ~{{{v}}_{2}})$ at the wavelength λ_Ss = 1242 nm occurred with a noticeable delay, which is explained by its development in a high-quality resonator (R₁₂₄₂ = 99.2% for concave mirrors 3 and 4 and R₁₂₄₂ = 98.5% for output mirror 6). At the same time, the train of the next (third) Stokes component with combined frequency shift $({{{v}}_{1}} + {{{v}}_{2}} + {{{v}}_{2}})$ at the wavelength λ_Sss = 1294 nm had no appreciable delay relative to the pulse train of the previous Stokes component with the wavelength λ_Ss = 1242 nm, which can be explained by the parametric Raman interaction on the low-frequency vibrational mode due to the fulfillment of the nonlinear phase capture condition. The pulse train of the third Stokes component (λ_Sss) was relatively short, i.e., it ended prematurely compared to the pulse train of the previous second Stokes component (λ_Ss) repeating the pattern of depletion of the pulse train of the first Stokes component (λ_S) during its conversion at the second SRS stage. This proves the participation of the first Stokes component not only in the process of SRS conversion into the second Stokes components (λ_Ss and λ_SS), but also in the process of parametric Raman interaction with the next two SRS components having low-frequency relative shifts (λ_Ss and λ_Sss).

The biggest question is the generation mechanism of the last Stokes component with the wavelength λ_SSs = 1396 nm. A simple explanation consisting in the third stage of the SRS conversion with low-frequency shift $({{{v}}_{2}})$ from the previous component (λ_SS) (the blue arrow in Fig. 4 for the last frequency shift) does not stand up to scrutiny because there is a generation delay although the resonator mirrors for λ_SSs have low reflection coefficients (R₁₃₉₆ = 15.3% for concave mirrors 3 and 4 and R₁₃₉₆ = 48.0% for output mirror 6) as is the case for the λ_SS. Besides, the relative proportion of the output SRS energy attributable to the λ_SS wavelength component is small (8%). The largest share of energy was attributable to the component with the wavelength λ_Ss (62%), so it can be assumed that the SRS generation of the last component (λ_SSs) originated from it with an additional high-frequency shift $({{{v}}_{1}})$ (the red arrow for the last frequency shift corresponds to it in Fig. 4). This is also indicated by the same generation delay for the components with wavelengths λ_Ss and λ_SSs (Fig. 6). However, the generation of the pulse train of the last component (λ_SSs) ended prematurely compared to the component at wavelength λ_Ss repeating the pattern of depletion of the pulse train of the first Stokes component (λ_S). This indicates the participation of the first Stokes component (λ_S) in the generation of the last Stokes component (λ_SSs), which could occur in four-wave parametric Raman interactions. First, it could be a four-wave interaction on the low-frequency vibrational mode $({{{v}}_{2}})$ involving components with wavelengths λ_S, λ_Ss, λ_SS, and λ_SSs. This process should be more efficient under high-intensity pumping (the condition of nonlinear phase capture is fulfilled). Second, there could be a four-wave interaction on the high-frequency vibrational mode (ν₁) that involves components with wavelengths λ_p, λ_S, λ_Ss, and λ_SSs (without participation of the λ_SS wavelength component). But the condition of nonlinear phase capture is not satisfied for this interaction. Thus, the most likely explanation for the generation of the last component (λ_SSs) is a combination of the four-wave interaction (λ_S, λ_Ss, λ_SSs, and λ_SSs) on the low-frequency vibrational mode $({{{v}}_{2}})$ and of the SRS conversion λ_Ss → λ_SSs on the high-frequency vibrational mode $({{{v}}_{1}})$. The latter occurs without the component (λ_SS), which is confirmed experimentally because Fig. 6 shows that the generation at the λ_SSs wavelength continued despite the fact that the generation at the λ_SS wavelength had stopped.

We also used a PS-1/S1-type streak camera [25] (developed by the Prokhorov General Physics Institute, Russian Academy of Sciences) to measure the duration of the generated pulses of the output SRS radiation. For the first Stokes component with a high-frequency shift (λ_S), the pulse duration λ_S was 20 ± 5 ps. A shortened pulse duration τ_Ss = 8 ± 2 ps was recorded for the second Stokes component with combined frequency shift (λ_Ss). These values are close to the theoretical estimate [26] τ_S ≈ $\sqrt {{{\tau }_{{\text{p}}}}{{\tau }_{1}}}$ and τ_Ss ≈ $\sqrt {{{\tau }_{{\text{p}}}}{{\tau }_{2}}}$, respectively.

5 CONCLUSIONS

Theoretical and experimental studies were carried out on conditions for the generation of multiple radiation components with a small wavelength spacing in a crystal SRS laser under synchronous pumping with combined frequency shift. A SrMoO₄ crystal possessing the first (high-frequency) and second (low-frequency) vibrational modes similar in Raman integral cross section values was used as an active medium. A theoretical analysis indicated an important role of four-wave parametric Raman interactions on the low-frequency vibrational mode of the SRS-active crystal when the conditions of coherence and nonlinear phase capture of such interactions are satisfied. The generation of a crystalline SRS laser in the near-infrared range for five closely spaced wavelengths with combined frequency shift was achieved for the first time. The use of high-intensity synchronous picosecond pumping with a wavelength of 1079 nm satisfying the condition of nonlinear phase capture of parametric Raman interaction on the second vibrational mode made possible efficient generation at wavelengths of 1194, 1242, 1294, 1336, and 1396 nm with various combinations of frequency shifts (888 и 327 cm^–1).