Unsteady Coupled Elastic Diffusion Processes in an Orthotropic Cylinder Taking into Account Relaxation of Diffusion Fluxes

Abstract

We consider the problem of determining the stress-strain state of an orthotropic multicomponent cylinder affected by unsteady surface elastic diffusive perturbations. The coupled system of elastic diffusion equations in the polar coordinate system is used as a mathematical model. Diffusion relaxation effects, implying finite rates of diffusion flux propagation, are taken into account. The solution to this problem is sought in the integral form and is represented as convolutions of Green’s functions with functions defining surface elastodiffusive perturbations. We use the Laplace transform by time and Fourier series expansion in Bessel functions of the first kind to find Green’s functions. The Laplace transform inversion is done analytically due to residues and operational calculus tables. An analytical solution to the problem is obtained. A numerical study of the interaction of mechanical and diffusion fields in a continuous orthotropic cylinder is performed. We used three-component material as an example. The cylinder is under pressure, which is uniformly distributed over it surface. We use three-component material as an example.

INTRODUCTION

In connection with the rapid development of technologies for the production of modern structural materials operating under conditions of multifactorial external influences, scientists are increasingly interested in the question of the interaction of fields of different physical natures in continuous media. To date, based on the known equations of continuum mechanics, equations of heat and mass transfer, equations of electrodynamics, and the laws of thermodynamics, models have been built that take into account the mutual influence of mechanical, temperature, diffusion, electromagnetic, chemical, and other fields. The most recent publications on this topic are works [1–6], where coupled thermomechanical diffusion processes are considered. Electromagnetic fields in continuous media are also studied in [7–10], in addition to the phenomena of heat and mass transfer.

In the publications listed above, when describing thermal diffusion processes, the generalized Fourier and Fick laws are used, which take into account the relaxation of thermal and diffusion flows. This is essential for describing high-frequency processes, examples of which are the propagation of ultrasound, shock waves, etc. Maxwell was the first to introduce inertia into the heat transfer equations, and in 1958 Cattaneo [11] proposed a variant of the Fourier law with a relaxation term. Vernott [12] and Lykov [13] independently arrived at the same result. Currently, there are various generalizations of the above laws, which can be found in [14–18].

The above list of studies does nowhere near fully cover the entire range of issues related to the analysis of the interaction of various fields of this nature. Proceeding from the closeness to the problem considered in this paper, the review includes papers devoted mainly to the formulation and solution of linear initial-boundary value problems in the mechanics of coupled fields. An analysis of these publications, as well as the publications of other authors, shows that these problems are considered both in the stationary (static) [4, 8, 9] and nonstationary formulations [2, 3, 5–7, 10], but mainly in a rectangular Cartesian coordinate system.

When solving problems in various curvilinear coordinate systems, the main problem is finding a system of eigenfunctions that is a solution to the corresponding Sturm–Liouville problem. Relatively few scientific papers are devoted to this issue, among which we can single out [19–27]. They consider models of thermomechanical diffusion, which include the analysis of nonstationary processes in single-component solid and hollow cylinders [19–21, 24, 25], the study of cylindrical Rayleigh waves [22], and polar–symmetric perturbations in a half-space [23] and layer [26, 27].

Elastic diffusion processes occurring in a continuous multicomponent orthotropic cylinder of infinite length, which is under the action of nonstationary elastic-diffusion surface perturbations, are discussed in this paper. It is assumed that all external influences have a uniform distribution over the surface of the cylinder, which allows us to consider this problem in a one-dimensional formulation.

1 STATEMENT OF THE PROBLEM

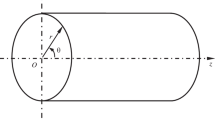
An orthotropic solid multicomponent cylinder is considered; on its surface, nonstationary elastic-diffusion perturbations are specified in the form of mechanical pressure and diffusion fields. Differential equations describing coupled elastic-diffusion processes without taking into account body forces in a polar-symmetric formulation have the form [28–30]

$$\begin{gathered} \ddot {u} = u{\kern 1pt} ''\, + \frac{{u'}}{r} - \frac{u}{{{{r}^{2}}}} - \sum\limits_{q = 1}^N {\alpha _{1}^{{(q)}}\eta _{q}^{'},\quad \eta {{}_{{N + 1}}} = - \sum\limits_{q = 1}^N {{{\eta }_{q}},} } \\ {{{\dot {\eta }}}_{q}} + {{\tau }_{q}}{{{\ddot {\eta }}}_{q}} = - \Lambda _{{11}}^{{(q)}}\left( {u{\kern 1pt} '''\, + \frac{{2u''}}{r} - \frac{{u'}}{{{{r}^{2}}}} + \frac{u}{{{{r}^{3}}}}} \right) + D_{1}^{{(q)}}\left( {\eta _{q}^{{''}} + \frac{{\eta _{q}^{'}}}{r}} \right). \\ \end{gathered} $$

(1)

The initial conditions are assumed to be zero. The boundary conditions corresponding to the problem statement are written as follows:

$${{\left. {\left( {u{\kern 1pt} '\, + {{c}_{{12}}}\frac{u}{r} - \sum\limits_{j = 1}^N {\alpha _{1}^{{(q)}}{{\eta }_{q}}} } \right)} \right|}_{{r = {{c}_{{12}}}}}} = {{f}_{1}}(\tau ),\quad {{\eta }_{q}}{{{\text{|}}}_{{r = {{c}_{{12}}}}}} = {{f}_{{q + 1}}}(\tau ).$$

(2)

In formulas (1) and (2), all quantities are dimensionless. Their relationship with their dimensional counterparts is determined by the following relationships:

$$\begin{gathered} u = \frac{{{{u}_{r}}}}{L},\quad \tau = \frac{{Ct}}{L},\quad {{C}^{2}} = \frac{{{{C}_{{1111}}}}}{\rho },\quad {{c}_{{\alpha \beta }}} = \frac{{{{C}_{{\alpha \alpha \beta \beta }}}}}{{{{C}_{{1111}}}}},\quad {{\tau }_{q}} = \frac{{C{{\tau }^{{(q)}}}}}{L}, \\ r = \frac{{r{\text{*}}}}{L},\quad \alpha _{1}^{{(q)}} = \frac{{\alpha _{{11}}^{{(q)}}}}{{{{C}_{{1111}}}}},\quad D_{1}^{{(q)}} = \frac{{D_{{11}}^{{(q)}}}}{{CL}},\quad \Lambda _{{11}}^{{(q)}} = \frac{{{{m}^{{(q)}}}\alpha _{{11}}^{{(q)}}D_{{11}}^{{(q)}}n_{0}^{{(q)}}}}{{\rho CLR{{T}_{0}}}}, \\ \end{gathered} $$

(3)

where t is time; u_r is the radial component of the mechanical displacement vector; r* is the radial coordinate; η_q is the increment in the concentration of the qth substance in the composition of a multicomponent continuous medium; $n_{0}^{{(q)}}$ and m^(q) are the initial concentration and molar mass of the qth component, respectively; ρ is the density of the continuous medium; τ^(q) is the relaxation time of diffusion processes; $\alpha _{{11}}^{{(q)}}$ is the coefficient characterizing the deformations arising due to diffusion; $D_{{11}}^{{(q)}}$ is the self-diffusion coefficient; R is the universal gas constant; and T₀ is the temperature of the continuum. The characteristic linear size L is chosen so that the dimensionless radius of the cylinder is equal to c₁₂.

2 SOLUTION ALGORITHM

The solution to the problem is sought in the integral form [29, 30]:

$$u(r,\tau ) = \sum\limits_{m = 1}^{N + 1} {\int\limits_0^\tau {{{G}_{{1m}}}(r,t){{f}_{m}}(\tau - t)dt,\quad {{\eta }_{q}}(r,\tau ) = \sum\limits_{m = 1}^{N + 1} {\int\limits_0^\tau {{{G}_{{q + 1,m}}}(r,t){{f}_{m}}(\tau - t)dt,} } } } $$

(4)

where G_nm(r, τ), n, m = $\overline {1,N + 1}$ are the surface Green’s functions of the problem under consideration, i.e., solutions to the following initial boundary value problems:

$$\begin{gathered} \left( {G_{{1m}}^{{''}} + \frac{{G_{{1m}}^{'}}}{r} - \frac{{{{G}_{{1m}}}}}{r}} \right) - \sum\limits_{j = 1}^N {\alpha _{j}^{{(j)}}G_{{j + 1,m}}^{'}} = {{{\ddot {G}}}_{{1m}}}, \\ D_{1}^{{(q)}}\left( {G_{{q + 1,m}}^{{''}} + \frac{{G_{{q + 1,m}}^{'}}}{r}} \right) - \Lambda _{{11}}^{{(q)}}\left( {G_{{1m}}^{{'''}} + \frac{{2G_{{1m}}^{{''}}}}{r} - \frac{{G_{{1m}}^{'}}}{{{{r}^{2}}}} + \frac{{{{G}_{{1m}}}}}{{{{r}^{3}}}}} \right) = {{{\dot {G}}}_{{q + 1,m}}} + {{\tau }_{q}}{{{\ddot {G}}}_{{q + 1,m}}}, \\ \end{gathered} $$

(5)

$$\begin{gathered} {{\left. {\left( {G_{{1m}}^{'} + \frac{{{{c}_{{12}}}}}{r}{{G}_{{1m}}} - \sum\limits_{j = 1}^N {\alpha _{1}^{{(j)}}{{G}_{{j + 1,m}}}} } \right)} \right|}_{{r = {{c}_{{12}}}}}} = {{\delta }_{{1m}}}\delta (\tau ),\quad {{G}_{{q + 1,m}}}{{{\text{|}}}_{{r = {{c}_{{12}}}}}} = {{\delta }_{{q + 1,m}}}\delta (\tau ), \\ {{G}_{{1m}}}{{{\text{|}}}_{{\tau = 0}}} = {{{\dot {G}}}_{{1m}}}{{{\text{|}}}_{{\tau = 0}}} = {{G}_{{q + 1,m}}}{{{\text{|}}}_{{\tau = 0}}} = 0. \\ \end{gathered} $$

(6)

Here, δ_ij is the Kronecker symbol and δ(τ) is the Dirac delta function.

To find Green’s functions, we apply the Laplace transform to (5) and (6). Then we multiply the first Eq. (5) by rJ₁(λ_nr/c₁₂) and the second by rJ₀(λ_nr/c₁₂) and integrate over r in the interval [0, c₁₂]. We get (the superscript L denotes the Laplace transform; s is the parameter of the Laplace transform)

$$\begin{gathered} \int\limits_0^{{{c}_{{12}}}} {\left( {G_{{1m}}^{{L''}} + \frac{{G_{{1m}}^{{L'}}}}{r} - \frac{{G_{{1m}}^{L}}}{{{{r}^{2}}}}} \right)} {{J}_{1}}\left( {\frac{{r{{\lambda }_{n}}}}{{{{c}_{{12}}}}}} \right)rdr - \sum\limits_{j = 1}^N {\alpha _{1}^{{(j)}}\int\limits_0^{{{c}_{{12}}}} {G_{{j + 1,m}}^{{L'}}{{J}_{1}}\left( {\frac{{r{{\lambda }_{{12}}}}}{{{{c}_{{12}}}}}} \right)rdr} } \\ = {{s}^{2}}\int\limits_0^{{{c}_{{12}}}} {G_{{1m}}^{L}{{J}_{1}}\left( {\frac{{r{{\lambda }_{n}}}}{{{{c}_{{12}}}}}} \right)rdr,} \\ \end{gathered} $$

(7)

$$\begin{gathered} - \Lambda _{{11}}^{{(q)}}\int\limits_0^{{{c}_{{12}}}} {\left( {G_{{1m}}^{{L'''}} + \frac{{2G_{{1m}}^{{L''}}}}{r} - \frac{{G_{{1m}}^{{L'}}}}{{{{r}^{2}}}} + \frac{{G_{{1m}}^{L}}}{{{{r}^{3}}}}} \right){{J}_{0}}\left( {\frac{{r{{\lambda }_{n}}}}{{{{c}_{{12}}}}}} \right)rdr} \\ + \,D_{1}^{{(q)}}\int\limits_0^{{{c}_{{12}}}} {\left( {G_{{q + 1,m}}^{{L''}} + \frac{{G_{{q + 1,m}}^{{L'}}}}{r}} \right){{J}_{0}}\left( {\frac{{r{{\lambda }_{n}}}}{{{{c}_{{12}}}}}} \right)rdr = (s + {{\tau }_{q}}{{s}^{2}})\int\limits_0^{{{c}_{{12}}}} {G_{{q + 1,m}}^{L}{{J}_{0}}\left( {\frac{{r{{\lambda }_{n}}}}{{{{c}_{{12}}}}}} \right)rdr,} } \\ {{\left. {\left( {G_{{1m}}^{{L'}} + \frac{{{{c}_{{12}}}}}{r}G_{{1m}}^{L} - \sum\limits_{j = 1}^N {\alpha _{1}^{{(j)}}G_{{j + 1,m}}^{L}} } \right)} \right|}_{{r = {{c}_{{12}}}}}} = {{\delta }_{{1m}}},\quad G_{{q + 1,m}}^{L}{{{\text{|}}}_{{r = {{c}_{{12}}}}}} = {{\delta }_{{q + 1,m}}}. \\ \end{gathered} $$

(8)

Here, J_ν(z) are the Bessel functions of the first kind of order ν and λ_n are the roots of the equation J₀(λ_n) = 0. It was shown in [31] that λ_n also satisfy the equation J₁(λ_n) + λ_n$J_{1}^{'}$(λ_n) = 0.

To calculate the integrals in (7), we use the formulas obtained in [30, 31]:

$$\int\limits_0^{{{c}_{{12}}}} {G_{{q + 1,m}}^{{L'}}{{J}_{1}}\left( {\frac{{r{{\lambda }_{n}}}}{{{{c}_{{12}}}}}} \right)rdr = - {{c}_{{12}}}{{\lambda }_{n}}\frac{{J_{1}^{2}({{\lambda }_{n}})}}{2}} G_{{q + 1,m}}^{{L{{H}_{0}}}}({{\lambda }_{n}},s) + {{c}_{{12}}}G_{{km}}^{L}({{c}_{{12}}},s){{J}_{1}}({{\lambda }_{n}}),$$

$$\int\limits_0^{{{c}_{{12}}}} {\left( {G_{{q + 1,m}}^{{L''}} + \frac{{G_{{q + 1,m}}^{{L'}}}}{r}} \right){{J}_{0}}\left( {\frac{{r{{\lambda }_{n}}}}{{{{c}_{{12}}}}}} \right)rdr = - \lambda _{n}^{2}\frac{{J_{1}^{2}({{\lambda }_{n}})}}{2}G_{{q + 1,m}}^{{L{{H}_{0}}}}({{\lambda }_{n}},s) + {{\lambda }_{n}}G_{{q + 1,m}}^{L}({{c}_{{12}}},s){{J}_{1}}({{\lambda }_{n}}),} $$

$$\begin{gathered} \int\limits_0^{{{c}_{{12}}}} {\left( {G_{{1m}}^{{L''}} + \frac{{G_{{1m}}^{{L'}}}}{r} - \frac{{G_{{1m}}^{L}}}{{{{r}^{2}}}}} \right){{J}_{1}}\left( {\frac{{r{{\lambda }_{n}}}}{{{{c}_{{12}}}}}} \right)rdr = - \frac{{\lambda _{n}^{2}}}{2}J_{1}^{2}({{\lambda }_{n}})G_{{1m}}^{{L{{H}_{1}}}}({{\lambda }_{n}},s)} \\ + \,{{J}_{1}}({{\lambda }_{n}})[{{c}_{{12}}}G_{{1m}}^{{L'}}({{c}_{{12}}},s) + G_{{1m}}^{L}({{c}_{{12}}},s)], \\ \end{gathered} $$

$$\begin{gathered} \int\limits_0^{{{c}_{{12}}}} {\left( {G_{{1m}}^{{L'''}} + \frac{{2G_{{1m}}^{{L''}}}}{r} - \frac{{G_{{1m}}^{{L'}}}}{{{{r}^{2}}}} + \frac{{G_{{1m}}^{L}}}{{{{r}^{3}}}}} \right){{J}_{0}}\left( {\frac{{r{{\lambda }_{n}}}}{{{{c}_{{12}}}}}} \right)rdr = - \frac{{\lambda _{n}^{3}}}{{2{{c}_{{12}}}}}J_{1}^{2}({{\lambda }_{n}})G_{{1m}}^{{L{{H}_{1}}}}({{\lambda }_{n}},s)} \\ + \,\frac{{{{\lambda }_{n}}}}{{{{c}_{{12}}}}}{{J}_{1}}({{\lambda }_{n}})[{{c}_{{12}}}G_{{1m}}^{{L'}}({{c}_{{12}}},s) + G_{{1m}}^{L}({{c}_{{12}}},s)], \\ \end{gathered} $$

where

$$G_{{1m}}^{L}(r,s) = \sum\limits_{n = 1}^\infty {G_{{1m}}^{{L{{H}_{1}}}}({{\lambda }_{n}},s){{J}_{1}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right),\quad G_{{q + 1,m}}^{L}(r,s) = \sum\limits_{n = 1}^\infty {G_{{q + 1,m}}^{{L{{H}_{0}}}}({{\lambda }_{n}},s){{J}_{0}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right),} } $$

(9)

$$G_{{1m}}^{{L{{H}_{1}}}}({{\lambda }_{n}},s) = \frac{2}{{c_{{12}}^{2}J_{1}^{2}({{\lambda }_{n}})}}\int\limits_0^{{{c}_{{12}}}} {rG_{{1m}}^{L}(r,s){{J}_{1}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right)dr,} $$

$$G_{{q + 1,m}}^{{L{{H}_{0}}}}({{\lambda }_{n}},s) = \frac{2}{{c_{{12}}^{2}J_{1}^{2}({{\lambda }_{n}})}}\int\limits_0^{{{c}_{{12}}}} {rG_{{q + 1,m}}^{L}(r,s){{J}_{0}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right)dr.} $$

As can be seen, the formulas for transforming differential operators in Eq. (7) can only be applied under the condition that the parameter c₁₂ in boundary conditions (8) is equal to one. Therefore, we will consider the problem in a simplified formulation, setting c₁₂ = 1 everywhere below.

Taking into account equalities (9), problem (7), (8) is transformed to the following system of linear algebraic equations:

$${{k}_{1}}({{\lambda }_{n}},s)G_{{1m}}^{{L{{H}_{1}}}}({{\lambda }_{n}},s) - {{c}_{{12}}}{{\lambda }_{n}}\sum\limits_{j = 1}^N {\alpha _{1}^{{(j)}}G_{{j + 1,m}}^{{L{{H}_{0}}}}} ({{\lambda }_{n}},s) = {{F}_{1}}({{\lambda }_{n}}),$$

$$\Lambda _{{11}}^{{(q)}}\lambda _{n}^{3}G_{{1m}}^{{L{{H}_{1}}}}({{\lambda }_{n}},s) - {{c}_{{12}}}{{k}_{{q + 1}}}({{\lambda }_{n}},s)G_{{q + 1,m}}^{{L{{H}_{0}}}}({{\lambda }_{n}},s) = {{F}_{{q + 1}}}({{\lambda }_{n}}),$$

$${{k}_{1}}({{\lambda }_{n}},s) = \lambda _{n}^{2} + {{s}^{2}},\quad {{k}_{{q + 1}}}({{\lambda }_{n}},s) = D_{1}^{{(q)}}\lambda _{n}^{2} + s + {{\tau }_{q}}{{s}^{2}},$$

$${{F}_{1}}({{\lambda }_{n}}) = \frac{2}{{{{J}_{1}}({{\lambda }_{n}})}}{{\delta }_{{1m}}},\quad {{F}_{{q + 1}}}({{\lambda }_{n}}) = \frac{{2{{\lambda }_{n}}\Lambda _{{11}}^{{(q)}}}}{{{{J}_{1}}({{\lambda }_{n}})}}\left( {{{\delta }_{{1m}}} + \sum\limits_{j = 1}^N {\alpha _{1}^{{(j)}}{{\delta }_{{j + 1,m}}} - {{c}_{{12}}}\frac{{D_{1}^{{(q)}}}}{{\Lambda _{{11}}^{{(q)}}}}{{\delta }_{{q + 1,m}}}} } \right).$$

Its solution has the form [14]

$$\begin{gathered} G_{{1k}}^{{L{{H}_{1}}}}({{\lambda }_{n}},s) = \frac{{2{{P}_{{1k}}}({{\lambda }_{n}},s)}}{{{{J}_{1}}({{\lambda }_{n}})P({{\lambda }_{n}},s)}},\quad G_{{q + 1,1}}^{{L{{H}_{0}}}}({{\lambda }_{n}},s) = \frac{2}{{{{J}_{1}}({{\lambda }_{n}})}}\left[ {\frac{{{{\lambda }_{n}}\Lambda _{{11}}^{{(q)}}}}{{{{c}_{{12}}}{{k}_{{q + 1}}}({{\lambda }_{n}},s)}} + \frac{{{{P}_{{q + 1,1}}}({{\lambda }_{n}},s)}}{{{{Q}_{q}}({{\lambda }_{n}},s)}}} \right], \\ G_{{q + 1,p + 1}}^{{L{{H}_{0}}}}({{\lambda }_{n}},s) = - \frac{2}{{{{J}_{1}}({{\lambda }_{n}})}}\left[ {\frac{{{{\lambda }_{n}}(\Lambda _{{11}}^{{(q)}}\alpha _{1}^{{(p)}} - {{c}_{{12}}}D_{1}^{{(q)}}{{\delta }_{{pq}}})}}{{{{c}_{{12}}}{{k}_{{q + 1}}}({{\lambda }_{n}},s)}} + \frac{{{{P}_{{q + 1,p + 1}}}({{\lambda }_{n}},s)}}{{{{Q}_{q}}({{\lambda }_{n}},s)}}} \right]. \\ \end{gathered} $$

(10)

Formulas (10) use the following notation:

$$\begin{gathered} P({{\lambda }_{n}},s) = {{k}_{1}}({{\lambda }_{n}},s)\Pi ({{\lambda }_{n}},s) - \lambda _{n}^{4}\sum\limits_{j = 1}^N {\alpha _{1}^{{(j)}}\Lambda _{{11}}^{{(j)}}{{\Pi }_{j}}({{\lambda }_{n}},s),\quad \Pi ({{\lambda }_{n}},s) = \prod\limits_{j = 1}^N {{{k}_{{j + 1}}}({{\lambda }_{n}},s),} } \\ {{Q}_{q}}({{\lambda }_{n}},s) = {{c}_{{12}}}{{k}_{{q + 1}}}({{\lambda }_{n}},s)P({{\lambda }_{n}},s),\quad {{\Pi }_{j}}({{\lambda }_{n}},s) = \prod\limits_{k = 1,k \ne j}^N {{{k}_{{k + 1}}}({{\lambda }_{n}},s),} \\ \end{gathered} $$

(11)

$${{P}_{{11}}}({{\lambda }_{n}},s) = \Pi ({{\lambda }_{n}},s) - \lambda _{n}^{2}\sum\limits_{j = 1}^N {\alpha _{1}^{{(j)}}\Lambda _{{11}}^{{(j)}}{{\Pi }_{j}}({{\lambda }_{n}},s),} $$

$${{P}_{{1,q + 1}}}({{\lambda }_{n}},s) = \lambda _{n}^{2}\alpha _{1}^{{(q)}}\left[ {{{c}_{{12}}}D_{1}^{{(q)}}{{\Pi }_{q}}({{\lambda }_{n}},s) - \sum\limits_{j = 1}^N {\alpha _{1}^{{(j)}}\Lambda _{{11}}^{{(j)}}{{\Pi }_{j}}({{\lambda }_{n}},s)} } \right],$$

$${{P}_{{q + 1,k}}}({{\lambda }_{n}},s) = - \Lambda _{{11}}^{{(q)}}\lambda _{n}^{3}{{P}_{{1k}}}({{\lambda }_{n}},s)$$

Since all functions in (10) and (11) are rational functions of the parameter s, the originals of the influence functions are found analytically using the theory of residues and tables of operational calculus [30, 32]:

$$G_{{1k}}^{{{{H}_{1}}}}({{\lambda }_{n}},\tau ) = \frac{2}{{{{J}_{1}}({{\lambda }_{n}})}}\sum\limits_{l = 1}^{2N + 2} {A_{{1k}}^{{(l)}}{{e}^{{{{s}_{l}}\tau }}}} ,\quad A_{{1k}}^{{(l)}} = \frac{{{{P}_{{1k}}}({{\lambda }_{n}},{{s}_{l}})}}{{P'({{\lambda }_{n}},{{s}_{l}})}},\quad A_{{q + 1,k}}^{{(l)}} = \frac{{{{P}_{{q + 1,k}}}({{\lambda }_{n}},{{s}_{l}})}}{{Q'({{\lambda }_{n}},{{s}_{l}})}},$$

$$G_{{q + 1,1}}^{{{{H}_{0}}}}({{\lambda }_{n}},\tau ) = - \frac{2}{{{{J}_{1}}({{\lambda }_{n}})}}\left[ {\sum\limits_{l = 1}^{2N + 4} {A_{{q + 1,1}}^{{(l)}}{{e}^{{{{s}_{l}}\tau }}} + \frac{{{{\lambda }_{n}}\Lambda _{{11}}^{{(q)}}}}{{{{c}_{{12}}}}}\sum\limits_{j = 1}^2 {\frac{{{{e}^{{{{\xi }_{j}}\tau }}}}}{{k_{{q + 1}}^{'}({{\lambda }_{n}},{{\xi }_{j}})}}} } } \right],$$

(12)

$$G_{{q + 1,p + 1}}^{{{{H}_{0}}}}({{\lambda }_{n}},\tau ) = - \frac{2}{{{{J}_{1}}({{\lambda }_{n}})}}\left[ {\sum\limits_{l = 1}^{2N + 4} {A_{{q + 1,p + 1}}^{{(l)}}{{e}^{{{{s}_{l}}\tau }}}} + \frac{{{{\lambda }_{n}}(\Lambda _{{11}}^{{(q)}}\alpha _{1}^{{(p)}} - {{c}_{{12}}}D_{1}^{{(q)}}{{\delta }_{{pq}}})}}{{{{c}_{{12}}}}}\sum\limits_{j = 1}^2 {\frac{{{{e}^{{{{\xi }_{j}}\tau }}}}}{{k_{{q + 1}}^{'}({{\lambda }_{n}},{{\xi }_{j}})}}} } \right],$$

where s_l(λ_n) are the zeros of the polynomial P(λ_n, s) and ξ_j(λ_n) are the additional zeros of the polynomial Q_q(λ_n, s) determined by the formulas

$${{\xi }_{{1,2}}}({{\lambda }_{n}}) = \frac{{ - 1 \mp \sqrt {1 - 4{{\tau }_{q}}D_{1}^{{(q)}}\lambda _{n}^{2}} }}{{2{{\tau }_{q}}}}.$$

3 LIMIT CASES

If we set τ_q = 0, then we obtain the classical model of elastic diffusion with an infinite propagation velocity of diffusion flows. For τ_q → 0, the degree of the polynomial P(λ_n, s) changes from 2N + 2 to N + 2, and the following passages to the limit take place for additional zeros:

$${{\xi }_{1}}({{\lambda }_{n}}) \to D_{1}^{{(q)}}\lambda _{n}^{2},\quad {{\xi }_{2}}({{\lambda }_{n}}) \to - \infty \quad ({{\tau }_{q}} \to 0).$$

Then ${{e}^{{{{\xi }_{1}}\tau }}}$ → ${{e}^{{ - D_{1}^{{(q)}}\lambda _{n}^{2}\tau }}}$, ${{e}^{{{{\xi }_{2}}\tau }}}$ → 0 (τ_q → 0). As a result, we arrive at the solution obtained in [30].

Assuming further $\alpha _{1}^{{(p)}}$ = 0, we pass to the classical models of elasticity and mass transfer for a solid cylinder. We will denote the Green’s functions corresponding to them ${{\tilde {G}}_{{11}}}$(r, τ), ${{\tilde {G}}_{{q + 1,p + 1}}}$(r, τ) and represent them as series similar to (9):

$${{\tilde {G}}_{{11}}}(r,\tau ) = \sum\limits_{n = 1}^\infty {\tilde {G}_{{11}}^{{{{H}_{1}}}}({{\lambda }_{n}},\tau ){{J}_{1}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right)} ,\quad {{\tilde {G}}_{{q + 1,p + 1}}}(r,\tau ) = \sum\limits_{n = 1}^\infty {\tilde {G}_{{q + 1,p + 1}}^{{{{H}_{0}}}}({{\lambda }_{n}},\tau ){{J}_{0}}} \left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right).$$

(13)

The coefficients of these series are found from equalities (11) and (12) by passing to the limit for $\alpha _{1}^{{(q)}}$ → 0. We have (here we take into account that $\Lambda _{{11}}^{{(q)}}$ → 0 for $\alpha _{1}^{{(q)}}$ → 0)

$$\mathop {\lim }\limits_{\alpha _{1}^{{(j)}} \to 0} {{P}_{{11}}}({{\lambda }_{n}},s) = \Pi ({{\lambda }_{n}},s),\quad \mathop {\lim }\limits_{\alpha _{1}^{{(j)}} \to 0} {{P}_{{1,q + 1}}}({{\lambda }_{n}},s) = 0,\quad \mathop {\lim }\limits_{\alpha _{1}^{{(j)}} \to 0} {{P}_{{q + 1,k}}}({{\lambda }_{n}},s) = 0,$$

$$\mathop {\lim }\limits_{\alpha _{1}^{{(j)}} \to 0} P({{\lambda }_{n}},s) = {{k}_{1}}({{\lambda }_{n}},s)\Pi ({{\lambda }_{n}},s),\quad \mathop {\lim }\limits_{\alpha _{1}^{{(j)}} \to 0} {{Q}_{q}}({{\lambda }_{n}},s) = {{c}_{{12}}}{{k}_{{q + 1}}}({{\lambda }_{n}},s){{k}_{1}}({{\lambda }_{n}},s)\Pi ({{\lambda }_{n}},s).$$

Then, in the space of the Laplace transform, the Green’s functions for uncoupled problems of elasticity and diffusion will be written as follows:

$$\tilde {G}_{{11}}^{{L{{H}_{1}}}}({{\lambda }_{n}},s) = \frac{2}{{{{J}_{1}}({{\lambda }_{n}}){{k}_{1}}({{\lambda }_{n}},s)}},\quad \tilde {G}_{{q + 1,p + 1}}^{{L{{H}_{0}}}}({{\lambda }_{n}},s) = \frac{{2{{\lambda }_{n}}{{c}_{{12}}}D_{1}^{{(q)}}{{\delta }_{{pq}}}}}{{{{c}_{{12}}}{{J}_{1}}({{\lambda }_{n}}){{k}_{{q + 1}}}({{\lambda }_{n}},s)}}.$$

(14)

Here, the transition to the original space is carried out in the same way as in the previous cases with the help of residues

$$\tilde {G}_{{11}}^{{{{H}_{1}}}}({{\lambda }_{n}},\tau ) = \frac{{2\sin {{\lambda }_{n}}\tau }}{{{{J}_{1}}({{\lambda }_{n}}){{\lambda }_{n}}}},\quad \tilde {G}_{{q + 1,p + 1}}^{{{{H}_{0}}}}({{\lambda }_{n}},\tau ) = \frac{{2{{\lambda }_{n}}D_{1}^{{(q)}}{{\delta }_{{pq}}}}}{{{{J}_{1}}({{\lambda }_{n}})}}\sum\limits_{j = 1}^2 {\frac{{{{e}^{{{{\xi }_{j}}\tau }}}}}{{k_{{q + 1}}^{'}({{\lambda }_{n}},{{\xi }_{j}})}}.} $$

Finally, assuming in the boundary conditions (2)

$${{f}_{k}}(\tau ) = {{\tilde {f}}_{k}}H(\tau ),$$

and passing to the limit at τ → ∞, we obtain the solution of the static elastic diffusion problem for a solid cylinder under the action of radially applied loads.

Green’s functions of the corresponding static problem $G_{{mk}}^{{{\text{st}}}}$(x) are expressed in terms of the Green’s functions G_mk(r, τ) of the dynamic problem using the equality [32]

$$G_{{mk}}^{{{\text{st}}}}(r) = \mathop {\lim }\limits_{\tau \to \infty } [{{G}_{{mk}}}(r,\tau )*H(\tau )] = \mathop {\lim }\limits_{s \to 0} \left[ {sG_{{mk}}^{L}(r,s)\frac{1}{s}} \right] = \mathop {\lim }\limits_{s \to 0} G_{{mk}}^{L}(r,s).$$

(15)

Transforming convolutions (4) with the help of the indicated passage to the limit, we obtain the solution of the static problem

$${{u}^{{{\text{(st)}}}}}(r) = \sum\limits_{m = 1}^{N + 1} {G_{{1m}}^{{{\text{(st)}}}}(r){{{\tilde {f}}}_{m}},\quad {{\eta }_{q}}(r) = \sum\limits_{m = 1}^{N + 1} {G_{{q + 1,m}}^{{{\text{(st)}}}}(r){{{\tilde {f}}}_{m}},} } $$

where Green’s functions $G_{{mk}}^{{{\text{st}}}}$(r) in accordance with Eqs. (10) and (11) have the form

$$\begin{gathered} G_{{11}}^{{{\text{(st)}}}}(r) = \sum\limits_{n = 1}^\infty {G_{{11}}^{{L{{H}_{1}}}}({{\lambda }_{n}},0){{J}_{1}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right) = 2\sum\limits_{n = 1}^\infty {\frac{1}{{{{J}_{1}}({{\lambda }_{n}})\lambda _{n}^{2}}}{{J}_{1}}} } \left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right), \\ G_{{q + 1,1}}^{{{\text{(st)}}}}(r) = \sum\limits_{n = 1}^\infty {G_{{q + 1,1}}^{{L{{H}_{0}}}}({{\lambda }_{n}},0){{J}_{0}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right)} = 0, \\ \end{gathered} $$

(16)

$$G_{{1,q + 1}}^{{{\text{(st)}}}}(r) = \sum\limits_{n = 1}^\infty {G_{{1,q + 1}}^{{L{{H}_{1}}}}({{\lambda }_{n}},0){{J}_{1}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right)} = 2\alpha _{1}^{{(q)}}[1 + ({{c}_{{12}}} - 1)\Phi ]\sum\limits_{n = 1}^\infty {\frac{1}{{{{J}_{1}}({{\lambda }_{n}})\lambda _{n}^{2}}}} {{J}_{1}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right),$$

$$G_{{q + 1,p + 1}}^{{{\text{(st)}}}}(r) = \sum\limits_{n = 1}^\infty {G_{{q + 1,p + 1}}^{{L{{H}_{0}}}}({{\lambda }_{n}},0){{J}_{0}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right)} = \left[ {{{\delta }_{{pq}}} + \frac{{\Lambda _{{11}}^{{(q)}}\alpha _{1}^{{(p)}}}}{{{{c}_{{12}}}}}({{c}_{{12}}} - 1){{\Phi }_{q}}} \right]\sum\limits_{n = 1}^\infty {\frac{1}{{{{J}_{1}}({{\lambda }_{n}}){{\lambda }_{n}}}}} {{J}_{0}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right),$$

$$\Phi = \frac{{\prod\limits_{j = 1}^N {D_{1}^{{(j)}}} }}{{\prod\limits_{j = 1}^N {D_{1}^{{(j)}}} - \sum\limits_{j = 1}^N {\alpha _{1}^{{(j)}}\Lambda _{{11}}^{{(j)}}\prod\limits_{r = 1,r \ne j}^N {D_{1}^{{(r)}}} } }},\quad {{\Phi }_{q}} = \frac{{\prod\limits_{j = 1,j \ne q}^N {D_{1}^{{(j)}}} }}{{\prod\limits_{j = 1}^N {D_{1}^{{(j)}}} - \sum\limits_{j = 1}^N {\alpha _{1}^{{(j)}}\Lambda _{{11}}^{{(j)}}\prod\limits_{r = 1,r \ne j}^N {D_{1}^{{(r)}}} } }}.$$

Based on the passages to the limit considered above, the following conclusions can be drawn:

(1) Since $G_{{q + 1,1}}^{{{\text{(st)}}}}$(r) = 0 (based on formulas (16)), we find that the static radial loads on the cylinder surface within the linear model (1), (2) do not affect to the diffusion field inside the cylinder. This agrees with experimental studies, according to which the diffusion rate in the first approximation is proportional to the strain rate [33]. Since the strain rate is zero in statics, we also obtain a zero diffusion rate.

(2) For unrelated problems, the static analogues of the Green’s functions ${{\tilde {G}}_{{km}}}$(r, τ) in (13) based on the passage to the limit (15) will be determined as follows:

$$\tilde {G}_{{11}}^{{{\text{(st)}}}}(r) = \sum\limits_{n = 1}^\infty {\tilde {G}_{{11}}^{{L{{H}_{1}}}}({{\lambda }_{n}},0){{J}_{1}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right),\quad \tilde {G}_{{q + 1,p + 1}}^{{{\text{(st)}}}}(r) = \sum\limits_{n = 1}^\infty {\tilde {G}_{{q + 1,p + 1}}^{{L{{H}_{0}}}}({{\lambda }_{n}},0)} } {{J}_{0}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right).$$

Using formulas (14), we obtain

$$\tilde {G}_{{11}}^{{L{{H}_{1}}}}({{\lambda }_{n}},0) = \frac{2}{{\lambda _{n}^{2}{{J}_{1}}({{\lambda }_{n}})}} = G_{{11}}^{{L{{H}_{1}}}}({{\lambda }_{n}},0).$$

Therefore, taking into account Eq. (16), we have

$$\tilde {G}_{{11}}^{{{\text{(st)}}}}(r) = 2\sum\limits_{n = 1}^\infty {\frac{1}{{{{J}_{1}}({{\lambda }_{n}})\lambda _{n}^{2}}}{{J}_{1}}\left( {\frac{{{{\lambda }_{n}}r}}{{{{c}_{{12}}}}}} \right) = G_{{11}}^{{{\text{(st)}}}}(r),} $$

(17)

i.e., in statics, the solutions of the problem of elastic diffusion and the problem of elasticity coincide. This means that diffusion processes under static radial loads do not affect the displacement field inside the cylinder.

4 CALCULATION EXAMPLE

As an example, we consider a three-component cylinder (N = 2, independent components zinc $n_{0}^{{(1)}}$ = 0.01, and copper $n_{0}^{{(2)}}$ = 0.045, which diffuse in aluminum). The physical characteristics of this material [34], after applying the procedure of transition to dimensionless quantities (3), are as follows:

$${{C}_{{12}}} = 4.92 \times {{10}^{{ - 1}}},\quad {{C}_{{66}}} = 2.54 \times {{10}^{{ - 1}}},\quad {{\alpha }_{1}} = 6.32 \times {{10}^{{ - 4}}},\quad {{\alpha }_{2}} = 5.92 \times {{10}^{{ - 4}}},$$

$${{D}_{1}} = 4.17 \times {{10}^{{ - 13}}},\quad {{D}_{2}} = 4.60 \times {{10}^{{ - 16}}},\quad {{\Lambda }_{1}} = 1.13 \times {{10}^{{ - 15}}},\quad {{\Lambda }_{2}} = 5.18 \times {{10}^{{ - 18}}}.$$

We assume for the calculation in the boundary conditions (2)

$${{f}_{1}}(\tau ) = H(\tau ),\quad {{f}_{{q + 1}}}(\tau ) = 0.$$

Then, calculating convolutions in time (4), we have

$$\begin{gathered} u(r,\tau ) = 2\sum\limits_{n = 1}^\infty {\sum\limits_{l = 1}^{2N + 2} {A_{{1k}}^{{(l)}}\frac{{({{e}^{{{{s}_{l}}\tau }}} - 1){{J}_{1}}({{\lambda }_{n}}r{\text{/}}{{c}_{{12}}})}}{{{{s}_{l}}{{J}_{1}}({{\lambda }_{n}})}}} ,} \\ {{\eta }_{q}}(r,\tau ) = - 2\sum\limits_{n = 1}^\infty {\left[ {\sum\limits_{l = 1}^{2N + 4} {A_{{q + 1,1}}^{{(l)}}\frac{{{{e}^{{{{s}_{l}}\tau }}} - 1}}{{{{s}_{l}}}} + \frac{{{{\lambda }_{n}}\Lambda _{{11}}^{{(q)}}}}{{{{c}_{{12}}}}}\sum\limits_{j = 1}^2 {\frac{{{{e}^{{{{\xi }_{j}}\tau }}} - 1}}{{{{\xi }_{j}}k_{{q + 1}}^{'}({{\lambda }_{n}},{{\xi }_{j}})}}} } } \right]} \frac{{{{J}_{0}}({{\lambda }_{n}}r{\text{/}}{{c}_{{12}}})}}{{{{J}_{1}}({{\lambda }_{n}})}}. \\ \end{gathered} $$

(18)

N_λ = 100 partition points were used to calculate the series (18). A further increase in the number of points does not lead to a visible change in the results.

Figure 1 shows the spacetime distribution of the displacement field inside the cylinder. Next, we compare the solution obtained in the work with the solution of the classical problem of elasticity theory for a solid cylinder (Figs. 2 and 3). It is shown that, starting from a certain moment of time (in this case τ ~ 10⁹), elastic-diffusion oscillations begin to lag behind elastic ones. A similar effect was established in the simulation of elastic-diffusion vibrations of Bernoulli–Euler and Timoshenko beams in [35, 36].

Fig. 1.

Displacement field u(r, τ).

Fig. 2.

Displacements u(0, τ). The solid line is the solution of the elastic-diffusion problem and the dotted line is the solution of the elastic problem.

Fig. 3.

Displacements u(0, τ). The solid line is the solution of the elastic-diffusion problem and the dotted line is the solution of the elastic problem.

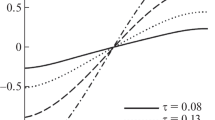
Figures 4 and 5 demonstrate the influence of relaxation effects on diffusion fields. It is shown that relaxation effects appear on a certain finite time interval and then disappear.

Fig. 4.

Increment of zinc concentration η₁(0, τ). The solid line corresponds to the relaxation time τ⁽¹⁾ = 200 s, the dotted line corresponds to τ⁽¹⁾ = 100 s, and the dashed line corresponds to τ⁽¹⁾ = 0.

Fig. 5.

Copper concentration increment η₂(0, τ). The solid line corresponds to the relaxation time τ⁽²⁾ = 200 s, the dotted line corresponds to τ⁽²⁾ = 100 s, and the dashed line corresponds to τ⁽²⁾ = 0.

Figure 6 shows the solutions of static problems obtained by formulas (16) and (17) (for calculation, we set ${{\tilde {f}}_{1}}$ = 1, ${{\tilde {f}}_{{q + 1}}}$ = 0). The solid line corresponds to the solution of the elastic-diffusion problem and the dotted line corresponds to the solution of the elastic one. The coincidence of the solutions of these problems illustrates equality (17).

Fig. 6.

Displacement field u(r) for a static problem. The solid line is the solution of the elastic-diffusion problem and the dotted line is the solution of the elastic one.

CONCLUSIONS

In this paper, we present an algorithm for solving a one-dimensional polar-symmetric nonstationary problem of elastic diffusion for an orthotropic solid multicomponent cylinder, taking into account the relaxation of diffusion processes. Influence functions are found that make it possible to determine the displacement fields and increments in the concentrations of the medium components from given surface perturbations. To demonstrate the operation of the algorithm, an example is considered that illustrates the effect of the coupling of mechanical and diffusion fields, as well as the influence of relaxation processes on diffusion fields in a three-component solid cylinder.

Limiting transitions to uncoupled problems of elasticity and diffusion, as well as to static elastic-diffusion problems, are studied. It is shown that, within the framework of linear models, the interaction of mechanical and diffusion fields does not manifest itself under static radial loads.

The calculation results are presented in the form of plots of the required fields versus time at various points of the cylinder.