Torsion is one of the types of deformation of solids, characterized by mutual rotations of its cross sections under the influence of the moments acting in these sections. Torsion of rods is quite common in engineering practice, especially in mechanical engineering. The torsion theory of isotropic and anisotropic rods made of an ideal rigid-plastic material is described in [1–4]. The transition to the case of a rod made of an inhomogeneous material leads to certain difficulties: the problem in the general case cannot be integrated. The torsion of composite prismatic and cylindrical rods is considered in [5, 7]. In [6], general relations of the torsion theory of rods made of an ideal rigid-plastic material were investigated.

The relations between the torsion theory of inhomogeneous cylindrical and prismatic rods made of ideally plastic material [6] can be written in the form:

$$\begin{array}{*{20}{c}} {{{{\sigma }}_{x}} = {{{\sigma }}_{y}} = {{{\sigma }}_{z}} = {{{\tau }}_{{xy}}} = 0,} \\ {{{{\tau }}_{{xz}}} = {{{\tau }}_{{xz}}}(x,~y),\quad {{{\tau }}_{{yz}}} = {{{\tau }}_{{yz}}}(x,~y);} \end{array}$$
(1)

—equilibrium equation

$$\frac{{\partial {{{\tau }}_{{xz}}}}}{{\partial x}} + \frac{{\partial {{{\tau }}_{{yz}}}}}{{\partial y}} = 0;$$
(2)

—field criterion

$$f\left( {{{{\tau }}_{{xz}}},{{{\tau }}_{{yz}}},x,y} \right) = 0;$$
(3)

—the ratio of the associated plastic flow rule

$$\frac{{{{{\varepsilon }}_{{xz}}}}}{A} = \frac{{{{{\varepsilon }}_{{yz}}}}}{B},\quad {{{\varepsilon }}_{x}} = {{{\varepsilon }}_{y}} = {{{\varepsilon }}_{z}} = {{{\varepsilon }}_{{xy}}} = 0,$$
(4)

where σij are stress components, εij are strain rate components,

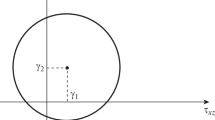
$$A = \frac{{\partial f}}{{\partial {{{\tau }}_{{xz}}}}}({{{\tau }}_{{xz}}},{{{\tau }}_{{yz}}},x,y),\quad ~B = \frac{{\partial f}}{{\partial {{{\tau }}_{{yz}}}}}({{{\tau }}_{{xz}}},{{{\tau }}_{{yz}}},x,y).$$
(5)

Yield criterion (3) in the plane τxz, τyz for fixed x, y represents a closed convex curve (Fig. 1), the origin is in the region bounded by this curve.

figure 1

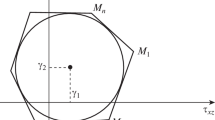
Fig. 1.

Let us assume that the yield curve (3) is replaced by a closed polygonal line \({{M}_{1}}{{M}_{2}}{{M}_{3}} \ldots {{M}_{n}}{{M}_{1}}\) (Fig. 1)

$${{A}_{i}}{{{\tau }}_{{xz}}} + {{B}_{i}}{{{\tau }}_{{yz}}} = {{K}_{i}},$$
(6)

where \(~{{A}_{i}} = \frac{{\partial f}}{{\partial {{{\tau }}_{{xz}}}}}({\tau }_{{xz}}^{{i0}},{\tau }_{{yz}}^{{i0}},{{x}_{0}},{{y}_{0}}),{{B}_{i}} = \frac{{\partial f}}{{\partial {{{\tau }}_{{yz}}}}}({\tau }_{{xz}}^{{i0}},{\tau }_{{yz}}^{{i0}},{{x}_{0}},{{y}_{0}}),f({\tau }_{{xz}}^{{i0}},{\tau }_{{yz}}^{{i0}},{{x}_{0}},{{y}_{0}}) = 0,\)

$${{K}_{i}} = {{A}_{i}}{\tau }_{{xz}}^{i} + {{B}_{i}}{\tau }_{{yz}}^{i},\quad {{A}_{i}} = {\mu }\frac{{\partial f}}{{\partial {{{\tau }}_{{xz}}}}}({\tau }_{{xz}}^{i},{\tau }_{{yz}}^{i},x,y),\quad {{B}_{i}} = {\mu }\frac{{\partial f}}{{\partial {{{\tau }}_{{yz}}}}}({\tau }_{{xz}}^{i},{\tau }_{{yz}}^{i},x,y),$$
$$f({\tau }_{{xz}}^{i},{\tau }_{{yz}}^{i},x,y) = 0,\quad {\mu }\,\,{\text{ = }}\,{\text{const}},\quad i = 1,2, \ldots ,n{\text{.}}$$

Criterion (6) represents on a certain segment the linearized yield criterion (3). Differentiating equation (6) with respect to the variable y, we obtain

$${{A}_{i}}\frac{{\partial {{{\tau }}_{{xz}}}}}{{\partial y}} + {{B}_{i}}\frac{{\partial {{{\tau }}_{{yz}}}}}{{\partial y}} = \frac{{\partial {{K}_{i}}}}{{\partial y}}.$$
(7)

Taking into account (2), from equation (7), we have

$${{A}_{i}}\frac{{\partial {{{\tau }}_{{xz}}}}}{{\partial y}} - {{B}_{i}}\frac{{\partial {{{\tau }}_{{xz}}}}}{{\partial x}} = \frac{{\partial {{K}_{i}}}}{{\partial y}}.$$
(8)

The system of equations for determining the characteristics of relation (8) and relations along the characteristics has the form

$$\frac{{dx}}{{ - {{B}_{i}}}} = \frac{{dy}}{{{{A}_{i}}}} = \frac{{d{{{\tau }}_{{xz}}}}}{{\frac{{\partial {{K}_{i}}}}{{\partial y}}}}$$
(9)

It follows from (9) that the straight lines

$${{A}_{i}}x + {{B}_{i}}y = {{C}_{{i1}}}\quad ({{C}_{{i1}}} = {\text{const}})$$
(10)

are characteristics of relation (8). The following relations hold along characteristics (10)

$${{A}_{i}}{{{\tau }}_{{xz}}} = \int {\frac{{\partial {{K}_{i}}}}{{\partial y}}\left( {{\alpha },y} \right)dy,\quad - {\kern 1pt} {{B}_{i}}{{{\tau }}_{{xz}}} = \int {\frac{{\partial {{K}_{i}}}}{{\partial y}}\left( {x,{\beta }} \right)dx} } ,$$
(11)

where \({\alpha } = \frac{1}{{{{A}_{i}}}}\left( {{{C}_{{i1}}} - {{B}_{i}}y} \right),~~{\beta } = \frac{1}{{{{B}_{i}}}}\left( {{{C}_{{i1}}} - {{A}_{i}}x} \right).\)

Similarly, differentiating equation (6) with respect to the variable x, taking into account (2), we obtain that along the characteristics (10) the following relations are valid for the stress components

$$ - {{A}_{i}}{{{\tau }}_{{yz}}} = \int {\frac{{\partial {{K}_{i}}}}{{\partial x}}\left( {{\alpha },y} \right)dy,\quad {{B}_{i}}{{{\tau }}_{{yz}}} = \int {\frac{{\partial {{K}_{i}}}}{{\partial x}}\left( {x,{\beta }} \right)dx} } .$$
(12)

Considering criterion (6) as a plastic potential, instead of (4) we obtain the relation

$$\frac{{{{{\varepsilon }}_{{xz}}}}}{{{{A}_{i}}}} = \frac{{{{{\varepsilon }}_{{yz}}}}}{{{{B}_{i}}}}.$$
(13)

Integrating relation (6) and part of relations (4) and taking into account that at the initial moment of torsion, the strain components eij are equal to 0, we obtain

$$\frac{{{{e}_{{xz}}}}}{{{{A}_{i}}}} = \frac{{{{e}_{{yz}}}}}{{{{B}_{i}}}},\quad {{e}_{x}} = {{e}_{y}} = {{e}_{z}} = {{e}_{{xy}}} = 0.$$
(14)

From (14) it follows that

$${{B}_{i}}{{e}_{{xz}}} - {{A}_{i}}{{e}_{{yz}}} = 0.$$
(15)

Let us assume that the displacement components u, \(v\), w have the form

$$u = {\theta }yz,\quad {v} = - {\theta }xz,\quad w = w\left( {x,y} \right),$$
(16)

where θ is the twist, w is the warping.

Expressing strain components in terms of displacement components

$${{e}_{{xz}}} = \frac{1}{2}\left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right),~\quad {{e}_{{yz}}} = \frac{1}{2}\left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial z}}} \right)$$
(17)

from (15) and (16), we obtain

$$ - {{B}_{i}}\frac{{\partial w}}{{\partial x}} + {{A}_{i}}\frac{{\partial w}}{{\partial y}} = {\theta }\left( {{{A}_{i}}x + {{B}_{i}}y} \right).$$
(18)

It follows from (18) that straight lines (10) are characteristics. Along characteristics (10), the following relations hold:

$${{B}_{i}}w + {\theta }{{C}_{{i1}}}x = {{C}_{{i2}}}\quad {\text{or}}\quad {{A}_{i}}w - {\theta }{{C}_{{i1}}}y = {{C}_{{i3}}},$$
(19)

where \({{C}_{{i2}}},{{C}_{{i3}}} = {\text{const}}~\) along the characteristic.

Differentiating relation (18) with respect to the variable x, we obtain the equation

$$ - {{B}_{i}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial w}}{{\partial x}}} \right) + {{A}_{i}}\frac{\partial }{{\partial y}}\left( {\frac{{\partial w}}{{\partial x}}} \right) = {\theta }{{A}_{i}}.$$
(20)

From equation (20) it follows that along characteristics (10) the following relations are valid:

$${{B}_{i}}\frac{{\partial w}}{{\partial x}} + {\theta }{{A}_{i}}x = {{C}_{{i4}}}\quad {\text{or}}\quad \frac{{\partial w}}{{\partial x}} - {\theta }y = {{C}_{{i5}}},$$
(21)

where \({{C}_{{i4}}},{{C}_{{i5}}} = {\text{const}}\) along the characteristic.

Similarly, differentiating relation (18) with respect to the variable y, we obtain the equation

$$ - {{B}_{i}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial w}}{{\partial y}}} \right) + {{A}_{i}}\frac{\partial }{{\partial y}}\left( {\frac{{\partial w}}{{\partial y}}} \right) = {\theta }{{B}_{i}}.$$
(22)

From Eq. (22) it follows that along characteristics (10) the following relations are valid:

$$\frac{{\partial w}}{{\partial x}} + {\theta }x = {{C}_{{i6}}}\quad {\text{or}}\quad {{A}_{i}}\frac{{\partial w}}{{\partial y}} - {\theta }{{B}_{i}}y = {{C}_{{i7}}},$$
(23)

where \({{C}_{{i6}}},{{C}_{{i7}}} = {\text{const}}\) along the characteristic.

Using the second relation (21) and the first relation (23), we obtain that along the characteristics (10) the relations

$${{e}_{{xz}}} - {\theta }y = \frac{1}{2}{{C}_{{i5}}},\quad {{e}_{{yz}}} + {\theta }x = \frac{1}{2}{{C}_{{i6}}}$$
(24)

are valid.

It should be noted that relations (24), (10), (15) imply

$${{A}_{i}}{{C}_{{i6}}} - {{B}_{i}}{{C}_{{i5}}} = 2{\theta }{{C}_{{i1}}}.$$
(25)

Let us consider the torsion of a rectangular cross-section rod m1m2m3m4 with sides 2a and 2b (Fig. 2). On the contour of the section, the shear stress vector \({\mathbf{\tau }} = \left( {{{{\tau }}_{{xz}}},{{{\tau }}_{{yz}}}} \right)\) is parallel to the contour.

figure 2

Fig. 2.

In the case of an isotropic ideally plastic material, the characteristics are directed perpendicular to the contour. In the case under consideration, the direction of characteristics (10) is fixed; therefore, for a given contour of the bar section, it is always possible to choose a linearized yield criterion (6) so that the characteristics remain perpendicular to the contour. For this, Ai, Bi in criterion (6) must be chosen so that the vector \({{{\mathbf{n}}}_{{\mathbf{i}}}} = \left( {{{A}_{i}},{{B}_{i}}} \right)\) is parallel to the segment mimi + 1 of the contour (Fig. 2).

Here we have four families of characteristics

$${{A}_{1}}x + {{B}_{1}}y = {{C}_{{11}}},$$
(26)
$${{A}_{2}}x + {{B}_{2}}y = {{C}_{{21}}},$$
(27)
$${{A}_{3}}x + {{B}_{3}}y = {{C}_{{31}}},$$
(28)
$${{A}_{4}}x + {{B}_{4}}y = {{C}_{{41}}}.$$
(29)

In order for the characteristics (26) to be orthogonal to the segment m1m2 of the contour of the cross-section of the rod, we should assume A1 = 0, B1 = –1. Yield criterion (6) takes the form

$${{{\tau }}_{{yz}}} = - {{K}_{1}}.$$
(30)

Characteristics (26) will be written in the form

$$y = - {{C}_{{11}}}.$$
(31)

From (25), it follows that

$${{C}_{{15}}} = 2{\theta }{{C}_{{11}}}.$$
(32)

Then from (11), (30), and (2) along characteristics (31) we have

$${{{\tau }}_{{yz}}} = - {{K}_{1}},\quad {{{\tau }}_{{xz}}} = \int {\frac{{\partial {{K}_{1}}}}{{\partial y}}\left( {x, - {{C}_{{11}}}} \right)dx = {{k}_{1}}} .$$
(33)

In order for characteristics (27) to be orthogonal to the segment m2m3 of the contour of the cross-section of the rod, we should assume A2 = –1, B2 = 0. The yield criterion (6) takes the form

$${{{\tau }}_{{xz}}} = - {{K}_{2}}$$
(34)

Characteristics (27) will be written in the form

$$x = - {{C}_{{21}}}$$
(35)

From (25), it follows that

$${{C}_{{26}}} = - 2{\theta }{{C}_{{21}}}$$
(36)

Then, from (12), (34), and (2) along characteristics (35), we have

$${{{\tau }}_{{xz}}} = - {{K}_{2}},\quad {{{\tau }}_{{yz}}} = \int {\frac{{\partial {{K}_{2}}}}{{\partial x}}\left( { - {{C}_{{21}}},y} \right)dy = {{k}_{2}}} .$$
(37)

In order for characteristics (28) to be orthogonal to the segment m3m4 of the contour of the cross-section of the rod, we should assume A3 = 0, B3 = 1. The yield criterion (6) takes the form

$${{{\tau }}_{{yz}}} = {{K}_{3}}.$$
(38)

Characteristics (28) will be written in the form

$$y = {{C}_{{31}}}.$$
(39)

From (25), it follows that

$${{C}_{{35}}} = - 2{\theta }{{C}_{{31}}}.$$
(40)

Then, from (11), (38), and (2) along characteristics (39), we have

$${{{\tau }}_{{yz}}} = {{K}_{3}},\quad {{{\tau }}_{{xz}}} = - \int {\frac{{\partial {{K}_{3}}}}{{\partial y}}\left( {x,{{C}_{{31}}}} \right)dx = - {{k}_{3}}} .$$
(41)

In order for characteristics (29) to be orthogonal to the segment m4m1 of the contour of the cross-section of the rod, we should assume A4 = 1, B4 = 0. The yield criterion (6) takes the form

$${{{\tau }}_{{xz}}} = {{K}_{4}}.$$
(42)

Characteristics (29) will be written in the form

$$x = {{C}_{{41}}}.$$
(43)

From (25), it follows that

$${{C}_{{46}}} = 2{\theta }{{C}_{{41}}}.$$
(44)

Then, from (12), (42), and (2) along characteristics (41), we have

$${{{\tau }}_{{xz}}} = {{K}_{4}},\quad {{{\tau }}_{{yz}}} = - \int {\frac{{\partial {{K}_{4}}}}{{\partial x}}\left( {{{C}_{{41}}},y} \right)dy = - {{k}_{4}}} .$$
(45)

Special attention should be paid to the stress discontinuity lines (lines \({{m}_{1}}L,~~{{m}_{2}}L,~{{m}_{3}}N\), \({{m}_{4}}N\), LN in Fig. 2), which arise when two or more characteristics pass through a given point of the cross-section.

Stress rupture lines are a trace of disappearing hard regions. They always satisfy the relations

$${{e}_{{xz}}} = {{e}_{{yz}}} = 0.$$
(46)

Curve m1L is the line of stress discontinuity emerging from the vertex m1 of the contour of the cross-section of the rod and formed due to the intersection of the family of characteristics (31) and (43).

From (33) and (45), we have the equation for the stress discontinuity line m1L

$$\frac{{dx}}{{{{K}_{4}} - {{k}_{1}}}} = \frac{{dy}}{{{{K}_{1}} - {{k}_{4}}}}.$$
(47)

Curve m2L is the line of stress discontinuity emerging from the vertex m2 of the contour of the cross-section of the rod and formed due to the intersection of the family of characteristics (31) and (35).

From (33) and (37), we have the equation for the stress discontinuity line m2L

$$\frac{{dx}}{{ - {{K}_{2}} - {{k}_{1}}}} = \frac{{dy}}{{{{K}_{1}} + {{k}_{2}}}}.$$
(48)

Curve m3N is the line of stress discontinuity emerging from the vertex m3 of the contour of the cross-section of the rod and formed due to the intersection of the family of characteristics (35) and (39).

From (37) and (41), we have the equation for the stress discontinuity line m3N

$$\frac{{dx}}{{{{K}_{2}} - {{k}_{3}}}} = \frac{{dy}}{{{{K}_{3}} - {{k}_{2}}}}.$$
(49)

Curve m4N is the line of stress discontinuity emerging from the vertex m4 of the contour of the cross-section of the rod and formed due to the intersection of the family of characteristics (39) and (43).

From (41) and (45), we have the equation for the stress discontinuity line m4N

$$\frac{{dx}}{{ - {{K}_{4}} - {{k}_{3}}}} = \frac{{dy}}{{{{K}_{3}} + {{k}_{4}}}}.$$
(50)

The NL curve is the stress discontinuity line formed due to the intersection of the family of characteristics (35) and (43).

From (37) and (45) we get the equation of the stress discontinuity line NL

$$\frac{{dx}}{{{{K}_{4}} + {{K}_{2}}}} = \frac{{dy}}{{ - {{k}_{4}} - {{k}_{2}}}}.$$
(51)

Let us consider the case when the yield criterion (3) has the form

$${{\left( {{{{\tau }}_{{xz}}} - {{{\gamma }}_{1}}} \right)}^{2}} + {{\left( {{{{\tau }}_{{yz}}} - {{{\gamma }}_{2}}} \right)}^{2}} = {{k}_{0}},$$
(52)

where \({{{\gamma }}_{1}} = {{a}_{1}}x + {{b}_{1}}y,{{{\gamma }}_{2}} = {{a}_{2}}x + {{b}_{2}}y,{{k}_{0}} = {\text{const}}\).

According to (6), (33), (37), (41), (45), the stress components are determined as follows:

—in the region \({{m}_{1}}L{{m}_{2}}\)

$${{{\tau }}_{{xz}}} = - {{b}_{2}}\left( {x - a} \right),\quad {{{\tau }}_{{yz}}} = - {{k}_{0}} + {{a}_{2}}x + {{b}_{2}}y;$$
(53)

—in the region \({{m}_{2}}LN{{m}_{3}}\)

$${{\tau }_{{xz}}} = - {{k}_{0}} + {{a}_{1}}x + {{b}_{1}}y,\quad {{{\tau }}_{{yz}}} = ~ - {{a}_{1}}\left( {y + b} \right);$$
(54)

—in the region \({{m}_{3}}N{{m}_{4}}\)

$${{{\tau }}_{{xz}}} = - {{b}_{2}}\left( {x + a} \right),\quad {{{\tau }}_{{yz}}} = {{k}_{0}} + {{a}_{2}}x + {{b}_{2}}y;$$
(55)

—in the region \({{m}_{4}}NL{{m}_{1}}\)

$${{{\tau }}_{{xz}}} = {{k}_{0}} + {{a}_{1}}x + {{b}_{1}}y,\quad {{{\tau }}_{{yz}}} = ~ - {{a}_{1}}\left( {y - b} \right).$$
(56)

From (53), (54), (55), (56) we obtain the equations for the lines of discontinuity of stresses

$${{m}_{1}}L~{\text{: }}\,~{{a}_{2}}{{x}^{2}} + 2\left( {{{a}_{1}} + {{b}_{2}}} \right)xy + {{b}_{1}}{{y}^{2}} - 2\left( {{{k}_{0}} + {{a}_{1}}b} \right)x + 2\left( {{{k}_{0}} - {{b}_{2}}a} \right)y = r,$$
(57)
$${{m}_{2}}L~{\text{: }}\,~{{a}_{2}}{{x}^{2}} + 2\left( {{{a}_{1}} + {{b}_{2}}} \right)xy + {{b}_{1}}{{y}^{2}} - 2\left( {{{k}_{0}} - {{a}_{1}}b} \right)x - 2\left( {{{k}_{0}} + {{b}_{2}}a} \right)y = r,$$
(58)
$${{m}_{3}}N{\text{: }}\,~{{a}_{2}}{{x}^{2}} + 2\left( {{{a}_{1}} + {{b}_{2}}} \right)xy + {{b}_{1}}{{y}^{2}} + 2\left( {{{k}_{0}} + {{a}_{1}}b} \right)x - 2\left( {{{k}_{0}} - {{b}_{2}}a} \right)y = r,$$
(59)
$${{m}_{4}}N~{\text{:}}~~{{a}_{2}}{{x}^{2}} + 2\left( {{{a}_{1}} + {{b}_{2}}} \right)xy + {{b}_{1}}{{y}^{2}} + 2\left( {{{k}_{0}} - {{a}_{1}}b} \right)x + 2\left( {{{k}_{0}} + {{b}_{2}}a} \right)y = r,$$
(60)
$$LN{\text{:}}\,~~ - {{a}_{1}}bx + {{k}_{0}}y = 0,$$
(61)

where \(~r = {{a}_{2}}{{a}^{2}} - 2{{k}_{0}}\left( {a - b} \right) + {{b}_{1}}{{b}^{2}}\).

Thus, in the article:

—integrals were obtained that determine the stress and strain states of an inhomogeneous ideal rigid-plastic rod during torsion for the linearized yield criterion; characteristics of the basic relations and relations for the components of stresses and strains are found;

—the limiting state of an inhomogeneous ideal rigid-plastic bar with a rectangular cross-section were investigated: the field of characteristics of the basic relations is determined, relations are found along the characteristics and the stress rupture line.