INTRODUCTION

Exposure-response analysis is important in drug development to optimize clinical dose and dosing regimens (1). Disease status measures in clinical studies are often bounded outcome scores (BOS) which take restricted values on finite intervals and achieve boundary value (2). An example of BOS is the Psoriasis Area and Severity Index (PASI), ranged 0–72 with 0.1 increments (3). Such endpoints are ordered categorical in nature, but due to the typically large (> 10) number of possible values, they are often analyzed as continuous data. The standard continuous data analysis approach, assuming normally distributed errors, may not handle skewed data well and may predict the data outside of its natural range. Several approaches have been proposed to describe BOS data distributions (2,4,5). The coarsened grid approach (2), assuming an underlying normal latent variable, predicts the data within its natural range but is still limited in its ability to handle skewed data. The censoring approach treats the boundary data as censored and applies a transformation to handle skewness (4), but treats data inside the boundary as continuous and thus violates the natural range of the data. The beta regression approach, perhaps the earliest and most often used in pharmacometrics, has its origin from psychology data analysis (5). An additional linear transformation Y* = Y(1 − δ) + δ/2 with a small correction factor δ, e.g., 0.01, is used to map the original BOS data Y inside the interval (0,1). Y* is then modeled with a beta distribution with density

$$ f(x)=\Gamma \left(\upalpha +\upbeta \right)/\left[\Gamma \left(\upalpha \right)\Gamma \left(\upbeta \right)\right]\ {y}^{\upalpha -1}{\left(1-y\right)}^{\upbeta -1} $$
(1)

where α > 0, β > 0, and Γ denotes the gamma function. It has recently been pointed out that the approach is ill-behaved at the boundary and lacks statistical rigor (6).

Clinical study endpoints may be either the direct disease status measure or derived metrics based on varying degrees of improvement from baseline, such as PASI 75, PASI 90, and PASI 100, defined as 75, 90, or 100% improvement from baseline in PASI, respectively (7). All of the existing BOS approaches, while having varied degrees of success in describing the original data, have not been shown to predict derived endpoints well, especially for PASI 75, PASI 90, and PASI 100 (7). For the PASI scores, while exposure-response (E-R) models have been developed (3,8,9,10), no published models has yet shown their ability to fully characterize the entire observed distributions (7). Because of this difficulty, PASI 75, PASI 90, and PASI 100 have been modeled directly as ordered categorical variables (7,11). However, these derived categorical endpoints reduce the granularity from the original PASI scores, as evidenced by the fact that the between-subject variability (BSV) could be modeled only at the average level (12). This inability in distinguishing between BSVs from different sources, e.g., potency, rate of onset, results in the limited ability of predicting subpopulations of different patient sensitivity, which is important in the analysis and design of response-adaptive clinical studies (13). The need of BOS analysis methodology development has recently been emphasized (14).

Recently, a new latent variable approach of using the beta distribution has been proposed in the statistical literature without a need for the problematic linear transformation (15). In the current manuscript, we applied this approach to the longitudinal E-R modeling of PASI scores, using data from two phase 3 clinical studies in patients with psoriasis (11). A previously established type I indirect response (IDR) model was used in the current modeling analysis (6,7,11,12,13,16,17). The results from this approach were compared with those from the standard continuous analysis approach, both for PASI scores and for the derived endpoints PASI 75, PASI 90, and PASI 100.

METHODS

Study Designs

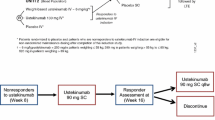
Model development and evaluation were performed using data from two pivotal phase 3 clinical studies of guselkumab (11). Briefly, these were randomized, double-blind, placebo-controlled, parallel, multicenter studies in patients who have moderate to severe plaque psoriasis. In study 1, approximately 450 patients, in a 2:1 ratio, were treated with guselkumab SC 100 mg at weeks 0, 4, 12, and every 8 weeks (q8w) through week 44; or placebo at weeks 0, 4, and 12 followed by guselkumab 100 mg at weeks 16 and 20, and q8w through week 44. Study 2 was similarly designed, enrolled approximately 750 patients to receive guselkumab or placebo (2:1 randomization), and included a randomized withdrawal portion beginning at week 28. In both phase 3 studies, guselkumab concentration and clinical efficacy were evaluated through week 48. More details of the study design have been reported in a previous analysis on PASI 75, PASI 90, and PASI 100 (11).

PK and PASI Assessments

In both studies, pre-dose PK samples were collected from each patient at weeks 0, 4, 8, 12, 16, 20, 24, 28, 36, and 44. Additionally, in study 1, a random PK sample was collected in actively treated patients between weeks 16 and 24; in study 2, PK samples were collected also at weeks 40 and 48. The PASI scores were collected at week 2, 4, and every 4 weeks (q4w) thereafter until week 40 (18,19). The final dataset contained 1218 patients with 16,531 PASI observations.

The “Sustained-Responder” Population

In the randomized withdrawal portion beginning at week 28 of study 2, it is of interest to understand the proportion of subjects maintaining PASI 100 over time without receiving additional active treatment. The ability to predict this “sustained-responder” population, who maintained clear skin (PASI 100) without receiving additional treatment after week 28, is important to the design of dose-optimization studies (20).

Population PK Model

A confirmatory population PK (21,22) analysis based on the previously developed model was implemented to describe guselkumab PK in patients with psoriasis. The structural model is one-compartment with first-order absorption and first-order elimination, with parameters including apparent clearance (CL/F), apparent volume of distribution (V/F), and absorption rate constant (ka). Between-subject random effects on CL/F, V/F, and ka were included using log-normal distributions. A correlation between the BSV on CL/F and V/F also was included, and the impact of baseline body weight effects on CL/F and V/F was described with a power model standardized to the median baseline body weight of 87.1 kg. This is consistent with previous psoriasis studies (23), but comparisons with other patient populations are less straightforward than using a standard weight of 70 kg with a theory-based allometric model (24). Diabetic comorbidity and race (Caucasian vs. non-Caucasian) both were identified as significant covariates on CL/F and were included in the final population PK model. Shrinkage estimates were low (15% and 4%, respectively) for random effects of V/F and CL/F. Details of the population PK modeling results have been reported elsewhere (23).

E-R: Continuous Analysis Model

In this approach, the PASI score was modeled by adopting a semi-mechanistic approach applied in an earlier E-R analysis (8) as

$$ \mathrm{PASI}(t)=b-{f}_{\mathrm{p}}(t)-{f}_{\mathrm{d}}(t)+\upvarepsilon $$
(2)

where PASI(t) is the observed PASI score at time t, b is the baseline PASI score, fp(t) is the placebo effect and fd(t) is the drug effect, and ε is the residual error with a normal distribution [N(0,σ2)]. The placebo effect was modeled empirically as

$$ {f}_{\mathrm{p}}(t)=b\ {F}_{\mathrm{p}}\ \left[1-\exp \left(-{k}_{\mathrm{p}}\ t\right)\right] $$
(3)

where 0 ≤ Fp ≤ 1 is the fraction of maximum placebo effect and kp is the rate of onset. It is plausible that placebo responses may decrease after week 12, however this is confounded with the drug effect. In our experience of analyzing placebo-controlled clinical trial data, more complex models usually could not be supported. For example, a Bateman function was attempted in a similar circumstance without success (6).

The drug effect was modeled as

$$ {f}_{\mathrm{d}}(t)=b\left(1-{F}_{\mathrm{p}}\right){E}_{\mathrm{max}}\left[1-R(t)\right] $$
(4)

where 0 ≤ Emax ≤ 1 represents maximum drug effect, with R(t) governed by:

$$ \frac{dR(t)}{dt}={k}_{\mathrm{in}}\left(1-\frac{C_{\mathrm{p}}}{I{C}_{50}+{C}_{\mathrm{p}}}\right)-{k}_{\mathrm{out}}R(t) $$
(5)

where Cp is the model estimated individual drug concentration at time t, and kin (disease formation rate), IC50 (half-maximal inhibitory concentration), and kout (disease amelioration rate) are the parameters in a type I indirect response model (25). It was further assumed that R = 1 at baseline, i.e., R(0) = 1, yielding kin = kout. Formally, this implies that there is no disease progression throughout the study. While disease progression is an actual possibility (26), its effect would be largely confounded with that of placebo, in part because the placebo effect was only observed for the initial 16 weeks. An alternative could be to interpret fp(t) as the combined effect of placebo and disease progression. Note that Eq. 4 links the placebo and drug effects such that the prediction of Eq. 2 remains ≥ 0. For more details on the theoretical characteristics of latent variable IDR models, see Hu (12).

BSVs on Fp and Emax were modeled assuming logit-normal distributions to restrict their values between (0, 1). In our previous experience with analyzing placebo-controlled clinical trial data, the currently applied placebo model seems sufficient (6,7,8,13,16,17,27,28). However, as a sensitivity analysis, the possibility of negative responses was assessed by assuming a proportional random effect on Fp and Emax (26). BSV on other parameters were modeled with lognormal distributions. The covariance between the random effects was modeled (see NM-TRAN code in the Supplementary material).

Latent-Beta BOS Analysis Model

As a general notation, the original BOS variable Y can be standardized onto the closed interval [0,1] by a linear transformation. Thus Y takes possible values in the form of k/m, where k = 0, 1, …, m. In the case of PASI scores, m = 720. Ursino and Gasparini (15) postulated that a latent variable Y* exists on the open interval (0,1) such that

$$ Y=k\ \mathrm{if}\ \mathrm{and}\ \mathrm{only}\ \mathrm{if}\kern0.75em {Y}^{\ast}\in \left[k/\left(m+1\right),\left(k+1\right)/\left(m+1\right)\right). $$

In a more compact mathematical notation, Y = ⌊(m + 1)Y*⌋/(m + 1), where ⌊·⌋ is the floor function. Y* is then modeled with a beta distribution given in Eq. 1 with a re-parameterization of

$$ \upalpha =\upmu \upphi, \upbeta =\left(1-\upmu \right)\upphi $$
(6)

where 0 < μ < 1 and ϕ > 0. The mean and variance of the beta distribution under this parameterization are μ and μ(1 − μ)/(1 + ϕ), respectively. This leads to the PASI score being analyzed as an ordered categorical variable, with the cumulative probability

$$ \mathrm{prob}\left(\mathrm{PASI}\ \mathrm{score}=k\right)=B\left(\left(k+1\right)/721\right)-B\left(k/721\right) $$
(7)

for k = 0, 1, …, 720, where B(x) = B(x, μ, ϕ) is the cumulative beta distribution. An implementation in NONMEM is given in Supplementary material.

The beta distribution is flexible enough to describe skewness. When μ = 0.5, the distribution is symmetrically centered on the interval (0,1), and the 3 statistics of mode, mean, and median are equal, similar to a normal distribution. As μ moves closer to 0 or 1, the 3 statistics differ more, which indicates the appropriate skewness that results in a shorter tail on the respective boundary. The larger the variance, scaled by (1 + ϕ), the wider the difference between the 3 statistics, which is conceptually appealing.

E-R: BOS Analysis Model

A semi-mechanistic model similar to that used in the continuous analysis approach was used to model the mean parameter μ under the beta distribution as follows:

$$ \mathrm{logit}\left(\upmu \right)=\mathrm{logit}\left({\mu}_{\mathrm{b}}\right)+{f}_{\mathrm{p}}(t)+{f}_{\mathrm{d}}(t) $$
(8)

where logit(x) = log[x/(1 − x)], μb is the baseline on the transformed scale (0,1), fp(t) is the placebo effect, and fd(t) is the drug effect (12).

The placebo effect was modeled empirically:

$$ {f}_{\mathrm{p}}(t)={P}_{\mathrm{max}}\ \left[1-\exp \left(-{k}_{\mathrm{p}}\ t\right)\right] $$
(9)

where Pmax is the maximum placebo effect and kp is the rate of onset.

The drug effect was modeled using a latent variable R(t) in the same form of Eq. 4, i.e.,

$$ \frac{dR(t)}{dt}={k}_{\mathrm{in}}\left(1-\frac{C_{\mathrm{p}}}{I{C}_{50}+{C}_{\mathrm{p}}}\right)-{k}_{\mathrm{out}}R(t) $$
(10)

where Cp is the drug concentration, and kin, IC50, and kout are the parameters in a type I IDR model. It was further assumed that at baseline R(0) = 1, yielding kin = kout. The reduction of R(t) was assumed to drive the drug effect through:

$$ {f}_{\mathrm{d}}(t)= DE\ \left[1-R(t)\right] $$
(11)

where DE is a parameter to be estimated that determines the magnitude of drug effect fd(t).

Theoretically, the representation of drug effect in Eqs. 8–11 has been shown to be equivalent to a change-from-baseline latent-variable IDR model (28), under which kout may be empirically interpreted as the rate constant of drug effect onset and offset, and DE may be interpreted as the baseline of the latent variable prior to normalization (12). Note that for latent variable IDR models, the Emax parameter under the standard IDR models (25) is not separately identifiable and is set to equal 1.

BSV on logit(μb) was modeled with a normal distribution. BSVs on other parameters were modeled with log-normal distributions. The covariance between the random effects was modeled (see NM-TRAN code in the Supplementary material). As a sensitivity analysis, the possibility of negative responses was assessed by assuming a proportional random effect on Pmax and DE.

Model Estimation and Evaluation

A sequential approach was used for the E-R model estimation by first fixing individual PK parameters to their respective empirical Bayesian parameter estimates obtained from the population PK model (29). Parameter estimation for the E-R model was implemented in the NONMEM (30) version 7.4.3 with a gFortran compiler, using the SAEM option followed by an importance sampling step for the objective function evaluation (31). E-R model selection was based on the NONMEM objective function values (OFVs), which are approximately − 2 times log-likelihood. A change in OFV of 10.83 corresponding to a nominal p value of 0.001 was judged as significant evidence for including an additional parameter for the comparisons within the continuous and the BOS analysis models, respectively. Conceptually, AIC and BIC are more appropriate for non-nested models, which were not used in this context. This is because the structural models were essentially pre-specified based on previous experiences, thus only the random effect models were compared. For more on BOS model comparisons, see (14).

Visual predictive checks (VPCs) (32) were used to evaluate model performance by simulating 500 replicates of the dataset and comparing simulated and model-predicted responses grouped by the planned observation times.

RESULTS

Continuous Analysis Model

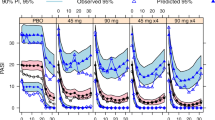
Equations 2–5 were fitted to the PASI score data. Model exploration based on changes in NONMEM OFV led to BSV terms on b, kout, and IC50, with a correlation between kout and IC50. The sensitivity analyses assuming a proportional random effect on Fp and Emax did not result in improved fit of the data. Parameter estimates are given in Table I. The relative standard errors (RSE) were all within 20%, which was reasonable. VPC results by treatment groups and studies were shown in Fig. 1. For the 100-mg treatment groups, the model reasonably described the median observed data median and the upper end, i.e., 95th percentile, of the observed data distribution. However the lower end, i.e., 5th percentile, of the model predicted distribution were negative and outside the data range after 8 weeks. For the placebo treatment groups, the 5th percentile of the model predicted distribution also became negative approximately 8 weeks after switching to the 100-mg treatment. In addition, the 5th percentile and the median of the model predictions were higher than the observed during the placebo-treated periods.

Table I Parameter Estimates for the Continuous and the BOS Exposure-Response Analysis Models
Full size table
Fig. 1
figure 1

The continuous analysis model predicted and observed PASI score median, 5th and 95th percentiles, at planned observation times. pbo, placebo

Full size image

For the derived PASI improvement criteria, i.e., PASI 75, PASI 90, and PASI 100, VPC results by treatment groups and studies are shown in Fig. 2. In general, the model consistently underpredicted the observed data. The difficulty of using PASI score models to predict the derived PASI improvement criteria has been previously noted (7).

Fig. 2
figure 2

The continuous analysis model predicted and observed PASI response criteria median, 5th and 95th percentiles, at planned observation times. pbo, placebo

Full size image

For the “sustained-responder” population, i.e., the proportion of subjects maintaining PASI 100 in the randomized withdrawal portion of study 2 without receiving active treatment after week 28, VPC results by treatment groups and studies are shown in Fig. 3. The model consistently underpredicted the observed data.

Fig. 3
figure 3

The continuous analysis model predicted and observed PASI 100 responder rates when active treatment was withdrawn after week 28

Full size image

Latent-Beta BOS Analysis Model

Equations 6–11 were fitted to the PASI score data. Model exploration based on the changes in NONMEM OFV led to BSV terms on b, kout, and DE, with a correlation between kout and DE. The sensitivity analyses assuming a proportional random effect on Pmax and DE did not result in improved fit of the data. Parameter estimates are given in Table I. The RSEs were all within 20%, which was reasonable. VPC results by treatment groups and studies are shown in Fig. 4. For the 100-mg treatment groups, the model reasonably described the observed data. For the placebo treatment groups, the 5th percentile and the median of the model predictions were also higher than the observed during the placebo-treated periods. Note that in all treatment groups, by 8 weeks after receiving the 100-mg treatment, the 5th percentiles of model predictions were no longer negative as compared with the continuous analysis model; they were now near 0 and overlapped with the observed data. The estimate of μb of 0.298, corresponding to a baseline PASI score of 21.5, is close to the observed data (median = 18.9, mean = 21.7). Considering the fact that the variance affects the mean for categorical data (12,33), this indicates that the baseline random effect variance was overestimated. The observed and model-predicted placebo effect trends parallel, suggesting accurate estimation of the magnitude of the placebo effect. As noted earlier in the “METHODS” section, this interpretation depends on the assumption of no disease progression throughout the study.

Fig. 4
figure 4

The BOS analysis model predicted and observed PASI score median, 5th and 95th percentiles, at planned observation times. pbo, placebo

Full size image

For the derived PASI improvement criteria, i.e., PASI 75, PASI 90, and PASI 100, VPC results by treatment groups and studies are shown in Fig. 5. In general, the model reasonably predicted observed data except after 28–40 weeks in study 2, which is the randomized withdrawal portion.

Fig. 5
figure 5

The BOS analysis model predicted and observed PASI response criteria median, 5th and 95th percentiles, at planned observation times. pbo, placebo

Full size image

For the “sustained-responder” population, VPC results by treatment groups and studies were shown in Fig. 6. The model reasonably predicted observed data.

Fig. 6
figure 6

The BOS analysis model predicted and observed PASI 100 responder rates when active treatment was withdrawn after week 28

Full size image

DISCUSSION

There are two main desirable goals in BOS data analysis: (1) to predict data within its natural range and (2) to accommodate skewed data distributions. Most of the existing methods can handle one goal but not both. An exception is the recent emergence of applying the standard ordered categorical analysis method (34), which has been shown to be accurate and robust when the sample size is sufficiently large. However, the method becomes impractical when the number of possible data categories becomes large, e.g., 721 in the case of PASI scores. The importance of accurately describing the data distribution has been emphasized for the accurate prediction of derived endpoints such as PASI 75, PASI 90, and PASI 100 (7). The flexibility of the beta distribution makes it appealing in BOS data analysis. However, the earlier attempt, in essence assuming the BOS data following the beta distribution (termed beta regression), is intuitive and lacks statistical rigor (6). The newly proposed beta-latent variable approach (15) corrects this problem. Consequently in this application, it has predicted the PASI scores within their natural bounds and showed superior performance in describing the derived endpoints of PASI 75, PASI 90, and PASI 100. In support of this, the outcome shown in Fig. 1 where the lower end, i.e., 5th percentile, of the model predicted distribution were negative and outside the data range after 8 weeks, was expected because the PASI score distributions become highly skewed after treatment, which the continuous analysis approach could not effectively handle.

While the beta distribution can accommodate skewed data distributions, it still has only 2 parameters, same as the normal distribution. In principle, more complex distributions could potentially improve the fit, depending on the application scenarios. For example, the components of PASI score involves multiples of 0.1, 0.2, 0.3, and 0.4 (35), therefore the distribution of PASI scores may not be homogenous in terms of 0.1 increments. Refining the beta distribution to accommodate this feature may warrant further investigation. In this regard, the most flexible distribution is that used in the standard ordered categorical data analysis (34), with the number of parameters close to the number of data categories. In addition, the latent-beta IDR model inherits all limitations of the latent variable IDR models (12), including those on parameter identification and interpretations. The over-estimation of baseline random effect by the latent-beta IDR model is in part because the data could not support the estimation of random effects for all parameters, e.g., Fp, IC50, and the random effects are usually confounded to certain degrees. This may also be in part due to the fact that 12 weeks of placebo data is too short to allow its variability to be fully characterized; indeed, model convergence could not be achieved when additional BSV terms were attempted. The latent-beta IDR model also appears to have some biases in the response-adaptive portion of study 2. The biases were unlikely to be caused by informative dropout (36,37) due to the low total dropout rates (near 6–7%) by the end of both studies. A difficulty of modeling data with such response-adaptive designs has been previously noted as the underidentification of random effects (13). The need of corrections due to the correlation between the response and dosing to avoid VPC bias has been proposed in the case of analyzing continuous response variables (38).

Although PASI 75, PASI 90, and PASI 100 could be directly modeled accurately with the standard ordered categorical analysis approach (7), the ability to estimate BSVs from different sources is limited and usually could not be separated from that of baseline (12). This is due to the loss of information caused by not fully using the granularity of the PASI scores. The importance of accurately identifying BSVs from different sources has been emphasized in the analysis of response-adaptive study data (13). In particular, accurately predicting the proportion of “sustained-responders” is important for the design of flexible-dose clinical studies. The previously developed model of direct modeling PASI 75, PASI 95, and PASI 100 falls short in this regard. In contrast, the current latent-beta BOS analysis approach performed reasonably well, as Fig. 3 and Fig. 6 show.

PASI scores have been analyzed numerous times before, and the difficulties of accommodating data skewness and predicting the derived endpoints have been duly noted (7). The current investigation has shown that the latent-beta BOS analysis approach could alleviate these difficulties. Furthermore, the approach could allow better characterization of BSVs, which in turn facilitates better predictions of population characteristics such as the “sustained-responders,” and thus the effective designs of dose-optimization clinical studies (20). The difficulty of predicting subpopulation responses with different sensitivity has been noted before (13).

CONCLUSION

The latent variable approach provides a more theoretically sound application of the beta distribution in BOS analysis than that was previously used in pharmacometrics publications. In the currently illustrated example, this approach showed the ability to (1) handle skewed BOS data, (2) describe derived endpoints, i.e., the PASI improvement criteria, and (3) describe a highly sensitive subpopulation.