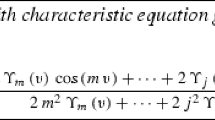1 Introduction

Our main goal is to discuss the one-dimensional radial Schrödinger equation of the form

$$ y''(x)= \biggl(\frac{l(l+1)}{x^{2}}+V(x)-E \biggr)y(x),\qquad y(0)=0, $$
(1)

where \(V(x)\) and E are the potential and energy, respectively. The second additional condition is obtained from the physical meaning of the problem. The numerical solution of equations of type (1) is of special importance for applied scientists, because they appear in many areas of science when formulating natural problems such as in chemical physics and in quantum physics, among others. Since the analytical solution for problem (1) has a special and complex structure, its numerical approximation and the construction of accurate approximation methods are of great importance. In recent years, various methods have been designed by different authors to solve the Schrödinger equation numerically. We will mention a limited number of these methods, such as Runge–Kutta methods [1–12], hybrid methods [21–23], EF and TF methods [13–20].

Since the method we propose here belongs to the category of linear multistep multiderivative methods, we turn our attention to presenting some properties of these methods. Consider the multiderivative symmetric multistep Obrechkoff method defined as

$$ \sum_{j=0}^{k}\alpha _{j}y_{n-j+1}=\sum_{i=1}^{l}h^{2i} \sum_{j=0}^{k} \beta _{ij} y_{n-j+1}^{(2i)}. $$
(2)

In the case \(\alpha _{j}=\alpha _{k-j}\) and \(\beta _{ij}=\beta _{i,k-j}\), for \(j=0,1,2,\ldots ,k\), method (2) will be symmetric. Also, its order will be q, provided the truncation error is

$$ \mathrm{TE}=C_{q+2}h^{q+2}y^{(q+2)}(\eta ),\quad x_{n-k+1}< \eta < x_{n+1}, $$

in which \(C_{q+2}\) is a constant. To study the properties of stability of a method for solving second-order differential equations, Lambert and Watson [10] offered the scalar test equation

$$ y''=-\omega ^{2}y,\quad \omega \in \mathbb{R}. $$
(3)

If we apply (2) to (3), then we have the characteristic equation

$$ \rho (\xi )-\sum_{i=1}^{l}(-1)^{i}v^{2i} \sigma _{i}(\xi )=0, $$
(4)

in which \(v=\omega h\) and

$$ \rho (\xi )=\sum_{j=0}^{k}\alpha _{j}\xi ^{k-j}, \qquad \sigma _{i}( \xi )= \sum _{j=0}^{k}\beta _{ij}\xi ^{k-j},\quad i=1,2,\ldots ,l. $$

Definition 1.1

The interval \((0,v_{0}^{2})\) is called the interval of periodicity of method (2) provided for each \(v^{2}\) in this interval (4) has complex roots so that at least two of the roots are on the unit circle and the rest are inside the unit circle. Also, if the interval of periodicity is \((0,\infty )\), then method (2) has the property of P-stability.

In general, if we apply a 2k-step symmetric scheme to (3), its difference equation is obtained in the form

$$ A_{k}(v) (y_{n+k}+y_{n-k} )+ \cdots +A_{1}(v) (y_{n+1}+y_{n-1} )+A_{0}(v)y_{n}=0, $$
(5)

in which \(A_{i}(v)\), \(i=0,1,\ldots ,k\), are polynomials depending on v. In addition, CE (the characteristic equation) corresponding to the difference equation (5) is

$$ A_{k}(v) \bigl(s^{k}+s^{-k} \bigr)+\cdots +A_{1}(v) \bigl(s+s^{-1} \bigr)+A_{0}(v)=0. $$
(6)

Definition 1.2

For any scheme with CE (6), PL (phase-lag) is defined as the first term in the expansion of

$$ t=v-\theta (v), $$

where \(\theta (v)\) is a real function of v. If we can write \(t=O(v^{q+1})\) as \(v\rightarrow \infty \), then the order of PL is q.

Theorem 1.3

The symmetric 2k-step scheme with CE (6) has PL order q and PL constant c, where

$$ -cv^{q+2}+O\bigl(v^{q+4}\bigr)= \frac{\sum_{i=1}^{k}2A_{i}(v)\cos (i v)+A_{0}(v)}{\sum_{i=1}^{k}2i^{2} A_{i}(v)}. $$

Proof

See [19]. □

Achieving the P-stability in numerical schemes is of great importance because with P-stability property, we can say with confidence that the step-size constraint is eliminated. In other words, differential equations with extreme oscillations can be easily solved with P-stable methods, and the desired solution can be approximated accurately. Of course, the P-stability property is a general concept and is used for differential equations involving multiple frequencies. The concept of singular P-stability has been applied to problems with only one frequency. So when we exclusively talk about the interval and distinguish it from the periodicity interval, we are, in fact, talking about the same concepts, and there is no difference between the P-stability and the singular P-stability. Indeed, singular P-stability is the same as P-stability with one frequency. On the other hand, given that the Schrödinger equation discussed in this paper has only one frequency, we use the expression singular P-stability. We will show this property in the section devoted to the periodicity analysis.

The paper is organized as follows. Introduction and review of multiderivative methods are presented in Sect. 1. In Sect. 2, we propose the main method, and its coefficients will be produced with a new approach. Periodicity analysis and Schrödinger error coefficient analysis are provided in Sect. 3. Finally, the efficiency of the new scheme is demonstrated in Sect. 4 by implementing the new method on the Schrödinger equation with several energy levels.

2 Development and analysis

2.1 Development

Since the main purpose of this paper is to solve numerically (1) using symmetric multiderivative multistep methods, we consider an eight-step fourth-derivative method of the form

$$ \begin{aligned} y_{n\pm 4}+a_{3}y_{n\pm 3}+a_{2}y_{n\pm 2}+a_{1}y_{n\pm 1}+a_{0}y_{n} &=h^{2} \bigl(b_{3}y''_{n\pm 3}+b_{2}y''_{n\pm 2}+b_{1}y''_{n\pm 1}+b_{0}y''_{n} \bigr) \\ &\quad {}+h^{4} \bigl(c_{3}y^{(4)}_{n\pm 3}+c_{2}y^{(4)}_{n\pm 2}+c_{1}y^{(4)}_{n \pm 1}+c_{0}y^{(4)}_{n} \bigr), \end{aligned} $$
(7)

where

$$\begin{aligned}& c_{3}=\frac{1}{500},\qquad c_{2}=- \frac{1}{500},\qquad c_{1}= \frac{1}{100},\qquad c_{0}=-\frac{1}{250}, \\& y_{n\pm i}=y_{n+i}+y_{n-i},\quad i=1,2,3,4, \end{aligned}$$

and \(a_{j}\), \(b_{j}\), \(j=0,1,2,3\), are real constant coefficients that should be computed. It is natural that all the properties and characteristics of any numerical method are deduced from its coefficients. However, the coefficients must be carefully generated in order to achieve superior properties. In this paper, several goals are pursued simultaneously so that we can produce a better and more accurate method. Not only do we want to control the interval of periodicity so that \((0,+\infty )\) is produced, but also we intend to have the Schrödinger error coefficient reduced. Applying the new method (7) to the scalar equation (3), CE of the method (7) will be as follows:

$$ A_{4}(v) (y_{n\pm 4})+A_{3}(v) (y_{n\pm 3})+A_{2}(v) (y_{n\pm 2})+A_{1}(v) (y_{n \pm 1})+A_{0}(v)y_{n}=0, $$
(8)

where

$$\begin{aligned}& A_{0}(v) =a_{0}+b_{0}v^{2}+ \frac{1}{250}v^{4}, \\& A_{1}(v) =a_{1}+b_{1}v^{2}- \frac{1}{100}v^{4}, \\& A_{2}(v) =a_{2}+b_{2}v^{2}+ \frac{1}{500}v^{4}, \\& A_{3}(v) =a_{3}+b_{3}v^{2}- \frac{1}{500}v^{4}, \\& A_{4}(v) =1. \end{aligned}$$

Now, to control the interval of periodicity, we will generate the coefficients so that CE of the scheme is

$$ \lambda ^{8}-2\cos (4v)\lambda ^{4}+1=0. $$
(9)

To this end, the polynomials \(A_{1}(v)\), \(A_{2}(v)\), and \(A_{3}(v)\) of the characteristic function must be equal to zero, which produces three equations. On the other hand, because the new method has eight free parameters, we need five more independent linear equations to obtain unique coefficients. Now, to control the Schrödinger error coefficient, suppose that PL and its derivatives up to four are zero. This leads to 8 equations with 8 unknowns. According to Theorem 1.3 with \(k=4\), PL is

$$ \mathrm{PL}= \frac{2A_{1}(v)\cos (v)+2A_{2}(v)\cos (2v)+2A_{3}(v)\cos (3v)+2A_{4}(v)\cos (4v)+A_{0}}{2A_{1}(v)+8A_{2}(v)+18A_{3}(v)+32A_{4}(v)}. $$

Using Maple 18, we have solved this system, and the obtained coefficients are given in Appendix A. The Taylor series expansions of the coefficients are

$$\begin{aligned}& a_{0}= -2+\frac{794\text{,}137}{47\text{,}250}v^{2}- \frac{1\text{,}190\text{,}687}{70\text{,}875}v^{4}+ \frac{109\text{,}930\text{,}193}{15\text{,}592\text{,}500}v^{6}- \cdots , \\& a_{1}= -\frac{424\text{,}453}{63\text{,}000}v^{2}+ \frac{108\text{,}841}{13\text{,}500}v^{4}- \frac{56\text{,}802\text{,}077}{15\text{,}592\text{,}500}v^{6}+ \cdots , \\& a_{2}= -\frac{13\text{,}103}{157\text{,}500}v^{2}-\frac{13\text{,}087}{236\text{,}250}v^{4} + \frac{595\text{,}357}{4\text{,}455\text{,}000}v^{6}-\cdots , \\& a_{3}= -\frac{1\text{,}495\text{,}957}{945\text{,}000}v^{2}+ \frac{557\text{,}087}{1\text{,}417\text{,}500}v^{4} - \frac{246\text{,}769}{15\text{,}592\text{,}500}v^{6}+ \cdots , \\& b_{0}= -\frac{38\text{,}137}{47\text{,}250}-\frac{643\text{,}193}{141\text{,}750}v^{2} + \frac{67\text{,}477\text{,}807}{15\text{,}592\text{,}500}v^{4}- \frac{811\text{,}862\text{,}971}{521\text{,}235\text{,}000}v^{6}+ \cdots , \\& b_{1}= \frac{424\text{,}453}{63\text{,}000}-\frac{54\text{,}353}{6750}v^{2} + \frac{56\text{,}802\text{,}077}{15\text{,}592\text{,}500}v^{4}- \frac{77\text{,}581\text{,}573}{90\text{,}090\text{,}000}v^{6}+ \cdots , \\& b_{2}= \frac{13\text{,}103}{157\text{,}500}+\frac{25\text{,}229}{472\text{,}500}v^{2} - \frac{595\text{,}357}{4\text{,}455\text{,}000}v^{4}+\frac{21\text{,}123\text{,}139}{1\text{,}351\text{,}350\text{,}000}v^{6}- \cdots , \\& b_{3}= \frac{1\text{,}495\text{,}957}{945\text{,}000}-\frac{138\text{,}563}{354\text{,}375}v^{2}+ \frac{246\text{,}769}{15\text{,}592\text{,}500}v^{4}-\frac{39\text{,}543\text{,}703}{36\text{,}486\text{,}450\text{,}000}v^{6}- \cdots . \end{aligned}$$

The local truncation error of (7), namely \(\mathrm{LTE} _{\mathrm{New}}\), is obtained using the usual Taylor series expansion and is given by

$$ \begin{aligned} \mathrm{LTE}_{\mathrm{New}}&=-\frac{326\text{,}687}{5\text{,}670\text{,}000}h^{10} \bigl[\omega ^{10}y_{n}+5 \omega ^{8}y^{(2)}_{n}+10 \omega ^{6}y^{(4)}_{n}+10\omega ^{4}y^{(6)}_{n} +5\omega ^{2}y^{(8)}_{n}+y^{(10)}_{n} \bigr] \\ &\quad {}+O \bigl(h^{12} \bigr). \end{aligned} $$
(10)

Then the local truncation error of the classical form of (7) (the same structure with constant coefficients), namely \(\mathrm{LTE} _{\mathrm{Class}}\), will be

$$ \mathrm{LTE}_{\mathrm{Class}}=- \frac{326\text{,}687}{5\text{,}670\text{,}000}h^{10}y^{(10)}_{n}+O \bigl(h^{12} \bigr). $$
(11)

To study the efficiency of the new scheme for solving (1), we have to have its Schrödinger error. To this end, we can transfer (1) to

$$ y''=f(x)y(x). $$

Now, as per Ixaru and Rizea’s paper [9], \(f(x)\) can be changed to \(f(x)=g(x)+G\), in which \(g(x)=V(x)-V_{c}\), and \(V_{c}\) is the constant approximation of the potential and \(G=v^{2}=V_{c}-E\) (see [9]).

Theorem 2.1

The Schrödinger error of the new method increases as the second power of G.

Proof

We know that, for any eighth algebraic-order linear multistep method, the general form of the LTEs is given by

$$ \mathrm{LTE}=h^{10}\sum_{i=0}^{j}N_{i}G^{i}, $$

where, in the classical case, \(N_{i}\) are constant numbers and in the frequency dependent cases, \(N_{i}\) are functions of v and G, and j is the maximum power of G. Since \(G=V_{c}-E\), we can assume two cases according to the values of E:

  1. 1.

    \(G = V_{c} - E \approx 0\).

  2. 2.

    \(G\gg 0\) or \(G\ll 0\), where \(|G|\) has a large value.

If \(G = V_{c} - E \approx 0\), then we have \(G^{r}=0\), \(r=1,2,\ldots \) . Obviously, the method with asymptotic form of LTE, which includes the minimum power of G, is the most accurate one. Now, \(G = V_{c} - E \approx 0\) implies \(\mathrm{LTE}=h^{10}N_{0}\), where \(N_{0}\) in (10) and (11) is \(-\frac{326\text{,}687}{5\text{,}670\text{,}000} [\omega ^{10}y_{n}+5\omega ^{8}y^{(2)}_{n}+10 \omega ^{6}y^{(4)}_{n}+10\omega ^{4}y^{(6)}_{n} +5\omega ^{2}y^{(8)}_{n}+y^{(10)}_{n} ]\) and \(-\frac{326\text{,}687}{5\text{,}670\text{,}000}y^{(10)}_{n}\), respectively. For the case \(G\gg 0\) or \(G\ll 0\), firstly, we should calculate higher derivatives of y. By simple calculation, we have

$$\begin{aligned}& y^{(2)}(x)= \bigl(V(x)-V_{c}+G\bigr)y(x), \\& y^{(4)}(x)= \biggl(\frac{d^{2}}{dx^{2}}V(x) \biggr)y(x)+2 \biggl( \frac{d}{dx}V(x) \biggr) \biggl(\frac{d}{dx}y(x) \biggr)+ \bigl(V (x)- V_{c} + G \bigr) \biggl(\frac{d^{2}}{dx^{2}}y(x) \biggr), \end{aligned}$$

etc. Therefore, by substituting the above derivatives in LTE, we can get the Schrödinger error for the new scheme. Hence, the principal term of the Schrödinger error of the new method is

$$ \mathrm{Err}_{\mathrm{Sch}}=\frac{326\text{,}687}{354\text{,}375} \biggl( \frac{d^{4}}{dx^{4}}g(x) \biggr)y(x)h^{10}G^{2}, $$

and thus, for this method, the error increases as the second power of G. □

2.2 Periodicity analysis

In order to confidently implement a numerical method on problems, we must have accurate information about how the method behaves. More specifically, we need to know the stability or instability, convergence or divergence of the method and even the maximum step length. For such studies, we must calculate the stability function of the method and then generate the stability region. This helps us to easily compare the proposed method with other methods. To generate the stability area of the scheme, we apply the main method to the problem

$$ y''(x)=-\phi ^{2}y(x) $$
(12)

and obtain its CE. Note that the frequency used in (12) is different from the frequency used in (3). If we assume \(s=\phi h\) and \(v=\omega h\), then we will produce y-axes with v and x-axis with s in the stability region. Therefore, the proposed method can be used for problems that have two frequencies. Applying (7) to (12), we will have

$$ \sum_{i=1}^{4}A_{i}(s,v) (y_{n+i}+y_{n-i} )+A_{0}(s,v)y_{n}=0, $$
(13)

in which \(v=\omega h\), \(s=\phi h\), and \(A_{i}(s,v)\) are functions of s and v. To save space, \(A_{i}(s,v)\) are given in Appendix B.

As explained at the beginning of this section, the stability function of the new method has two parameters, s and v, each of which is derived from a frequency. We are looking for P-stability of the method to solve more problems with the proposed method. The colored parts in Fig. 1, which is the figure for the stability area of the method, show the stability parts, and the white parts show the instability region of the method. The method will be P-stable when the entire \(s-v\) plane is colored. But this is when we talk about two-frequency issues. Since the equation discussed in this paper has one frequency, the concept of P-stability changes to the one of singular P-stability. It is enough that the bisector of the first quarter belongs to the colored part. Hence, the method is singular P-stable. Now we prove the property of singular P-stability in the next theorem algebraically.

Figure 1
figure 1

The periodicity region of the new scheme

Full size image

Theorem 2.2

The explicit eight-step scheme (7) is singularly P-stable.

Proof

If we take \(s=v\), then CE of (7) can be written as

$$ \mathrm{CE}=\lambda ^{8}-2\lambda ^{4} \bigl(8\cos ^{4} v-8\cos ^{2} v+1 \bigr)+1. $$

Since \(\cos (4v)=8\cos ^{4} v-8\cos ^{2} v+1\), CE of the new scheme may be rewritten as

$$ \mathrm{CE}=\lambda ^{8}-2\lambda ^{4}\cos (4v)+1. $$
(14)

Note that (14) is a polynomial of degree eight with real coefficients. So, it has eight roots namely \(\lambda _{i}\), \(i=0,1,2,\ldots ,7\). According to these roots, \(\mathrm{CE}=0\) is equivalent to

$$ \prod_{k=0}^{3} (\lambda -\lambda _{2k} ) (\lambda - \lambda _{2k+1} )=0. $$

If we assume \(\lambda _{2k}=\exp (I\frac{2k\pi }{m} )\exp (Iv)\) (see [22]), where \(k=0,1,2,3\) and \(I=\sqrt{-1}\), then

$$ \begin{aligned} &(\lambda _{2k} )^{8}-2\cos (mv) (\lambda _{2k} )^{4}+1 \\ &\quad = \biggl[\exp \biggl(I\frac{2k\pi }{m} \biggr)\exp (Iv) \biggr]^{8}-2 \cos (mv) \biggl[\exp \biggl(I\frac{2k\pi }{m} \biggr) \exp (Iv) \biggr]^{4}+1 \\ &\quad =\exp (I2mv)-2\cos (mv)\exp (Imv)+1 \\ &\quad =0. \end{aligned} $$
(15)

Also, if for \(k=0,1,2,3\) we set \(\lambda _{2k+1}=\exp (I\frac{2k\pi }{m} )\exp (-Iv)\), then we have

$$ \begin{aligned} &(\lambda _{2k+1} )^{8}-2\cos (mv) (\lambda _{2k+1} )^{4}+1 \\ &\quad = \biggl[\exp \biggl(I\frac{2k\pi }{m} \biggr)\exp (-Iv) \biggr]^{8}-2 \cos (mv) \biggl[\exp \biggl(I\frac{2k\pi }{m} \biggr) \exp (-Iv) \biggr]^{4}+1 \\ &\quad =\exp (I2mv)-2\cos (mv)\exp (-Imv)+1 \\ &\quad =0. \end{aligned} $$
(16)

So, from (15) and (16), the characteristic roots of the new method are obtained as

$$\begin{aligned}& \lambda _{0}=\exp (Iv), \qquad \lambda _{1}=\exp (-Iv),\qquad \lambda _{2}=I \exp (Iv),\qquad \lambda _{3}=I\exp (-iv), \\& \lambda _{4}=-\exp (Iv), \qquad \lambda _{5}=-\exp (-Iv),\qquad \lambda _{6}=-I \exp (Iv),\qquad \lambda _{7}=-I\exp (-iv). \end{aligned}$$

Clearly, for these roots we have \(|\lambda _{0}|=|\lambda _{1}|=1\) and \(|\lambda _{i}|\leq 1\), \(i=2,3,\ldots ,7\). Accordingly, when \(s=v\), the periodicity interval of the new scheme is equal to \((0,\infty )\), and the method is P-stable. Therefore, it is singularly P-stable. □

Remark 2.3

The characteristic equation (14) is the same as the one obtained in [18, Theorem 5]. To explain this, since to prove the P-stability property of a linear multistep method, we have to show that the characteristic roots have modulus less (or equal) than one. In other words, they must lie in or on the unit circle. Although the structure of the proposed method in [18] is different from the method presented in this paper, we know the characteristic equation of an eight-step linear multistep method is equal to (8), and also its two variable characteristic equation is (13). Singularly P-stability means P-stability when \(s=v\). To generate a system of equations for calculating the coefficients of the method, we have assumed that \(A_{1}(v)\), \(A_{2}(v)\), and \(A_{3}(v)\) are equal to zero and the remaining equations are obtained from vanishing phase-lag and some of its derivatives. Now, by substituting \(s=v\) in \(A_{i}(s,v)\), \(i=0,1,2,3,4\), we have \(y_{n+4}+B(v)y_{n}+y_{n-4}=0\), where \(B(v)=-2(8\cos ^{4} v-8\cos ^{2} v+1)\). Hence, the characteristic polynomial will be \(\lambda ^{8}+B(v)\lambda ^{4}+1=0\), and then all characteristic roots are equal or less than one.

3 Numerical results

This section is devoted to implementing the method built on the Schrödinger problem. In order to better judge the quality of the method, we have implemented it on two energy levels \(E=341.495874\) and \(E=989.701916\). We have compared the produced results with those of the other methods which are of the same order as the new one, and we showed the superiority of the new method. Since we need a value ω in numerical implementation, we need to specify this value. Different methods have been proposed in different papers to consider ω. We may mention \(\omega =\sqrt{|V(x)-E|}\) in which \(v(x)\) is the potential; in this article, we will use the Woods–Saxon potential function. The definition of the function V is (see Fig. 2)

$$ V(x)=u_{0}(1+z)^{-1} \bigl[1-z \bigl(a(1+z) \bigr)^{-1} \bigr],\quad z=e^{\frac{x-x_{0}}{a}}, a = 0.6, x_{0} = 7.0, u_{0} =-50. $$
(17)

Here, in order to implement and produce numerical results of the new method (see [8]), we let

$$ \omega = \textstyle\begin{cases} \sqrt{E-50},&0\leq x\leq 6.5-2h, \\ \sqrt{E-37.5},&x=6.5-h, \\ \sqrt{E-25},&x=6.5, \\ \sqrt{E-12.5},&x=6.5+h, \\ \sqrt{E},&6.5+2h\leq x\leq 15. \end{cases} $$

This value is considered for the interval \([0,15]\).

Figure 2
figure 2

The Woods–Saxon potential

Full size image

3.1 Schrödinger equation-resonance problem

Consider the numerical solution of the radial time-independent Schrödinger equation (1) in the well-known case of the Woods–Saxon potential (17). To numerically solve this problem, we should approximate the true or infinite interval of integration by applying a finite interval. Since we need to illustrate our problem numerically, we take the domain of integration as \(x\in [0,15]\). We consider (1) in a relatively large domain of energies, i.e., \(E \in [1,1000]\). When it comes to positive energies, \(E=k^{2}\), the potential fades faster than the term \(\frac{l(l+1)}{x^{2}}\), and the Schrödinger equation effectively reduces to

$$ y''(x)= \biggl( \frac{l(l+1)}{x^{2}}-E \biggr)y(x), $$
(18)

for x greater than some value X. Equation (18) has two linearly independent solutions \(kxj_{l}(kx)\) and \(kxn_{l}(kx)\), where \(j_{l}\) and \(n_{l}\) are the spherical Bessel and Neumann functions, respectively. When \(x\rightarrow \infty \), the solution takes the asymptotic form

$$\begin{aligned} y(x) \approx & A k x j_{l}(k x)-B k x n_{l} (k x) \\ \approx & D \bigl[\sin (k x-\pi l/2)+\tan (\delta _{ l})\cos (kx- \pi l/2)\bigr], \end{aligned}$$

where \(\delta _{ l}\) is called scattering phase shift that may be calculated from the formula

$$ \tan (\delta _{ l} )= \frac{y(x_{1}) S(x_{2})-y(x_{2}) S(x_{1})}{y(x_{2}) C(x_{1})-y(x_{1}) C(x_{2})}, $$

where \(x_{1}\) and \(x_{2}\) are distinct points in the asymptotic region (we choose \(x_{1}\) as the right-hand end point of the interval of integration and \(x_{2}=x_{1}-h\)) with \(S(x)=kxj_{l}(kx)\) and \(C(x)=-kxn_{l} (kx)\). The problem is dealt with as an initial value problem; thus, we have to have \(y_{0}\). We obtain \(y_{0}\) from the initial condition. With these starting values, we evaluate at \(x_{1}\) of the asymptotic region the phase shift \(\delta _{l}\).

For positive energies, we have resonance problem which is comprised either of finding the phase-shift \(\delta _{l}\) or finding those E, for \(E\in [1,1000]\), at which \(\delta _{l}=\frac{\pi }{2}\). We solve the problem when the positive energies lie under potential barrier. The boundary conditions for this problem are

$$ y(0)=0,\qquad y(x)=\cos (\sqrt{E} x)\quad \text{for large }x. $$

The following methods have been used to compare the new method:

  • The twelve-step thirteenth algebraic-order method developed by Quinlan and Tremaine [15] which is indicated as I;

  • The eight-step method with PL and its first derivative equal to zero obtained in [5] which is indicated as II;

  • The ten-step method with PL and its first, second, and third derivatives equal to zero obtained in [7] which is indicated as III;

  • The exponentially-fitted four-step method developed by Raptis [16] which is indicated as IV;

  • The eight-step method with PL and its first and second derivative equal to zero obtained in [6] which is indicated as V;

  • The trigonometrically-fitted six-step method developed by Wang [22] which is indicated as VI;

  • The new explicit eight-step singularly P-stable multiderivative method developed in this paper which is indicated as New.

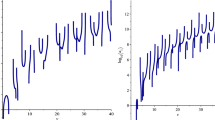
The computed eigenenergies are compared with the exact ones. In Fig. 3, we present the digits of accuracy given by \(\log _{10}(\mathrm{Err})\), where

$$ \mathrm{Err} = \vert E_{\mathrm{calculated}}-E_{\mathrm{accurate}} \vert , $$
(19)

versus the CPU times for several methods used for calculating the eigenenergy \(E_{2}=341.495874\). In Fig. 4, we present the maximum absolute error \(\log _{10}(\mathrm{Err})\) of the eigenenergy \(E_{3}=989.701916\). In addition, it is pointed out in Fig. 5 that the new method shows a better long time behavior than other ones when applied to the Schrödinger equation for various eigenenergies. All computations were carried out on a PC(i5 @2.67 GHz) using Maple 18 with 16 significant digits accuracy (IEEE standard).

Figure 3
figure 3

Digits of accuracy versus CPU times (in seconds) for different methods, corresponding to the eigenvalue \(E_{2}=341.495874\)

Full size image
Figure 4
figure 4

Digits of accuracy versus CPU times (in seconds) for different methods, corresponding to the eigenvalue \(E_{3}=989.701916\)

Full size image
Figure 5
figure 5

Digits of accuracy versus energy levels for different methods

Full size image

4 Conclusion

By using higher-order derivatives in classical methods and combining them with the system of PL and its derivatives, we were able to create a new high-efficiency method (with lower CPU time) that can approximate different types of energy levels of the Schrödinger equation with high accuracy. In fact, by keeping the computation time low, we were able to produce better quality results, which is very important in numerical analysis.