Mathematical analysis of a fractional resource-consumer model with disease developed in consumer

Abstract

The research presents a qualitative investigation of a fractional-order consumer-resource system with the hunting cooperation interaction functional and an infection developed in the resources population. The existence of the equilibria is discussed where there are many scenarios that have been distinguished as the extinction of both populations, the extinction of the infection, the persistence of the infection, and the two populations. The influence of the hunting cooperation interaction functional is also investigated where it can influence the existence of equilibria and their stability. A proper numerical scheme is used for building a proper graphical representation for the goal of confirming the theoretical results.

1 Introduction

Interaction functional is the number of resources (prey) successfully hunted per predator consumer, and it highlights the degree of successfulness of the consumer attacks to the predators, also the behavior of both resources and consumers. How to choose a reasonable interaction function in population dynamics is an interesting subject which gets increased attention in mathematics ecology, biology, and eco-epidemiology. One of the first interaction functionals is the Holling type functional response where he proposes three different interaction functionals for modeling different behavior of some animals. His functionals were used widely, see for example the papers [1–4]. The main remark for Holling interaction functional is the dependence of the behavior of the resources population, which has been named the prey dependent interaction functional. The dependence can be on the consumer population also, there are some works that model this case as Hassell–Varley intermingling functional [5, 6], ratio-dependent intermingling functional [7], Beddington–DeAngelis intermingling functional [8], Crowley–Martin intermingling functional [9], and fractional calculus or different applications [10–34].

In nature, the consumers that live in packs, such as lions, hyenas, African wild dogs, wolves, orcas, give increased foraging adequacy. These living organisms have high-efficiency rates, and their behavior is called cooperation. The responsible interaction functional was derived by Conser et al. [35], and it is expressed in the following structure:

$$ \Psi (N,P)=\frac{Ce_{0}NP}{1+hCe_{0}NP}, $$

(1)

where N is the resource density, P is the consumer density, $e_{0}$ is the encounter coefficient per consumer per resource unit time, h is the handling period per resource item, C is the fraction of the resource item consumed per consumer per encounter. Many ongoing research works analyze the rich behavior by considering the interaction functional (2), see for example [36, 37]. Another interaction functional appears in the interface to model this behavior, which is investigated and studied in the paper [38]. The considered interaction functional is

$$ \Psi (N,P)=(\lambda +aP)N, $$

(2)

where λ is the hunting coefficient per consumer, a is the hunting cooperation rate. Based on the above discussion, we set the following model:

$$ \textstyle\begin{cases} \frac{dN}{dt}= rN(1-\frac{N}{k})-(\lambda +aP)NP, \\ \frac{dP}{dt}= e(\lambda +aP)NP-\mu P, \end{cases} $$

(3)

where $r(1-\frac{N}{k})$ is the logistic reproduction of the resources with the coefficient r and the environmental carrying capacity k. μ is the mortality coefficient for the consumer, e is the conversion coefficient. This case of interaction has been studied on many occasions, see [37, 39–45], which shows the huge importance of such interaction. Further, the influence of infectious diseases in the evolution of predator–prey interaction is seen, for example, in the papers [46–49]. In this research, we consider an infection developed in the consumer population, which means that this population will be split into two categories, susceptible consumer S and infected consumer I, i.e., $P=S+I$. The two categories cooperate in hunting. Also, we presume that there is no vertical transmission, which means that the newborn consumer cannot be infected. Further, we presume that both types of consumers have the same efficiency of hunting, which highlights that this infection cannot influence the performance of the consumer in hunting. As a result, we consider the following model:

$$ \textstyle\begin{cases} \frac{dN}{dt}= rN(1-\frac{N}{k})-(\lambda +a(S+I))N(S+I), \\ \frac{dS}{dt}= e(\lambda +a(S+I))N(S+I)-\beta SI -\mu S, \\ \frac{dI}{dt}= \beta SI -\eta I -\mu I. \end{cases} $$

(4)

β is the transmission rate of this infection, η is the mortality rate of this infection for the consumer. It is highlighted in [1, 2] that the time-fractional derivative is responsible for biological fluctuation in different cases and explains the influence of memory on the dynamical system. The memory rate is the order of this derivative, the memory function is the kernel of this derivative. The influence of memory on the biological and ecological interaction has attracted many researchers, we mention a few [1–4, 50–57]. For more examples of modeling animals social behavior and other approximations, we cite the research works [58–69]. As a result, we consider it in our mathematical model which can be expressed as

$$ \textstyle\begin{cases} \frac{d^{\alpha }N}{dt}= rN(1-\frac{N}{k})-(\lambda +a(S+I))N(S+I), \\ \frac{d^{\alpha }S}{dt}= e(\lambda +a(S+I))N(S+I)-\beta SI -\mu S, \\ \frac{d^{\alpha }I}{dt}= \beta SI -\eta I -\mu I, \end{cases} $$

(5)

where $\frac{d^{\alpha }}{dt}$ is Caputo’s derivative with respect to t, which is defined by

$$ \frac{d^{\alpha }\varphi }{dt} (t)=\frac{1}{\Gamma (m-\alpha )} \int _{0}^{t}\frac{\varphi ^{m}(s)}{(t-s)^{\alpha +s-i}}\,ds,\quad m-1< \alpha < m, m\in \mathbb{N} . $$

Our goal is to investigate maximally model (5), thus we will provide a mathematical and numerical investigation of this model. Also, we will use these results for our biological interpretation and provide some useful suggestions for conserving the ecological species. For that purpose, we arrange the manuscript as follows:

• The 2nd section is devoted to calculating the equilibria of (5) and the epidemiological, ecological relevance of these equilibria.

• The stability of the equilibria is offered in Sect. 3 where the linearized stability is offered.

• The numerical scheme is provided in Sect. 4 using the trapezoidal product-integration rule.

• Some numerical representations are provided for the biological relevance, which helps in confirming the mathematical results and in giving a proper biological conclusion.

2 Mathematical analysis and asymptotic behaviors of the solution

2.1 Equilibria of the model

Obviously, the equilibrium points are positive solutions of the system

$$ \textstyle\begin{cases} 0= rN(1-\frac{N}{k})-(\lambda +a(S+I))N(S+I), \\ 0= e(\lambda +a(S+I))N(S+I)-\beta SI -\mu S, \\ 0= \beta SI -\eta I -\mu I. \end{cases} $$

(6)

As a first remark we can derive that (6) has $\Lambda _{0}=(0,0,0)$, $\Lambda _{1}=(k,0,0)$ as equilibrium points. Now we look for the disease-free equilibrium (DFE) which is written as $\Lambda _{3}=(N,S,0)$, where $(N,S)$ is the positive solution of the following system:

$$ \textstyle\begin{cases} 0= erN(1-\frac{N}{k})-e(\lambda +aS)NS, \\ 0= e(\lambda +aS)NS-\mu S. \end{cases} $$

(7)

By summing the two equations in (7), we get

$$ S=\frac{erN}{\mu }\biggl(1-\frac{N}{k}\biggr). $$

By replacing this result in the first equation of (6), we find the following third-order polynomial:

$$ \frac{ae^{2}r}{k\mu ^{2}}N^{3}-\frac{ae^{2}r}{\mu ^{2}}N^{2}- \frac{\lambda e}{\mu }N+1=0. $$

(8)

As a first remark, and using the Descartes rule, we can deduce that equation (8) has either two or no positive solutions in the positive quadrant. The number of positive solutions in the interval $[0,k]$ dominates the number of the DFEs. Now we set

$$ f(N)=\frac{ae^{2}r}{k\mu ^{2}}N^{3}-\frac{ae^{2}r}{\mu ^{2}}N^{2}- \frac{\lambda e}{\mu }N+1. $$

At first, we can highlight that f verifies

$$ f(0)=1>0,\qquad f(k)=-\frac{\lambda k e}{\mu }+1, $$

also,

$$ f'(N)=\frac{3ae^{2}r}{k\mu ^{2}}N^{2}- \frac{2ae^{2}r}{\mu ^{2}}N- \frac{\lambda e}{\mu } $$

and

$$ f'(0)=-\frac{\lambda e}{\mu }. $$

Using the fact that $f(x)$ is a third-order polynomial and using $f'(0)<0$, we can deduce that f has a unique global minimum at $N_{\min }$, where

$$ N_{\min }= \frac{aerk+\sqrt{a^{2}e^{2}r^{2}k^{2}+3\lambda a e r k \mu }}{3aer}. $$

By a simple discussion on the positivity of $f(N_{\min })$ and $f(k)$, we resume the existence conditions for the DFEs (see also Fig. 1) in the following theorem.

Figure 1

Existence of DFE for the values $r=1.2$, $\lambda =0.02$, $\mu =2.5$, $e=0.8$, $a=0.5$, $\beta =3.5$, $\eta =0.5$, where for $(A)$ we considered $k=8.5$. We have no existence of the DFE for $(B)$, we take $k=10.15$, hence we have the existence of a unique DFE. For $k=12.5$, we guarantee the existence of two DFEs

Theorem 2.1

The existence of the DFE for system (5) is arranged in the following aspects:

• (i) System (5) has no DFE if

  $$ \biggl(N_{\min }< k\textit{ and }\frac{ae^{2}r}{k\mu ^{2}}N^{3} _{\min }+1> \frac{ae^{2}r}{\mu ^{2}}N^{2} _{\min }+ \frac{\lambda e}{\mu }N_{\min } \biggr). $$

• (ii) System (5) has one DFE denoted by $\Lambda _{3} =(N_{3},S_{3},0)$ if $\mu <\lambda ke$ or

  $$ \biggl(N_{\min }< k\textit{ and }\frac{ae^{2}r}{k\mu ^{2}}N^{3} _{\min }+1= \frac{ae^{2}r}{\mu ^{2}}N^{2} _{\min }+ \frac{\lambda e}{\mu }N_{\min } \biggr). $$

• (iii) System (5) has two DFEs denoted by $\Lambda _{3} =(N_{3},S_{3},0)$ and $\Lambda _{4} =(N_{4},S_{4},0)$ if $\mu >\lambda ke$, and

  $$ \biggl(N_{\min }< k \textit{ and }\frac{ae^{2}r}{k\mu ^{2}}N^{3} _{\min }+1< \frac{ae^{2}r}{\mu ^{2}}N^{2} _{\min }+ \frac{\lambda e}{\mu }N_{\min } \biggr). $$

Next, we investigate the existence of endemic equilibrium EE which highlights the persistence of the three populations. From the third equation of (6) we deduce that the susceptible density equilibrium is

$$ S^{*}=\frac{\mu +\eta }{\beta }. $$

Note that the infected density equilibrium and the resource density equilibrium are the solution of the system

$$ \textstyle\begin{cases} 0= r(1-\frac{N}{k})-(\lambda +a(S^{*}+I))(S^{*}+I), \\ 0= e(\lambda +a(S^{*}+I))N(S^{*}+I)-(\beta I+\mu ) S^{*}. \end{cases} $$

(9)

From the first equation of (9) we get

$$ N=f_{1}(I)=k \biggl(1-\frac{\lambda }{r}S^{*}- \frac{a}{r}\bigl(S^{*}\bigr)^{2} \biggr)-( \lambda +2a)\frac{kI}{r}-\frac{ka}{r}I^{2}. $$

(10)

It is easy to see that $f_{1}$ is a strictly decreasing concave function; also, for guaranteeing the positivity of $f_{1}$ for some values of I, we assume that $1>\frac{\lambda }{r}S^{*}+\frac{a}{r}(S^{*})^{2}$ and intersects the horizontal axis at

$$ I_{\mathrm{int}}=a^{-1} \bigl[-(\lambda +2a)+\sqrt{(\lambda +2a)^{2}+4a\bigl(r- \lambda S^{*}-a\bigl(S^{*} \bigr)^{2}\bigr)} \bigr]. $$

Using the second equation of (9), we have

$$ N=f_{2}(I)= \frac{(\beta I+\mu ) S^{*}}{e(\lambda +a(S^{*}+I))(S^{*}+I)}, $$

(11)

which is a positive functional. Under the condition $\beta <\frac{\mu }{S^{*}}$ and $a< a^{*}:=\frac{\mu \lambda -\beta S*\lambda }{\beta (S^{*})^{2}}$, we get that $f_{2}$ is strictly decreasing in I. Hence, we can draw the following result.

Theorem 2.2

Assume that $1>\frac{\lambda }{r}S^{*}+\frac{a}{r}(S^{*})^{2}$, $\beta <\frac{\mu }{S^{*}}$, $a< a^{*}:=\frac{\mu \lambda -\beta S^{*}\lambda }{\beta (S^{*})^{2}}$, then system (5) has an interior equilibrium denoted by $\Lambda ^{*}=(N^{*},S^{*},I^{*})$ where

$$ S^{*}=\frac{\mu +\eta }{\beta },\qquad N^{*}= \frac{(\beta I^{*}+\mu ) S^{*}}{e(\lambda +a(S^{*}+I^{*}))(S^{*}+I^{*})}, $$

and $I^{*}$ is the positive intersection between the graphical representation of $f_{1}$ and $f_{2}$.

2.2 Asymptotic behaviors (5)

In this part, we are interested in determining the asymptotic stability of the equilibria obtained in the previous section.

Letting $(N,S,I)$ be an equilibrium for system (5), the Jacobian matrix (J-matrix) of (5) at $(N,S,I)$ is

$$ J(N,S,I)= \begin{pmatrix} r(1-\frac{2N}{k})-(\lambda +a(S+I))(S+I) & -N(\lambda +2a(S+I)) & -N( \lambda +2a(S+I)) \\ e(\lambda +a(S+I))(S+I) & eN(\lambda +2a(S+I))-\mu -\beta I & eN( \lambda +2a(S+I))-\beta S \\ 0 & \beta I & \beta S-(\mu +\eta ) \end{pmatrix}. $$

(12)

For defining the concept of the local stability for the fractional-order system, we set the following theorem.

Theorem 2.3

At a random equilibrium for fractional system (5), the local stability of the equilibrium occurs if the eigenvalues θ of the J-matrix (12) verify $\vert \arg (\theta ) \vert >\frac{\alpha \pi }{2}$ for each eigenvalue λ of J. The equilibrium for (6) is unstable if $\vert \arg (\theta ) \vert <\frac{\gamma \pi }{2}$ for some eigenvalues θ.

At the origin $\Lambda _{0}$, J-matrix (12) becomes

$$ J(0,0,0)= \begin{pmatrix} r & 0&0 \\ 0 & -\mu & 0 \\ 0 & 0 & -(\mu +\eta ) \end{pmatrix} . $$

(13)

J-matrix (13) has the eigenvalues $\theta _{1}=r>0$, $\theta _{2}=-\mu <0$, $\theta _{3}=-(\mu +\eta )$. This equilibrium is always unstable.

Now, we evaluate the J-matrix at $\Lambda _{1}$, we get

$$ J(k,0,0)= \begin{pmatrix} -r & -k\lambda &-k\lambda \\ 0 & ek\lambda -\mu & ek\lambda \\ 0 & 0 & -(\mu +\eta ) \end{pmatrix} . $$

(14)

J-matrix (14) has the eigenvalues $\theta _{1}=-r<0$, $\theta _{2}=ek\lambda -\mu$, $\theta _{3}=-( \mu +\eta )$. Then the sign of $\theta _{2}$ dominates the stability/instability of the equilibrium $\Lambda _{1}$. Hence,

$$ \theta _{2}= \textstyle\begin{cases} < 0 &\text{for } k< \frac{\mu }{e\lambda } , \\ >0 &\text{for } k>\frac{\mu }{e\lambda } . \end{cases} $$

The stability conditions are summarized in the following lemma.

Lemma 2.4

$\Lambda _{1}$ is locally stable if $k<\frac{\mu }{e\lambda }$ and unstable if $k>\frac{\mu }{e\lambda }$.

Now, we focus on analyzing the stability of $\Lambda _{i}$, $i=3,4$,

$$ J(N_{i},S_{i},0)= \begin{pmatrix} -\frac{rN_{i}}{k} & -N_{i}(\lambda +2aS_{i}) & -N_{i}(\lambda +2aS_{i}) \\ \frac{\mu S_{i}}{N_{i}} & eN_{i}aS_{i} & eN_{i}(\lambda +2aS_{i})- \beta S_{i} \\ 0 & 0 & \beta S_{i}-(\mu +\eta ) \end{pmatrix},\quad i=3,4 . $$

(15)

Obviously, $\theta _{3}=\beta S_{i}-(\mu +\eta )$ can be considered as an eigenvalue of J-matrix (15), hence, if $\beta S_{i}>(\mu +\eta )$, then these equilibria are unstable. Now, we assume that $\beta S_{i}<(\mu +\eta )$, which means that $\theta _{3}<0$, hence the other two eigenvalues dominate the stability of the DFEs. The other two are the solution of the equation

$$ \theta ^{2}-\operatorname{Tr}_{i} \theta +\mathrm{Det}_{i}=0,\quad i=3,4, $$

(16)

where

$$ \textstyle\begin{cases} \operatorname{Tr}_{i}= -\frac{rN_{i}}{k}+ eN_{i}aS_{i} \\ \mathrm{Det}_{i}= -\frac{eraS_{i}N_{i} ^{2}}{k} + \mu S_{i} (\lambda +2aS_{i}) \end{cases}\displaystyle i=3,4. $$

(17)

Clearly, if $\mathrm{Det}_{i}<0$, $i=3,4$, hence we get the instability of the equilibria $\Lambda _{i}$, $i=3,4$. Now we consider that $\mathrm{Det}_{i}>0$ $i=3,4$, then if $\operatorname{Tr}_{i}<0$, $i=3,4$, we conclude that $\Lambda _{i}$, $i=3,4$, are stable. Now we consider that $\mathrm{Det}_{i}>0$, $\operatorname{Tr}_{i}>0$, $i=3,4$, hence, these equilibria are unstable for the first-order derivative. However, for the FOD we have a possibility of the stability of this equilibrium. Note that in this situation (16) has two complex roots $\theta _{j}=\tilde{\theta }_{j} \pm \bar{\theta }_{j} i$, $\theta _{j} \in \mathbb{R}$, $j=3,4$. Then these roots verify the following:

$$ \tan ^{2} \bigl( \arg \{ \theta _{i} \} \bigr) = \frac{4 (-\frac{eraS_{i}N_{i} ^{2}}{k} + \mu S_{i} (\lambda +2aS_{i}) )}{ (-\frac{rN_{i}}{k}+ eN_{i}aS_{i} )^{2}}-1,\quad i=3,4. $$

For guaranteeing the stability of $\Lambda _{i}$, $i=3,4$, we must obtain $\tan ^{2} ( \arg \{ \theta _{i} \} ) >\tan ^{2} ( \frac{\alpha \pi }{2} )$, $i=3,4$, which is equivalent to

$$ (H_{1}):\quad \frac{4 (-\frac{eraS_{i}N_{i} ^{2}}{k} + \mu S_{i}(\lambda +2aS_{i}) )}{ (-\frac{rN_{i}}{k}+ eN_{i}aS_{i} )^{2}}>1+ \tan ^{2} \biggl( \frac{\alpha \pi }{2} \biggr). $$

Then, if $(H_{1})$ holds, then we get the stability of the DFEs, else it is instable. The obtained results are resumed in the following theorem.

Theorem 2.5

Assume that condition (ii) or (iii) in Theorem 2.1is verified, then we get:

• (i) If $\beta S_{i}>(\mu +\eta )$, then DFE is unstable.

• (ii) If $\beta S_{i}<(\mu +\eta )$ and $(H_{1})$ holds, then DFEs is stable, otherwise it is unstable.

Now, determining the stability of the endemic equilibrium (EE), the J-matrix at this equilibrium takes the following form:

$$ J\bigl(N^{*},S^{*},I^{*}\bigr)= \begin{pmatrix} -\frac{rN^{*}}{k} & -N^{*}(\lambda +2a(S^{*}+I^{*})) & -N^{*}( \lambda +2a(S^{*}+I^{*})) \\ e(\lambda +a(S^{*}+I^{*}))(S^{*}+I^{*}) & eN^{*}(\lambda +2a(S^{*}+I^{*}))- \mu -\beta I^{*} & eN^{*}(\lambda +2a(S^{*}+I^{*}))-\beta S^{*} \\ 0 & \beta I^{*} & 0 \end{pmatrix} , $$

(18)

the characteristic equation corresponding to J-matrix (18) is

$$ \Delta =\theta ^{3}+\omega _{2}\theta ^{2}+ \omega _{1}\theta +\omega _{0}, $$

where

$$\begin{aligned}& \omega _{2}= \frac{rN^{*}}{k}-\bigl(eN^{*}\bigl( \lambda +2a\bigl(S^{*}+I^{*}\bigr)\bigr)- \mu -\beta I^{*}\bigr), \\& \begin{aligned} \omega _{1}={}& {-} \frac{rN^{*}(S^{*}+I^{*})(eN^{*}(\lambda +2a(S^{*}+I^{*}))-\mu -\beta I^{*})}{k}\\ &{}+eN^{*}\bigl( \lambda +a\bigl(S^{*}+I^{*} \bigr)\bigr) \bigl(S^{*}+I^{*}\bigr) \bigl(\lambda +2a \bigl(S^{*}+I^{*}\bigr)\bigr) \\ &{}-\beta I^{*} \bigl( eN^{*}\bigl(\lambda +2a \bigl(S^{*}+I^{*}\bigr)\bigr)-\beta S^{*} \bigr) , \end{aligned} \\& \begin{aligned} \omega _{0}={}& {-} \frac{r\beta I^{*}N^{*}}{k} \bigl( eN^{*} \bigl(\lambda +2a\bigl(S^{*}+I^{*}\bigr)\bigr)\\ &{}- \beta S^{*} \bigr) -\beta I^{*} N^{*} \bigl(e\bigl( \lambda +a\bigl(S^{*}+I^{*}\bigr)\bigr) \bigl(S^{*}+I^{*}\bigr) \bigr) \bigl(\lambda +2a \bigl(S^{*}+I^{*}\bigr) \bigr). \end{aligned} \end{aligned}$$

Put $\Delta =18\omega _{2}\omega _{1}\omega _{0}+ ( \omega _{2} \omega _{1} ) ^{2}-4\omega _{0} \omega _{2} ^{3}-4 \omega _{1} ^{3}-27 \omega _{0} ^{3}$. By using the Routh–Hurwitz criterion defined in [2, 3], we find the local stability of the EE, which is highlighted in the following theorem.

Theorem 2.6

Assume that the condition mentioned in Theorem 2.2holds, then the EE is stable if

• (i) $\Delta >0$, $\omega _{2}>0$, $\omega _{0}>0$, $\omega _{2}\omega _{1}>\omega _{0}$, or

• (ii) $\Delta <0$, $\omega _{2}\geq 0$, $\omega _{1}\geq 0$, $\omega _{0}\geq 0$, and $\alpha <\frac{2}{3}$.

2.3 Numerical scheme

Our goal in this subsection is to build a numerical scheme for our graphical representations for confirming the results found in the previous section. At first, we consider the following fractional problem:

$$ \frac{d^{\alpha }\chi }{dt}= {G}\bigl(t, \chi (t)\bigr). $$

(19)

The employment of the principal theorem of fractional calculus on (5) yields

$$ \chi (t) - \chi (0) = \frac{1}{\Gamma (\alpha )} \int _{0}^{t} {G}\bigl( \upsilon , \chi ( \upsilon )\bigr) (t-\upsilon )^{\alpha -1}\,d\upsilon . $$

(20)

We set $t=t_{n}=n\hslash$ in (20), we find

$$ \chi (t_{n}) = \chi (0)+\frac{1 }{\Gamma (\alpha )}\sum _{i=0}^{n-1} \int _{t_{i}}^{t_{i+1}} {G}\bigl(\upsilon , \chi ( \upsilon )\bigr) (t_{n}- \upsilon )^{\alpha -1}\,d\upsilon . $$

(21)

By approximating the functional ${G}(t, \chi (t))$ by

$$ {G}\bigl(t, \chi (t)\bigr)\approx {G}(t_{i+1}, \chi _{i+1} )+ \frac{t-t_{i+1}}{\hslash } \bigl( {G}(t_{i+1}, \chi _{i+1} )\bigr)- {G}(t_{i}, \chi _{i} ) ) , \quad t\in [t_{i},t_{i+1}], $$

(22)

where $\chi _{i}= \chi (t_{i})$.

The substitution of Eq. (22) into (21) gives (for more details, see [70])

$$ \chi _{n}= \chi _{0} +\hslash ^{\alpha } \Biggl(A _{n} {G}(t_{0}, \chi _{0} )+\sum_{i=1}^{n}B_{n-i} {G}(t_{i}, \chi _{i} ) \Biggr), $$

(23)

where

$$ \begin{gathered} A _{n}= \frac{(n-1)^{\alpha +1}-n^{\alpha }(n-\alpha -1)}{\Gamma (\alpha +2)} \\ B_{n}=\textstyle\begin{cases} \frac{1}{{\Gamma (\alpha + 2)}},& n = 0 \\ \frac{{{{(n - 1)}^{\alpha }} - 2{n^{\alpha }} + {{(1+n)}^{\alpha }}}}{{\Gamma ( \alpha + 2)}}, & n = 1,2, \ldots \end{cases}\displaystyle \end{gathered} $$

(24)

The application of the numerical method (23) to solve (5) yields

$$ \begin{gathered} N_{n} = N_{0} +\hslash ^{\alpha } \Biggl(A _{n} {G}_{1}( N_{0},S_{0},I_{0})+ \sum _{i=1}^{n}B_{n-i} {G}_{1}( N_{i},S_{i},I_{i}) \Biggr), \\ S_{n} = S_{ 0} +\hslash ^{\alpha } \Biggl(A _{n} {G}_{2}( N_{0},S_{0},I_{0})+ \sum_{i=1}^{n}B_{n-i} {G}_{2}( N_{i},S_{i},I_{i}) \Biggr), \\ I_{n} = I_{0} +\hslash ^{\alpha } \Biggl(A _{n} {G}_{3}( N_{0},S_{0},I_{0})+ \sum_{i=1}^{n}B_{n-i} {G}_{3}( N_{i},S_{i},I_{i}) \Biggr), \end{gathered} $$

(25)

with

$$ \begin{gathered} {G}_{1} ( N,S,I ) = rN\biggl(1- \frac{N}{k}\biggr)-\bigl(\lambda +a(S+I)\bigr)N(S+I), \\ {P}_{2} (N,S,I ) = e\bigl(\lambda +a(S+I)\bigr)N(S+I)-\beta SI - \mu S, \\ {P}_{3} ( N,S,I )=\beta SI -\eta I -\mu I. \end{gathered} $$

(26)

3 Numerical analysis of system (5)

3.1 Graphical representations

In this subsection, we show that our mathematical analysis represents perfectly what we have in the real life through several examples with different values.

Fig. 3::

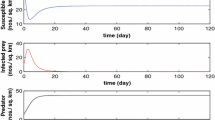
Here we consider $\alpha =0.9$, $r=1.2$, $k=2.5$, $\eta =0.5$, $\lambda =0.5$, $\mu =0.5$, $a=3.5$, $\beta =0.5$, $e=0.5$. Hence we get the stability of the DFE $\Lambda _{3}=(0.45,0.46,0)$.

Fig. 4::

In this figure we have the instability of the DFE and the existence of oscillations in time. The following values $\Lambda _{5}=(0.27,0.64,0.11)$, where the following values $\alpha =0.9$, $r=3.2$, $k=10.5$, $\mu =2.5$, $e=0.5$, $\lambda =1.5$, $a=3.5$, $\beta =1.5$, $\eta =0.5$ are considered.

Fig. 5::

This figure shows the stability of the EE $\Lambda _{5}=(0.27,0.64,0.11)$ where the following values $\alpha =0.9$, $r=3.2$, $k=10.5$, $\mu =0.5$, $e=0.5$, $\lambda =1.5$, $a=3.5$, $\beta =1.5$, $\eta =0.5$ are used.

Fig. 6::

The persistence of the three populations in the case of the instability of the EE, the following values $\alpha =0.9$, $r=5.2$, $k=30.5$, $\lambda =1.5$, $\mu =2.5$, $e=0.8$, $a=4.5$, $\beta =3.5$, $\eta =0.5$ are utilized.

Fig. 7::

We consider the values $\alpha =0.9$, $r=5.2$, $k=30.5$, $\mu =2.5$, $e=0.8$, $\lambda =1.5$, $a=0.5$, $\beta =3.5$, $\eta =0.5$ are utilized.

Fig. 8::

We put $\alpha =0.9$, $r=5.2$, $k=30.5$, $\lambda =4.5$, $\mu =2.5$, $e=0.8$, $a=0.5$, $\beta =3.5$, $\eta =0.5$.

Fig. 9::

We set $\alpha =0.9$, $r=5.2$, $k=30.5$, $\mu =2.5$, $e=0.8$, $a=0.5$, $\beta =3.5$, $\eta =0.5$, and multi-values of λ.

Fig. 10::

We use the following set of the parameters: $\alpha =0.9$, $r=5.2$, $k=30.5$, $\mu =2.5$, $e=0.8$, $\lambda =0.2$, $\beta =3.5$, $\eta =0.5$, and multi-values of a.

Fig. 11::

We use the following set of the parameters: $r=5.2$, $k=30.5$, $\mu =2.5$, $e=0.8$, $a=1.5$, $\lambda =0.1$, $\beta =3.5$, $\eta =0.5$, and multi-values of α.

4 Conclusion

We dealt in this research with the consumer-resource system where we investigated the influence of the hunting cooperation on the spread of the disease developed in the consumer population. Note that the cooperation of consumers gives more accuracy in hunting, and it has been discussed throughout the paper. The purpose of this research is to determine the impact of this cooperation on the prevalence of infection and the interaction between resources and consumers. To mention that in the case of the presence of contagion disease in the consumer, this last will still use cooperation in hunting, which increases the contact between the populations, which can lead to the persistence of the infection in populations.

The mathematical analysis of the considered system (5) is also considered, where the equilibria of this system are successfully determined. The hunting cooperation can generate two DFEs, which is investigated through Theorem 2.1, and it is proved numerically using Fig. 1, where many scenarios can behold as the nonexistence of DFE, the existence of one DFE, or two. The existence of two DFEs highlights the possibility of the extinction of the infection for consumer populations but in different levels (which is affected by the degree of cooperation between the two populations), which is affected principally by the value of the hunting cooperation rate a as it has been shown in Fig. 2 where the rate a can dominate the existence and the multiplicity of DFE. Further, the stability of this equilibrium can hold, which is considered through numerical simulation in different scenarios, as in Fig. 3 we have the stability of DFE, and in Figs. 4, 8 we have the extinction of infected consumers as a form of oscillations. Besides, the persistence of the epidemic is also probably where the stability of the EE shows this result. Indeed, this stability can be seen through Theorem 2.6, and it is confirmed using graphical representation in Fig. 5. Further, the persistence of the infection can be seen differently through the occurrence of oscillations guaranteed by the instability of EE (see Fig. 6), which shows the richness of the dynamics generated by model (5).

Figure 2

Influence of the hunting cooperation rate a on the existence of the DFE for the values $r=1.2$, $\mu =2.5$, $e=0.8$, $\lambda =0.02$, $k=12.5$, $\beta =3.5$, $\eta =0.5$

Figure 3

Extinction of the infection which is elaborated by the stability of the DFE

Figure 4

Extinction of the infection elaborated by the instability of the DFE, which is by the existence of oscillations in time

Figure 5

Persistence of the three populations which is elaborated by the stability of the EE

Figure 6

Persistence of the three populations in the case of the instability of EE

Figure 7

Local stability of the EE

Figure 8

Local stability of the DFE

Furthermore, we investigated the influence of solitary hunting and cooperation hunting on the degree of the spread of the disease, wherein Fig. 9 we obtained that this parameter can influence the stability of the EE, which shows a big impact on the behavior of animals. Also, the cooperation hunting affects the stability of EE, as it has been shown in (10) where there are oscillations for multi-values of a but in different levels. Also, the memory plays an important role in measuring the memory raised by taking advantage of the previous experiments done by the animal for more accuracy in hunting for consumers and avoiding predation for the resources. This rate influences the behavior of solution where it appears in the stability of equilibrium states as in Theorem 2.6 and Theorem 2.5 (condition $(H_{1})$), and it is confirmed through graphical representation (Fig. 11), which shows a huge impact on the evolution of the studied species.

Figure 9

Influence of the solitary hunting on the coexistence of the population

Figure 10

Influence of the hunting cooperation coefficient on the evolution of the species

Figure 11

Influence of the memory rate on the stability of the equilibria