Herd behavior in a predator–prey model with spatial diffusion: bifurcation analysis and Turing instability

Abstract

We consider in this paper an ecological model, in a predator–prey interaction with the presence of a herd behavior. For the analysis of the model, the existence of positive solution and also the existence Hopf bifurcation, Turing driven instability, and Turing–Hopf bifurcation point have bee proved. Then by calculating the normal form, on the center of the manifold associated to the Hopf bifurcation points, the stability of the periodic solution has been proved. In the last part of the paper, numerical simulations has been given to illustrate our theoretical analysis.

1 Introduction

Since the works of Volterra [1] a huge improvement has been noticed in population dynamics in general and ecosystems in particular; from a half century, several mathematicians followed their steps and proposed several models for modeling the interaction between the two species “predators” and “preys”, and each time it was intended to include a new population phenomenon. someone of them assumed that predator population has hyperbolic mortality for instance [2], and others assumed that the predators has a quadratic mortality [3], others changed the interaction functional to considering a specific population phenomenon. For instance Holling I interaction functional [4,5,6], models only the predation of the preys, but for Holling II interaction functional [4], models both the predation of the preys and the search of the predators for the preys. For more examples of interaction types, we cit Beddington–DeAngelis interaction type [7,8,9], Holling I–III interaction type [4, 10,11,12,13], Ratio dependent interaction type [14, 15].

Recently, herd behavior has been included. It is a behavior that the preys population uses to defend against predators population. It make a group called “group defense”, such that when the predators make contact with the preys population, they can’t reach the inside of the preys group which means that the predators hunt only on the boundary of preys herd. It is the reason of defining this dynamic of preys by the square root of the preys population; for instance the works of [3, 16,17,18,19,20]; and several models in the same orientation to appear in the interface. Now calling the works of E. Venturino and Y. Song; in [3, 17, 18, 21,22,23], they assumed that this phenomenon is a natural behavior of prey, but in [16] it has been assumed that is an instant cause of a disease that infects the preys population.

In the present work a standard method has been given to include herd behavior in some interaction functionals, and a difference between this functionals has been given, and therefor it is the master key of the present work work. Motivated by the previous works the proposed model is the following one:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dR}{dt}=rR\left( 1-\frac{R}{k}\right) -\frac{aRP}{1+b\sqrt{R}+cR}, \\ \frac{dP}{dt}=-mP+\frac{eaRP}{1+b\sqrt{R}+cR}, \end{array} \right. \end{aligned}$$

(1.1)

where R(t) and P(t) stand respectively for the preys and the predators densities at the time t, r is the reproduction rate of prey population and k the carrying capacity, e is the conversion rate of preys biomass into predators biomass and note that $0<e<1, m$ is the mortality rate, b and c related to search coefficient of the predator for the prey, a represents the hunting rate, where $\frac{a}{c}$ is the maximum quantity of preys can be captured by a predator.

In the case of herd behavior, the predators hunt exclusively on the boundary of preys herd. For the ecological meaning of the interaction functional in system (1.1) $h(R,P)= \frac{aRP}{1+b\sqrt{R}+cR}$ some previous works are recalled including herd behavior. In [2, 16] the authors use the interaction functional $h_{1}(R,P)=a\sqrt{R}P$ where $\sqrt{R}$ models the preys herd. This functional is the Holling I interaction functional with the presence of prey group. In [3], the authors propose the interaction functional $h_{2}(R,P)=\frac{a\sqrt{R}P}{1+b\sqrt{R}}$ which is the Holling II interaction functional in the presence of preys herd where b is the search rate of P for R. In this work, the generalized Holling III interaction functional [11, 13, 24] defined by $h_{3}(R,P)=\frac{aR^{2}P}{ 1+bR+cR^{2}}$ has been considered, and a simple assumption on this functional has been used to include the preys herd. In the presence of this behavior the predators hunt only in the boundary of the preys group which means that the functional $h_{3}(R,P)$ becomes $h_{4}(R,P)=h_{3}(\sqrt{R},P)=\frac{aRP}{1+b\sqrt{R}+cR}$; where $h_{4}(R,.)$ saturates at large prey population densities comparing $h_{1}(R,.)$ and $h_{2}(R,.)$ (see Fig. 1).

Fig. 1

Three types of modified Holling interaction functionals in the presence of herd behavior for $a=0.5, b=0.5, c=0.5$

In real world, the prey and the predator always in movement, for modeling this dynamic we will consider that the two populations has a spatial disperse; the spatial dynamic of the predator–prey models including spatial diffusion has been widely studied in literature, see [13,14,15, 25,26,27,28]. Here, we will consider that both considered population are in an insolated patch, which means that the immigration is neglected using the Neumann boundary conditions. Considering the above discussion the system (1.1) can be rewritten in the presence of spatial diffusion as follows:

$$\begin{aligned} \left\{ \begin{array}{l} R_{t}(x,t)-d_{1}R_{xx}(x,t)=rR(x,t)\left( 1-\dfrac{R(x,t)}{k}\right) \\ \qquad -\dfrac{aR(x,t)P(x,t) }{1+b\sqrt{R(x,t)}+cR(x,t)}\,\, x\in (0,L), \\ P_{t}(x,t)-d_{2}P_{xx}(x,t)=-mP(x,t)+\dfrac{eaR(x,t)P(x,t)}{1+b\sqrt{R(x,t)} +cR(x,t)}{ \, \, \, \, \,}t\ge 0, \end{array} \right. \end{aligned}$$

(1.2)

with the associated Neumann boundary conditions

$$\begin{aligned} \left\{ \begin{array}{l} R_{x}(0,t)=R_{x}(L,t)=P_{x}(0,t)=R_{x}(L,t)=0{ \, \,}\forall t\ge 0, \\ R(x,0)=R_{0}(x)\ge 0{ \, \,}P(x,0)=P_{0}(x)\ge 0{ \, \ } x\in (0,L); \end{array} \right. \end{aligned}$$

(1.3)

where x is the covered distance by P or R, and L is the maximum distance that can be covered by the prey or the predator, $d_{1},d_{2}$ are the positive diffusion constants for the preys and the predators , respectively.

The paper is organized as follow. In Sect. 2, the existence of a positive solution of the system (1.2) and a priori bound of solution and also the global stability of the equilibrium state $E_{0}$ have been proved. In Sect. 3, the roots of the characteristic equation have been calculated and the existence of Hopf bifurcation and Turing driven instability also have been proved and the Turing–Hopf bifurcation points has been calculated. In Sect. 4 the normal form on the center of the manifold of Hopf bifurcation has been calculated for determining the direction and the stability of Hopf bifurcation, also some numerical simulations is used to illustrate the analytic results. A conclusion section ends the paper. We also mention the works [29,30,31,32] for further reading.

2 Existence of a positive solution, a priori bound of solution, global stability

In this section the existence of a positive solution of the system (1.2) has been proved under Neumann boundary condition, then some estimation of the solution has been given, at last the global stability of the equilibrium (k, 0) has been shown under some condition of the parameters.

Obviously the system (1.2) has three equilibrium states $E_{0}=(0,0), E_{1}=(k,0)$ and $E^{*}=(R^{*},P^{*})$ such that

$$\begin{aligned} \left\{ \begin{array}{l} R^{*}=\left( \dfrac{b+\sqrt{b^{2}+4(\tfrac{ae}{m}-c)}}{2(\tfrac{ae}{m}-c) }\right) ^{2},\\ P^{*}=\frac{er}{m}R^{*}\left( 1-\dfrac{R^{*}}{k}\right) >0, \end{array} \right. \end{aligned}$$

(2.1)

which exists if and only if

$$\begin{aligned} k>R^{*} \,and \,\tfrac{ae}{m}>c, \end{aligned}$$

(2.2)

(there may exist a fourth equilibrium state, which is strictly non positive and thus not biologically significant) for the existence of a positive solution and the bounders of the solution the following theorem is used:

Theorem 2.1

For $P_{0}(x)\ge 0, R_{0}(x)\ge 0$ and $R_{0}(x),P_{0}(x)$ not identically null, then the system (1.2) has a unique solution (R(x, t), P(x, t)) such that $0<R(x,t)<R^{*}(t)$ and $0<P(x,t)<P^{*}(t)$ for $\ t>0$ and $x\in (0,L)$ where $(R^{*}(t),P^{*}(t))$ is the unique solution of the ordinary differential equation:

$$\begin{aligned} \left\{ \begin{array}{l} R_{t}=rR(x)\left( 1-\dfrac{R(x)}{k}\right) { \, \, \, \, \, \, \, \, \, \, \ }t>0, \\ P_{t}=-mP(x)+\dfrac{eaR(x)P(x)}{1+b\sqrt{R(x)}+cR(x)}\, t>0 ,\\ R(0)=R_{0}^{*}=\sup \limits _{x\in (0,L)}R_{0}(x) , \ P(0)=P_{0}^{*}=\sup \limits _{x\in (0,L)}P_{0}(x). \end{array} \right. \end{aligned}$$

(2.3)

Further we have $\lim \nolimits _{t\rightarrow +\infty }\sup R(x,t)=k$ and

$$\begin{aligned} \lim _{t\rightarrow +\infty }\sup \frac{1}{L}\times \displaystyle \int \limits _{\Omega }P(x,t)dx\le \frac{m+r}{m}ek. \end{aligned}$$

(2.4)

Proof

By putting

$$\begin{aligned} f(R,P)= & {} rR\left( 1-\frac{R}{k}\right) -\dfrac{aRP}{1+b\sqrt{R}+cR}, \nonumber \\ g(R,P)= & {} -mP+\dfrac{eaRP}{1+b\sqrt{R}+cR}, \end{aligned}$$

(2.5)

where f and g verify the condition:

$$\begin{aligned} f_{P}= & {} -\dfrac{aR}{1+b\sqrt{R}+cR}<0 ,\nonumber \\ g_{R}= & {} \dfrac{eaP}{(1+b\sqrt{R}+cR)^{2}}>0. \end{aligned}$$

(2.6)

It is obvious to see that the functionals f and g are Lipschitz functions which means there exist $c_{1}, c_{2}$ such that for positive $R_{1}, R_{2},P_{1},P_{2}$ we have

$$\begin{aligned} \begin{array}{c} \left| f(R_{1},P_{1})-f(R_{2},P_{2})\right| \le c_{1}(\left| R_{1}-R_{2}\right| +\left| P_{1}-P_{2}\right| ), \\ \left| f(R_{1},P_{1})-f(R_{2},P_{2})\right| \le c_{2}(\left| R_{1}-R_{2}\right| +\left| P_{1}-P_{2}\right| ). \end{array} \end{aligned}$$

(2.7)

From (2.6) to (2.7) then f and g is mixed quasi monotone functional in ${\mathbb {R}}$(see [33]); now putting $(R_{2}(x,t),P_{2}(x,t))=(R^{ *}(t),P^{*}(t))$ satisfying the equation:

$$\begin{aligned} \left\{ \begin{array}{c} \frac{\partial R_{2}}{\partial t}-d_{1} R_{2xx}-f(R_{2},P_{2})=0\ge 0, \\ \frac{\partial P_{2}}{\partial t}-d_{2}P_{2xx}-g(R_{2},P_{2})=0\ge 0, \end{array} \right. \end{aligned}$$

(2.8)

and $(R_{1}(x,t),P_{1}(x,t))=(0,0)$ satisfying:

$$\begin{aligned} \left\{ \begin{array}{c} \frac{\partial R_{1}}{\partial t}-d_{1} R_{1xx}-f(R_{1},P_{1})=0\le 0, \\ \frac{\partial P_{1}}{\partial t}-d_{2}P_{1xx}-g(R_{1},P_{1})=0\le 0, \end{array} \right. \end{aligned}$$

(2.9)

and $0\le R_{0}(x)\le R_{0}^{*}, \ 0\le P_{0}(x)\le P_{0}^{*}$ . $(R_{1}(x,t),P_{1}(x,t))$ and $(R_{2}(x,t),P_{2}(x,t))$ called the lower and the upper solution (or sub- and super-solution) of the system (1.2); it is obvious to see that the functions f and g in addition of being Lipschitz, are homogenous which means $f(R_{1},P)-f(R_{2},P) \ge -c_{1}(R_{1}-R_{2})$ and $f(R,P_{1})-f(R,P_{2})\ge -c_{1}(P_{1}-P_{2})$ for $R_{1}>R_{2}$ and $P_{1}>P_{2}$ where $c_{1}$ is Lipchitz constant of the functional f and the same idea for the functional g that means all the conditions of the Theorem 2.1 in [33] are verified, which leads to the global existence of the solution of the system (1.2) satisfying the condition $0\le R(x,t)\le R^{*}(t)$ and $0\le P(x,t)\le P^{*}(t)$ for $\ t>0$ and $x\in (0,L).$

The strong maximum principle implies that $0<R(x,t) , 0<P(x,t)$ for $t>0$ and $x\in (0,L)$ that completes the first part of the proof.

Note that $R(x,t)\le R^{*}(t)$ and $P(x,t)\le P^{*}(t)$ where $R^{*}(t)$ is the unique solution of the equation $R_{t}=rR(x)(1-\dfrac{R(x) }{k})$ and $R(0)=R_{0}^{*}>0$.

It is easy to verify that $R^{*}(t)\rightarrow k$ as $t\rightarrow +\infty$ so for any $\varepsilon >0$ there exist $T_{0}>0$ such that $R(x,t)\le k+\varepsilon$  for $t>T_{0},\,x\in [0,L]$ witch leads to $\lim \nolimits _{t\rightarrow +\infty }\sup R(x,t)=k$.

Putting

$$\begin{aligned} \beta (t)=\displaystyle \int \limits _{0}^{L}R(x,t)dx{ \, \ }\delta (t)=\displaystyle \int \limits _{0}^{L}P(x,t)dx, \end{aligned}$$

(2.10)

and

$$\begin{aligned} w(t)=e\beta (t)+\delta (t), \end{aligned}$$

(2.11)

then

$$\begin{aligned} \dfrac{d\beta }{dt}= & {} \displaystyle \int \limits _{0}^{L}d_{1}R_{xx}dx+\displaystyle \int \limits _{0}^{L}\left[ rR\left( 1-\frac{R}{k}\right) -\dfrac{aRP}{1+b\sqrt{R}+cR}\right] dx,\nonumber \\ \dfrac{d\delta }{dt}= & {} \displaystyle \int \limits _{0}^{L}d_{2}P_{xx}dx+\displaystyle \int \limits _{0}^{L}\left[ -mP+\dfrac{eaRP}{1+b\sqrt{R}+cR}\right] dx. \end{aligned}$$

(2.12)

Using Neumann boundary condition $\dfrac{dw}{dt}$ becomes

$$\begin{aligned} \begin{array}{l} \dfrac{dw}{dt}=e\dfrac{d\beta }{dt}+\dfrac{d\delta }{dt}, \\ =-m\delta (t)+er\displaystyle \int \limits _{0}^{L}R\left( 1-\frac{R}{k}\right) dx. \\ \end{array} \end{aligned}$$

(2.13)

Adding and subtracting the term $me \beta (t)$

$$\begin{aligned} \dfrac{dw}{dt}=-m(e\beta (t)+\delta (t))+me\beta (t)+er\displaystyle \int \limits _{0}^{L}R\left( 1-\frac{R}{k}\right) dx, \end{aligned}$$

(2.14)

which leads to

$$\begin{aligned} \dfrac{dw}{dt}\le -mw+e\beta (t)(m+r). \end{aligned}$$

(2.15)

From $\lim \nolimits _{t\rightarrow +\infty }\sup R(x,t)=k$ we have $\lim \nolimits _{t\rightarrow +\infty }\beta (t)\le Lk$ thus for small $\varepsilon >0$ there exists $T>0$ such that

$$\begin{aligned} \dfrac{dw}{dt}\le -mw+eLk(m+r), \end{aligned}$$

(2.16)

and note that w(t) is the solution of

$$\begin{aligned} \dfrac{dw}{dt}=-mw+eL(k+\varepsilon )(m+r), \end{aligned}$$

(2.17)

then

$$\begin{aligned} \lim _{t\rightarrow +\infty }w(t)=\frac{m+r}{m}e(k+\varepsilon )L, \end{aligned}$$

(2.18)

using the comparison principle and (2.16) we can obtain for $T_{2}>T_{1}$

$$\begin{aligned} \displaystyle \int \limits _{0}^{L}P(x,t)dx=\delta (t)<w(t)\le \frac{m+r}{m} e(k+\varepsilon )L+\varepsilon { \, }t>T_{2}, \end{aligned}$$

(2.19)

that means

$$\begin{aligned} \lim _{t\rightarrow +\infty }\sup \frac{1}{L}\times \displaystyle \int \limits _{0}^{L}P(x,t)dx\le \frac{m+r}{m}ek. \end{aligned}$$

(2.20)

This completes the proof. $\square$

Now we consider the carrying capacity of the prey k as a bifurcation parameter, and the Jacobian matrix of the system (1.1) can be defined as follows:

$$\begin{aligned} J(R,P)=\left( \begin{array}{cc} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \end{array} \right) , \end{aligned}$$

(2.21)

where

$$\begin{aligned} a_{11}= & {} r\left( 1-\frac{2R}{k}\right) -aP\frac{1+b\sqrt{R}+cR-R\left( \frac{b}{2\sqrt{R}}+c\right) }{ (1+b\sqrt{R}+cR)^{2}}, \nonumber \\ a_{12}= & {} -\dfrac{aR}{1+b\sqrt{R}+cR}<0, \nonumber \\ a_{21}= & {} eaP\frac{1+b\sqrt{R}+cR-R\left( \frac{b}{2\sqrt{R}}+c\right) }{(1+b\sqrt{R}+cR)^{2} }>0, \nonumber \\ a_{22}= & {} -m+\dfrac{eaR}{1+b\sqrt{R}+cR}, \end{aligned}$$

(2.22)

and $D=diag(d_{1},d_{2})$ and corresponding the Neumann boundary condition the real-valued Sobolev space can be defined as follows.

$$\begin{aligned} \chi =\left\{ U=(R,P)^{T}\in H^{2}(0,L)\diagup \frac{\partial R}{\partial x}= \frac{\partial R}{\partial x}=0\text { at }x=0,L\right\} , \end{aligned}$$

(2.23)

For $U_{1},U_{2}\in \chi$, defining the usual inner product $\langle U_{1},U_{2}\rangle =\int \nolimits _{0}^{L}(R_{1}R_{2}+P_{1}P_{2})dx$ and the associated Hilbertian norm of $\chi$ noted by $\Vert \cdot \Vert _{2,2}$

The associated eigenvalue problem is given by:

$$\begin{aligned} \left\{ \begin{array}{c} -\Phi ^{\prime \prime }=\mu \Phi { \,}x\in (0,L), \\ \Phi ^{\prime }(0)=\Phi ^{\prime }(L)=0, \end{array} \right. \end{aligned}$$

(2.24)

it is well known that $\mu _{n}=( \dfrac{n\pi }{L})^{2}$ and $\cos (\dfrac{n\pi }{L}x)\,(n=0,1\ldots )$ are the eigenvalues and the eigenfunctions of the problem (2.24) on $\chi$, respectively.

Under the boundary condition of we look for the solution of the form:

$$\begin{aligned} U=\sum _{i=0}^{+\infty }\left( \begin{array}{c} a_{n} \\ b_{n} \end{array} \right) \cos \left( \dfrac{n\pi }{L}x\right) e^{\lambda t}. \end{aligned}$$

(2.25)

In order of the global stability of $E_{1}$ we have the following results

Theorem 2.2

The equilibrium state $E_{1}=(k,0)$ of the system (1.2) is globally asymptotically stable when $R^{*}>k$ and $E^{*}$ does not exist.

Proof

The linearized system around the stationary state $E_{1}=(k,0)$ is given by:

$$\begin{aligned} U_{t}=D\Delta U+J(k,0). \end{aligned}$$

(2.26)

The eigenvalues of the matrix $-(\dfrac{n\pi }{L})^{2}D+J(k,0)$ are:

$$\begin{aligned} \begin{array}{l} \lambda _{1}=-r-d_{1}\left( \dfrac{n\pi }{L}\right) ^{2}<0, \\ \lambda _{2}=-m+\dfrac{eak}{1+b\sqrt{k}+ck}-d_{2}\left( \dfrac{n\pi }{L}\right) ^{2}, \end{array} \end{aligned}$$

(2.27)

$-m+\dfrac{eak}{(b+\sqrt{k})(c+\sqrt{k})}=0$ is equivalent to $R^{*}=k$

which means when $R^{*}>k$ then $\lambda _{2}<0$ for any $n\ge 0$ leads to the local stability of the equilibrium $E_{1}$ for $R^{*}>k$, and it is obvious to see that $k={\tilde{k}}(n)$ are the bifurcating points of the forward bifurcation where ${\tilde{k}}$ are the solution of the equation of the variable k:

$$\begin{aligned} \left( m+d_{2}\left( \frac{n\pi }{L}\right) ^{2}\right) +b\left( m+d_{2}\left( \frac{n\pi }{L}\right) ^{2}\right) \sqrt{k} +\left( cm+cd_{2}\left( \frac{n\pi }{L}\right) ^{2}-ae\right) k=0. \end{aligned}$$

(2.28)

Now for the global attraction of $E_{1}$ the proof of Theorem 2.1 in [33] has been used, and defining respectively the upper constant and the lower solution of the system (1.2) by $(R_{1},P_{1})=(k+\varepsilon ,M)$ and $(R_{2},P_{2})=(\varepsilon ,0)$ where $\varepsilon$ and M are positive constants and $\varepsilon$ is sufficiently small; and also the monotone sequences for coupled parabolic equation defined in [33] by $(\overline{R}^{(m)},\overline{P}^{(m)})$ and $(\underline{R}^{(m)},\underline{P}^{(m)})$ for $m=1,2,\ldots$ such that

$$\begin{aligned} \left\{ \begin{array}{c} \overline{R}^{(m)}=\overline{R}^{(m-1)}+\dfrac{1}{c_{1}}f(\overline{R} ^{(m-1)},\underline{P}^{(m-1)}), \\ \overline{P}^{(m)}=\overline{P}^{(m)}+\dfrac{1}{c_{2}}g(\overline{R}^{(m-1)}, \overline{P}^{(m-1)}), \end{array} \right. \end{aligned}$$

(2.29)

and

$$\begin{aligned} \left\{ \begin{array}{c} \underline{R}^{(m)}=\underline{R}^{(m-1)}+\dfrac{1}{c_{1}}f(\underline{R} ^{(m-1)},\overline{P}^{(m-1)}), \\ \underline{P}^{(m)}=\underline{P}^{(m)}+\dfrac{1}{c_{2}}g(\underline{R} ^{(m-1)},\underline{P}^{(m-1)}), \end{array} \right. \end{aligned}$$

(2.30)

such that $(\overline{R}^{(0)},\overline{P}^{(0)})=(k+\varepsilon ,M)$ and $( \underline{R}^{(0)},\underline{P}^{(0)})=(\varepsilon ,0)$.

From Lemma 2.1 in Pao [33], $(\overline{R}^{(m)}, \overline{P}^{(m)})\rightarrow (\overline{R},\overline{P})$ and $(\underline{ R}^{(m)},\underline{P}^{(m)})\rightarrow (\underline{R},\underline{P})$ such that

$$\begin{aligned} \begin{array}{c} \varepsilon \le \underline{R}^{(m)}\le \underline{R}^{(m+1)}\le \underline{R}\le \overline{R}\le \overline{R}^{(m+1)}\le \overline{R} ^{(m)}\le k+\varepsilon , \\ \varepsilon \le \underline{P}^{(m)}\le \underline{P}^{(m+1)}\le \underline{P}\le \overline{P}\le \overline{P}^{(m+1)}\le \overline{P} ^{(m)}\le M, \end{array} \end{aligned}$$

(2.31)

if $\varepsilon =0$ then $(\underline{R}^{(0)},\underline{P} ^{(0)})=(0,0)$ leads to $\underline{P}=0$ from [33] $(\overline{R}, \overline{P})$ and $(\underline{R},\underline{P})$ verify:

$$\begin{aligned} \begin{array}{c} f(\overline{R},\underline{P})=0 ,\ f(\underline{R},\overline{P})=0 ,\\ g(\overline{R},\overline{P})=0 ,\,g(\underline{R},\underline{P})=0 ,\\ \end{array} \end{aligned}$$

(2.32)

which is equivalent to

$$\begin{aligned} \begin{array}{cc} r\overline{R}\left( 1-\frac{\overline{R}}{k}\right) =0, &{} -m\overline{P}+\dfrac{ea \overline{R}\overline{P}}{1+b\sqrt{\overline{R}}+c\overline{R}}=0, \\ r\underline{R}\left( 1-\frac{\underline{R}}{k}\right) -\dfrac{a\underline{R}\overline{P}}{ 1+b\sqrt{\underline{R}}+c\underline{R}}=0, &{} -m\underline{P}+\dfrac{ea \underline{R}\underline{P}}{1+b\sqrt{\underline{R}}+c\underline{R}}=0. \end{array} \end{aligned}$$

(2.33)

From the first equation of (2.33), $\overline{R}=k$ can be deduced, and the other equations implies that $\overline{P}=0, \underline{R}=k$ and from Theorem 2.2 of Pao [33] the solution (R, P) satisfies:

$(R,P)\rightarrow (k,0)$ as $t\rightarrow +\infty$ when $\varepsilon <R_{0}(x)\le k+\varepsilon$.

Using the comparison theorem the functional $\eta (x,t)$ that verify $R(x,t)\le \eta (x,t)$ can be defined where $(x,t)\in [0,L]\times [0,+\infty )$ by the following parabolic equation

$$\begin{aligned} \left\{ \begin{array}{l} \eta _{t}=d_{1}\eta _{xx}+r\eta \left( 1-\frac{\eta }{k}\right) { \, \,} t>0,x\in (0,L), \\ \frac{\partial \eta }{\partial x}(0,t)=\frac{\partial \eta }{\partial x} (L,t)=0 \, \, t>0, \\ \eta (x,0)=R_{0}(x), \end{array} \right. \end{aligned}$$

(2.34)

and $\eta (x,t)\rightarrow k$ as $t\rightarrow +\infty$ and there exists $t_{0}>0$ such that $R(x,t)\le k+\varepsilon$ in $[0,L]\times [t_{0},+\infty )$ which means the equilibrium state $E_{1}$ globally attracts the solutions and is locally asymptotically stable, leads to the global stability of $E_{1}$. Which completes the proof $\square$

3 Linear stability, Turing instability and bifurcation analysis

In this section the stability of the positive equilibrium $E^{*}$ has been analyzed, the existence of the Hopf bifurcation, and Turing–Hopf bifurcation points for the system (1.2), Throughout the rest part of the paper, the condition (2.2) has been assumed; for the simplicity to the readers the section has been splitted into three subsections.

3.1 The characteristic equation

The system (1.2) can be rewritten as follows:

$$\begin{aligned} U_{t}=D\Delta U+J(R^{*},P^{*})U+F(U), \end{aligned}$$

(3.1)

with

$$\begin{aligned} J(R^{*},P^{*})=\left( \begin{array}{cc} A(k) &{} B \\ C(k) &{} 0 \end{array} \right) , \end{aligned}$$

(3.2)

where

$$\begin{aligned} A(k)= & {} r\left( 1-\frac{2R^{*}}{k}\right) -aP^{*}\frac{1+b\sqrt{R^{*}}+cR^{*}-R^{*}\left( \frac{b}{2\sqrt{R^{*}}}+c\right) }{(1+b\sqrt{R^{*}}+cR^{*})^{2}}, \end{aligned}$$

(3.3)

$$\begin{aligned} B= & {} \frac{-m}{e}<0, \end{aligned}$$

(3.4)

$$\begin{aligned} C(k)= & {} eaP^{*}\frac{1+b\sqrt{R^{*}}+cR^{*}-R^{*}\left( \frac{b}{2 \sqrt{R^{*}}}+c\right) }{(1+b\sqrt{R^{*}}+cR^{*})^{2}}>0, \end{aligned}$$

(3.5)

and

$$\begin{aligned} D\Delta= & {} diag\left( d_{1}\frac{\partial ^{2}}{\partial x^{2}},d_{2}\frac{\partial ^{2}}{\partial y^{2}}\right) , \end{aligned}$$

(3.6)

$$\begin{aligned} F(U)= & {} \left( \begin{array}{c} rR\left( 1-\dfrac{R}{k}\right) -\dfrac{aPR}{1+b\sqrt{R}+cR}-A(k)R-BP \\ -m+\dfrac{eaR}{1+b\sqrt{R}+cR}-C(k)R \end{array} \right) . \end{aligned}$$

(3.7)

Where F(U) is a nonlinear function around the equilibrium $E^{*}$. The linearized system of (1.2) around $E^{*}$ is given by:

$$\begin{aligned} U_{t}=D\Delta U+J(R^{*},P^{*})U. \end{aligned}$$

(3.8)

The matrix $-(\dfrac{n\pi }{L})^{2}D+J(R^{*},P^{*})$ is given by

$$\begin{aligned} -\left( \dfrac{n\pi }{L}\right) ^{2}D+J(R^{*},P^{*})=\left( \begin{array}{cc} A(k)-d_{1}\left( \dfrac{n\pi }{L}\right) ^{2} &{} B \\ C(k) &{} -d_{2}\left( \dfrac{n\pi }{L}\right) ^{2} \end{array} \right) . \end{aligned}$$

(3.9)

The eigenvalues of the matrix (3.9) are the solution of the characteristic equation given by

$$\begin{aligned} \lambda ^{2}-T_{n}(k)\lambda +D_{n}(k)=0, \end{aligned}$$

(3.10)

with

$$\begin{aligned} \begin{array}{l} T_{n}(k)=A(k)-(d_{1}+d_{2})\left( \dfrac{n\pi }{L}\right) ^{2}, \\ D_{n}(k)=d_{1}d_{2}\left( \dfrac{n\pi }{L}\right) ^{4}-d_{2}A(k)\left( \dfrac{n\pi }{L} \right) ^{2}-BC(k). \end{array} \end{aligned}$$

(3.11)

3.2 Hopf bifurcation

In this subsection, the existence of the Hopf bifurcation and the bifurcation points have been calculated, further we will give the order of this last. Recall the existence of Hopf bifurcation occurs if and only if $T_{n}(k)=0$ and $D_{n}(k)>0$.

Obviously $D_{0}(k)>0$ and $\lim \nolimits _{n\rightarrow +\infty }D_{n}(k)=+\infty$.

Lemma 3.1

The positive equilibrium $E^{*}$, whenever exists, verify the following condition:

$$\begin{aligned} T=R^{*}-\frac{m}{ae}\left( 1+\frac{1}{2}b\sqrt{R^{*}}\right) >0. \end{aligned}$$

(3.12)

It is easy to prove the Lemma 3.1 using the equation of the existence of equilibrium point $R^{*}=\dfrac{b\sqrt{R^{*}}+1}{(\frac{ ae}{m}-c)}$ and under the condition (2.2) T can be written as follows

$$\begin{aligned} T\left( \frac{ae}{m}-c\right)= & {} b\sqrt{R^{*}}+1-\frac{m}{ae}\left( 1+\frac{1}{2}b\sqrt{ R^{*}}\right) \left( \frac{ae}{m}-c\right) , \end{aligned}$$

(3.13)

$$\begin{aligned}= & {} b\sqrt{R^{*}}\left( 1+\frac{mc}{ae}\right) +\frac{mc}{ae}>0. \end{aligned}$$

(3.14)

Recall that the eventual Hopf bifurcation points must be the solution of the equation in the variable k

$$\begin{aligned} A(k)-(d_{1}+d_{2})\left( \dfrac{n\pi }{L}\right) ^{2}=0, \end{aligned}$$

(3.15)

which is equivalent to

$$\begin{aligned} r\left( 1-\frac{2R^{*}}{k}\right) -aP^{*}\frac{1+b\sqrt{R^{*}}+cR^{*}-R^{*}\left( \frac{b}{2\sqrt{R^{*}}}+c\right) }{(1+b\sqrt{R^{*}}+cR^{*})^{2}}-(d_{1}+d_{2})\left( \dfrac{n\pi }{L}\right) ^{2}=0. \end{aligned}$$

(3.16)

Using $P^{*}=\frac{er}{m}R^{*}(1-\dfrac{R^{*}}{k})$ and $\frac{ae }{m}R^{*}=1+b\sqrt{R^{*}}+cR^{*}$ then (3.15) becomes:

$$\begin{aligned} r\left( 1-\frac{2R^{*}}{k}\right) -\frac{mr}{eaR^{*}}\left( 1-\frac{R^{*}}{k}\right) \left( 1+ \frac{1}{2}b\sqrt{R^{*}}\right) -(d_{1}+d_{2})\left( \dfrac{n\pi }{L}\right) ^{2}=0,\qquad \end{aligned}$$

(3.17)

then the eventuels bifurcating points are given by

$$\begin{aligned} k(n)=\frac{2r(R^{*})^{2}-\dfrac{rm}{ae}R^{*}\left( 1+\frac{1}{2}b\sqrt{ R^{*}}\right) }{\left( r-(d_{1}+d_{2})\left( \dfrac{n\pi }{L}\right) ^{2}\right) R^{*}-\dfrac{rm}{ae} \left( 1+\frac{1}{2}b\sqrt{R^{*}}\right) }. \end{aligned}$$

(3.18)

Lemma 3.2

Putting

$$\begin{aligned} N_{1}=\left[ \sqrt{\tfrac{rT}{R^{*}}\left( \tfrac{L}{\pi }\right) ^{2}\tfrac{1}{ (d_{1}+d_{2})} }\right] . \end{aligned}$$

(3.19)

Where [.] is the integer part and k(n) is defined in (3.18); Hopf bifurcation occurs for the system (1.2) at $k=k(n)$ and for $n\le N_{1}$ and k(n) verify the following estimation:

$$\begin{aligned} R^{*}<k(0)<k(1)<\cdots<k(n)<k(n+1)<\cdots <k(N_{1})\le T_{\infty }, \end{aligned}$$

(3.20)

with

$$\begin{aligned} T_{\infty } =\frac{r}{R^{*}}T>0. \end{aligned}$$

(3.21)

Where T is defined in (3.12).

Proof

Note that Hopf bifurcation occurs if and only if $T_{n}(k)=0,$ leads to

$$\begin{aligned} T_{0}(k)=(d_{1}+d_{2})\left( \dfrac{n\pi }{L}\right) ^{2}, \end{aligned}$$

(3.22)

with

$$\begin{aligned} T_{0}(k)=A(k)=r\left( 1-\frac{2R^{*}}{k}\right) -\frac{mP^{*}}{eR^{*2}}\left( 1+ \dfrac{1}{2}b\sqrt{R^{*}}\right) , \end{aligned}$$

(3.23)

and it is easy to see that $\lim \nolimits _{k\rightarrow R^{*}}T_{0}(k)=-r<0$

$$\begin{aligned} A(k)=\frac{r}{k}\left( -2R^{*}+\frac{mr}{ea}\left( 1+\frac{1}{2}b\sqrt{R^{*}}\right) \right) + \frac{r}{R^{*}}\left( R^{*}-\frac{mr}{ea}\left( 1+\frac{1}{2}b\sqrt{R^{*}}\right) \right) , \end{aligned}$$

(3.24)

then

$$\begin{aligned} T_{0}^{\prime }(k)=\frac{r}{k^{2}}\left( 2R^{*}-\frac{mr}{ea}\left( 1+\frac{1}{2}b \sqrt{R^{*}}\right) \right) >0, \end{aligned}$$

(3.25)

which means

$$\begin{aligned} T_{0}^{\prime }(k)=\frac{r}{k^{2}}(R^{*}+T)>0, \end{aligned}$$

(3.26)

and

$$\begin{aligned} \lim \limits _{k\rightarrow +\infty }T_{0}(k)=T_{\infty }>0. \end{aligned}$$

(3.27)

Where $T_{\infty }$ is defined by (3.21); from (3.22) to (3.26), $T_{0}(k)$ is strictly increasing as a function of k and intersect the horizontal axis at

$$\begin{aligned} k^{*}=\frac{(R^{*}+T)R^{*}}{T}>0, \end{aligned}$$

(3.28)

the Eq. (3.22) possesses a solution if and only if

$$\begin{aligned} (d_{1}+d_{2})\left( \dfrac{n\pi }{L}\right) ^{2}<\lim \limits _{k\rightarrow +\infty }T_{0}(k)=\frac{r}{R^{*}}T, \end{aligned}$$

(3.29)

in other words, the Eq. (3.22) posses solutions if and only if $n<N_{1}$ where $N_{1}$ is defined in (3.19).

The function $(d_{1}+d_{2})(\dfrac{n\pi }{L})^{2}$ is strictly increasing as a function of n then the estimation in (3.20) is obviously verified (see Fig. 2) and this completes the proof. $\square$

Fig. 2

Numerical simulation for the existence and the order of Hopf bifurcation points the solution of the Eq. (3.22) where $a=1.5; b=1.02; c=1.02; e=0.5; m=0.5; r=1.2; d_{1}=0.02; d_{2}=0.1$ and $L=5$. Which means $R^{*}=8.1497;\,N_{1}=4; T=7.7404$ and $T_{\infty }=1.1397$ and its obvious to see that Fig. 2 show the order of Hopf bifurcation points shown in (3.20)

Now we put $\lambda (k)=\alpha (k)\pm i\omega (k)$ as the solution of the characteristic equation with:

$\alpha (k(n))=0$  and  $\omega (k(n))=\sqrt{D(k(n))}$

$$\begin{aligned} \alpha ^{\prime }(k(n))=\frac{r}{2k^{2}(n)}(R^{*}+T)>0. \end{aligned}$$

(3.30)

Under the condition (3.30) the bifurcation points and their order is given by the following theorem

Theorem 3.3

If there exists $N^{*}\le N_{1}$ a critical value $j_{0},\ldots ,j_{N^{*}}$ such that $j_{0}=0<j_{1}<\cdots<j_{N^{*}}<N_{1}$ and $D_{i\xi }(k(i\xi ))>0, \,\xi =0\ldots N^{*}$ we have the following estimation:

$$\begin{aligned} R^{*}<k(0)<k(1)<\cdots<k(n)<k(n+1)<\cdots <k(j_{N^{*}}). \end{aligned}$$

(3.31)

3.3 Linear stability and Turing instability

In this subsection, a sufficient condition for Turing instability has been given, before that recall that the existence of Turing instability exhibit when the two following conditions holds:

• (i) The equilibrium point is linearly stable in the absence of diffusion.

• (ii) The equilibrium point becomes instable in the presence of diffusion.

Obviously $D_{0}(k)>0$, then $D_{n}(k)<0$ need to be proved for some values of n.

$$\begin{aligned} D_{n}(k)=D\left( \left( \dfrac{n\pi }{L}\right) ^{2}\right) =d_{1}d_{2}\left( \left( \dfrac{n\pi }{L} \right) ^{2}\right) ^{2}-d_{2}A(k)\left( \dfrac{n\pi }{L}\right) ^{2}-BC(k).\quad \end{aligned}$$

(3.32)

Note that $D_{0}(k)>0$ so the minimum of the function (3.32) occurs when

$$\begin{aligned} \left( \dfrac{n\pi }{L}\right) ^{2}=\left( \dfrac{n\pi }{L}\right) _{cr}^{2}, \end{aligned}$$

(3.33)

with

$$\begin{aligned} \left( \dfrac{n\pi }{L}\right) _{cr}^{2}=\frac{A(k)}{2d_{1}}>0, \end{aligned}$$

(3.34)

and $D((\dfrac{n\pi }{L})_{cr}^{2})<0$ is a sufficient condition for Turing instability, that is

$$\begin{aligned}&\displaystyle d_{1}d_{2}\left( \frac{A(k)}{2d_{1}}\right) ^{2}-d_{2}A(k)\frac{A(k)}{2d_{1}}-BC(k)<0, \end{aligned}$$

(3.35)

$$\begin{aligned}&\displaystyle -\frac{d_{2}}{4d_{1}}(A(k))^{2}-BC(k)<0, \end{aligned}$$

(3.36)

$$\begin{aligned}&\displaystyle \frac{d_{2}}{4d_{1}}(A(k))^{2}>-BC(k)>0, \end{aligned}$$

(3.37)

then

$$\begin{aligned} A(k)>2\sqrt{\frac{md_{1}}{ed_{2}}c(k)}>0, \end{aligned}$$

(3.38)

It is a sufficient condition for having Turing driven instability. for the time biens we should be focus on studying the intersection between the Hopf bifurcation curve and Turing driven instability curve, not that this point (whenever it exists) is called Turing–Hopf bifurcation point.

Obviously the condition $T_{n}=0$ and $D_{n}>0$ is a necessary condition for the existence of Hopf bifurcation and $T_{n}=0$ which equivalent to

$$\begin{aligned} A(k)-(d_{1}+d_{2})\left( \dfrac{n\pi }{L}\right) ^{2}=0, \end{aligned}$$

(3.39)

leads to

$$\begin{aligned} k_{H}(d_{1},n)=\frac{R^{*}r(R^{*}+T)}{-(d_{1}+d_{2})\left( \dfrac{n\pi }{L} \right) ^{2}R^{*}+rT}, \end{aligned}$$

(3.40)

and $D_{n}=0$ equivalent to

$$\begin{aligned} d_{1}d_{2}\left( \dfrac{n\pi }{L}\right) ^{4}-d_{2}A(k)\left( \dfrac{n\pi }{L}\right) ^{2}-BC(k)=0, \end{aligned}$$

(3.41)

replacing $A(k)=-\dfrac{r}{k}(R^{*}+T)+\dfrac{r}{R^{*}}T$ and $C(k)= \dfrac{ae^{2}r}{mR^{*}}(R^{*}-T)-\dfrac{ae^{2}r}{mk}(R^{*}-T)$ in (3.41)

$$\begin{aligned} k_{T}(d_{1},n)=r\frac{ae(R^{*}-T)-(R^{*}+T)\left( \dfrac{n\pi }{L}\right) ^{2}}{ d_{1}d_{2}\left( \dfrac{n\pi }{L}\right) ^{4}-\dfrac{r}{R^{*}}T\left( \dfrac{n\pi }{L}\right) ^{2}+ \dfrac{aer}{mR^{*}}(R^{*}-T)}, \end{aligned}$$

(3.42)

The two curves defined in (3.40) and (3.42) intersect at

$$\begin{aligned} d_{1}= & {} d_{1}^{*}=\left( \frac{L}{n\pi }\right) ^{2}\left[ -d_{2}^{2}\left( \frac{ n\pi }{L}\right) ^{4}\frac{R^{*}}{a}\left( \frac{R^{*}+T}{R^{*}-T} \right) \right. \nonumber \\&\left. +Tr+rR^{*}(R^{*}+T)-d_{2}\left( \frac{n\pi }{L}\right) ^{2}\right] . \end{aligned}$$

(3.43)

Defining the functional

$$\begin{aligned} f(x)= & {} \left( \frac{L}{\pi }\right) ^{2}\frac{1}{x}\left[ -d_{2}^{2}\left( \frac{\pi }{L}\right) ^{4} \frac{R^{*}}{a}\left( \frac{R^{*}+T}{R^{*}-T}\right) x^{2}+Tr\right. \nonumber \\&\left. +rR^{*}(R^{*}+T)-d_{2}\left( \frac{\pi }{L}\right) ^{2}x\right] , \end{aligned}$$

(3.44)

with

$$\begin{aligned} f^{\prime }(x)=\left( \frac{\pi }{L}\right) ^{2}\frac{1}{x^{2}}\left[ -d_{2}^{2}\left( \frac{ \pi }{L}\right) ^{4}\frac{R^{*}}{a}\left( \frac{R^{*}+T}{R^{*}-T} \right) x^{2}-Tr-rR^{*}(R^{*}+T)\right] <0, \end{aligned}$$

(3.45)

which means that the functional f is strictly decreasing as n growth and $\lim \nolimits _{n\rightarrow 0^{+}}f(x)=+\infty$ and $\lim \nolimits _{n \rightarrow +\infty }f(x)=-\infty$ and there exist a positive integer $n^{*}$ such that

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} >0&{} \text {if}\quad 1\le n<n^{*}, \\ <0&{}\text {if}\quad n^{*}\le n. \end{array} \right. \end{aligned}$$

(3.46)

leads to $1\le n_{*}<n^{*}$ such that the Hopf bifurcation curve defined in (3.40) intersects the Turing instability curve (3.42) noted by $L_{n_{*}},$ at the point $(k^{*},d_{2}^{*})$ this point called Turing–Hopf bifurcation point, for the existence of homogenous and nonhomogeneous periodic solution is given by the following theorem:

Theorem 3.4

We assume that the existence condition of the positive equilibrium $E^{*}$ (2.2) holds, and defining the Hopf curve by $H_{n}$ in the $k-d_{1}$ plane defined in (3.40)

• (i) If $n=0$ the equilibrium $E^{*}$ is asymptotically stable when $0<k<\dfrac{R^{*}(R^{*}+T)}{T}=k^{*}$ and instable when $k> \dfrac{R^{*}(R^{*}+T)}{T}$

• (ii) The system (1.2) has a Hopf bifurcation near $E^{*}$ when $k=k_{H}(d_{1},n)$ and has a homogenous periodic solution for n=0, and nonhomogeneous periodic solution when $n=1,2,\ldots ,j_{N^{*}}$

4 Normal form on the center of manifold for Hopf bifurcation

In this section the papers [15, 34,35,36,37] has been followed and k has been used as a bifurcation parameter. Assuming that $k^{*}=k_{H}^{*}(n)$ where $k_{H}^{*}(n)$ is defined by the Eq. (3.15) and introducing the variable $\mu =k-k_{H}^{*}(n)$ and rewriting the positive equilibrium $E^{*}$ point in function of $\mu$ by putting $k=\mu +k_{H}^{*}(n)$ then we have:

$$\begin{aligned} u^{*}(\mu )=R^{*}\text { and } v^{*}(\mu )=P^{*}(\mu +k^{*}). \end{aligned}$$

(4.1)

Putting

$$\begin{aligned} {\tilde{R}}(.,t)=R(.,t)-u^{*}(\mu ){ \, \, \, \ }{\tilde{P}} (.,t)=P(.,t)-v^{*}(\mu ), \end{aligned}$$

(4.2)

and

$$\begin{aligned} {\tilde{U}}(t)=({\tilde{R}}(.,t),{\tilde{P}}(.,t))^{T}\text { and }{\tilde{U}} ^{*}=(u^{*}(\mu ),v^{*}(\mu ))^{T}, \end{aligned}$$

(4.3)

Rewriting system (1.2) in the form:

$$\begin{aligned} \frac{d{\tilde{U}}(t)}{dt}=D\Delta {\tilde{U}}+L_{0}({\tilde{U}})+g({\tilde{U}},\mu ), \end{aligned}$$

(4.4)

with $D=diag(d_{1},d_{2})$ and $L_{0}({\tilde{U}})=J({\tilde{U}}^{*})\tilde{U }$

and

$$\begin{aligned} g({\tilde{U}},\mu )= & {} \sum _{i+j+l\ge 2 }\frac{1}{i!j!l!}g_{ijl}{\tilde{R}}^{i} {\tilde{P}}^{j}\mu ^{l}, \end{aligned}$$

(4.5)

$$\begin{aligned} g_{ijl}= & {} \left( g_{ijl}^{(1)},g_{ijl}^{(2)}\right) , \end{aligned}$$

(4.6)

with

$$\begin{aligned} g_{ijl}^{(k)}= & {} \frac{\partial ^{i+j+l}g^{(k)}(0,0,0)}{\partial ^{i}R\partial ^{j}P\partial ^{il}\mu },\quad k=1,2, \end{aligned}$$

(4.7)

$$\begin{aligned} g^{(1)}({\tilde{R}},{\tilde{P}},\mu )= & {} r({\tilde{R}}+u^{*}(\mu ))\left( 1-\frac{ {\tilde{R}}+u^{*}(\mu )}{\mu +k^{*}}\right) \nonumber \\&-\dfrac{a({\tilde{P}}+v^{*}(\mu ))({\tilde{R}}+u^{*}(\mu ))}{1+b\sqrt{{\tilde{R}}+u^{*}(\mu )}+c(\tilde{R }+u^{*}(\mu ))}, \nonumber \\ g^{(2)}({\tilde{R}},{\tilde{P}},\mu )= & {} -m({\tilde{P}}+v^{*}(\mu ))+\dfrac{ae( {\tilde{P}}+v^{*}(\mu ))({\tilde{R}}+u^{*}(\mu ))}{1+b\sqrt{{\tilde{R}} +u^{*}(\mu )}+c({\tilde{R}}+u^{*}(\mu ))}.\nonumber \\ \end{aligned}$$

(4.8)

The linearized system of (4.4) around the origin is:

$$\begin{aligned} \frac{d{\tilde{U}}(t)}{dt}=\Gamma ({\tilde{U}}). \end{aligned}$$

(4.9)

Now defining the normalized eigenfunction of the problem (2.6)

$$\begin{aligned} \varphi _{n}(x)=\frac{\cos \left( \dfrac{n\pi }{L}x\right) }{\left\| \cos \left( \dfrac{n\pi }{L}x\right) \right\| _{2,2}}, \end{aligned}$$

(4.10)

and putting

$$\begin{aligned} \beta _{n}^{1}(x)=(\varphi _{n}(x),0)^{T}{ \, \, \,}\beta _{n}^{2}(x)=(0,\varphi _{n}(x))^{T}. \end{aligned}$$

(4.11)

Let $\Lambda _{n}$ be the set of all eigenvalues of (4.9), under the form $\lambda =\pm i\omega _{n}$ and the associated invariant manifold set is:

$$\begin{aligned} \Upsilon _{n}=span\{<\varphi (.),\beta _{n}^{i}>\beta _{n}^{i} \ /\varphi (.)\in \chi ,i=1,2\}. \end{aligned}$$

(4.12)

It is easy to see that $\Gamma (\Upsilon _{n})\subset span\{\beta _{n}^{i},i=1,2\}\,n\in {\mathbb {N}} _{0}$; and let $Y(t)\in {\mathbb {R}}^{2}$ be such that $Y^{T}(t)(\beta _{n}^{1},\beta _{n}^{2})^{T}\in \Upsilon _{n}$.

In the invariant manifold $\Gamma$ the linear partial differential equation (4.9) is equivalent to the linear system:

$$\begin{aligned} {\dot{Y}}(t)=-\left( \frac{n\pi }{L}\right) ^{2}diag(d_{1},d_{2})+L_{0}(Y(t)){ \, } Y(t)\in {\mathbb {R}} ^{2}. \end{aligned}$$

(4.13)

It is obvious to see that (4.9) has the same characteristic equation ( 3.1), now defining the matrix

$$\begin{aligned} M_{n}=-\left( \frac{n\pi }{L}\right) ^{2}diag(d_{1},d_{2})+J(R^{*},P^{*}) . \end{aligned}$$

(4.14)

Assume there exist $n\in {\mathbb {N}} _{0}$ such that $T_{n}=0$ with $k=k^{*}(n)$ then the eigenvalues are $\pm i\omega _{n}$ (or $\pm \sqrt{D_{n}}$) leads to

$\Lambda _{n}=\{i\omega _{n},-i\omega _{n}\}; B_{n}=diag(i\omega _{n},-i\omega _{n}); z=(z_{1},z_{2})^{T}$

Now defining

$$\begin{aligned} p_{n}= & {} \left( {\begin{array}{c}p_{n1}\\ p_{n2}\end{array}}\right) =\left( \begin{array}{c} \dfrac{d_{2}\left( \frac{n\pi }{L}\right) ^{2}+i\omega _{n}}{c_{n}(k^{*})} \\ 1 \end{array} \right) , \end{aligned}$$

(4.15)

$$\begin{aligned} q_{n}= & {} \left( {\begin{array}{c}q_{n1}\\ q_{n2}\end{array}}\right) =\left( \begin{array}{c} \dfrac{c_{n}(k^{*})}{2i\omega _{n}} \\ \dfrac{d_{1}\left( \frac{n\pi }{L}\right) ^{2}-A(k^{*})+i\omega _{n}}{2i\omega _{n}} \end{array} \right) . \end{aligned}$$

(4.16)

Note that $p_{n}$ and $q_{n}$ verified the conditions

$$\begin{aligned} M_{n}p_{n}= & {} i\omega _{n}p_{n};\, M_{n}^{T}q_{n}=i\omega _{n}q_{n}, \end{aligned}$$

(4.17)

$$\begin{aligned} q_{n}^{T}p_{n}= & {} 1, \end{aligned}$$

(4.18)

and the decomposition of $\chi$ into two subspaces

$$\begin{aligned} \chi =\chi ^{{\mathbb {C}}} \oplus \chi ^{{\mathbb {S}}}, \end{aligned}$$

(4.19)

with $\chi ^{{\mathbb {C}}}:=\{zq+{\bar{z}}\bar{q}:z\in {\mathbb {C}}\}$ and the stable subspace $\chi ^{{\mathbb {S}}} :=\{U\in \chi :\langle q,U\rangle =0\}$ for any $U\in \chi$ there exists $z\in {\mathbb {C}}$ and $w\in \chi ^{{\mathbb {S}}}$; and defining the $2\times 2$ matrices $\Omega _{n}=(p_{n},{\bar{p}}_{n})$  $\Psi _{n}=col(q_{n}^{T},{\bar{q}}_{n}^{T})$ where ${\bar{p}}_{n}$ (resp $\bar{q }_{n}$) is the conjugate of $p_{n}$ (resp $q_{n}$); and $\Psi _{n}\Omega _{n}=diag(1,1)=I_{2}$.

Using the decomposition of the space $\chi$ to write ${\tilde{U}}$ as follows:

$$\begin{aligned} {\tilde{U}}=z_{1}p_{n}\varphi _{n}(x)+z_{2}{\bar{p}}_{n}\varphi _{n}(x)+w \, z_{1},z_{2}\in {\mathbb {R}} \ ;w\in \chi ^{s}. \end{aligned}$$

(4.20)

Following the same ideas in [15, 26, 38], the normal forms can be written as follows

$$\begin{aligned} z=B_{n}z+\left( {\begin{array}{c}B_{n1}z_{1}\mu \\ {\bar{B}}_{n1}z_{2}\mu \end{array}}\right) +\left( {\begin{array}{c} B_{n2}z_{1}^{2}z_{2}\\ {\bar{B}}_{n2}z_{1}z_{2}^{2}\end{array}}\right) +O(z\left| \mu \right| ^{2}+\left| z\right| ^{4}){,} \end{aligned}$$

(4.21)

with

$$\begin{aligned} B_{n1}= & {} q_{n2}(g_{101}^{(2)}p_{n1}+g_{011}^{(2)}p_{n2}){,} \end{aligned}$$

(4.22)

$$\begin{aligned} B_{n2}= & {} \left\{ \begin{array}{ll} \frac{1}{2\pi }Q_{021}+\frac{1}{4\pi }F_{021}+\frac{1}{2\sqrt{\pi }}G_{00}&{} \text {if}\quad n=0{,} \\ \frac{3}{4}Q_{n21}+\frac{1}{2\sqrt{\pi }}G_{n0}+\frac{1}{2\sqrt{2\pi }} G_{n(2n)}&{}\text {if}\quad n\ne 0{,} \end{array}\right. \end{aligned}$$

(4.23)

where

$$\begin{aligned} Q_{n21}= & {} q_{n}^{T}\left[ g_{300}p_{n1}\left| p_{n1}\right| ^{2}+g_{030}p_{n2}\left| p_{n2}\right| ^{2}+g_{210}(p_{n1}^{2}{\bar{p}} _{n2}+2p_{n2}\left| p_{n1}\right| ^{2})\right. \nonumber \\&\left. +g_{120}(p_{n2}^{2}{\bar{p}} _{n1}+2p_{n1}\left| p_{n2}\right| ^{2})\right] , \end{aligned}$$

(4.24)

$$\begin{aligned} F_{k21}= & {} \frac{i}{\omega _{n}}\left[ (q_{n}^{T}C_{n20})(q_{n}^{T}C_{n11})-\left| q_{n}^{T}C_{n11}\right| ^{2}-\frac{2}{3}\left| q_{n}^{T}C_{n02}\right| ^{2}\right] , \end{aligned}$$

(4.25)

$$\begin{aligned} C_{n20}= & {} {\bar{C}} _{n02}=g_{200}p_{n1}^{2}+2g_{110}p_{n1}p_{n2}+g_{020}p_{n2}^{2}, \end{aligned}$$

(4.26)

$$\begin{aligned} C_{n11}= & {} g_{200}\left| p_{n1}^{2}\right| +4g_{110}Re\{p_{n1}{\bar{p}} _{n2}\}+2g_{020}\left| p_{n2}^{2}\right| , \end{aligned}$$

(4.27)

and

$$\begin{aligned} G_{ni}= & {} q_{n}^{T}[(g_{200}p_{n1}+g_{110}p_{n2})A_{ni11}+(g_{110}p_{n1}+g_{020}p_{n2})A_{ni11}\nonumber \\&+A_{ni20}(g_{200} {\bar{p}}_{n1}+g_{110}{\bar{p}}_{n2}) \nonumber \\&+(g_{110}{\bar{p}}_{n1}+g_{020}{\bar{p}}_{n2})A_{ni20}], \end{aligned}$$

(4.28)

with

$$\begin{aligned} A_{ni20}=\left\{ \begin{array}{l} \frac{1}{\sqrt{\pi }}(2i\omega _{0}diag(1,1)-M_{0})^{-1}(C_{020}-q_{0}^{T}C_{020}p_{0}-{\bar{q}} _{0}^{T}C_{020}{\bar{p}}_{0})\text { if }n,j=0, \\ c_{ni}(2i\omega _{0}diag(1,1)-M_{0})^{-1}C_{n20}\text { if }n\ne 0,j=0,2n, \end{array} \right. \end{aligned}$$

(4.29)

and

$$\begin{aligned} A_{ni11}= & {} \left\{ \begin{array}{l} -\frac{1}{\sqrt{\pi }}M_{0}{}^{-1}(C_{011}-q_{0}^{T}C_{011}p_{0}-{\bar{q}} _{0}^{T}C_{011}{\bar{p}}_{0})\text { if }n,j=0, \\ -c_{ni}M_{i}{}^{-1}C_{n11}\text { if }n\ne 0,j=0,2n, \end{array} \right. \end{aligned}$$

(4.30)

$$\begin{aligned} c_{ni}= & {} \langle \varphi _{n}^{2}(x)\varphi _{i}(x)\rangle . \end{aligned}$$

(4.31)

Note that

$$\begin{aligned} c_{ni}=\left\{ \begin{array}{c} \frac{1}{\sqrt{\pi }} \, i=n=0, \\ \frac{1}{\sqrt{\pi }} \, i=0,n\ne 0, \\ \frac{1}{\sqrt{\pi }} \, i=2n\ne 0, \\ 0~\text {otherwise}. \end{array} \right. \end{aligned}$$

(4.32)

Fig. 3

Numerical simulation for the intersection point between Hopf bifurcation curve (3.40) and Turing instability curve (3.42) when $n=3$ ; $a=3.5;\,b=1.02;\,c=1.02;\,e=0.5;\,m=0.75;\,r=1.2; d_{2}=0.1$ and $L=5.$ which means $R^{*}=0.3863; ; T=0.2452$ and $T_{\infty }=0.7616$, and it is obvious to see that the conditions (2.2) is verified (for the existence of the positive equilibrium $E^{*}$)

Fig. 4

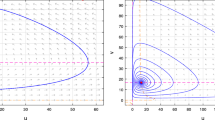
Trajectory and phase portraits of the system (1.1) when $E^{*}$ is locally asymptotically stable and $k=14.75<k^{*}=16.7304$

Fig. 5

Trajectory and phase portraits of the system (1.1) when $E^{*}$ is instable and $k=19>k^{*}=16.7304$

Fig. 6

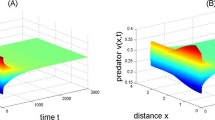
Numerical simulation of the system (1.2) when the equilibrium $(R^{*},P^{*})=(6.5394,11.4886)$ is locally asymptotically stable for $k=14.5<k(0)=14.75$ and $d_{1}=0.2; d_{2}=0.1; a=1.75; b=1.22; c=1.12\,e=0.5; m=0.5; r=3.2$ with the initial condition $R(0,x)=5$ and $P(0,x)=10$

Fig. 7

Numerical simulation of the system (1.2) when the equilibrium $(R^{*},P^{*})=(6.5394,11.4886)$ is instable when $k=15>k(0)=14.75$ and $d_{1}=0.2; d_{2}=0.1; a=1.75; b=1.22; c=1.12\, e=0.5; m=0.5; r=3.2$ with the initial condition $R(0,x)=5$ and $P(0,x)=10$ and shows the existence of a homogenous periodic solution

Fig. 8

Numerical simulation of the system (1.2) when the equilibrium $E^{*}$ does not exist and $E_{1}$ is globally asymptotically stable when $k=6<R^{*}=6.5394$ and $d_{1}=0.02; d_{2}=0.01; a=1.75; b=1.22; c=1.12\, e=0.5; m=0.5; r=3.2$ with the initial condition $R(0,x)=7$ and $P(0,x)=3$

Fig. 9

Numerical simulation of the system (1.2) when the equilibrium $E^{*}$ does not exist and $E_{1}$ is globally asymptotically stable when $k=6<R^{*}=6.5394$ and $d_{1}=0.02,d_{2}=0.01\,a=1.75 , b=1.22 , c=1.12\, e=0.5; m=0.5, r=3.2$ with the initial condition $R(0,x)=1$ and $P(0,x)=4$

Using the change of variables

$$\begin{aligned} z_{1}=V_{1}-iV_{2},{ \, }z_{2}=V_{1}-iV_{2}, \end{aligned}$$

(4.33)

and

$$\begin{aligned} V_{1}=\rho \cos \theta , { \, \, \,}V_{2}=\rho \sin \theta , \end{aligned}$$

(4.34)

then the normal form (4.21) can be written in the real coordinate using the above change of variable, and becomes:

$$\begin{aligned} \left\{ \begin{array}{c} \dot{\rho }=V_{n1}\mu \rho +V_{n2}\rho ^{3}+O(\mu \rho ^{2}+\left| (\mu ,\rho )\right| ^{4}), \\ \theta =-\omega _{n}+O(\left| (\mu ,\rho )\right| ), \end{array} \right. \end{aligned}$$

(4.35)

with

$$\begin{aligned} V_{n1}=Re\{B_{n1}\} \, V_{n2}=Re\{B_{n2}\}. \end{aligned}$$

(4.36)

The dynamic of the system (1.2) near the bifurcation point is topologically equivalent to (4.35) in the neighborhood of $\mu =0$ ($\mu$ sufficiently small) and using Lemma 3.1.2 in Wiggins [39, 40] and [27, 41]. $V_{n2}$ determines the direction of Hopf bifurcation and the stability of periodic solutions, it is given by the following theorem:

Theorem 4.1

(i) If $V_{n2}<0$ then the system (4.20) has a supercritical Hopf bifurcation in $k=k_{H}^{*}(n)$ (that means the periodic solutions are stable) and the periodic solution exist if $V_{n1}>0$ and $\mu >0$ or $V_{n1}<0$ and $\mu <0$

(ii) If $V_{n2}>0$ then the system (4.20) has a subcritical Hopf bifurcation in $k=k_{H}^{*}(n)$ (that means the periodic solutions are instable) and the periodic solution exist if $V_{n1}>0$ and $\mu <0$ or $V_{n1}<0$ and $\mu >0$.

5 Conclusion

We have dealt in this paper with a predator prey model with a spatial diffusion, a linear mortality and a herd behavior. the generalized Holling III interaction functional with the presence of herd behavior and a Neumann boundary condition have been chosen.

In Sect. 1, a presentation of our model is given and also the ecological meaning of the parameters is provided. In Sect. 2, the existence of a unique positive solution was proved using the upper-lower solution (sub super-solution) method, it is also proved that the solution of the system (1.2) is bounded. Furthermore, the global stability of $E_{1}$ in the absence of $E^{*}$ is proved.

In Sect. 3, the local stability of the positive equilibrium $E^{*}$ has been studied in the presence of diffusion and also Hopf bifurcation has been analyzed (calculating the Hopf bifurcation points and their order), also a sufficient condition for Turing driven instability has been given; and the presence of homogenous periodic solution when $n=0$ and nonhomogeneous periodic solution when $n=1,2,\ldots ,N_{1}$ is shown. At last, the intersection between bifurcation curve and Turing driven instability curve is analyzed to prove the existence of a Turing–Hopf bifurcation point.

In the next section, the normal form of Hopf bifurcation is calculated beside some properties of the periodic solution (the stability and the instability of the periodic homogenous and inhomogeneous solution).

At the end of the paper, numerical simulation has been used to illustrate the theoretical results, for instance Fig. 2 represents the order of Hopf bifurcation points shown in Lemma 3.2, Fig. 3 the existence of Turing–Hopf bifurcation point; Figs. 4 and 5 the presence of a periodic solution of the system (1.1) such that for $k<k^{*}$, the positive equilibrium $E^{*}$ is locally asymptotically stable, but when $k>k^{*}$, it becomes instable and there exists a stable periodic orbit. Figure 6 shows the existence of a periodic spiral to $E^{*}$ when $k<k(0)$; Fig. 7 the existence of a stable periodic homogenous solution of the system (1.2) for $k>k(0)$. Finally Figs. 8 and 9 represent the global stability of the equilibrium $E_{1}$ for two different initial conditions when $k<R^{*}$.