1 Introduction

A thermostat is a device that senses a physical system’s temperature and performs actions to maintain the system’s temperature at a desired set point. A thermostat maintains the exact temperature, by controlling the switching on or off of the heating or cooling devices or by controlling the flow of heat-transfer fluid as necessary. In applications, ranging from ambient air control to automotive coolant control, a thermostat may often be the only control unit for a heating or cooling system.

Thermostats are used in an appliance or a system that heats or cools at a set-point temperature, such as house heating, air conditioning, central heating, water heaters, kitchen equipment like stoves and refrigerators, and medical and scientific incubators. Thermostats use various sensor types to measure the temperature. For one type, the mechanical thermostat, a coil-shaped bimetallic strip directly controls electrical contacts that control the source of heating or cooling. Alternatively, electronic thermostats use a thermistor or other semiconductor sensor to monitor the heating or cooling equipment, which includes amplification and processing.

Due to the rapid expansion in the literature of fractional calculus, there are many advanced techniques in the development of fractional-order ordinary and partial differential equations. They were used as excellent sources and methods for modeling many phenomena in the various fields of science, engineering, and technology, see the monographs [1–3]. Furthermore, the thermostat model, Burgers equation, Navier–Stokes equations, or Kirchhoff–Schrodinger-type equations are some of the real-world problems. Thus, different methods and techniques have been suggested for modeling these types of problems [4, 5].

Over the past three decades, many researchers have widely studied the topic of the classical initial boundary value problem (BVP) for ordinary and partial differential equations with integer and fractional order by using different methods. Stability analysis is an important branch of the qualitative theory of differential equations, as we know that sometimes finding the exact solution is quite challenging. Therefore, various numerical techniques were developed to find a solution. The most important type of stability is Ulam–Hyers stability. From a numerical and optimization point of view, Ulam–Hyers stability is essential because it provides a bridge between the exact and numerical solutions. Ulam–Hyers (or Ulam–Hyers–Rasssias) stability has been used extensively to study stability and has found applications in real-life problems such as in economics, biology, population dynamics, etc. [6–21].

However, only a few results have been obtained for linear and nonlinear ordinary and partial differential equations with the Caputo fractional derivative method and nonlocal boundary conditions [22–25]. The Caputo time fractional derivative can be used to model memory systems, since it includes all the context of the past. One of the most important classes of the thermostat models is the fractional thermostat equations that has been discussed and used in various fields of science. As is well known, different types of thermostat models have been studied by several researchers [26–34]. Very recently, Kaabar et al. [35] proved the existence of solutions for the fractional strongly singular thermostat model using nonlinear fixed-point techniques and investigated a hybrid version of the fractional thermostat control model. The study of thermostat models enables the development of efficient equipment used in several mechanical and electronic devices.

In 2006 [31], Infante and Webb developed a thermostat model, insulated at \(\kappa = 0\) with a controller adding or removing heat at \(\kappa = 1\) depending on the temperature detected by a sensor point at η

$$\begin{aligned} \textstyle\begin{cases} u^{\prime \prime }(\kappa )+\psi (\kappa,u(\kappa ))=0,\quad \kappa \in [0,1], \\ u^{\prime }(0)=0,\qquad \delta u^{\prime }(1)+u(\eta )=0, \end{cases}\displaystyle \end{aligned}$$

where \(\eta \in [0,1]\) is a real constant and δ is a positive parameter. By applying the fixed-point index theory on Hammerstein integral equations, they obtained existence results for the BVP. Recently, Nieto and Pimentel [32] extended the fractional thermostat model to the three-point boundary conditions (BCs) of order \(\vartheta \in (1,2]\)

$$\begin{aligned} \textstyle\begin{cases} {}^{C} D^{\vartheta }u(\kappa )+\psi (\kappa,u(\kappa ))=0, \quad\kappa \in [0,1], \\ u^{\prime }(0)=0,\qquad \delta {}^{C} D^{\vartheta -1}u(1)+u(\eta )=0, \end{cases}\displaystyle \end{aligned}$$
(1)

where \({}^{C} D^{\vartheta }\) and \({}^{C} D^{\vartheta -1}\) denote the Caputo fractional derivatives, \(\delta >0\) and \(\eta \in [0,1]\) are real constants.

In recent years, a new field for researchers has become available, which is fractional difference equations (FDE). With the fractional difference operators, some real-world phenomena are being studied, see, e.g., [36]. Nevertheless, quite recently some researchers have developed much interest in the study of discrete fractional calculus (DFC). The study of DFC was initiated by Miller and Ross [37]. The authors [38–48] have recently recorded significant developments in that direction. Further, the existence and uniqueness of solutions and various kinds of Ulam-stability analysis for Caputo fractional difference equations have been established by several authors [49–57]. Motivated by the previously mentioned works [31, 32, 34, 58, 59], in this paper, we aim to investigate the following discrete fractional thermostat model (DFTM) with three-point BCs of the form

$$\begin{aligned} \textstyle\begin{cases} {}^{C}\Delta ^{\vartheta }u(\kappa )+\mathcal{F}(\kappa +\vartheta -1, u( \kappa +\vartheta -1))=0, \quad\kappa \in {\mathbb{N}_{0}^{\ell +1}}, \\ \Delta u(\vartheta -2)=0, \qquad \delta {}^{C}\Delta ^{\vartheta -1} u( \vartheta +\ell )+\gamma u(\eta )=0, \end{cases}\displaystyle \end{aligned}$$
(2)

for \(\vartheta \in (1,2]\), \(\vartheta -1\in (0,1]\), δ & \(\gamma >0\) are a positive real parameter and a sensor point \(\eta \in \mathbb{N}_{\vartheta -1}^{\vartheta +\ell }\) is a constant, where \({}^{C}\Delta ^{p}\) is the CFDO of order \(p\in \{ \vartheta, \vartheta -1 \} \), \(\mathcal{F}: \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1} \times \mathbb{R} \rightarrow \mathbb{R}\) is a continuous function and \(\ell \in \mathbb{N}_{0}\). Also, we consider various types of Ulam stability for DFTM with four-point BCs

$$\begin{aligned} \textstyle\begin{cases} {}^{C}\Delta ^{\vartheta }u(\kappa )=\mathcal{F}(\kappa +\vartheta -1, u( \kappa +\vartheta -1)),\quad \kappa \in {\mathbb{N}_{0}^{\ell +1}}, \\ \Delta u(\vartheta -2)=\beta u(\zeta ), \qquad \delta {}^{C}\Delta ^{ \vartheta -1} u(\vartheta +\ell )+\gamma u(\eta )=0, \end{cases}\displaystyle \end{aligned}$$
(3)

for \(\vartheta \in (1,2]\), \(\vartheta -1\in (0,1]\), δ, β & \(\gamma >0\) and sensor points \(\zeta, \eta \in \mathbb{N}_{\vartheta -1}^{\vartheta +\ell }\) are constants with \(\zeta \leq \eta \). Comparing (3) with (1), we have \(\mathcal{F}(\kappa,u)=-\psi (\kappa,u)\).

This paper is organized as follows. Some definitions and properties of DFC used to establish the main results are provided in Sect. 2. Existence and uniqueness of solutions for a DFTM with three-point BCs (2) are obtained by using a contraction mapping theorem and the Brouwer fixed-point theorem in Sect. 3.1. In Sect. 3.2, we introduce some new results for various forms of Ulam stability analysis of a DFTM with four-point BCs (3). In Sect. 4, suitable examples are discussed as applications to show the applicability of our obtained results, and the paper ends with a conclusion in Sect. 5.

2 Basic preliminaries

This section consists of definitions and preliminary lemmas, which are essential for the discussion of our results.

Definition 2.1

(see [39])

For \(\vartheta > 0\), the ϑth-order fractional sum of \(\mathcal{F}:\mathbb{N}\rightarrow \mathbb{R}\) is defined as

$$\begin{aligned} \Delta ^{-\vartheta } \mathcal{F}(\kappa )= \frac{1}{\Gamma (\vartheta )} \sum _{\xi =a}^{\kappa -\vartheta } \bigl( \kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)} \mathcal{F}(\xi ), \end{aligned}$$

for \(\kappa \in {\mathbb{N}_{a+\vartheta }}\), \(\sigma (\kappa )=\xi +1\) and \(\kappa ^{(\vartheta )}:= \frac{\Gamma (\kappa +1)}{\Gamma (\kappa +1-\vartheta )}\).

Moreover, Composition rules [39] are;

  • Assume \(\mathcal{F}\) is defined on \(\mathbb{N}_{a}\) and \(\mu, \vartheta \) are positive numbers. Then,

    $$\begin{aligned} \bigl[\Delta ^{-\mu }_{a+\vartheta } \bigl(\Delta ^{-\vartheta }_{a} \mathcal{F}\bigr) \bigr](\kappa ) = \bigl(\Delta _{a} ^{-(\mu + \vartheta )} \mathcal{F} \bigr) (\kappa ) = \bigl[\Delta _{a+\mu }^{- \vartheta } \bigl( \Delta _{a} ^{-\mu } \mathcal{F}\bigr) \bigr] (\kappa ), \end{aligned}$$

    for \(\kappa \in \mathbb{N}_{a+\mu +\vartheta }\).

  • Assume \(\mathcal{F}: \mathbb{N}_{a} \to \mathbb{R}\) with \(\vartheta, \mu >0\) and \(0\leq \mathcal{N}-1 < \vartheta \leq \mathcal{N}\). Then,

    $$\begin{aligned} \Delta _{a+\mu }^{\vartheta } \Delta _{a} ^{-\mu } \mathcal{F}(\kappa ) = \Delta _{a} ^{\vartheta -\mu } \mathcal{F}(\kappa ), \end{aligned}$$

    for \(\kappa \in \mathbb{N}_{a+\mu +\mathcal{N}-\vartheta }\) and \(\mathcal{N} \in \mathbb{N}\).

Definition 2.2

(see [38])

For \(\vartheta >0\) and \(\mathcal{F}\) being defined on \(\mathbb{N}_{a}\), the ϑth Caputo fractional difference of \(\mathcal{F}\) is

$$\begin{aligned} {}^{C}\Delta ^{\vartheta } \mathcal{F}(\kappa )= \Delta ^{-(\mathcal{N}- \vartheta )}\Delta ^{\mathcal{N}} \mathcal{F}(\kappa ) = \frac{1}{\Gamma (\mathcal{N}-\vartheta )} \sum_{\xi =a}^{\kappa - \mathcal{N}+\vartheta } \bigl(\kappa -\sigma (\xi ) \bigr)^{(\mathcal{N}- \vartheta -1)}\Delta ^{\mathcal{N}} \mathcal{F}(\xi ), \end{aligned}$$

for \(\kappa \in {\mathbb{N}_{a+\mathcal{N}-\vartheta }}\) and \(\mathcal{N}\in \mathbb{N}\) such that \(0\leq \mathcal{N}-1<\vartheta \leq \mathcal{N}\). If \(\vartheta =\mathcal{N}\), then \({}^{C}\Delta ^{\vartheta } \mathcal{F}(\kappa )=\Delta ^{\mathcal{N}} \mathcal{F}(\kappa )\), for \(\kappa \in \mathbb{N}_{a}\).

Lemma 2.3

(see [41, 52])

Assume \(\kappa, \vartheta >0\) for which \(\kappa ^{(\vartheta )}\), \(\kappa ^{(\vartheta -1)}\) are defined. Then, \(\Delta \kappa ^{(\vartheta )}=\vartheta \kappa ^{(\vartheta -1)}\).

Lemma 2.4

(see [38])

Suppose that \(\vartheta >0\) and \(\mathcal{F}\) is defined on \({\mathbb{N}_{a}}\). Then,

$$\begin{aligned} \Delta ^{-\vartheta } {}^{C}\Delta ^{\vartheta }u(\kappa )=u(\kappa )+ \mathcal{A}_{0}+\mathcal{A}_{1}\kappa ^{(1)}+ \mathcal{A}_{2} \kappa ^{(2)}+\cdots+ \mathcal{A}_{N-1} \kappa ^{(N-1)}, \end{aligned}$$

for some \(\mathcal{A}_{i} \in {\mathbb{R}}\), with \(0\leq i \leq \mathcal{N}-1\).

Lemma 2.5

(see [49])

Assume κ, ϑ and ℓ are positive numbers for which \(\kappa ^{(\vartheta )}\) is defined. Then,

  1. (a)

    \(\sum_{\xi =0}^{\kappa -\vartheta } (\kappa -\sigma ( \xi ) )^{(\vartheta -1)}=\frac{1}{\vartheta }\kappa ^{( \vartheta )} \),

  2. (b)

    \(\sum_{\xi =0}^{\ell } (\vartheta +\ell -\sigma (\xi ) )^{(\vartheta -1)}=\frac{1}{\vartheta }(\vartheta +\ell )^{( \vartheta )}\).

Lemma 2.6

(see [38])

Let \(\vartheta, j>0\). Then,

$$\begin{aligned} \Delta ^{-\vartheta }\kappa ^{(j)}= \frac{\Gamma (j+1)}{\Gamma (j+\vartheta +1)}\kappa ^{(j+\vartheta )}\quad \textit{{and}}\quad {}^{C} \Delta ^{\vartheta }\kappa ^{(j)}= \frac{\Gamma (j+1)}{\Gamma (j-\vartheta +1)}\kappa ^{(j-\vartheta )}. \end{aligned}$$

3 Main results

3.1 Thermostat model with one sensor

This section studies the existence and uniqueness results to the DFTM with three-point BCs (2). First, we introduce some notations that are used in this paper. Let \(\mathcal{B}\) be a Banach space with norm \(\Vert u \Vert =\max \vert u(\kappa ) \vert \) for \(\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\). Now, we state and prove an important theorem that deals with a linear variant of the solution of DFTM with three-point BCs (2) and we give a representation of the solution.

Theorem 3.1

Let real-valued function \(\mathcal{F}\) be defined on \(\mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\). Then, for \(\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\) the following DFTM

$$\begin{aligned} \textstyle\begin{cases} - {}^{C}\Delta ^{\vartheta }u(\kappa )=\mathcal{F}(\kappa +\vartheta -1),\quad \kappa \in {\mathbb{N}_{0}^{\ell +1}}, \\ \Delta u(\vartheta -2)=0, \qquad \delta {}^{C}\Delta ^{\vartheta -1} u( \vartheta +\ell )+\gamma u(\eta )=0, \end{cases}\displaystyle \end{aligned}$$
(4)

has a unique solution that is obtained by

$$\begin{aligned} \begin{aligned} u(\kappa )={}&{-}\frac{1}{\Gamma (\vartheta )}\sum _{\xi =0}^{ \kappa -\vartheta }\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)}\mathcal{F}( \xi +\vartheta -1)+\frac{\delta }{\gamma } \sum _{\xi =0}^{\ell +1} \mathcal{F}(\xi +\vartheta -1) \\ &{}+\frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)}\mathcal{F}(\xi +\vartheta -1). \end{aligned} \end{aligned}$$
(5)

Proof

Let \(u(\kappa )\) be a solution to (4). Using Lemma 2.4, for some constants \(\mathcal{A}_{i} \in \mathbb{R}\), for \(i=0, 1\), we have

$$\begin{aligned} u(\kappa )=-\Delta ^{-\vartheta } \mathcal{F}(\kappa +\vartheta -1)+ \mathcal{A}_{0}+\mathcal{A}_{1} \kappa. \end{aligned}$$

Using the fractional sum of order \(\vartheta \in (1,2]\), we obtain

$$\begin{aligned} u(\kappa )= -\frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa - \vartheta } \bigl(\kappa -\sigma (\xi )\bigr)^{(\vartheta -1)}\mathcal{F}(\xi + \vartheta -1)+ \mathcal{A}_{0}+\mathcal{A}_{1} \kappa, \quad\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}. \end{aligned}$$
(6)

By applying Δ to the parts of (6), we have

$$\begin{aligned} \Delta u(\kappa )={}&{ -}\Delta ^{-(\vartheta -1)}\mathcal{F}(\kappa + \vartheta -1)+\mathcal{A}_{0}\Delta (1)+ \mathcal{A}_{1} \Delta \kappa \\ ={}&{-}\frac{1}{\Gamma (\vartheta -1)}\sum_{\xi =0}^{\kappa -\vartheta +1} \bigl( \kappa -\sigma (\xi )\bigr)^{(\vartheta -2)}\mathcal{F}(\xi +\vartheta -1)+ \mathcal{A}_{1}. \end{aligned}$$
(7)

Due to the first boundary condition \(\Delta u(\vartheta -2)=0\) in (7), we obtain \(\mathcal{A}_{1}=0\). Using the CFDO \({}^{C}\Delta ^{\vartheta -1}\) of order \(\vartheta -1\in (0,1]\) on both the sides of (6) with \(\mathcal{A}_{1}=0\), it provides

$$\begin{aligned} {}^{C}\Delta ^{\vartheta -1} u(\kappa )= - {}^{C}\Delta ^{\vartheta -1} \bigl[\Delta ^{-\vartheta }\mathcal{F}(\kappa +\vartheta -1) \bigr]+{}^{C} \Delta ^{\vartheta -1} \mathcal{A}_{0}. \end{aligned}$$

Here, using the Definition 2.2 that for constant \(\mathcal{A}_{0}\), \({}^{C}\Delta ^{\vartheta -1}\mathcal{A}_{0}= \Delta ^{-(2-\vartheta )} \Delta \mathcal{A}_{0}=\Delta ^{-(2-\vartheta )}(0) = 0\), yields

$$\begin{aligned} {}^{C} \Delta ^{\vartheta -1} u(\kappa )= -\Delta ^{-1}\mathcal{F}( \kappa +\vartheta -1)=-\sum _{\xi =0}^{\kappa -1}\mathcal{F}(\xi + \vartheta -1). \end{aligned}$$
(8)

Using the second boundary condition \(\delta {}^{C}\Delta ^{ \vartheta -1} u(\vartheta +\ell )+\gamma u(\eta )=0\) in (6) and (8), we obtain

$$\begin{aligned} \delta {}^{C}\Delta ^{\vartheta -1} u(\vartheta +\ell )= -\delta \sum _{\xi =0}^{\vartheta +\ell -1}\mathcal{F}(\xi +\vartheta -1)= - \delta \sum_{\xi =0}^{ \lceil (\vartheta -1)+\ell \rceil } \mathcal{F}(\xi + \vartheta -1). \end{aligned}$$

Since \(\vartheta -1\leq 1\), we obtain

$$\begin{aligned} \delta {}^{C}\Delta ^{\vartheta -1} u(\vartheta +\ell )= -\delta \sum_{\xi =0}^{\ell +1}\mathcal{F}(\xi + \vartheta -1) \end{aligned}$$
(9)

and

$$\begin{aligned} \gamma u(\eta )= -\frac{\gamma }{\Gamma (\vartheta )}\sum _{\xi =0}^{ \eta -\vartheta }\bigl(\eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\mathcal{F}( \xi +\vartheta -1)+\gamma \mathcal{A}_{0}. \end{aligned}$$
(10)

From (9) and (10) in \(\delta {}^{C}\Delta ^{\vartheta -1} u(\vartheta +\ell )+u(\eta )=0\), we arrive at

$$\begin{aligned} -\delta \sum_{\xi =0}^{\ell +1}\mathcal{F}(\xi + \vartheta -1)- \frac{\gamma }{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta -\vartheta } \bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)}\mathcal{F}(\xi +\vartheta -1)+ \gamma \mathcal{A}_{0}=0. \end{aligned}$$

This leads to

$$\begin{aligned} \mathcal{A}_{0}=\frac{\delta }{\gamma } \sum _{\xi =0}^{\ell +1} \mathcal{F}(\xi +\vartheta -1)+ \frac{1}{\Gamma (\vartheta )}\sum_{ \xi =0}^{\eta -\vartheta }\bigl(\eta -\sigma (\xi )\bigr)^{(\vartheta -1)} \mathcal{F}(\xi +\vartheta -1). \end{aligned}$$
(11)

Using the values of \(\mathcal{A}_{i} \in \mathbb{R}\), for \(i=0, 1\) in \(u(\kappa )\), we obtain

$$\begin{aligned} \begin{aligned} u(\kappa )={}&{-}\frac{1}{\Gamma (\vartheta )}\sum _{\xi =0}^{ \kappa -\vartheta }\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)}\mathcal{F}( \xi +\vartheta -1)+\frac{\delta }{\gamma } \sum _{\xi =0}^{\ell +1} \mathcal{F}(\xi +\vartheta -1) \\ &{}+\frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)}\mathcal{F}(\xi +\vartheta -1), \end{aligned} \end{aligned}$$
(12)

for \(\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\). The proof is completed. □

We introduce the notation \(\Phi _{u}^{\vartheta }(\kappa )=\mathcal{F}(\kappa +\vartheta -1, u( \kappa +\vartheta -1))\). To transform the above DFTM with three-point BCs (2) to a fixed-point theorem, we define the operator \(\mathcal{T}:\mathcal{B}\rightarrow \mathcal{B}\) by

$$\begin{aligned} \begin{aligned} (\mathcal{T}u) (\kappa )={}&{-} \frac{1}{\Gamma (\vartheta )} \sum_{\xi =0}^{\kappa -\vartheta }\bigl( \kappa -\sigma (\xi )\bigr)^{( \vartheta -1)}\Phi _{u}^{\vartheta }(\xi )+\frac{\delta }{\gamma } \sum_{\xi =0}^{\ell +1}\Phi _{u}^{\vartheta }(\xi ) \\ &{}+ \frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)}\Phi _{u}^{\vartheta }(\xi ), \end{aligned} \end{aligned}$$
(13)

for \(\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\). We know that the fixed point of \(\mathcal{T}\) is a solution to (2).

We consider the following hypotheses:

(\(\mathcal{H}_{1}\)):

The Lipschitz-type inequality: There exists \(\mathcal{K}>0\) such that \(\vert \mathcal{F}(\kappa,u)-\mathcal{F}(\kappa,\hat{u}) \vert \leq \mathcal{K} \vert u-\hat{u} \vert \) for all \(u,\hat{u}\in \mathcal{B}\) and each \(\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\).

\((\mathcal{H}_{2})\):

There exists a bounded function \(\mathcal{L}:\mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1} \rightarrow \mathbb{R}\) with \(\vert \mathcal{F}(\kappa,u) \vert \leq \mathcal{L}(\kappa ) \vert u \vert \) for all \(u\in \mathcal{B}\).

Theorem 3.2

If the hypothesis (\(\mathcal{H}_{1}\)) holds, then the DFTM with three-point BCs (2) has a unique solution in \(\mathcal{B}\) provided

$$\begin{aligned} \begin{aligned} \frac{1}{\Gamma (\vartheta +1)} \bigl[(\vartheta + \ell +1)^{( \vartheta )}+\eta ^{(\vartheta )} \bigr]+\frac{\delta }{\gamma } ( \ell +2)< \frac{1}{\mathcal{K}}. \end{aligned} \end{aligned}$$
(14)

Proof

Let \(u,\hat{u}\in \mathcal{B}\). Then, for each \(\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\), we have

$$\begin{aligned} \begin{aligned} \bigl\vert (\mathcal{T}u) (\kappa )-( \mathcal{T}\hat{u}) ( \kappa ) \bigr\vert \leq {}& \frac{1}{\Gamma (\vartheta )}\sum _{\xi =0}^{ \kappa -\vartheta }\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)} \bigl\vert \Phi _{u}^{\vartheta }(\xi )-\Phi _{\hat{u}}^{\vartheta }(\xi ) \bigr\vert \\ &{}+\frac{\delta }{\gamma } \sum_{\xi =0}^{\ell +1}(1) \bigl\vert \Phi _{u}^{ \vartheta }(\xi )-\Phi _{\hat{u}}^{\vartheta }( \xi ) \bigr\vert \\ &{}+\frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)} \bigl\vert \Phi _{u}^{\vartheta }( \xi )-\Phi _{\hat{u}}^{\vartheta }(\xi ) \bigr\vert , \end{aligned} \end{aligned}$$
(15)

where \(\Phi _{u}^{\vartheta },\Phi _{\hat{u}}^{\vartheta }\in \mathcal{C} (\mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}, \mathbb{R} )\) satisfies the functional equations

$$\begin{aligned} \Phi _{u}^{\vartheta }(\kappa )=\mathcal{F}\bigl( \kappa +\vartheta -1, u( \kappa +\vartheta -1)\bigr),\qquad \Phi _{\hat{u}}^{\vartheta }( \kappa )= \mathcal{F}\bigl(\kappa +\vartheta -1, \hat{u}(\kappa +\vartheta -1) \bigr). \end{aligned}$$
(16)

From the assumption \((\mathcal{H}_{1})\), we obtain

$$\begin{aligned} \bigl\vert \Phi _{u}^{\vartheta }(\kappa )-\Phi _{\hat{u}}^{\vartheta }( \kappa ) \bigr\vert &= \bigl\vert \mathcal{F}\bigl(\kappa +\vartheta -1, u(\kappa + \vartheta -1)\bigr)-\mathcal{F} \bigl(\kappa +\vartheta -1, \hat{u}(\kappa + \vartheta -1)\bigr) \bigr\vert \\ &\leq \mathcal{K} \bigl\vert u(\kappa +\vartheta -1)-\hat{u}(\kappa + \vartheta -1) \bigr\vert , \\ \bigl\vert \Phi _{u}^{\vartheta }(\kappa )-\Phi _{\hat{u}}^{\vartheta }( \kappa ) \bigr\vert &\leq \mathcal{K} \Vert u-\hat{u} \Vert . \end{aligned}$$
(17)

Substituting the inequality (17) into (15), it follows that

$$\begin{aligned} \begin{aligned} \Vert \mathcal{T}u-\mathcal{T}\hat{u} \Vert \leq {}& \frac{\mathcal{K} \Vert u-\hat{u} \Vert }{\Gamma (\vartheta )} \sum_{\xi =0}^{\kappa -\vartheta }\bigl( \kappa -\sigma (\xi )\bigr)^{( \vartheta -1)}+\frac{\delta }{\gamma } \mathcal{K} \Vert u-\hat{u} \Vert \sum_{\xi =0}^{\ell +1}(1) \\ &{}+\frac{\mathcal{K} \Vert u-\hat{u} \Vert }{\Gamma (\vartheta )} \sum_{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)}. \end{aligned} \end{aligned}$$

In view of Lemma 2.5 of (a), we obtain

$$\begin{aligned} \begin{aligned} \Vert \mathcal{T}u-\mathcal{T}\hat{u} \Vert &\leq \biggl[\frac{1}{\Gamma (\vartheta +1)} \bigl(\kappa ^{(\vartheta )}+ \eta ^{(\vartheta )} \bigr)+\frac{\delta }{\gamma } (\ell +2) \biggr] \mathcal{K} \Vert u-\hat{u} \Vert \\ &\leq \biggl[ \frac{1}{\Gamma (\vartheta +1)} \bigl[(\vartheta + \ell +1)^{(\vartheta )}+\eta ^{(\vartheta )} \bigr]+ \frac{\delta }{\gamma } (\ell +2) \biggr]\mathcal{K} \Vert u-\hat{u} \Vert , \end{aligned} \end{aligned}$$

therefore, it follows that \(\mathcal{T}\) is a contraction and has a unique fixed point that is the solution of (2). □

Theorem 3.3

The DFTM with three-point BCs (2) has at least one solution under the assumption (\(\mathcal{H}_{2}\)) and the inequality

$$\begin{aligned} \begin{aligned} \mathcal{L}^{*} \leq \frac{\gamma \Gamma (\vartheta +1)}{\gamma [ (\vartheta +\ell +1)^{(\vartheta )}+\eta ^{(\vartheta )} ]+\delta (\ell +2)\Gamma (\vartheta +1)}, \end{aligned} \end{aligned}$$
(18)

where \(\mathcal{L}^{*}=\max \{ \mathcal{L}(\kappa ):\mathbb{N}_{ \vartheta -2}^{\vartheta +\ell +1} \} \).

Proof

Suppose that \(\mathfrak{M}>0\) and \(\mathcal{S}_{u}= \{ u(\kappa ) | \mathbb{N}_{\vartheta -2}^{ \vartheta +\ell +1}\rightarrow \mathbb{R}, \Vert u \Vert \leq \mathfrak{M} \} \). We must first show that \(\mathcal{T}\) maps \(\mathcal{S}_{u}\) in \(\mathcal{S}_{u}\).

For \(u(\kappa )\in \mathcal{S}_{u}\), we have

$$\begin{aligned} \begin{aligned} \bigl\vert (\mathcal{T}u) (\kappa ) \bigr\vert \leq {}& \frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa -\vartheta } \bigl( \kappa -\sigma (\xi )\bigr)^{(\vartheta -1)} \bigl\vert \Phi _{u}^{\vartheta }( \xi ) \bigr\vert +\frac{\delta }{\gamma } \sum _{\xi =0}^{\ell +1}(1) \bigl\vert \Phi _{u}^{\vartheta }(\xi ) \bigr\vert \\ &{}+\frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)} \bigl\vert \Phi _{u}^{\vartheta }( \xi ) \bigr\vert , \end{aligned} \end{aligned}$$
(19)

where \(\Phi _{u}^{\vartheta }(\kappa )\) is given in (16). Using (\(\mathcal{H}_{2}\)), we arrive at

$$\begin{aligned} \begin{aligned} \bigl\vert \Phi _{u}^{\vartheta }( \kappa ) \bigr\vert = \bigl\vert \mathcal{F}\bigl(\kappa +\vartheta -1, u( \kappa +\vartheta -1)\bigr) \bigr\vert \leq \mathcal{L}(\kappa ) \bigl\vert u( \kappa +\vartheta -1) \bigr\vert \leq \mathcal{L}^{*} \Vert u \Vert . \end{aligned} \end{aligned}$$
(20)

Hence, putting the inequality (19) and (20) together, we conclude that

$$\begin{aligned} \Vert \mathcal{T}u \Vert \leq \Biggl[ \frac{1}{\Gamma (\vartheta )} \Biggl(\sum _{\xi =0}^{\kappa - \vartheta }\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)}+\sum_{\xi =0}^{ \eta -\vartheta }\bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)} \Biggr)+ \frac{\delta }{\gamma } \sum _{\xi =0}^{\ell +1}(1) \Biggr]\mathcal{L}^{*} \Vert u \Vert . \end{aligned}$$

From Lemma 2.5 of (a), we have

$$\begin{aligned} \begin{aligned} \Vert \mathcal{T}u \Vert &\leq \biggl[ \frac{1}{\Gamma (\vartheta +1)} \bigl(\kappa ^{(\vartheta )}+\eta ^{( \vartheta )} \bigr)+ \frac{\delta }{\gamma } (\ell +2) \biggr] \mathcal{L}^{*} \Vert u \Vert \\ &\leq \frac{\gamma [(\vartheta +\ell +1)^{(\vartheta )}+\eta ^{(\vartheta )} ]+\delta (\ell +2)\Gamma (\vartheta +1)}{\gamma \Gamma (\vartheta +1)} \mathcal{L}^{*}\mathfrak{M}. \end{aligned} \end{aligned}$$

In view of (18), we obtained \(\Vert \mathcal{T}u \Vert \leq \mathfrak{M}\). Thus, \(\mathcal{T}\) maps \(\mathcal{S}_{u}\) in \(\mathcal{S}_{u}\) and has at least one fixed point that is a solution to (2), according to the Brouwer fixed-point theorem. □

3.2 Thermostat model with two sensors

This section discusses the stability results for the DFTM with four-point BCs (3).

Theorem 3.4

Assume \(\mathcal{F}: \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1} \rightarrow \mathbb{R}\) is given. A unique solution to the DFTM with four-point BCs

$$\begin{aligned} \textstyle\begin{cases} {}^{C}\Delta ^{\vartheta }u(\kappa )=\mathcal{F}(\kappa +\vartheta -1),\quad \kappa \in {\mathbb{N}_{0}^{\ell +1}}, \\ \Delta u(\vartheta -2)=\beta u(\zeta ),\qquad \delta {}^{C}\Delta ^{ \vartheta -1} u(\vartheta +\ell )+\gamma u(\eta )=0, \end{cases}\displaystyle \end{aligned}$$
(21)

has the form

$$\begin{aligned} \begin{aligned} u(\kappa )={}& \Biggl[\frac{1}{\Gamma (\vartheta )} \sum_{ \xi =0}^{\kappa -\vartheta }\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)}+ \frac{\beta \mathcal{D}_{1}(\kappa )}{\Gamma (\vartheta )}\sum_{ \xi =0}^{\zeta -\vartheta } \bigl(\zeta -\sigma (\xi )\bigr)^{(\vartheta -1)} \Biggr]\mathcal{F}(\xi +\vartheta -1) \\ &{}-\mathcal{D}_{2}(\kappa ) \Biggl[\frac{\gamma }{\Gamma (\vartheta )} \sum _{\xi =0}^{\eta -\vartheta }\bigl(\eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}+ \delta \sum_{\xi =0}^{\ell +1}(1) \Biggr]\mathcal{F}(\xi +\vartheta -1), \end{aligned} \end{aligned}$$
(22)

where \(\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\), \(\mathcal{D}_{1}(\kappa )= \frac{[\delta \mu +\gamma (\eta -\kappa )]}{\mathcal{Q}}\), \(\mathcal{D}_{2}(\kappa )= \frac{[\beta (\zeta -\kappa )-1]}{\mathcal{Q}}\) such that \(\mathcal{Q}=\gamma (\beta \zeta -1)-\beta ( \delta \mu + \gamma \eta )\) and \(\mu =\frac{1}{\Gamma (3-\vartheta )}(\vartheta +\ell )^{(2- \vartheta )}\).

Proof

For the fractional sum of order \(\vartheta \in (1,2]\) for (21) and using Lemma 2.4, we obtain

$$\begin{aligned} u(\kappa )= \frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa - \vartheta } \bigl(\kappa -\sigma (\xi )\bigr)^{(\vartheta -1)}\mathcal{F}(\xi + \vartheta -1)+ \mathcal{A}_{2}+\mathcal{A}_{3} \kappa, \end{aligned}$$
(23)

where \(\mathcal{A}_{i} \in \mathbb{R}\), for \(i=2,3\). Applying the operators Δ and \({}^{C}\Delta ^{\vartheta -1}\) on both sides of (23) together with Definitions 2.1 and 2.2, we obtain

$$\begin{aligned} \Delta u(\kappa )=\frac{1}{\Gamma (\vartheta -1)}\sum _{\xi =0}^{ \kappa -\vartheta +1}\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -2)} \mathcal{F}(\xi +\vartheta -1)+ \mathcal{A}_{3} \end{aligned}$$
(24)

and

$$\begin{aligned} {}^{C}\Delta ^{\vartheta -1} u(\kappa )= \sum _{\xi =0}^{\kappa -1} \mathcal{F}(\xi +\vartheta -1)+ \mathcal{A}_{3} \mu. \end{aligned}$$
(25)

In view of \(\Delta u(\vartheta -2)= \beta u(\zeta )\), we obtain

$$\begin{aligned} \beta u(\zeta )= \frac{\beta }{\Gamma (\vartheta )}\sum _{\xi =0}^{ \zeta -\vartheta }\bigl(\zeta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\mathcal{F}( \xi +\vartheta -1)+\beta \mathcal{A}_{2}+ \beta \mathcal{A}_{3} \zeta \end{aligned}$$
(26)

and

$$\begin{aligned} \Delta u(\vartheta -2)= \mathcal{A}_{3}. \end{aligned}$$
(27)

From (26) and (27) and employing the first boundary condition (21), we obtain

$$\begin{aligned} \frac{\beta }{\Gamma (\vartheta )}\sum_{\xi =0}^{\zeta -\vartheta } \bigl( \zeta -\sigma (\xi )\bigr)^{(\vartheta -1)}\mathcal{F}(\xi +\vartheta -1)+ \beta \mathcal{A}_{2}+\mathcal{A}_{3}(\beta \zeta -1)=0. \end{aligned}$$
(28)

In view of \(\delta {}^{C}\Delta ^{\vartheta -1} u(\vartheta +\ell )+\gamma u( \eta )=0\), we obtain

$$\begin{aligned} \gamma u(\eta )= \frac{\gamma }{\Gamma (\vartheta )}\sum _{\xi =0}^{ \eta -\vartheta }\bigl(\eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\mathcal{F}( \xi +\vartheta -1)+\gamma \mathcal{A}_{2}+ \gamma \mathcal{A}_{3} \eta \end{aligned}$$
(29)

and

$$\begin{aligned} \delta {}^{C} \Delta ^{\vartheta -1} u(\vartheta +\ell ) = \delta \sum _{\xi =0}^{ \lceil (\vartheta -1)+\ell \rceil } \mathcal{F}(\xi +\vartheta -1)+ \delta \mathcal{A}_{3} \mu. \end{aligned}$$

Since \(\vartheta -1\leq 1\), we arrive at

$$\begin{aligned} \delta \Delta ^{\vartheta -1} u(\vartheta +\ell )= \delta \sum _{\xi =0}^{ \ell +1}\mathcal{F}(\xi +\vartheta -1)+ \delta \mathcal{A}_{3} \mu. \end{aligned}$$
(30)

From (29) and (30) with the help of the second boundary condition (21), we have

$$\begin{aligned} &\gamma \mathcal{A}_{2}+\mathcal{A}_{3}( \delta \mu +\gamma \eta ) \\ &\quad{} +\frac{\gamma }{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta -\vartheta } \bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)}\mathcal{F}(\xi +\vartheta -1)+ \delta \sum_{\xi =0}^{\ell +1}\mathcal{F}(\xi + \vartheta -1)=0. \end{aligned}$$
(31)

The constant \(\mathcal{A}_{3}\) can be obtained by solving equations (28) and (31),

$$\begin{aligned} &\mathcal{A}_{3} \mathcal{Q}+ \frac{\gamma \beta }{\Gamma (\vartheta )}\sum _{\xi =0}^{\zeta - \vartheta }\bigl(\zeta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\mathcal{F}(\xi + \vartheta -1) \\ &\quad{} -\frac{\gamma \beta }{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta - \vartheta } \bigl(\eta -\sigma (\xi )\bigr)^{(\vartheta -1)}\mathcal{F}(\xi + \vartheta -1)- \delta \beta \sum_{\xi =0}^{\ell +1}\mathcal{F}(\xi + \vartheta -1)=0, \end{aligned}$$

which implies

$$\begin{aligned} &\mathcal{A}_{3}=\frac{1}{\mathcal{Q}} \Biggl[ \frac{\gamma \beta }{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta - \vartheta }\bigl(\eta -\sigma (\xi )\bigr)^{(\vartheta -1)}\mathcal{F}(\xi + \vartheta -1) \\ &\quad{}\times \delta \beta \sum_{\xi =0}^{\ell +1} \mathcal{F}(\xi + \vartheta -1) -\frac{\gamma \beta }{\Gamma (\vartheta )}\sum _{\xi =0}^{ \zeta -\vartheta }\bigl(\zeta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\mathcal{F}( \xi +\vartheta -1) \Biggr]. \end{aligned}$$
(32)

Substituting \(\mathcal{A}_{3}\) into (28), we have

$$\begin{aligned} \beta \mathcal{A}_{2}={}& \frac{\beta [\gamma (\beta \zeta -1)-\mathcal{Q}]}{\mathcal{Q} \Gamma (\vartheta )} \sum _{\xi =0}^{\zeta -\vartheta }\bigl(\zeta -\sigma (\xi ) \bigr)^{(\vartheta -1)} \mathcal{F}(\xi +\vartheta -1) \\ &{} -\frac{\beta [\beta \zeta -1]}{\mathcal{Q}} \Biggl[ \frac{\gamma }{\Gamma (\vartheta )}\sum _{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\mathcal{F}(\xi +\vartheta -1)+ \delta \sum _{\xi =0}^{\ell +1}\mathcal{F}(\xi +\vartheta -1) \Biggr]. \end{aligned}$$

This implies,

$$\begin{aligned} \mathcal{A}_{2}={}&\frac{1}{\mathcal{Q}} \Biggl[ \frac{\beta (\delta \mu +\gamma \eta )]}{ \Gamma (\vartheta )}\sum _{ \xi =0}^{\zeta -\vartheta }\bigl(\zeta -\sigma (\xi ) \bigr)^{(\vartheta -1)} \mathcal{F}(\xi +\vartheta -1)- [\beta \zeta -1] \\ &{} \times \Biggl(\frac{\gamma }{\Gamma (\vartheta )}\sum_{\xi =0}^{ \eta -\vartheta } \bigl(\eta -\sigma (\xi )\bigr)^{(\vartheta -1)}\mathcal{F}( \xi +\vartheta -1)+ \delta \sum_{\xi =0}^{\ell +1}\mathcal{F}(\xi + \vartheta -1) \Biggr) \Biggr]. \end{aligned}$$

Using the constants \(\mathcal{A}_{i} \in \mathbb{R}\), for \(i=2, 3\) in (23), we obtain u in the form

$$\begin{aligned} \begin{aligned} u(\kappa )={}& \Biggl[\frac{1}{\Gamma (\vartheta )}\sum _{ \xi =0}^{\kappa -\vartheta }\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)}+ \frac{\beta \mathcal{D}_{1}(\kappa )}{\Gamma (\vartheta )}\sum_{ \xi =0}^{\zeta -\vartheta } \bigl(\zeta -\sigma (\xi )\bigr)^{(\vartheta -1)} \Biggr]\mathcal{F}(\xi +\vartheta -1) \\ &{}-\mathcal{D}_{2}(\kappa ) \Biggl[\frac{\gamma }{\Gamma (\vartheta )} \sum _{\xi =0}^{\eta -\vartheta }\bigl(\eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}+ \delta \sum_{\xi =0}^{\ell +1}(1) \Biggr]\mathcal{F}(\xi +\vartheta -1), \end{aligned} \end{aligned}$$

for \(\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\). □

We assume that \(\mathcal{F}\) is a real-valued continuous function on \({\mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}}\) such that \(\Phi _{\hat{u}}^{\vartheta }(\kappa )=\mathcal{F}(\kappa +\vartheta -1, \hat{u}(\kappa +\vartheta -1))\). Now, we introduce the definitions of Ulam stability for DFC given on the basis of [60, 61].

Definition 3.5

If for every function \(\hat{u}(\kappa )\in \mathbb{B}\) of

$$\begin{aligned} \bigl\vert {}^{C}\Delta ^{\vartheta } \hat{u}(\kappa )-\Phi _{\hat{u}}^{ \vartheta }(\xi ) \bigr\vert \leq \epsilon, \end{aligned}$$
(33)

where \(\kappa \in {\mathbb{N}_{0}^{\ell +1}}\), \(\epsilon >0\), there exists a solution \(u(\kappa )\in \mathbb{B}\) of (3) and a positive constant \(\mathcal{P}_{1}>0\) such that

$$\begin{aligned} \bigl\vert \hat{u}(\kappa )-u(\kappa ) \bigr\vert \leq \mathcal{P}_{1} \epsilon,\quad \kappa \in {\mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}}. \end{aligned}$$
(34)

Then, the DFTM with four-point BCs (3) is Hyers–Ulam (HU) stable. Equation (3) is also said to be generalized HU stable if we substitute \(\Theta (\epsilon )=\mathcal{P}_{1} \epsilon \) in inequality (34), where \(\Theta (\epsilon )\in \mathbb{C} (\mathbb{R}^{+}, \mathbb{R}^{+} )\) and \(\Theta (0)=0\).

Definition 3.6

Let ∀ \(\hat{u}(\kappa )\in \mathbb{B}\), then the following inequality holds

$$\begin{aligned} \bigl\vert {}^{C}\Delta ^{\vartheta } \hat{u}(\kappa )-\Phi _{\hat{u}}^{ \vartheta }(\xi ) \bigr\vert \leq \epsilon \phi ( \kappa +\vartheta -1), \end{aligned}$$
(35)

where \(\kappa \in {\mathbb{N}_{0}^{\ell +1}}\), \(\epsilon >0\), there is a solution \(u(\kappa )\in \mathbb{B}\) of (3) and a positive constant \(\mathcal{P}_{2}>0\) such that

$$\begin{aligned} \bigl\vert \hat{u}(\kappa )-u(\kappa ) \bigr\vert \leq \delta _{2} \epsilon \Phi (\kappa +\vartheta -1), \quad\kappa \in { \mathbb{N}_{\vartheta -2}^{ \vartheta +\ell +1}}. \end{aligned}$$
(36)

Then, the DFTM with four-point BCs (3) is Hyers–Ulam–Rassias (HUR) stable. Equation (3) is generalized HUR stable if we substitute \(\phi (\kappa +\vartheta -1)= \epsilon \phi (\kappa +\vartheta -1)\) in inequalities (35) and (36).

Remark 3.7

A function \(\hat{u}(\kappa )\in \mathcal{B}\) is a solution to the inequalities (33) and (35) if there exists a function \(f:\mathbb{N}_{\beta -2}^{\beta +\ell +1}\rightarrow \mathbb{R}\) satisfying, for \(\kappa \in \mathbb{N}_{0}^{\ell +1}\)

  1. (i)

    \(\vert f(\kappa +\vartheta -1) \vert \leq \epsilon \),

  2. (ii)

    \({}^{C}\Delta ^{\vartheta } \hat{u}(\kappa )=\Phi _{\hat{u}}^{\vartheta }( \kappa )+f(\kappa +\vartheta -1)\),

  3. (iii)

    \(\vert f(\kappa +\beta -1) \vert \leq \epsilon \phi (\kappa +\beta -1)\),

  4. (iv)

    \({}^{C} \Delta ^{\beta } \hat{u}(\kappa )=\Phi _{\hat{u}}^{\vartheta }( \kappa )+f(\kappa +\beta -1)\).

Lemma 3.8

If \(\hat{u}(\kappa )\) solves the inequality (33) for \(\kappa \in \mathbb{N}_{0}^{\ell +1}\), then

$$\begin{aligned} \begin{aligned} & \Biggl\vert \hat{u}(\kappa ) - \frac{1}{\Gamma (\vartheta )} \sum_{\xi =0}^{\kappa -\vartheta }\bigl( \kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)}\Phi _{\hat{u}}^{\vartheta }( \xi )-\frac{\beta \mathcal{D}_{1}(\kappa )}{\Gamma (\vartheta )} \sum_{\xi =0}^{\zeta -\vartheta }\bigl(\zeta -\sigma (\xi ) \bigr)^{(\vartheta -1)} \Phi _{\hat{u}}^{\vartheta }(\xi ) \\ &\quad{} +\mathcal{D}_{2}(\kappa ) \Biggl[ \frac{\gamma }{\Gamma (\vartheta )}\sum _{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\Phi _{\hat{u}}^{\vartheta }(\xi )+ \delta \sum _{\xi =0}^{\ell +1}\Phi _{\hat{u}}^{\vartheta }( \xi ) \Biggr] \Biggr\vert \leq \frac{\epsilon }{\Gamma (\vartheta +1)}( \vartheta +\ell +1)^{(\vartheta )}, \end{aligned} \end{aligned}$$

where \(\mathcal{D}_{1}(\kappa )\) and \(\mathcal{D}_{2}(\kappa )\) are defined in Theorem 3.4.

Proof

If \(\hat{u}(\kappa )\) solves the inequality (33), then from (ii) of Remark 3.7 and Lemma 2.4, the solution to (ii) of Remark 3.7 satisfies

$$\begin{aligned} \begin{aligned} \hat{u}(\kappa )={}& \frac{1}{\Gamma (\vartheta )} \sum_{ \xi =0}^{\kappa -\vartheta }\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)} \Phi _{\hat{u}}^{\vartheta }(\xi )+ \frac{\beta \mathcal{D}_{1}(\kappa )}{\Gamma (\vartheta )}\sum_{ \xi =0}^{\zeta -\vartheta }\bigl(\zeta -\sigma (\xi )\bigr)^{(\vartheta -1)} \Phi _{\hat{u}}^{\vartheta }(\xi ) \\ &{}-\mathcal{D}_{2}(\kappa ) \Biggl[\frac{\gamma }{\Gamma (\vartheta )} \sum _{\xi =0}^{\eta -\vartheta }\bigl(\eta -\sigma (\xi ) \bigr)^{(\vartheta -1)} \Phi _{\hat{u}}^{\vartheta }(\xi )+\delta \sum _{\xi =0}^{\ell +1} \Phi _{\hat{u}}^{\vartheta }( \xi ) \Biggr] \\ &{}+\frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa -\vartheta }\bigl( \kappa -\sigma (\xi )\bigr)^{(\vartheta -1)}f(\xi +\vartheta -1). \end{aligned} \end{aligned}$$
(37)

Using (a) of Lemma 2.5 together with (i) of Remark 3.7, we arrive at

$$\begin{aligned} & \Biggl\vert \hat{u}(\kappa ) - \frac{1}{\Gamma (\vartheta )}\sum _{\xi =0}^{ \kappa -\vartheta }\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)}\Phi _{ \hat{u}}^{\vartheta }(\xi )- \frac{\beta \mathcal{D}_{1}(\kappa )}{\Gamma (\vartheta )} \sum_{ \xi =0}^{\zeta -\vartheta }\bigl(\zeta -\sigma (\xi ) \bigr)^{(\vartheta -1)} \Phi _{\hat{u}}^{\vartheta }(\xi ) \\ &\qquad{} +\mathcal{D}_{2}(\kappa ) \Biggl[ \frac{\gamma }{\Gamma (\vartheta )}\sum _{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\Phi _{\hat{u}}^{\vartheta }(\xi )+ \delta \sum _{\xi =0}^{\ell +1}\Phi _{\hat{u}}^{\vartheta }( \xi ) \Biggr] \Biggr\vert \\ &\quad = \Biggl\vert \frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa - \vartheta } \bigl(\kappa -\sigma (\xi )\bigr)^{(\vartheta -1)}f(\xi +\vartheta -1) \Biggr\vert \\ &\quad \leq \frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa -\vartheta } \bigl( \kappa -\sigma (\xi )\bigr)^{(\vartheta -1)} \bigl\vert f(\xi +\vartheta -1) \bigr\vert \\ &\quad \leq \frac{\epsilon }{\Gamma (\vartheta +1)}\kappa ^{(\vartheta )} \\ &\quad \leq \frac{\epsilon }{\Gamma (\vartheta +1)}(\vartheta +\ell +1)^{( \vartheta )}. \end{aligned}$$

This completes the proof. □

Theorem 3.9

Assume that the following inequalities and (\(\mathcal{H}_{1}\)) hold at the same time

$$\begin{aligned} \begin{aligned} \Lambda =\mathcal{K} \biggl( \frac{(\vartheta +\ell +1)^{(\vartheta )}+\beta \mathcal{G}_{1} \zeta ^{(\vartheta )}+\mathcal{G}_{2} [\gamma \eta ^{(\vartheta )}+\delta (\ell +2)\Gamma (\vartheta +1) ]}{\Gamma (\vartheta +1)} \biggr)< 1, \end{aligned} \end{aligned}$$
(38)

then the DFTM with four-point BCs (3) is HU stable and generalized HUR stable.

Proof

From solution (22), for \(\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\), it follows that

$$\begin{aligned} \bigl\vert \hat{u}(\kappa ) - u(\kappa ) \bigr\vert \leq{} & \Biggl\vert \hat{u}( \kappa ) - \Biggl[\frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{ \kappa -\vartheta } \bigl(\kappa -\sigma (\xi )\bigr)^{(\vartheta -1)}+ \frac{\beta \mathcal{D}_{1}(\kappa )}{\Gamma (\vartheta )}\sum _{ \xi =0}^{\zeta -\vartheta }\bigl(\zeta -\sigma (\xi ) \bigr)^{(\vartheta -1)} \Biggr]\Phi _{\hat{u}}^{\vartheta }(\xi ) \\ &{} +\mathcal{D}_{2}(\kappa ) \Biggl[ \frac{\gamma }{\Gamma (\vartheta )}\sum _{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\Phi _{\hat{u}}^{\vartheta }(\xi )+ \delta \sum _{\xi =0}^{\ell +1}\Phi _{\hat{u}}^{\vartheta }( \xi ) \Biggr] \Biggr\vert \\ &{}+ \frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa -\vartheta } \bigl( \kappa -\sigma (\xi )\bigr)^{(\vartheta -1)} \bigl\vert \Phi _{\hat{u}}^{ \vartheta }(\xi ) - \Phi _{u}^{\vartheta }(\xi ) \bigr\vert \\ &{}+ \frac{\beta \vert \mathcal{D}_{1}(\kappa ) \vert }{\Gamma (\vartheta )} \sum_{\xi =0}^{\zeta -\vartheta } \bigl(\zeta -\sigma (\xi )\bigr)^{(\vartheta -1)} \bigl\vert \Phi _{\hat{u}}^{\vartheta }(\xi ) - \Phi _{u}^{\vartheta }(\xi ) \bigr\vert \\ &{}+ \bigl\vert \mathcal{D}_{2}(\kappa ) \bigr\vert \Biggl[ \frac{\gamma }{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)}+\delta \sum_{\xi =0}^{\ell +1}(1) \Biggr] \bigl\vert \Phi _{\hat{u}}^{\vartheta }(\xi ) - \Phi _{u}^{ \vartheta }(\xi ) \bigr\vert , \end{aligned}$$

where \(\mathcal{D}_{1}(\kappa )\), \(\mathcal{D}_{2}(\kappa )\) are defined in Theorem 3.4 and \(\Phi _{u}^{\vartheta }(\kappa )\), \(\Phi _{\hat{u}}^{\vartheta }(\kappa )\) are given in (16). Using the inequality (17) and Lemma 3.8 along with an application of Lemma 2.5 of (a), implies that

$$\begin{aligned} \Vert \hat{u} - u \Vert \leq {}& \frac{\epsilon }{\Gamma (\vartheta +1)}(\vartheta +\ell +1)^{( \vartheta )}+ \frac{\mathcal{K} \Vert \hat{u}-u \Vert }{\Gamma (\vartheta +1)} \bigl[(\vartheta +\ell +1)^{(\vartheta )}+\beta \mathcal{G}_{1} \zeta ^{(\vartheta )} \bigr] \\ &{}+\mathcal{K}\mathcal{G}_{2} \Vert \hat{u}-u \Vert \biggl[ \frac{\gamma \eta ^{(\vartheta )}}{\Gamma (\vartheta +1)}+\delta ( \ell +2) \biggr], \end{aligned}$$
(39)

where \(\mathcal{G}_{1}= \vert \frac{\delta \mu +\gamma [\eta -(\vartheta +\ell +1)]}{\mathcal{Q}} \vert \) and \(\mathcal{G}_{2}= \vert \frac{[\beta (\zeta -[\vartheta +\ell +1])-1]}{\mathcal{Q}} \vert \).

Inequality (39) yields \(\Vert \hat{u}-u \Vert \leq \mathcal{P}_{1}\epsilon \), where

$$\mathcal{P}_{1}= \frac{(\vartheta +\ell +1)^{(\vartheta )}}{\Gamma (\vartheta +1)-\mathcal{K} [(\vartheta +\ell +1)^{(\vartheta )}+\beta \mathcal{G}_{1} \zeta ^{(\vartheta )} +\mathcal{G}_{2} (\gamma \eta ^{(\vartheta )}+\delta (\ell +2)\Gamma (\vartheta +1) ) ]}. $$

Thus, the solution to (3) is HU stable.

Further, by taking \(\Theta (\epsilon )=\mathcal{P}_{1} \epsilon \) with \(\Theta (0)=0\), we have

$$\begin{aligned} \Vert \hat{u}- u \Vert \leq \Theta (\epsilon ). \end{aligned}$$

Hence, the solution to (3) becomes generalized HU stable. □

Finally, we consider the following hypotheses to discuss the HUR stability and generalized HUR stability in the next results.

(\(\mathcal{H}_{3}\)):

For an increasing function \(\phi \in \mathcal{C} ({\mathbb{N}_{\vartheta -2}^{\vartheta + \ell }}, \mathbb{R}^{+} )\), there exists \(\lambda _{\phi }>0\) such that, for \(\kappa \in {\mathbb{N}_{0}^{\ell +1}}\)

  1. (i)

    \(\frac{\epsilon }{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa - \vartheta }(\kappa -\sigma (\xi ))^{(\vartheta -1)}\phi (\xi + \vartheta -1)\leq \lambda _{\phi } \epsilon \phi (\kappa +\vartheta -1)\), consequently

  2. (ii)

    \(\frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa - \vartheta }(\kappa -\sigma (\xi ))^{(\vartheta -1)}\phi (\xi + \vartheta -1)\leq \lambda _{\phi } \phi (\kappa +\vartheta -1)\).

Lemma 3.10

If \(\hat{u}(\kappa )\) solves the inequality (35) for \(\kappa \in \mathbb{N}_{0}^{\ell +1}\), then

$$\begin{aligned} & \Biggl\vert \hat{u}(\kappa ) - \frac{1}{\Gamma (\vartheta )}\sum _{\xi =0}^{ \kappa -\vartheta }\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)}\Phi _{ \hat{u}}^{\vartheta }(\xi )- \frac{\beta \mathcal{D}_{1}(\kappa )}{\Gamma (\vartheta )} \sum_{ \xi =0}^{\zeta -\vartheta }\bigl(\zeta -\sigma (\xi ) \bigr)^{(\vartheta -1)} \Phi _{\hat{u}}^{\vartheta }(\xi ) \\ &\quad{} +\mathcal{D}_{2}(\kappa ) \Biggl[ \frac{\gamma }{\Gamma (\vartheta )}\sum _{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\Phi _{\hat{u}}^{\vartheta }(\xi )+ \delta \sum _{\xi =0}^{\ell +1}\Phi _{\hat{u}}^{\vartheta }( \xi ) \Biggr] \Biggr\vert \leq \lambda _{\phi }\epsilon \phi (\kappa + \vartheta -1), \end{aligned}$$

where \(\mathcal{D}_{1}(\kappa )\) and \(\mathcal{D}_{2}(\kappa )\) are defined in Theorem 3.4.

Proof

From inequality (35), we obtain a solution to (iv) of Remark 3.7 that satisfies (37). Using (\(\mathcal{H}_{3}\)) of (i), for \(\kappa \in \mathbb{N}_{0}^{\ell +1}\) and Remark 3.7 of (iii), it follows that

$$\begin{aligned} &\Biggl\vert \hat{u}(\kappa ) - \frac{1}{\Gamma (\vartheta )}\sum _{\xi =0}^{ \kappa -\vartheta }\bigl(\kappa -\sigma (\xi ) \bigr)^{(\vartheta -1)}\Phi _{ \hat{u}}^{\vartheta }(\xi )- \frac{\beta \mathcal{D}_{1}(\kappa )}{\Gamma (\vartheta )} \sum_{ \xi =0}^{\zeta -\vartheta }\bigl(\zeta -\sigma (\xi ) \bigr)^{(\vartheta -1)} \Phi _{\hat{u}}^{\vartheta }(\xi ) \\ &\qquad{} +\mathcal{D}_{2}(\kappa ) \Biggl[ \frac{\gamma }{\Gamma (\vartheta )}\sum _{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\Phi _{\hat{u}}^{\vartheta }(\xi )+ \delta \sum _{\xi =0}^{\ell +1}\Phi _{\hat{u}}^{\vartheta }( \xi ) \Biggr] \Biggr\vert \\ &\quad \leq \frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa -\vartheta } \bigl( \kappa -\sigma (\xi )\bigr)^{(\vartheta -1)} \bigl\vert f(\xi +\vartheta -1) \bigr\vert \\ &\quad \leq \frac{\epsilon }{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa - \vartheta } \bigl(\kappa -\sigma (\xi )\bigr)^{(\vartheta -1)}\phi (\xi + \vartheta -1) \\ &\quad\leq \lambda _{\phi }\epsilon \phi (\kappa +\vartheta -1). \end{aligned}$$

This completes the proof. □

Theorem 3.11

If the hypothesis (\(\mathcal{H}_{1}\)) holds with the inequality (38), then the DFTM with four-point BCs (3) is HUR stable and generalized HUR stable.

Proof

From the solution (22), for \(\kappa \in \mathbb{N}_{\vartheta -2}^{\vartheta +\ell +1}\), we obtain

$$\begin{aligned} \bigl\vert \hat{u}(\kappa ) - u(\kappa ) \bigr\vert \leq {}& \Biggl\vert \hat{u}( \kappa ) - \frac{1}{\Gamma (\vartheta )}\sum_{\xi =0}^{\kappa - \vartheta } \bigl(\kappa -\sigma (\xi )\bigr)^{(\vartheta -1)}\Phi _{u}^{ \vartheta }( \xi ) \\ &{} -\frac{\beta \mathcal{D}_{1}(\kappa )}{\Gamma (\vartheta )}\sum_{ \xi =0}^{\zeta -\vartheta } \bigl(\zeta -\sigma (\xi )\bigr)^{(\vartheta -1)} \Phi _{u}^{\vartheta }( \xi ) \\ &{} +\mathcal{D}_{2}(\kappa ) \Biggl[ \frac{\gamma }{\Gamma (\vartheta )}\sum _{\xi =0}^{\eta -\vartheta }\bigl( \eta -\sigma (\xi ) \bigr)^{(\vartheta -1)}\Phi _{u}^{\vartheta }(\xi )+ \delta \sum _{\xi =0}^{\ell +1}\Phi _{u}^{\vartheta }( \xi ) \Biggr] \Biggr\vert , \end{aligned}$$

where \(\mathcal{D}_{1}(\kappa )\) and \(\mathcal{D}_{2}(\kappa )\) are defined in Theorem 3.4. Using Lemma 3.10 and the procedure used in Theorem 3.9, we obtain

$$\begin{aligned} \Vert \hat{u} - u \Vert \leq {}& \lambda _{\phi }\epsilon \phi ( \kappa +\vartheta -1)+\frac{\mathcal{K}}{\Gamma (\vartheta )}\sum_{ \xi =0}^{\kappa -\vartheta } \bigl(\kappa -\sigma (\xi )\bigr)^{(\vartheta -1)} \Vert \hat{u} - u \Vert \\ &{}+ \frac{\mathcal{K}\beta \vert \mathcal{D}_{1}(\kappa ) \vert }{\Gamma (\vartheta )} \sum_{\xi =0}^{\zeta -\vartheta } \bigl(\zeta -\sigma (\xi )\bigr)^{( \vartheta -1)} \Vert \hat{u} - u \Vert \\ &{}+\mathcal{K} \bigl\vert \mathcal{D}_{2}(\kappa ) \bigr\vert \Biggl[ \frac{\gamma }{\Gamma (\vartheta )}\sum_{\xi =0}^{\eta -\vartheta } \bigl( \eta -\sigma (\xi )\bigr)^{(\vartheta -1)}+\delta \sum _{\xi =0}^{\ell +1}(1) \Biggr] \Vert \hat{u} - u \Vert . \end{aligned}$$

By an application of Lemma 2.5 of (a), the above inequality becomes

$$\begin{aligned} \begin{aligned} \Vert \hat{u} - u \Vert \leq{} & \lambda _{\phi }\epsilon \phi (\kappa +\vartheta -1)+ \frac{\mathcal{K} \Vert \hat{u}-u \Vert }{\Gamma (\vartheta +1)} \bigl[(\vartheta +\ell +1)^{(\vartheta )}+\beta \mathcal{G}_{1} \zeta ^{(\vartheta )} \bigr] \\ &{}+\mathcal{K}\mathcal{G}_{2} \Vert \hat{u}-u \Vert \biggl[\gamma \frac{\eta ^{(\vartheta )}}{\Gamma (\vartheta +1)}+\delta (\ell +2) \biggr], \end{aligned} \end{aligned}$$
(40)

where \(\mathcal{G}_{1}\) and \(\mathcal{G}_{2}\) are defined in Theorem 3.9. From which, the inequality (40) yields

$$\begin{aligned} \Vert \hat{u}- u \Vert \leq \mathcal{P}_{2} \epsilon \phi ( \kappa +\vartheta -1), \end{aligned}$$

where \(\mathcal{P}_{2} = \frac{\lambda _{\phi }\Gamma (\vartheta +1)}{\Gamma (\vartheta +1)-\mathcal{K} [(\vartheta +\ell +1)^{(\vartheta )}+\beta \mathcal{G}_{1} \zeta ^{(\vartheta )}+\mathcal{G}_{2} (\gamma \eta ^{(\vartheta )}+\delta (\ell +2)\Gamma (\vartheta +1) ) ]}\).

Hence, the solution of (3) is HUR stable.

Also, by setting \(\phi (\kappa +\vartheta -1)=\epsilon \phi (\kappa +\vartheta -1)\), we have

$$\begin{aligned} \Vert \hat{u} - u \Vert \leq \mathcal{P}_{2} \phi (\kappa + \vartheta -1). \end{aligned}$$

Therefore, the solution of (3) is generalized HUR stable. □

4 Examples

In this section, we validate the theoretical results by providing examples for discrete fractional thermostat models with three-point BCs (2) and four-point BCs (3) by using CFDO.

Example 4.1

Consider the linear DFTM with three-point BCs (4)

$$\begin{aligned} \textstyle\begin{cases} - {}^{C}\Delta ^{1.67}u(\kappa )= (\kappa +0.67 )^{(8)}, \quad \kappa \in {\mathbb{N}_{0}^{5}}, \\ \Delta u (-0.33 )=0,\qquad 0.8 {}^{C}\Delta ^{0.67} u (5.67 )+0.9 u(\eta )=0. \end{cases}\displaystyle \end{aligned}$$
(41)

Here, \(\vartheta =1.67\), \(\ell =4\), \(\delta =0.8\), \(\gamma =0.9\) and \(\mathcal{F}(\kappa )=\kappa ^{(8)}\). Applying Theorem 3.1, we obtain that \(u(\kappa )\) is a solution of (41) that is given by

$$\begin{aligned} \begin{aligned} u(\kappa )={}&{-}\frac{1}{\Gamma (1.67)}\sum _{\xi =0}^{ \kappa -1.67}\bigl(\kappa -\sigma (\xi ) \bigr)^{(0.67)} (\xi +0.67 )^{(8)}+ \biggl( \frac{0.8}{0.9} \biggr) \sum_{\xi =0}^{5}( \xi +0.67)^{(8)} \\ &{}+\frac{1}{\Gamma (1.67)}\sum_{\xi =0}^{\eta -1.67}\bigl( \eta - \sigma (\xi )\bigr)^{(0.67)}(\xi +0.67)^{(8)}, \end{aligned} \end{aligned}$$
(42)

for \(\kappa \in \mathbb{N}_{-0.33}^{6.67}\). Now, solving the solution (42) by using Definition 2.1 and Lemma 2.6, we obtain

$$\begin{aligned} \frac{1}{\Gamma (1.67)}\sum_{\xi =0}^{\kappa -1.67} \bigl(\kappa - \sigma (\xi )\bigr)^{(0.67)}(\xi +0.67)^{(8)}&= \Delta ^{-1.67}(\kappa +0.67)^{(8)} \\ &=\frac{\Gamma (9)}{\Gamma (10.67)}\cdot \frac{\Gamma (\kappa +1.67)}{\Gamma (\kappa -8)}. \end{aligned}$$
(43)

Similarly, we obtain

$$\begin{aligned} \frac{1}{\Gamma (1.67)}\sum_{\xi =0}^{\eta -1.67} \bigl(\eta - \sigma (\xi )\bigr)^{(0.67)}(\xi +0.67)^{(8)}= \frac{\Gamma (9)}{\Gamma (10.67)}\cdot \frac{\Gamma (\eta +1.67)}{\Gamma (\eta -8)}. \end{aligned}$$
(44)

Also, we find

$$\begin{aligned} \sum_{\xi =0}^{5}(\xi +0.67)^{(8)}=\Delta ^{-1}( \kappa +0.67)^{(8)}\bigg|_{\kappa ={5.67}}= \frac{\Gamma (9)}{\Gamma (10)}\cdot \frac{\Gamma (7.67)}{\Gamma (-1.33)}. \end{aligned}$$
(45)

Combining (42), (43), (44), and (45), we obtain a solution to (41) as follows:

$$\begin{aligned} \begin{aligned} u(\kappa )={}&{-} \biggl[\frac{\Gamma (9)}{\Gamma (10.67)} \cdot \frac{\Gamma (\kappa +1.67)}{\Gamma (\kappa -8)} \biggr]+ \biggl[\frac{\Gamma (9)}{\Gamma (10.67)}\cdot \frac{\Gamma (\eta +1.67)}{\Gamma (\eta -8)} \biggr] \\ &{}+ \biggl(\frac{0.8}{0.9} \biggr) \biggl[ \frac{\Gamma (9)}{\Gamma (10)}\cdot \frac{\Gamma (7.67)}{\Gamma (-1.33)} \biggr], \quad\text{{for }} \kappa \in \mathbb{N}_{-0.33}^{6.67}. \end{aligned} \end{aligned}$$
(46)

Furthermore, we also consider the linear DFTM with four-point BCs (21)

$$\begin{aligned} \textstyle\begin{cases} {}^{C}\Delta ^{1.67}u(\kappa )= (\kappa +0.67 )^{(8)}, \quad\kappa \in {\mathbb{N}_{0}^{5}}, \\ \Delta u (-0.33 )=0.2 u(\zeta ),\qquad 0.8 {}^{C}\Delta ^{0.67} u (5.67 )+0.9 u(\eta )=0. \end{cases}\displaystyle \end{aligned}$$
(47)

Here, \(\vartheta =1.67\), \(\ell =4\), \(\delta =0.8\), \(\beta =0.2\), \(\gamma =0.9\), and \(\mathcal{F}(\kappa )=\kappa ^{(8)}\). From Theorem 3.4, we obtain \(u(\kappa )\) as a solution to (47) that is given by

$$\begin{aligned} \begin{aligned} u(\kappa )={}& \Biggl[\frac{1}{\Gamma (1.67)} \sum_{\xi =0}^{ \kappa -1.67}\bigl(\kappa -\sigma (\xi )\bigr)^{(0.67)}\\ &{}+ \frac{(0.2) \mathcal{D}_{1}(\kappa )}{\Gamma (1.67)}\sum_{\xi =0}^{ \zeta -1.67} \bigl(\zeta -\sigma (\xi )\bigr)^{(0.67)} \Biggr] (\xi +0.67 )^{(8)} \\ &{}-\mathcal{D}_{2}(\kappa ) \Biggl[\frac{0.9}{\Gamma (1.67)}\sum _{ \xi =0}^{\eta -1.67}\bigl(\eta -\sigma (\xi ) \bigr)^{(0.67)} (\xi +0.67 )^{(8)}+0.8 \sum _{\xi =0}^{5} (\xi +0.67 )^{(8)} \Biggr], \end{aligned} \end{aligned}$$
(48)

where \(\kappa \in \mathbb{N}_{-0.33}^{6.67}\), \(\mathcal{D}_{1}(\kappa )\) and \(\mathcal{D}_{2}(\kappa )\) are defined in Theorem 3.4. From (43), (44), (45), and (48), we obtain a solution to (47) as follows:

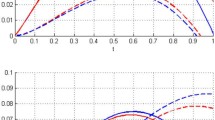
$$\begin{aligned} \begin{aligned} u(\kappa )={}& \biggl[\frac{\Gamma (9)}{\Gamma (10.67)} \cdot \frac{\Gamma (\kappa +1.67)}{\Gamma (\kappa -8)} \biggr]+(0.2) \mathcal{D}_{1}(\kappa ) \biggl[ \frac{\Gamma (9)}{\Gamma (10.67)} \cdot \frac{\Gamma (\zeta +1.67)}{\Gamma (\zeta -8)} \biggr] \\ &{}-\mathcal{D}_{2}(\kappa ) \biggl[0.9 \biggl( \frac{\Gamma (9)}{\Gamma (10.67)}\cdot \frac{\Gamma (\eta +1.67)}{\Gamma (\eta -8)} \biggr)+0.8 \biggl( \frac{\Gamma (9)}{\Gamma (10)}\cdot \frac{\Gamma (7.67)}{\Gamma (-1.33)} \biggr) \biggr]. \end{aligned} \end{aligned}$$
(49)

Using the solutions (46) and (49) along with \(\zeta =0.67\) and various values of \(\eta =1.67, 2.67\), we obtain different solutions to the corresponding DFTMs with three-point BCs (41) and four-point BCs (47), as seen in Fig. 1 and Table 1. Figure 2 illustrates the solution surface plots over different values of η and κ.

Figure 1
figure 1

Solutions curves of the DFTMs (41) and (47): (a) \(\kappa -u\) plane with sensor point η; (b) \(\kappa -u\) plane with sensor points ζ and η

Full size image
Figure 2
figure 2

Surface corresponding to the graphs in Fig. 1

Full size image
Table 1 Numerical values of \(u(\kappa )\) with step size 1
Full size table

Example 4.2

Let us consider the parameters \(\vartheta =1.6\), \(\ell =0\), \(\delta =0.5\), \(\gamma =0.4\), and \(\eta =0.6\) with \(\mathcal{F}(\kappa,u(\kappa ))=\frac{1}{20} [ \frac{\kappa }{3}\cos ^{2} (\frac{\pi }{2}(\kappa ) )+ \sin (u(\kappa )) ]\). Then, we obtain a DFTM with three-point BCs (2) in the form

$$\begin{aligned} \textstyle\begin{cases} -{}^{C}\Delta ^{1.6}u(\kappa )=\frac{1}{20} [ \frac{(\kappa +0.6)}{3}\cos ^{2} (\frac{\pi }{2}(\kappa +0.6) )+\sin (u(\kappa +0.6)) ],\quad \kappa \in {\mathbb{N}_{0}^{1}}, \\ \Delta u (-0.4 )=0, \qquad 0.5 {}^{C} \Delta ^{0.6}u (1.6 )+0.4 u(0.6)=0. \end{cases}\displaystyle \end{aligned}$$
(50)

We now show that (50) has a unique solution. Since \((\mathcal{H}_{1})\), holds for each \(\kappa \in {\mathbb{N}_{-0.4}^{2.6}}\), we obtain

$$\begin{aligned} \begin{aligned} \bigl\vert \mathcal{F}\bigl(\kappa,u(\kappa )\bigr)- \mathcal{F}\bigl( \kappa,\hat{u}(\kappa )\bigr) \bigr\vert ={}& \biggl\vert \frac{1}{20} \biggl[ \frac{\kappa }{3}\cos ^{2} \biggl( \frac{\pi }{2}(\kappa ) \biggr)+ \sin \bigl(u(\kappa )\bigr) \biggr] \\ &{} -\frac{1}{20} \biggl[\frac{\kappa }{3}\cos ^{2} \biggl(\frac{\pi }{2}( \kappa ) \biggr)+\sin \bigl(\hat{u}(\kappa )\bigr) \biggr] \biggr\vert \\ ={}& \frac{1}{20} \bigl\vert \sin \bigl(u(\kappa )\bigr) - \sin \bigl( \hat{u}(\kappa )\bigr) \bigr\vert , \\ \bigl\vert \mathcal{F}\bigl(\kappa,u(\kappa )\bigr)-\mathcal{F}\bigl(\kappa, \hat{u}( \kappa )\bigr) \bigr\vert \leq{}& \frac{1}{20} \bigl\vert u( \kappa ) - \hat{u}( \kappa ) \bigr\vert , \end{aligned} \end{aligned}$$

so for \(\mathcal{K}=\frac{1}{20}\). Thus, for inequality (14), we have

$$\begin{aligned} \mathcal{K} \biggl[\frac{1}{\Gamma (\vartheta +1)} \bigl[(\vartheta + \ell +1)^{(\vartheta )}+\eta ^{(\vartheta )} \bigr]+ \frac{\delta }{\gamma } (\ell +2) \biggr]\approx 0.2550< 1. \end{aligned}$$

Therefore, from Theorem 3.2 we come to the conclusion that (50) has a unique solution.

Example 4.3

Suppose that \(\vartheta =1.4\), \(\ell =1\), \(\delta =0.4\), \(\gamma =0.3\), \(\mathfrak{M}=150\), and \(\eta = 0.4\) with \(\mathcal{F}(\kappa,u(\kappa ))=\kappa ^{2} e^{-u^{2}(\kappa )}\). Then, we obtain the following Caputo DFTM with three-point BCs (2)

$$\begin{aligned} \textstyle\begin{cases} -{}^{C}\Delta ^{1.4}u(\kappa )=(\kappa +0.4)^{2} e^{-u^{2}(\kappa +0.4)},\quad \kappa \in {\mathbb{N}_{0}^{2}}, \\ \Delta u (-0.6 )=0, \qquad 0.4 {}^{C} \Delta ^{0.4}u (2.4 )+0.3 u(0.4)=0. \end{cases}\displaystyle \end{aligned}$$
(51)

Consider the Banach space \(\mathcal{B}:= \{ u(\kappa ) | \mathbb{N}_{-0.6}^{3.4} \rightarrow \mathbb{R}, \Vert u \Vert \leq 150 \} \). We note that

$$\begin{aligned} \frac{\mathfrak{M} \gamma \Gamma (\vartheta +1)}{\gamma [(\vartheta +\ell +1)^{(\vartheta )}+\eta ^{(\vartheta )} ]+\delta (\ell +2)\Gamma (\vartheta +1)} \approx 18.5644. \end{aligned}$$

It is clear that \(\vert \mathcal{F}(\kappa,u(\kappa )) \vert = 11.5600<18.5644\), whenever \(u\in [-150, 150]\). Therefore, having at least one solution for (51) concluded from Theorem 3.3.

Example 4.4

Assume that \(\vartheta =1.5\), \(\ell =1\), \(\delta =0.5\), \(\beta =0.2\), \(\gamma =0.4\), \(\zeta =0.5\), \(\eta =1.5\), and \(\mathcal{F}(\kappa,u(\kappa ))=\frac{2}{\sqrt{\pi }} (\kappa -0.5 )^{(0.5)}+\frac{u(\kappa )}{20}\). Then, for the following Caputo DFTM with four-point BCs (3)

$$\begin{aligned} \textstyle\begin{cases} {}^{C}\Delta ^{1.5}u(\kappa )=\frac{2}{\sqrt{\pi }}\kappa ^{(0.5)}+ \frac{u(\kappa +0.5)}{20}, \quad \kappa \in {\mathbb{N}_{0}^{2}}, \\ \Delta u (-0.5 )= 0.2 u(0.5),\qquad 0.5 {}^{C} \Delta ^{0.5}u (2.5 )+0.4u(1.5)=0, \end{cases}\displaystyle \end{aligned}$$
(52)

we prove that (52) is HU stable. To begin with, we need to verify that \(\mathcal{F}\) satisfies \((\mathcal{H}_{1})\) for \(\kappa \in {\mathbb{N}_{-0.5}^{3.5}}\), we obtain

$$\begin{aligned} \begin{aligned} \bigl\vert \mathcal{F}\bigl(\kappa,\hat{u}(\kappa ) \bigr)-\mathcal{F}\bigl( \kappa,u(\kappa )\bigr) \bigr\vert ={}& \biggl\vert \frac{2}{\sqrt{\pi }} ( \kappa -0.5 )^{(0.5)}+\frac{\hat{u}(\kappa )}{20}- \biggl( \frac{2}{\sqrt{\pi }} (\kappa -0.5 )^{(0.5)}+ \frac{u(\kappa )}{20} \biggr) \biggr\vert \\ \leq {}& \frac{1}{20} \bigl\vert \hat{u}(\kappa ) - u(\kappa ) \bigr\vert . \end{aligned} \end{aligned}$$

Hence, \(\mathcal{K}=\frac{1}{20}\) and \(\mathcal{F}\) is Lipschitz continuous for \(\kappa \in {\mathbb{N}_{-0.5}^{3.5}}\). Since

$$\begin{aligned} \frac{\Gamma (\vartheta +1)}{(\vartheta +\ell +1)^{(\vartheta )}+\mathcal{G}_{1}\beta \zeta ^{(\vartheta )}+\mathcal{G}_{2} [\gamma \eta ^{(\vartheta )}+\delta (\ell +2)\Gamma (\vartheta +1) ]} \approx 0.1120, \end{aligned}$$

for \(\mathcal{K}=\frac{1}{20}<0.1120\), we obtain \(\Lambda =0.4465<1\). This shows (52) is HU stable with \(\mathcal{P}_{1}=7.9038\). Further, it is also generalized HU stable. To check this, put \(\epsilon =0.1563\) and \(\hat{u}(\kappa )=\frac{\kappa ^{2}}{2}\), \(\kappa \in {\mathbb{N}_{0}^{2}}\) and also prove that (33) holds. Indeed,

$$\begin{aligned} & \bigl\vert {}^{C}\Delta ^{1.5} \hat{u}( \kappa )-\mathcal{F}\bigl(\kappa +0.5, \hat{u}(\kappa +0.5)\bigr) \bigr\vert \\ &\quad = \biggl\vert {}^{C}\Delta ^{1.5}\hat{u}(\kappa )- \frac{2}{\sqrt{\pi }} \kappa ^{(0.5)}-0.05\hat{u}(\kappa +0.5) \biggr\vert \\ &\quad = \biggl\vert \Delta ^{-0.5}\Delta ^{2} \biggl( \frac{\kappa ^{2}}{2} \biggr)-\frac{2}{\sqrt{\pi }}\kappa ^{(0.5)}-0.05 \biggl( \frac{(\kappa +0.5)^{2}}{2} \biggr) \biggr\vert \\ &\quad = \biggl\vert \Delta ^{-0.5}1-\frac{2}{\sqrt{\pi }}\kappa ^{(0.5)}-0.025( \kappa +0.5)^{2} \biggr\vert . \end{aligned}$$
(53)

Using (iii) of Lemma 2.6 in (53), we have

$$\begin{aligned} & \bigl\vert {}^{C}\Delta ^{1.5} \hat{u}(\kappa )- \mathcal{F}\bigl(\kappa +0.5, \hat{u}(\kappa +0.5)\bigr) \bigr\vert \\ &\quad = \biggl\vert \frac{2}{\sqrt{\pi }}\kappa ^{(0.5)}-\frac{2}{\sqrt{\pi }} \kappa ^{(0.5)}-0.025(\kappa +0.5)^{2} \biggr\vert \\ &\quad \leq 0.025(\kappa +0.5)^{2} \\ &\quad \leq 0.1563, \\ & \bigl\vert {}^{C}\Delta ^{1.5} \hat{u}(\kappa )- \mathcal{F}\bigl(\kappa +0.5, \hat{u}(\kappa +0.5)\bigr) \bigr\vert \leq \epsilon,\quad \text{{for }} \kappa \in {\mathbb{N}_{0}^{2}}. \end{aligned}$$

Example 4.5

Consider the following Caputo DFTM with four-point BCs (3)

$$\begin{aligned} \textstyle\begin{cases} {}^{C}\Delta ^{1.6}u(\kappa )=0.1(\kappa +0.6)+0.03\sin (u(\kappa +0.6)),\quad \kappa \in {\mathbb{N}_{0}^{2}}, \\ \Delta u (-0.4 )=0.3u(0.6),\qquad 0.6 {}^{C} \Delta ^{0.6}u (2.6 )+0.2u(1.6)=0. \end{cases}\displaystyle \end{aligned}$$
(54)

Here, \(\vartheta =1.6\), \(\ell =1\), \(\delta =0.6\), \(\beta =0.3\), \(\gamma =0.2\), \(\zeta =0.6\), \(\eta =1.6\), and \(\mathcal{F}(\kappa,u(\kappa ))=0.1\kappa +0.03\sin (u(\kappa ))\). Now, we prove that (54) is HUR stable. Since \((\mathcal{H}_{1})\) holds for each \(\kappa \in {\mathbb{N}_{-0.4}^{3.6}}\), we obtain

$$\begin{aligned} \begin{aligned} \bigl\vert \mathcal{F}\bigl(\kappa,\hat{u}(\kappa ) \bigr)-\mathcal{F}\bigl( \kappa,u(\kappa )\bigr) \bigr\vert ={}& \bigl\vert 0.1 \kappa +0.03\sin \bigl(\hat{u}( \kappa )\bigr)-0.1\kappa -0.03\sin \bigl(u(\kappa )\bigr) \bigr\vert \\ = {}& 0.03 \bigl\vert \sin \bigl(\hat{u}(\kappa )\bigr)-\sin \bigl(u(\kappa ) \bigr) \bigr\vert , \\ \bigl\vert \mathcal{F}\bigl(\kappa,\hat{u}(\kappa )\bigr)-\mathcal{F}\bigl( \kappa,u( \kappa )\bigr) \bigr\vert \leq {}& 0.03 \bigl\vert \hat{u}(\kappa ) - u(\kappa ) \bigr\vert , \end{aligned} \end{aligned}$$

so for \(\mathcal{K}=0.03\). Further, assuming \(\epsilon =0.29\) and \(\phi (\kappa +0.6)=1\), we have

$$\begin{aligned} \begin{aligned} \frac{0.29}{\Gamma (1.6)}\sum_{\xi =0}^{ \kappa -1.6} \bigl(\kappa -\sigma (\xi )\bigr)^{(0.6)}(1)={} & \frac{(0.29)\Gamma (\kappa +1)}{\Gamma (2.6)\Gamma (\kappa -0.6)} \\ \leq {}& \frac{(0.29) \Gamma (3)}{\Gamma (2.6)\Gamma (1.4)}, \\ \frac{0.29}{\Gamma (1.6)}\sum_{\xi =0}^{\kappa -1.6}\bigl( \kappa -\sigma (\xi )\bigr)^{(0.6)}(1)\leq & 0.4572. \end{aligned} \end{aligned}$$

Thus, inequality \((\mathcal{H}_{3})\), of (i), holds with \(\lambda _{\phi }=1.5767\), \(\epsilon =0.29\), and \(\phi (\kappa +0.6)=1\), for \(\kappa \in \mathbb{N}_{0}^{2}\). Since

$$\begin{aligned} \frac{\Gamma (\vartheta +1)}{(\vartheta +\ell +1)^{(\vartheta )}+\mathcal{G}_{1}\beta \zeta ^{(\vartheta )}+\mathcal{G}_{2} [\gamma \eta ^{(\vartheta )}+\delta (\ell +2)\Gamma (\vartheta +1) ]} \approx 0.0882, \end{aligned}$$

if \(\mathcal{K}=0.03<0.0882\), from Theorem 3.11, we see that \(\Lambda =0.3400<1\). Hence, HUR stablity of the solution (54) is obtained from \(\mathcal{P}_{2}=2.3890\). To verify this, put \(\epsilon =0.29\), \(\hat{u}(\kappa )=\kappa \) for \(\kappa \in {\mathbb{N}_{0}^{2}}\). We prove that (35) holds. Indeed,

$$\begin{aligned} & \bigl\vert {}^{C}\Delta ^{1.6} \hat{u}(\kappa )- \mathcal{F}\bigl(\kappa +0.6, \hat{u}(\kappa +0.6)\bigr) \bigr\vert \\ &\quad = \bigl\vert {}^{C}\Delta ^{1.6}\hat{u}(\kappa )-0.1( \kappa +0.6)-0.03 \sin \bigl(\hat{u}(\kappa +0.6)\bigr) \bigr\vert \\ &\quad = \bigl\vert \Delta ^{-0.4}\Delta ^{2} \kappa -0.1( \kappa +0.6)-0.03 \sin (\kappa +0.6) \bigr\vert \\ & \quad= \bigl\vert -0.1(\kappa +0.6)-0.03 \sin (\kappa +0.6) \bigr\vert \\ &\quad \leq 0.1(\kappa +0.6)+0.03 \\ &\quad \leq 0.29, \\ &\bigl\vert {}^{C}\Delta ^{1.6} \hat{u}(\kappa )- \mathcal{F}\bigl(\kappa +0.6, \hat{u}(\kappa +0.6)\bigr) \bigr\vert \leq \epsilon \phi (\kappa +0.6), \quad\text{{for }} \kappa \in {\mathbb{N}_{0}^{2}}. \end{aligned}$$

Consequently, it is obviously generalized HUR stable by using Theorem 3.11.

5 Conclusion

It is essential that we enhance our ability to understand complicated discrete fractional thermostat models. One of the strategies is to apply well-known models to various complicated sensor problems. In this paper, we have studied a new form of DFTMs with the three-point and four-point BCs by the Caputo difference operator. Existence and uniqueness results and various forms of HU stability are discussed with the aid of properties of the fractional operator and different fixed-point techniques for the concerned problems. Also, we presented sufficient conditions for stable solutions by using the Caputo difference operator in the discrete case. On the basis of our theoretical findings, we have presented suitable examples with numerical solutions to different values of κ and η supported with graphical illustrations. The findings of this study can be seen as a contribution to the developing area of discrete fractional thermostat models that describe mathematical models of engineering and applied-science applications.