Optimal sensor placement for the spatial reconstruction of sound fields

Abstract

The estimation sound fields over space is of interest in sound field control and analysis, spatial audio, room acoustics and virtual reality. Sound fields can be estimated from a number of measurements distributed over space yet this remains a challenging problem due to the large experimental effort required. In this work we investigate sensor distributions that are optimal to estimate sound fields. Such optimization is valuable as it can greatly reduce the number of measurements required. The sensor positions are optimized with respect to the parameters describing a sound field, or the pressure reconstructed at the area of interest, by finding the positions that minimize the Bayesian Cramér-Rao bound (BCRB). The optimized distributions are investigated in a numerical study as well as with measured room impulse responses. We observe a reduction in the number of measurements of approximately 50% when the sensor positions are optimized for reconstructing the sound field when compared with random distributions. The results indicate that optimizing the sensors positions is also valuable when the vector of parameters is sparse, specially compared with random sensor distributions, which are often adopted in sparse array processing in acoustics.

1 Introduction

A room impulse response (RIR) describes the acoustic transfer function between a sound source and a receiver inside a room. The RIR is a function of both the source and receiver positions, so that there is a different RIR for each source-receiver combination. Knowledge of RIRs over space is required in sound field control and spatial audio, where the goal is to modify, control or reproduce the sound field in a given area, taking its spatial characteristics into account [1,2,3]. Furthermore, characterizing acoustic fields over space is also central to other applications within acoustic engineering and signal processing, such as room acoustics, sound field analysis, acoustic holography, in-situ characterization of acoustic properties, and dereverberation. However, measuring the acoustic pressure at many closely spaced locations is, if at all possible, very time consuming and expensive. In addition, there are often restrictions as to where the measurements can be collected, so that it might not be possible to place sensors inside the area of interest. Because of this, the acoustic field over space is often estimated from a small set of pressure measurements. That is, sound field reconstruction corresponds to estimating the acoustic pressure at unobserved locations by interpolating and/or extrapolating the pressure values at a set of sampled locations using a suitable model for the propagation of acoustic waves.

This study is concerned with the selection of the measurement positions for estimating sound fields over space. Given the sensor budget (i.e., the maximum number of spatial locations that can be sampled), and the candidate positions (i.e, the positions in which measurements can potentially be collected), optimal sensor placement aims at finding the combination of measurement positions that is optimal for estimating the sound field. It is highly valuable to optimize the sensor positions, as this can extend the bandwidth and size of the reconstructed sound field for a fixed number of sensors, or alternatively, lessen the sampling requirements for a given reconstruction accuracy, ultimately reducing the experimental effort and costs.

Previous studies have shown that, in general, it is beneficial to place a large fraction of the sensor budget close to the boundary of the measurement domain [4, 5]. The rest of the available sensors are distributed inside the domain for increased stability, since distributions with all the measurements on the boundary are unstable at the eigenfrequencies of the domain shape¹. The optimization of interior positions to increase the array stability has been investigated for a number of domain shapes [5, 6]. Besides stability, statistical criteria are generally adopted in the optimization of measurement distributions and design of measurement set selection [7,8,9,10,11,12]. In particular, as the parameters describing the sound field are estimated from a finite set of noisy measurements, it is of interest to optimize the measurement positions with respect to the statistics, such as variance, of the estimator. Multiple optimal sensor placement algorithms based on statistical criteria have been developed and applied to sound field control and reproduction [13,14,15,16,17]. Yet, the highly sparse structure present in many sound fields of interest is normally not accounted for in these optimal sensor placement strategies.

Compressive sensing (CS) is a relevant framework that makes it possible to vastly reduce the number of measurements required to reconstruct a signal [18]. CS is based on the assumption that the signal is sparse in a given basis—which implies a certain underlying structure—and that the sampling process is incoherent. The application of CS to the sound field reconstruction problem has been investigated in a number of studies [19,20,21,22,23,24,25], yet the placement of sensors remains an open question. Randomized measurement positions are usually favored over regular distributions, as this helps to lower the coherence of the sampling matrix. Nonetheless, high coherence between the columns of the sampling matrix is often unavoidable as this stems from the interpolation functions used (e.g., plane waves) rather than from the sampling locations. On the other had, coherence might not be a good indicator of how well a signal can be reconstructed [26]. At any rate, naive random selections of measurements do not provide any optimality guarantees.

Recently, data-driven approaches to the sensor placement problem have been proposed [27]. In this case, sensor selection algorithms are applied to a basis learned from representative data. Data-driven sensor placement has proved successful in exploiting patterns in the data, resulting in large reductions in the number of measurements. On the downside, data-driven methods require large datasets that are generalizable, and a new tailored basis must be learned for each problem. A different data-driven approach is active learning, in which data is gathered sequentially and used to train the model as the signal is sampled. In this case, the learner has the ability to select which data point to sample next, sequentially gathering the most informative data to add to the training set [28]. In acoustics, active learning has recently been applied to design microphone arrays for source localization [29].

In this work we investigate optimal sensor distributions that are generalizable across different sound fields, rooms and source positions. We study two approaches, in which the sensor positions are optimized with respect to the estimation of (a) the parameters describing a sound field, or (b) the pressure reconstructed at the positions of interest. In the optimization problem, we seek to minimize average variance (of the estimated parameters or the reconstructed pressure, respectively), which is akin to minimizing the (sum of the diagonal elements of the) Bayesian Cramér-Rao bound (BCRB). The optimal sensor placement is approximately found by convex relaxation of the original combinatorial problem. Formulating the problem in a Bayesian probabilistic framework enables us to easily include prior information, e.g., the amplitude of the sound field relative to the noise level, or data obtained through an active learning approach. We discuss whether this framework could be used to take into account the structure/sparsity of sound fields when selecting the sensor positions. The optimization procedure is investigated in a numerical study as well as with measured RIRs. We observe a reduction in the number of measurements by approximately one half when the sensor positions are optimized for reconstructing the sound field when compared with uniform and random distributions. The results indicate that optimizing the sensors positions is also valuable when the vector of parameters is sparse, specially compared with a random distribution, often adopted in CS studies.

In earlier studies [30, 31], we developed an optimal selection method for sampling and reconstructing sound fields. In the current work, we focus on the generalizability across sound fields (rooms, source positions, etc.), and we derive general advice for sampling distributions in sound field control scenarios. In addition, we thoroughly investigate optimal selections for reconstructing the sound field, rather than estimating the wave parameters, which has been the main focus in the general sensor selection literature. We show that distributions optimized for reconstruction outperform other optimization approaches. This is very valuable as the end goal of many applications is to recover the acoustic pressure rather than the wave parameters. Furthermore, we introduce a hierarchical Bayesian model in the optimal sensor selection methodology, which makes it possible to take into account potential prior information about the sampled sound field.

The following notation is used throughout: $\textbf{I}$, $\textbf{0}$, and $\textbf{1}$ are the appropriate-size identity matrix, vector of zeros and vector of ones, respectively. Furthermore, $\text {Diag}(\textbf{a})$ is the square diagonal matrix with vector $\textbf{a}$ in its main diagonal, $\text {diag}(\textbf{A})$ is the main diagonal of matrix $\textbf{A}$ in vector form, $\circ$ represents the Hadamard product, $E_x\{\cdot \}$ indicates expectation with respect to the probability law of the random variable x, and $\nabla _\textbf{x}$ is the gradient with respect to $\textbf{x}$.

2 Wave propagation model

Let us define a measurement region, $\Omega _A \subset \mathbb {R}^3$, in which acoustic sensors can be placed, and a reconstruction region, $\Omega _B \subset \mathbb {R}^3$, in which the acoustic pressure is to be determined. The measurement and reconstruction region may overlap, completely or partially, or they can be separate from one another. It is important to clarify that this study is not concerned with solving a boundary value problem. Instead, the sound field reconstruction problem is formulated as the interpolation or extrapolation in between or away from points of measured pressure values. For that, a model for the propagation of acoustics waves is introduced.

The acoustic pressure at any position $\textbf{r}\in \Omega _A \cup \Omega _B$ can be expressed as

$$\begin{aligned} \hat{y}(\textbf{r},t) = \frac{1}{2\pi }\int _{-\infty }^{\infty } y(\textbf{r},\omega )e^{\text {j}\omega t}d\omega , \end{aligned}$$

(1)

where $y(\textbf{r},\omega )$ is the pressure at position $\textbf{r}$ and frequency $\omega$. The pressure field is modeled as the superposition of propagating plane waves [32]. Accordingly, $y(\textbf{r},\omega )$ can be expressed as

$$\begin{aligned} y(\textbf{r},\omega ) = \int \!\!\int _S x(\textbf{k})e^{\text {j}\textbf{k}\cdot \textbf{r}}dS, \end{aligned}$$

(2)

where $x(\textbf{k})$ is the wavenumber spectrum, $\textbf{k}$ is the wavenumber vector, S is the surface of the radiation sphere with radius $\omega /c$, and c is the speed of sound. The plane wave model is physically motivated, as plane waves are elementary solutions to the wave equation. The model does not assume specular reflections on the boundaries of the room nor any specific room geometry, yet it is required that $\Omega _A \cup \Omega _B$ does not include the source position and can be inscribed in a star-convex region [4].

We define m candidate positions, $\textbf{r}_1,\dots ,\textbf{r}_m \in \Omega _A$, in which sensors can potentially be placed. The following system of equations is then formed by discretizing the integral in (2) and introducing a term to account for measurement noise,

$$\begin{aligned} \textbf{y} = \textbf{Ax} + \textbf{e}, \end{aligned}$$

(3)

where $\textbf{y} \in \mathbb {C}^m$ is the vector of pressure values at the candidate positions, with the $i^\text {th}$ element $y_i = y(\textbf{r}_i,\omega )$. The vector $\textbf{x} \in \mathbb {C}^n$ contains the amplitudes of the n plane waves taken in the approximation, $x_j = x(\textbf{k}_j)$, where $\textbf{k}_1,\dots ,\textbf{k}_n$ are uniformly sampled over S. The elements of $\textbf{A}$ are the complex exponential terms, $a_{ij} = e^{\text {j}\textbf{k}_j\cdot \textbf{r}_i}$, and the vector $\textbf{e} \in \mathbb {C}^{m}$ represents the measurement noise. It is noted that for each frequency $\omega$ there is one system like the one in (3).

3 Sound field reconstruction

Sound field reconstruction consists in (a) estimating the parameters $\textbf{x}$ from a small number of pressure measurements, and then (b) estimating the pressure in $\Omega _B$ by multiplying the estimated parameter vector $\textbf{x}$ with the reconstruction matrix $\textbf{B}$, with $b_{ij}=e^{\text {j}\textbf{k}_j\cdot \textbf{r}_i}$ and $\textbf{r}_i \in \Omega _B$.

The estimation of $\textbf{x}$ is an ill-posed problem that requires regularization or prior information about $\textbf{x}$ in order to arrive to a unique, stable solution. The ill-posedness stems from having a number of measurements, k, smaller than the number of parameters to estimate, n.

Sparse signal recovery methods, such as CS, can recover apparently undersampled signals ($k<n$). In particular, CS theory determines that an undersampled signal can be recovered under two conditions: the signal $\textbf{x}$ is sparse (i.e., it has few non-zero elements), and the sensing process is incoherent (i.e., the columns of $\textbf{A}$ are sufficiently uncorrelated). The less sparse the signal is, the more restrictive the incoherence condition [18]. Several sparse representations, including elementary wave functions [19,20,21,22] and functions learned from representative data [23, 24, 33], have been exploited to reconstruct sound fields from a small number of measurements. It has been shown that the RIR at low frequencies can be sparsely represented by a plane wave expansion, like the one in (2) and (3), in acoustically damped rooms [22] and as well as in rectangular rooms [20]. Yet, the number of non-zero elements in $\textbf{x}$ depends on the frequency, size, geometry and acoustic treatment of each particular room.

In this work, we do not assume a priori that $\textbf{x}$ is sparse in order to keep the optimized sensor distributions as general as possible. We study two approaches to the sensor selection problem: one optimizes the sensor positions with respect to the estimation of $\textbf{x}$, while the other one does it with respect to the estimation of $\textbf{Bx}$. In sound field reconstruction (as in many other reconstruction problems [26]), it is not the exact recovery of $\textbf{x}$, as much as the estimation of $\textbf{Bx}$ what is of interest. Thus, optimizing the sensor distribution to estimate $\textbf{Bx}$ could be advantageous.

4 Bayesian estimation

The estimation of $\textbf{x}$ is formulated in the Bayesian probabilistic framework. The measurement noise is assumed to be i.i.d. complex, circularly symmetric Gaussian with variance $\beta ^{-1} \in \mathbb {R}$, i.e., $\textbf{e}\sim \mathcal{C}\mathcal{N}(\textbf{0},\beta ^{-1}\textbf{I})$. From (3) and the Gaussian noise assumption, the likelihood function can be written as

$$\begin{aligned} p(\textbf{y}|\textbf{x},\beta ) = \prod _i\mathcal{C}\mathcal{N}\left(y_i|\textbf{a}_i \textbf{x},\beta ^{-1}\right), \end{aligned}$$

(4)

where $\textbf{a}_i$ denotes the $i^\text {th}$ row of $\textbf{A}$. A hierarchical prior is assigned to $\textbf{x}$ so that each parameter $x_j$ follows an independent Gaussian distribution with variance $\alpha _j^{-1} \in \mathbb {R}$,

$$\begin{aligned} p(\textbf{x}|\pmb {\alpha }) = \prod _j\mathcal{C}\mathcal{N}\left(x_j|0,\alpha _j^{-1}\right), \end{aligned}$$

(5)

where $\pmb {\alpha } \equiv \left[ \alpha _1,\dots ,\alpha _{n}\right] ^\text {T}$ is the vector of hyperparameters that control the strength of each $x_j$ (e.g., an element $x_j$ that is zero or very small will have a large associated $\alpha _j$, resulting in a normal prior with zero mean and very small variance). To complete the hierarchical prior, we assign non-informative hyperpriors on $\pmb {\alpha }$ and $\beta$,

$$\begin{aligned} p(\pmb {\alpha }) = \prod _j \text {Gamma}(\alpha _j; a,b), \end{aligned}$$

(6)

and

$$\begin{aligned} p(\beta ) = \text {Gamma}(\beta ;c,d), \end{aligned}$$

(7)

where $\text {Gamma}(\alpha ; a,b) \equiv \Gamma (a)^{-1} b^a \alpha ^{a-1} e^{-b\alpha }$, and $\Gamma (a)$ is the gamma function. The parameters a, b, c, and d are set to a small value so that the hyperpriors are broad/non-informative. The hierarchical prior described by (5) and (6) permits solutions with a small number of non-zeros (i.e., a sparse $\textbf{x}$), should the data support this. Such a model is the basis of sparse Bayesian learning [34, 35].

Given the likelihood and prior of (4) and (5), it can be shown that the posterior over the parameters is also a Gaussian distribution [34],

$$\begin{aligned} p(\textbf{x}|\textbf{y},\pmb {\alpha },\beta ) = \mathcal{C}\mathcal{N}(\textbf{x}|\pmb {\mu },\pmb {\Sigma }), \end{aligned}$$

(8)

where the mean is

$$\begin{aligned} \pmb {\mu } = \beta \pmb {\Sigma }\textbf{A}^\text {H} \textbf{y}, \end{aligned}$$

(9)

and the covariance matrix is

$$\begin{aligned} \pmb {\Sigma } = \left[ \beta \textbf{A}^\text {H}\textbf{A} + \text {Diag}(\pmb {\alpha })\right] ^{-1}. \end{aligned}$$

(10)

In this study, we choose the maximum a posteriori as point estimate, which coincides with the mean, $\tilde{\textbf{x}}=\pmb {\mu }$.

The hyperparamerters, $\pmb {\alpha }$ and $\beta$, can be determined by finding the values that maximize the marginal likelihood [34]

$$\begin{aligned} p(\textbf{y}|\pmb {\alpha },\beta ) = \int p(\textbf{y}|\textbf{x},\beta )p(\textbf{x}|\pmb {\alpha }) \text {d}\textbf{x}. \end{aligned}$$

(11)

Therefore, the number of non-zeros and support of $\textbf{x}$, as well as the noise level are learned from the data $\textbf{y}$.

5 Sensor selection

In this work, the sensor positions are optimized in terms of the BCRB, which states that the mean-square error matrix of any estimator, $\textbf{R}(\tilde{\textbf{x}})$, is lower bounded by the inverse of the Fisher information matrix,

$$\begin{aligned} \textbf{R} \succcurlyeq \textbf{F}^{-1}, \end{aligned}$$

(12)

where the matrix inequality indicates that $(\textbf{R}-\textbf{F}^{-1})$ is a non-negative definite matrix. The Bayesian Fisher information matrix is defined as [36]

$$\begin{aligned} \textbf{F} \equiv E_{\textbf{y},\textbf{x}} \left\{ \left[ \nabla _\textbf{x} \ln p(\textbf{y},\textbf{x}) \right] \left[ \nabla _\textbf{x} \ln p(\textbf{y},\textbf{x})\right] ^\text {H}\right\} . \end{aligned}$$

(13)

In the selection problem, the hyperparameters $\pmb {\alpha }, \beta$ are considered to be fixed variables, previously learned from data or preselected, and therefore they do not appear in (13). The estimator described by (9) and (10) is unbiased, which means that $\pmb {\Sigma }=\textbf{R}$, and Bayesian efficient, which means that $\textbf{R}=\textbf{F}^{-1}$. This can be shown by inserting $p(\textbf{y}|\textbf{x})$ and $p(\textbf{x})$ in (13). Therefore, the diagonal elements of $\textbf{F}^{-1}$ contain the variance of the estimator, i.e., they correspond to the mean-square error when estimating the parameters $x_1,\dots ,x_n$.

We introduce the binary selection vector, $\textbf{z}\equiv [z_1,\dots ,z_m]^\text {T}$, with $z_i\in \{0, 1\},\ i=1,\dots ,m$. The elements of the selection vector indicate whether the $i^\text {th}$ sensor is selected or not. The selected measurements can be expressed as

$$\begin{aligned} \textbf{Zy} = \textbf{ZAx} + \textbf{Ze}, \end{aligned}$$

(14)

where $\textbf{Z} \in \{0,1\}^{k\times m}$ is the selection matrix that results from removing the zero-rows from $\text {Diag}(\textbf{z})$. The BCRB as a function of the selection vector is

$$\begin{aligned} \textbf{F}^{-1}(\textbf{z}) = \left[ \beta \textbf{A}^\text {H}\textbf{Z}^\text {H}\textbf{Z}\textbf{A} + \text {Diag}(\pmb {\alpha })\right] ^{-1}, \end{aligned}$$

(15)

which follows from (10) and (14).

Therefore, by finding the sensors that minimize the trace of $\textbf{F}^{-1}(\textbf{z})$ one effectively minimizes the average variance when estimating the parameters $\textbf{x}$. The optimal sensor selection problem is therefore formulated as

$$\begin{aligned} \begin{array}{rl} \underset{\textbf{z}}{\mathrm {minimize\ }} & \textrm{tr}\left( \textbf{F}^{-1}\right) \\ \mathrm {subject\ to\ } & \textbf{1}^\text {T} \textbf{z} = k,\\ & z_i\in \{0, 1\},\ i=1,\dots ,m. \end{array} \end{aligned}$$

(16)

Sound field reconstruction involves estimating the pressure in some region of interest $\Omega _B$ by multiplying the estimated parameters $\textbf{x}$ with the reconstruction matrix $\textbf{B}$. Therefore, as discussed in Section 2, it can be advantageous to optimize the sensor selection for reconstructing the pressure, instead of for estimating $\textbf{x}$. If the reconstructed pressure is $\textbf{y}_B=\textbf{Bx}$, its covariance can be expressed as a function of the covariance matrix for $\textbf{x}$, such that $\text {cov}(\textbf{y}_B,\textbf{y}_B) = \textbf{B} \pmb {\Sigma } \textbf{B}^\text {H} = \textbf{B} \textbf{F}^{-1} \textbf{B}^\text {H}$. The optimal sensor placement problem for reconstruction is therefore

$$\begin{aligned} \begin{array}{rl} \underset{\textbf{z}}{\mathrm {minimize\ }} & \textrm{tr}\left( \textbf{B}\textbf{F}^{-1}\textbf{B}^\text {H}\right) \\ \mathrm {subject\ to\ } & \textbf{1}^\text {T} \textbf{z} = k,\\ & z_i\in \{0, 1\},\ i=1,\dots ,m. \end{array} \end{aligned}$$

(17)

It is worth noting that objective functions other than the average estimation variance (i.e., $\textrm{tr}\left( \textbf{F}^{-1}\right)$ and $\textrm{tr}\left( \textbf{B}\textbf{F}^{-1}\textbf{B}^\text {H}\right)$) can be used for optimizing the sensor locations as well. In this study, the average variance is chosen because it is easy to interpret and very general. Should one use a different the sound field model (e.g., other physically motivated models like equivalent sources, or models learned from data), the overall optimization problem would not change, and the method could be readily applied. In addition, the mean-square error provides a good way of describing the average reconstruction error over a reconstruction area, and it is a common metric to assess the sound field reconstruction accuracy.

5.1 Sensor selection for sparse signals

A distribution of sensors tailored to recover a particular sound field can easily be designed using the hierarchical model described in (4)–(7). The number of non-zeros and support of $\textbf{x}$ enter in the selection procedure through the role of the hyperparameters $\pmb {\alpha }$ in forming $\textbf{F}$. This would involve having information about $\pmb {\alpha }$ prior to selecting the measurement positions. An active sequential selection based on this idea is summarized as follows: after initializing $\pmb {\alpha }$ and $\beta$, the sensor position that minimizes $\textrm{tr}(\textbf{F}^{-1})$ or $\textrm{tr}(\textbf{B}\textbf{F}^{-1}\textbf{B}^\text {H})$ is added to the selection. The pressure at such position is then measured, and the values of $\pmb {\alpha }$ and $\beta$ are updated through (11). The process is repeated until the number of selected sensors is equal to k. As the data is gathered, the sparsity and support of $\textbf{x}$ is learned through the update of the hyperparameters $\pmb {\alpha }$, such that the resulting distribution of sensors adapts to the particular sound field.

However, the active scheme described above is not well suited for designing sensor distributions to estimate RIRs: the support and number of non-zeros of $\textbf{x}$ is different for each room and source position, resulting in a sensor distribution that is not generalizable. Every room and every source position would lead to a different selection of sensors. In this study we consider a prior in which all the hyperparameters $\pmb {\alpha }$ share the same value, such that $\alpha _i=\alpha , \ i=1,\dots ,n$, $\alpha \in \mathbb {R}$. The only assumed prior information is a (rough) approximation of the measurements signal-to-noise ratio (SNR), from which the ratio $\beta /\alpha$ is obtained. The resulting optimal sensor distribution is generalizable across rooms and source positions, as all parameters in $\textbf{x}$ are regarded equally. It is worth remarking that even though the sensor selection does not assume sparsity, a sparse $\textbf{x}$ can still be obtained (should the data support this) through the Bayesian estimation described in Section 4. The experimental results of Section 6.1 show an improved reconstruction accuracy also for sparse $\textbf{x}$, specially when compared to random distributions normally adopted in CS studies.

5.2 Approximate solution

Finding the exact solution to the optimization problems (16) and (17) is normally not feasible. Given m candidate positions and a sensor budget k, an exhaustive search over all $\left( {\begin{array}{c}m\\ k\end{array}}\right)$ possible combinations is computationally intractable, unless m and k are very small. In this section, we describe a two-stage method for approximating the optimal solution of (16) and (17). The first stage is based on the convex relaxation of the original (non-convex) problem, originally proposed by Joshi and Boyd [9]. The second stage takes the the convex relaxed solution as input and performs a greedy search to select an integer number of sensors.

5.2.1 Convex relaxation

The objective function of problems (16) and (17) is convex, and the only non-convexity stems from the constraint $z_i\in \{0, 1\},\ i=1,\dots ,m$. The relaxation of such constraint in (16) results in

$$\begin{aligned} \begin{array}{rl} \hat{\textbf{z}} = \underset{\textbf{z}}{\mathrm {arg\ min\ }} & \textrm{tr}\left( \textbf{F}^{-1}\right) \\ \mathrm {subject\ to\ } & \textbf{1}^\text {T} \textbf{z} = k,\\ & 0 \le z_i \le 1,\ i=1,\dots ,m. \end{array} \end{aligned}$$

(18)

A convex relaxation of (17) can be done in a similar manner. The optimization problem (18) is convex, and a global optimum can be found via suitable convex optimization algorithms [37]. The convex-relaxed inequality constraint, $0 \le z_i \le 1, i=1,\dots ,m$, implies that the elements of the relaxed selection vector, $\hat{\textbf{z}}$, might take values between 0 and 1. There are several ways of selecting an integer number of sensors. The simplest one consists on setting the k largest entries of $\hat{\textbf{z}}$ to one and the rest to zero, forming the approximate, thresholded solution $\tilde{\textbf{z}}$. While this simple thresholding method works well when the approximate solution $\hat{\textbf{z}}$ has values close to one and close to zero, this is not always the case. In the following section, we describe a more elaborate way of selecting k integer sensors via a greedy search.

The convex-relaxed approximation can be examined by observing that the set of all possible solutions that satisfy the constraints of the relaxed problem, (18), contains the set of the possible solutions of the original problem, (16). Therefore, the optimal objective value of the relaxed problem is upper bounded by the optimal value of the original problem. Following the same logic, one can see that the objective function evaluated at the approximate, thresholded solution is lower bounded by the optimal value of the original problem. More concisely,

$$\begin{aligned} \textrm{tr}\left( \textbf{F}^{-1}(\hat{\textbf{z}})\right) \le \textrm{tr}\left( \textbf{F}^{-1}(\tilde{\textbf{z}})\right) . \end{aligned}$$

(19)

The difference $\delta \equiv \textrm{tr}\left( \textbf{F}^{-1}(\tilde{\textbf{z}})\right) - \textrm{tr}\left( \textbf{F}^{-1}(\hat{\textbf{z}})\right)$ indicates how far the approximate solution is from the solution to the original problem. If $\delta =0$ then $\tilde{\textbf{z}}$ is the solution to the original problem.

Problem (18) can be approximately solved by defining logarithmic barrier functions for the inequality constraints [37], so that it becomes

$$\begin{aligned} \begin{array}{rl} \hat{\textbf{z}} = \underset{\textbf{z}}{\mathrm {arg\ min\ }} & \textrm{tr}\left( \textbf{F}^{-1}\right) - \kappa \textbf{1}^\text {T}[\log (\textbf{z})+\log (\textbf{1}-\textbf{z})]\\ \mathrm {subject\ to\ } & \textbf{1}^\text {T} \textbf{z} = k, \end{array} \end{aligned}$$

(20)

where the parameter $\kappa \in \mathbb {R}^+$ determines the accuracy of the approximation. The problem (20) can be solved very efficiently via Newton’s method, for which one has to compute the gradient and Hessian of the objective functions. The expressions are given in the Appendix.

5.2.2 Greedy selection

The second stage of the proposed algorithm is a greedy search to select k sensors from the convex relaxed solution $\hat{\textbf{z}}$ since it is likely that this contains values different from zero and one. The greedy stage starts with the convex relaxed solution $\hat{\textbf{z}}$ as input. A threshold is applied to remove the candidates with very small $\hat{z}_i$ and keep only $m_\text {convx}$ candidates, where $k< m_\text {convx} < m$. Specifically, the selection of $m_\text {convx}$ is performed by sorting $\hat{\textbf{z}}$ in descending order, computing the cumulative sum and normalizing it by k. Only the $m_\text {convx}$ candidates whose cumulative sum is below a certain value (e.g., 0.9) are kept to continue with the greedy search. These are the most relevant candidates according to the convex relaxed procedure. The greedy search is then initialized. The first sensor is selected by computing the objective value (either $\textrm{tr}\left( \textbf{F}^{-1}\right)$ or $\textrm{tr}\left( \textbf{B} \textbf{F}^{-1} \textbf{B}^\text {H}\right)$, depending whether we want to solve (16) or (17)) for each one of the $m_\text {convx}$ candidates and selecting the one that minimizes the objective. The search then progresses by computing the objective value with the already selected sensors plus one of the remaining (non-selected) candidates. A sweep through all the remaining candidates is performed and the one that minimizes the objective is kept. The process is repeated until the sensor budget k is reached. In this way, instead of simply applying a threshold to $\hat{\textbf{z}}$, the greedy approach sequentially selects the sensors that locally minimize the objective function one at a time.

In each iteration, the objective needs to be evaluated as many times as there are remaining sensors left, which can be time-consuming (specially if $m_\text {convx}$ is large). The efficiency of the greedy search can be improved by performing a rank-one update instead of computing $\textbf{F}^{-1}$ from scratch every time the objective needs to be evaluated [9]. When a new candidate is evaluated, the row of $\textbf{A}$ that corresponds to the previously tested candidate, $\textbf{a}_i$, is replaced by that of the new candidate, $\textbf{a}_j$. To compute the updated $\textbf{F}^{-1}$ one can make use of the Woodbury identity,

$$\begin{aligned} \textbf{F}^{-1}_{updated} = \textbf{F}^{-1} - \textbf{F}^{-1}(\textbf{U}\textbf{S}^{-1}\textbf{V})\textbf{F}^{-1} \end{aligned}$$

(21)

where

$$\begin{aligned} \textbf{U} & = \beta \left[ \begin{array}{cc} -\textbf{a}_i^\text {H}&\textbf{a}_j^\text {H} \end{array}\right] , \\ \textbf{V} & = \left[ \begin{array}{c} \textbf{a}_i\\ \textbf{a}_j \end{array}\right] , \\ \textbf{S} & = \textbf{I} + \textbf{V}\textbf{F}^{-1}\textbf{U}. \end{aligned}$$

Therefore, only a $2\times 2$ matrix, $\textbf{S}$, has to be inverted every time objective function is evaluated.

5.3 Multi-frequency selection

The estimation and selection framework described so far is frequency-dependent, since there is a different system (Eq. 3) for each frequency $\omega$. In practice, the sensors deployed measure the entire pressure signal, $\hat{y}(\textbf{r},t)$. The optimal sensor selection can be modified to take into account several frequencies simultaneously, resulting in the optimization problem

$$\begin{aligned} \begin{array}{rl} \underset{\textbf{z}}{\mathrm {minimize\ }} & \sum \limits _j w_j \textrm{tr}\left( \textbf{F}_j^{-1}\right) \\ \mathrm {subject\ to\ } & \textbf{1}^\text {T} \textbf{z} = k,\\ & z_i\in \{0, 1\},\ i=1,\dots ,m, \end{array} \end{aligned}$$

(22)

where $\textbf{F}_j$ is the Fisher information matrix at frequency $\omega _j$, and $\omega _j$ are the frequency bins after discretization. The scalar $w_j\in \mathbb {R}$ represent a weight given to $\omega _j$. In preliminary experiments, we observed slightly worse results when optimizing for several frequencies simultaneously compared to when optimizing only for the highest frequency considered. Since the reconstruction becomes more challenging with increasing frequency, it seems sensible to focus on the higher frequencies when optimizing the sensor positions. While in our experiments we consider optimal distributions with respect to a single frequency, we show results over a broadband frequency range.

6 Experiments and results

6.1 Numerical study

The selection methods are investigated in a numerical study. The reconstruction area $\Omega _B$ is defined as the area enclosed by two ellipses of principal axes 0.4 m and 0.3 m, and whose centers are 1 m apart. The measurement area $\Omega _A$ is defined as the difference between the reconstruction area and a rectangle of sides 2.4 m and 1.6 m. The combined area $\Omega _A \cup \Omega _B$ is discretized using a grid with 5 cm spacing, resulting in $m = 1333$ candidate positions ($\textbf{r}_1,\dots ,\textbf{r}_m, \textbf{r}_i \in \Omega _A$), and $m_B=284$ positions inside the reconstruction area ($\textbf{r}_1,\dots ,\textbf{r}_{m_B}, \textbf{r}_i \in \Omega _B$). These areas are chosen to showcase the flexibility of the sensor selection method, where the shape of both the measurement and reconstruction regions can be arbitrarily defined. While the areas represent a typical setup where the goal is to create two different sound zones, the study does not directly deal with sound zoning.

The sensor budget is set to $k=101$. The frequency used for the optimization is 860 Hz, which is the theoretical cut-off frequency for a uniform distribution with 101 sensors equally spaced over the measurement area. The wavenumber vectors $\textbf{k}_1, \dots , \textbf{k}_n$, are obtained by uniformly sampling the radiation sphere (S in (2)) using 200 points, so that $n=200$. The matrices $\textbf{A}$ and $\textbf{B}$ (with elements $a_{ij}=e^{\text {j}\textbf{k}_j\cdot \textbf{r}_i}$, $\textbf{r}\in \Omega _A$, and $b_{ij}=e^{\text {j}\textbf{k}_j\cdot \textbf{r}_i}$, $\textbf{r}\in \Omega _B$, respectively) are then formed. The noise precision is set to $\beta =1$ and the parameters precision is set to $\alpha =2$, which results in a measurement SNR of 20 dB. It is worth noting that in (15), when $\alpha _i=\alpha , \ i=1,\dots ,n$, $\alpha \in \mathbb {R}$, the BCRB does not depend on $\textbf{x}$, so that we can compute the estimator mean-square error without generating instances of $\textbf{x}$ as one would do in a Monte Carlo simulation.

6.1.1 Tested methods

The sensor selection methods described in Section 5 are compared with other sensor placement strategies. Table 1 summarizes the examined distributions. A uniform distribution (uni), where the sensors positions are equally spaced forming a regular lattice, is considered (Fig. 1a). Uniform distributions are one of the most common ways of arranging acoustic sensors due to their simplicity and well-studied performance. A random placement strategy (rand), where the selected candidates are drawn from a uniform random distribution, is considered as well. Random arrays are common in the CS in acoustics literature as randomness helps to lower the coherence of the sensing matrices. In the numerical study the results for rand show the average and standard deviation of 200 realizations of a random selection. We found this to be representative of the expected performance of a naive random selection. A selection optimized using a proper orthogonal decomposition-based method (pod) is also considered (Fig. 1b). Sensor selections operating on a dictionary learned from data were recently proposed as a way to take into account the structure/sparsity of the reconstructed signal in the selection process [27]. As the pod selection method incorporates representative data of the sound field to be reconstructed, it focuses on reconstruction, rather than on parameter estimation. For this reason, we found it to be a good benchmark for the selection optimized to reconstruct the pressure, i.e., the proposed solution to (17). The original pod method starts by collecting representative data at the candidate locations. A dictionary of pod-modes (i.e., principal components) is computed via the singular value decomposition of the training data. A greedy selection algorithm is then applied to the learned dictionary. In our study, we modify this method in order to be able to compare it with the rest of selection approaches. Training data is generated by synthesizing $10^4$ random sound fields. The sound field coefficients $\textbf{x}$ are drawn from a Gaussian distribution with variance $\alpha ^{-1}$, and the pressure data is generated by computing $\textbf{Ax}$ and adding Gaussian noise with variance $\beta ^{-1}$. The singular value decomposition of the data arranged in a matrix is then computed to obtain the left singular vectors. The pod dictionary, $\textbf{U}$, is obtained by truncating the singular vectors, keeping only the first 150. This number is determined by observing a plateau in the (log scaled) singular value decay after 150 modes. A list of the sensors sorted by relevance is found by computing the QR decomposition with column pivoting of $\textbf{U}\textbf{U}^\text {H}$, as described in [27]. The pod selection corresponds to the first k positions of such list. Once the relevant sensors are selected, the analysis is carried out in a similar way as the other selection methods (i.e., on a dictionary of plane waves rather than on the pod dictionary) in order to be able to compare it with the rest of selection approaches.

The distributions obtained from the proposed method are shown in Fig. 1c for the selection optimized to estimate the wave amplitudes, opt$_\textbf{x}$, and Fig. 1d for the selection optimized to reconstruct the pressure, opt$_\textbf{Bx}$. Figure 1e shows the convex relaxed solution $\hat{\textbf{z}}_{\textbf{x}}$ obtained from (18). Figure 1f shows the convex relaxed solution $\hat{\textbf{z}}_{\textbf{Bx}}$ obtained when minimizing $\text {tr}(\textbf{B}\textbf{F}^{-1}\textbf{B}^\text {H})$.

Table 1 Sensor selections examined

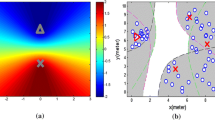
The pod-based method (Fig. 1b) places most of the sensors close to the outer boundary of the measurement area (along the sides of the rectangle), while the remaining sensors are placed around the reconstruction area ellipses. The selection optimized for estimating the parameters $\textbf{x}$ (Fig. 1c) distributes the sensors rather evenly across the measurement area, yet it is different from the uniform distribution (Fig. 1a). The selection optimized for estimating the sound field inside the reconstruction area $\textbf{Bx}$ (Fig. 1c) concentrates samples close to the boundary of $\Omega _B$, but many sensors are also placed towards the upper-left and lower-right corners of the measurement area. An analysis of the convex relaxed solutions, $\hat{\textbf{z}}_{\textbf{x}}$ and $\hat{\textbf{z}}_{\textbf{Bx}}$ shown in Fig. 1e and f, shows many values in between 0 and 1. A simple thresholding (without the second-stage greedy search) would have resulted in a different selection, with a higher sampling density on the outer edges of the measurement domain for opt$_\textbf{x}$ and a higher sampling density on the boundary of the reconstruction area for opt$_\textbf{Bx}$.

It may be noted that none of the selection methods places all of the sensors on the boundaries of the measurement domain, which could cause instabilities at the domain’s eigenfrequencies.

Fig. 1

Sensor distributions studied. a Uniform distribution. b Distribution optimized using the proper orthogonal decomposition-based method method. c Distribution optimized to minimize the variance when estimating the parameters $\textbf{x}$ d Distribution optimized to minimize the variance when estimating the pressure in the reconstructed area $\textbf{Bx}$. e Convex relaxed solution $\hat{\textbf{z}}_\textbf{x}$ obtained when minimizing $\text {tr}(\textbf{F}^{-1})$. f Convex relaxed solution $\hat{\textbf{z}}_\textbf{Bx}$ obtained when minimizing $\text {tr}(\textbf{B}\textbf{F}^{-1}\textbf{B}^\text {H})$. The random distribution is not shown in the figure

6.1.2 Results

The selections are compared in terms of the normalized root-mean-square error for estimating the parameters $\textbf{x}$, calculated as

$$\begin{aligned} \text {nrmse}(\textbf{x})\% = 100\sqrt{\frac{\text {tr}(\textbf{F}^{-1})\alpha }{n}}, \end{aligned}$$

(23)

and the normalized root-mean-square error for estimating the pressure in the reconstruction region $\textbf{Bx}$, calculated as

$$\begin{aligned} \text {nrmse}(\textbf{Bx})\% = 100\sqrt{\frac{\text {tr}(\textbf{B}\textbf{F}^{-1}\textbf{B}^\text {H})\alpha }{nm_B}}. \end{aligned}$$

(24)

Figure 2a shows the $\text {nrmse}(\textbf{x})$ over frequency. As the frequency increases, the estimation $\textbf{x}$ improves for all selections. The larger error at low frequencies is due to the high correlation of the columns of $\textbf{A}$, which makes it difficult to recover $\textbf{x}$. Since the acoustic wavelength ($\lambda =2 \pi c/\omega$) is large at low frequencies, two wave functions $e^{\text {j}\textbf{k}_i \cdot \textbf{r}}$ and $e^{\text {j}\textbf{k}_j \cdot \textbf{r}}$ can be highly correlated even when their propagation directions, $\textbf{k}_i c/\omega$ and $\textbf{k}_j c/\omega$, are not the same. If the two columns corresponding to the i and j waves are correlated, it is not be possible to distinguish whether the wave is propagating in one direction or the other, making the estimation of $\textbf{x}$ challenging and resulting in a larger nmse($\textbf{x}$). The uni and opt$_\textbf{x}$ selections achieve the lowest $\text {nrmse}(\textbf{x})$, performing very similarly up until 800 Hz. Above 800 Hz, opt$_\textbf{x}$ performs slightly better. Figure 2b shows the $\text {nrmse}(\textbf{Bx})$. For all selections the reconstruction error increases with frequency. At low frequencies, the sound field does not present large variations over space, which results in accurate reconstructions even if $\textbf{x}$ is not recovered exactly. The best performing selection is opt$_\textbf{Bx}$, with improvements of approximately 10 to 25% above 400 Hz with respect to the other selection methods.

Fig. 2

Normalized root-mean-square error over frequency a for the estimation of $\textbf{x}$ and b for the estimation of $\textbf{Bx}$

The $\text {nrmse}(\textbf{x})$ as a function of the number of available sensors k is shown in Fig. 3a (the uniform selection is not shown in this figure as in this case k cannot be chosen arbitrarily). The opt$_\textbf{x}$ and pod methods achieve similar performance. In this experiment, the benefit of optimizing the sensor positions in contrast to a naive random selection is clearly seen for a budget above 80 sensors. The gray line in Fig. 3a corresponds to the nmse($\textbf{x}$) lower bound obtained from the convex relaxed solution, $\text {tr}(\textbf{F}^{-1}(\hat{\textbf{z}}))$ in (19). As the sensors budget increases, the approximate solution $\tilde{\textbf{z}}$ is closer to the solution to the original problem (16). In Fig. 3b, the $\text {nrmse}(\textbf{Bx})$ as a function of k is shown. In this figure, the gray line corresponds to the nmse($\textbf{Bx}$) lower bound obtained from the convex relaxed solution. The largest improvement of opt$_\textbf{Bx}$ over the other selections is around $k=80$ (approximately 20% improvement). The selection opt$_\textbf{Bx}$ achieves a $\text {nrmse}(\textbf{Bx})$ of 40% with a budget of $k=80$ measurements, while pod requires $k=120$ and rand requires $k=200$ to achieve the same performance.

Fig. 3

Normalized root-mean-square error as a function of the number of sensors, for a fixed frequency of 860 Hz. a $\text {nrmse}(\textbf{x})$. Gray line: lower bound for $\text {nrmse}(\textbf{x})$ obtained from the convex relaxed solution $\hat{\textbf{z}}_\textbf{x}$ b $\text {nrmse}(\textbf{Bx})$. Gray line: lower bound for $\text {nrmse}(\textbf{Bx})$ obtained from the convex relaxed solution $\hat{\textbf{z}}_\textbf{Bx}$

The results shown in Figs. 2 and 3 consider an equal $\alpha$ for all the parameters, so that the computed errors are the average error when estimating all the n parameters. We study the case in which $\textbf{x}$ is sparse, i.e., when only a few of the parameters are non-zero, by generating different realizations of $\textbf{x}$ with a varying number of non-zeros. For each number of non-zeros considered, 1000 realizations of a sparse $\textbf{x}$ are generated, where the support is randomly selected. Therefore, the results depend on the sparsity degree of $\textbf{x}$ but are generalizable over different rooms and source positions. The nrmse is then computed as in (23) and (24) but only taking the relevant rows in $\textbf{A}$ and $\textbf{B}$ (the rows corresponding to the non-zeros in $\textbf{x}$) and replacing n by the number of non-zeros. Figure 4 shows the error as a function of the sparsity degree for $k=101$ and 860 Hz. When the number of non-zeros is very small (about 10% of all the parameters) there are no large differences between selections, as $\textbf{x}$ is easily recovered. When the number of non-zeros is larger than approximately 20% of the total number of parameters, the differences between distributions become significant. The largest improvement in terms of reconstruction error corresponds to opt$_\textbf{Bx}$ (green line in Fig. 4b).

For the estimation of $\textbf{x}$, Fig. 4a, the uni and opt$_\textbf{x}$ selections outperform the random selection. For the estimation $\textbf{Bx}$, Fig. 4b, the random selection is (by far) the worst performing from the studied selections. This results indicate that a random distribution of sensors is very likely suboptimal for recovering $\textbf{x}$ or $\textbf{Bx}$, even when $\textbf{x}$ is sparse.

Fig. 4

Normalized root-mean-square error as a function of the number of parameters that are non-zero over the total number of parameters

6.2 Sound field in a room

The selection methods are investigated with RIR data measured in a reverberant room. The setup (reconstruction and measurements areas and discretization) is the same as for the numerical study (Section 6.1). The RIRs are processed to mimic an acoustically damped room, since the original RIRs were acquired in a highly reverberant laboratory room that is not representative of common rooms. The processing consists on applying a time window to the RIRs so that the reverberation time is reduced. Details about the dataset can be found in [24] and [38].

The reconstruction performance is assessed in terms of the spatially averaged normalized error,

$$\begin{aligned} \text {error}(\textbf{Bx})\% = 100\frac{\Vert \textbf{B}\tilde{\textbf{x}} - \textbf{y}_B \Vert _2}{\Vert \textbf{y}_B \Vert _2}, \end{aligned}$$

(25)

and the spatial similarity [39],

$$\begin{aligned} \text {similarity}\% = 100\frac{|\textbf{y}_B^\text {H}\textbf{B}\tilde{\textbf{x}}|^2}{[\textbf{y}_B^\text {H}\textbf{y}_B][(\textbf{B}\tilde{\textbf{x}})^\text {H} \textbf{B}\tilde{\textbf{x}}]}, \end{aligned}$$

(26)

where $\tilde{\textbf{x}}$ is the maximum a posteriori estimate (Eq. 9), and the reference $\textbf{y}_B$ are the measured RIRs in the reconstruction area. The similarity takes values between 0 (reference and reconstruction are orthogonal) and 100 (reference and reconstruction are parallel).

Figure 5 shows the reconstruction results over frequency. The opt$_\textbf{Bx}$ selection achieves the best performance, with improvements of 10 to 20% for frequencies above 600 Hz with respect to the other selections, both in terms of error and similarity. The second best performing methods is opt$_\textbf{x}$, followed by pod, uni and rand. The frequency response at the center of the right ellipse of the reconstruction region is shown in Fig. 6. The reconstruction using the opt$_\textbf{Bx}$ selection is shown at the top of the figure, and the reconstruction corresponding to the pod selection is shown at the bottom. The opt$_\textbf{Bx}$ reconstruction is closer to the reference frequency response, particularly at frequencies above 500 Hz. The sound field over space at the optimization frequency (860 Hz) is studied in Fig. 7. The opt$_\textbf{Bx}$ reconstruction (Fig. 7b) recovers the spatial pattern of the reference sound field (Fig. 7a) while the pod reconstruction (Fig. 7c) differs significantly. This can also be seen in Fig. 7d and e, which show the difference between reference and reconstruction for the two methods.

Fig. 5

a Reconstruction error and b spatial similarity over frequency for the experiment in the reverberant room. A smoothing filter is applied to the results for better readability (the error and similarity shown at frequency f is the average of each metric in a band of 50 Hz center around f)

Fig. 6

Room frequency response at the center of the right ellipse in the reconstruction area for a the opt$_\textbf{Bx}$ selection and b pod selection. Black: reference (measured response). Color: reconstruction

Fig. 7

Sound field over space for a fixed frequency of 860 Hz (absolute values). a Reference sound field (measured). b Reconstructed with opt$_\textbf{Bx}$ selection. c Reconstructed with pod selection. d Difference between reference and opt$_\textbf{Bx}$ reconstruction. e Difference between reference and pod reconstruction

7 Conclusions

In this work, we have investigated the optimal positioning of sensors for sound field reconstruction. We examined two approaches: one optimizes the sensor positions with respect to the estimation of the parameters that describe the sound field, while the other one does it with respect to the reconstructed pressure in the area of interest. The results show a clear advantage of taking into account the reconstruction area when optimizing the sensors positions, specially compared to distributing the sensors randomly over space. It is worth noticing that this type of random microphone arrays are commonly used in CS and sparse recovery in acoustics as a means to lower the coherence of the sensing matrix.

While the selection optimized for estimating the parameters distributes the sensors evenly over the measurement area, the selection optimized for estimating the pressure concentrates more samples close to the reconstruction area. This type of distributions were also observed for geometries and frequencies different from the ones reported in Section 6. As a general guiding advise for designing sampling strategies, it seems to be advantageous to distribute the available sensors over the entire measurement domain, with a higher sensor density closer to the reconstruction area.

A hierarchical Bayesian formulation makes it possible to include sparsity promoting priors in the estimation problem. In this study, we focused on optimal distributions that are generalizable across rooms and source positions, and thus, we consider a prior in which all the hyperparameters share the same value. Nonetheless, a sensor selection tailored to a given sound field could easily be obtained as well via this formulation when sufficient data is available.

While this study focused on the reconstruction of RIRs, the sensor selection method can easily be applied to other types of sound field reconstruction problems (e.g., acoustic holography, sound field analysis, and in situ characterization of acoustic materials) by using a suitable model for the studied sound field (e.g., equivalent sources and data-driven models).

An implementation of the sensor selection method as well as the code necessary to reproduce the results of this study are available in the repository https://github.com/samuel-verburg/optimal_sensor_placement.git.

Appendix

The gradient of the objective function in (16) is

$$\begin{aligned} \nabla \textrm{tr}\left( \textbf{F}^{-1}\right) = - \beta \textrm{diag} \left( \textbf{A} \textbf{F}^{-1}\textbf{F}^{-1} \textbf{A}^\text {H} \right) , \end{aligned}$$

(27)

and the Hessian is

$$\begin{aligned} \nabla ^2 \textrm{tr}\left( \textbf{F}^{-1}\right) = 2(\beta \textbf{A}\textbf{F}^{-1}\textbf{A}^\text {H})\circ (\beta \textbf{A}\textbf{F}^{-1}\textbf{F}^{-1}\textbf{A}^\text {H}). \end{aligned}$$

(28)

For (17), the expressions for the gradient and Hessian are

$$\begin{aligned} \nabla \textrm{tr}\left( \textbf{B} \textbf{F}^{-1} \textbf{B}^\text {H}\right) = - \beta \textrm{diag} \left( \textbf{C}\textbf{C}^\text {H}\right) \end{aligned}$$

(29)

and

$$\begin{aligned} \nabla ^2 \textrm{tr}\left( \textbf{B} \textbf{F}^{-1} \textbf{B}^\text {H}\right) = 2\left(\beta \textbf{A}\textbf{F}^{-1}\textbf{A}^\text {H}\right)\circ \left(\sigma ^{-2}\textbf{C}\textbf{C}^\text {H}\right), \end{aligned}$$

(30)

where $\textbf{C} \equiv \textbf{A}\textbf{F}^{-1}\textbf{B}^\text {H}$.