Introduction

Complex networks are common in real life and the research has shifted from discovering the macro laws of structure and dynamics to uncovering the role of macro elements as nodes in real systems [1,2,3,4,5]. In the past several decades, designing effective centrality methods to identify critical nodes in complex networks has become a significant topic. Many methods have been designed to measure the importance of nodes in static networks, such as degree [6], closeness [7] and betweenness [8, 9]. Those centrality measures have been used in predicting essential proteins [10], identifying influential nodes from social networks [11, 12], finding critical links [13]. With the development and evolution of organisms, the structure of biological networks changes dynamically over time [14,15,16,17], by increasing or decreasing the number of nodes or edges [18, 19]. The research on dynamic biological networks and the identification of critical nodes are helpful to better understand biological processes [20].

At present, several methods have paying attention to identify critical genes in biological networks [21,22,23]. Liu et al. [24] identified potential critical genes related to the pathogenesis and prognosis of gastric cancer by protein-protein interaction (PPI) network and Cox proportional hazards. Li et al. [25] identified critical miRNAs, genes and transcription factors of lung adenocarcinoma by analyzing Gene Ontology terms, pathways, and PPI networks. Liu et al. [26] used the robust rank aggregation method, re-constructed the PPI network and performed modules analysis to identify critical genes. However, most of those methods are based on static network and ignoring the stage heterogeneity of complex diseases. He et al. [20] investigated miRNAs in serum exosome-like microvesicles to identify stage-common and stage-specific miRNAs, but ignored the connections between stages. Kim et al. [27] defined the temporal version of degree, closeness and betweenness on temporal networks, which reduced a dynamic network to a static one with directed flows. Nevertheless, those methods simply calculated the degree, closness and betweenness centrality of nodes in different time snapshots and obtained a mean value. The information of nodes changing with time would be lost. In our previous studies, we have proven that the studies of cancer stages is important for understanding the evolution of cancers [28, 29].

Fig. 1
figure 1

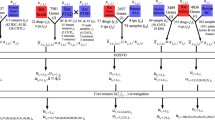
The module of forming the tensor and decomposing tensor. a The way of constructing temporal network into tensor. The edges, consist of inter-stage edges and intra-stage edges are both taken into consideration. The yellow one is the network of Stage I, the green one is Stage II, the blue one is Stage III and the red one is Stage IV. The black represents inter-stage network. b The decomposition of tensor

Full size image

In this study, a lightweight and effective method that quantify the importance of genes with tensor decomposition (QIGTD) was proposed to identify the critical genes along with the progression of lung adenocarcinoma (LUAD). To start with, a time-series network was constructed to represent the molecular connections of individual pathological stages of LUAD, and a third-order tensor was employed to capture topological information of both intra-stage and inter-stage. The intra-stage topological connections were obtained from gene co-expression relationships, while the inter-stage topological connections were calculated by combining both local similarities and a pre-defined parameters. Then, a tensor decomposition method was proposed to identify critical gene from the temporal network, which considers not only the intra-stage topological information, but also the inter-stage temporal characteristics. It is also a learning free method, which can work well with a small amount of samples. The precision and mAP are presented to evaluate the performance of QIGTD, and the other three state-of-the-art methods: temporal versions of degree, betweenness and closeness [30, 31] were employed as benchmark methods. The overall framework of the proposed method was show in Fig. 1.

Materials and methods

Data collection and processing

The critical genes are identified in the Stage I - Stage IV temporal networks of LUAD. The LUAD related gene expression dataset were downloaded from Xena (https://xenabrowser.net/), where there are 206 samples in Stage I, 93 samples in Stage II, 59 samples in Stage III, and 20 samples in Stage IV.

The networks of the four stages are constructed separately according to the PCC and the obtained p-value. In this study, the selection criteria were p-value\(< 0.01\) and \(|PCC| > 0.8\) according to the characteristics of biological networks. As a result, there are 17,830 edges in Stage I, 21,951 in Stage II, 11,170 in Stage III and 611 edges in Stage IV.

The known critical genes can be obtained from DisGeNET (https://www.disgenet.org/), where there are 3,899 genes appearing in the temporal network, and 566 of them have been verified to be associated with LUAD.

The temporal network construction

The network representing each stage of LUAD was constructed with pearson correlation coefficient (PCC) calculated with gene expression. Besides the connections within stage, there was also a fixed set of genes connected between different stages of LUAD.

Currently, there are two typical ways to construct connections between networks of adjacent stages. One is to use a fixed constant to represent the interlayer relationship, and the value of the parameter can indicate the strength of the interlayer relationship. The other method is to use similarity metrics to measure inter layer relationships. It was stated that the features in temporal networks are studied by converting time into a snapshot sequence of the network, so the similarity measurement method between nodes in static networks can be extended to the node relationships between adjacent layers.

In this study, a novel method for measuring inter layer node similarity in temporal networks was proposed by combining the calculation of node local similarity index with fixed parameters, which is

$$\begin{aligned} TLS_{i}^{(t, t+1)}= C + \frac{\sum _{j}w_{ij}^{t} + \sum _{j}w_{ij}^{t+1}}{2N} + \frac{| SN_{i}^{(t, t+1)} |}{N} \end{aligned}$$
(1)

where C is a constant parameter that indicate the strength of the interlayer relationship, N is the number of vertices in the network, if \(\sum _{j}w_{ij}^{t} = 1\), then the vertex i and vertex j has connection in the network of \(G_t\), while if \(\sum _{j}w_{ij}^{t} = 0\), then the vertex i and vertex j does not have connection. \(SN_{i}^{(t, t+1)}\) represents the number of common vertices in two adjacent network \(G_t\) and \(G_{t+1}\).

The first part of Eq. 1 is a constant parameter, which can be setup according to the experimental requirement. If a relatively small parameter was used, then it enhances the importance of vertices with high inter layer similarity in temporal networks, while selecting larger fixed parameters strengthens the importance of isolated vertices. In this study, the value of C was set to 0.5 based on the characteristics of the biological network. The second part of Eq. 1 is network local similarity, which represents the proportion of local neighbors of adjacent snapshot nodes in the entire network at different times. The third part of Eq. 1 represents the proportion of shared neighbors of adjacent snapshot vertices in the entire network. Hence, the overall value of TLS can characterize the degree of vertices in a temporal network and the inter layer relationship of node adjacency in different time snapshots. The larger the TLS value, the higher the probability of the node continuously appearing on two snapshot layers, and the more stable the node adjacency relationship.

The tensor description of the temporal network

The temporal network was represented as \(X= \left\{ G_{t},C \right\}\). The \(G_{t}\) is the network of different stages of LUAD and C is the set of interconnections between different networks. The elements in C were concerned as ‘cross network’. The temporal network could be represented in tensor as follows. Let \(X\in \mathbb {R}^{I\times J\times K}\). The elements can be defined according to Formula 2.

$$\begin{aligned} \ X_{ijk}=\left\{ \begin{array}{ll} w_{ijk}& \text { if } X_{ijk}\in G_{t} \\ c_{ijk}& \text { if } X_{ijk}\in C \\ 0& \text { otherwise } \end{array}\right. \end{aligned}$$
(2)

where \(0\le i<I,0\le j<J,0\le k<K\), the \(w_{ijk}\) is the element in \(G_{t}\) and \(c_{ijk}\) is the element in C.

The process to form the tensor from temporal network is shown in Fig. 1a, where different colors represent different stages. The edges between the different stages compose the cross network. There are four kinds of networks in \(G_{t}\) and three kinds of cross networks in C.

The tensor could be transformed into matrix by unfolding or flattening. In this study, we expanded the n-order tensor X along mode-n into a matrix \(X_{n}\). The mode-1 corresponds to the 1-order of tensor, mode-2 corresponds to the 2-order of tensor and mode-3 corresponds to the 3-order of tensor. After the matricization of the tensor, the Kronecker, Khatri-Rao, and Hadamard products can be calculated respectively as follows.

$$\begin{aligned} A\odot B=\left[ a_{1}\otimes b_{1} a_{1}\otimes b_{1} a_{2}\otimes b_{3} \cdots a_{N}\otimes b_{N} \right] \end{aligned}$$
(3)
$$\begin{aligned} A\otimes B = \left| \begin{array}{ccc} a_{11}B & \cdots & a_{1N}B\\ \vdots & \ddots & \vdots \\ a_{N1}B & \cdots & a_{NN}B\\ \end{array}\right| \end{aligned}$$
(4)
$$\begin{aligned} A*B = \left| \begin{array}{ccc} a_{11}B_{11} & \cdots & a_{1N}B_{1N}\\ \vdots & \ddots & \vdots \\ a_{N1}B_{N1} & \cdots & a_{NN}B_{NN}\\ \end{array}\right| \end{aligned}$$
(5)

The Canonical Polyadic (CP) decomposition of tensor

A tensor can be expressed as the sum of finite rank tensors. In this study, the 3-order could be decomposed as follows.

$$\begin{aligned} X\approx [\left[ A,B,C \right] ] = \sum \limits _{r=1}^{R}a_{r}\circ b_{r}\circ c_{r} \end{aligned}$$
(6)

where

$$\begin{aligned} & X\in \mathbb {R}^{I\times J\times K} \\ & A=(a_{1},a_{2},a_{3},...,a_{R}) \in \mathbb {R}^{I\times R}\\ & B=(b_{1},b_{2},b_{3},...,b_{R}) \in \mathbb {R}^{J\times R}\\ & C=(c_{1},c_{2},c_{3},...,c_{R}) \in \mathbb {R}^{K\times R}\\ \end{aligned}$$

The symbol “\(\circ\)” is the outer product, the vector \(a_{r}\in \mathbb {R}^{I}\) is column r of factor matrix \(A\in \mathbb {R}^{I\times R}\), the vector \(b_{r}\in \mathbb {R}^{J}\) is column r of factor matrix \(B\in \mathbb {R}^{J\times R}\), and the vector \(c_{r}\in \mathbb {R}^{K}\) is column r of factor matrix \(C\in \mathbb {R}^{K\times R}\).

The outer product of these vectors is a rank one tensor, so the R rank-one tensors was used to approximate the original data, which is shown in Fig. 1b. By utilizing the factor matrix, the 3-order tensor can be decomposed as follows.

$$\begin{aligned} \begin{array}{l} min_{A}\sum \limits _{i,j,k} \left(x_{ijk}-\sum \limits _{r=1}^{R}a_{ir}b_{jr}c_{kr}\right)^2 = min_{A}\left\| X_{(1)}-A(C\odot B)\top \right\| ^2_{F} \\ min_{B}\sum \limits _{i,j,k} \left(x_{ijk}-\sum \limits _{r=1}^{R}a_{ir}b_{jr}c_{kr}\right)^2 = min_{B}\left\| X_{(2)}-B(C\odot A)\top \right\| ^2_{F} \\ min_{C}\sum \limits _{i,j,k} \left(x_{ijk}-\sum \limits _{r=1}^{R}a_{ir}b_{jr}c_{kr}\right)^2 = min_{B}\left\| X_{(2)}-B(C\odot A)\top \right\| ^2_{F} \\ \end{array} \end{aligned}$$
(7)

The formulas can be approximately as

$$\begin{aligned} \begin{array}{l} X_{(1)}\approx [A(C\odot B)\top ] \\ X_{(2)}\approx [B(C\odot A)\top ] \\ X_{(3)}\approx [C(B\odot A)\top ] \\ \end{array} \end{aligned}$$
(8)

Consequently, the \(A_{[n]}\) could be calculated with back propagation and gradient descent. Since the goal is to make the tensor \(\hat{X}\) estimated by A, B, C as close as possible to the original tensor X, the loss function is set as follows.

$$\begin{aligned} \begin{array}{l} Loss_{1} = \frac{1}{2}[X_{(1)}-A(C\odot B)\top ] \\ Loss_{2} = \frac{1}{2}[X_{(2)}-B(C\odot A)\top ] \\ Loss_{3} = \frac{1}{2}[X_{(3)}-C(B\odot A)\top ] \\ \end{array} \end{aligned}$$
(9)

The partial derivative of A, B and C could be quantified and the parameters could be updated by the following formulas.

$$\begin{aligned} \begin{array}{l} A = A-\alpha * \frac{\partial Loss_{1}}{\partial A} \\ B = B-\alpha * \frac{\partial Loss_{2}}{\partial B} \\ C = C-\alpha * \frac{\partial Loss_{3}}{\partial C} \\ \end{array} \end{aligned}$$
(10)

where \(\alpha\) is the learning rate. The vertex centrality is now can be calculated as

$$\begin{aligned} s_i = \frac{1}{T}\sum \limits _{t=1}^{T}((a_1)_i (c_1)_t + (b_1)_i (c_1)_t) \end{aligned}$$
(11)

In this study, where \(I=J\) represents the number of genes, and \(K=4\) represents the number of layers in the network. The importance score of every gene could be determined with either \(I = A\odot C\) or \(I = B\odot C\). Additionally, if R is set to 1, so \(I = A\) or \(I = B\).

Results

The evaluation indices

The performance of QIGTD is evaluated by the precision, mean average precision (mAP) and fold enrichment.

The precision show the true positive ratio by giving a list of predictions, which is

$$\begin{aligned} precision = \frac{TP}{TP + FP} \end{aligned}$$
(12)

The primary objective revolves around the task of ranking, where precision alone may not insufficiently reflect the algorithm’s performance. The mAP does not only consider the accuracy of identifying the critical genes, but also considers the differences in genes order. More robustly, the mAP is utilized to reflect the model’s performance, which can be defined as Formula 13.

$$\begin{aligned} AP\left( q_{i} \right) = \frac{\sum _{i\in i_{1},i_{2},...,i_{M}} P_{i}\times L_{i}}{M} \end{aligned}$$
(13)

where \(P_{i}=\frac{1}{\sum _{j=1}^{i}j}\), and the \(L_{i}\) is the label of the i-th gene. In this study, the label comprises 0 and 1. Since there is only one query in the problem, so the mAP is equal to the AP.

Comparing with the benchmark methods

The important score of every gene in temporal network were calculated with three benchmark methods: T-degree, T-closeness, T-betweenness and the proposed QIGTD method.

The T-degree is defined as

$$\begin{aligned} T\text {-}deg(v) = \frac{\sum _{t=1}^{T} D_t(v)}{T} \end{aligned}$$
(14)

where \(D_t(v)\) represents the degree of vertex v at the \(t^{th}\) network snapshot, and T is the total number of network snapshot.

The T-closeness is defined as

$$\begin{aligned} T\text {-}clo(v) = \sum \limits _{1 \le t \le T} \sum \limits _{u \in V\setminus v} \frac{1}{\Delta _{t,T(u,v)}} \end{aligned}$$
(15)

where \(\Delta _{t,T(u,v)}\) represents the shortest path length between vertex u and vertex v.

The T-betweenness is defined as

$$\begin{aligned} T\text {-}bet(v) = \sum \limits _{1 \le t \le T} \sum \limits _{s \ne v \ne d \in V} \frac{\sigma (s,d,v)}{\sigma (s,v)} \end{aligned}$$
(16)

where \(\sigma (s,d,v)\) represents the number of shortest path between vertex s and vertex v that through vertex d, while\(\sigma (s,v)\) represents the number of all shortest path between vertex s and vertex v.

The precision of different methods are summarized in Table 1. The QIGTD consistently performs better than the other three state-of-the-art methods from the top 10 to top 500 predictions. In top 10, the precision of QIGTD is 0.50, while the best in the other three methods is T-betweenness with the precision of only 0.20. This situation also hold for predictions from the top 50 to top 500. The top three important genes calculated by QIGTD are highly related to LUAD.

Table 1 The precision of QIGTD and the three SOTA methods
Full size table

The results of mAP@M, presented in Table 2, indicate that QIGTD outperforms the other three methods. QIGTD exhibits superior performance in accurately identifying the LUAD related genes without learning.

Table 2 The mAP of the four methods
Full size table

The fold enrichment is carried out to measure the performance of the model, which indicates how precisely the method can locate disease-related genes. QIGTD consistently exhibits significantly higher values compared to the other three methods as shown in Fig. 2.

Fig. 2
figure 2

The curve of fold enrichment in the top 500 genes. The x axis is the rank of genes in every method. The y axis is the score of fold enrichment. The fold enrichment could be calculated with precision and the correlation rate between all genes and LUAD

Full size image

Biological evidences of the predictions

Table 3 illustrated top 10 genes identified by the four methods as well as their rank. Among the top 10 genes identified by QIGTD, 5 genes are associated with LUAD in DisGenNET, indicating a higher level of association with the disease compared to the other methods.

Additionally, the rest 5 genes have the potential to become biomarkers of LUAD. The NCAPH was verified to be negatively associated with Mcl-1 in non-small cell lung cancer [32]. Nguyen et al. [33] found that CDCA5 (cell division cycle associated 5) upregulated in the majority of lung cancers. The study of Wei et al. [34] found that the knockdown of HJURP inhibits non-small cell lung cancer cell proliferation, migration, and invasion. Coincidentally, there are many researchers found that BUB1 may hopefully become a novel marker and therapeutic target for LUAD [35,36,37]. The BUB1B was also identified to be a significant biomarker for a poor prognosis and poor clinicopathological outcomes in patients with LUAD [38].

Table 3 The top 10 genes identified by the four methods and verified by DisGeNET
Full size table

The differentially expressed analysis is also performed on the top 10 genes, which is shown in Fig. 3. The blue box is the gene expression in control and the rest 4 boxes are that in four stages. The top 10 genes are obviously differentially expressed in stages compared to control.

Fig. 3
figure 3

The boxplot of the expression of top 10 genes. The different color in the plots is different stages. The blue box represents the expression in control. It shows that the genes identified with QIGTD are differentially expressed genes

Full size image

Moreover, in top 50 genes identified by QIGTD, 29 genes are verified have a strong association with the disease, which is demonstrated in Table 4.

Table 4 The top 50 genes identified by QIGTD and verified in DisGeNET
Full size table

The sub-networks of top 10 genes are extracted as Fig. 4a. The figure shows the subgraphs of top 10 genes of Stage I to Stage IV respectively. The thickness of the edge in the figure indicates the weight of the edge. The thick edges gradually decrease from Stage I to Stage IV, and some edges also disappear at Stage IV, thus the subgraphs of top 10 genes exhibit the evolution of LUAD.

The sub-networks of top 50 genes are extracted as Fig. 4b. The red nodes are top 10 genes, the purple are top 20 genes and the green are top 50. The thickness of the edges is not obviously as there are too many edges in the networks, but the sub-networks gradually become sparse with the stages, which shows a signal of the evolution of LUAD.

Fig. 4
figure 4

The sub networks of Top 10 genes and Top 50 genes

Full size image

Among top 50 genes, 36 genes are enriched to 5 GO terms in Fig. 5. The GO terms are nuclear division, mitotic nuclear division, chromosome segregation, organelle fission and mitotic sister chromatid segregation, all of which have been verified to be associated with LUAD [39,40,41]. The different color of the ribbon represents the different GO terms. The numbers of ribbon means the number of GO terms that genes enrich. For example, the DLGAP5 has five ribbons, which means it enriches all 5 GO terms. The SPC25 has a green ribbon, which means it only enriches the chromosome segregation.

Fig. 5
figure 5

The GO enrichment of top 50 genes. 5 Go terms chosen from the result of the enrichment are exhibited. The ribbons in different colors represents different GO terms. The number of the ribbons in gene is the number of GO terms it enriches. The boxed genes are LUAD-related genes. There are 32 genes enriched on nuclear division, 29 enriched on mitotic nuclear division, 30 on chromosome segregation, 32 on organelle fission and 25 enriched on mitotic sister chromatid segregation

Full size image

Discussion

The investigation of critical genes in temporal networks has become increasingly prevalent. Most of previous studies concentrate on the the structure of the network itself, but ignore the connections and changes between network at adjacent stages. Inspired by tensor decomposition, QIGTD is proposed in this research. Both the connections of genes inter and intra are taken into consideration.

The experimental results show that QIGTD outperforms the other three SOTA methods, especially in identifying the most critical genes. In the result, 5 genes in top 10 identified by QIGTD have been verified to be critical. At the same time, the other five genes may also be critical according to recent researches. The top 10 genes also differentially expression in stages compared to control. Furthermore, 29 genes are highly related to LUAD in top 50. The GO terms show indicate the top 50 genes ranked by QIGTD is associated with LUAD. The sub network of top 10 to top 50 undergoes changes across stages, which means the genes identified are potential to be biomarkers of the evolution of LUAD.

Additionally, QIGTD is a learning free and effective method, which does not require too many samples. The QIGTD has a low computational complexity and can be utilized in large-scale networks, which also could be easily embedded into the research of other complex problems.