1 Introduction

The current outbreak of coronavirus disease 2019 (COVID-19) has significantly affected public health and the economy worldwide. As of 21 November 2021, more than 257 million COVID-19 cases and 5 million deaths have been reported globally [6]. COVID-19 is an emerging respiratory infectious disease that was first detected in early December 2019 in Wuhan, China. The virus that causes COVID-19 is severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), which spread rapidly throughout the globe. The World Health Organization (WHO) initially declared the COVID-19 outbreak as a public health emergency of international concern but with the spread across and within countries leading to a rapid increase in the number of cases, the outbreak was officially declared a global pandemic on 11 March 2020 [47]. Given the global scenario on the series of waves and unprecedented strains of COVID-19, there is a need for more investigation to timely and effectively curtail the spread of the disease.

Mathematical modelling is a very versatile and effective instrument for understanding infectious disease transmission dynamics and helps us to develop preventive measures for controlling the infection spread both qualitatively and quantitatively. To model the epidemiological data of infectious diseases, compartmental models are widely used due to their simplicity and well-studied applications [18]. In this regard, the recent epidemiological threat of COVID-19 is not an exception. In such types of models, the population is categorized into several classes, or compartments, based on the stage of the infection that is affecting them. These models are governed by a system of ordinary differential equations that take into account the time-discoursed infection status of the population compartments. Wu et al. [49] first developed a mathematical model for COVID-19 which is based on Susceptible–Exposed–Infectious–Recovered (SEIR) model and explains the transmission dynamics and estimate the national and global spread of COVID-19. After that, various mathematical models were proposed by considering several stages of susceptible and infected populations [19, 36]. Many researchers studied the dynamics of COVID-19 using real incidence data of the affected countries and examined different characteristics of the outbreak as well as evaluated the effect of intervention strategies implemented to suppress the outbreak in respective countries [14, 27, 41]. In addition, a comparative analysis of the most affected countries during the second wave of COVID-19 was done by Easwaramoorthy et al. [10] using fractal-based prognostic model.

Presently, the second wave of COVID-19 is affecting most of the countries in the world. In a densely populated country like India, this scenario is more threatening. On April 15, 2021, the daily cases of COVID-19 were double the first peak. However, The epidemic evolution of the country is quite complex due to regional inhomogeneities. Thus, governments of various states in India are adopting different strategies to control the outbreak, such as wearing masks, vaccination drives, social distancing guidelines, partial lockdowns, and restricted store hours in place. Thus, gaining an understanding of how this outbreak spread in the form of waves and possible interventions on a short-term basis is urgent. As of 21 November 2021, more than 34 million COVID-19 cases and more than 465 thousand deaths are reported in India [7]. We have chosen to concentrate on two major districts namely, Bangalore urban and Chennai of India for our case studies. These two districts are very crucial hubs of south India and are experiencing a severe second wave of COVID-19. Additionally, taking small regions is also necessary to make reliable projections using mechanistic mathematical models. Due to the small area and populations, it is also easy to implement and supervise specific control measures.

As a case study in India, several researchers proposed models that are fitted to the daily COVID-19 cases and deaths, and examined different control strategies [13, 15, 17, 19, 28, 34, 36]. Some of the studies explore the vaccine allocation strategy in India due to limited supply and to support relevant policies [12]. Regarding the upcoming wave of COVID-19 in India, Kavitha et al. [17] discussed the epidemic rate in the provinces of India by considering the SIR and fractal models and notifying that there is a possibility of a third wave during the first week of August 2021. However, none of the above studies has considered the airborne transmission of the SARS-COV-2 virus in their respective models with application to Indian districts.

To control a pandemic outbreak, it is necessary to understand how the virus transmits to a susceptible individual and eventually spreads in the community. The primary transmission pathway of COVID-19 is human-to-human propagation through infectious droplets [45]. However, a recent study by Greenhalgh et al. [16] suggests that SARS-COV-2 can be transmitted through the air and they showed 10 scientific reasons behind this. Later on, Addleman et al. [1] commented that Canadian public health guidance and policies should be updated to address the airborne mode of transmission. The authors also suggested that addressing airborne transmission requires the expertise of interdisciplinary teams to inform solutions that can end this pandemic faster. Motivated by these scientific pieces of evidence, we consider a compartmental model of SEIR-type including shedding of free virus in the air by infectious persons. To the best of our knowledge, this is the first modelling study that considers the airborne transmission of COVID-19 with applications to Indian districts. We consider that the susceptible population becomes exposed in two different ways: firstly through direct contact with an infected population or touches a surface that has been contaminated. This transmission also occurs through large and small respiratory droplets that contain the virus, which would occur when near an infected person. The next is through the airborne transmission of smaller droplets and particles that are suspended in the air over longer distances and time [11]. We also study the effect of immigration along with popular control strategies. The main focus of our study is to explore the following epidemiological issues:

  • Mathematically analyze the COVID-19 transmission dynamics by incorporating the airborne pathway of free SARS-CoV-2 virus into the model structure.

  • Impact of anti-COVID drugs on the reduction of hospitalized persons.

  • Individual and combined effects of various control measures (use of face mask, vaccination) as well as immigration of infectious persons on the COVID-19 pandemic.

The remainder of this paper is organized as follows. In the next section, we propose a deterministic compartmental model to describe the disease transmission mechanism. We consider the amount of free virus in the air as a dynamic variable. Section 3 describes the theoretical analysis of the model, which incorporates the existence of positive invariance region, boundedness of solutions, computation of the basic reproduction number, and stability of disease-free equilibrium. Also, in this section, the existence of forward bifurcation of the model system is explored. In Sect. 4, we fit the mathematical model using nonlinear least-squares technique from the observed mortality data and estimate unknown parameters. Section 5 describe several control mechanisms and immigration of infectives through numerical simulation. We examine the effects of vaccination, treatment by drugs, and use of face masks with different degrees of efficacy as intervention strategies. Finally, in Sect. 6 we discuss the findings and some concluding remarks about mitigation strategy obtained from our study.

2 Model description

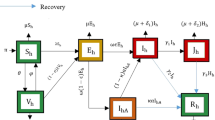
To design the basic mathematical model for COVID-19 transmission dynamics, some general epidemiological factors are considered including the airborne transmission of the free virus. Several studies of novel coronavirus suggest that an infected person can be asymptomatic (infectious but not symptomatic) or symptomatic with small, moderate, severe, or critical symptoms [23, 46, 50, 51]. For simplicity of model formulation, we break the infected individuals into two separated classes, notified and un-notified. Here, the un-notified class contains untested asymptomatic, asymptomatic who are tested negative, untested symptomatic, and symptomatic who are tested negative, whereas notified class contains those symptomatic and asymptomatic persons who are tested COVID-19 positive. Population among both the notified and un-notified class can be hospitalized, when they have a critical health situation. Thus the entire population can be stratified into six main compartments based on the status of the disease: susceptible (S(t)), exposed (E(t)), un-notified (\(I_u(t)\)), notified (\(I_n(t)\)), hospitalized (\(I_h(t)\)), and recovered (R(t)), at time t. Consequently, the total population size is given by \(N(t)=S(t)+E(t)+I_u(t)+I_n(t)+I_h(t)+R(t)\). In addition, V(t) describes the amount of free virus in the environment.

Now, we consider individuals from each human class have a per capita natural mortality rate \(\mu \). The net influx rate of susceptible population per unit time is \(\Pi \). This parameter includes new births, immigration, and emigration of susceptible persons. Also, the susceptible population decrease after infection, acquired through the direct contact of notified or un-notified infected individuals. Let \(\beta _1\) be the transmission rate for direct contact with the modification factor \(\nu \) for notified infected individuals. Then \(\nu \in (0,1)\), since the notified persons are advised to take preventive measures like face mask use, social distancing more seriously. In addition, the susceptible population is infected through the contact of the free virus in air [1, 16]. Let \(\beta _2\) be the transmission rate for free virus contact. The interaction of susceptible individuals with infected individuals (un-notified or notified) follows standard mixing incidence and with free virus follows mass action incidence. For basic details and difference between standard mixing incidence and mass action incidence, interested readers are referred to the third chapter of Martcheva’s book [29]. Then the differential equation that describes the rate of change of susceptible individuals at time t, is given by

$$\begin{aligned} \displaystyle {\frac{{\mathrm{d}}S}{{\mathrm{d}}t}} =\Pi -\frac{\beta _1 S( I_u+ \nu I_n)}{N} - \beta _2 SV -\mu S + \theta R. \end{aligned}$$

Here, \(\theta \) be the rate at which recovered individuals eventually lose the temporal immunity from the infection and become susceptible [12, 35].

Alongside, the exposed population (E(t)) who are infected individuals, however still not infectious for the community. By making successful contact with infectives, susceptible individuals become exposed. Also, these people decrease at a rate \(\gamma \) and become notified or un-notified. The probability that exposed individuals progress to the notified infectious class is p and that of the un-notified class is \(1-p\). This assumption leads to the following rate of change in E:

$$\begin{aligned} \displaystyle {\frac{{\mathrm{d}}E}{{\mathrm{d}}t}} = \frac{\beta _1 S( I_u+ \nu I_n)}{N} + \beta _2 SV - (\gamma + \mu ) E. \end{aligned}$$

The un-notified individuals (\(I_u\)), who are transferred from exposed class at a rate \((1-p)\gamma \) are the population who are un-notified from COVID-19 disease. Also, the un-notified individuals progress to hospitalized class at a rate \(\eta _u\) and recovered at a rate \(\sigma _u\). The un-notified individuals are assumed to have no disease-induced mortality rate as most of them will not develop severe symptoms. However, if some of the un-notified persons develop sudden severe symptoms, they will be transferred to the hospital and die as a hospitalized patients. Thus, the equation governing the rate of change of un-notified persons is

$$\begin{aligned} \displaystyle {\frac{{\mathrm{d}}I_u}{{\mathrm{d}}t}} =(1-p)\gamma E- (\eta _u+\sigma _u+\mu )I_u. \end{aligned}$$

The notified individuals (\(I_n\)), who are transferred from exposed class at a rate \(p\gamma \) are the population who are notified as COVID-19 positive people. Also, the notified individuals reduced by progressing to hospitalized class at a rate \(\eta _n\), by recovery at a rate \(\sigma _n\), and COVID-19 induced mortality rate \(\delta _n\). Therefore, we have the following equation

$$\begin{aligned} \displaystyle {\frac{{\mathrm{d}}I_n}{{\mathrm{d}}t}} = p \gamma E-(\eta _n + \sigma _n + \mu + \delta _n) I_n. \end{aligned}$$

The hospitalized individuals (\(I_h\)) increase from un-notified or notified people at rates \(\eta _n\) or \(\eta _u\), respectively. Also, this class of people recover at a rate \(\sigma _h\) and decrease through COVID-19 induced mortality rate \(\delta _h\). Thus, we have the following rate of change of \(I_h\):

$$\begin{aligned} \displaystyle {\frac{{\mathrm{d}}I_h}{{\mathrm{d}}t}} = \eta _u I_u+ \eta _n I_n - (\sigma _h + \mu + \delta _h)I_h. \end{aligned}$$

The recovered individuals (R) increase by recovering from each of the infected classes (un-notified, notified and hospitalized) at rates \(\sigma _u\), \(\sigma _n\), and \(\sigma _h\) respectively. As mentioned earlier, \(\theta \) is the rate at which the recovered population loses immunity against COVID-19 and becomes susceptible again. Thus, the following differential equation leads to the rate of change of R:

$$\begin{aligned} \displaystyle {\frac{{\mathrm{d}}R}{{\mathrm{d}}t}} =\sigma _u I_u+\sigma _n I_n + \sigma _h I_h - (\theta + \mu )R. \end{aligned}$$

The differential equation describing the rate of change of free virus, increased from the shedding rate of un-notified and notified patients at rates \(\alpha _u\) and \(\alpha _n\), respectively with a natural clearance rate \(\mu _c\). Thus

$$\begin{aligned} \displaystyle {\frac{{\mathrm{d}}V}{{\mathrm{d}}t}} = \alpha _u I_u+ \alpha _n I_n - \mu _c V. \end{aligned}$$
Fig. 1
figure 1

Schematic diagram of the proposed model. Solid arrows represent the transmission rate from one compartment to other, whereas dashed arrows represent the interaction between compartments

Full size image

Figure 1 describes the flow patterns of individuals between compartments over time.

Assembling all the above differential equations, we have the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{lll} \displaystyle {\frac{{\mathrm{d}}S}{{\mathrm{d}}t}} &{}=&{} \Pi -\frac{\beta _1 S( I_u+ \nu I_n)}{N} - \beta _2 SV -\mu S + \theta R, \\ \displaystyle {\frac{{\mathrm{d}}E}{{\mathrm{d}}t}} &{}=&{} \frac{\beta _1 S( I_u+ \nu I_n)}{N} + \beta _2 SV - (\gamma + \mu ) E, \\ \displaystyle {\frac{{\mathrm{d}}I_u}{{\mathrm{d}}t}} &{}=&{} (1-p) \gamma E - (\eta _u + \sigma _u +\mu )I_u, \\ \displaystyle {\frac{{\mathrm{d}}I_n}{{\mathrm{d}}t}} &{}=&{} p \gamma E-(\eta _n + \sigma _n + \mu + \delta _n) I_n, \\ \displaystyle {\frac{{\mathrm{d}}I_h}{{\mathrm{d}}t}} &{}=&{} \eta _u I_u+ \eta _n I_n - (\sigma _h + \mu + \delta _h)I_h, \\ \displaystyle {\frac{{\mathrm{d}}R}{{\mathrm{d}}t}} &{}=&{} \sigma _u I_u+\sigma _n I_n + \sigma _h I_h - (\theta + \mu )R, \\ \displaystyle {\frac{{\mathrm{d}}V}{{\mathrm{d}}t}} &{}=&{} \alpha _u I_u+ \alpha _n I_n - \mu _c V. \end{array} \end{array}\right. } \end{aligned}$$
(1)

All the parameters involved in the above system are positive. We present the parameters with their biological interpretation, dimensions, and realistic values in Table 1.

Table 1 Description of model parameters used in the model (1)
Full size table

3 Mathematical analysis

3.1 Basic properties

Here, we explore the basic dynamical properties of the model (1). Let us first consider the initial conditions of the model as

$$\begin{aligned} S(0)>0,~E(0),~I_u(0),~I_n(0),~I_h(0),~R(0),~V(0)\ge 0.\nonumber \\ \end{aligned}$$
(2)

The dynamical system (1) is well posed as shown in the following theorem.

Theorem 1

Consider the model (1) with initial conditions (2). The nonnegative orthant \({\mathbb {R}}_+^7\) is invariant under the flow of (1), including S remaining positive with the advancement of time. Moreover, the solutions of the system (1) are bounded in the region

$$\begin{aligned} \Omega= & {} \left\{ (S,~E,~I_u,~I_n,~I_h,~R,~V)|~~0<S+E+I_u+I_n\right. \\&\left. +I_h+R\le \frac{\Pi }{\mu },~~ 0\le V<\frac{\Pi (\alpha _u+\alpha _n)}{\mu \mu _c}\right\} . \end{aligned}$$

Proof

Consider the initial conditions (2). Suppose that at time \(t=t_1\), \(S(t_1)=0\). Then from (1) at \(t=t_1\), \(\frac{{\mathrm{d}}S}{{\mathrm{d}}t}=\Pi +\theta R>0\) which implies that \(\frac{{\mathrm{d}}S}{{\mathrm{d}}t}>0\) when S is positive and small. Thus, there is no time \(t_1\) such that \(S(t_1)=0\). Therefore, S stays positive for \(t>0\) with the initial condition \(S(0)>0\). Now, for the other components

$$\begin{aligned}&\frac{{\mathrm{d}}E}{{\mathrm{d}}t}{\bigg |}_{E=0}=\frac{\beta _1 S( I_u+ \nu I_n)}{N} + \beta _2 SV\ge 0,\\&\frac{{\mathrm{d}}I_u}{{\mathrm{d}}t}{\bigg |}_{I_u=0}= (1-p) \gamma E\ge 0, \\&\frac{{\mathrm{d}}I_n}{{\mathrm{d}}t}{\bigg |}_{I_n=0} = p \gamma E\ge 0, \\&\frac{{\mathrm{d}}I_h}{{\mathrm{d}}t}{\bigg |}_{I_h=0} = \eta _u I_u+ \eta _n I_n,\ge 0, \\&\frac{{\mathrm{d}}R}{{\mathrm{d}}t}{\bigg |}_{R=0} = \sigma _u I_u+\sigma _n I_n + \sigma _h I_h,\ge 0, \\&\frac{{\mathrm{d}}V}{{\mathrm{d}}t}{\bigg |}_{V=0}\quad =\alpha _u I_u+ \alpha _n I_n\ge 0. \end{aligned}$$

Thus, all the other components are nonnegative and the orthant \({\mathbb {R}}_+^7\) is invariant under (1).

To show the boundedness of solutions of the system (1), we add all the equations except the last one of (1) to get

$$\begin{aligned} \frac{{\mathrm{d}}N}{{\mathrm{d}}t}&=\frac{{\mathrm{d}}}{{\mathrm{d}}t}(S+E+I_u+I_n+I_h+R)\\&=\Pi -\mu N-\delta _nI_n-\delta _hI_h\\&\le \Pi -\mu N. \end{aligned}$$

Using the results of differential inequality, we have

$$\begin{aligned} \limsup _{t\rightarrow \infty }N(t)\le \frac{\Pi }{\mu }. \end{aligned}$$

Since the total population is bounded, so the individual components are also bounded.

Also, from the last equation of (1), the rate of change of free virus is given by

$$\begin{aligned} \frac{{\mathrm{d}}V}{{\mathrm{d}}t}&= \alpha _u I_u+ \alpha _n I_n - \mu _c V\\&< (\alpha _u+ \alpha _n)\frac{\Pi }{\mu }- \mu _c V \end{aligned}$$

Again, using the results of differential inequality, we have

$$\begin{aligned} \limsup _{t\rightarrow \infty }V(t)<\frac{\Pi (\alpha _u+ \alpha _n)}{\mu \mu _c}. \end{aligned}$$

This completes the proof. \(\square \)

3.2 Disease-free equilibrium and basic reproduction number

As of many epidemiological models, our model (1) also exhibits the disease-free equilibrium (DFE). At this equilibrium, the population persists in the absence of disease. Mathematically, DFE is obtained by assuming all the infected compartments to be zero, i.e., \(E, I_u, I_n, I_h\), and V to be zero. Then from the model, \(S=\frac{\Pi }{\mu }\) and \(R=0\). Thus, the DFE is given by \({\mathscr {E}}_s=(\frac{\Pi }{\mu },0,0,0,0,0,0)\).

The basic reproduction number \({\mathscr {R}}_0\) is interpreted as the average number of secondary cases produced by one infected individual introduced into a population of susceptible individuals. This dimensionless number is a measure of the potential for disease outbreaks. Now to obtain \({\mathscr {R}}_0\), we use next-generation operator method [9, 43].

First we assemble the compartments which are infected (i.e., E, \(I_u\), \(I_n\), \(I_h\), and V) and decomposing the right hand side of the system (1) as \({\mathscr {F}}-{\mathscr {W}}\), where \({\mathscr {F}}\) is the transmission part, expressing the production of new infection, and the transition part is \({\mathscr {W}}\), which describe the rate of transfer of individuals from one compartment to another. Then we have for the model (1)

$$\begin{aligned} {\mathscr {F}}= & {} \begin{pmatrix} \frac{\beta _1 S( I_u+ \nu I_n)}{N}+ \beta _2 SV\\ 0\\ 0\\ 0\\ 0 \end{pmatrix}\quad \text {and}\quad \\ {\mathscr {W}}= & {} \begin{pmatrix} (\gamma + \mu ) E \\ -(1-p) \gamma E+\phi _uI_u \\ -p\gamma E+\phi _n I_n \\ -\eta _u I_u- \eta _n I_n +\phi _hI_h \\ -\alpha _u I_u-\alpha _n I_n+ \mu _c V \end{pmatrix}, \end{aligned}$$

with \(\phi _u=\eta _u+\sigma _u+\mu \), \(\phi _n=\eta _n+\sigma _n+\mu +\delta _n\), and \(\phi _h=\sigma _h+\mu +\delta _h\).

Consider \(X=(E, I_u, I_n, I_h, V)\). Then the derivatives of \({\mathscr {F}}\) and \({\mathscr {W}}\) at the DFE \({\mathscr {E}}_s\) are given by

$$\begin{aligned} F= & {} \frac{{\partial }{\mathscr {F}}}{{\partial }X}=\begin{pmatrix} 0 &{} \beta _1 &{} \beta _1\nu &{} 0 &{}\frac{\beta _2\Pi }{\mu }\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix}\quad \text {and}\quad \\ W= & {} \frac{{\partial }{\mathscr {W}}}{{\partial }X}=\begin{pmatrix} (\gamma + \mu ) &{} 0 &{} 0 &{} 0 &{} 0\\ -(1-p) \gamma &{} \phi _u &{} 0 &{} 0 &{} 0\\ -p\gamma &{} 0 &{} \phi _n &{} 0 &{} 0 \\ 0 &{} -\eta _u &{} -\eta _n &{}\phi _h&{} 0\\ 0 &{} -\alpha _u &{} -\alpha _n &{} 0 &{}\mu _c \end{pmatrix}. \end{aligned}$$

Now, we calculate the next-generation matrix \(FW^{-1}\), whose (i, j)-th entry describes the expected number of new infections in compartment i produced by the infected individual originally introduced into compartment j. According to Diekmann et al. [9], the basic reproduction number is given by \({\mathscr {R}}_0=\rho (FW^{-1})\), where \(\rho \) is the spectral radius of the next-generation matrix \(FW^{-1}\). A simple calculation leads to the following expression for \({\mathscr {R}}_0\):

$$\begin{aligned} {\mathscr {R}}_0= & {} \frac{(1-p)\gamma \beta _1}{\phi _u( \gamma +\mu )}+\frac{p\gamma \nu \beta _1}{\phi _n( \gamma +\mu )}+\frac{(1-p)\gamma \alpha _u\beta _2(\Pi /\mu )}{\mu _c \phi _u( \gamma +\mu )}\nonumber \\&+\frac{p\gamma \alpha _n\beta _2(\Pi /\mu )}{\mu _c\phi _n( \gamma +\mu )}. \end{aligned}$$
(3)

Epidemiologically, the first and second terms of \({\mathscr {R}}_0\) can be interpreted as the number of secondary infections that one un-notified and notified individual will produce in a completely susceptible population during its infectious period, respectively. Here, the infection occurs due to direct contact. Also, the last two terms represent the same but for free virus contact. Thus, both transmission pathways have impacts on the dynamics of COVID-19 spread in the community.

3.3 Stability of disease-free equilibrium

Following theorem gives the local stability properties of the DFE \({\mathscr {E}}_s=(\frac{\Pi }{\mu },0,0,0,0,0,0)\).

Theorem 2

The disease-free equilibrium (DFE) \({\mathscr {E}}_s=(\frac{\Pi }{\mu },0,0,0,0,0,0)\) of the system (1) is locally asymptotically stable if \({\mathscr {R}}_0<1\) and unstable if \({\mathscr {R}}_0>1\).

Proof

The Jacobian matrix at the DFE \({\mathscr {E}}_s\) is given by

$$\begin{aligned} J_{{\mathscr {E}}_s}= \left[ \begin{array}{ccccccc} -\mu &{} 0 &{}-\beta _1 &{}-\nu \beta _1 &{} 0 &{} \theta &{} -\frac{\Pi \beta _2}{\mu }\\ 0 &{} -(\gamma +\mu )&{} \beta _1 &{} \nu \beta _1 &{} 0 &{} 0 &{} \frac{\Pi \beta _2}{\mu }\\ 0 &{} (1-p)\gamma &{}-\phi _u &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} p\gamma &{} 0 &{} -\phi _n &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{}\eta _u &{} \eta _n &{}-\phi _h &{} 0 &{} 0\\ 0 &{} 0 &{}\sigma _u &{}\sigma _n &{}\sigma _h &{}-(\theta +\mu ) &{} 0 \\ 0 &{}0 &{}\alpha _u &{}\alpha _n &{} 0 &{}0 &{}-\mu _c \end{array} \right] ,\nonumber \\ \end{aligned}$$
(4)

with \(\phi _u=\eta _u+\sigma _u+\mu \), \(\phi _n=\eta _n+\sigma _n+\mu +\delta _n\), and \(\phi _h=\eta _h+\mu +\delta _h\).

The above Jacobian matrix possess three obvious eigenvalues \(-\mu \), \(-(\theta +\mu )\) and \(-\phi _h=-(\sigma _h+\mu +\delta _h)\), which are all negative. Also, the remaining eigenvalues (\(\lambda \)) are the roots of the equation \(\det (M-\lambda I)=0\), where I is the \(4\times 4\) identity matrix and

$$\begin{aligned} M= \left[ \begin{array}{ccccccc} -(\gamma +\mu ) &{} \beta _1 &{} \nu \beta _1 &{} \frac{\Pi \beta _2}{\mu } \\ (1-p)\gamma &{}-\phi _u &{} 0 &{} 0 \\ p\gamma &{} 0 &{} -\phi _n &{} 0 \\ 0 &{}\alpha _u &{} \alpha _n &{}-\mu _c \\ \end{array} \right] . \end{aligned}$$

Now, \(\det (M-\lambda I)=0\) gives

$$\begin{aligned}&(\lambda +\mu _c)(\lambda +\phi _n)(\lambda +\phi _u)(\lambda +\gamma +\mu )\\&\quad -(1-p)\gamma \beta _1(\lambda +\mu _c)(\lambda +\phi _n)\\&\quad -p\gamma \nu \beta _1(\lambda +\mu _c)(\lambda +\phi _u)\\&\quad -(1-p)\gamma \alpha _u\frac{\Pi \beta _2}{\mu }(\lambda +\phi _n)-\frac{\Pi \beta _2}{\mu }p\gamma \alpha _n(\lambda +\phi _u)=0. \end{aligned}$$

The above equation can be written as \(H(\lambda )=1\), where

$$\begin{aligned} \begin{aligned} H(\lambda )=&\frac{(1-p)\gamma \beta _1}{(\lambda +\phi _u)(\lambda +\gamma +\mu )}+\frac{p\gamma \nu \beta _1}{(\lambda +\phi _n)(\lambda +\gamma +\mu )}\\&+\frac{(1-p)\gamma \alpha _u\beta _2(\Pi /\mu )}{(\lambda +\mu _c)(\lambda +\phi _u)(\lambda +\gamma +\mu )}\\&+\frac{p\gamma \alpha _n\beta _2(\Pi /\mu )}{(\lambda +\mu _c)(\lambda +\phi _n)(\lambda +\gamma +\mu )}. \end{aligned} \end{aligned}$$
(5)

We also rewrite \(H(\lambda )\) as

$$\begin{aligned} H(\lambda )=H_1(\lambda )+H_2(\lambda )+H_3(\lambda )+H_4(\lambda ), \end{aligned}$$

where \(H_j(\lambda )\), \(j=1,2,3,4\), are the respective term of (5). Now, if \(Re(\lambda )\ge 0\) with \(\lambda =x+iy\), then

$$\begin{aligned} |H_1(\lambda )|=\frac{(1-p)\gamma \beta _1}{|\lambda +\phi _u||\lambda +\gamma +\mu |}\le H_1(x)\le H_1(0). \end{aligned}$$

Analogously,

$$\begin{aligned} |H_j(\lambda )|\le H_j(x)\le H_j(0),\quad \text {for}~j=2,3,4. \end{aligned}$$

Then

$$\begin{aligned} |H(\lambda )|\le&|H_1(\lambda )|+|H_2(\lambda )|+|H_3(\lambda )|+|H_4(\lambda )|\\ \le&H_1(0)+H_2(0)+H_3(0)+H_4(0)\\ =&H(0). \end{aligned}$$

From (3) and (5), we have \(H(0)={\mathscr {R}}_0\). Then \({\mathscr {R}}_0<1\) \(\implies \) \(|H(\lambda )|<1\), which implies there does not exist any solutions of \(H(\lambda )= 1\) with \(Re(\lambda )\ge 0\).

Therefore if \({\mathscr {R}}_0<1\), all the eigenvalues of \(H(\lambda )= 1\) have negative real parts and hence the DFE \({\mathscr {E}}_s\) of the system (1) is locally asymptotically stable.

Now for the case of \({\mathscr {R}}_0>1\), i.e., \(H(0)>1\)

$$\begin{aligned} \lim _{\lambda \rightarrow \infty }H(\lambda )=0. \end{aligned}$$

Then there exists \(\lambda ^*>0\) such that \(H(\lambda ^*)=1\), which confirm the existence of positive eigenvalue of the Jacobian matrix \(J_{{\mathscr {E}}_s}\). Thus the DFE \({\mathscr {E}}_s\) is unstable for \({\mathscr {R}}_0>1\). \(\square \)

Moreover, when \({\mathscr {R}}_0<1\) the DFE \({\mathscr {E}}_s\) is globally asymptotically stable, which can be assured by the following theorem.

Theorem 3

The disease-free equilibrium (DFE) \({\mathscr {E}}_s=(\frac{\Pi }{\mu },0,0,0,0,0,0)\) of the system (1) is globally asymptotically stable if \({\mathscr {R}}_0<1\).

Proof

First we rewrite the model (1) into the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{lll} \displaystyle {\frac{{\mathrm{d}}{\mathbb {X}}}{{\mathrm{d}}t}} &{}=&{} P({\mathbb {X}},{\mathbb {Z}}), \\ \displaystyle {\frac{{\mathrm{d}}{\mathbb {Z}}}{{\mathrm{d}}t}} &{}=&{} Q({\mathbb {X}},{\mathbb {Z}}) \end{array} \end{array}\right. } \end{aligned}$$
(6)

where \({\mathbb {X}}^\mathrm{{T}}=(S,R)\in {\mathbb {R}}^2_+\) with \(S>0\), describe the uninfected compartments and \({\mathbb {Z}}^\mathrm{{T}}=(E,I_u,I_n,I_h,V)\in {\mathbb {R}}^5_+\) describe the infected compartments with free virus. Also, T denoting the transpose of the matrix. Note that \(Q({\mathbb {X}},{\mathbf {0}})={\mathbf {0}}\), where \({\mathbf {0}}\) is a zero vector.

Following Castillo-Chavez et al. [4], the DFE \({\mathscr {E}}_s\) of the system (6) is globally asymptotically stable if it is locally asymptotically stable and satisfy following two conditions:

  1. (H1)

    For the subsystem \(\frac{{\mathrm{d}}{\mathbb {X}}}{{\mathrm{d}}t}=P({\mathbb {X}},{\mathbf {0}})\), the equilibrium \({\mathbb {X}}^*\) is globally asymptotically stable,

  2. (H2)

    \(Q({\mathbb {X}},{\mathbb {Z}})=B{\mathbb {Z}}-{\widetilde{Q}}({\mathbb {X}},{\mathbb {Z}})\), \({\widetilde{Q}}({\mathbb {X}},{\mathbb {Z}})\ge 0\) for \(({\mathbb {X}},{\mathbb {Z}})\in \Omega \),

where \(B=\frac{\partial Q}{\partial {\mathbb {Z}}}{\bigg |}_{({\mathbb {X}},{\mathbf {Z}})=({\mathbb {X}}^*,{\mathbf {0}})}\) is a Metzler matrix (a matrix whose off diagonal elements are nonnegative) and \(\Omega \) is the positive invariant set for the model (1) as described in Sect. 3.1.

Now, for the model (1),

$$\begin{aligned} P({\mathbb {X}},{\mathbf {0}})= \begin{pmatrix} \Pi -\mu S\\ 0 \end{pmatrix}. \end{aligned}$$

Since all the infected compartments are zero, so there is no infection, and thus, no recovery. For this reason, we consider \(R=0\). Clearly, \({\mathbb {X}}^*=(\frac{\Pi }{\mu },0)\) is a globally asymptotically equilibrium for the system \(\frac{{\mathrm{d}}{\mathbb {X}}}{{\mathrm{d}}t}=P({\mathbb {X}},{\mathbf {0}})\). So the condition (H1) is satisfied. Now,

$$\begin{aligned} B= & {} \begin{pmatrix} -(\gamma +\mu ) &{} \beta _1 &{} \beta _1\nu &{} 0 &{} \frac{\beta _2\Pi }{\mu }\\ (1-p)\gamma &{} -\phi _u &{} 0 &{} 0 &{} 0\\ p\gamma &{} 0 &{} -\phi _n &{} 0 &{} 0\\ 0 &{} \eta _u &{} \eta _n &{} -\phi _h &{} 0\\ 0 &{} \alpha _u &{} \alpha _n &{} 0 &{} -\mu _c\\ \end{pmatrix}\quad \text {and} \\ {\widetilde{Q}}({\mathbb {X}},{\mathbb {Z}})= & {} \begin{pmatrix} \beta _1\left( 1-\frac{S}{N}\right) I_u+\beta _1\nu \left( 1-\frac{S}{N}\right) I_n +\beta _2\left( \frac{\Pi }{\mu }-S\right) V\\ 0\\ 0\\ 0\\ 0 \end{pmatrix}, \end{aligned}$$

with \(\phi _u=\eta _u+\sigma _u+\mu \), \(\phi _n=\eta _n+\sigma _n+\mu +\delta _n\), and \(\phi _h=\eta _h+\mu +\delta _h\).

The matrix B is a Metzler matrix and \({\widetilde{Q}}({\mathbb {X}},{\mathbb {Z}})\ge 0\) whenever the state variables are inside the invariant set \(\Omega \). Thus (H2) is also satisfied. This completes the proof. \(\square \)

3.4 Existence of endemic equilibrium

Here, we discuss the existence of endemic equilibrium of the model (1). The endemic equilibrium \({\mathscr {E}}^*=(S^*,E^*,I_u^*,I_n^*,I_h^*,R^*,V^*)\) is given by \(I_u^*=A_1E^*\), \(I_n=A_2E^*\), \(I_h^*=A_3E^*\), \(R=A_4E^*\), \(V^*=A_5E^*\), \(S^*=\frac{\Pi +(\theta A_4-(\gamma +\mu ))E^*}{\mu }=\frac{(\gamma +\mu )(\Pi -A_7E^*)}{A_6+\beta _2A_5(\Pi -A_7E^*)}\), where all the \(A_i\), \(i=1,2,\ldots ,7\), are positive and given by

$$\begin{aligned}&A_1=\frac{(1-p)\gamma }{\eta _u+\sigma _u+\mu },\; \quad A_2\quad =\frac{p\gamma }{\eta _n+\sigma _n+\mu +\delta _n},\\&A_3\quad =\frac{\eta _u A_1+\eta _n A_2}{\sigma _h+\mu +\delta _h},\\&A_4=\frac{\sigma _u A_1+\sigma _n A_2+\sigma _h A_3}{\theta +\mu },\;\quad A_5\quad =\frac{\alpha _u A_1+\alpha _n A_2}{\mu _c},\\&A_6\quad =\mu \beta _1(A_1+\nu A_2),\;\\&A_7=\delta _n A_2+\delta _h A_3, \end{aligned}$$

and \(E^*\) is a positive root of the quadratic equation

$$\begin{aligned} \rho _0E^2+\rho _1E+\rho _2=0 \end{aligned}$$
(7)

with

$$\begin{aligned} \rho _0&=-\beta _2 A_5 A_7(\theta A_4-(\gamma +\mu )),\\ \rho _1&=(A_6+\beta _2 A_5 \Pi )(\theta A_4-(\gamma +\mu ))-\beta _2 A_5 A_7\Pi \\&\quad +\mu (\gamma +\mu )A_7\\&=\mu (\gamma +\mu ){\mathscr {R}}_0(\theta A_4-(\gamma +\mu ))+\mu (\gamma +\mu )(1-{\mathscr {R}}_0)A_7\\&\quad +A_6A_7,\\ \rho _2&=(A_6+\beta _2 A_5 \Pi )\Pi -\mu (\gamma +\mu )\Pi =\mu (\gamma +\mu )\Pi ({\mathscr {R}}_0-1). \end{aligned}$$

For the existence of real roots of (7), we must have \(\rho _1^2-4\rho _0\rho _2\ge 0\). Without loss of generality, assume that \(E_1^*>E_2^*\), when Eq. (7) have two real roots. From the expression of \(S^*\), \(S^*=\frac{\Pi }{\mu }+\frac{(\theta A_4-(\gamma +\mu ))}{\mu }E^*\). Since the upper bound of total population is \(\Pi /\mu \), so we must have \(\theta A_4-(\gamma +\mu )< 0\). Then \(\rho _0\) is always positive. Note that, for \(\theta A_4-(\gamma +\mu )= 0\), \(S^*=\frac{\Pi }{\mu }\) and thus the endemic equilibrium becomes DFE. Also, \(\rho _2<(>)0\iff {\mathscr {R}}_0<(>)1\). At the equilibrium density, \(N^*=\frac{\Pi -A_7E^*}{\mu }\). Thus, \(N^*>0\iff \Pi -A_7E^*>0\). Keeping all the conditions in mind, in the next theorem, we state the existence and the possible number of endemic equilibrium points.

Theorem 4

When \({\mathscr {R}}_0<1\), the model (1) has unique endemic equilibrium if \(\Pi -A_7E^*>0\). When \({\mathscr {R}}_0>1\), the model (1) has

  1. 1.

    two endemic equilibrium if \(\rho _1<0\), \(\rho _1^2-4\rho _0\rho _2>0\), and \(\Pi -A_7E_i^*>0\), \(i=1,2\).

  2. 2.

    unique endemic equilibrium if any of the following cases holds

    1. (a)

      \(\rho _1<0\), \(\rho _1^2-4\rho _0\rho _2>0\), and \(E_1^*>\frac{\Pi }{A_7}>E_2^*\),

    2. (b)

      \(\rho _1<0\), \(\rho _1^2-4\rho _0\rho _2=0\), \(\Pi -A_7E^*>0\),

  3. 3.

    no endemic equilibrium otherwise.

3.5 Analysis of the center manifold near DFE \({\mathscr {E}}_s\) when \({\mathscr {R}}_0=1\)

In this subsection, we discuss the nature of DFE \({\mathscr {E}}_s\) when \({\mathscr {R}}_0=1\). Recall the Jacobian matrix \(J_{{\mathscr {E}}_s}\) from (4). Notice that, when \({\mathscr {R}}_0=1\), \(J_{{\mathscr {E}}_s}\) possess a zero eigenvalue. So the equilibrium \({\mathscr {E}}_s\) becomes non-hyperbolic. Then the center manifold theory is the best approach to study the behaviour of this equilibrium. In this regard, we follow Theorem 4.1 described in Castillo-Chavez and Song [5].

To proceed, first we write the mathematical model (1) into the vector form \(\frac{{\mathrm{d}}{\mathbf {x}}}{{\mathrm{d}}t}=f({\mathbf {x}})\), with \({\mathbf {x}}=(x_1,~ x_2,~ x_3,~ x_4,~ x_5,~ x_6,~ x_7)^\mathrm{{T}}=(S,~E,~I_u,~I_n,~I_h,~R, V)^\mathrm{{T}}\) and \(f({\mathbf {x}})=(f_1({\mathbf {x}}), ~f_2({\mathbf {x}}),~ \ldots ,~ f_7({\mathbf {x}}))^\mathrm{{T}}\). Since \({\mathscr {R}}_0\) is often inconvenient to use directly as a bifurcation parameter, we introduce \(\beta _1\) as a bifurcation parameter. Then \({\mathscr {R}}_0=1\) gives

$$\begin{aligned} \beta _1= & {} \frac{\mu _c (\gamma +\mu )\phi _u \phi _n -\gamma \beta _2(\Pi /\mu )((1-p)\alpha _u\phi _n+p\alpha _n\phi _u)}{\mu _c \gamma ((1-p)\phi _n+\nu p\phi _u)}\\= & {} \beta _1^* ~~(\text {say}). \end{aligned}$$

Moreover, \({\mathscr {R}}_0<1\) for \(\beta _1<\beta _1^*\) and \({\mathscr {R}}_0>1\) for \(\beta _1>\beta _1^*\). Now, consider the system \(\frac{{\mathrm{d}}{\mathbf {x}}}{{\mathrm{d}}t}=f({\mathbf {x}},\beta _1)\) and at \(\beta _1=\beta _1^*\) the Jacobian matrix \(J_{{\mathscr {E}}_s}\) have simple zero eigenvalue and all the other eigenvalues have negative real parts. Let \({\mathbf {v}}=(v_1,~ v_2,~ \ldots ~, v_7)\) and \({\mathbf {w}}=(w_1,~ w_2,~ \ldots ~, w_7)^\mathrm{{T}}\) are the respective left and right eigenvectors corresponding to zero eigenvalue. Simple algebraic calculations lead us to the following expressions of \(v_i\) and \(w_i\), \(i=1,2,\ldots , 7\):

$$\begin{aligned}&v_1=0=v_5=v_6, \quad v_2=v_2>0,\\&v_3=\frac{1}{\phi _u}\left( \beta _1^*+\frac{\beta _2\alpha _u\Pi }{\mu \mu _c}\right) v_2,\\ v_4&=\frac{1}{\phi _n}\left( \beta _1^*\nu +\frac{\beta _2\alpha _n\Pi }{\mu \mu _c}\right) v_2,\\&v_7=\frac{\beta _2\Pi }{\mu \mu _c}v_2, \end{aligned}$$

and

$$\begin{aligned} w_1&=\frac{1}{\mu }\left[ \frac{\theta }{\theta +\mu }\left\{ \frac{(1-p)\gamma }{\phi _u}\left( \sigma _u+\frac{\sigma _h\eta _u}{\phi _h}\right) \right. \right. \\&\quad \left. \left. +\frac{p\gamma }{\phi _n}\left( \sigma _n+\frac{\sigma _h\eta _n}{\phi _h}\right) \right\} -(\gamma +\mu )\right] w_2,\\ w_2&=w_2>0,\quad w_3=\frac{(1-p)\gamma }{\phi _u}w_2,\quad w_4=\frac{p\gamma }{\phi _n}w_2,\\ w_5&=\frac{1}{\phi _h}\left( \frac{(1-p)\gamma \eta _u}{\phi _u}+\frac{p\gamma \eta _n}{\phi _n}\right) w_2,\\ w_6&=\frac{1}{\theta +\mu }\left[ \frac{(1-p)\gamma }{\phi _u}\left( \sigma _u+\frac{\sigma _h\eta _u}{\phi _h}\right) \right. \\&\quad \left. +\frac{p\gamma }{\phi _n}\left( \sigma _n+\frac{\sigma _h\eta _n}{\phi _h}\right) \right] w_2,\\ w_7&=\frac{1}{\mu _c}\left( \frac{(1-p)\gamma \alpha _u}{\phi _u}+\frac{p\gamma \alpha _n}{\phi _n}\right) w_2. \end{aligned}$$

Clearly, all the \(v_i\) and \(w_i\) (\(i=1,2,\ldots ,7\)) are positive except \(w_1\). From the expression of \(w_1\), note that \(w_1=\frac{1}{\mu }(\theta A_4-(\gamma +\mu ))w_2\). Also, since \(\theta A_4-(\gamma +\mu )<0\), so \(w_1<0\). Now, according to the Theorem 4.1 [5], we calculate the quantities a and b, which are defined by

$$\begin{aligned} a&=\sum _{k,i,j=1}^{7}v_kw_iw_j\frac{\partial ^2 f_k}{\partial x_i \partial x_j}, \end{aligned}$$
(8)
$$\begin{aligned} b&=\sum _{k,i=1}^{7}v_kw_i\frac{\partial ^2 f_k}{\partial x_i \partial \beta _1}, \end{aligned}$$
(9)

where all the partial derivatives are evaluated at the DFE \({\mathscr {E}}_s\) and \(\beta _1=\beta _1^*\). Since \(v_1\) is zero and \(f_k\), \(k=3,4,\ldots 7\) are linear functions of the state variables, so we need to calculate only \(\frac{\partial ^2 f_2}{\partial x_i \partial x_j}\). Then we have

$$\begin{aligned}&\frac{\partial ^2 f_2}{\partial x_1 \partial x_7}=\beta _2, \quad \frac{\partial ^2 f_2}{\partial x_2 \partial x_3}=-\frac{\beta _1^*\mu }{\Pi }=\frac{\partial ^2 f_2}{\partial x_3 \partial x_5}=\frac{\partial ^2 f_2}{\partial x_3 \partial x_6},\\&\frac{\partial ^2 f_2}{\partial x_3 \partial x_4}=-\frac{\beta _1^*\mu (1+\nu )}{\Pi },\\&\frac{\partial ^2 f_2}{\partial x_3^2}=-\frac{2\beta _1^*\mu }{\Pi },\quad \frac{\partial ^2 f_2}{\partial x_2 \partial x_4}=-\frac{\beta _1^*\mu \nu }{\Pi }=\frac{\partial ^2 f_2}{\partial x_4 \partial x_5}=\frac{\partial ^2 f_2}{\partial x_4 \partial x_6}, \\&\frac{\partial ^2 f_2}{\partial x_4^2}=-\frac{2\beta _1^*\mu \nu }{\Pi }, \end{aligned}$$

and the rest of the derivatives are zero. Thus from (8), we have

$$\begin{aligned} a= & {} v_2\left[ \beta _2w_1w_7-\frac{\beta _1^*\mu }{\Pi }\left\{ w_3(w_2+2w_3+w_4+w_5+w_6)\right. \right. \\&\left. \left. +\nu w_4(w_2+w_3+2w_4+w_5+w_6)\right\} \right] . \end{aligned}$$

Again, since \(v_1\) is zero and \(\frac{\partial ^2 f_k}{\partial x_i \partial \beta _1}=0\) for \(k=3,4,\ldots ,7\), then from (9) we have

$$\begin{aligned} b=v_2\left[ w_3\frac{\partial ^2 f_2}{\partial x_3 \partial \beta _1}+w_4\frac{\partial ^2 f_2}{\partial x_4 \partial \beta _1}\right] =v_2(w_3+\nu w_4)>0. \end{aligned}$$

Since \(w_1<0\), so \(a<0\). Hence, for the system (1), \(a<0\) and \(b>0\). Thus the system exhibit forward bifurcation at \(\beta _1=\beta _1^*\), and an endemic equilibrium appears which is locally asymptotically stable.

We numerically verify the existence of forward bifurcation with respect to the basic reproduction number \({\mathscr {R}}_0\). Since \({\mathscr {R}}_0\) is not a model parameter and it depends on \(\beta _1\), so we vary \(\beta _1\). When \({\mathscr {R}}_0\) crosses the threshold value 1, the system transits from the stable DFE to the stable endemic equilibrium and the DFE becomes unstable (Fig. 2). In the figure, the blue-coloured line depicts the stable DFE and the red curve depicts the stable endemic equilibrium.

Fig. 2
figure 2

Forward bifurcation of the system (1) with respect to the basic reproduction number \({\mathscr {R}}_0\). The parameter values are taken as \(\Pi =496.68615\), \(\beta _2=6.6248\times 10^{-8}\), \(\eta _u=0.0223\), \(\eta _n = 0.7846\), \(\sigma _h= 0.9181\), \(\delta _h = 0.0046\), \(\alpha _u = 1.3232\times 10^{-6}\), \(\alpha _n = 0.0741\) and the other parameter values are same as Table 1

Full size image

We also draw the time series plot by choosing two different values of \(\beta _1\). For \(\beta _1=0.15\), \({\mathscr {R}}_0<1\) and all the infected compartments (un-notified, notified and hospitalized) becomes zero and for \(\beta _1=0.3\), \({\mathscr {R}}_0>1\) and infected compartments persists in a stable manner as time evolves (Fig. 3).

Fig. 3
figure 3

Time series evaluation of infected compartments for the system (1). In A–C, \(\beta _1=0.15\) where \({\mathscr {R}}_0<1\), and for D–F, \(\beta _1=0.3\) where \({\mathscr {R}}_0>1\). The other parameter values are same as Fig. 2

Full size image

4 Model calibration

Daily new deaths between the period 16 January 2021 (start date of vaccination in India) to 31 October 2021 for the districts Bangalore Urban and Chennai are used to calibrate the model. The rationale behind using mortality data is that this data is more reliable than the incidence data due to limited testing capacities [20, 30]. We fit the model output (\(\int _{t=1}^{T} [\delta _n I_n + \delta _h I_h] dt\), where T=289) to daily new deaths and cumulative deaths due to COVID-19 for both districts. Fixed parameters and initial conditions of the model (1) are given in Tables 1 and 2, respectively. Eight unknown model parameters are estimated, namely \(\beta _1\), \(\beta _2\), \(\nu _u\), \(\nu _h\), \(\sigma _h\), \(\delta _h\), \(\alpha _u\) and \(\alpha _n\). In addition, the initial number of exposed people E(0) is also estimated from the mortality data. During the specified time period, nonlinear least square solver lsqnonlin (in MATLAB) is used to fit simulated daily mortality data to the reported COVID-19 deaths in Bangalore urban and Chennai districts. MATLAB codes for generating the fitting figures for Chennai have been uploaded to the GitHub repository https://github.com/indrajitg-r/ODE_model_fitting. The fitting of the daily new deaths and cumulative deaths due to COVID-19 are displayed in Figs. 4 and 5 for Bangalore urban and Chennai, respectively.

Table 2 Initial conditions used to simulate the model (1) in Bangalore urban and Chennai
Full size table
Fig. 4
figure 4

Fitting model solution to A new deaths and B cumulative death data due to COVID-19 in Bangalore urban district

Full size image

From Fig. 4, it can be argued that the model output fits the mortality data well. Estimated parameter values for Bangalore urban are as follows: \(\beta _1=0.2277\), \(\beta _2=4.5394 \times 10^{-6}\), \(\eta _u =0.0104\), \(\eta _n =0.3908\), \(\sigma _h =0.7564\), \(\delta _h =0.0028\), \(\alpha _u =0.0055\), \(\alpha _n = 4.8891 \times 10^{-6}\) and \(E(0)= 121\). The data trend is well captured by the model output as seen in Fig. 5. Estimated parameter values for Chennai district data are as follows: \(\beta _1=0.1962\), \(\beta _2=6.4749 \times 10^{-6}\), \(\eta _u =2.4095 \times 10^{-7}\), \(\eta _n =0.9997\), \(\sigma _h =0.8244\), \(\delta _h =0.0019\), \(\alpha _u =0.0011\), \(\alpha _n = 0.0538\) and \(E(0)= 718\). Using these estimated parameters for both the districts, we investigate different control strategies.

Fig. 5
figure 5

Fitting model solution to A new deaths and B cumulative deaths data due to COVID-19 in Chennai district

Full size image

5 Control interventions and immigration of infectives

In this section, we investigate different control mechanisms and immigration of infectives through numerical simulation. We examine the effects of vaccination, treatment by drugs, and use of face masks with different degrees of efficacy.

5.1 Use of face mask

Although several vaccines are discovered and people are vaccinated in a rapid process, several drugs are in the trial stage and few of them are implemented for hospitalized patients, nevertheless, the use of face mask still could offer as a non-pharmaceutical intervention, to avoid transmission of direct contact and airborne transmission of free virus. In a densely populated country like India, it is almost impossible to determine how many people have come in contact with an infected person. Thus, wearing a face mask properly is an important control strategy for the current epidemic outbreak. The idea of using a face mask to combat respiratory infections in the community was not new [44]. Face masks reduce the amount of droplet inoculum discharging from infectious individuals by capturing a proportion of droplets within the mask [40, 44]. Face masks also reduce the amount of droplet inoculum inhaled by susceptible individuals by capturing a proportion of droplets in the inhaled air and hence reducing the airborne transmission rate. Let \(0\le c_m\le 1\) is the community-wide compliance in the face mask usage and \(0<\epsilon _m\le 1\) is the face mask efficiency for preventing the disease. Then the term \(1- c_m \epsilon _m\) describes a measure of reduction in community contacts and free virus contacts due to the use of face mask [30, 40]. Note that, \(0\le 1- c_m \epsilon _m\le 1\). We consider three different efficiency levels, depending on the material and layering of the face masks viz. N95 masks are 95% effective; Surgical masks are 55% effective and Multi-layered cloth masks are 38% effective [37]. Community-wide compliance in the face mask usage is chosen at three different levels namely, High 75%, Medium 50%, and low 25%. The baseline values for \(c_m\) and \(\epsilon _m\) are taken to be 10% and 0.1, respectively.

5.2 Treatment by drugs: faster recovery

In recent times, several drugs are developed for moderate to severe COVID-19 patients and some of them are in a different phase of the trial period. The 3rd phase trial of Soin et al. [39] in India predict that tocilizumab plus standard care in patients admitted to hospital with moderate to severe COVID-19 have a faster recovery and reduce the burden of intensive care. Recently, Institute of Nuclear Medicine and Allied Sciences (DRDO-INMAS) and Dr. Reddy’s laboratories, Hyderabad jointly developed a drug, 2-deoxy-d-glucose (2-DG) for emergency use in symptomatic COVID-19 patients [3, 33]. On 8th May 2021, the Drugs Controller General of India (DCGI) approved this drug [31]. As per the government release, clinical trial data shows that the drug helps in the recovery timelines of hospitalized patients and reduces supplemental oxygen dependence. Latterly, pfizer’s novel COVID-19 oral antiviral treatment candidate \(\hbox {PAXLOVID}^{TM}\) (PF-07321332; ritonavir) is showing significant reduction in deaths or hospitalization in high risk groups. Consider \(\epsilon _t\ge 1\) be the factor describing the faster recovery of hospitalized patients. Taking the base value of the \(\epsilon _t\) as 1, we vary this parameter up to 1.3 while evaluating control strategies.

5.3 Effect of vaccination

To control the ongoing global pandemic, vaccine is a critical tool as a pharmaceutical intervention. At present, Covaxin and Covishield vaccines are being used for the vaccination drive against COVID-19 in India and also, several vaccines are in trial process [38]. To extend our mathematical model under the effect of vaccination, we introduced a new compartment of population, namely protected (P(t)), those who are vaccinated. Now, the Susceptible and recovered populations both can progress to the protected population at rates \(\xi _s\) and \(\xi _r\), respectively, through vaccination. For simplicity, we consider that the protected population completed the required doses of vaccine (and also completed 14 days after the last dose) and thus does not consider any intermediate stage (i.e., the time gap between doses or before 14 days of the last dose). The base values for vaccination rates are chosen to be 0.00085 for both susceptibles and recovered people. This value is calculated from the vaccination data of India [7]. Simulations are performed by increasing the vaccination rates to 0.05 for both sub-populations.

5.4 Immigration of infectives

Communicable diseases like the current COVID-19 epidemic may be introduced into a community by the arrival of infectives outside the community. Indeed, in India, the first COVID-19 case was reported in Trissur, Kerala, on January 30, 2020, who was returned from Wuhan, China [2]. Thus, the immigration of infectives in a disease-free community played a crucial role for the spread of the disease. We extend the mathematical model (1) by assuming a constant flow of new members of an un-notified person. Recruitment of notified person was not considered as they are restricted for travelling. On the other hand, immigration is necessary for many people to maintain a livelihood. Thus, individuals from neighbouring locations must be allowed to immigrate for the well-being of the overall community. Let \(\Lambda \) be the recruitment rate of un-notified infected individuals through immigration. We consider three levels of immigration as low, medium, and high with \(\Lambda \) = 1, 5, and 10 respectively.

By considering the above control interventions and immigration of infectives, the model (1) can be extended to the following model:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{l} \displaystyle {\frac{{\mathrm{d}}S}{{\mathrm{d}}t}} = \Pi -\frac{\beta _1 (1- c_m \epsilon _m) S( I_u+ \nu I_n)}{N} - \beta _2 (1- c_m \epsilon _m) SV\\ \qquad \quad -(\mu + \xi _s) S + \theta R, \\ \displaystyle {\frac{{\mathrm{d}}E}{{\mathrm{d}}t}} = \frac{\beta _1 (1- c_m \epsilon _m) S( I_u+ \nu I_n)}{N} + \beta _2 (1- c_m \epsilon _m) SV - (\gamma + \mu ) E, \\ \displaystyle {\frac{{\mathrm{d}}I_u}{{\mathrm{d}}t}} = \Lambda + (1-p) \gamma E - (\eta _u + \sigma _u +\mu )I_u, \\ \displaystyle {\frac{{\mathrm{d}}I_n}{{\mathrm{d}}t}} = p \gamma E-(\eta _n + \sigma _n + \mu + \delta _n) I_n, \\ \displaystyle {\frac{{\mathrm{d}}I_h}{{\mathrm{d}}t}} = \eta _u I_u+ \eta _n I_n - ( \epsilon _t \sigma _h + \mu + \delta _h)I_h, \\ \displaystyle {\frac{{\mathrm{d}}R}{{\mathrm{d}}t}} = \sigma _u I_u+\sigma _n I_n + \epsilon _t \sigma _h I_h - (\theta + \mu +\xi _r)R, \\ \displaystyle {\frac{{\mathrm{d}}P}{{\mathrm{d}}t}} = \xi _s S + \xi _r R - \mu P, \\ \displaystyle {\frac{{\mathrm{d}}V}{{\mathrm{d}}t}} =\alpha _u I_u+ \alpha _n I_n - \mu _c V. \end{array} \end{array}\right. } \end{aligned}$$
(10)
Table 3 Percentage reduction in the total number of notified and hospitalized COVID-19 patients for different levels of interventions
Full size table

Intensive numerical simulations are performed to quantify the effects of various strategies in the Bangalore urban and Chennai districts. The fixed parameters and initial conditions are taken from Tables 1 and  2, respectively. The initial number of protected/vaccinated people is estimated using vaccination coverage data from both the districts [7]. Estimated parameters for both districts are mentioned in the model calibration section. Using these parameters and control parameters at various levels we simulate the model (10) with 3 months ahead of projections.

For both the districts, the projection period is 1 November 2021 to 31 January 2022. To quantify the effects of single control strategies more precisely, we calculate the percentage reduction of notified and hospitalized persons in the 3 month projection period. We use the following basic formula

$$\begin{aligned}&Percentage reduction \nonumber \\&\quad =\frac{Baseline cases - Cases with control }{Baseline cases }\times 100. \end{aligned}$$
(11)

The percentage reduction in notified and hospitalized cases are reported in Table 3 for Bangalore urban and Chennai districts. We can see that the face mask-related controls when applied individually have a moderate impact on the notified and hospitalized populations of both locations. On the other hand, treatment of hospitalized population has a large positive impact on the percentage reduction of hospitalized patients. However, treatment does not show any impact on the notified patients for both the locations. This might be due to the fact that the hospitalized patients are not responsible for new infections directly. Comparing the vaccination rates of susceptible and recovered people, it can be inferred from the table that vaccinating susceptibles has a better impact than that of recovered people. At least in the short-term (3 months) scenario, it is beneficial to vaccinate susceptible people than to vaccinate recovered people. Furthermore, while evaluating the effects of immigration, we noticed that a high level of immigration has a significant negative impact on the percentage reduction. Thus, the immigration of un-notified COVID-19 patients has to be as low as possible. This can be done by allowing people from low incidence neighbour districts and restricting immigration from highly affected areas. From the single control results, it is evident that pharmaceutical mitigation strategies like treatment of hospitalized patients and vaccination of susceptible individuals are most effective. Additionally, non-pharmaceutical measures such as face mask use have minimal effects on the reduction of notified and hospitalized COVID-19 cases.

To investigate the combined effects of control interventions, we examine four different combinations on the total number of hospitalized patients (\(I_h^\mathrm{{tot}}\)) in the 3-month projection period. The parameter values are taken as mentioned earlier in this section. We draw contour plots with respect to the control parameters with response variable \(I_h^\mathrm{{tot}}=\int _{t=289}^{381} I_h(t) \mathrm{{d}}t\). Contour plots depicting combination of interventions are displayed in Figs. 6 and 7 for Bangalore urban and Chennai districts, respectively.

Fig. 6
figure 6

Combination of control strategies and immigration of infectives in Bangalore urban. A efficacy of face mask usage—community-wide compliance in face mask usage (\(\epsilon _m-c_m\)), B increase in recovery rate of hospitalized patients—vaccination rate of susceptible individuals (\(\epsilon _t-\xi _s\)), C increase in recovery rate of hospitalized patients—immigration of infectives (\(\epsilon _t-\Lambda \)), D vaccination rate of susceptible individuals—immigration of infectives (\(\epsilon _s-\Lambda \))

Full size image

For both of the locations, similar scenarios are seen with varying control interventions and immigration of un-notified infectious patients. Simultaneously increasing face mask efficacy and population-wide compliance level will decrease \(I_h^\mathrm{{tot}}\) in the 3 month projection period (Figs. 6A, 7A). Thus, both the face mask-related parameters will have a stronger impact on the reduction of \(I_h^\mathrm{{tot}}\). On the other hand, the vaccination rate of susceptibles and increase in the treatment rate of hospitalized patients will have similar effects for both the locations (as seen in Figs. 6B, 7B). Further, the immigration of un-notified COVID-19 patients will obviously show an increase in \(I_h^\mathrm{{tot}}\). But, keeping \(\Lambda \) low and increasing treatment rate simultaneously will keep \(I_h^\mathrm{{tot}}\) under control (see Figs. 6C, 7C). From the number of \(I_h^{tot}\), it should be noted that this combination is risky if there is no other intervention in action. However, if the vaccination of susceptibles is performed at an increased rate, then the immigration may not have very adverse effects (see Fig. 6D and 7D). It can be noted that a high level of face mask use with maximum efficacy is more effective than the other combined strategies in terms of reduction in \(I_h^\mathrm{{tot}}\). But the feasibility of face mask usage in such intensity may be critical. From the contour plot analysis, it can be argued that the combination of \(\xi _s\) and \(\epsilon _t\) is more feasible and has competitive effects on \(I_h^\mathrm{{tot}}\). Further numerical simulations are necessary to study the combination of more than two control interventions and the immigration of un-notified infectives.

Fig. 7
figure 7

Combination of control strategies and immigration of infectives in Chennai. A efficacy of face mask usage—community-wide compliance in face mask usage (\(\epsilon _m-c_m\)), B increase in recovery rate of hospitalized patients—vaccination rate of susceptible individuals (\(\epsilon _t-\xi _s\)), C increase in recovery rate of hospitalized patients—immigration of infectives (\(\epsilon _t-\Lambda \)), D vaccination rate of susceptible individuals—immigration of infectives (\(\epsilon _s-\Lambda \))

Full size image

Three or more control interventions and the immigration of infectives are now applied to examine their combined impact on the COVID-19 cases in the 3 months projection period. We calculate the percentage reduction in notified COVID-19 patients and hospitalized COVID-19 patients using the formula (11). The fixed parameters and initial conditions are taken from Tables 1 and 2 . Four different combination strategies are investigated namely, strategy I: face mask efficacy-community level usage of face masks-vaccination of susceptibles (\(\epsilon _m\)–\(c_m\)–\(\xi _s\)), strategy II: face mask efficacy-community level usage of face masks-vaccination of susceptibles-increase in treatment rate (\(\epsilon _m\)–\(c_m\)–\(\xi _s\)–\(\epsilon _t\)), strategy III: face mask efficacy-community level usage of face masks-vaccination of susceptibles-increase in treatment rate-immigration of un-notified infectives (\(\epsilon _m\)–\(c_m\)–\(\xi _s\)-\(\epsilon _t\)–\(\Lambda \)) and strategy IV: combination of all control interventions with immigration of un-notified infectives (\(\epsilon _m\)–\(c_m\)–\(\xi _s\)–\(\epsilon _t\)–\(\Lambda \)-\(\xi _r\)). The parameter values are chosen for the feasibility of the strategies, i.e., we do not consider hypothetically high values of the parameters. The percentage reduction of \(I_n\) and \(I_h\) for Bangalore urban and Chennai are reported in Table 4.

Table 4 Percentage reduction in total number of notified and hospitalized COVID-19 patients for different strategies
Full size table

From the combinations of strategy I and strategy II, we observe that the second case of strategy II has most the positive reduction for both the districts. However, the travel restrictions are being eased and more people tend to come to these districts. Thus, the immigration of un-notified infectives is also evident and hence it is necessary to consider non-zero values of \(\Lambda \). It can be observed that strategy IV (first case) with specified control parameter values and low immigration has the most feasible results on both the locations (marked bold in Table 4). Alternatively, the second case of strategy II shows a similar case reduction in both the locations. This strategy does not include immigration and therefore is not feasible. It can be seen that the second case of strategy III also shows competitive results in terms of percentage reduction of both populations. This strategy is feasible and can be implemented with less effort by the policy makers.

6 Results and conclusions

An SEIR-type compartmental model for the transmission dynamics of COVID-19 outbreak incorporating free virus concentration of the environment is considered in this paper. The model assumes standard incidence function while COVID-19 transmission by un-notified and notified individuals. Mass action incidence is considered for the airborne transmission of the virus. The mathematical model consists of a seven-dimensional system of ordinary differential equations. The model is mathematically analysed to obtain insight into the long-term dynamic features of the disease. Basic properties of the model are studied by finding positivity and boundedness of the solutions when the initial conditions are taken non-negative for all the state variables. The disease-free equilibrium (DFE) of the model is found to be unique and the basic reproduction number is found using the next-generation matrix method. The model has a locally stable DFE whenever the basic reproduction number is less than unity otherwise the DFE becomes unstable. Moreover, the global stability of the DFE is guaranteed when \({\mathscr {R}}_0<1\). This can be inferred that COVID-19 will be mitigated from the community if the corresponding parameters are in the range to ensure \({\mathscr {R}}_0<1\). The existence of the endemic equilibrium is investigated and it is found that at most two endemic equilibria may exist for the system. Forward transcritical bifurcation is established both analytically and numerically between DFE and one of the endemic equilibrium (see Fig. 2). Further, it is numerically shown that all the infected compartments tend to vanish in the long run when \({\mathscr {R}}_0<1\) and approaches a non-zero equilibrium when \({\mathscr {R}}_0>1\) (shown in Fig. 3).

We calibrated the proposed model parameters to fit daily mortality data of two districts of India during the period of January \(16^{th}\), 2021 to October \(31^{st}\), 2021. From the fitting of the model output to mortality data, it can be seen that the model output closely anticipates the real data for both the districts. Afterwards we investigate the impacts of control strategies and immigration of un-notified persons on the number of hospitalized patients. We concentrate on both pharmaceutical and non-pharmaceutical control measures as they are being implemented simultaneously to combat the deadly disease. Two pharmaceutical measures namely, treatment of hospitalized persons and vaccination of susceptibles as well as recovered persons are considered. On the other hand, face mask efficacy and community-wide compliance of face masks are considered as non-pharmaceutical control measures. Along with these interventions, we also study the effect of immigrating un-notified persons from other communities. We calculated the percentage reduction in total hospitalized patients to get a quantitative idea of the control measures and immigration. It is found that treatment of hospitalized patients and vaccination of susceptible impacts has a significant impact on the reduction of hospitalized cases (see Table 3). Therefore, pharmaceutical measures are more reliable than non-pharmaceutical controls. Additionally, immigration of un-notified infected persons may drive the hospitalized cases to higher prevalence. It is noted that face mask-related controls have a lower impact than pharmaceutical measures like treatment and vaccination. The immigration of un-notified patients has a negative impact on the total hospitalized cases and thus this should be kept as low as possible. Low immigration of infectives can be maintained by restricting immigration from highly affected neighbouring districts. Further, we investigate the combined effect of two strategies on the total number of hospitalized patients for both districts. We found that the combination of treatment and vaccination of susceptible individuals will be very effective to reduce the disease. Finally, we compare three or more interventions by calculating the percentage reduction of notified and hospitalized patients with different levels of feasible control measures and immigration rates. We examine strategy I–strategy IV (as defined in the previous section) and find that the combination of all controls with low immigration will have the best effect on the reduction of the disease. However, the second case of strategy III also shows competitive results in terms of percentage reduction of both populations. This strategy differs from strategy IV by the vaccination of recovered people. Therefore, it can be concluded that when vaccine crisis is there, the public health authorities may not vaccinate the recovered people. In other words, the people who were tested COVID-19 positive in past and are now healthy (they may have developed natural antibodies against SARS-CoV-2) may be vaccinated later when vaccines are available. Low immigration of un-notified patients can be regulated by restricting the movement of people from high prevalence adjacent districts. This analysis can be made with data from other profoundly affected districts with proper parametrization.

In summary, the results indicate that vaccination of susceptible individuals and treatment of hospitalized patients are very crucial to control COVID-19 in the two locations. In the 3 months short-term period, vaccination of susceptible people should be prioritized over vaccination of recovered people for a better outcome. Whenever vaccine crisis is there, governments may avoid the vaccination of people who were tested COVID-19 positive and are now healthy. However, increased quality and quantity of mask use are also helpful. Along with face mask use, treatment of hospitalized patients, and vaccination of susceptibles, immigration should be allowed in a supervised manner so that economy of the overall society remains healthy.