Chiral solitons with W-shaped and other profiles in (1 + 2) dimensions

Abstract

In the present work, we investigate the dynamical behaviours of solitons in the quantum field theory. The medium is described by the chiral nonlinear Schrödinger equation in $(1+2)$-dimensions. The study is carried out by three integration methodologies including extended auxiliary equation method, functional variable method and Kudryashov method. Different types of soliton structures such as W-shaped, bright, dark and singular solitons are derived. The obtained results show that the W-type structure is transmitted to bright and dark solitons under specific conditions. The physical interpretations of soliton behaviours are presented so as to pave the way for likely engineering or industrial applications.

1 Introduction

Soliton has become one of the important wave solutions for nonlinear evolution equations. It has the ability to describe the physics of media in many fields of sciences such as fluid dynamics, plasma physics, nonlinear optics and many other fields [1,2,3,4,5]. Mostly, the dynamics of solitons are described by the model of nonlinear Schrödinger equation (NLSE) and its generalized forms. It is known that this type of waves arises in a nonlinear media because of the balance between the dispersion and nonlinearity. In the field of photonics, for example, the soliton solutions of NLSE are classified into different structures such as bright, dark and singular solitons [6, 7]. During the last two decades, there is a remarkable intention directed to a new type of solitons having the shape of W. To study the features of this wave, several mechanisms have been applied to analyse the mathematical models that describe various physical phenomena [8,9,10,11,12,13,14].

Solitons are found to arise in the context of quantum hall effect where chiral excitations are detected. The governing model of soliton propagation in this field of science is the chiral nonlinear Schrödinger equation (CNLSE) which is formed in a process of one dimensional reduction for a system describing fractional quantum Hall effect. The derived soliton solution for this equation is known as chiral solitons which have an essential role in nonlinear optics. Numerous studies have been devoted towards examining exact analytic solutions for CNLSE. For example, Nishino et al. [15] investigated CNLSE in (1 + 1) dimensions and found two kinds of the progressive wave solutions characterizing bright and dark solitons, see also [16, 17]. In the presence of the quantum potential perturbation, this model was examined in literature [18,19,20,21], where the potential is known as Bohm potential and it has the role on changing the dispersion of the CNLSE. To shed light thoroughly on the behaviour of chiral solitons, the problem of CNLSE in (1 + 2) dimensions was studied with constant coefficients and time-dependent coefficients by Biswas [22] where both bright and dark soliton solutions were extracted. In order to retrieve chiral solitons of different forms in (1 + 2) dimensions, many powerful approaches have been exploited such as trial solution technique, sine-Gordon expansion method, modified simple equation method and $\exp (-\psi (\rho ))$-expansion method, Lie symmetry analysis, first integral method, extended Fan sub-equation technique, modified Jacobi elliptic expansion method. For more details about the methodologies applied to (1 + 2)-dimensional CNLSE, the reader is referred to the references [23,24,25,26,27,28,29,30,31].

The target of the current study is to investigate various soliton solutions of the (1 + 2)-dimensional Chiral nonlinear Schrödinger equation. Three mathematical techniques, namely extended auxiliary equation method, functional variable method and Kudryashov method, are employed to deal with the dominating model. The rest of the paper is organized as follows. In Sect. 2, the governing model is analysed and its traveling wave reduction is derived. Then, Sect. 3 describes the extraction of soliton solutions by the proposed integration schemes where the behaviours of solitons are examined. In Sect. 4, the main outlook of results and remarks are presented. Section 5 displays the stability investigation for the constructed solutions by using linear stability analysis. Finally, the conclusion of work is given in Sect. 6.

2 Governing equation and mathematical pen-picture

The model of (1 + 2)-dimensional Chiral nonlinear Schrödinger equation discussed in the present work is given by

$$\begin{aligned} iQ_t + \alpha (Q_{xx}+Q_{yy}) + i \left\{ \beta _1 (Q Q_x^* - Q^* Q_x) + \beta _2 (Q Q_y^* - Q^* Q_y) \right\} Q= 0, \end{aligned}$$

(1)

where the dependent variable Q(x, y, t) refers to the optical soliton profile, whereas the independent variables x and y are the space coordinates and t is the time coordinate. The superscript $*$ indicates the complex conjugate. In equation above, the first term denotes the temporal evolution of the pulse. The second term with the coefficient of $\alpha$ stands for the dispersion term. The nonlinear terms given by the coefficients of $\beta _1$ and $\beta _2$ represent the self-steepening effect. This type of nonlinearity is known as current density. Equation (1) is found to fail the Painleve test of integrability, and thus, it is not integrable by inverse scattering transform method. Moreover, it is noteworthy that this equation is not invariant under the Galilean transformation [22].

Now, we intend to obtain the traveling wave reduction of Eq. (1) so as to derive the soliton solutions. Thus, we introduce the traveling wave transformation of the form

$$\begin{aligned} Q(x, y, t) = q(\xi )e^{i\phi (x,y,t)}, \end{aligned}$$

(2)

where $q(\xi )$ accounts for the amplitude of the soliton while $\phi (x,y,t)$ denotes the phase component. The wave variable $\xi$ is given by

$$\begin{aligned} \xi =\kappa _1 x+\kappa _2 y - \nu t, \end{aligned}$$

(3)

and the phase component is presented as

$$\begin{aligned} \phi (x,y,t)=\lambda _1 x+\lambda _2 y + \omega t+\theta (\xi ), \end{aligned}$$

(4)

where $\kappa _1$ and $\kappa _2$ are the inverse width of the soliton along x- and y-directions, respectively, whereas $\nu$ is the velocity of the soliton. The parameters $\lambda _1$ and $\lambda _2$ indicate the frequencies in the x- and y-directions, respectively, and $\omega$ represents the soliton frequency. The function $\theta (\xi )$ is defined as a nonlinear phase shift which is more general than the one considered as a constant parameter in many previous studies [23,24,25,26,27,28,29,30,31].

Applying the transformation (2) to Eq. (1) and separating the real and imaginary parts, this leads to a pair of equations having the form

$$\begin{aligned}&[-\nu + 2\alpha ( \kappa _1 \lambda _1 + \kappa _2 \lambda _2)] q' + 2\alpha (\kappa _1^2 + \kappa _2^2) q' \theta ' + \alpha (\kappa _1^2 + \kappa _2^2) q \theta '' =0, \end{aligned}$$

(5)

$$\begin{aligned}&\alpha (\kappa _1^2 + \kappa _2^2) q'' - [\omega +\alpha (\lambda _1^2+\lambda _2^2 )] q + 2(\beta _1 \lambda _1+\beta _2 \lambda _2 ) q^3 + [\nu -2\alpha ( \kappa _1\lambda _1+\kappa _2\lambda _2)] q \theta ' \nonumber \\&\qquad - \alpha (\kappa _1^2 + \kappa _2^2) q\theta '^2 + 2 (\kappa _1\beta _1 +\kappa _2 \beta _2 ) q^3 \theta '=0, \end{aligned}$$

(6)

where the prime denotes the derivative with respect to $\xi$. Once we multiply Eq. (5) by q, we arrive at the first integral given by

$$\begin{aligned} \frac{[-\nu + 2\alpha ( \kappa _1 \lambda _1 + \kappa _2 \lambda _2)]}{2} q^2 + \alpha (\kappa _1^2 + \kappa _2^2) q^2 \theta ' = C, \end{aligned}$$

(7)

where C is the constant of integration. Rearranging Eq. (7), one can obtain

$$\begin{aligned} \theta ' = \frac{C q^{-2}}{\alpha (\kappa _1^2 + \kappa _2^2)} + \frac{[\nu - 2\alpha ( \kappa _1 \lambda _1 + \kappa _2 \lambda _2)]}{2\alpha (\kappa _1^2 + \kappa _2^2)}. \end{aligned}$$

(8)

Substituting Eqs. (8) into (6) gives rise to

$$\begin{aligned} q''+A_1q+A_2q^{3}-A_3q^{-3}=0. \end{aligned}$$

(9)

Multiplying Eq. (9) by $q'$ and integrating with respect to $\xi$, we find

$$\begin{aligned} q'^2 + A_1q^2 + \frac{A_2}{2}q^{4} + A_3q^{-2}+2A_0=0, \end{aligned}$$

(10)

where $A_0$ is an arbitrary constant of integration and the rest of constants are defined by

$$\begin{aligned} A_1= & {} \frac{8C(\beta _1 \kappa _1+\beta _2 \kappa _2 ) - 4\alpha (\kappa _1^2 + \kappa _2^2) [\omega +\alpha (\lambda _1^2+\lambda _2^2 )] + [\nu - 2\alpha ( \kappa _1 \lambda _1 + \kappa _2 \lambda _2)]^2 }{4\alpha ^2 (\kappa _1^2 + \kappa _2^2)^2}, \end{aligned}$$

(11)

$$\begin{aligned} A_2= & {} \frac{\nu (\kappa _1\beta _1 + \kappa _2\beta _2 ) + 2\alpha ( \kappa _1 \lambda _2 - \kappa _2 \lambda _1)( \kappa _1\beta _2 - \kappa _2 \beta _1) }{ \alpha ^2 (\kappa _1^2 + \kappa _2^2)^2}, \end{aligned}$$

(12)

$$\begin{aligned} A_3= & {} \frac{C^2}{\alpha ^2 (\kappa _1^2 + \kappa _2^2)^2}. \end{aligned}$$

(13)

To avoid the complexity caused by the term of negative power in Eq. (10), we make use of the variable transformation given by

$$\begin{aligned} q^2=V. \end{aligned}$$

(14)

Hence, Eq. (10) reduces to

$$\begin{aligned} V'' + 4A_0 + 4A_1 V + 3A_2 V^2 =0. \end{aligned}$$

(15)

The solutions to Eq. (15) along with the relations (2) and (14) construct the general form of exact solutions for Eq. (1) addressed as

$$\begin{aligned} Q(x,y, t) = V^{1/2}e^{i[\lambda _1 x+\lambda _2 y + \omega t+\theta (\xi )]}, \end{aligned}$$

(16)

where the phase variable $\theta (\xi )$ can be turned up through integrating Eq. (8) with respect to $\xi$ as

$$\begin{aligned} \theta (\xi )= \frac{C }{\alpha (\kappa _1^2 + \kappa _2^2)} \int \frac{\mathrm {d}\xi }{V}+ \frac{[\nu - 2\alpha ( \kappa _1 \lambda _1 + \kappa _2 \lambda _2)]}{2\alpha (\kappa _1^2 + \kappa _2^2)}(\kappa _1 x+\kappa _2 y - \nu t) + \theta _0, \end{aligned}$$

(17)

where $\theta _0$ is the phase constant.

It can be noted that Eq. (10) is converted to an elliptic type equation given in [32] when $C=0$. This equation possesses various types of exact analytic solutions including Jacobi elliptic function solutions, trigonometric function solutions and hyperbolic function solutions. In that case, the phase function given by (17) collapses to a linear function.

3 Chiral soliton solutions

In this section, various structures of exact solutions representing W-shaped and other solitons for Eq. (1) are derived through applying different techniques. These solutions are obtained via solving Eq. (15) and then its solutions are plugged into (2) in company with (14) and (17).

3.1 Extended auxiliary equation method

Now, our goal is to extract several types of solitary waves solutions of Eq. (1). The analytical solutions are obtained upon the use of the auxiliary equation method to solve Eq. (15).

We assume that Eq. (15) has a solution expressed as

$$\begin{aligned} V(\xi )= C_0 + C_1 F(\xi ) + C_2 F^2(\xi ), \end{aligned}$$

(18)

where $C_0, C_1$ and $C_2$ are constants to be determined whereas $F(\xi )$ satisfies

$$\begin{aligned} F'^2(\xi )=4L_0 F(\xi ) + 4 L_2 F^2(\xi ) + 4L_4 F^3(\xi ) + 4L_6 F^4(\xi ), \end{aligned}$$

(19)

which is equivalent to

$$\begin{aligned} u'^2(\xi )= L_0 + L_2 u^2(\xi ) + L_4 u^4(\xi ) + L_6 u^6(\xi ), \end{aligned}$$

(20)

where $F(\xi )\equiv u^2(\xi )$ and $L_i (i=0,2,4,6)$ are constants to be identified. It is well known that Eqs. (19) and (20) admit solutions in the form

$$\begin{aligned} F(\xi )=u^2(\xi )=-\frac{L_4}{4L_6} (1\pm f(\xi )), \end{aligned}$$

(21)

where the function $f(\xi )$ could be expressed in terms of the Jacobi elliptic functions (JEFs) ${{\,\mathrm{sn}\,}}(\xi ,m), {{\,\mathrm{cn}\,}}(\xi ,m), {{\,\mathrm{dn}\,}}(\xi ,m)$ and so on [33]. The parameter m with $0< m < 1$ represents the modulus of JEFs. Substituting (18) and (19) into Eq. (15), a polynomial in $F^i(\xi ), (i=0,1,\dots ,6)$ will be constructed. Equating the coefficients with the same power of $F^i(\xi )$ in this polynomial to zero leads to a system of algebraic equations. Solving this system gives rise to the following cases of solutions.

Case I. If $L_0=\frac{L_4^3(m^2-1)}{32L_6^2m^2}, \; L_2=\frac{L_4^2(5m^2-1)}{16L_6m^2}$, then this brings about

$$\begin{aligned} C_0=\frac{L_4^2(1-2m^2) - 4A_1 L_6m^2}{6A_2 L_6 m^2}, C_1=-\frac{4 L_4}{A_2}, C_2= -\frac{8 L_6}{A_2}, A_0=\frac{16 A_1^2 L_6^2m^4 - L_4^4(m^4-m^2+1)}{48A_2 L_6^2 m^4}. \end{aligned}$$

(22)

Substituting (22) in conjunction with (21) into (18) and using (2) with (14), one can obtain JEF solutions to Eq. (1) in the form

$$\begin{aligned} Q(x,y,t)= & {} \left\{ \frac{-4A_1 L_6 m^2 + L_4^2 \left[ 1+m^2-3 m^2 {{\,\mathrm{sn}\,}}^2\left( \frac{L_4}{2m\sqrt{L_6}}\xi \right) \right] }{6A_2 L_6 m^2} \right\} ^{\frac{1}{2}}e^{i\phi (x,y,t)}, \end{aligned}$$

(23)

$$\begin{aligned} Q(x,y,t)= & {} \left\{ \frac{-4A_1 L_6 m^2 + L_4^2 \left[ 1+m^2-3 {{\,\mathrm{ns}\,}}^2\left( \frac{L_4}{2m\sqrt{L_6}}\xi \right) \right] }{6A_2 L_6 m^2} \right\} ^{\frac{1}{2}}e^{i\phi (x,y,t)}, \end{aligned}$$

(24)

where $L_6>0$. As $m\rightarrow 1$, solutions (23) and (24) reduce to the soliton solution presented as

$$\begin{aligned} Q(x,y,t)=\left\{ \frac{-4A_1 L_6 + L_4^2 \left[ 2-3 \tanh ^2\left( \frac{L_4}{2\sqrt{L_6}}\xi \right) \right] }{6A_2 L_6} \right\} ^{\frac{1}{2}}e^{i\phi (x,y,t)}, \end{aligned}$$

(25)

and the singular soliton solution introduced as

$$\begin{aligned} Q(x,y,t)=\left\{ \frac{-4A_1 L_6 + L_4^2 \left[ 2-3 \coth ^2\left( \frac{L_4}{2\sqrt{L_6}}\xi \right) \right] }{6A_2 L_6} \right\} ^{\frac{1}{2}}e^{i\phi (x,y,t)}, \end{aligned}$$

(26)

under the constraint

$$\begin{aligned} A_0=\frac{16 A_1^2 L_6^2-L_4^4}{48A_2 L_6^2}. \end{aligned}$$

(27)

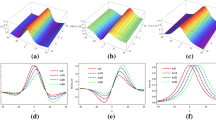
Figures 1, 2 and 3 describe the evolution of solution (25) which embodies three types of solitons under specific limits. As one can see from Fig. 1, the plots present soliton waves of W shape. The graph is depicted for the parameters given as $\alpha =1$, $\beta _1=\beta _2=\kappa _2=\lambda _1=0.5$, $\nu =\omega =\lambda _2=-0.5$, $\kappa _1=0.8$, $C=0.3$, $L_4=L_6=4$. Then, Fig. 2 illustrates the behaviour of bright soliton with the parameter values $\alpha =\beta _1=\beta _2=\kappa _2=\lambda _1= \lambda _2=\nu =\omega =0.5$, $\kappa _1=0.8$, $C=-0.3$, $L_4=L_6=4$. The emergence of the bright soliton is subject to the condition $A_2>0, 4A_1L_6/L_4^2\le -1$. Under the restriction $A_2<0, 4A_1L_6/L_4^2\ge 2$, it is clear that Fig. 3 shows dark soliton which is depicted with the values $\alpha =\beta _1=\beta _2=\kappa _2=\lambda _1= \lambda _2=0.5$, $\nu =\omega =-0.5$, $\kappa _1=0.8$, $C=0.1$, $L_4=L_6=4$.

Fig. 1

W-shaped soliton solution given by (25) with $\alpha =1$, $\beta _1=\beta _2=\kappa _2=\lambda _1=0.5$, $\nu =\omega =\lambda _2=-0.5$, $\kappa _1=0.8$, $C=0.3$, $L_4=L_6=4$

Fig. 2

Bright soliton solution given by (25) with $\alpha =\beta _1=\beta _2=\kappa _2=\lambda _1= \lambda _2=\nu =\omega =0.5$, $\kappa _1=0.8$, $C=-0.3$, $L_4=L_6=4$

Fig. 3

Dark soliton solution given by (25) with $\alpha =\beta _1=\beta _2=\kappa _2=\lambda _1= \lambda _2=0.5$, $\nu =\omega =-0.5$, $\kappa _1=0.8$, $C=0.1$, $L_4=L_6=4$

Case II. If $L_0=\frac{L_4^3(1-m^2)}{32L_6^2}, \; L_2=\frac{L_4^2(5-m^2)}{16L_6}$, then this results in

$$\begin{aligned} C_0=\frac{L_4^2(m^2-2) - 4A_1 L_6}{6A_2 L_6}, C_1=-\frac{4 L_4}{A_2}, C_2= -\frac{8 L_6}{A_2}, A_0=\frac{16 A_1^2 L_6^2-L_4^4(m^4-m^2+1)}{48A_2 L6^2}. \end{aligned}$$

(28)

Inserting (28) along with (21) into (18) and using (2) with (14), we reach JEF solutions to Eq. (1) as

$$\begin{aligned} Q(x,y,t)= & {} \left\{ \frac{-4A_1 L_6 + L_4^2 \left[ 1+m^2-3 m^2 {{\,\mathrm{sn}\,}}^2\left( \frac{L_4}{2\sqrt{L_6}}\xi \right) \right] }{6A_2 L_6} \right\} ^{\frac{1}{2}}e^{i\phi (x,y,t)}, \end{aligned}$$

(29)

$$\begin{aligned} Q(x,y,t)= & {} \left\{ \frac{-4A_1 L_6 + L_4^2 \left[ 1+m^2-3 {{\,\mathrm{ns}\,}}^2\left( \frac{L_4}{2\sqrt{L_6}}\xi \right) \right] }{6A_2 L_6} \right\} ^{\frac{1}{2}}e^{i\phi (x,y,t)}, \end{aligned}$$

(30)

where $L_6>0$. As $m\rightarrow 1$, solutions (29) and (30) degenerate to the soliton solutions (25) and (26) under the same constraint conditions given in (27).

Case III. If $L_0=\frac{L_4^3}{32L_6^2m^2}, \; L_2=\frac{L_4^2(4m^2+1)}{16L_6m^2}$, then this contributes to

$$\begin{aligned} C_0=-\frac{L_4^2(m^2+1) + 4A_1 L_6m^2}{6A_2 L_6 m^2}, C_1=-\frac{4 L_4}{A_2}, C_2= -\frac{8 L_6}{A_2}, A_0=\frac{16 A_1^2 L_6^2m^4 - L_4^4(m^4-m^2+1)}{48A_2 L_6^2 m^4}. \end{aligned}$$

(31)

Plugging (31) in company with (21) into (18) and using (2) with (14), we secure JEF solution to Eq. (1) in the form

$$\begin{aligned} Q(x,y,t)=\left\{ \frac{-4A_1 L_6 m^2 - L_4^2 \left[ 1+m^2-3 m^2 {{\,\mathrm{sn}\,}}^2\left( \frac{L_4}{2m\sqrt{-L_6}}\xi \right) \right] }{6A_2 L_6 m^2} \right\} ^{\frac{1}{2}}e^{i\phi (x,y,t)}, \end{aligned}$$

(32)

where $L_6<0$. As $m\rightarrow 1$, solution (32) changes into the soliton solution written as

$$\begin{aligned} Q(x,y,t)=\left\{ \frac{-4A_1 L_6 - L_4^2 \left[ 2-3 \tanh ^2\left( \frac{L_4}{2\sqrt{-L_6}}\xi \right) \right] }{6A_2 L_6} \right\} ^{\frac{1}{2}}e^{i\phi (x,y,t)}, \end{aligned}$$

(33)

under the same constraint condition given in (27).

Figures 4, 5 and 6 show the dynamic behaviours of solution (33) which yields three shapes of solitons demonstrated as follows. Figure 4 represents the profile of W-shaped soliton where it is plotted with the same parameter values given in Fig. 1 except that $L_6=-4$. Following the condition $A_2>0, 4A_1L_6/L_4^2\ge 1$, the bright soliton is exhibited in Fig. 5 with the same values of parameters as in Fig. 2 but with $L_6=-4$. Figure 6 depicts the dark soliton which comes into view under the condition $A_2<0, 4A_1L_6/L_4^2\le -2$. The graphs are plotted with the same parameter values given in Fig. 3 except that $L_6=-4$.

Fig. 4

W-shaped soliton solution given by (33) with the same parameter values given in Fig. 1 except that $L_6=-4$

Fig. 5

Bright soliton solution given by (33) with the same values of parameters as in Fig. 2 but with $L_6=-4$

Fig. 6

Dark soliton solution given by (33) with the same parameter values given in Fig. 3 except that $L_6=-4$

Case IV. If $L_0=\frac{L_4^3m^2}{32L_6^2}, \; L_2=\frac{L_4^2(m^2+4)}{16L_6}$, then this generates

$$\begin{aligned} C_0=-\frac{L_4^2(m^2+1) + 4A_1 L_6}{6A_2 L_6}, C_1=-\frac{4 L_4}{A_2}, C_2= -\frac{8 L_6}{A_2}, A_0=\frac{16 A_1^2 L_6^2-L_4^4(m^4-m^2+1)}{48A_2 L6^2}. \end{aligned}$$

(34)

Inserting (34) along with (21) into (18) and using (2) with (14), we arrive at JEF solution to Eq. (1) as

$$\begin{aligned} Q(x,y,t)=\left\{ \frac{-4A_1 L_6 m^2 - L_4^2 \left[ 1+m^2-3 m^2 {{\,\mathrm{sn}\,}}^2\left( \frac{L_4}{2\sqrt{-L_6}}\xi \right) \right] }{6A_2 L_6} \right\} ^{\frac{1}{2}}e^{i\phi (x,y,t)}, \end{aligned}$$

(35)

where $L_6<0$. As $m\rightarrow 1$, solution (35) degenerates to the soliton solution (33) with the same constraint condition given in (27).

3.2 Functional variable approach

Here, we derive the soliton solutions of Eq. (1) with the aid of functional variable technique. To start with, we introduce the transformation

$$\begin{aligned} V(\xi )=a+b\, W(\zeta ), \qquad \zeta =\Omega \, \xi , \end{aligned}$$

(36)

where a, b and $\Omega$ are constants to be identified. Substituting (36) into Eq. (15), we arrive at

$$\begin{aligned} b \Omega ^2 W'' + (3A_2a^2+4A_1a+4A_0) + (6A_2 a b +4 A_1 b) W + (3A_2 b^2) W^2 =0, \end{aligned}$$

(37)

where the prime stands for the derivative with respect to $\zeta$. According to functional variable method [34], Eq. (37) satisfies

$$\begin{aligned} \begin{aligned}&W_\zeta = Y(W),\\&W_{\zeta \zeta } = \frac{1}{2}(Y^2)', \\&W_{\zeta \zeta \zeta } = \frac{1}{2}(Y^2)'' \sqrt{Y^2},\\&W_{\zeta \zeta \zeta \zeta } = \frac{1}{2}\left[ (Y^2)''' Y^2 + (Y^2)'' (Y^2)' \right] , \end{aligned} \end{aligned}$$

(38)

and so on, where the prime indicates the derivative with respect to W. Substituting (38) into Eq. (37), one can reach

$$\begin{aligned} \frac{b \Omega ^2(Y^2)'}{2} + (3A_2a^2+4A_1a+4A_0) + (6A_2 a b +4 A_1 b) W + (3A_2 b^2) W^2 =0. \end{aligned}$$

(39)

Rearranging Eq. (39) and integrating with respect to W, we acquire

$$\begin{aligned} Y(W)=\frac{1}{\Omega } \sqrt{B_1 W + B_2 W^2 + B_3 W^3}, \end{aligned}$$

(40)

where the constants $B_1, B_2$ and $B_3$ are defined as

$$\begin{aligned} B_1= -\frac{6A_2a^2+8A_1a+8A_0}{b}, \quad B_2=-(6A_2 a + 4 A_1), \quad B_3=-2A_2 b. \end{aligned}$$

(41)

Taking into account $W_\zeta = Y(W)$ and making use of the technique given in [35], the following cases of solutions are extracted.

Case I. If $a=-\frac{2}{3 A_2} \left[ A_1+(2m^2-1)\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}}\right] , b=\frac{2 m^2}{A_2}\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}}, \Omega =\left( \frac{A_1^2-3A_0A_2}{m^4-m^2+1}\right) ^{\frac{1}{4}}$, then $W(\zeta )={{\,\mathrm{cn}\,}}^2(\zeta )$. Employing (16) and (36), we come by JEF solution to Eq. (1) as

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{2}{3 A_2}\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}} \left[ A_1 \sqrt{\frac{m^4-m^2+1}{A_1^2-3A_0A_2}} + (2m^2-1) - 3m^2 {{\,\mathrm{cn}\,}}^2(\Omega \xi ) \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}. \end{aligned}$$

(42)

As $m\rightarrow 1$, solution (42) converts to soliton solution having the form

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{2}{3 A_2}\sqrt{A_1^2-3A_0A_2} \left[ \frac{A_1}{\sqrt{A_1^2-3A_0A_2}} +1 - 3{{\,\mathrm{sech}\,}}^2(\Omega \xi ) \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}, \end{aligned}$$

(43)

provided $A_1^2-3A_0A_2>0$.

Figures 7, 8 and 9 show the dynamic behaviours of solution (43) which constructs three types of soliton structures according to specific conditions. As we can see that Fig. 7 illustrates W-shaped soliton where the graph is plotted by selecting appropriate values for the parameters given as $\alpha =\beta _1=\beta _2=\kappa _2=\lambda _1=0.5$, $\nu =\omega =\lambda _2=-0.5$, $\kappa _1=0.8$, $C=0.3$, $A_0=1$. However, as long as the condition $A_1<0$, $4A_0 A_2>3A_0 A_2>0$ takes place, the bright soliton wave will emerge in the medium as displayed in Fig. 8 with the parameter values $\alpha =\beta _1=\beta _2=\kappa _2=\lambda _1= \lambda _2=\nu =\omega =0.5$, $\kappa _1=0.8$, $C=-0.3$, $A_0=1$. Further to this, Fig. 9 demonstrates the dark soliton structure which exists in the limit $A_2<0$, $4A_0 A_2\ge A_1^2>3A_0 A_2$, where the plot is depicted with the values $\alpha =\omega =1$, $\beta _1=\beta _2=\kappa _2=\lambda _1= \lambda _2=0.5$, $\nu =-0.5$, $\kappa _1=0.8$, $C=1.01$, $A_0=-0.7$.

Fig. 7

W-shaped soliton solution given by (43) with $\alpha =\beta _1=\beta _2=\kappa _2=\lambda _1=0.5$, $\nu =\omega =\lambda _2=-0.5$, $\kappa _1=0.8$, $C=0.3$, $A_0=1$

Fig. 8

Bright soliton solution given by (43) with $\alpha =\beta _1=\beta _2=\kappa _2=\lambda _1= \lambda _2=\nu =\omega =0.5$, $\kappa _1=0.8$, $C=-0.3$, $A_0=1$

Fig. 9

Dark soliton solution given by (43) with $\alpha =\omega =1$, $\beta _1=\beta _2=\kappa _2=\lambda _1= \lambda _2=0.5$, $\nu =-0.5$, $\kappa _1=0.8$, $C=1.01$, $A_0=-0.7$

Case II. If $a=-\frac{2}{3 A_2} \left[ A_1-(m^2+1)\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}}\right] , b=-\frac{2 m^2}{A_2}\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}}, \Omega =\left( \frac{A_1^2-3A_0A_2}{m^4-m^2+1}\right) ^{\frac{1}{4}}$, then $W(\zeta )={{\,\mathrm{sn}\,}}^2(\zeta )$. From (16) and (36), Eq. (1) has JEF solution in the form

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{2}{3 A_2}\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}} \left[ A_1 \sqrt{\frac{m^4-m^2+1}{A_1^2-3A_0A_2}} - (m^2+1) + 3m^2 {{\,\mathrm{sn}\,}}^2(\Omega \xi ) \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}. \end{aligned}$$

(44)

As $m\rightarrow 1$, solution (44) degenerates to soliton solution given by

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{2}{3 A_2}\sqrt{A_1^2-3A_0A_2} \left[ \frac{A_1}{\sqrt{A_1^2-3A_0A_2}} - 2 + 3\tanh ^2(\Omega \xi ) \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}, \end{aligned}$$

(45)

provided $A_1^2-3A_0A_2>0$. According to the relation $\tanh ^2(\Omega \xi )=1-{{\,\mathrm{sech}\,}}^2(\Omega \xi )$, solution (45) turns to solution (43). Hence, this solution generates W-shaped, bright and dark solitons which are exactly exhibited in Figs. 7, 8 and 9.

Case III. If $a=-\frac{2}{3 A_2} \left[ A_1-(m^2+1)\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}}\right] , b=-\frac{2}{A_2}\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}}, \Omega =\left( \frac{A_1^2-3A_0A_2}{m^4-m^2+1}\right) ^{\frac{1}{4}}$, then $W(\zeta )={{\,\mathrm{ns}\,}}^2(\zeta )$. Utilizing (16) and (36), we secure JEF solution to Eq. (1) as

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{2}{3 A_2}\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}} \left[ A_1 \sqrt{\frac{m^4-m^2+1}{A_1^2-3A_0A_2}} - (m^2+1) + 3 {{\,\mathrm{ns}\,}}^2(\Omega \xi ) \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}. \end{aligned}$$

(46)

As $m\rightarrow 1$, solution (46) changes to singular soliton solution presented as

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{2}{3 A_2}\sqrt{A_1^2-3A_0A_2} \left[ \frac{A_1}{\sqrt{A_1^2-3A_0A_2}} - 2 + 3\coth ^2(\Omega \xi ) \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}, \end{aligned}$$

(47)

provided $A_1^2-3A_0A_2>0$.

Case IV. If $a=-\frac{2}{3 A_2} \left[ A_1-(m^2-2)\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}}\right] , b=-\frac{2}{A_2}\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}}, \Omega =\left( \frac{A_1^2-3A_0A_2}{m^4-m^2+1}\right) ^{\frac{1}{4}}$, then $W(\zeta )={{\,\mathrm{cs}\,}}^2(\zeta )$. Using (16) and (36), we recover JEF solution to Eq. (1) as

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{2}{3 A_2}\sqrt{\frac{A_1^2-3A_0A_2}{m^4-m^2+1}} \left[ A_1 \sqrt{\frac{m^4-m^2+1}{A_1^2-3A_0A_2}} - (m^2-2) + 3 {{\,\mathrm{cs}\,}}^2(\Omega \xi ) \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}. \end{aligned}$$

(48)

As $m\rightarrow 1$, solution (48) decays to singular soliton solution addressed as

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{2}{3 A_2}\sqrt{A_1^2-3A_0A_2} \left[ \frac{A_1}{\sqrt{A_1^2-3A_0A_2}} +1 + 3{{\,\mathrm{csch}\,}}^2(\Omega \xi ) \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}, \end{aligned}$$

(49)

provided $A_1^2-3A_0A_2>0$.

Case V. If $a=-\frac{2}{3 A_2} \left[ A_1-2 (2m^2-1)\sqrt{\frac{A_1^2-3A_0A_2}{16m^4-16m^2+1}}\right] , b=-\frac{2}{A_2}\sqrt{\frac{A_1^2-3A_0A_2}{16m^4-16m^2+1}}$,

$\Omega =2\left( \frac{A_1^2-3A_0A_2}{16m^4-16m^2+1}\right) ^{\frac{1}{4}}$, then $W(\zeta )=\frac{{{\,\mathrm{sn}\,}}^2(\zeta )}{(1+{{\,\mathrm{cn}\,}}(\zeta ))^2}$. Exploiting (16) and (36), we obtain JEF solution to Eq. (1) as

$$\begin{aligned} \begin{aligned} Q(x, y, t)=&\left\{ -\frac{2}{3 A_2}\sqrt{\frac{A_1^2-3A_0A_2}{16m^4-16m^2+1}} \left[ A_1 \sqrt{\frac{16m^4-16m^2+1}{A_1^2-3A_0A_2}} \right. \right. \\&\quad \left. \left. - 2(2m^2-1) + 3 \frac{{{\,\mathrm{sn}\,}}^2(\Omega \xi )}{\left( 1+{{\,\mathrm{cn}\,}}(\Omega \xi )\right) ^2} \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}. \end{aligned} \end{aligned}$$

(50)

As $m\rightarrow 1$, solution (50) collapses to soliton solution of the form

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{2}{3 A_2}\sqrt{A_1^2-3A_0A_2} \left[ \frac{A_1}{\sqrt{A_1^2-3A_0A_2}} +1 - \frac{6{{\,\mathrm{sech}\,}}(\Omega \xi )}{1+{{\,\mathrm{sech}\,}}(\Omega \xi )} \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}, \end{aligned}$$

(51)

provided $A_1^2-3A_0A_2>0$.

The evolution of solution (51) is illustrated in Figs. 10, 11 and 12 which display three shapes of waves including W-shaped, bright and dark solitons. The behaviour of W-shaped soliton is presented in Fig. 10 with the same values of parameters as in Fig. 7. Under the condition $A_1<0$, $4A_0 A_2>3A_0 A_2>0$, the propagation of bright soliton is shown in Fig. 11 using the same values of parameters as in Fig. 8. The dark soliton wave which evolves based on the restriction of $A_2<0$, $4A_0 A_2\ge A_1^2>3A_0 A_2$ is plotted in Fig. 12 with the same values of parameters taken in Fig. 9.

Fig. 10

W-shaped soliton solution given by (51) with the same values of parameters as in Fig. 7

Fig. 11

Bright soliton solution given by (51) with the same values of parameters as in Fig. 8

Fig. 12

Dark soliton solution given by (51) with the same values of parameters taken in Fig. 9

3.3 Kudryashov method

Our purpose herein is to reveal distinct structures of solitons for Eq. (1) using another integration scheme. The Kudryashov method [36] is the main mathematical tool implemented to seek the exact solution. Let us first rewrite Eq. (15) to take the form

$$\begin{aligned} r^2 P'' + 4A_0 + 4A_1 P + 3A_2 P^2 =0, \end{aligned}$$

(52)

where $P(\zeta )=V(\xi )$, $\zeta =r \, \xi$ and r is a constant to be detected. We assume that the solution of Eq. (52) is introduced as

$$\begin{aligned} P(\zeta )= a_0 + a_1 F(\zeta ) + a_2 F^2(\zeta ), \end{aligned}$$

(53)

where $a_0, a_1$ and $a_2$ are constants to be determined whereas $F(\zeta )$ satisfies

$$\begin{aligned} F'(\zeta )=F^2(\zeta ) - F(\zeta ), \end{aligned}$$

(54)

which has the solution of the form

$$\begin{aligned} F(\zeta )= \frac{1}{1+\sigma e^{\zeta }}, \end{aligned}$$

(55)

where $\sigma$ is an arbitrary constant.

Substituting (53) together with (54) into Eq. (52), a polynomial of different powers of $F^j{(\zeta )}$, ($j=0,1, \dots , 4$) will be created. Equating each coefficient with the same power of $F^j{(\zeta )}$ in this polynomial to zero gives rise to a system of algebraic equations for $a_0, a_1, a_2$ and r. The system is given by

$$\begin{aligned} \left. \begin{aligned}&F^4{(\zeta )}: 3 A_2 a_2^2 + 6 r^2 a_2=0,\\&F^3{(\zeta )}: 6A_2 a_1a_2 + 2 r^2 a_1 - 10 r^2 a_2=0,\\&F^2{(\zeta )}: 6 A_2 a_0 a_2 + 3 A_2 a_1^2 - 3 r^2 a_1 + 4 r^2 a_2 + 4 A_1a_2=0,\\&F^1{(\zeta )}: 6 A_2 a_0 a_1 + r^2 a_1+ 4A_1 a_1=0, \\&F^0{(\zeta )}: 3 A_2 a_0^2 + 4 A_1 a_0+ 4A_0=0. \end{aligned} \right\} \end{aligned}$$

(56)

Solving this system of equations, one can arrive at the following values of $a_i$ and r.

$$\begin{aligned} a_0= & {} -\frac{2(A_1+\sqrt{A_1^2-3A_0A_2})}{3 A_2}, \end{aligned}$$

(57)

$$\begin{aligned} a_1= & {} \frac{8\sqrt{A_1^2-3A_0A_2}}{A_2}, \end{aligned}$$

(58)

$$\begin{aligned} a_2= & {} -\frac{8\sqrt{A_1^2-3A_0A_2}}{A_2}, \end{aligned}$$

(59)

$$\begin{aligned} r= & {} 2\left( A_1^2-3A_0A_2\right) ^{1/4}. \end{aligned}$$

(60)

Exploiting these findings, we can obtain an exact soliton solution to Eq. (1) written as

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{2\sqrt{A_1^2-3A_0A_2}}{3 A_2}\left[ 1 + \frac{A_1}{\sqrt{A_1^2-3A_0A_2}} - \frac{12}{1+\sigma e^{(r \xi )}} + \frac{12}{\left[ 1+\sigma e^{(r \xi )}\right] ^2} \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}, \end{aligned}$$

(61)

provided that $A_1^2-3A_0A_2>0$ for the validity of solitons with real values for the pulse width and amplitude. The solution (61) leads to formation of W-shaped soliton. Despite its propagation, W-shaped wave is subject to decay to bright or dark solitons under specific restrictions. For instance, it is found that W-shaped solitons degenerate to bright solitons in case that the parameters satisfy the condition $A_1<0$, $4A_0 A_2>3A_0 A_2>0$. Further to this, W-shaped soliton does not exist in the limit $A_2<0$, $4A_0 A_2\ge A_1^2>3A_0 A_2$, where the dark soliton wave is exclusively constructed. Afterwards, W-shaped soliton is formed as soon as $A_1^2>4A_0A_2$ occurs.

Figures 13, 14 and 15 display the behaviours of solitons given in (61) for the same values of parameters as in Figs. 7, 8 and 9. The value of parameter $\sigma$ is set to be 1. It is clear that Fig. 13 shows the 2D and 3D plots for the evolution of W-shaped soliton. The propagation of bright soliton is described in Fig. 14 where the appearance of this pulse is dominated by the constraint $A_1<0$, $4A_0 A_2>3A_0 A_2>0$. Figure 15 demonstrates the behaviour of dark soliton which is purely created under the condition $A_2<0$, $4A_0 A_2\ge A_1^2>3A_0 A_2$.

Fig. 13

W-shaped soliton solution given by (61) with the same values of parameters as in Fig. 7

Fig. 14

Bright soliton solution given by (61) with the same values of parameters as in Fig. 8

Fig. 15

Dark soliton solution given by (61) with the same values of parameters as in Fig. 9

Fig. 16

The effect of $\sigma$ on the propagation of W-shaped soliton given by (61) with the same values of parameters as in Fig. 7

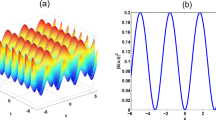
Indeed, the parameter $\sigma$ has a remarkable influence on the evolution of wave propagation. As displayed in Fig. 16, it plays a significant role on handling the horizontal shift of the wave graph. For example, when $\sigma >1$ the wave is shifted to the left direction while for $0<\sigma <1$ the graph of wave is shifted to the right direction. The graph shows the 2D plots for the situation of shifting W-shaped soliton (61) due to the variations of the parameter $\sigma$. The plots are depicted for the same values of parameters taken in Fig. 7. On the contrary, the negative value of the parameter $\sigma$ leads to the emergence of a singular soliton wave.

4 Results and remarks

We have seen that the utilized methods provide soliton solutions having a variety of structures classified into W-shaped, bright, dark and singular solitons. Solutions (25), (33), (43), (45), (51), (61) which generate W-shaped solitons are also found to yield bright and dark solitons under some restrictions. Further to this fascinating outcome, in case that $A_0=0$ each of those solutions reduces to two separate expressions characterizing W-type and bright solitons under specific conditions as follows.

Solutions(25), (33), (43), (45) turn into solution representing W-shaped solitons given by

$$\begin{aligned} Q(x, y, t) =\left\{ -\frac{4A_1}{3A_2}\left[ 1 - \frac{3}{2} {{\,\mathrm{sech}\,}}^2\left( \sqrt{A_1} \xi \right) \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}, \end{aligned}$$

(62)

when $A_1>0$, $A_2<0$ and they collapse to solution describing bright solitons in the form

$$\begin{aligned} Q(x, y, t) =\sqrt{-\frac{2A_1}{A_2}} {{\,\mathrm{sech}\,}}\left( \sqrt{-A_1} \xi \right) e^{i\phi (x,y,t)}, \end{aligned}$$

(63)

if $A_1<0$, $A_2>0$. Figure 17 exhibits W-shaped and bright solitons given by (62) and (63).

Fig. 17

W-shaped and bright soliton solutions given by (62) and (63) with the parameter values $\beta _1=\kappa _2=\lambda _1= \lambda _2=\omega =\nu =0.5$, $\kappa _1=0.8$; for a $\alpha =\beta _2=0.5$ and for b $\alpha =1, \beta _2=0.3$

Similarly, as $A_0=0$, solution (51) generates solitons with shape of W and is written as

$$\begin{aligned} Q(x, y, t) =\left\{ -\frac{4A_1}{3A_2}\left[ 1 - \frac{3 {{\,\mathrm{sech}\,}}\left( 2\sqrt{A_1} \xi \right) }{1+{{\,\mathrm{sech}\,}}\left( 2\sqrt{A_1} \xi \right) } \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}, \end{aligned}$$

(64)

provided $A_1>0$, $A_2<0$ and it is converted to bright solitons of the form

$$\begin{aligned} Q(x, y, t) =\left\{ -\frac{4A_1}{3A_2} \frac{ {{\,\mathrm{sech}\,}}\left( 2\sqrt{-A_1} \xi \right) }{1+{{\,\mathrm{sech}\,}}\left( 2\sqrt{-A_1} \xi \right) } \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}, \end{aligned}$$

(65)

when $A_1<0$, $A_2>0$. Figure 18 represents W-shaped and bright solitons given by (64) and (65).

Fig. 18

W-shaped and bright soliton solutions given by (64) and (65) with the same parameter values as in Fig. 17

Likewise, once $A_0=0$ solution (61) changes to W-shaped solitons given by

$$\begin{aligned} Q(x, y, t)= \left\{ -\frac{4A_1}{3 A_2}\left[ 1 - \frac{6}{1+\sigma e^{(2\sqrt{A_1}) \xi )}} + \frac{6}{\left[ 1+\sigma e^{(2\sqrt{A_1} \xi )}\right] ^2} \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}, \end{aligned}$$

(66)

provided $A_1>0$ and $A_2<0$. On the other hand, if $A_1<0$ and $A_2>0$, it is transformed into bright solitons introduced as

$$\begin{aligned} Q(x, y, t)=\left\{ -\frac{8A_1}{A_2}\left[ \frac{1}{1+\sigma e^{(2\sqrt{-A_1} \xi )}} - \frac{1}{\left[ 1+\sigma e^{(2\sqrt{-A_1} \xi )}\right] ^2} \right] \right\} ^{\frac{1}{2}} e^{i\phi (x,y,t)}. \end{aligned}$$

(67)

Figure 19 demonstrates W-shaped and bright solitons given by (66) and (67).

Fig. 19

W-shaped and bright soliton solutions given by (66) and (67) with the same parameter values as in Fig. 17

In addition to W-shaped, bright, dark and singular solitons, the obtained JEFs solutions can degenerate to periodic-type solutions in terms of trigonometric functions as the modulus of JEFs approaches zero. However, these periodic function solutions are omitted in this work since we only focus on soliton type solutions.

The various structures of chiral solitons constructed in the present study are completely different in comparison with those reported in the previous studies in literature.

5 Stability analysis

In this section, the stability of the obtained solutions is examined by means of the standard linear stability analysis. Accordingly, we introduce the perturbed solution of the form

$$\begin{aligned} Q(x,y,t)=\left[ \sqrt{P} + U(x,y,t) \right] e^{i P t}, \quad \end{aligned}$$

(68)

where P is the incident power at the point of $t=0$ while U(x, y, t) is a small perturbation and $U(x,y,t)\ll P$.

Substituting Eqs. (68) into (1) and linearizing, we arrive at

$$\begin{aligned} i \frac{\partial U}{\partial t} - P U + \alpha \left( \frac{\partial ^2U}{\partial x^2} + \frac{\partial ^2U}{\partial y^2} \right) - i P \beta _1 \left( \frac{\partial U}{\partial x} - \frac{\partial U^*}{\partial x}\right) - i P \beta _2 \left( \frac{\partial U}{\partial y} - \frac{\partial U^*}{\partial y}\right) =0, \end{aligned}$$

(69)

where $*$ denotes the conjugate of the complex function U(x, y, t). Assuming that the solution of Eq. (69) is given as

$$\begin{aligned} U(x,y, t)=\gamma _1 e^{i(K_1 x + K_2 y -\Omega t )} + \gamma _2 e^{-i(K_1 x + K_2 y -\Omega t)}, \end{aligned}$$

(70)

where $\Omega$ and $K_1, K_2$ are the frequency of perturbation and normalized wave numbers. Inserting ansatz (70) into Eq. (69), we find two equations in $\gamma _1$ and $\gamma _2$ upon separating the coefficients of $\exp \{i(K_1 x + K_2 y -\Omega t )\}$ and $\exp \{-i(K_1 x + K_2 y -\Omega t)\}$ defined as

$$\begin{aligned} \begin{aligned}&\left[ (\beta _1K_1 + \beta _2 K_2) (\gamma _1 - \gamma _2) - \gamma _2 \right] P - \left[ \alpha (K_1^2+K_2^2) + \Omega \right] \gamma _2 =0,\\&\left[ (\beta _1K_1 + \beta _2 K_2) (\gamma _1 - \gamma _2) - \gamma _1 \right] P - \left[ \alpha (K_1^2+K_2^2) - \Omega \right] \gamma _1 =0. \end{aligned} \end{aligned}$$

(71)

The system of Eq. (71) yields the coefficient matrix of $\gamma _1$ and $\gamma _2$ in the form

$$\begin{aligned} \begin{bmatrix} (\beta _1K_1 + \beta _2 K_2) P &{} -(\beta _1K_1 + \beta _2 K_2 +1)P \\ &{} - \alpha (K_1^2+K_2^2) - \Omega \\ \\ (\beta _1K_1 + \beta _2 K_2 - 1)P &{} -(\beta _1K_1 + \beta _2 K_2) P \\ - \alpha (K_1^2+K_2^2) + \Omega &{} \end{bmatrix} \begin{bmatrix} \gamma _1\\ \\ \\ \gamma _2\\ \\ \end{bmatrix} = \begin{bmatrix} 0\\ \\ \\ 0\\ \\ \end{bmatrix}. \end{aligned}$$

(72)

In order to extract nontrivial solution for the coefficient matrix, the determinant has to be vanished. From this determinant, we obtain the dispersion relation as

$$\begin{aligned} \Omega ^2 + 2\Omega P(\beta _1K_1 + \beta _2 K_2) - \left( P+\alpha (K_1^2+K_2^2) \right) ^2 =0. \end{aligned}$$

(73)

The solution of the dispersion relation (73) for $\Omega$ is presented by

$$\begin{aligned} \Omega =-(\beta _1K_1 + \beta _2 K_2)P \pm \sqrt{(\beta _1K_1 + \beta _2 K_2)^2 P^2 + \left( P+\alpha (K_1^2+K_2^2) \right) ^2}. \end{aligned}$$

(74)

This expression diagnoses the steady-state stability that depends on the dispersion, self-steepening effect and wave numbers. It is obviously noticed that $(\beta _1K_1 + \beta _2 K_2)^2 P^2 + \left( P+\alpha (K_1^2+K_2^2) \right) ^2$ is always $\ge 0$. This means that $\Omega$ is real for all values of wave numbers $K_1, K_2$. Hence, the steady state is stable against wave number perturbations.

6 Conclusion

This paper has concentrated on investigating the behaviours of chiral solitons in (1+2) dimensions. Three efficient approaches are implemented to secure the soliton solutions of the governing model. All derived solutions are extracted based on nonlinear phase shift in contrast of all previous studies. The obtained chiral solitons have different profiles including W-shaped, bright, dark and singular solitons. The graphical representations of W-shaped, bright and dark solitons are presented with distinct values of model parameters to enable a clear view of wave behaviours. The stability of the retrieved solutions has been investigated by utilizing the linear stability analysis which shows that all solutions are stable. To the best of our knowledge, the results obtained here are entirely new and may enhance the understanding of soliton dynamics in nonlinear phenomena that appear in various scientific fields.