1 Introduction

The issue of dark matter is one of the important problems in modern cosmology and galactic astronomy. Two very well-known observations, namely galactic rotation curves and mass discrepancy in galactic clusters, suggest the existence of dark matter [1, 2]. The observations show that the velocity of a star or an interstellar cloud rotating in the disk of a spiral galaxy increases linearly with distance from the centre of the galaxy and attains approximately constant values in the outer range of the baryonic matter disk. This is in contrast to Newtonian gravity where it predicts the reduction of velocity in the halo region, assuming a centrally dominated mass associated with the observed luminous matter. Such behaviour of galactic rotation curves is explained by the existence of some mysterious invisible matter distribution, known as dark matter [3, 4].

The mass difference of clusters is another evidence for the existence of dark matter which can be understood by measuring the mass of a cluster in two different ways: either measuring the total mass obtained from the sum of all observable mass members within the cluster or by using the virial theorem, which provides an estimated mass of the cluster called the virial mass. The comparison between the virial mass and total baryonic mass shows that the former is almost 20–30 times greater than the latter. This fact is known as the virial mass discrepancy and is explained by postulating the existence of dark matter in clusters [1, 5].

The most acceptable model to describe evolution of the universe, known as \(\Lambda CDM\), proposes cold dark matter (CDM) to explain rotational velocity of spiral galaxies, virial mass discrepancy, observed CMB anisotropies, large-scale structure, galactic formation processes and gravitational lensing of distant objects [6,7,8]. Despite the simplicity, beauty and efficiency of \(\Lambda CDM\) in describing the large-scale evolution of the universe, the theory faces serious challenges at small scales such as the Cusp-core problem, fewer observed massive satellites around Milky Way (MW)-like galaxies than what the theory predicts, reproducing the phase-space distribution of satellites around MW and Andromeda galaxies and early formation of large galaxies at high redshifts [6]. Hence other alternatives to CDM have been proposed and attracted considerable attention, among which one comes across warm dark matter, self-interacting dark matter, brane world models, modified gravity (MG) [9,10,11,12,13,14,15,16,17,18,19,20,21,22] and scalar field dark matter (SFDM) [6]. Of such models, we focus on SFDM which assumes dark matter as an ultra-light scalar field. The scalar field in SFDM can form Bose–Einstein condensates (BEC) at cosmological scales and behaves like CDM at large scales. Contrary to \(\Lambda CDM\), fewer satellite halos were predicted in SFDM and formation of massive galaxies would occur at high redshifts [6]. Scalar fields with positive quadratic [23,24,25] or quartic self-interacting potential have been studied before [26]. In this work we consider a symmetron-like model of SFDM as an alternative to CDM. Similar to other screening mechanisms such as Chameleon, dilaton and Vainshtein scenario; in this model, there exists an interaction between matter content and the scalar field due to a conformal factor so that the effective potential of the scalar field depends on the matter density of the environment. The model is consistent with results from GR in local experiments, while significantly deviates from GR in cosmological scale [27,28,29]. The screening mechanism is proposed in order to modify GR at cosmological scales, while the effects of extra degrees of freedom are screened from local gravitational experiments. For symmetron, the modification of GR occurs when the matter content inside the system becomes smaller than a critical density. In this case the shape of the effective potential changes, figuratively speaking, from U to the W at cosmic scales. Since in a static system, the scalar field takes values which minimize the effective potential, under proper conditions the system undergoes a transition and the scalar field leaves the unstable position to settle in a true stable vacuum. Assuming that matter content inside the Milky Way to be larger than the critical density, one may use symmetron mechanism to explain late time cosmic acceleration [27, 29].

Moreover, the curvature of space–time near any mass, including dark matter, deflects the passing photons and distorts the images of the background galaxies which means that gravity acts as a lens around the massive object. Accordingly, the lensing of light by galaxies in a halo where galaxy rotation curves are constant is an important observational test showing the effects of dark matter. This effect was first observed during a solar eclipse in front of the Hyades star cluster, where stars appeared to move as they passed behind the sun [30]. The impression was then improved by Zwicky when he suggested that the ultimate measurement of cluster masses would be accomplished from gravitational lensing [31]. Hence investigating the light deflection angle shows whether or not any proposed model can be a proper alternative to dark energy.

In this work, we use the symmetry breaking mechanism based on symmetron model and investigate dark matter effects on galaxy scales. Unlike [32] where the modification to GR occurs in high-density environments trough the symmetron field, we consider a Higgs-like potential for the scalar field and let the transition occur when the baryonic matter is subdominant in the halo region. Our results show that rotation curves of a spiral galaxy and light deflection would be explained by the effect of a symmetron field in the halo region. The paper is organized as follows: Sect. 2 deals with a review of the symmetron model as an example of SFDM models and continues by considering a spherically symmetric space–time. In Sect. 3 the field equations for the symmetron model are obtained, and then in Sect. 4, the metric components in the region of the flat rotation curves are derived. The light deflection angle for this model is investigated in Sect. 5. Finally, conclusions are drawn in the last section.

2 The symmetron model

In this section, we briefly introduce the symmetron model and derive field equations in a four-dimensional space–time. The action of the model is in the form

$$\begin{aligned} S = \int {{d^4}x\sqrt{ - g} } \left[ {\frac{{M_{Pl}^2}}{2}R - \frac{1}{2}{g^{\mu \nu }}{\partial _\mu }\phi {\partial _\nu }\phi - V\left( \phi \right) } \right] + \int {{d^4}x\sqrt{ - \tilde{g}} } {L_m}\left[ {{{\tilde{g}}_{\mu \nu }},\psi } \right] , \end{aligned}$$
(1)

where \(M_\mathrm{Pl}\equiv (8\pi G)^{-1/2}\) is the reduced Planck mass, \(V(\phi )\) is a self-interacting potential, \(\psi \) is the matter field, and \({L_\mathrm{m}}\) is the Lagrangian of the matter. The metric in the Jordan frame, \(\tilde{g}_{\mu \nu }\), is conformally related to that of the Einstein frame according to

$$\begin{aligned} {\tilde{g}}_{\mu \nu }={A^2}\left( \phi \right) {g}_{\mu \nu }. \end{aligned}$$
(2)

As an example of the scalar potentials \( V(\phi )\) and \( A(\phi ) \), which must have \( {\mathbb {Z}_2} \) symmetry, one may consider

$$\begin{aligned} V\left( \phi \right) = - \frac{1}{2}{\mu ^2}{\phi ^2} + \frac{1}{4}\lambda {\phi ^4}, \end{aligned}$$
(3)

and

$$\begin{aligned} A\left( \phi \right) = 1 + \frac{{{\phi ^2}}}{{2{M^2}}}, \end{aligned}$$
(4)

where \( {\mu ^2} \) and M are mass scales of the model and \( \lambda \) is a positive dimensionless coupling constant [27]. Variation of action (1) with respect to the metric tensor \(g_{\mu \nu }\) associated with the Einstein frame gives the field equations

$$\begin{aligned} {G_{\mu \nu }} \equiv \frac{1}{M_\mathrm{Pl}^2}\left( T_{\mu \nu }^{[m]}+T_{\mu \nu }^{[\phi ]}\right) = \frac{1}{M_\mathrm{Pl}^2}\left( {A^2}\left( \phi \right) \tilde{T}_{\mu \nu }^{[m]}+T_{\mu \nu }^{[\phi ]} \right) , \end{aligned}$$
(5)

where \(\tilde{T}_{\mu \nu }^{[m]}\) is the energy-momentum tensor of the matter which is conserved in the Jordan frame and defined as

$$\begin{aligned} \tilde{T}_{\mu \nu }^{[m]}=-\frac{2}{\sqrt{-\tilde{g}}}\frac{\left( \delta {\sqrt{-\tilde{g}}}{L_{m}}\right) }{\delta {\tilde{g}}^{\mu \nu }}, \end{aligned}$$
(6)

and \( T_{\mu \nu }^{[\phi ]} \) is the energy-momentum tensor of the scalar field, given by

$$\begin{aligned} T_{\mu \nu }^{[\phi ]} = - \frac{1}{2}{g_{\mu \nu }}{\partial ^\alpha }\phi {\partial _\alpha }\phi - {g_{\mu \nu }}V\left( \phi \right) + {\partial _\mu }\phi {\partial _\nu }\phi . \end{aligned}$$
(7)

In addition, variation with respect to the scalar field gives the following field equation

$$\begin{aligned} \Box \phi = \frac{{dV\left( \phi \right) }}{{d\phi }} - {A^3}\left( \phi \right) \frac{{dA\left( \phi \right) }}{{d\phi }}\tilde{T}^{[m]}, \end{aligned}$$
(8)

where \( {\tilde{T}}^{[m]} \) is the trace of energy-momentum tensor (6) and turns to

$$\begin{aligned} {\tilde{T}}^{[m]}={\tilde{g}}^{\mu \nu }{\tilde{T}}_{\mu \nu }^{[m]} =-{{\tilde{\rho }}^{\left[ m \right] }}, \end{aligned}$$
(9)

in the case of nonrelativistic matter.Footnote 1 The relation of the matter density in the Einstein frame to that of the Jordan frame is given by

$$\begin{aligned} \rho ^{[m]}= {A^4}\left( \phi \right) \tilde{\rho }^{[m]}. \end{aligned}$$
(10)

Note that \( \rho ^{[m]}=-T^{\left[ m \right] }=- {g^{\mu \nu }}T_{\mu \nu }^{\left[ m \right] } \) where \( T_{\mu \nu }^{\left[ m \right] } \) is the Einstein frame energy-momentum tensor which is not covariantly conserved (i.e. \( {\nabla ^\mu }T_{\mu \nu }^{\left[ m \right] } \ne 0 \) ) because matter moves on geodesics in the Jordan frame that satisfies \( {\tilde{\nabla }^\mu }\tilde{T}_{\mu \nu }^{\left[ m \right] } = 0 \). By defining \( \rho \equiv {A^3}\left( \phi \right) \tilde{\rho }^{[m]} ={A^{-1}\left( \phi \right) } \rho ^{[m]}\) as an independent quantity of the symmetron scalar field, which is conserved in the Einstein frame, and substituting this definition in (8) one can see that the dynamics of the scalar field is actually governed by an effective potential, i.e.

$$\begin{aligned} \Box \phi =\frac{{d{V_\mathrm{eff}}\left( \phi \right) }}{{d\phi }}, \end{aligned}$$
(11)

where

$$\begin{aligned} {V}_\mathrm{eff}(\phi )\equiv V(\phi )+A(\phi )\rho . \end{aligned}$$
(12)

Keep in mind that \( \rho \) is not a physical matter density, but it is used for more conveniences and mathematical facilities. We therefore have

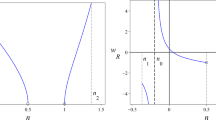
$$\begin{aligned} {V_\mathrm{eff}}\left( \phi \right) = \frac{1}{2}\left( {\frac{\rho }{{{M^2}}} - {\mu ^2}} \right) {\phi ^2} + \frac{1}{4}\lambda {\phi ^4}, \end{aligned}$$
(13)

obviating the name screening mechanism embodied in effective potential (13). According to this relation the effective mass \( {m^{2}_\mathrm{eff}} = {\frac{\rho }{{{M^2}}} - {\mu ^2}}\) depends on local density of the environment. Hence in regions of high density where \( {\rho }\gg {M^{2}} {\mu ^2}\), the effective potential is U-shaped and the system settles in the vacuum expectation value (VEV) \(\Phi _{VEV}=0\), while in regions where \( {\rho }\ll {M^{2}} {\mu ^2}\) and environment is rare, the effective potential is W-shaped. Figure 1 shows behaviour of the effective potential schematically; the left plot refers to the region of high density, while the right plot shows the effective potential where density of the environment is rare. Starting from a region where \( {\rho }\gg {M^{2}} {\mu ^2}\) and assuming the scalar field settles in the minimum of the effective potential, that is having \(\phi _{VEV}=0\) as the initial condition, then in the case of density reduction the shape of the effective potential will undergo a change to become W-shaped. So as the result of quantum fluctuations the system may leave the unstable initial point and tends to the true vacuum \(\Phi _{VEV}=\frac{\mu }{\sqrt{\lambda }}\). In other words, symmetry is spontaneously broken where density of the environment is less than a critical density \(\rho _{crit}= M^{2}\mu ^{2}\). The authors in [27] used this simple and beautiful mechanism to answer why the symmetron field can be effective at cosmic scales and play the role of dark energy while being screened in local experiments and remain undetectable.

Fig. 1
figure 1

Schematic behaviour of the effective potential as a function of scalar field \(\phi \), left: for regions where the matter density is dominant, right: for regions where the matter density is subdominant

Full size image

In the rest of the paper we try to use the same mechanism for a different purpose; we consider galactic scales where the baryonic density diminishes as one moves from the centre of a typical spiral galaxy to the galactic halo and investigate the effects of the scalar field on galactic rotation curves and deflection of light.

3 Equations of motion for a static, spherically symmetric space–time

In the following, we derive the field equations for a static spherically symmetric space–time and obtain the metric components for the model under consideration. Note that, the static spherically symmetric space–time is produced by a spherically symmetric body at rest. The static coordinate system means that the metric is independent of the time, and the spherically symmetric means that the metric components are a function of radius only. Hence, we assume that the scalar field inherits the space–time symmetry and depends only on radial coordinate, i.e. \(\phi =\phi (r)\). Let us now consider an isolated system described by a static and spherically symmetric metric given by

$$\begin{aligned} d{s^2} = - {e^{a\left( r \right) }}d{t^2} + {e^{b\left( r \right) }}d{r^2} + {r^2}d{\theta ^2} + {r^2}{\sin ^2}\theta d{\varphi ^2}, \end{aligned}$$
(14)

wherein a and b as a function of r must be chosen to satisfy the Einstein equations. Now, inserting metric (14) into Eq. (5) gives the field equations as

$$\begin{aligned}&G_t^t = - \frac{1}{{{r^2}}} + \frac{1}{{{r^2}{e^b}}} - \frac{{b'}}{{r{e^b}}} =-\frac{1}{{M_{Pl}^2}}\left( {{ \rho }^{\left[ m \right] }} +{\rho ^{\left[ \phi \right] }} \right) , \end{aligned}$$
(15)
$$\begin{aligned}&G_r^r = - \frac{1}{{{r^2}}} + \frac{1}{{{r^2}{e^b}}} + \frac{{a'}}{{r{e^b}}} =\frac{p_r^{\left[ \phi \right] }}{{M_{Pl}^2}}, \end{aligned}$$
(16)

and

$$\begin{aligned} G_\theta ^\theta = G_\varphi ^\varphi = \frac{1}{{4{e^b}}}\left( {2a'' + {{a'}^2} - a'b'} \right) + \frac{{a' - b'}}{{2r{e^b}}} =\frac{p_ \bot ^{\left[ \phi \right] } }{{M_{Pl}^2}}, \end{aligned}$$
(17)

where a prime represents derivative with respect to the radial coordinate r. In the above relations, \( T_\mu ^{\nu {\left[ \phi \right] }} = \text{ diag }\left( - {\rho ^{\left[ \phi \right] }},p_r^{\left[ \phi \right] },p_ \bot ^{\left[ \phi \right] },p_ \bot ^{\left[ \phi \right] } \right) \) where \( {p_r^{\left[ \phi \right] }} \) and \( {p_ \bot ^{\left[ \phi \right] } } \) correspond to the radial and tangential pressure components of the energy-momentum tensor of the scalar field, respectively. From relation (7), one finds

$$\begin{aligned}&{\rho ^{\left[ \phi \right] }} = - T_t^{t\left[ \phi \right] } = \frac{{{{\phi '}^2}}}{{2{e^{b\left( r \right) }}}} + V\left( \phi \right) , \end{aligned}$$
(18)
$$\begin{aligned}&p_r^{[ \phi ]} = T_r^{r\left[ \phi \right] }= \frac{{{{\phi '}^2}}}{{2{e^{b\left( r \right) }}}} - V\left( \phi \right) , \end{aligned}$$
(19)
$$\begin{aligned}&p_{\bot }^{[ \phi ]} =T_\theta ^{\theta \left[ {{\phi } } \right] } = T_\varphi ^{\varphi \left[ {{\phi } } \right] } = -\left( \frac{{{{\phi '}^2}}}{{2{e^{b\left( r \right) }}}} + V\left( \phi \right) \right) . \end{aligned}$$
(20)

Manipulation of Eqs. (15)–(17) leads to

$$\begin{aligned} \frac{{M_{Pl}^2}}{{{e^{b\left( r \right) }}}}\left( {a'' + \frac{{{{a'}^2}}}{2} - \frac{{a'b'}}{2} + \frac{{2a'}}{r}} \right) = {\rho ^{\left[ m \right] }} + {\rho ^{\left[ \phi \right] }} + p_r^{\left[ \phi \right] } + 2p_ \bot ^{\left[ \phi \right] }. \end{aligned}$$
(21)

To move on, we assume that \( a' \) and \( b' \) are slowly varying functions of the radial coordinate so that the first three terms in (21) can be neglected. Moreover, we define \({{\bar{\rho }}^{\left[ \phi \right] }} \equiv {\rho ^{\left[ \phi \right] }} + p_r^{\left[ \phi \right] } + 2p_ \bot ^{\left[ \phi \right] } \) as purely the effect of the scalar field which we call the effective scalar field density [20, 21]. Thus relation (21) changes to

$$\begin{aligned} \frac{{M_{Pl}^2}}{{{e^{b\left( r \right) }}}}\left( {\frac{{2a'}}{r}} \right) = {\rho ^{\left[ m \right] }}+ {{\bar{\rho }}^{\left[ \phi \right] }}, \end{aligned}$$
(22)

where using relations (18)–(20) leads to \( {{\bar{\rho }}^{\left[ \phi \right] }} = -2V\left( \phi \right) \). Furthermore, using metric (14), the right-hand side of (11) becomes

$$\begin{aligned} \Box \phi = \frac{1}{{{e^{b\left( r \right) }}}}\left[ {\left( {\frac{{a' - b'}}{2} + \frac{2}{r}} \right) \phi ' + \phi ''} \right] , \end{aligned}$$
(23)

so that (11) turns to

$$\begin{aligned} \left( {\frac{{a' - b'}}{2} + \frac{2}{r}} \right) \phi ' + \phi '' = {e^{b\left( r \right) }}\frac{{d{V_\mathrm{eff}}\left( \phi \right) }}{{d\phi }}. \end{aligned}$$
(24)

As was mentioned above, we focus on deriving the metric components for this model which slightly differs from that of the GR. Hence, we choose \( {e^{a(r)}}{e^{b(r)}} = F(r) \), where the function F(r) would be a slightly different from 1. For instance, if one considers

$$\begin{aligned} F\left( r \right) = {\left( {\frac{r}{s}} \right) ^\alpha } \Rightarrow a' + b' = \frac{\alpha }{r}, \end{aligned}$$
(25)

where s is the length scale of the system and \( \alpha \) is a dimensionless parameter, then the model will remain in the vicinity of GR [22, 33]. In this relation if \(\alpha \ll 1\), we have \( F(r)\approx 1 + \alpha \ln \left( {r/s} \right) \) and the above assumption would be satisfied. Since in the inner parts of galaxies the baryonic matter is dominant, it is reasonable to take the length scale of the system to be the radius of the baryonic in the galaxy, i.e. \( s=r_B \), hence we have

$$\begin{aligned} {e^{a\left( r \right) }} = {\left( {\frac{r}{{{r_B}}}} \right) ^\alpha }{e^{ - b\left( r \right) }}. \end{aligned}$$
(26)

In the next section, we propose to determine the metric components in this model using flat rotation curves of galactic halos.

4 Galactic rotation curves

The observational data show that as one moves away from the core of a galaxy up to several luminous radii, the rotational velocity increases linearly within the bulge and approaches a constant value of about \( {v_{tg}} \approx \) 200–500 km/s [1, 3]. In this section, we consider a test particle which moves in a timelike geodesic in a static and spherically symmetric system in the Einstein frame. The Newtonian limit of the geodesic equation is [34]

$$\begin{aligned} \frac{{{d^2}{x^\mu }}}{{d{\tau ^2}}} + \Gamma _{\nu \sigma }^\mu \frac{{d{x^\nu }}}{{d\tau }}\frac{{d{x^\sigma }}}{{d\tau }} = -{\frac{{d\ln A}}{{d\phi }}} {\nabla ^\mu }\phi , \end{aligned}$$
(27)

wherein \( \tau \) is an affine parameter along the geodesics of \( g_{\mu \nu } \). This equation illustrates that there is a fifth force proportional to the gradient of \( \phi \) that couples to any massive test particle. Hence, the corresponding geodesic equation for the r–coordinate in the Einstein frame will be

$$\begin{aligned} \frac{{{d^2}r}}{{d{\tau ^2}}} + \Gamma _{tt}^r = - {\frac{{d\ln A}}{{d\phi }}} {g^{rr}}{\nabla _r}\phi , \end{aligned}$$
(28)

where the Christoffel symbol \( \Gamma _{tt}^r \) contains the Newtonian force that interpreted as the fifth force [34,35,36]. For the stable circular orbits, i.e. \( dr/d\tau = 0\), inserting metric (14) into Eq. (28) gives the following relation

$$\begin{aligned} {e^a}a' = - \frac{2}{A}\left( {\frac{{dA}}{{d\phi }}} \right) \phi ', \end{aligned}$$
(29)

therefore, we have

$$\begin{aligned} {e^{a\left( r \right) }} = \ln \left( {\frac{{{C_0}}}{{{A^2}}}} \right) , \end{aligned}$$
(30)

where \( C_0 \) is a constant of integration. Moreover, in the Newtonian limit the \( g_{tt} \) component of the metric is given by \({g_{tt}} = - {e^a} \approx - 1 - 2{\psi _N} \) where \( \psi _N \) is the Newtonian potential. By regarding the Poisson equation, the force in this region is equal to \( v^{2}/r \), which respective the Newtonian potential will be as \( {\psi _N}\left( r \right) \propto {v^2}\ln r \) [37]. Also, as mentioned before, the \(\alpha \) parameter in (25) must be much smaller than 1 in order to have the theory close to GR in the constant velocity dark matter-dominated region. We consider that \(\alpha \) is approximately equal to the second power of tangential velocity, i.e. \(\alpha \approx v^{2}={v_{tg}^2}/c^{2} \approx \mathcal {O}(10^{-6}) \) [22, 33], which is compatible with our requirement. For this purpose, in the galactic halo where the dark matter dominated, we assume the metric components as the following

$$\begin{aligned} {e^{a\left( r \right) }} = C{\left( {\frac{r}{{{r_B}}}} \right) ^{2{v^2}}}, \end{aligned}$$
(31)

and

$$\begin{aligned} {e^{b\left( r \right) }} = \frac{1}{C}{\left( {\frac{r}{{{r_B}}}} \right) ^{ - {v^2}}}, \end{aligned}$$
(32)

where C is a constant. Now, using (31) we have

$$\begin{aligned} {e^a} \approx {\left( {\frac{r}{{{r_B}}}} \right) ^{2{v^2}}} = \exp \left\{ {\ln {{\left( {\frac{r}{{{r_B}}}} \right) }^{2{v^2}}}} \right\} \approx 1 + 2{v^2}\ln {\left( {\frac{r}{{{r_B}}}} \right) } = 1 + 2{\psi _N}\left( r \right) . \end{aligned}$$
(33)

Therefore our model has a well-defined Newtonian limit, and metric components (31) and (32) can describe the geometry of the space–time in the region of the flat rotation curves. Furthermore, metric component (31) should be equal to relation (30) in the radius of the galactic halo. Hence, by using relation (4) we can obtain \( {\left. A \right| _{r = {r_B}}} = 1 \), which leads to have \( {C_0} = {e^C} \) as a constraint.

Now, we want to investigate the flat rotation curve in the halo of galaxies by using metric components (31) and (32). Considering the fact that the density of baryonic matter in a galactic halo rapidly decreases with radius, we argue that the mass assigned to the effects of the symmetron field density can explain the flat rotation curves without resorting to a dark matter. Since in this region, the baryonic matter is subdominant, we consider \( {\rho ^{\left[ m \right] }} \ll {{\bar{\rho }}^{\left[ \phi \right] }} \) which is equivalent to \( {\rho } \ll {\mu ^2}{M^2} \). In the region of our consideration, i.e. \(r_{B}<r<r_{D}\), where the baryonic density is subdominant, one can use (22) to obtain the effect of the scalar field density as

$$\begin{aligned} {{\bar{\rho }}^{\left[ \phi \right] }} \simeq \frac{{4M_{Pl}^2C{v^2}}}{{r_B^{{v^2}}}}{r^{{v^{2}- 2}}}. \end{aligned}$$
(34)

This relation clearly shows that \( {{\bar{\rho }}^{\left[ \phi \right] }} \propto {r^{ - 2}} \), which means that the effect of the symmetron mass varies linearly with r, i.e.

$$\begin{aligned} {\overline{M} ^{\left[ \phi \right] }} = \int \limits _0^{{r_D}} {4\pi {r^2}} {\overline{\rho }^{\left[ \phi \right] }}dr, \end{aligned}$$
(35)

so the symmetron mass can be held responsible for flat rotation curves in the halo of galaxies and plays the role of dark matter.Footnote 2

At the end of this section, we investigate the symmetron profile for \(r_{B}<r<r_{D}\) and show that the field starts from an initial zero value at \(r_{B}\) and, as a result of baryonic density reduction, tends to a final nonzero value which is the true minimum of the effective potential. To do so, using metric components (31) we rewrite Eq. (24) in terms of dimensionless variables

$$\begin{aligned} \tilde{\phi }=\frac{\phi }{\phi _{VEV}}=\frac{\phi \sqrt{\lambda }}{\mu }, \quad \tilde{r}=\frac{r}{r_{B}}, \quad \tilde{\mu }=\mu r_{B}, \end{aligned}$$
(36)

giving

$$\begin{aligned} \frac{d^{2}\tilde{\phi }}{d\tilde{r}^2}+ \frac{2}{\tilde{r}}\frac{d\tilde{\phi }}{d\tilde{r}}=\frac{\tilde{\mu }^{2}}{C}\tilde{r}^{-v^{2}} (-\tilde{\phi }+\tilde{\phi }^{3}). \end{aligned}$$
(37)

By numerically integrating Eq. (37), the behaviour of the symmetron field in a galaxy halo is revealed. Figure 2 shows the behaviour of the symmetron profile as a function of dimensionless variable \(\tilde{r}\). As can be seen, the scalar moves from the initial value \(\phi _{0}=0\) at \(r_{B}\) to the final value \(\phi _{VEV}=\frac{\mu }{\sqrt{\lambda }}\) at \(r_{D}\) which, according to Sect. 2, is compatible with the expected effect of baryonic density reduction on the dynamic of the symmetron field. Thus, our proposed model for the space–time geometry in the dark matter halo range, i.e. metric components (31) and (32), is appropriate for describing symmetron field behaviour in the dark matter-dominated area.

Fig. 2
figure 2

Symmetron profile as a function of \(\tilde{r}=\frac{r}{r_{B}}\) in halo region for \(\frac{\tilde{\mu }^{2}}{C}=0.001\) , \(v^{2}= 10^{-6}\) and \(r_{D}=10 r_{B}\). The plot shows the proper evolution of symmetron field from initial zero value to the true nonzero value which is the true minimum of the effective potential \(\phi _{VEV}\)

Full size image

5 Light deflection angle

Let us now concentrate on the deflection angle of light as an effect of dark matter in our symmetron model. For this purpose, we consider a photon approaching a galaxy from afar. The gravitational field leads to the bending of light at a deflection angle \( \Delta \varphi \) given by

$$\begin{aligned} \Delta \varphi = 2\left| {\varphi \left( {{r_0}} \right) - \varphi \left( \infty \right) } \right| - \pi , \end{aligned}$$
(38)

where \( r_{0} \) is the radius of the closest approach to the centre of the galaxy and \( \varphi \left( \infty \right) \) is the incident direction.Footnote 3 Generally, the geodesic equation for a photon reduces to [38]

$$\begin{aligned} \varphi \left( {{r_0}} \right) - \varphi \left( \infty \right) = {\int _{{r_0}}^{\infty } {{e^{\frac{{b \left( r \right) }}{2}}}\left[ {{e^{a\left( {{r_0}} \right) - a\left( r \right) }}{{ \left( {\frac{r}{{{r_0}}}} \right) }^2} - 1} \right] } ^{ - \frac{1}{2}}}\frac{{dr}}{r}. \end{aligned}$$
(39)

Considering the metric components in the region of flat rotation curves, i.e. relations (31) and (32), the above equation leads to

$$\begin{aligned} \varphi \left( {{r_0}} \right) - \varphi \left( \infty \right)= & {} \sqrt{\frac{{r_B^{{v^2}}}}{C}} {\int _{{r_0}}^{{r_D}} {\left[ {{{\left( {\frac{{{r_0}}}{r}} \right) }^{2{v^2} - 2}} - 1} \right] } ^{ - \frac{1}{2}}}\frac{{dr}}{{{r^{1 + \frac{{{v^2}}}{2}}}}}\nonumber \\&+\, \int _{{r_D}}^{{\infty }} {\frac{1}{{\sqrt{1 - \frac{{M}}{4\pi M_{Pl}^2 r}} }}} {\left[ {\frac{{1 - \frac{{M}}{{4\pi M_{Pl}^2{r_0}}}}}{{1 - \frac{{M}}{4\pi M_{Pl}^2 r}}}{{\left( {\frac{r}{{{r_0}}}} \right) }^2} - 1} \right] ^{ - \frac{1}{2}}}\frac{{dr}}{r}, \end{aligned}$$
(40)

where, in the first integral, we have considered \( r_{0} \) to be in the region of flat rotation curves, i.e. \( r_{B} \leqslant r_{0}<r_{D} \). Now, one can exactly integrate the first term in Eq. (40) which corresponds to the dark matter-dominated region where flat rotation curves are under consideration. Also, the second integral in Eq. (40) relates to the exterior region of dark matter halo whose integration with Schwarzschild metric using Robertson expansion [38] results in

$$\begin{aligned} \Delta \varphi= & {} 2\left| \frac{1}{{\sqrt{C} \left( {1 - {v^2}} \right) }}{\left( {\frac{{{r_B}}}{{{r_0}}}} \right) ^{\frac{{{v^2}}}{2}}}\arctan \left( {\sqrt{{{\left( {\frac{{{r_0}}}{{{r_D}}}} \right) }^{2{v^2} - 2}} - 1} } \right) \right. \nonumber \\&+\, \left. {\arcsin \left( {\frac{{{r_0}}}{{{r_D}}}} \right) + \frac{{M}}{{8\pi {M_{Pl}^2}{r_0}}} \left[ {2 - \sqrt{1 - {{\left( {\frac{{{r_0}}}{{{r_D}}}} \right) }^2}} - \sqrt{\frac{{{r_D} - {r_0}}}{{{r_D} + r_{0}}}} } \right] } \right| - \pi . \end{aligned}$$
(41)

Variation of the light deflection angle, as a function of \( r_{0}/r_{D} \) in a galactic halo by using the data from Ref. [33], is plotted in Fig. 3 with the NGC 5533 galaxy with \( {v_{tg}} = 250\) km/s, the NGC 4138 galaxy with \( {v_{tg}} = 147\) km/s and the UGC 6818 galaxy with \( {v_{tg}} = 73\) km/s, and all with \( C=10^{12} \). Moreover, we assume that the halo cut-off, i.e. \({r_D} \) to be at \( {r_D} = 10{r_B} \), which is consistent with observation. Also, in the second and third terms of Eq. (41), obtained from the second integral of Eq. (40), when \(r_0=r_D\), Eq. (41) yields \(\Delta \varphi =M/2\pi M_{Pl}^2{r_D} = 4GM/r_D\) as in GR, see e.g. [33].

Fig. 3
figure 3

Light deflection angle as a function of \( r_{0}/r_{D}\) for the galaxies NGC 5533 (dash), NGC 4138 (dot), UGC 6818 (solid) and \( C=10^{12} \)

Full size image

The comparison of the result of this diagram with other dark matter models such as generalized pseudo-isothermal dark matter [39, 40], brane F(R) gravity [21] or F(R, T) gravity [22], demonstrates that all such models have similar behaviour in general in the sense that the deflection angle reduces in the halo of dark matter with radius.

6 Conclusions

In this work, we have considered the symmetron model to describe dark matter effects on galaxies as inferred from flat rotation curves. We have shown that our suggested model for the metric components has a well-defined Newtonian limit in the halo of the galaxies. In addition, the comparison between our model and the metric component obtained from the geodesic equation in the Einstein frame causes to appearing a constraint on the constant of integration. Also, the effective scalar field density \( {{\bar{\rho }}^{\left[ \phi \right] }} \), as a pure effect of the symmetron scalar field in the model presented here, can be considered as an alternative for dark matter effects in galaxies. Taking into account that the density of the baryonic matter in a galaxy’s halo is feeble, we have shown that the assumption \( {\rho ^{\left[ m \right] }} \ll {{\bar{\rho }}^{\left[ \phi \right] }} \) can lead to a symmetron mass term in modified Einstein field equations which varies linearly with radius, hence resulting in flat rotation curves in a galactic halo. Note that the special feature of the effective potential of the symmetron field leads to spontaneous symmetry breaking in the halo region, so the flatness of rotation curves of galaxies can be explained without the need of the mysterious dark matter.

Furthermore, to investigate another effect of dark matter on galaxies we studied the propagation of light in our model. For this purpose, we obtained the light deflection angle in galactic halos by using metric components proposed for the space–time geometry in this range. The diagram indicates that the angle representing the deflection of light reduces in the halo of a galaxy with radius, showing that its behaviour in our model is generally similar to a number of other models, namely the generalized pseudo-isothermal dark matter model with exponential matter density, brane F(R) gravity and F(R, T) gravity. It is, therefore, reasonable to consider the symmetron field as an alternative to dark matter by using our proposed model for the metric components in galactic halos.