Computational techniques for highly oscillatory and chaotic wave problems with fractional-order operator

Abstract

In this paper, we study the dynamic evolution of chaotic and oscillatory waves arising from dissipative dynamical systems of elliptic and parabolic types of partial differential equations. In such a system, the classical second-order partial derivatives are modeled with the Riesz fractional-order operator in one and two dimensions. We employ both finite difference schemes and the Fourier spectral methods for the approximation of fractional derivatives. We examined the accuracy of the schemes by reporting their convergence results. These numerical techniques are applied to solve two practical problems that are of current and recurring interests, namely the fractional multi-wing chaotic system and fractional Helmholtz equation in one and two spatial dimensions. In the computational experiments, it was observed that under certain conditions, nonlinear dynamical system which depends on some variables is able to produce the so-called chaotic patterns. The present example shows a sensitive dependence on the choice of parameters and initial conditions. Some numerical results are presented for different instances of fractional power.

1 Introduction

Nonlinear chaotic models are dynamical systems that are widely celebrated in the literature due to their useful applications in many areas of applied sciences and engineering. Based on chaotic system, an increasing number of research papers has been published over the years, for instance, the chaotic circuit based on memristor [63], Chen and Ueta’s system [11], Lorenz’s system [28], simple chaotic flows [52], Rössler’s system [47], memristive chaotic model with bird- and heart-shaped attractors [5, 62], CMOS transistor oscillators [43], digital and circuit realization of chaotic systems [30], analog digital designs [44], chaotic mythical bird system [5], butterfly wings and paradise bird map model [1].

Nowadays, oscillatory and complex chaotic processes have been used for theoretical, practical or experimental purposes in different application areas, which include the pathological image encryption [26], chaotic communication [12], image watermarking [61], chaotic video communication scheme via WAN remote transmission [25] autonomous mobile robots [58], control and synchronization [45], audio and image encryption effects [27, 32] and electromechanical oscillators [10], among several others.

Over the last few decades the concept of fractional calculus (which involves the extension of standard differentiation and integration to fractional cases) has become a strong tool for describing the dynamics of complex scenarios which appear most often in virtually all application field of engineering and sciences. Fractional differentiation and their methods of solution have a lot of applications in the areas of physics, electrochemistry, control theory, finance and economics, electrical circuits, robotics, viscoelasticity, ecology, biology and other physical systems [7, 36, 37, 41]. Majority of the work reported on the dynamics of chaotic systems which attract a great attention of researchers are either based on integer-order or fractional-order ordinary differential equations.

Recently, the study of fractional differential equations such as the fractional wave and diffusion equations [41], control systems [49], biological systems, ecological and chemical systems, chaotic systems [36, 39, 40], subdiffusion and superdiffusion processes [35], finance, electrical problems, viscoelasticity theory [49] and bioengineering [29] has been arisen in many applications of the applied sciences, engineering and technology. Over the years, the concept of fractional calculus which is the generalization of the classical integration and differentiation to fractional-order derivatives and integrals has been applied and used to model many physical and real-life phenomena in physics, biology, groundwater and economics [23].

In real sense, partial differential equations (PDEs) have been used to describe a wide variety of phenomena such as diffusion, electrostatics, sound, fluid dynamics, heat, electrodynamics, elasticity, gravitation and quantum mechanics. Most of these models that are governed by PDE combine low-order nonlinear with higher-order linear terms. For instance, the time-dependent models such as Allen–Cahn, Fisher–KPP, Gray–Scott, KdV, Navier–Stokes, Schroödinger, Bugers, Burger–Huxley, Hodgkin–Huxley, Cahn–Hilliard, FitzHugh–Nagumo and nonlinear KiSS equations, among several others. It is desirable to utilize higher-order approximations in both time and space, in order to obtain accurate numerical results. Due to some computational challenges imposed as by the combination of nonlinearity and stiffness which lead many authors to restrict their computational to second-order schemes in time, we are motivated in this work with the formulation of higher-order numerical schemes which are capable of handling both elliptic and parabolic types of fractional partial differential equations (FPDEs).

In this work, we shall consider the solution of a time-dependent reaction–diffusion equation of the form

$$\begin{aligned} \varvec{w}_t={\mathcal {L}}^\alpha \varvec{w} + \mathcal {N}(\varvec{w},t), \end{aligned}$$

(1.1)

where $\varvec{w}$ is the species concentrations or densities, ${\mathcal {L}}$ is the linear or nonlinear (stiff) fractional operator of order $\alpha \in (1,2]$, which requires a fast solver to formulate into higher dimensions, and $\mathcal {N}$ denotes nonlinear (nonstiff or mildly stiff) operator which accounts for all the local kinetics in the equation. Equations of the form (1.1) have been solved using different numerical methods, such as the implicit–explicit (IMEX) schemes [3, 4, 24, 48], finite difference methods [31, 53, 56], finite element [9, 46] and spectral algorithms [8, 38].

Here, in one dimension, we define the Riesz fractional derivative of order $\alpha \in (1,2]$, as

$$\begin{aligned} {\mathcal {L}}^\alpha \varvec{w}=\frac{\partial ^\alpha \varvec{w}(x,t)}{\partial x^\alpha }=-c_\alpha (_0D_x^\alpha +{_xD^\alpha _L})\varvec{w}(x,t), \end{aligned}$$

(1.2)

where

$$\begin{aligned}&c_\alpha =\frac{1}{2\cos \left( \frac{\pi \alpha }{2}\right) },\;\;\;\alpha \ne 1,\\&_0D_x^\alpha \varvec{w}(x,t)=\frac{1}{\Gamma (2-\alpha )} \frac{\partial ^2}{\partial x^2}\int _{0}^{x} \frac{\varvec{w}(\tau ,t)}{(x-\tau )^{\alpha -1}}\mathrm{d}\tau ,\\&_xD_L^\alpha \varvec{w}(x,t)=\frac{1}{\Gamma (2-\alpha )} \frac{\partial ^2}{\partial x^2}\int _{x}^{L}\frac{\varvec{w}(\tau ,t)}{(\tau -x)^{\alpha -1}}\mathrm{d}\tau . \end{aligned}$$

The terms $_0D_x^\alpha$ and $_xD_L^\alpha$ are expressed as the left- and right-hand side of the Riemann–Liouville fractional derivatives. The fractional reaction–diffusion model described in (1.1) has a lot of physical meaning and applications; see [41, 65] for details. The aim of the present work is to explore the dynamic richness in chaotic and oscillatory fractional diffusive models of either parabolic or elliptic type of PDEs, and to seek appropriate numerical techniques of arriving at solution.

The remainder part of this paper is organized into sections as follows. In Sect. 2, we give detailed definitions, theorems and some useful results for subdifussive and superdiffusive cases of the fractional operator. In Sect. 3, we introduced some numerical schemes based on the finite difference and spectral methods for the approximation of the Riesz fractional derivatives. The accuracy, applicability and suitability of the proposed schemes are tested on some practical problems taken from the literature in Sect. 4. We conclude with the last section.

2 Preliminaries on Riesz fractional operator

We begin this section with a quick tour of some useful definitions and theorem used for subdiffusion $(0<\alpha \le 1)$ and superdiffusion $(1<\alpha \le 2)$ cases in one component [35].

Definition 2.1

[41, 51, 64] The Riesz fractional derivative for $\alpha \in (n-1, n]$ defined on interval $x\in (0,L]$ is given by

$$\begin{aligned} \frac{\partial ^\alpha {w}(x,t)}{\partial x^\alpha }=-c_\alpha (_0D_x^\alpha +{_xD^\alpha _L}){w}(x,t), \end{aligned}$$

where

$$\begin{aligned}&c_\alpha =\frac{1}{2\cos \left( \frac{\pi \alpha }{2}\right) },\;\;\;\alpha \ne 1,\\&_0D_x^\alpha {w}(x,t)=\frac{1}{\Gamma (n-\alpha )}\frac{\partial ^n}{\partial x^n}\int _{0}^{x}\frac{{w}(\tau ,t)}{(x-\tau )^{\alpha +1-n}}\mathrm{d}\tau ,\\&_xD_L^\alpha {w}(x,t)=\frac{1}{\Gamma (n-\alpha )}\frac{\partial ^n}{\partial x^n}\int _{x}^{L}\frac{{w}(\tau ,t)}{(\tau -x)^{\alpha +1-n}}\mathrm{d}\tau . \end{aligned}$$

Theorem 2.2

For a continuous function w(x) defined on $-\infty< x<\infty$, the following inequality is satisfied.

$$\begin{aligned} {\mathcal {L}}^\alpha w(x)=\frac{\partial ^\alpha u(x)}{\partial |x|^\alpha }=-(-\Delta )^{\alpha /2}\varvec{w}(x)=-\frac{1}{2\cos \left( \frac{\pi \alpha }{2}\right) }\left[ _{-\infty }D^\alpha _x{w}(x)+ {_xD_\infty ^\alpha w(x)}\right] . \end{aligned}$$

Proof

By following [35, 51], the fractional Laplacian operator is defined as

$$\begin{aligned} -(-\Delta )^{\alpha /2}w(x)=-\mathscr {F}^{-1}|x|^\alpha \mathscr {F}w(x), \end{aligned}$$

(2.3)

where $\mathscr {F}$ represents the Fourier transform, and $\mathscr {F}^{-1}$ denotes the inverse Fourier transform of function w(x), so that

$$\begin{aligned} -(-\Delta )^{\alpha /2}w(x)=-\frac{1}{2\pi }\int _{-\infty }^{\infty }e^{ix\tau }| \tau |^\alpha \int _{-\infty }^{\infty }e^{i\tau \xi }w(\xi )\mathrm{d}\xi \mathrm{d}\tau . \end{aligned}$$

In the function, w(x) vanishes at $x=\pm \infty$, by applying integration by parts

$$\begin{aligned} \int _{-\infty }^{\infty }e^{i\tau \xi }w(\xi )\mathrm{d}\xi =-\frac{1}{i\tau } \int _{-\infty }^{\infty }e^{i\tau \xi }w'(\xi )\mathrm{d}\xi , \end{aligned}$$

which implies that

$$\begin{aligned} -(-\Delta )^{\alpha /2}w(x)=-\frac{1}{2\pi }\int _{-\infty }^{\infty }w'(\xi )\ \left( i\int _{-\infty }^{\infty }e^{i\tau (\xi -x)}\frac{|\tau |^\alpha }{\tau }\mathrm{d}\tau \right) \mathrm{d}\xi . \end{aligned}$$

For simplicity, we denote

$$\begin{aligned} G_1=i\int _{-\infty }^{\infty }e^{i\tau (\xi -x)}\frac{|\tau |^\alpha }{\tau }\mathrm{d}\tau , \end{aligned}$$

so that

$$\begin{aligned} G_1=i\left( \int _{0}^{\infty }e^{i\tau (\xi -x)}\tau ^{\alpha -1}\mathrm{d}\tau - \int _{0}^{\infty } e^{i\tau (x-\xi )}\tau ^{\alpha -1}\mathrm{d}\tau \right) . \end{aligned}$$

Bear in mind that

$$\begin{aligned} \mathscr {L}(t^{\sigma -1})=\int _{0}^{\infty }e^{-st}t^{\sigma }\mathrm{d}t= \frac{\Gamma (\sigma )}{s^\sigma },\;\;\mathfrak {R}(\sigma )>0, \end{aligned}$$

and for case $0<\alpha <1$, we get

$$\begin{aligned} G_1=i\left( \frac{\Gamma (\alpha )}{[i(x-\xi )]^\alpha }-\frac{\Gamma (\alpha )}{[i(\xi -x)]^\alpha }\right) =\frac{\text {sign}(x-\xi )\Gamma (\alpha )\Gamma (1-\alpha )}{|x-\xi |^\alpha \Gamma (1-\alpha )}\left[ i^{\alpha -1}+(-i)^{\alpha -1}\right] . \end{aligned}$$

By applying the known result $\Gamma (\alpha )\Gamma (1-\alpha )=\pi /\sin \pi \alpha$ and $i^{\alpha -1}+(-i)^{\alpha -1}=2\sin \left( \frac{\pi \alpha }{2}\right)$, we get

$$\begin{aligned} G_1=\frac{\text {sign}(x-\xi )\pi }{2\cos \left( \frac{\pi \alpha }{2}\right) |x -\xi |^\alpha \Gamma (1-\alpha )}. \end{aligned}$$

Therefore, for subdiffusion interval $0<\alpha <1$,

$$\begin{aligned} -(-\Delta )^{\alpha /2}w(x)= & {} -\frac{1}{2\pi }\int _{-\infty }^{\infty }w'(\xi ) \frac{\text {sign}(x-\xi )\pi }{2\cos \left( \frac{\pi \alpha }{2}\right) |x-\xi |^\alpha \Gamma (1-\alpha )}\mathrm{d}\xi \nonumber \\= & {} -\frac{1}{2\cos \left( \frac{\pi \alpha }{2}\right) }\left( \frac{1}{\Gamma (1-\alpha )}\int _{-\infty }^{x}\frac{w'(\xi )}{(x-\xi )^\alpha }\mathrm{d}\xi - \frac{1}{\Gamma (1-\alpha )}\int ^{\infty }_{x}\frac{w'(\xi )}{(\xi -x)^\alpha }\mathrm{d}\xi \right) .\nonumber \\ \end{aligned}$$

(2.4)

According to Podlubny [41], the Grünwald–Letnikov fractional operator of order $\alpha \in (0,1]$ in [a, x] is defined by

$$\begin{aligned} _aD^\alpha _xw(x)=\frac{w(a)(x-a)^{-\alpha }}{\Gamma (1-\alpha )}+\frac{1}{\Gamma (1 -\alpha )}\int _{a}^{x}\frac{w'(\xi )}{(x-\xi )^\alpha }\mathrm{d}\xi . \end{aligned}$$

If $a\rightarrow -\infty$, we have

$$\begin{aligned} _{-\infty }D^\alpha _xw(x)=\frac{1}{\Gamma (1-\alpha )}\int _{-\infty }^{x}\frac{w'(\xi )}{(x-\xi )^\alpha }\mathrm{d}\xi . \end{aligned}$$

In the same manner, if $u(x)\rightarrow 0$ for $b\rightarrow \infty$, we obtain

$$\begin{aligned} _xD^\alpha _xw(x)=\frac{-1}{\Gamma (1-\alpha )}\int ^{\infty }_{x}\frac{w'(\xi )}{(\xi -x)^\alpha }\mathrm{d}\xi . \end{aligned}$$

Therefore, since w(x) is integrable and continuous for $x\ge a$ for all $\alpha \in (0,1)$, then the Riemann–Liouville fractional derivative is the same as the Grünwald–Letnikov fractional operator. Hence, for all $\alpha \in (0,1)$, we say

$$\begin{aligned} {\mathcal {L}}^\alpha w(x)=\frac{\partial ^\alpha w(x)}{\partial |x|^\alpha }=-(-\Delta )^{\alpha /2}{w}(x)=-\frac{1}{2\cos \left( \frac{\pi \alpha }{2}\right) }\left[ _{-\infty }D^\alpha _x{w}(x)+ {_xD_\infty ^\alpha w(x)}\right] , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} _{-\infty }D^\alpha _xw(x)&=\frac{1}{\Gamma (1-\alpha )}\int _{-\infty }^{x}\frac{w'(\xi )}{(x-\xi )^\alpha }\mathrm{d}\xi \\ _xD^\alpha _xw(x)&=\frac{-1}{\Gamma (1-\alpha )}\int ^{\infty }_{x}\frac{w'(\xi )}{(\xi -x)^\alpha }\mathrm{d}\xi . \end{aligned} \end{aligned}$$

Again, we consider the superdiffusive case we follow a similar derivation in the interval $\alpha \in (1,2]$. We assume that the function w(x) and its derivative $w'(x)$ both vanish as $x\rightarrow \pm \infty$. And by integration by parts, we have

$$\begin{aligned} \int _{-\infty }^{\infty }e^{i\tau \xi }w(\xi )\mathrm{d}\xi =-\tau ^{-2}\int _{-\infty }^{\infty } e^{i\tau \xi }w''(\xi )\mathrm{d}\xi , \end{aligned}$$

so that

$$\begin{aligned} -(-\Delta )^{\alpha /2}w(x)= & {} -\frac{1}{2\pi }\int _{-\infty }^{\infty }e^{-ix\tau }|\tau |^\alpha \left[ -\tau ^{-2} \int _{-\infty }^{\infty }e^{i\tau \xi }w''(\xi )d\xi \right] \mathrm{d}\tau \nonumber \\= & {} \frac{1}{2\pi }\int _{-\infty }^{\infty }w''(\xi )\left( \int _{-\infty }^{\infty }e^{i\tau (\xi -x)} |\tau |^{\alpha -2}d\tau \right) \mathrm{d}\xi . \end{aligned}$$

(2.5)

We assume

$$\begin{aligned} G_2=\int _{-\infty }^{\infty }e^{i\tau (\xi -x)}|\tau |^{\alpha -2}\mathrm{d}\tau , \end{aligned}$$

then

$$\begin{aligned} G_2=\int _{0}^{\infty }e^{i\tau (x-\xi )}|\tau |^{\alpha -2}\mathrm{d}\tau +\int _{0}^{\infty } e^{i\tau (\xi -x)}|\tau |^{\alpha -2}\mathrm{d}\tau . \end{aligned}$$

Also bear in mind that

$$\begin{aligned} \mathscr {L}(t^{\sigma -2})=\int _{0}^{\int }e^{-st}t^{\sigma -2}\mathrm{d}t= \frac{\Gamma (\sigma -1)}{s^{\sigma -1}},\;\;\;\mathfrak {R}(\sigma )>1, \end{aligned}$$

we obtain

$$\begin{aligned} G_2=\frac{\Gamma (\alpha -1)}{[i(\xi -x)]^{\alpha -1}}+\frac{\Gamma (\alpha -1)}{[i(x-\xi )]^{\alpha -1}}=\frac{\Gamma (\alpha -1)\Gamma (2-\alpha )}{|x-\xi |^{\alpha -1}\Gamma (2-\alpha )} \left[ i^{\alpha -1}+(-i)^{\alpha -1}\right] . \end{aligned}$$

By applying $\Gamma (\alpha -1)\Gamma (2-\alpha )=\pi /\sin \pi (\alpha -1) =-\pi /\sin (\pi \alpha )$ and $i^{\alpha -1}+(-i)^{\alpha -1}=2\sin \left( \frac{\pi \alpha }{2}\right)$, we get

$$\begin{aligned} G_1=\frac{\pi }{\cos \left( \frac{\pi \alpha }{2}\right) |x-\xi |^(\alpha -1)\Gamma (2-\alpha )}. \end{aligned}$$

Hence, for superdiffusion case $1<\alpha <2$,

$$\begin{aligned} \begin{aligned}&-(-\Delta )^{\alpha /2}w(x)=-\frac{1}{2\pi }\int _{-\infty }^{\infty }w''(\xi ) \frac{\pi }{\cos \left( \frac{\pi \alpha }{2}\right) |x-\xi |^{\alpha -1}\Gamma (2-\alpha )}\mathrm{d}\xi \\&=-\frac{1}{2\cos \left( \frac{\pi \alpha }{2}\right) }\left( \frac{1}{\Gamma (2-\alpha )}\int _{-\infty }^{x}\frac{w''(\xi )}{(x-\xi )^{\alpha -1}}\mathrm{d}\xi + \frac{1}{\Gamma (2-\alpha )}\int ^{\infty }_{x}\frac{w''(\xi )}{(\xi -x)^{\alpha -1}}\mathrm{d}\xi \right) . \end{aligned}\nonumber \\ \end{aligned}$$

(2.6)

According to Podlubny [41], the Grünwald–Letnikov fractional operator for superdiffusive order $\alpha \in (1,2]$ in [a, x] is defined by

$$\begin{aligned} _aD^\alpha _xw(x)=\frac{w(a)(x-a)^{-\alpha }}{\Gamma (1-\alpha )} \frac{w'(a)(x-a)^{1-\alpha }}{\Gamma (2-\alpha )}+\frac{1}{\Gamma (2-\alpha )}\int _{a}^{x} \frac{w''(\xi )}{(x-\xi )^{\alpha -1}}\mathrm{d}\xi . \end{aligned}$$

So, if w(x) and $w'(x)$ both tend to zero as $a\rightarrow -\infty$, we have

$$\begin{aligned} _{-\infty }D^\alpha _xw(x)=\frac{1}{\Gamma (2-\alpha )}\int _{a}^{x} \frac{w''(\xi )}{(x-\xi )^{\alpha -1}}\mathrm{d}\xi . \end{aligned}$$

Also, if $w(x),w'(x)\rightarrow 0$ for $b\rightarrow \infty$, we obtain

$$\begin{aligned} _xD^\alpha _xw(x)=\frac{1}{\Gamma (2-\alpha )}\int ^{\infty }_{x} \frac{w''(\xi )}{(\xi -x)^{\alpha -1}}\mathrm{d}\xi . \end{aligned}$$

If both w(x) and $w'(x)$ are integrable and continuous for $x\ge a$, then Riemann–Liouville fractional derivative coincides with the Grünwald–Letnikov operator. Hence, for superdiffusive process we have

$$\begin{aligned} {\mathcal {L}}^\alpha w(x)=\frac{\partial ^\alpha w(x)}{\partial |x|^\alpha } =-(-\Delta )^{\alpha /2}{w}(x)=-\frac{1}{2\cos \left( \frac{\pi \alpha }{2}\right) }\left[ _{-\infty }D^\alpha _x{w}(x)+ {_xD_\infty ^\alpha w(x)}\right] , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} _{-\infty }D^\alpha _xw(x)&=\frac{1}{\Gamma (2-\alpha )}\frac{\partial ^2}{\partial x^2}\int _{-\infty }^{x}\frac{w(\xi )}{(x-\xi )^{\alpha -1}}\mathrm{d}\xi \\ _xD^\alpha _xw(x)&=\frac{1}{\Gamma (2-\alpha )}\frac{\partial ^2}{\partial x^2}\int ^{\infty }_{x}\frac{w(\xi )}{(\xi -x)^{\alpha -1}}\mathrm{d}\xi . \end{aligned} \end{aligned}$$

Finally, if $n-1<\alpha <n$ then

$$\begin{aligned} {\mathcal {L}}^\alpha w(x)=\frac{\partial ^\alpha w(x)}{\partial |x|^\alpha }=-(-\Delta )^{\alpha /2}{w}(x)=-\frac{1}{2\cos \left( \frac{\pi \alpha }{2}\right) }\left[ _{-\infty }D^\alpha _x{w}(x)+ {_xD_\infty ^\alpha w(x)}\right] , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} _{-\infty }D^\alpha _xw(x)&=\frac{1}{\Gamma (n-\alpha )}\frac{\partial ^n}{\partial x^n}\int _{-\infty }^{x}\frac{w(\xi )}{(x-\xi )^{\alpha +1-n}}\mathrm{d}\xi ,\\ _xD^\alpha _xw(x)&=\frac{(-1)^n}{\Gamma (n-\alpha )}\frac{\partial ^n}{\partial x^n}\int ^{\infty }_{x}\frac{w(\xi )}{(\xi -x)^{\alpha +1-n}}\mathrm{d}\xi . \end{aligned} \end{aligned}$$

3 Approximation techniques

In this segment, we use results of definition2.1 and Theorem 2.2 and give numerical approximation to the following Riesz fractional diffusion equation [19, 20, 55, 64, 66]

$$\begin{aligned} \frac{\partial w}{\partial t}=\delta \frac{\partial ^\alpha w(x,t)}{\partial x^\alpha },\;\;\;0<x<L,\;\;0<t\le T,\;\;1<\alpha \le 2 \end{aligned}$$

(3.7)

subject to initial and boundary conditions

$$\begin{aligned} \begin{aligned} w(x,0)&=\beta (x),\\ w(0,t)&=0,\;\;w(L,t)=0, \end{aligned} \end{aligned}$$

(3.8)

where $\delta >0$ is the diffusion coefficient, and both functions w(x, t) are real-valued.

The Riesz fractional derivative of order $1<\alpha \le 2$ is given by the left- and right-hand Grünwald-Letnikov (GL) fractional operator on finite interval [0, L] as

$$\begin{aligned} _0\mathcal {D}_x^\alpha w(x)= & {} \frac{w(0)x^{-\alpha }}{\Gamma (1-\alpha )}+\frac{w'(0)x^{1-\alpha }}{\Gamma (2-\alpha )}+\frac{1}{\Gamma (2-\alpha )}\int _{0}^{x}\frac{w^{(2)}(\tau )}{(x-\tau )^{\alpha -1}}\mathrm{d}\tau ,\nonumber \\ _x\mathcal {D}_L^\alpha w(x)= & {} \frac{w(L)(L-x)^{-\alpha }}{\Gamma (1-\alpha )}+\frac{w'(L)(L-x)^{1-\alpha }}{\Gamma (2-\alpha )}+\frac{1}{\Gamma (2-\alpha )}\int _{x}^{L}\frac{w^{(2)}(\tau )}{(\tau -x)^{\alpha -1}}\mathrm{d}\tau .\qquad \nonumber \\ \end{aligned}$$

(3.9)

It should be noted that the infinite space domain $(-\infty ,\infty )$ as discussed in the above section is now truncated with the finite case [0, L]. The space $L>0$ should be adjusted in the computation to ensure that there is enough space for waves to propagate. By following [19, 41, 64], the mesh is N equal intervals of $h=L/N$, $x_s=sh$ for $0\le s\le N$. Next we approximate (3.9) term by term. Beginning with the right-hand side, we approximate the second term by

$$\begin{aligned} \frac{w'(0)x^{1-\alpha }}{\Gamma (2-\alpha )}\approx \frac{h^{-\alpha }}{\Gamma (2-\alpha )t^{\alpha -1}} (w_1-w_0). \end{aligned}$$

(3.10)

Also, we approximate the third term by

$$\begin{aligned} \begin{aligned} \frac{1}{\Gamma (2-\alpha )}\int _{0}^{x}\frac{w^{(2)}(x-\tau )}{(\tau )^{\alpha -1}} \mathrm{d}\tau&=\frac{1}{\Gamma (2-\alpha )}\int _{0}^{x}\frac{w^{(2)}(\tau )}{(x-\tau )^{\alpha -1}}\mathrm{d}\tau \\&=\frac{1}{\Gamma (2-\alpha )}\sum _{i=0}^{s-1}\int _{ih}^{h(i+1)}\frac{w^{(2)} (\tau )}{(x-\tau )^{\alpha -1}}\mathrm{d}\tau \\&\approx \frac{1}{\Gamma (2-\alpha )}\sum _{i=0}^{s-1}\frac{w(x-h(i-1))-2w(x-ih) +w(x-h(i+1))}{h^2}\\&\;\;\;\;\times \int _{ih}^{h(i+1)}\frac{\mathrm{d}\tau }{\tau ^{\alpha -1}}\\&=\frac{h^{-\alpha }}{\Gamma (3-\alpha )}\sum _{i=0}^{s-1}(w_{s-i+1}-2w_{s-i}+w_{s-i-1})\\&\;\;\;\;\times \left\{ (i+1)^{2-\alpha }-i^{2-\alpha } \right\} ,\;\;\text {for}\;w(x-ih)=w_{s-i}. \end{aligned}\nonumber \\ \end{aligned}$$

(3.11)

By adding Eqs. (3.10) and (3.11), we obtain the numerical approximation for the left-hand side of fractional operator in (3.9) as follows

$$\begin{aligned} \begin{aligned} _0\mathcal {D}_x^\alpha w(x_s)&\approx \frac{h^{-\alpha }}{\Gamma (3-\alpha )} \left[ \frac{(1-\alpha )(2-\alpha )w_0}{s^\alpha }+ \frac{(2-\alpha )(w_1-w_0)}{s^{\alpha -1}} \right. \\&\left. \;\;\;+\sum _{i=0}^{s-1}(w_{s-i+1}-2w_{s-i}+w_{s-i-1})\left\{ (i+1)^{2-\alpha }-i^{2-\alpha } \right\} \right] . \end{aligned} \end{aligned}$$

(3.12)

In a similar fashion, we formulate an approximation for the right-hand operator in (3.9) as

$$\begin{aligned} _x\mathcal {D}_L^\alpha w(x_s)\approx & {} \frac{h^{-\alpha }}{\Gamma (3-\alpha )} \left[ \frac{(1-\alpha )(2-\alpha )w_N}{(N-s)^\alpha }+ \frac{(2-\alpha ) (w_N-w_{N-1})}{(N-s)^{\alpha -1}} \right. \nonumber \\&\left. \;\;\;+\sum _{i=0}^{N-s-1}(w_{s+i-1}-2w_{s+i}+w_{s+i+1})\left\{ (i+1)^{2-\alpha }-i^{2-\alpha } \right\} \right] . \end{aligned}$$

(3.13)

Finally, by using the GL definitions in (3.9) in conjunction with left- and right- approximations (3.12) and (3.13), the time fractional-in-space diffusion Eq. (3.7) is transformed to system of fractional ODEs

$$\begin{aligned} \frac{dw_s}{dt}\approx & {} -\frac{\delta h^{-\alpha }}{2\cos \left( \frac{\pi \alpha }{2} \right) \Gamma (3-\alpha )}\left[ \frac{(1-\alpha )(2-\alpha )w_0}{s^\alpha }+ \frac{(2-\alpha )(w_1-w_0)}{s^{\alpha -1}} \right. \nonumber \\&+\sum _{i=0}^{s-1}(w_{s-i+1}-2w_{s-i}+w_{s-i-1})\left\{ (i+1)^{2 -\alpha }-i^{2-\alpha } \right\} \nonumber \\&+\frac{(1-\alpha )(2-\alpha )w_N}{(N-s)^\alpha }+ \frac{(2-\alpha ) (w_N-w_{N-1})}{(N-s)^{\alpha -1}} \nonumber \\&\left. +\sum _{i=0}^{N-s-1}(w_{s+i-1}-2w_{s+i}+w_{s+i+1})\left\{ (i+1)^{2-\alpha }-i^{2-\alpha } \right\} \right] , s=1,2,\ldots ,N-1.\nonumber \\ \end{aligned}$$

(3.14)

We denote (3.14) as finite difference (FD) scheme.

The second method we utilize in this work is based on the Fourier spectral method. According to Illć et al. [19, 20], the power $(-\Delta )^{\alpha /2}$ of the Laplacian operator $(-\Delta )$, in a domain $\Omega$ with zero Neumann or Dirichlet boundary conditions, is defined via the spectral decomposition of the eigenvalues of the original operator. Denote $(\varphi _{j} , \lambda _{j})$ as respective eigenfunctions and eigenvectors of operator $(-\Delta )$ in $\Omega$ with zero Neumann or Dirichlet boundary conditions. It implies that $(\varphi _{j} , \lambda _{j}^{\alpha /2})$ are the eigenfunctions and eigenvectors of $(-\Delta )^{\alpha /2}$, subject to the Neumann or Dirichlet boundary conditions.

Obviously, the fractional Laplacian operator $(-\Delta )^{\alpha /2}$ is well defined in the space of functions

$$\begin{aligned} H_{0}^{\alpha /2}(\Omega )=\left\{ w=\sum _{j=0}^{\infty } a_{j}\lambda ^{\alpha /2}\in L^{2}(\Omega ):\Vert w\Vert _{H_{0}^{\alpha /2}(\Omega )}=\left( \sum _{j=0}^{\infty }a_{j}^{2}\lambda ^{\alpha /2}\right) ^{1/2}<\infty \right\} \nonumber \\ \end{aligned}$$

(3.15)

where

$$\begin{aligned} \Vert w\Vert _{H_{0}^{\alpha /2}(\Omega )}=\Vert (-\Delta )^{\alpha /4}w\Vert _{L^{2}(\Omega )}. \end{aligned}$$

(3.16)

Hence, for any $w\in H_{0}^{\alpha /2}$, the Laplacian $(-\Delta )^{\alpha /2}$ is defined by

$$\begin{aligned} (-\Delta )^{\alpha /2}w=\sum _{i=0}^{\infty }a_{j}\lambda ^{\alpha /2}_{j}\varphi _{j}, \end{aligned}$$

(3.17)

where $\varphi _{j}$ and $\lambda _{j}$ depend on any boundary condition as specified.

The homogeneous Neumann and Dirichlet boundary condition are given as

$$\begin{aligned} \left( \varphi _{j} , \lambda _{j}\right) =\left( \left[ \frac{\pi j}{b-a}\right] ^2, \sqrt{\frac{2}{b-a}}\sin \left[ \frac{(x-a)\pi j}{b-a}\right] \right) , \end{aligned}$$

(3.18)

and

$$\begin{aligned} \left( \varphi _{j} , \lambda _{j}\right) =\left( \left[ \frac{(j+1)\pi }{b-a}\right] ^2, \sqrt{\frac{2}{b-a}}\sin \left[ \frac{(x-a)\pi (j+1)}{b-a}\right] \right) , \end{aligned}$$

(3.19)

respectively. The approach illustrated the above results in a full diagonal representation of the fractional operator, and it achieves spectral convergence regardless of the chosen value of fractional power $\alpha$. Another advantage of the spectral method is that it is easy to adapt and extend to high dimensions.

In practice, we use the MATLAB fast Fourier transform (fft) to transform the general fractional-in-space reaction–diffusion equation of the form

$$\begin{aligned} w_t=\delta (\Delta ^{\alpha /2})w + f(w,t), \end{aligned}$$

(3.20)

which leads to two-dimensional representation in the Fourier space as

$$\begin{aligned} W_t(\omega _x,\omega _y,t)=-\delta \left( (\omega _x^2)^{\alpha /2}+(\omega _y^2)^{\alpha /2} \right) W(\omega _x,\omega _y,t)+\mathcal {F}[f(w(x,y,t))], \end{aligned}$$

(3.21)

where W is the double Fourier transform of w(x, y, t), that is,

$$\begin{aligned} \mathcal {F}[w(x,y,t)]=W(\omega _x,\omega _y,t)=\int _{0}^{\infty } \int _{0}^{\infty } w(x,y,t)e^{-i(\omega _x x+\omega _y y)}\mathrm{d}x\mathrm{d}y. \end{aligned}$$

(3.22)

We let

$$\begin{aligned} \Omega ^{\alpha /2}=\left( (\omega _x^2)^{\alpha /2}+(\omega _y^2)^{\alpha /2}\right) , \end{aligned}$$

so as to explicitly remove the linear pieces of the transformed equations, and set

$$\begin{aligned} W=e^{-\delta \Omega ^{\alpha /2}t}\bar{W}, \end{aligned}$$

so that we now obtain

$$\begin{aligned} \partial _t\bar{W}=e^{\delta \Omega ^{\alpha /2}t}\mathcal {F}[f(w)]. \end{aligned}$$

(3.23)

At this junction, in practice, we have discretized the spatial domain, using the equispaced points in the directions of x and y. Apply the discrete fft so that (3.23) becomes a system of ODEs represented by the Fourier modes

$$\begin{aligned} \partial _t\bar{W}_{i,j}=e^{\delta \Omega ^{\alpha /2}_{i,j}t}\mathcal {F}[f(w_{i,j})], \end{aligned}$$

(3.24)

where $w_{i,j}=w(x_i,y_j)$ and $\Omega ^{\alpha /2}_{i,j}=\left( \chi _x^2(i)\right) ^{\alpha /2}+\left( \chi _y^2(j)\right) ^{\alpha /2}$. In the computation, the boundary conditions are now mounted at extremes of the domain. Since the PDE has been transformed to an ODEs, any explicit solver can be employed to integrate in time. Specifically here, we utilize the improved version of the fourth-order exponential time differencing Runge–Kutta (ETD4RK) [22] given by

(3.25)

with the stages $\chi _i$ given as

$$\begin{aligned} \begin{aligned} \chi _{2}&=e^{\mathbf {L}h/2}\mathcal {W}_{n}+(\mathbf {L}h/2)\zeta _{1} (\mathbf {L}h/2)\mathbf {F}(w_{n},t_{n}) \\ \chi _{3}&=e^{\mathbf {L}h/2}\mathcal {W}_{n}+(\mathbf {L}h/2)[\zeta _{1} (\mathbf {L}h/2)-2\zeta _{2}(\mathbf {L}h/2)]\mathbf {F}(w_{n},t_{n})\\&\;\;\;\;+ h\zeta _{2}(\mathbf {L}h/2)\mathbf {F}(\chi _{2},t_{n}+h/2) \\ \chi _{4}&=e^{\mathbf {L}h}\mathcal {W}_{n}+h[(\zeta _{1}(\mathbf {L}h)-2 \zeta _{2}(\mathbf {L}h)]\mathbf {F}(w_{n},t_{n})+2h\zeta _{2}(\mathbf {L}h) \mathbf {F}(\chi _{3},t_{n}+h), \end{aligned} \end{aligned}$$

(3.26)

with functions $\zeta _{1,2,3}$ defined as

$$\begin{aligned} \zeta _{1}(z)=\frac{e^{z}-1}{z}, \quad \zeta _{2}=\frac{e^{z}-1-z}{z^{2}},\quad \zeta _{3}=\frac{e^{z}-1-z-z^{2}/2}{z^{3}} \end{aligned}$$

which coincide with the terms in the Munthe-Kaas [34] Lie group methods; see [22] for details.

In what follows, we demonstrate the applicability and accuracy of the numerical schemes by considering the one-dimensional fractional-in-space diffusion Eq. (3.7) on $0<x<\pi$ subject to initial and boundary conditions $w(x,0)=\beta (x)=x^2(\pi -x)$ and $w(0,t)=w(\pi ,t)=0$, respectively. Talking of the classical case, when $\alpha =2$, $\delta =0.25$ and $_0\mathcal {D}_x^\alpha =-(-\Delta )^{\alpha /2}$, the exact solution is calculated as

$$\begin{aligned} w(x,t)=\sum _{n=1}^{\infty }\left[ \frac{8(-1)^{n+1}-4}{n^3}\right] \sin (nx)\exp (-n^2\delta t). \end{aligned}$$

With $\alpha \ne 2$, the exact equation is given as

$$\begin{aligned} w(x,t)=\sum _{n=1}^{\infty }\left[ \frac{8(-1)^{n+1}-4}{n^3}\right] \sin (nx)\exp (-(n^2)^{\alpha /2}\delta t). \end{aligned}$$

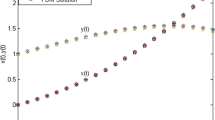
It should be mentioned that we obtain the classical result when $\alpha =2$. We illustrate the convergence of the schemes as shown in Figs. 1 and 2 for some instances of $\alpha$. It is obvious that the spectral method has better accuracy.

Fig. 1

Numerical solution of (3.7) showing the convergence of the finite difference scheme for different $\alpha$ at $t=1.00$

Fig. 2

Numerical solution of (3.7) showing the convergence of the spectral method for some instances of $\alpha$ and $\delta$. The upper and lower rows correspond to $\delta =(0.25, 0.50)$ at $t=1.00$

4 Applications to models in physics and engineering

The methods we described above are capable of solving higher-dimensional problems and further coupled reaction–diffusion systems; however, we shall restrict our study to consider one and two space dimensions of two different PDEs that abound in mathematical physics, biology, chemistry and ecology, and many intriguing mathematical phenomena and patterns that may naturally arise.

4.1 Fractional chaotic model

Chaos theory is an aspect of mathematics that focuses on the study of chaos states of dynamical problems which have some irregular behaviors that are highly sensitive to initial conditions. Chaotic phenomena occurs in many natural and physical systems, such as fluid flow, weather and climate, heartbeat irregularities, road traffic and stock market, among several others [21, 28, 50]. Chaotic behavior can be studied via the analysis of a chaotic mathematical model. Chaos theory has many applications in various disciplines, like physics, engineering, meteorology, sociology, anthropology, environmental science, computer science, economics and finance, biology, pandemic crisis management, medicine, ecology and security in communication technology.

Over the years, a reasonable number of research work has been published based on the study and application of chaotic systems, for instance, the Lorenz system [28], Rössler system [47], Chen and Ueta system [11], and other applications such as simple chaotic flows [52], MOS transistor-based oscillators, heart-shaped memristive and memristor chaotic attractors [62, 63], digital realization of chaotic system, transition to turbulence in incompressible fluid flows [14, 15] and electromechanical oscillator [68]. Complexity of chaotic systems has been applied in different engineering applications ranging from asymmetric color pathological image encryption [26], to control and synchronization [45] and so many others that are classified in [6].

Standing on the success and useful applications of chaotic processes as widely reported, we consider a three-species chaotic fractional-in-space system

$$\begin{aligned} \begin{aligned}&\frac{\partial u}{\partial t}=\delta _1\Delta ^\alpha u+f_1(u,v,w),(x,y)\in \Omega ,\;0<t\le T,\\&\frac{\partial v}{\partial t}=\delta _2\Delta ^\alpha v +f_2(u,v,w),(x,y)\in \Omega ,\;0<t\le T,\\&\frac{\partial w}{\partial t}=\delta _3\Delta ^\alpha w +f_3(u,v,w),(x,y)\in \Omega ,\;0<t\le T, \end{aligned} \end{aligned}$$

(4.27)

subject to initial and boundary conditions

$$\begin{aligned} \begin{aligned}&u(x,y,0)=\rho _1(x,y),\;v(x,y,0)=\rho _2(x,y),\;v(x,y,0)=\rho _2(x,y),\;\;0\le x,y\le L,\\&\left. \frac{\partial u}{\partial \varvec{n}}\right| _{\partial \Omega }=\left. \frac{\partial v}{\partial \varvec{n}}\right| _{\partial \Omega }=\left. \frac{\partial w}{\partial \varvec{n}}\right| _{\partial \Omega }=0, (x,y)\in \partial \Omega , \end{aligned} \end{aligned}$$

(4.28)

where $u, v,w\mathbf {R}^n$ represent a group of physical or biological species, $\delta _i\in \mathbf {R}^{n\times n},\;i=1,2,3$ is the diffusion coefficient matrix, $\Delta ^\alpha$ is the fractional Laplacian operator of order $\alpha \in (1, 2]$ associated with the diffusion of the species u, v and w, $\Omega =\{0<x\le L, 0<y\le L \}$ for $L\gg 0$, and $\varvec{n}$ is the outward unit normal of vector of the boundary $\partial \Omega$. Then, $f_i(u,v,w)$ for $i=1,2,3$ are nonlinear functions of u, v and w which describe the chemical or biological reactions, given here as

$$\begin{aligned} \begin{aligned} f_1(u,v,w)&=\phi _1 u+\varphi _1 vw,\\ f_2(u,v,w)&=\phi _2 u+\varphi _2 v-uw,\\ f_3(u,v,w)&=\psi _1 uv+\psi _2w. \end{aligned} \end{aligned}$$

(4.29)

The system of ordinary differential equations (ODEs), that is, the spatially homogeneous form of system (4.27) with kinetic (4.29), has been investigated [59, 60]. The corresponding ODE system is sometimes referred to as the three-dimensional four-wing chaotic model

$$\begin{aligned} \begin{aligned} u'(t)&=f_1(u,v,w)=\phi _1 u(t)+\varphi _1 v(t)w(t),\\ v'(t)&=f_2(u,v,w)=\phi _2 u(t)+\varphi _2 v(t)-u(t)w(t),\\ w'(t)&=f_3(u,v,w)=\psi _1 u(t)v(t)+\psi _2w(t), \end{aligned} \end{aligned}$$

(4.30)

where u(t), v(t) and w(t) are state variables given as functions of time only, $\phi _1,\phi _2$, $\varphi _2$ and $\psi _2\in {\mathbb {R}}$, $\varphi _1>0$ and $\psi _1<0$ are real all real numbers. If model (4.30) is dissipative, then the sum $\left( \frac{\partial u'}{u}+\frac{\partial v'}{v}+\frac{\partial w'}{w}=\phi _1+\varphi _2+\psi _2=\mathfrak {V}\right) <0$. This means that $\mathfrak {V}_0$ which represent the volume element is contracted into $\mathfrak {V}_0\exp (\phi _1+\varphi _2+\psi _2)$ by the flow at time t. In what follows, we give a quick tour of the local dynamics of the reaction–diffusion system. This gives conditions on the choice of parameters necessary for the solution to have physically or biologically meaningful equilibria, and it will also help in making the choice of parameters when numerically dealing with the solutions of the full fractional reaction–diffusion model.

To derive the equilibrium points of the autonomous model (4.30), we require to set $f_i(u,v,w)=0$, which implies that $u'(t)=0, v'(t)=0$ and $w'(t)=0$. The points $E_0=(0,0,0)$ is trivial which corresponds to the washout of the species. We are only interested in the coexistence of the three components.

With conditions $\frac{\phi _1\psi _2}{\varphi _1\psi _1}>0$, the discriminant $\phi _2^2\varphi _1^2-4\phi _1\varphi _1\varphi _2>0$ and $\varphi _1\ne 0$, we obtain the following nontrivial states

$$\begin{aligned} \begin{aligned} E_1^*&=\left( -\left( \frac{\varphi _1}{\phi _1}\right) v_ew_e^a,v_e,w_e^a\right) ,\\ E_2^*&=\left( \left( \frac{\varphi _1}{\phi _1}\right) v_ew_e^a,-v_e,w_e^a\right) \\ E_3^*&=\left( -\left( \frac{\varphi _1}{\phi _1}\right) v_ew_e^b,v_e,w_e^b\right) ,\\ E_4^*&=\left( \left( \frac{\varphi _1}{\phi _1}\right) v_ew_e^b,-v_e,w_e^b\right) \end{aligned} \end{aligned}$$

(4.31)

where

$$\begin{aligned} \begin{aligned} u_e&=\sqrt{\frac{\phi _1\psi _2}{\varphi _1\psi _1}},\\ w_e^a&=\frac{\phi _2+\text {sign}(\phi _1)\sqrt{\phi _2^2\varphi _1^2-4\phi _1 \varphi _1\varphi _2}}{2\varphi _1},\\ w_e^b&=\frac{\phi _2-\text {sign}(\phi _1)\sqrt{\phi _2^2\varphi _1^2-4\phi _1 \varphi _1\varphi _2}}{2\varphi _1}, \end{aligned} \end{aligned}$$

(4.32)

where $\text {sign}(\cdot )$ denotes a sign function. So, by linearizing (4.30) at point $E_0$, we have the Jacobian

$$\begin{aligned} A(E_0)= \begin{pmatrix} \phi _1&{}\quad 0&{}\quad 0\\ \phi _2&{}\quad \varphi _2&{}\quad 0\\ 0&{}\quad 0&{}\quad \psi _2 \end{pmatrix}. \end{aligned}$$

(4.33)

Obviously, the eigenvalues of matrix $A({E_0})$ correspond to

$$\begin{aligned} \lambda _a=\phi _1,\lambda _b=\varphi _2,\lambda _c=\psi _2. \end{aligned}$$

With these findings, we can remark that since $\phi _1,\varphi _2,\psi _2$ are all real numbers, then there is no imaginary eigenvalue arising from matrix $A(E_0)$, and near the state $E_0=(0,0,0)$, there is no Hopf bifurcation. It is important to note that the states $E_1^*$ and $E_2^*$ are symmetric in nature with respect to the w direction and same is applicable to the points $E_3^*$ and $E_4^*$. The corresponding Jacobian at points $E_i^*,i=1,\dots ,4$, as

$$\begin{aligned} A(E_1^*)= \begin{pmatrix} \phi _1&{}\varphi _1w_e^a&{}\varphi _1v_e\\ \\ \phi _2-w_e^a &{}\varphi _2&{}\frac{\varphi _1v_ew_e^a}{\phi _1}\\ \\ \psi _1v_e&{}-\frac{\psi _1\varphi _1v_ew_e^a}{\phi _1}&{}\psi _2 \end{pmatrix}, A(E_2^*)= \begin{pmatrix} \phi _1&{}\varphi _1w_e^a&{}-\varphi _1v_e\\ \\ \phi _2-w_e^a &{}\varphi _2&{}-\frac{\varphi _1v_ew_e^a}{\phi _1}\\ \\ -\psi _1v_e&{}\frac{\psi _1\varphi _1v_ew_e^a}{\phi _1}&{}\psi _2 \end{pmatrix},\nonumber \\ \end{aligned}$$

(4.34)

and

$$\begin{aligned} A(E_3^*)= \begin{pmatrix} \phi _1&{}\varphi _1w_e^b&{}\varphi _1v_e\\ \\ \phi _2-w_e^b &{}\varphi _2&{}\frac{\varphi _1v_ew_e^b}{\phi _1}\\ \\ \psi _1v_e&{}-\frac{\psi _1\varphi _1v_ew_e^b}{\phi _1}&{}\psi _2 \end{pmatrix}, A(E_4^*)= \begin{pmatrix} \phi _1&{}\varphi _1w_e^b&{}-\varphi _1v_e\\ \\ \phi _2-w_e^b &{}\varphi _2&{}-\frac{\varphi _1v_ew_e^b}{\phi _1}\\ \\ -\psi _1v_e&{}\frac{\psi _1\varphi _1v_ew_e^b}{\phi _1}&{}\psi _2 \end{pmatrix}\nonumber \\ \end{aligned}$$

(4.35)

Since the pairs of matrices are symmetric, and from the Jacobian matrices in (4.34) and (4.35), we have the transformation $\mathbf{B}$, in such that

$$\begin{aligned} \mathbf{B}^{-1}A(E_1^*)\mathbf{B}=A(E_2^*), \mathbf{B}^{-1}A(E_3^*)\mathbf{B}=A(E_4^*), \end{aligned}$$

(4.36)

where $\mathbf{B}=\text {diag}(-1, -1,1)$ and $\mathbf{B}$ represents the orthogonal matrix for $\mathbf{B}^{-1}=\mathbf{B}^T=\mathbf{B}$. If we set $Z_i=[z_{i1},z_{i2},z_{i3}]$ be matrix which consists the eigenvectors of $E_i^*,$ for $i=1,2,3,4$, we obtain

$$\begin{aligned} \mathbf{B}^{-1}Z_1\mathbf{B}=Z_2,\;\;\mathbf{B}^{-1}Z_3\mathbf{B}=Z_4. \end{aligned}$$

Therefore, it is obvious that $E_1^*,E_2^*$ and $E_3^*,E_4^*$ are two distinct states, and each pair of the equilibrium state is locally stable, unstable and center manifolds. When $\phi _1=0.2, \phi _2=-0.01,\varphi _1=1,\varphi _2=-0.4,\psi _1=-1$ and $\psi _2=-1$. The equilibrium states are calculated as $E_1=(-0.62,0.45,0.28), E_2=(0.62,-0.45,0.28), E_3=(0.64,0.45,-0.29)$ and $E_4=(0.62,-0.45,-0.29)$.

Since the sum $\frac{\partial u'}{u}+\frac{\partial v'}{v}+\frac{\partial w'}{w}=\phi _1+\varphi _2+\psi _2=-1.2<0$, it implies that system (4.30) is dissipative. To examine the stability of the equilibrium states $E_0,E_1,\ldots ,E_4$, we require to consider the Jacobian matrix at all the equilibrium points and find all their eigenvalues. These results are calculated as

$$\begin{aligned} \begin{aligned} E^1_0&=(\lambda _1,\lambda _2,\lambda _3)=(-0.40,0.20,-1.00)\\ E^1_1&=(\lambda _1,\lambda _2,\lambda _3)=(-1.357,0.082+0.467i,0.082-0.467i)\\ E^1_2&=(\lambda _1,\lambda _2,\lambda _3)=(-1.357,0.082+0.467i,0.082-0.467i)\\ E^1_3&=(\lambda _1,\lambda _2,\lambda _3)=(-1.379,0.089+0.48i,0.089-0.48i)\\ E^1_4&=(\lambda _1,\lambda _2,\lambda _3)=(-1.379,0.089+0.48i,0.089-0.48i). \end{aligned} \end{aligned}$$

(4.37)

We can deduce based on the above eigenvalues that the equilibria of model (4.30) are saddle and unstable.

The Lyapunov exponent measures the degree of sensitivity to initial conditions that is, local instability in a state space. Such local instability can evolve for a variety of reasons in different types of systems [17]. Lyapunov exponents have proved useful in various contexts. For instance, within the dynamical system, it gives a detailed characterization of chaotic dynamics and can assist to achieve various forms of synchronization. With parameters $\phi _1=0.25, \phi _2=0.05,\varphi _1=1.2,\varphi _2=-0.2,\psi _1=-1$, $\psi _2=-1$ and $(u_0,v_0,w_0)=(2,1,2)$, the Lyapunov exponents (LEs) for different time levels are calculated as

and the corresponding graphical representation of the Lyapunov exponents for $t=200$ and $t=1000$ is shown in Fig. 3. Since the sum of the Lyapunov exponents at any time t here is negative, it implies that system (4.30) is dissipative, and the fractional dimension for $t=200$ is 2.05, which leads the dynamical system with attractors as shown in Figs. 4 and 5. Figure 6 shows time series results for different instances of $\phi _1$ as given in the figure caption. With $\phi _2=0$, it should be noted that model (4.30) cannot leads to a desired chaotic attractor, causing the number of scroll wings to reduce from four to two. Also, if at any point we have at least two of the Lyapunov exponents to be positive maybe due to the perturbation of the initial data, then the system is hyper-chaotic.

Fig. 3

Dynamics of the Lyapunov exponents of system (4.30) computed for $t=200$ (left) and $t=1000$ (right). Initial condition and parameters are chosen as: $(u_0,v_0,w_0)=(2,1,2), \phi _1=1/4, \phi _2=0.01, \varphi _1=1.2, \varphi _2=-0.2, \psi _1=-1$ and $\psi _2=-1$

In one dimension, we experiment fractional model (4.27) with kinetics (4.29) using the zero-flux boundary conditions and random initial data emanating from small perturbation of the steady state, which we compute as

for $N=200$, The parameters are taken as

$$\begin{aligned} \phi _1=0.25, \phi _2=0.1, \varphi _1=1.20, \varphi _2=-0.2, \psi _1=-1.2, \psi _2=-1. \end{aligned}$$

(4.38)

Figures 7 and 8 show one-dimensional chaotic oscillations for $\alpha =1.55$ and $\alpha =1.92$, respectively.

In two dimensions, we solve system (4.27) using the zero-flux boundary conditions with two different initial functions. We employ both the MATLAB random data

and smooth initial functions

$$\begin{aligned} \begin{aligned} u(x,y,0)&=1-u^*\sin (\pi (x-\nu )/(2\nu ))^\gamma \sin (\pi (y-\nu )/(2\nu ))^\gamma ,\\ v(x,y,0)&=v^*\sin (\pi (x-\nu )/(2\nu ))^\gamma \sin (\pi (y-\nu )/(2\nu ))^\gamma \\ w(x,y,0)&=1.5-w^*\sin (\pi (x-\nu )/(2\nu ))^\gamma \sin (\pi (y-\nu )/(2\nu ))^\gamma \end{aligned} \end{aligned}$$

(4.39)

where $(u^*,v^*,w^*)=(0.5,0.25,0.25)$, $\gamma =0.8$ and $\nu =0.05$ to obtain the distributions in Figs. 9 and 10, respectively. The effect of initial functions is justified here for some $\alpha$.

Fig. 4

3-D and 2-D chaotic attractors of system (4.30) for $\phi _1=1/4, \phi _2=0.01, \varphi _1=1.2, \varphi _2=-0.2, \psi _1=-1.2, \psi _2=-1$, with initial conditions $(u_0,v_0,w_0)=(2,1,2)$ at $t=1000$

Fig. 5

3-D and 2-D chaotic attractors of system (4.30) for $\phi _1=1/4, \phi _2=0.05, \varphi _1=1.2, \varphi _2=-0.2, \psi _1=-1.0, \psi _2=-1$, with initial conditions $(u_0,v_0,w_0)=(2,1,2)$ at $t=1000$

Fig. 6

Time series solution system (4.30) showing chaotic distribution of species different instances of (a) $\phi _1=1/2$ and (b) (a) $\phi _1=1/4$ at $t=1000$, other parameters are given in Fig. 4

Fig. 7

One-dimensional solution of system (4.27) with kinetics (4.29) showing chaotic behaviors for $\alpha =1.55$ at $t=200$. Other parameters are given in (4.38)

Fig. 8

One-dimensional solution of system (4.27) with kinetics (4.29) showing chaotic behaviors for $\alpha =1.92$ at $t=200$. Other parameters are given in (4.38)

Fig. 9

Two-dimensional evolution of system (4.27) with kinetics (4.29) showing chaotic oscillations for $\alpha =1.75$ at $t=200$. Other parameters are given in (4.38)

Fig. 10

Two-dimensional evolution of system (4.27) with kinetics (4.29) showing spatiotemporal oscillations for $\alpha =1.88$ at $t=200$. Other parameters are given in (4.38)

Fig. 11

Two-dimensional solution of the Helmholtz Eq. (4.27) with $\kappa =6$ for different values of $\alpha$

Fig. 12

Two-dimensional solution of the Helmholtz Eq. (4.27) with $\kappa =9$ for different values of $\alpha$

4.2 Fractional Helmholtz equation

Helmholtz equation is known to be the variation of the Poisson equation. Helmholtz equation or reduced wave equation belongs to a family of an elliptic type of partial differential equation with broad utility in mechanical engineering and theoretical physics, whose derivation can be drawn directly from the known wave equation. It arises, for instance, to describe the potential field caused by a given charge or mass density distribution; with the potential field known, one can then calculate gravitational or electrostatic field. It is a generalization of Laplace’s equation, which is also frequently seen in physics.

In this work, we consider on Cartesian coordinate the two- or three-dimensional nonhomogeneous isotropic medium whose wave speed is denoted by c. The corresponding wave solution to harmonic source f(x, y) is u(x, y), vibrating at frequency $\omega >0$ satisfying the scalar fractional Helmholtz equation defined on region $\mathbf {R}$ by

$$\begin{aligned} \Delta ^\alpha u +\kappa ^2 u=f(x,y)\;\; u=u_0,\;\frac{\partial u}{\partial \mathbf{n} },\;\Omega \in {\mathbb {R}}^d, d=2,3 \end{aligned}$$

(4.40)

where u is a sufficiently differentiable function on the boundary $\partial \Omega$, n is the outward unit normal to the boundary, $\kappa >0$ is a wave number, and $\sqrt{\kappa }=\omega /c$ denotes the wave number with wavelength $2\pi /\sqrt{\kappa }$. $\Delta ^\alpha$ is usual fractional Laplacian operator of order $1<\alpha \le 2$ in two $\Delta ^\alpha u=\left( \frac{\partial ^\alpha u}{\partial x^\alpha }+\frac{\partial ^\alpha u}{\partial y^\alpha }\right)$ or three dimensions $\Delta ^\alpha u=\left( \frac{\partial ^\alpha u}{\partial x^\alpha }+\frac{\partial ^\alpha u}{\partial y^\alpha }+\frac{\partial ^\alpha u}{\partial z^\alpha }\right)$.

Helmholtz equation has application in Physics problem-solving concepts like seismology, acoustics and electromagnetic radiation. Seismology: The scientific study of earthquake and its propagating elastic waves is known as seismology, electrodynamics, most especially in optics and acoustics involving time harmonic wave distribution. Other study areas are the volcanic eruptions due to seismic source and tsunamis as a result of environmental effects. If the plus (+) sign before the term $\kappa$ is changed to minus (−) sign, then the Helmholtz equation can be used to describe the mass transfer processes with volume chemical reactions of first order [42]. It should be mentioned that whenever the wave number $\kappa \gg 1$, the solution of (4.40) becomes highly oscillatory which makes it very challenging to design an effective numerical algorithm to solve the Helmholtz equation in higher dimensions. A lot of numerical methods based on the finite difference approximations [13, 67], Adomian decomposition method [16], reduced differential transform method [2], homotopy perturbation method [18] and finite elements and Galerkin methods [33, 57] have been reported in the literature.

To experiment (4.40) in two dimensions, we set $f(x,y)=\exp (-10(y-1)^2+(x-0.5)^2)$ and utilize a square domain size $x,y\in [-L,L]\times [-L,L]$ for $L=1$. The wave evolution showing chaotic oscillations is displayed in Figs. 11 and 12 for different values of fractional-order $\alpha \in (1,2]$ and $\kappa \gg 1$. It should be noted that when $\kappa =0$, the Helmholtz equation (4.40) reduces to the Poisson. When $\kappa <4$, we get a stationary (pattern) solution.

5 Conclusion

Numerical solution of fractional-in-space advection or reaction equations in two and higher dimensions has been the major setback some researchers are facing, most simulations that are based on conventional ideas are time consuming. As a result, the majority of work reported is restricted to one-dimensional case problems of PDEs. The aim of the present work is to report a good, clear, working versatile technique based on both finite difference and spectral methods to explore the dynamic richness of chaotic and oscillatory waves models. We realized that the spectral scheme avoids the issue of stiffness, and they can be applied and built upon by other scientists and engineers. This technique is used to explore the dynamic richness of chaotic systems and the Helmholtz equation in one and two dimensions. The methods reported in this work can be extended higher dimensions and more coupled practical problems in physics and engineering.