1 Introduction

In order to present OCP solved in this manuscript, firstly, we give an introduction to the OCP and provide an explanation of the functions and parameters defined in this problem. A brief review and history of these equations and spectral and pseudospectral methods are in the following subsections.

1.1 The governing equations

Optimum control problems arise in the minimization of a functional over a set of admissible control functions subject to dynamic constraints on the state and control functions [1, 2]. Regarding that the equations of dynamics in the system are reformed by a partial differential equation—with time and space variables—this OCP is known as an optimal control of a distributed system [1]. The formulation of this optimal control problem is [3]:

$$\begin{aligned} \mathrm{min} ~~ J=\frac{1}{2}\int _0^1\int _0^R x^r\big (c_1z^2(x,t)+c_2y^2(x,t)\big )\text {d}x\text {d}t, \end{aligned}$$
(1)

subject to

$$\begin{aligned} \frac{\partial z}{\partial t}=k(\frac{\partial ^2 z}{\partial x^2}+\frac{r}{x}\frac{\partial z}{\partial t})+y(x,t), \end{aligned}$$
(2)

with initial and boundary conditions

$$\begin{aligned} z(x,0)= & {} z_0(x),~~0<x<R,\nonumber \\ z(R,t)= & {} 0,~~~~~~~t>0. \end{aligned}$$
(3)

In fact, this is a nonlinear quadratic optimal control problem with the dynamic system of the classical diffusion equation.

In Eqs. (1)–(3), y(x, t) is the optimization function that must be calculated so that it and the function of z(x, t) are held in Eqs. (1)–(3) and the value of J is minimized. z(x, t) and y(x, t) are called the state and control functions and usually calculated in such a way that they are smooth and the derivatives and integral in Eqs. (1) and (2) can be calculated analytically or numerically. \(z_0(x)\) is a known real function, \(c_1\) and \(c_2\) are two arbitrary constants, k is a numerical constant that is specified in the problem, and r and R are positive real constants. Here, \(t>0\) and its upper bound is 1. The parameter r is specified in numerical examples as \(r=1\) or \(r=2\).

The purpose of solving this problem is to approximate the control and state functions that minimize the J.

This OCP arises in a variety of biological, chemical, and physical applications; for more details, see Refs. [4,5,6].

1.2 The literature on optimal control problems

Two-dimensional (2D) systems and their beneficial applications in many different industrial fields draw the attention of scientists presently. These applications rise in heat transfer, image processing, seismological and geophysical data processing, distributed systems, restoration of noisy images, earthquake signal processing, water stream heating gas absorption, smart materials, and transmission lines [7,8,9,10]. The miscellaneous chemical, biological, and physical problems are modeled by diffusion processes involving control function mentioned in Eqs. (1)–(3). By the aid of Roesser’s model [10], Attasi’s model [11, 12], Fornasini–Marchesini’s models [13, 14], the state-space models of 2D systems are organized [7]. Remarkable studies have been done in the area of optimal controls, and excellent articles are written hereby [15,16,17,18,19]. Among these studies, numerical techniques have been used to solve optimal control problems [17, 20]. Moreover, Agrawal [1] presented a general formulation and a numerical scheme for fractional optimal control for a class of distributed systems. He used eigenfunctions to develop his method. In other works, Manabe [21], Bode et al. [22] and Rabiee et al. [23] studied fractional-order optimal control problems. Additionally, Mamehrashia and Yousefi [3, 7] and Lotfi et al. [24] employed the Ritz method to solve optimal control problems. With the variational method, Yousefi et al. [25] found the solution of the optimal control of linear systems, approximately. Li et al. [26] considered a continuous-time 2D system and converted it to the discrete-time 2D model. In other works, Wei et al. [27] and Zhang et al. [28] investigated an optimal control problem in continuous-time 2D Roesser’s model. They employed iterative adaptive critic design algorithm and the adaptive dynamic programming method to approximate the solution. Sabeh et al. [29] introduced a pseudo-spectral method for the solution of distributed optimal control problem with the viscous Burgers equation.

1.3 The literature of spectral and pseudospectral methods

The main feature of spectral methods is to use different orthogonal polynomials/functions as trial functions. These polynomials/functions are global and infinitely differentiable. These methods are applied to four types of problems: periodic problems, nonperiodic problems, whole-line problems, and half-line problems. These can be categorized as: Trigonometric polynomials for periodic problems; classical Jacobi, ultraspherical, Chebyshev and Legendre polynomials for non-periodic problems; Hermite polynomials for problems on the whole line; and Laguerre polynomials for problems on the half line [30]. With the truncated series of smooth global functions, spectral methods are giving the solution of a particular problem [31, 32]. These methods, with a relatively limited number of degrees of freedom, provide such an accurate approximation for a smooth solution. Spectral coefficients tend to zero faster than any algebraic power of their index n; see page 2 in [33].

Spectral methods can fall into three categories: Tau, Collocation and Galerkin methods [34].

  • The Tau spectral method is used to approximate numerical solutions of various differential equations. This method considers the solution as an expansion of orthogonal polynomials/functions. Such coefficients, in this expansion, are set to approximate the solution correctly [35].

  • Collocation method helps obtain highly accurate solutions to nonlinear/linear differential equations; see page 2 in [36,37,38,39]. Two common steps in collocation methods are: First, suitable nodes (Gauss/Gauss–Radau/Gauss–Lobatto) are selected to restate a finite or discrete form of the differential equations. Second, a system of algebraic equations from the discretization of the original equation is achieved [40, 41].

  • In the Galerkin spectral method, trial and test functions are chosen the same [42]; This method can result in a highly accurate solution.

It is said that spectral Galerkin methods are similar to Tau methods where in approximation by Tau method, the differential equation is enforced [33].

Furthermore, some other numerical methods like finite difference method (FDM) and finite element method (FEM) need network construction of data and they perform locally. Although spectral methods are continuous and globally performing, they do not require network construction of data [43].

In addition to spectral methods, pseudospectral methods have also attracted researchers recently [44,45,46,47]. As mentioned previously, Sabeh et al. [29] investigated a pseudospectral method to solve the optimal control problem. Pseudospectral methods are also utilized in the solution of other optimal control problems as well [48,49,50,51]. These methods become popular because of their computational feasibility and efficiency. In fact, in standard pseudospectral methods, interpolation operators are used to reduce the cost of computation of the inner product we encounter in some of the spectral methods. For this purpose, a set of distinct interpolation points \(\{x_i\}_{i=0}^{n}\) is considered by which the corresponding Lagrange interpolants are achieved. Besides, when applying collocation points, \(\{x_i\}_{i=0}^{n}\), the residual function is set to vanish on the same set of points. Notwithstanding, the collocation points do not need to be chosen the same as the interpolation nodes. Indeed, just for having the Kronecker delta property, they are considered to be the same: as a consequence, this property helps reduce computational cost noticeably as well. There are such authors who utilized pseudospectral methods for the solution of optimal control as well. William [52] introduced a Jacobi pseudospectral method for solving an optimal control problem. He reported that significant differences in computation time can be seen for different parameters of the Jacobi polynomial. Jacobi pseudospectral method endowed with Lagrange basis is also in [53] to solve a problem defined in semi-infinite domain problem. In another work in [54], a set of nonlinear PDEs was solved by applying this Jacobi pseudospectral method. Garge et al. [50] presented a unified framework for the numerical solution of optimal control problems using collocation at Legendre–Gauss (LG), Legendre–Gauss–Radau (LGR), and Legendre–Gauss–Lobatto (LGL) points and discussed the advantages of each for solving optimal control problems. Chebyshev pseudospectral method was utilized by Fahroo et al. [49] to provide an optimal solution for the optimal control problem.

1.4 The main aim of this paper

To the best of our knowledge, the use of pseudospectral methods for solving optimal control problems has been limited in the literature to either Chebyshev or Legendre methods. Noteworthily, the pseudospectral method based on Jacobi can encompass a wide range of other pseudospectral methods since the Legendre and Chebyshev nodes can be obtained as particular cases of the general Jacobi. Therefore, examining different choices of the parameters in the Jacobi polynomials and a proper selection of the Jacobi parameters will allow us to obtain more accurate real-time solutions to nonlinear optimal control problems. Meanwhile, an arbitrary and not precise selection of nodes may result in poor interpolation characteristics such as the Runge phenomenon; therefore, the nodes in pseudospectral methods are selected as the Gauss–Radau points [52].

In this paper, we present a general formulation and a suitable numerical method called the GLJGR collocation method to solve OCP for a class of distributed systems. Using GLJGR collocation method helps lessen the computational and CPU time. The developed method is exponentially accurate and obtained by a generalization of classical Lagrange polynomials [55]. Additionally, the equation of the dynamics of optimal control problem is reformed as a partial differential equation.

This paper is arranged as follows: In Sect. 2, we present some preliminaries and drive some tools for introducing GL function, GLJGR collocation method, and their relevant derivative matrices. In Sect. 3, we apply the GLJGR collocation method to the solution of the OCP. Section 4 shows numerical examples to demonstrate the effectiveness of the proposed method. Also, a conclusion is given in Sect. 5.

2 Preliminaries, conventions, and notations

In this section, we review some necessary definitions and relevant properties of Jacobi polynomials. In the next step, we introduce generalized Lagrange (GL) functions. Then, we state some theorems on GL functions and develop GLJGR collocation method. Finally, in terms of GLJGR collocation method, we give a formula that expresses the derivative matrix of the mentioned functions.

2.1 Jacobi polynomials

A basic property of the Jacobi polynomials is that they are the eigenfunctions to a singular Sturm–Liouville problem. Jacobi polynomials are defined on \([-1,1]\) and are of high interest recently [56,57,58,59]. The following recurrence relation generates the Jacobi polynomials [60]:

$$\begin{aligned} P_{k+1}^{\alpha ,\beta }(x)= & {} (a_k^{\alpha ,\beta }x-b_k^{\alpha ,\beta })P_k^{\alpha ,\beta }-c_k^{\alpha ,\beta }P_{k-1}^{\alpha ,\beta }(x),~k\ge 1\\ P_0^{\alpha ,\beta }(x)= & {} 1,~P_1^{\alpha ,\beta }(x)=\frac{1}{2}(\alpha +\beta +2)x+\frac{1}{2}(\alpha -\beta ), \end{aligned}$$

where

$$\begin{aligned} a_k^{\alpha ,\beta }= & {} \frac{(2k+\alpha +\beta +1)(2k+\alpha +\beta +2)}{2(k+1)(k+\alpha +\beta +1)},\\ b_k^{\alpha ,\beta }= & {} \frac{(\beta ^2-\alpha ^2)(2k+\alpha +\beta +1)}{2(k+1)(k+\alpha +\beta +1)(2k+\alpha +\beta )},\\ c_k^{\alpha ,\beta }= & {} \frac{(k+\beta )(k+\alpha )(2k+\alpha +\beta +2)}{(k+1)(k+\alpha +\beta +1)(2k+\alpha +\beta )}, \end{aligned}$$

The Jacobi polynomials satisfy the following identities:

$$\begin{aligned} P_{n}^{\alpha ,\beta }(-x)= & {} (-1)^nP_{n}^{\beta ,\alpha }(x),\\ P_{n}^{\alpha ,\beta }(-1)= & {} \frac{(-1)^n\varGamma (n+\beta +1)}{n!\varGamma (\beta +1)},\\ P_{n}^{\alpha ,\beta }(1)= & {} \frac{\varGamma (n+\alpha +1)}{n!\varGamma (\alpha +1)}\\, \bigg (P_{n}^{\alpha ,\beta }(x)\bigg )^{(m)}= & {} 2^{-m}\frac{\varGamma (m+n+\alpha +\beta +1)}{\varGamma (n+\alpha +\beta +1)}P_{n-m}^{\alpha +m,\beta +m}(x), \end{aligned}$$

and its weight function is \(w^{\alpha ,\beta }(x)=(1-x)^{\alpha }(1+x)^{\beta }\).

Moreover, the Jacobi polynomials are orthogonal on \([-1,1]\):

$$\begin{aligned} \int _{-1}^{1}{P_{n}^{\alpha ,\beta }(x)P_{m}^{\alpha ,\beta }(x)}w^{\alpha ,\beta }(x)= & {} \delta _{m,n}\gamma _n^{\alpha ,\beta },\\ \gamma _n^{\alpha ,\beta }= & {} \frac{2^{\alpha +\beta +1}\varGamma (n+\alpha +1)\varGamma (n+\beta +1)}{(2n+\alpha +\beta +1)\varGamma (n+1)\varGamma (n+\alpha +\beta +1)}, \end{aligned}$$

where \(\delta _{m,n}\) is the Kronecker delta function and \(L_{w^{\alpha ,\beta }}^2[-1,1]\) is the weighted space. The inner product and the norm of \(L_{w^{\alpha ,\beta }}^2[-1,1]\) with respect to the weight function are defined as:

$$\begin{aligned} (g,h)_{w^{\alpha ,\beta }}=\int _{-1}^{1}g(x)h(x){w^{\alpha ,\beta }(x)}\text {d}x,~~\Vert g\Vert _{w^{\alpha ,\beta }}=(g,g)^{\frac{1}{2}}_{w^{\alpha ,\beta }} \end{aligned}$$

It is noted that the set of Jacobi polynomials forms a complete \(L_{w^{\alpha ,\beta }}^2[-1,1]\) system [36].

It is known that the \((n+1)\) points of Gauss–Radau are the n roots of \(P_{n}^{\alpha ,\beta +1}(x)\) over \((-1,1)\) and one particular root as \(-1\) or 1. Similarly, for the interval [a,b] with the shifting parameter u(x), these points are n roots of \(P_{n}^{\alpha ,\beta +1}(u(x))\) over (a, b) and one particular root as a or b on the boundaries, where more details on u(x) are discussed in the following sections.

2.2 Generalized Lagrange (GL) functions

In this section, generally, the GL functions are introduced and the suitable formulas for the first- and second-order derivative matrices of these functions are presented.

Definition 1

Let \(w(x)=\prod _{i=0}^N\big (u(x)-u(x_i)\big )\), then the generalized Lagrange (GL) formula is shown as [55]

$$\begin{aligned} L_j^u(x)=\frac{w(x)}{ (u-u_j)\partial _uw(x_j)}=\frac{u'_jw(x)}{(u-u_j)\partial _x w(x_j)}=\kappa _j\frac{w(x)}{(u-u_j)}, \end{aligned}$$
(4)

where \(\partial _uw(x)=\frac{1}{u'}\partial _xw(x)\), \(\kappa _j=\frac{u'_j}{\partial _x w(x_j)}\), u(x) is a continuous, arbitrary, and sufficiently differentiable function, \(x_i\)s are arbitrary distinct points on domain of u(x) such that \(u'_i\ne 0\) for any \(i=0,\cdots ,N\) and \(u_i \ne u_j\) for all \(i \ne j\).

For simplicity, \(u=u(x)\) and \(u_i=u(x_i)\) are considered.

Theorem 1

Considering the GL functions \(L_j^u(x)\) in Eq. (4), one can exhibit the first-order derivative matrices of GL functions as

$$\begin{aligned} D^{(1)}=[d_{kj}]\in \mathfrak {R}^{(n+1)\times (n+1)},~~~ 0\le j,k \le n, \end{aligned}$$

where

$$\begin{aligned} d_{kj} = {\left\{ \begin{array}{ll} \kappa _j\frac{\partial _xw(x_k)}{u_k-u_j} ,&{}j\ne k, \\ \\ \kappa _j\frac{u'_j\partial _x^2 w(x_j)-u''_j\partial _xw(x_j)}{2{u'_j}^2}, &{} j=k.\\ \end{array}\right. } \end{aligned}$$

Proof

As the GL functions defined in Eq. (4), the first-order derivative formula for the case \(k \ne j\) can be achieved as follows:

$$\begin{aligned} d_{kj}=\partial _xL_j^u(x_k)\overset{Eq. (4)}{=} \kappa _j\frac{\partial _xw(x_k)(u_k-u_j)-u_k'w(x_k)}{(u_k-u_j)^2} = \kappa _j\frac{\partial _xw(x_k)}{u_k-u_j}. \end{aligned}$$
(5)

But, when \(k=j\), with L’Hopital’s rule:

$$\begin{aligned} d_{jj}= & {} \partial _xL_j^u(x_j)=\lim _{x\rightarrow x_j}\kappa _j\frac{(u-u_j)\partial _xw(x)-u'w(x)}{(u-u_j)^2}\overset{\mathrm {Hop}}{=}\\&\lim _{x\rightarrow x_j}\kappa _j\frac{(u-u_j)\partial _x^2w(x)-u''w(x)}{2u'(u-u_j)}\overset{\mathrm {Hop}}{=}\kappa _j\frac{u'_j\partial _x^2w(x_j)-u''_j\partial _xw(x_j)}{2{u'_j}^2}. \end{aligned}$$

This completes the proof. \(\square \)

Theorem 2

Let \(D^{(1)}\) be the above matrix (first-order derivative matrix of GL functions) and define matrix Q such that \(Q=Diag(u'_0,u'_1,...,u'_N)\), \(Q^{(1)}=Diag(u''_0,u''_1,...,u''_N)\); then, the second-order derivative matrix of GL functions can be formulated as:

$$\begin{aligned} D^{(2)}=(Q^{(1)}+QD^{(1)})Q^{-1}D^{(1)}. \end{aligned}$$
(6)

Proof

See Ref. [55]. \(\square \)

For simplicity, from now on, \(D^{(1)}\) is considered D.

2.3 Generalized Lagrange–Jacobi–Gauss–Radau (GLJGR) collocation method

It is a well-established fact that a proper choice of collocation points is crucial in terms of accuracy and computational stability of the approximation by Lagrange basis [61]. As an appropriate choice of such collocation points, we can refer to the well-known Gauss–Radau points in which points lie inside (a,b) and one point is clustered near the endpoints [29, 61]. In this sequel, we use Jacobi–Gauss–Radau nodes.

In the case of GLJGR collocation method, w(x) in Eq. (4) can be considered as two approaches: in the first approach, one point is clustered near the end of the interval:

$$\begin{aligned} w(x)=\lambda P_{n}^{\alpha ,\beta +1}(u)(u-u_n), \end{aligned}$$
(7)

and in the second approach, one point at the beginning of the interval is clustered:

$$\begin{aligned} w(x)=\lambda (u-u_0)P_{n}^{\alpha ,\beta +1}(u), \end{aligned}$$
(8)

where \(\lambda \) is a real constant. As a matter of simplification, we write

$$\begin{aligned} G(u)=P_{n}^{\alpha ,\beta +1}(u), \end{aligned}$$
(9)

with the following important properties:

$$\begin{aligned} \partial _x G(u)= & {} u'\frac{\varGamma (\alpha +\beta +n+3)}{2\varGamma (\alpha +\beta +n+2)}P_{n-1}^{\alpha +1,\beta +2}(u), \end{aligned}$$
(10)
$$\begin{aligned} \partial _x^2 G(u)= & {} \frac{\varGamma (\alpha +\beta +n+3)}{4\varGamma (\alpha +\beta +n+2)}\bigg (2u''P_{n-1}^{\alpha +1,\beta +2}(u)+(u')^2(\alpha +\beta +n+3)P_{n-2}^{\alpha +2,\beta +3}(u)\bigg ),\nonumber \\ \end{aligned}$$
(11)

Let us speak of the first approach as in Eq. (7). Assuming

$$\begin{aligned} w(x)=\lambda P_{n}^{\alpha ,\beta +1}(u)(u-u_n), \end{aligned}$$

then we have:

$$\begin{aligned} \partial _x w(x)= & {} \lambda \big [u'G(u)+(u-u_n)\partial _xG(u)~\big ], \end{aligned}$$
(12)
$$\begin{aligned} \partial _x^2 w(x)= & {} \lambda \big [u''G(u)+2u'\partial _x G(u)+(u-u_n)\partial _x^2G(u)\big ]. \end{aligned}$$
(13)
$$\begin{aligned} G(u_n)= & {} \frac{\varGamma (\alpha +1+n)}{(n)!\varGamma (\alpha +1)},~~~ \partial _x G(u_n)=u'_n\frac{\varGamma (\alpha +\beta +n+3)}{2\varGamma (\alpha +\beta +n+2)}\frac{\varGamma (\alpha +1+n)}{(n-1)!\varGamma (\alpha +2)}.\nonumber \\ \end{aligned}$$
(14)

We can rewrite the formula in Theorem 1 for a Jacobi–Gauss–Radau specific case: It is easy to do this by setting \(w(x)=\lambda (u-u_0)P_{n}^{\alpha ,\beta +1}(u)\) and recalling that \(\{P_{n}^{\alpha ,\beta +1}(u_j)=0\}_{j=0}^{n-1}\). So, by this, the formula in Theorem 1 can be obtained as a Jacobi–Gauss–Radau case, and the entry of the first-order derivative matrix of GL functions will be:

$$\begin{aligned} d_{kj} = {\left\{ \begin{array}{ll} \frac{u'_kP_{n-1}^{\alpha +1,\beta +2}(u_k)(n!)(\alpha +\beta +n+2)\varGamma (\alpha +1)}{2\varGamma (\alpha +1+n)} ,&{}j=n, 0\le k\le n-1, \\ \\ \frac{2u_k'\varGamma (\alpha +n+1)}{\varGamma (\alpha +1)(n!)(\alpha +\beta +n+2)P_{n-1}^{\alpha +1,\beta +2}(u_j)(u_k-u_j)(u_j-u_k)}, &{} k=n, 0\le j \le n-1,\\ \\ \frac{u_k'(u_k-u_n)}{(u_j-u_n)(u_k-u_j)}\frac{P_{n-1}^{\alpha +1,\beta +2}(u_k)}{P_{n-1}^{\alpha +1,\beta +2}(u_j)} ,&{} 0\le j\ne k\le n-1, \\ \\ \frac{u_j'}{u_j-u_n}+u_j'(\alpha +\beta +n+3)\frac{P_{n-3}^{\alpha +3,\beta +3}(u_j)}{4P_{n-2}^{\alpha +2,\beta +2}(u_j)},&{}0\le k=j\le n-1,\\ \\ \frac{u_k' (n-1)(\alpha +\beta +n+2)}{2(\alpha +1) },&{} ~~k=j=n ,\\ \end{array}\right. } \end{aligned}$$

Similar to this fashion, for the second approach shown in Eq. (8), one can write:

$$\begin{aligned} w(x)= & {} \lambda (u-u_0)P_{n}^{\alpha ,\beta +1}(u),\nonumber \\ G(u_0)= & {} \frac{\varGamma (\beta +2+n)(-1)^n}{(n)!\varGamma (\beta +2)},~~~ \partial _x G(u_0)\nonumber \\= & {} u'_0\frac{\varGamma (\alpha +\beta +n+3)}{2\varGamma (\alpha +\beta +n+2)}\frac{(-1)^{n-1}\varGamma (\beta +2+n)}{(n-1)!\varGamma (\beta +3)}. \end{aligned}$$
(15)

Now this is obvious that \(\{P_{n}^{\alpha ,\beta +1}(u_j)=0\}_{j=1}^{n}\). Therefore, by the second approach, the entries of defined matrix D can be filled as:

$$\begin{aligned} d_{kj} = {\left\{ \begin{array}{ll} \frac{u'_kP_{n-1}^{\alpha +1,\beta +2}(u_k)(n!)(\alpha +\beta +n+2)\varGamma (\beta +2)}{2\varGamma (\beta +2+n)(-1)^n} ,&{}j=0, 1\le k\le n, \\ \\ \frac{2u_k'\varGamma (\beta +n+2)(-1)^n}{\varGamma (\beta +2)(n!)(\alpha +\beta +n+2)P_{n-1}^{\alpha +1,\beta +2}(u_j)(u_k-u_j)(u_j-u_k)}, &{} k=0, 1\le j \le n,\\ \\ \frac{u_k'(u_k-u_0)}{(u_j-u_0)(u_k-u_j)}\frac{P_{n-1}^{\alpha +1,\beta +2}(u_k)}{P_{n-1}^{\alpha +1,\beta +2}(u_j)} ,&{} 1\le j\ne k\le n, \\ \\ \frac{u_j'}{u_j-u_0}+u_j'(\alpha +\beta +n+3)\frac{P_{n-3}^{\alpha +3,\beta +3}(u_j)}{4P_{n-2}^{\alpha +2,\beta +2}(u_j)},&{}1\le k=j\le n,\\ \\ \frac{-u_k' (n)(\alpha +\beta +n+2)}{2(\beta +2) },&{} ~~k=j=0 ,\\ \end{array}\right. } \end{aligned}$$

More specifically, Legendre, Chebyshev, and ultraspherical polynomials can be obtained as special cases from the proposed method. These cases are summarized in the following remark:

Remark 1

We have all the mentioned formulas of GL functions, i.e., D, \(D^{(2)}\) for Gegenbauer (ultraspherical), Legendre, Chebyshev (the first, second, third, and fourth kinds) polynomials by simply setting \(\alpha =\beta \), \(\alpha =\beta =0\), \(\alpha =\beta =-0.5\), \(\alpha =\beta =0.5\), \(\alpha =-0.5\), \(\beta =0.5\), and \(\alpha =0.5\), \(\beta =-0.5\), respectively. These specifications can be named generalized Lagrange–[Gegenbauer, Legendre, Chebyshev (first, second, third, fourth)]–Gauss–Radau for that manner.

2.4 Operational matrix of GL functions

In this subsection, we intend to clarify that when it comes to the collocation method, the operational matrix of derivative for GL functions is equal to transpose of the derivative matrix mentioned in 2.3.

Defining the one-column vectors

$$\begin{aligned} {\hat{L}}_n^u(x)=\begin{bmatrix} L_0^u(x)\\ L_1^u(x)\\ \vdots \\ \L _n^u(x)\\ \end{bmatrix}, {\hat{H}}_n^u(x)=\begin{bmatrix} \partial _xL_0^u(x)\\ \partial _xL_1^u(x)\\ \vdots \\ \partial _xL_n^u(x)\\ \end{bmatrix}, C=\begin{bmatrix} c_0\\ c_1\\ \vdots \\ c_n\\ \end{bmatrix},\end{aligned}$$

for the approximation of a function \(\xi (x)\), one can write

$$\begin{aligned} \xi (x) \approx \sum _{i=0}^{n}c_iL_i^u(x)=C^T{\hat{L}}_n^u(x), \end{aligned}$$

and similarly for the derivative of this function, one can rewrite it as

$$\begin{aligned} \partial _x\xi (x)=C^TK{\hat{L}}_n^u(x), \end{aligned}$$
(16)

where \(K\in \mathfrak {R}^{(n+1)\times (n+1)}\) is the operational matrix of derivative where

$$\begin{aligned} K{\hat{L}}_n^u(x)={\hat{H}}_n^u(x), \end{aligned}$$

and in other words,

$$\begin{aligned} \begin{bmatrix} K_{00}&{}K_{01}&{}\dots &{}K_{0n}\\ K_{10}&{}K_{11}&{}\dots &{}K_{1n}\\ \vdots \\ K_{n0}&{}K_{n1}&{}\dots &{}K_{nn} \end{bmatrix}\begin{bmatrix} L_0^u(x)\\ L_1^u(x)\\ \vdots \\ L_n^u(x)\\ \end{bmatrix} =\begin{bmatrix} \partial _xL_0^u(x)\\ \partial _xL_1^u(x)\\ \vdots \\ \partial _xL_n^u(x)\\ \end{bmatrix}. \end{aligned}$$

To prove it, take the jth row

$$\begin{aligned} \begin{bmatrix} K_{j0}&K_{j1}&\dots&K_{jn} \end{bmatrix}\begin{bmatrix} L_0^u(x)\\ L_1^u(x)\\ \vdots \\ L_n^u(x)\\ \end{bmatrix} = \partial _xL_j^u(x) , \end{aligned}$$

and by collocating the Jacobi–Gauss–Radau nodes (\(\{x_i\}_{i=0}^{n}\)) in this equation, we obtain:

$$\begin{aligned} K_{ji}= & {} \partial _xL_j^u(x_i),\\ K_{ji}= & {} d_{ij}. \end{aligned}$$

This means that the operational matrix for these functions is

$$\begin{aligned} K=D^{T}, \end{aligned}$$
(17)

where D is defined in Sect. 2.3. Similarly, for \(\partial _{xx}\xi (x)\), one can also say

$$\begin{aligned} \partial _{xx}\xi (x)=C^T\big (D^{(2)}\big )^{T}{\hat{L}}_i^u(x), \end{aligned}$$
(18)

where \(D^{(2)}\) is defined in Eq. (6).

3 Numerical method

The main objective of this section is to develop the GLJGR collocation method to solve OCP. In this section, firstly, a promising function approximation method has been presented. Then, GLJGR collocation is implemented so as to accomplish the introduction of the presented numerical method for OCP of interest.

3.1 Function approximation

If \(H=L^2(\eta )\), \(\eta =0\cup (0,1)\times (0,1)\cup 1\), where

$$\begin{aligned} s=\{L_i^u(x)L_j^u(t)~ | ~0\le i\le n, 0\le j\le m\}, \end{aligned}$$

\(s\subset H \), s is the set of GL functions product and

$$\begin{aligned} V_{nm}=Span\{L_i^u(x)L_j^u(t) ~| ~0\le i \le n ,~0\le j \le m\}, \end{aligned}$$

where \(V_{nm}\) is a finite-dimensional vector space. For any \(q\in S\), one can find the best approximation of q in space \(V_{nm}\) as \(P_{nm}(x,t)\) such that

$$\begin{aligned} \exists P_{nm}(x,t) \in V_{nm}, \forall l_{nm}(x,t)\in V_{nm}, \Vert q-P_{nm}(x,t)\Vert _2 \le \Vert q-l_{nm}(x,t)\Vert _2, \end{aligned}$$

where \( \Vert f \Vert _2=\sqrt{\langle f,f\rangle } \) and \(\langle .,.\rangle \) is the inner product. Therefore, for any \(P_{nm}(x,t)\in V_{nm}\), one can write

$$\begin{aligned} P_{nm}(x,t)=\sum _{i=0}^{n}\sum _{j=0}^{m} c_{ij}L_i^u(x)L_j^u(t)=({\hat{L}}_n^u(x))^TC{\hat{L}}_m^u(t), \end{aligned}$$
(19)

in which C is a matrix of \(\mathfrak {R}^{(m+1)\times (n+1)}\), and \(c_{ij}\) are the relevant coefficients and calculable. \(L_i^u(x)\) is considered by the first approach mentioned in Sect. 2.3 in which \(u(x)=\frac{2}{R}x-1\), and \(L_j^u(t)\) is based on the second approach and considered as \(u(t)=2t-1\). This can be proved that as n and m increase, the approximate solution tends to the exact solution [3].

3.2 Implementation of GLJGR collocation method for solving the OCP

Now, for the approximation of state and control functions

$$\begin{aligned} y(x,t)\approx y_{nm}(x,t)= & {} \sum _{i=0}^{n}\sum _{j=0}^{m} a_{ij}L_i^u(x)L_j^u(t)=({\hat{L}}_n^u(x))^TA{\hat{L}}_m^u(t), \end{aligned}$$
(20)
$$\begin{aligned} z(x,t)\approx z_{nm}(x,t)= & {} \sum _{i=0}^{n}\sum _{j=0}^{m} b_{ij}L_i^u(x)L_j^u(t)=({\hat{L}}_n^u(x))^TB{\hat{L}}_m^u(t), \end{aligned}$$
(21)

where

$$\begin{aligned} A=\begin{bmatrix} a_{00}&{}a_{01}&{}\dots &{}a_{0m}\\ a_{10}&{}a_{11}&{}\dots &{}a_{1m}\\ \vdots \\ a_{n0}&{}a_{n1}&{}\dots &{}a_{nm} \end{bmatrix}, B=\begin{bmatrix} b_{00}&{}b_{01}&{}\dots &{}b_{0m}\\ b_{10}&{}b_{11}&{}\dots &{}b_{1m}\\ \vdots \\ b_{n0}&{}b_{n1}&{}\dots &{}b_{nm} \end{bmatrix}, {\hat{L}}_m^u(t)=\begin{bmatrix} L_0^u(t)\\ L_1^u(t)\\ \vdots \\ L_m^u(t)\\ \end{bmatrix}, {\hat{L}}_n^u(x)=\begin{bmatrix} L_0^u(x)\\ L_1^u(x)\\ \vdots \\ L_n^u(x)\\ \end{bmatrix}, \end{aligned}$$

We define residual functions res(x, t) by substituting Eqs. (20) and (21) in Eq. (2)

$$\begin{aligned} res(x,t)=-\frac{x\partial z_{nm}(x,t)}{\partial t}+k\left( \frac{x\partial ^2 z_{nm}(x,t)}{\partial x^2}+r\frac{\partial z_{nm}(x,t)}{\partial t}\right) +xy_{nm}(x,t); \end{aligned}$$
(22)

in terms of Eqs. (17) and (18), one can write

$$\begin{aligned} \frac{\partial z_{nm}(x,t)}{\partial x}= & {} \bigg (D^T{\hat{L}}_n^u(x)\bigg )^TB{\hat{L}}_m^u(t)={\hat{L}}_n^u(x)^TDB{\hat{L}}_m^u(t), \end{aligned}$$
(23)
$$\begin{aligned} \frac{\partial ^2 z_{nm}(x,t)}{\partial x^2}= & {} \bigg ((D^{(2)})^T{\hat{L}}_n^u(x)\bigg )^TB{\hat{L}}_m^u(t)={\hat{L}}_n^u(x)^TD^{(2)}B{\hat{L}}_m^u(t), \end{aligned}$$
(24)
$$\begin{aligned} \frac{\partial z_{nm}(x,t)}{\partial t}= & {} {\hat{L}}_n^u(x)^TB{\hat{D}}^T{\hat{L}}_m^u(t), \end{aligned}$$
(25)

\(A,B\in \mathfrak {R}^{(n+1)\times (m+1)} \), \(D\in \mathfrak {R}^{(n+1)\times (n+1)} \) and \({\hat{D}}\in \mathfrak {R}^{(m+1)\times (m+1)} \) so Eq. (22) can be restated as

$$\begin{aligned} res(x,t)= & {} -x{\hat{L}}_n^u(x)^TB{\hat{D}}^T{\hat{L}}_m^u(t)+k\bigg (x{\hat{L}}_n^u(x)^TD^{(2)}B{\hat{L}}_m^u(t)\nonumber \\&+r{\hat{L}}_n^u(x)^TB{\hat{D}}^T{\hat{L}}_m^u(t)\bigg )+x{\hat{L}}_n^u(x)^TA{\hat{L}}_m^u(t), \end{aligned}$$
(26)

and the initial and boundary conditions of the problem are obtained as

$$\begin{aligned} z_{nm}(x,0) \approx z_0(x), 0<x<R,~~~~~~~z_{nm}(R,t) \approx 0,t>0, \end{aligned}$$
(27)

and within the assumption of Eqs. (21) and (20)

$$\begin{aligned} {\hat{L}}_n^u(x)^TB{\hat{L}}_m^u(0)\approx z_0(x),~~{\hat{L}}_n^u(R)^TB{\hat{L}}_m^u(t)\approx 0. \end{aligned}$$
(28)

As 0 and R are the \( t_0 \) and \( x_n \), with the aid of the characteristic of Lagrange polynomials, we write

$$\begin{aligned} {\hat{L}}_n^u(x)^TB \begin{bmatrix} 1\\ 0\\ \vdots \\ 0\\ \end{bmatrix} ={\hat{L}}_n^u(x)^TB[:,0],~~~ \begin{bmatrix} 0&0&...&1 \end{bmatrix}B{\hat{L}}_m^u(t)=B[n,:]{\hat{L}}_m^u(t), \end{aligned}$$
(29)

where B[ : , 0] and B[n,  : ] are the first column and \((n+1)\)th row of Matrix B.

Then, with (\(n+1\)) collocation nodes in x space and (\(m+1\)) collocation nodes in t space, a set of algebraic equations is constructed by using Eq. (26) together with the conditions in Eq. (28). (Simplification of Eq. (29) is also used.)

$$\begin{aligned} {\left\{ \begin{array}{ll} F[i]={\hat{L}}_n^u(x_i)^TB[:,0]- z_0(x_i)=B_{i0}- z_0(x_i), ~i=0,\dots ,n,\\ F[n+j]=B[n,:]{\hat{L}}_m^u(t_j)=B_{nj}, ~j=1,\dots ,m,\\ F[n+m+(i)(m+1)+j+1]=res(x_i,t_j),~i=0,...,n,~j=0,...,m,\\ \end{array}\right. } \end{aligned}$$
(30)

in which \( res(x_i,t_j) \) can be considered as

$$\begin{aligned} res(x_i,t_j)=-x_iB[i,:]{\hat{D}}^T[:,j]+k\bigg (x_iD^{(2)}[i,:]B[:,j]+rB[i,:]{\hat{D}}^T[:,j]\bigg )+x_ia_{ij}. \end{aligned}$$

or

$$\begin{aligned} res(x_i,t_j)=(kr-x_i)B[i,:]{\hat{D}}^T[:,j]+kx_iD^{(2)}[i,:]B[:,j]+x_ia_{ij}. \end{aligned}$$
(31)

The reason why j starts from 1 (in the second case of Eq. (30)) is that: in both examples we will consider later, for the first case of Eq. (30), we have \(z_0(x_n=R)=0\) and this makes a redundancy with the second case of Eq. (30) at \(j=0\). To avoid this, j starts from 1.

We now describe the method of the selection of points in this paper. In what follows, we have used \(x_i\) and \(t_j\) which are considered as the following statements. Firstly,

$$\begin{aligned} \{x_i\}_{i=0}^{n}=\{x|(P_{n}^{\alpha ,\beta +1}(u(x))(u(x)-u(x_n)))=0\}, \end{aligned}$$
(32)

which should \(x\in (0,R]\). Therefore, we set \(u(x)=\frac{2x}{R}-1\), and we have:

$$\begin{aligned} \{x_i\}_{i=0}^{n-1}=\{x|P_{n}^{\alpha ,\beta +1} \left( \frac{2x}{R}-1\right) =0\},~~~ and ~~~ x_n=R. \end{aligned}$$
(33)

One can see that this assignment is based on the first approach in Sect. 2.3.

With the same fashion, for variable t we have

$$\begin{aligned} \{t_j\}_{j=0}^{m}=\left\{ t|(u(t)-u(t_0))P_{n}^{\alpha ,\beta +1}(u(t))=0\right\} \end{aligned}$$
(34)

that should \(t \in [0,1)\). Therefore, we set \(u(t)=2t-1\), and we have:

$$\begin{aligned} t_0=0,~~~ and ~~~ \{t_j\}_{j=1}^{m}= \left\{ t|P_{n}^{\alpha ,\beta +1}(2t-1)=0\right\} \end{aligned}$$
(35)

Again, one can consider this assignment based on the second approach shown by Eq. (8) in Sect. 2.3.

At the next step, we approximate the integral existing in the OCP. For this, we exploit Gauss–Jacobi quadrature.

For estimating an integral by Gauss–Jacobi quadrature, we do as follows:

$$\begin{aligned} \int _a^bf(v)w^{\alpha ,\beta }\left( \frac{2(v-a)}{b-a}-1\right) dv\approx & {} \left( \frac{b-a}{2}\right) \int _{-1}^1f\left( \frac{b-a}{2}s+\frac{b+a}{2}\right) w^{\alpha ,\beta }(s)\text {d}s,\nonumber \\= & {} \frac{b-a}{2}\sum _{i=0}^{N}f\left( \frac{b-a}{2}s_i+\frac{b+a}{2}\right) \varpi _i\nonumber \\= & {} \frac{b-a}{2}\sum _{i=0}^{N}f(v_i)\varpi _i, \end{aligned}$$
(36)

where \(v\in [a,b]\) and \(s\in [-1,1]\) , and Eq. (36) is exact when \(degree \big (f(v)\big )\le (2N+1)\) for Gauss–Jacobi quadrature.

\(\{s_i\}_{i=0}^{N}\) are Gauss–Jacobi nodes, and their relevant weights \(\{\varpi \}_{i=0}^{N}\) are [64]

$$\begin{aligned} \varpi _i=\frac{\varGamma (N+\alpha +2)\varGamma (N+\beta +2)}{\bigg (P_{N+1}^{\alpha ,\beta }(s_i)\bigg )'(1-s_i^2)}\frac{2^{\alpha +\beta +1}}{\varGamma (N+2+\alpha +\beta )\varGamma (N+2)}, \end{aligned}$$
(37)

The cost functional J is estimated by a numerical integration method. For this, we applied Gauss–Jacobi quadratures in Eq. (36) for both variables t and x.

$$\begin{aligned} \mathrm{min} ~~ J= & {} \frac{1}{2}\int _0^1\int _0^R x^r\big (c_1z_{nm}^2(x,t)+c_2y_{nm}^2(x,t)\big )\text {d}x\text {d}t,\nonumber \\\approx & {} \frac{R}{8}\bigg (c_1\sum _{i=0}^{N}\sum _{j=0}^{M}\frac{\varpi _x^i {(\frac{\hat{x_i}+1}{2})}^r \varpi _t^j z_{nm}^2(\frac{\hat{x_i}+1}{2},\frac{\hat{t_j}+1}{2})}{w^{\alpha ,\beta }(\hat{x_i})w^{\alpha ,\beta }(\hat{t_i})}\nonumber \\&+c_2\sum _{i=0}^{N}\sum _{j=0}^{M}\frac{\varpi _x^i {(\frac{\hat{x_i}+1}{2})}^r \varpi _t^j y_{nm}^2(\frac{\hat{x_i}+1}{2},\frac{\hat{t_j}+1}{2})}{w^{\alpha ,\beta }(\hat{x_i})w^{\alpha ,\beta }(\hat{t_i})}\bigg ), \end{aligned}$$
(38)

where \(\varpi _x^i\), \(\varpi _t^j\), \(\hat{x_i}\), \(\hat{t_j}\) are as follows

$$\begin{aligned} \{\hat{x_i}\}_{i=0}^{N}= & {} \{x|P_{N+1}^{\alpha ,\beta }(x)=0\}, \end{aligned}$$
(39)
$$\begin{aligned} \{\hat{t_j}\}_{j=0}^{M}= & {} \{t|P_{M+1}^{\alpha ,\beta }(t)=0\}, \end{aligned}$$
(40)
$$\begin{aligned} \varpi _x^i= & {} \frac{\varGamma (N+\alpha +2)\varGamma (N+\beta +2)}{\bigg (P_{N+1}^{\alpha ,\beta }(\hat{x_i})\bigg )'(1-\hat{x_i}^2)}\frac{2^{\alpha +\beta +1}}{\varGamma (N+2+\alpha +\beta )\varGamma (N+2)}, \end{aligned}$$
(41)
$$\begin{aligned} \varpi _t^j= & {} \frac{\varGamma (M+\alpha +2)\varGamma (M+\beta +2)}{\bigg (P_{M+1}^{\alpha ,\beta }(\hat{t_j})\bigg )'(1-\hat{t_j}^2)}\frac{2^{\alpha +\beta +1}}{\varGamma (M+2+\alpha +\beta )\varGamma (M+2)}. \end{aligned}$$
(42)

From Eq. (38) to Eq. (42) for both variables t and x, we consider 15 Gauss–Jacobi nodes (\(M=N=14\)).

Table 1 Numerical results of Example 1
Full size table
Fig. 1
figure 1

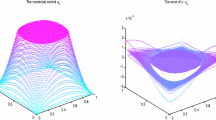
Plots of approximate state and control functions for Example  1.

Full size image

Thus, on the basis of what we have just discussed, the optimal control problem is reduced to a parameter optimization problem. This can be stated as follows:

$$\begin{aligned} L(A,B,{\hat{\lambda }})=J+\sum _{i=0}^{2(n+m)+nm+1}\lambda _iF[i], \end{aligned}$$
(43)

\({\hat{\lambda }}=\{\lambda _i\}_{i=0}^{2(n+m)+nm+1}\) are Lagrange multipliers. Therefore, the minimization problem can, under these new conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial L}{\partial a_{ij}}=0,~~i=0,\dots ,n,~j=0,\dots ,m,\\ \frac{\partial L}{\partial b_{ij}}=0,~~i=0,\dots ,n,~j=0,\dots ,m,\\ \frac{\partial L}{\partial \lambda _{i}}=0,~~i=0,\dots ,2(n+m)+nm+1, \end{array}\right. } \end{aligned}$$

produce a system of \(4(n+m+1)+3nm\) algebraic equations which can be solved by a mathematical software for achieving the unknowns. This system is solved by Newton’s method via ”fsolve” command in Maple. The solution of this system is given by using Maple software.

4 Numerical examples

In this section, the GLJGR collocation method is used to solve two cases of aforementioned OCP in Eq. (1). The aim is to find the state and control functions z(x, t), y(x, t) that minimize the cost function J.

Example 1

Consider the aforementioned OCP with \(c_1=c_2=r=R=k=1\) and initial condition [3, 62]

$$\begin{aligned} z(x,0)=z_0(x)=1-\big (\frac{x}{R}\big )^2,~0<x<R. \end{aligned}$$

so the optimal control problem of Eq. (1) would be

$$\begin{aligned} \mathrm{min} ~~ J=\frac{1}{2}\int _0^1\int _0^1 x\big (z^2(x,t)+y^2(x,t)\big )\text {d}x\text {d}t, \end{aligned}$$
(44)

subject to

$$\begin{aligned} x\frac{\partial z}{\partial t}=x\left( \frac{\partial ^2 z}{\partial x^2}+\frac{1}{x}\frac{\partial z}{\partial t}\right) +xy(x,t), \end{aligned}$$
(45)

with boundary and initial conditions

$$\begin{aligned} z(x,0)=z_0(x)=1-x^2, 0<x<1,~~~~~~~z(1,t)=0,t>0. \end{aligned}$$
(46)

Consider the assumptions mentioned in Example 1. With the methodology presented in Sects. 2 and  3, we approximate the function z(x, t) and y(x, t). In Table 1, the presented method is used to solve the OCP of Example 1. This table, by presenting the value of cost functional, simply shows the accuracy of the presented method for the different choices of n and m. The effect of \(\alpha \) and \(\beta \) is shown as well to provide Chebyshev (all four kinds), Legendre cases, and other different cases. As the aim of this paper is to find z(x, t), y(x, t) in order to minimize J, we plot these state and control functions in Fig. 1a, c. Also, the graph of these functions for the different number of bases is illustrated in Fig. 1b, d; they are the surface plots of the state and control functions. The comparison with the Ritz method by Mamehrashi and Yousefi [3] is made in Table 2. These results show that the presented method is accurate and provides such solutions rather faster than the Ritz method. In other words, with \(n=1,m=4\), we obtained such a result that the Ritz method, somehow, provides with \(n=2,m=7\). Similar to what has been concluded in [3], we obtained that the control and state functions initially have distinct values over the x-axis and as time goes by they tend to reach the same value: This phenomenon is representative of a diffusion process.

Table 2 Numerical results for J in Example 1 with the presented method and the Ritz method [3] (\(\alpha =0\), \(\beta =2\))
Full size table

Example 2

In this example, the \(r=2\), \(c_1=c_2=R=k=1\) and the initial condition is [3, 63]

$$\begin{aligned} z(x,0)=z_0(x)=sin(2\pi x),~0<x<R. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \mathrm{min} ~~ J=\frac{1}{2}\int _0^1\int _0^1 x^2\big (z^2(x,t)+y^2(x,t)\big )\text {d}x\text {d}t, \end{aligned}$$
(47)

subject to

$$\begin{aligned} x\frac{\partial z}{\partial t}=x\left( \frac{\partial ^2 z}{\partial x^2}+\frac{2}{x}\frac{\partial z}{\partial t}\right) +xy(x,t), \end{aligned}$$
(48)

with boundary and initial conditions

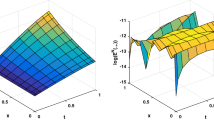
$$\begin{aligned} z(x,0)=z_0(x)=sin(2\pi x), 0<x<1,~~~~~~~z(1,t)=0,t>0. \end{aligned}$$
(49)

Like Example 1, the method discussed in Sects. 2,  3 is utilized to approximate the solution of Example 2. The cost functional J for the different selection of n, m, \(\alpha \), \(\beta \) is calculated in Table 3. Figure 2a, c shows numerical results for state and control functions, i.e., z(x, t) and y(x, t), respectively. These results are plotted in Fig. 2b, d at \(x=0.5\) in a surface plot. Note that initially the state and control at two different locations differ, but as time progresses, the two values become very close. As said in Example 1, this is because of diffusion. A comparison with the Ritz method [3] is made and reported in Table 4. The results in this table demonstrate that the presented method is accurate and reliable, and these results seem to be reached faster than the Ritz method.

Table 3 Numerical results of Example 2
Full size table
Fig. 2
figure 2

Plots of approximate state and control functions for Example 2

Full size image
Table 4 Numerical results for J in Example. 2 with the presented method and the Ritz method [3] (\(\alpha =0\), \(\beta =2\))
Full size table

5 Conclusion

In this study, an OCP is investigated. This problem has beneficial applications in many chemical, biological, and physical fields of studies. The goal of this article is to develop an efficient and accurate method to solve this nonlinear OCP. The method is based upon GLJGR collocation method. Firstly, GL functions are introduced so as to satisfy in delta Kronecker function and GLJGR collocation method is described. The advantage of employing this method is that it reduces the computational and CPU time remarkably. As expressed, these functions are a generalization of the classical Lagrange polynomials. The corresponding differentiation matrices of \(D^{(1)}\) and \(D^{(2)}\) can be obtained by simple formulas. The main benefit of the proposed formulas is that these formulas are derivative-free. Additionally, the accuracy of the presented method by GL function has an exponential convergence rate. Secondly, the obtained results compared with those provided by Mamehrashi and Yousefi [3] show the accuracy and reliability of the presented method. This numerical approach is applicable and effective for such kind of nonlinear OCPs and other problems that can be approximated by Gauss–Radau nodes.