1 Introduction

Theory of free boundary problems for the Navier–Stokes equations is developed intensely during last 50 years. Formation of singularities in viscous flows with a free boundary has a special interest. Monograph [1] contains a number of examples of such kind, where the flow domain changes its topology with time. Corresponding solutions are described by invariant solutions of the Navier–Stokes equations. At the same time, there is another scenario for arising of singularity: Flow domain expands indefinitely at finite time. This phenomenon is studied in present paper on the base of partially invariant solutions to the Navier–Stokes equations.

2 Strip deformation

Plane motion of a viscous incompressible fluid is considered. In what follows, x and y are the Cartesian coordinates, \(\mathbf{u} = (u^x, \ u^y)\) is the velocity vector, p is the pressure, \(\nu \) is the kinematic viscosity, and \(\rho \) is the fluid density. The parameters \(\nu \) and \(\rho \) are assumed to be positive constants. It is also assumed that there are no external body forces. The functions \(\mathbf{u} ,\ p\) satisfy the Navier–Stokes equations

$$\begin{aligned} \mathbf{u} _t + \mathbf{u} \cdot \nabla \mathbf{u} = -\rho ^{-1} \nabla p + \nu \Delta \mathbf{u} , \quad \nabla \cdot \mathbf{u} = 0. \end{aligned}$$
(1)

It is known (see [1, 2] and the references therein) that system (1) has solutions of the form

$$\begin{aligned} u^x = - x v(y,t),\ u^y = \int _0^y v(z,t)\ \mathrm{d}z, \quad p = q(y,t). \end{aligned}$$
(2)

It turned out that class (2) of solutions of system (1) can be used to describe the motion of a viscous fluid in a strip \(\omega _T = \{x,y,t: x \in R, 0< y< s(t), 0< t < T \}\) whose lower boundary is a solid wall and whose upper boundary is free. Indeed, if the function v satisfies the condition

$$\begin{aligned} v(0,t) = 0,\ t \in [0,T], \end{aligned}$$
(3)

then the no-slip condition \(\mathbf{u} = 0\) is satisfied on the line \(y = 0\). In accordance with the kinematic condition on the free boundary, the velocity of its motion in the external normal direction coincides with the normal velocity of the fluid. This condition is satisfied if the following equality is valid:

$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}t} = \int _0^s v(y,t)\ \mathrm{d}y, \quad \ 0 \le t \le T. \end{aligned}$$
(4)

The condition of the absence of shear stresses on the free boundary yields the relation

$$\begin{aligned} v_y (s,t) = 0, \ 0 \le t \le T. \end{aligned}$$
(5)

Finally, the condition of the absence of normal stresses reduces to the equality \(q(s,t) = 0\). It can be satisfied a posteriori because the pressure in the solution of system (1) of the form (2) is determined with accuracy to the additive function of time.

Let us use l to determine the initial thickness of the layer and introduce dimensionless variables by choosing \(l, \ l^2\nu ^{-1},\ \nu l^{-1}, \ \rho \), and \(\nu ^2 l^{-2}\) as scales of length, time, velocity, and pressure. Let the new variables retain their previous notations. Then, by virtue of Eqs. (1) and (2), the function v in the strip \(\omega _T\) satisfies the equation

$$\begin{aligned} v_t = v_{yy} + v^2 - v_{y} \int _0^y v(z,t)\ \mathrm{d}z. \end{aligned}$$
(6)

The boundary conditions (3)–(5) in the new variables retain the previous form. We also add the initial conditions

$$\begin{aligned} v(y,0) = v_0(y),\ 0 \le y \le 1, \ s(0) = 1. \end{aligned}$$
(7)

As a result, we obtain a problem formulation with an unknown boundary: We have to find a function s(t) and a solution v(y, t) of Eq. (6) in the domain \(\omega _T\) satisfying the boundary conditions (3)–(5) and the initial condition (7).

The problem with a free boundary for the Navier–Stokes equations (3)–(7) was first formulated in [3], where self-similar solutions of this problem were also found. The effect of solution blowup was numerically discovered in [4]. This effect is manifested as follows: The free boundary moves to infinity within a finite time. Similar solutions of ideal fluid equations were obtained by Ovsiannikov [5] and by Longuet-Higgins [6]. In these solutions, the strip width is described by a simple formula

$$\begin{aligned} s = \frac{s_0}{1-kt}, \end{aligned}$$
(8)

where \(k = \text {const}\). If \(k < 0\), then the problem solution exists for all \(t>0\), and the strip width tends to zero as \(t \rightarrow \infty \). If \(k > 0\), the solution fails within a finite time. In this case, the solution lifetime is 1/k. It turned out that the inviscid asymptotic yields the principal term of the singularity in the behavior of the function s(t) when approaching the catastrophe instant [4]. Figure 1 shows the plot of \(1/s'(t)\) for the initial function \( v_0(y) = 0.8 \sin (\pi y/2)\), and the dotted curve is the Ovsiannikov solution for an ideal fluid.

Fig. 1
figure 1

Asymptotic tending of the viscous fluid strip width when approaching the catastrophe instant to the Ovsiannikov solution for an ideal fluid

Full size image

The problem of deformation of a viscous strip with two free boundaries was also considered in [3], where sufficient conditions both for the existence of the solution for all \(t>0\) and for solution blowup within a finite time were formulated. The structure of the collapsing solutions of this problem was considered by Galaktionov and Vazquez [7].

3 Self-similar solution

Let us assume that the initial function \(v_0\) satisfies the conditions of smoothness and consistency

$$\begin{aligned} v_0(y) \in C^{2+\beta }[0,1], \ 0< \beta < 1; \ v_0(0) = 0,\ v'_0(1)= 0. \end{aligned}$$
(9)

(In Eq. (9), the symbol \(C^{2+\beta }[0,1]\) indicates the class of functions having continuous derivatives up to the second-order inclusive, which satisfy the Hölder condition with the index \(\beta \)). Then, problem (3)–(7) has the only classical solution in the domain \(\omega _T\) if T is sufficiently small. This statement is proved by the method described in the monograph [8]; it is not presented here.

The sufficient conditions of solvability of the problem as a whole in the course of time are provided below; here, we give an example of its exact solution possessing this property. Equation (6) and the boundary conditions remain unchanged under the action of the stretching transformation \(y = c {\bar{y}}\), \(t = c^2 {\bar{t}}\), \(v = c^{-2} {\bar{v}}\), \(s = c {\bar{s}}\) \((c = \text {const})\). This fact allows us to seek for the self-similar solutions of the problem

$$\begin{aligned} v = t^{-1} \psi (\xi ), \ s = \kappa t^{1/2}, \end{aligned}$$
(10)

where \(\xi = y/\sqrt{t}, \ \kappa = \text {const} > 0, \) and the function \(\psi (\xi )\) satisfies the equation

$$\begin{aligned} \frac{\mathrm{d}^3 \psi }{\mathrm{d}\xi ^3} + \left( \frac{\xi }{2} -\psi \right) \frac{\mathrm{d}^2 \psi }{\mathrm{d}\xi ^2} + \left( \frac{\mathrm{d}^2 \psi }{\mathrm{d}\xi ^2}\right) ^2 + \frac{\mathrm{d} \psi }{\mathrm{d}\xi } = 0, \ 0< \xi < \kappa \end{aligned}$$
(11)

and the boundary conditions

$$\begin{aligned} \psi= & {} \frac{\mathrm{d} \psi }{\mathrm{d}\xi } = 0, \ \ \xi = 0; \nonumber \\ \frac{\mathrm{d}^2 \psi }{\mathrm{d}\xi ^2}= & {} 0, \ \ \xi = \kappa . \end{aligned}$$
(12)

The variable \(\kappa \) is also to be sought; it is determined from the relation

$$\begin{aligned} \psi (\kappa ) = \frac{\kappa }{2}. \end{aligned}$$
(13)

The existence of the self-similar solution of problem (3)–(6) was established in [3]. Obviously, solution (10) is determined for all \(t > 0\). The numerical solution of problem (11)–(13) (Fig. 2) yields the value \(\kappa \approx 1.315. \)

Fig. 2
figure 2

Numerical solution of problem (11)–(13)

Full size image

4 Blowup of the solution

Here, we formulate the sufficient conditions of blowup of the solution of problem (3)–(7). Our formulation is based on the properties of the Lyapunov functional

$$\begin{aligned} L_t[v] = \int \limits _0^{s(t)} \left( \frac{v^3}{3} - \frac{v_y^2}{2} \right) \ \mathrm{d}y, \end{aligned}$$
(14)

associated with its solution. (Here, the subscript t marks the dependence of the functional \(L_t\) on time.)

Statement 1. Let us assume that there exists a classical solution of problem (3)–(7) in the domain \(\omega _T\). Let the following conditions be satisfied:

$$\begin{aligned} v_0 \ge 0, \ y\in [0,1]; \qquad \int \limits _0^{1} \left( \frac{v_0^3}{3} - \frac{(v'_0)^2}{2} \right) \ \mathrm{d}y \equiv L_0 > 0. \end{aligned}$$
(15)

Then, the functional \(L_t\) is a non-decreasing function of t on the segment [0, T].

To prove this fact, we calculate the derivative \(\mathrm{d}L_t/\mathrm{d}t\) and take into account that the inequality \(v \ge 0\) is satisfied everywhere in the domain \(\omega _T\) by virtue of the maximum principle [9] and the first condition of (15). We have

$$\begin{aligned} \frac{\mathrm{d}L_t}{\mathrm{d}t}= & {} \int \limits _0^{s} \left( v^2 v_t - v_y v_{y t}\right) \ \mathrm{d}y + \frac{s'}{3} \ v^3(s,t)\nonumber \\= & {} \int \limits _0^{s} \left( v^4 + v^2 v_{y y} - v^2 v_y \int \limits _0^{y} v(z,t)\ \mathrm{d}z\right. \nonumber \\&\left. - v_y v_{yyy} - v v^2_y + v_y v_{yy} \int \limits _0^{y} v(z,t) \ \mathrm{d}z \right) \ \mathrm{d}y = \frac{s'}{3} v^3(s,t) \nonumber \\&- \frac{1}{3} v^3(s,t) \int \limits _0^{s} v(y,t) \ \mathrm{d}y + \int \limits _0^{s} \left[ v^4 + v^2 v_{yy} + v^2_{yy}\right. \nonumber \\&\left. + \frac{1}{3} v^4 - v v^2_y + \frac{1}{2} (v^2_{y})_y \int \limits _0^{y} v(z,t) \ \mathrm{d}z \right] \ \mathrm{d}y \nonumber \\= & {} \int \limits _0^{s} \left[ v^4 + 2 v^2 v_{yy} + v^2_{yy} + \frac{1}{3} v^4 - v^2 v_{yy} - \frac{3}{2} v v^2_y \right] \ \mathrm{d}y\nonumber \\= & {} \int \limits _0^{s} \left[ \left( v^2 + v_{yy}\right) ^2 + \frac{1}{3} \ v^4 + \frac{1}{2} v v^2_y \right] \ \mathrm{d}y\ge 0. \end{aligned}$$
(16)

Let us introduce the notations

$$\begin{aligned} \eta = \frac{y}{s(t)}, \ w(\eta , t) = v(y,t),\ I(t) = \int \limits _0^{1} w^2(\eta , t) \ \mathrm{d}\eta ,\ I_0 = I(0). \end{aligned}$$
(17)

Thus, we have

Statement 2. Let us assume that conditions (15) are satisfied. Then, the lifetime \(t_{*}\) of the solution of problem (3)–(7) is estimated from above as \(3 I^{-1/2}_0\).

The proof of Statement 2 is based on the inequality \(L_t[v] > 0\) at \( 0< t < T\), which follows from Eqs. (14) to (16), and on the identity to which the solution of problem (3)–(7) satisfies:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \int \limits _0^{s} v^2 \ \mathrm{d}y = \int \limits _0^{s} (3 v^3 - 2 v^2_y) \ \mathrm{d}y, \quad 0< t < T. \end{aligned}$$

By virtue of definition (14) of the functional \(L_t[v]\), the last identity can be rewritten as

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \int \limits _0^{s} v^2 \ \mathrm{d}y = \frac{5}{3}\int \limits _0^{s} v^3 \ \mathrm{d}y + 4 L_t[v], \quad 0< t < T. \end{aligned}$$

Passing here to the variables \(\eta \) and w by formulas (17) and taking into account the definition of the functional I and equality (4), we obtain

$$\begin{aligned} \frac{\mathrm{d}I}{\mathrm{d}t} = \frac{5}{3}\int \limits _0^{1} w^3 \ \mathrm{d}\eta - \left( \int \limits _0^{1} w \ \mathrm{d}\eta \right) \ \left( \int \limits _0^{1} w^2 \ \mathrm{d}\eta \right) + 4 L_t[v]. \end{aligned}$$

Owing to Statement 2, we have \(L_t[v] \ge L_0 > 0\) for all \(t \in [0,T]\). Using the property of nonnegativeness of the function w and the Hölder inequality, we derive the differential inequality

$$\begin{aligned} \frac{\mathrm{d}I}{\mathrm{d}t} > \frac{2}{3} I^{3/2}, \ t \in [0,T]. \end{aligned}$$

Integrating this inequality, we obtain the desired estimate of \( t_{*} < 3 I^{-1/2}_0\).

5 Compression of the strip

Let us now consider the case where the function \(v_0(y)\) is non-positive, \(v_0 = - u_0\), and \(0 \le u_0 \le a,\) \(y \in (0,1]\). Let us pass to the new sought function \(u = -v\) in problem (3)–(7):

$$\begin{aligned} u_t= & {} u_{yy} - u^2 + u_{y} \int _0^y u(z,t)\ \mathrm{d}z, \quad (y,t) \in \omega _T, \end{aligned}$$
(18)
$$\begin{aligned} u(0,t)= & {} 0,\quad \frac{\mathrm{d}s}{\mathrm{d}t} = - \int _0^s u(y,t)\ \mathrm{d}y, \quad u_y(s,t) = 0,\ 0 \le t \le T, \end{aligned}$$
(19)
$$\begin{aligned} u(y,0)= & {} u_0(y), \ 0 \le y \le 1. \end{aligned}$$
(20)

As the function \(u_0\) is nonnegative, the solution of problem (18)–(20) possesses the same property. This fact follows from the maximum principle applicable to Eq. (18) [9]. Moreover, the following estimates are valid: \(0 \le u \le a, \ (y,t) \in {\overline{\omega _T}}\). The solution of problem (18)–(20) describes the process of strip compression, which goes on for an infinite time. It is assumed that the function \(u_0 = - v_0\) satisfies the conditions of smoothness and consistency (9). Under these conditions, the following statement is valid.

Statement 3. For an arbitrary value \(T > 0\), there exists the only classical solution (u, s) of problem (18)–(20), with \(s(t) \ge \exp (-8 a/\pi ^3)\) for \(t > 0\), where \(a = \) max \(u_0 (y), \ y \in [0,1]\).

The two-sided estimate of the function u allows one to use the method described in [8] to prove the solvability of the problem. The layer thickness can be estimated by the inequality

$$\begin{aligned} u \le {\widehat{u}} = a \exp \left( - \frac{\pi ^2 t}{4}\right) \sin \left( \frac{\pi y}{2 s}\right) . \end{aligned}$$

In turn, this inequality is based on the theorem of comparison [9] of the function \({\widehat{u}}\) and the solution of problem (18)–(20). The resultant estimate is of principal importance. It follows from this estimate that the limiting thickness of the strip is positive as \(t \rightarrow \infty \) owing to the action of viscosity. This is the difference between the problem considered here from the problem of inviscid strip deformation, where its thickness tends to zero with increasing t [5, 6].

Fig. 3
figure 3

Time evolution of the layer thickness: stabilization to the quiescent state \((c=0.6)\) (curve 1), solution failure \((c=0.75)\) (curve 2), and self-similar solution (curve 3)

Full size image

6 Numerical solution

The results of the numerical solution of problem (3)–(7) are presented below. Let us introduce a new spatial variable \(\zeta \) (Lagrangian coordinate) and a new sought function V by the relations

$$\begin{aligned} y_t = \int \limits _0^{y} v(z,t) \mathrm{d}z, \quad t > 0; \qquad y = \zeta , \quad t = 0; \qquad V(\zeta , t) = v[y(\zeta ,t)]. \end{aligned}$$
(21)

Then, the domain \(\omega _T\) transforms to the rectangle \(\Pi _T = \{ \zeta , t: 0<\zeta<1, \ 0<t <T \}\), and the original problem transforms to

$$\begin{aligned} V_t= & {} \lambda ^{-1} (\lambda ^{-1} V_{\zeta })_{\zeta } + V^2, \quad \lambda _t = \lambda V, \qquad (\zeta ,t) \in \Pi _T, \end{aligned}$$
(22)
$$\begin{aligned} V(\zeta , 0)= & {} v_0(\zeta ), \quad \lambda (\zeta , 0) = 1, \qquad 0 \le \zeta \le 1, \end{aligned}$$
(23)
$$\begin{aligned} V( 0, t)= & {} 0, \quad V_{\zeta }(1,t) = 0, \qquad 0\le t \le T. \end{aligned}$$
(24)

The additional sought function \(\lambda \) has the meaning of deformation: \(\lambda = x_\zeta \). The strip thickness s is expressed by the formula \(s(t) = \int \nolimits _0^{1} \lambda (\zeta ,t) \mathrm{d}\zeta \). Problem (22)–(24) is solved by the finite difference method. The calculations were performed with the initial function \(v_0 = c \sin (\pi \zeta /2), \ c = \text {const}\). Figure 3 demonstrates the plots of s(t) for \(c= 0.6\) (curve 1) and \(c= 0.75\) (curve 3). In the first case, the motion becomes stabilized to the quiescent state with time despite the fact that the initial function \(v_0\) is positive. The second case demonstrates solution blowup. Curve 2 separating these two plots corresponds to the self-similar solution of problem (10), where t is replaced by \(t+1\). In this solution, \(s = \kappa (t+1)^{1/2}\). The original problem (3)–(7) was also solved by the Galerkin method. The approximate solution was sought in the form

$$\begin{aligned} V_N = \sum _{k=1}^{N} a_k(t) \sin \left[ \pi (2k-1) y/s(t) \right] , \quad N = 1,2, \ldots \end{aligned}$$
(25)
Fig. 4
figure 4

Initial function \(v_0\) (a) and the corresponding plot of the free boundary (b)

Full size image

The functions s and \(a_k \ (k=1,2,\ldots , N)\) form the solution of the dynamic system. This system is presented below for the case \(N=3\):

$$\begin{aligned} \frac{\mathrm{d} a_1}{\mathrm{d}t}= & {} -\frac{77 a_1 a_2}{30 \pi } - \frac{107 a_1 a_3}{210 \pi }-\frac{ \pi ^2 a_1}{4 s^2}\\&+\frac{3 a_1^2}{\pi }-\frac{430 a_2 a_3}{189 \pi }+\frac{9 a_2^2}{2 \pi }+\frac{25 a_3^2}{6 \pi }, \\ \frac{\mathrm{d} a_2}{\mathrm{d}t}= & {} \frac{263 a_1 a_2}{70 \pi }-\frac{865 a_1 a_3}{252 \pi }-\frac{a_1^2}{6 \pi }\\&+\frac{1351 a_2 a_3}{220 \pi }-\frac{9 \pi ^2 a_2}{4 s^2} + \frac{a_2^2}{\pi }+\frac{25 a_3^2}{12 \pi }, \\ \frac{\mathrm{d} a_3}{\mathrm{d}t}= & {} -\frac{5 a_1 a_2}{756 \pi }+\frac{259 a_1 a_3}{66 \pi }-\frac{a_1^2}{30 \pi }\\&+\frac{961 a_2 a_3}{1092 \pi }-\frac{9 a_2^2}{20 \pi }-\frac{25 \pi ^2 a_3}{4 s^2}+\frac{3 a_3^2}{5 \pi }, \\ \frac{\mathrm{d}s}{\mathrm{d}t}= & {} \frac{2 s \left( a_1+a_2/3 + a_3/5 \right) }{\pi }. \end{aligned}$$

It turned out that acceptable accuracy can be provided by taking solution (25) with \(N = 3\). The numerical solutions obtained by the Galerkin method and by the finite difference method agree well with each other.

Thus, we can conclude that the effect of solution blowup within a finite time has a threshold character. The sufficient conditions of solution blowup in Statement 2 are not necessary. The condition of nonnegativeness of the initial function \(v_0\) is not necessary either for the existence of the solution of problem (3)–(7) for all \(t > 0\). This is demonstrated by calculations illustrated in Fig. 4. The initial function \(v_0\) is plotted in Fig. 4a, and the behavior of the free boundary is illustrated in Fig. 4b. We have \(v_0 (x) = 3 \sin (\pi x/2)\) in the first case, \(v_0 (x) = 2 \sin (\pi x/2)-\sin (3 \pi x/2)\) in the second case, and \(v_0(x) = 2 \sin (\pi x/2)+\sin (5 \pi x/2)\) in the third case. It is seen that neither nonnegativeness of the initial function in the second case nor the absence of monotonicity in the third case prevents solution collapse within a finite time; these factors only slightly change the time of this event.

In addition to the mode where the strip width tends to a positive constant as \(t \rightarrow \infty \), there is a close-to-self-similar mode with the asymptotic behavior of the strip width \( s = \kappa t^{1/2} + O(t^{-1/2})\). This mode has a moderate reserve of stability. Figure 5 illustrates the behavior of the strip width obtained for the case where the initial value is the self-similar solution or a small perturbation of this solution. It is seen that the predicted strip thickness coincides with the self-similar law only if the perturbation applied to the initial function is symmetric with respect to the self-similar solution. In other cases, the strip thickness either tends to a constant or passes to infinity within a finite time.

Fig. 5
figure 5

Perturbation of the initial conditions with respect to the self-similar solution (a) and the resultant position of the free boundary with respect to the self-similar law (b)

Full size image

7 Rotation of the layer

In what follows, \(r, \varphi \), and z are the cylindrical coordinates, and \(\mathbf{u} = (u^{r}, u^{\varphi }, u^{z})\) is the velocity vector. In this section, we study the rotationally symmetric solutions of the Navier–Stokes equations

$$\begin{aligned} \mathbf{u} _t + \mathbf{u} \cdot \nabla \mathbf{u} = - \nabla p + \Delta \mathbf{u} , \quad \nabla \cdot \mathbf{u} = 0 \end{aligned}$$
(26)

in the layer \(Q_T = \{r,z,t: r>0, 0< z< s(t), 0< t < T \}.\) System (26) is written in dimensionless variables. They are chosen in the same way as those in Sect. 1, but l now means the initial thickness of the layer. It is known that system (26) admits solutions of the form

$$\begin{aligned} u^r = - r f(z,t),\ u^\varphi = r g(z,t), \ u^z = 2 \int _0^z f(y,t)\ \mathrm{d}y, \quad p = q(z,t). \end{aligned}$$
(27)

The class of these solutions was discovered by Karman [10]. The functions f and g form a closed system of equations

$$\begin{aligned} f_t= & {} f_{zz} + f^2 - g^2 - 2 f_{z} \int _0^z f(y,t)\ \mathrm{d}y, \nonumber \\ g_t= & {} g_{zz} + 2 f g - 2 g_{z} \int _0^z f(y,t)\ \mathrm{d}y \end{aligned}$$
(28)

System (28) is supplemented with the following boundary and initial conditions:

$$\begin{aligned} f(0,t)= & {} 0,\ g(0,t) = \Omega (t),\ 0 \le t \le T, \end{aligned}$$
(29)
$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}t}= & {} 2 \int _0^s f(z,t)\ \mathrm{d}z, \quad f_z (s,t) = 0, \ g_z (s,t) = 0, \ 0 \le t \le T, \end{aligned}$$
(30)
$$\begin{aligned} f(z,0)= & {} f_0(z),\ g(z,0) = g_0(z),\ 0 \le z \le 1, \ s(0) = 1. \end{aligned}$$
(31)

Here, \(\Omega ,\ f_0\), and \(g_0\) are specified smooth functions of their arguments. The solution of problem (28)–(31) describes the fluid motion in a layer of thickness \(Q_T\) whose upper boundary is free and whose lower boundary is a solid plane rotating with an angular velocity \(\Omega (t)\).

In a particular, case with \( f_0 = 0\), problem (28)–(31) was considered in [11], where its local solvability at small values of T was established. The theorem of existence and uniqueness of this problem “as a whole” in time was derived in [1]. It should be noted that this problem has engineering applications (see [12] and references therein). Lavrent’eva [13] studied self-similar and steady-state solutions of problem (28)–(31) with \(f_0 = 0\). In her co-authored paper with Volkova ( [14], see also [1]), they derived a numerical solution of this problem for different forms of the dependence of \(\Omega \) on t and found the asymptotic curve of the solution for \(\Omega \rightarrow \) const as \(t \rightarrow \infty \). Another particular case of problem (28)–(31) occurs if it is assumed that \(\Omega = 0\) and \(g_0 = 0\). Then, it is necessary that \(g = 0 \), and the motion becomes axisymmetric. The axisymmetric case of this problem was considered in [15]. The results of that study are in good qualitative agreement with the results of the analysis of the problem of strip deformation described in Sect. 1 of the present paper. Let us assume that the function \(f_0\) is positive on the interval (0, 1] and “sufficiently large.” If \(g_0 = 0\) and \(\Omega = 0\) (i.e., rotation is absent), then the layer starts to expand, and its thickness turns to infinity at a certain time instant. The specific features of the arising collapse are caused by the presence of the free boundary, while there is no energy concentration inside the flow domain.

Fig. 6
figure 6

Function s(t) without (curve 1) and with (curve 2) rotation

Full size image
Fig. 7
figure 7

Functions f(z, t) and g(z, t) without (curve 1) and with (curve 2) rotation at the time \(t=1\)

Full size image

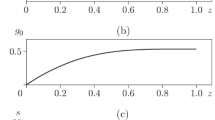
The situation becomes qualitatively different if the plane starts to rotate. At a certain time instant, expansion of the layer transforms to its compression. One can see that plane rotation can prevent the collapse of the solution of problem (28)–(31). Figure 6 shows the function s(t) in the absence of rotation (curve 1) and in the presence of rotation (curve 2). The results were obtained for identical initial data: \(f_0(z) = 0.9 \sin (\pi z/2),\) \(g_0(z)=0,\) \(\Omega (t) = 4 - 4/(1+t^2)\), except for the angular velocity \(\Omega (t)\), which is equal to zero in the first case.

Figure 7a shows the function f(z, t) without (curve 1) and with (curve 2) rotation at the time \(t=1\). It is at this time that the layer thickness for these two cases becomes different. It is seen that rotation leads to principal changes in the character of the vertical component of the velocity vector: There even arises a counterflow region near the rotation axis. Figure 7b shows the function g(z, 1). Clearly, this function is equal to zero if there is no rotation. It characterizes the angular velocity and naturally decreases with distance from the rotation axis.

8 Conclusions

Both solutions considered in the present study have a group-theoretical nature: They are partially invariable (in the sense of Ovsiannikov [16]) solutions of the Navier–Stokes equations [1, 2]. A method of constructing invariant and partially invariant solutions of the Navier–Stokes equations a priori consistent with the conditions on the free surface, which is an invariant manifold of the corresponding group admitted by these equations, was developed in [11]. It is also possible to find other solutions of the Navier–Stokes equations, which describe motions with flat free surfaces. The plane bounding the flow can perform translational or rotational motions. It can be permeable; moreover, the density of sources or sinks should be independent of the longitudinal coordinates, but can depend on time. The fluid may be affected by the gravity force in the vertical direction. In this case, the function p(z, t) determining the pressure should be supplemented with the term \(\rho g (s(t)-z)\), where g is the acceleration due to gravity.