Utilizing passive elements to break time reversibility at low Reynolds number: a swimmer with one activated element

Abstract

In the realm of low Reynolds number, the shape-changing biological and artificial matters need to break time reversibility in the course of their strokes to achieve motility. This necessity is well described in the so-called scallop theorem. In this work, considering low Reynolds number, a novel and versatile swimmer is proposed as an example of a new scheme to break time reversibility kinematically and, in turn, produce net motion. The swimmer consists of one sphere as a cargo or carried body, joined by one activated link with time-varying length, to another perpendicular rigid link, as the support of two passively flapping disks, at its end. The disks are free to rotate between their fixed minimum and maximum angles. The system’s motion in two dimensions is simulated, and the maneuverability of the swimmer is discussed. The minimal operating parameters for steering of the swimmer are studied, and the limits of the swimmer are identified. The introduced swimming mechanism can be employed as a simple model system for biological living matters as well as artificial microswimmers.

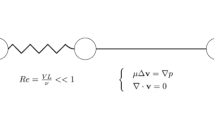
Graphic abstract

Introduction

Microswimmers are cutting-edge technology, with many potential biomedical applications spanning from drug delivery, artificial insemination, and imaging to microsurgery [1,2,3,4]. They are a class of micromachines with the ability to harness external chemical, electrical or acoustic fields to produce net motion [5, 6]. Seminal studies of translation of microorganisms, prominently, first started in the 1950 s [7,8,9,10], focusing mainly on their interactions, energy consumption, and kinematics [10,11,12,13]. In 1977, Purcell’s so-called scallop theorem broadened our understanding of microorganism motility [14]. According to this theory, a swimmer at low Reynolds number swimming condition must change its shape so that the time-symmetry is broken. Physically, this restriction arises since, at low Reynolds number condition, which includes the microscale realm of motile living matters, the inertial forces are less effective than viscous forces [15]. Here, similar to Purcell’s original paper, we will only focus on self-propelling microswimmers by their shape change, and we will not consider phoretic motions [16,17,18,19] and chemically or externally driven swimmers [20, 21]. To overcome the constraint of this theory, many strategies can be deployed mainly to change the assumptions of the theory [10]. These include the introduction of inertia in the microswimmer body [22, 23], having more than one swimmer [24], moving close to an interface or deformable boundaries [25], considering non-Newtonian fluids [26], and owing elastic components [27].

Following Purcell, many swimming mechanisms have been designed or inspired by living matters or biological microswimmers [28,29,30,31]. The proposed self-propelling mechanisms are configurated from the simplest ones, such as the three-link swimmer by Purcell [14], three-sphere swimmer by Najafi and Golestanian [32], and the circle swimmer by Ledesma-Aguilar et al. [33], an elastic two-sphere swimmer by Nasouri et al. [34], etc., to the complex ones such as two varying radii bladder spheres by Avron et al., [35], Quadroar swimmer proposed by Jalali et al. [36], snapping elastic disk swimmer by Wischnewski and Kierfeld [37], etc.

Reviewing the proposed self-propelling mechanisms in recent decades shows that many of them have more than one active element. Moreover, when owing one degree of freedom, they are mainly able to move forward and backward. For instance, Montino and DeSimone [27] considered a variant of the linear three-sphere swimmer [32] with one of the active links replaced with an elastic spring. Upon actuating the active link with different frequencies, their swimmer can move forward and backward. The net displacement of this swimmer is frequency dependent as opposed to its original counterpart, where the net displacement only depends on the sequence and range of the links’ deformation.

The orientation control as a key factor for the maneuverability of the mechanism may be achieved by external fields, but reorientation strategies by versatile reshaping is still a desired topic.

Here, we introduce a strategy to circumvent the time reversibility by considering a passive element, only allowed to have restricted motion. In fact, an extra degree of freedom that is constrained between two values, despite being passive, along with an actively varying degree of freedom, can result in a sequence of body movements that are not time reversible. The proposed mechanism is an instance of such strategies. This mechanism consists of one active link. It may be arranged in both symmetric and asymmetric configurations so that both straight and curved (simple and complex) trajectories and pseudo-self-rotational motion can be achieved. The proposed mechanism can be utilized as an autonomous swimming microrobots, drug delivery system, microcarrier, mixing element, etc., involving simple (straight or curved) or complex trajectories. The swimmer consists of two flapping disks connected via a rigid link and one sphere, as a cargo container, perpendicularly linked to the middle of the connecting link by a time-varying telescopic arm. Disks are free to rotate passively about their revolute joint between their preset minimum and maximum angles.

The rest of the paper is organized as follows: In Sect. 2, we introduce geometry, describe the motion and the phases of the swimmer’s cycle, and subsequently discuss the governing dynamics of the motion. The case of symmetric constraining angles or straight propulsion is discussed in Sect. 3 while Sect. 4 is dedicated to the asymmetric case of the constraining angles, and we also discuss the possible trajectories of the swimmer. Finally, we conclude in Sect. 5.

1 Geometry and Description of the cycle of motion

Our swimmer consists of two identical, very thin disks of radius a, a sphere of radius b, and two slender links with a T-shape arrangement as shown in Fig. 1. The length of the body link, which connects the center of the sphere, B, to the middle of the front link is $h+l$, where $l\ge 0$ is the time-dependent deformation of the body link and h is a constant length. The front link has a constant length of 2g (Fig. 1). Consider a body-fixed coordinate system $(x_1,x_2,x_3)$ with the unit vectors $({\hat{i}}_1,{\hat{i}}_2,{\hat{i}}_3)$, whose $x_1$ and $x_2$ axis is along the body link and front link respectively, with origin O at the intersection of two links. The plane of each disk is perpendicular to the connecting link. Each disk is hinged at its circumference to its corresponding end of the front link and can rotate about an axis perpendicular to the plane of the links until reaching its designated limiting angles. The angle of rotation of the nth disk, $\theta _n$ ($n=1,2$), is defined as the angle between $x_1$ and the plane of each disk, as shown in Fig. 1. Each of these angles is constrained by constant minimum and maximum angles, $\theta _{n,min}$ and $\theta _{n,max}$, respectively, such that $-90^{\circ }<\theta _{n,\text {min}}\le \theta _n\le \theta _{n,\text {max}}<90^{\circ }$. In this study, we assume $\theta _{1,\text {max}}=\theta _{2,\text {max}}=0^{\circ }$, where each limit occurs when the corresponding disk is along the front link (see Fig. 1). Hence, each disk rotates along or below the front link. Without loss of generality, we further assume $|\theta _{1,\text {min}} |\le |\theta _{2,\text {min}} |$. The swimmer can swim by extending and contracting its body repeatedly. Due to symmetry, motion can only occur in the plane of links, which we assume to be the xy plane of the global coordinate system, (x, y, z). Hence the orientation of the swimmer can be determined by a single angle $\phi$, the angle between x and $x_1$ axis of global and body-fixed coordinate systems, respectively. Thus, the positive direction of the x and y axes can be transformed into the ${\hat{i}}_1$ and ${\hat{i}}_2$ directions, respectively, using the rotation matrix [38],

$$\begin{aligned} {\varvec{R}}_\phi =\begin{bmatrix} \cos {\phi }&{}\quad -\sin {\phi }&{}\quad 0\\ \sin {\phi }&{}\quad \cos {\phi }&{}\quad 0\\ 0&{}\quad 0&{}\quad 1 \end{bmatrix} \end{aligned}$$

(1)

Point C is considered in the middle of points B and O, ${\varvec{x}}_C=-\frac{h+l}{2}{\hat{i}}_2$, to describe the position and motion of the swimmer.

Fig. 1

a Geometry of the swimmer. b The body link, the only active part, is a prismatic actuator. Disks are hinged to the front link and can have a limited rotation. c The $x_1x_2$ plane of the body-fixed coordinate system $(x_1,x_2,x_3)$ lies in the plane of links, which coincide with xy plane of the global frame. As an example, the angle of disk-1, $\theta _1$, and its constraining angles, $\theta _{1,min}$ and $\theta _{1,max}$, are shown

We consider the initial state of the swimmer such that the body link is initially at its minimum size ($l=0$) and disks are along the front link ($\theta _1=\theta _{1,\text {max}}=0^{\circ }$, $\theta _2=\theta _{2,\text {max}}=0^{\circ }$). We denote the designated maximum length of l (the deformable part of the body link) by $l_{max}$ (Fig. 2). The complete cycle of non-reciprocal motion can be presented in six phases as follows:

• 1. In the first phase of the motion, the body link extends with the expansion rate ${\dot{l}}>0$, ${\dot{l}}=dl/dt$, and due to the induced flow of fluid, the disks rotate and translate similarly (symmetrically) until reaching the limit of disk-1, angle $\theta _{1,\text {min}}$. We denote the extension of the body link, corresponding to this phase, by $l_1$.

• 2. The body link keeps extending similar to the preceding phase, while disk-1 translates without rotating relative to the front link, $\theta _1=\theta _{1,\text {min}}$, and disk-2 translates and rotates relative to the front link until reaching the limit $\theta _2=\theta _{2,\text {min}}$. We denote the extension of the body link, corresponding to this phase, by $l_2$.

• 3. In this phase, the body link extends until reaching its maximum length, $h+l_{\text {max}}$, while both disks translate without rotating relative to the front link ($\theta _1=\theta _{1,\text {min}}$, $\theta _2=\theta _{2,\text {min}}$).

• 4. The body link contracts with the expansion rate ${\dot{l}}<0$, which has the same magnitude as the previous phase, and disks rotate and translate until disk-1 retains its initial orientation relative to the main body, i.e., it orients along the front link. We denote the contraction of the body link, corresponding to this phase, by $l_4$.

• 5. The body link keeps contracting the same as the preceding phase, while disk-1 translates and remains along the front link, and disk-2 translates and rotates relative to the front link until it orients along the front link. We denote the contraction of the body link, corresponding to this phase, by $l_5$.

• 6. Finally, the body link contracts, until reaching its initial length, h, while both disks translate as they remain along the front link.

These phases and the corresponding configuration of the swimmer are depicted in Fig. 2 (for straight and curved motion). To have a complete cycle, the maximum deformation length of the body link ($l_{\text {max}}$) must satisfy $\max \{l_1+l_2, l_4 +l_5\}<l_{\text {max}}$. Deformation lengths $l_i$ ($i=1,2,4,5$) are parts of stroke length in which disks transform in designated orientations, while during the rest of each stroke, disks retain their orientations relative to the links. Hence, analogous to push-me-pull-you [35], the swimmer extends or contracts while being transformed into a new configuration.

Fig. 2

The swimmer’s cycle of motion, for straight and curved motion, versus time. Vertical dashed lines indicate the initial position of the swimmer, and curved dashed lines correspond to the position of the swimmer throughout its cycle for each class

1.1 Dynamics of the motion

Denoting velocity of the center of the disk-1, disk-2, sphere and origin O by ${\varvec{v}}_1$, ${\varvec{v}}_2$, ${\varvec{v}}_3$ and ${\varvec{v}}_O$, respectively, we obtain

$$\begin{aligned} {\varvec{v}}_1&={\varvec{v}}_O+\dot{\varvec{\phi }}\times {\varvec{r}}_1+\dot{\varvec{\theta }}_1\times (a\cos {\theta _1}{\hat{i}}_1+a\sin {\theta _1}{\hat{i}}_2) \end{aligned}$$

(2a)

$$\begin{aligned} {\varvec{v}}_2&={\varvec{v}}_O+\dot{\varvec{\phi }}\times {\varvec{r}}_2+\dot{\varvec{\theta }}_2\times (-a\cos {\theta _2}{\hat{i}}_1+a\sin {\theta _2}{\hat{i}}_2) \end{aligned}$$

(2b)

$$\begin{aligned} {\varvec{v}}_3&={\varvec{v}}_O+\dot{\varvec{\phi }}\times {\varvec{r}}_3-{\dot{l}}{\hat{i}}_2 \end{aligned}$$

(2c)

where the over-dot denotes $\frac{d}{dt}$, $\dot{\varvec{\phi }}={\dot{\phi }}{\hat{i}}_3$, $\dot{\varvec{\theta }}_1={\dot{\theta }}_1{\hat{i}}_3$, $\dot{\varvec{\theta }}_2=-{\dot{\theta }}_2{\hat{i}}_3$, and the positions of the centers of disk-1, disk-2, and the sphere (all in the body frame), are written as

$$\begin{aligned} {\varvec{r}}_1&=(g+a\cos {\theta _1}){\hat{i}}_1+a\sin {\theta _1}{\hat{i}}_2 \ \end{aligned}$$

(3a)

$$\begin{aligned} {\varvec{r}}_2&=-(g+a\cos {\theta _2}){\hat{i}}_1+a\sin {\theta _2}{\hat{i}}_2 \end{aligned}$$

(3b)

$$\begin{aligned} {\varvec{r}}_3&=-(h+l){\hat{i}}_2 \end{aligned}$$

(3c)

We assume that hydrodynamic perturbation of the T-frame is negligible compared to disks and the sphere, and also, the disks and the sphere are far enough, $a,b\ll h,g$, that we can neglect hydrodynamic interactions between them. The translation tensor for a circular disk of radius a and sphere of radius b can be obtained as [39]

$$\begin{aligned}&{\varvec{K}}_{\text {disk}}=\frac{16}{3}a(2{\hat{e}}_1{\hat{e}}_1+3{\hat{e}}_2{\hat{e}}_2+2{\hat{e}}_3{\hat{e}}_3) \ \end{aligned}$$

(4)

$$\begin{aligned}&{\varvec{K}}_{\text {sphere}}=6\pi b{\varvec{I}} \end{aligned}$$

(5)

where ${\varvec{I}}$ is an identity matrix and $({\hat{e}}_1,{\hat{e}}_2,{\hat{e}}_3)$ are basis vectors of an orthogonal coordinate system fixed to the center of the disk with ${\hat{e}}_2$ directed normal to the disk. Assuming ${\hat{e}}_3$ to be directed along the positive ${\hat{i}}_3$ axis of the body frame, to obtain the translation tensor of the nth disk ($n=1,2$) with respect to the frame of the swimmer, we use the rotation matrix [38]

$$\begin{aligned} {\varvec{R}}_n=\begin{bmatrix} (-1)^{n+1}\cos {\theta _n}&{}\quad \sin {\theta _n}&{}\quad 0\\ -\sin {\theta _n}&{}\quad (-1)^{n+1}\cos {\theta _n}&{}\quad 0\\ 0&{}\quad 0&{}\quad 1 \end{bmatrix}\nonumber \\ \end{aligned}$$

(6)

which yields:

$$\begin{aligned} {\varvec{K}}_n={\varvec{R}}_{n}^T{\varvec{K}}_{\text {disk}}{\varvec{R}}_n \end{aligned}$$

(7)

The background fluid exerts a hydrodynamic force on each part of the swimmer as it moves. The hydrodynamic forces that disk-1, disk-2, and the sphere experience as they move are denoted by ${\varvec{F}}_1$, ${\varvec{F}}_2$, and ${\varvec{F}}_3$ respectively, which reads [39]

$$\begin{aligned}&{\varvec{F}}_i=-\mu {\varvec{K}}_i{\varvec{v}}_i \text { } (i=1,2,3) \end{aligned}$$

(8)

$$\begin{aligned}&{\varvec{K}}_3={\varvec{K}}_{\text {sphere}} \end{aligned}$$

(9)

The hydrodynamic torques exerted on the disks can be obtained as [39]

$$\begin{aligned} {\varvec{T}}_n=-\mu \varvec{\Omega }_{\text {disk}}(\dot{\varvec{\phi }}+\dot{\varvec{\theta }}_n) \hbox { }\ (n=1,2) \end{aligned}$$

(10)

where $\varvec{\Omega }_{\text {disk}}=\frac{32}{3}a^3{\varvec{I}}$, and for the case of a sphere, we have

$$\begin{aligned} {\varvec{T}}_3=-\mu \varvec{\Omega }_{\text {sphere}}\dot{\varvec{\phi }} \end{aligned}$$

(11)

where $\varvec{\Omega }_{\text {sphere}}=8\pi b^3{\varvec{I}}$. In the absence of external forces and torques, the swimmer will be force and torque-free, meaning the swimmer is subjected to the constraints

$$\begin{aligned}&\sum _{j=1}^3{\varvec{F}}_j=0 \end{aligned}$$

(12)

$$\begin{aligned}&\sum _{j=1}^3({\varvec{r}}_j\times {\varvec{F}}_j+{\varvec{T}}_j)=0 \end{aligned}$$

(13)

where ${\varvec{r}}_j\times {\varvec{F}}_j$ are the torque vectors due to the first moment of the hydrodynamic force about the origin of the body frame. If the nth disk ($n \in \{1,2\}$) rotates relative to the links during a phase, it must be torque-free; thus, it is subjected to the constraint

$$\begin{aligned} {\varvec{T}}_n+((-1)^{n+1} a\cos {\theta _n}{\hat{i}}_1+a\sin {\theta _n}{\hat{i}}_2)\times {\varvec{F}}_n=0\nonumber \\ \end{aligned}$$

(14)

Eq. 14 puts a constraint on both disks during phase 1 and phase 4, as disks are free to rotate. It also applies to disk-2 during phase 2 and phase 5.

Considering each phase separately, upon substituting from Eqs. 2 and 3 into Eqs. 12–14, we drive first-order ODEs, describing the motion of the swimmer that can be used to find the position and orientation of the swimmer in each phase. In the proceeding sections, analytical solutions are calculated for the case of the symmetric constraining angles of the disks, while we use a numerical approach in general. We first treat the problem for the case of symmetric constraining angles of the disks and then for the asymmetric one.

2 Pure translational (straight) motion: symmetric constraining angles of disks

In the case of symmetric constraining angles, $\theta _{2,\text {min}}=\theta _{1,\text {min}}$, simplifies phases of the cycle of motion to 4 phases by eliminating phases 2 and 5. Therefore, the swimmer’s phases 1, 2, 3, and 4 of this case will be the same as general phases 1, 3, 4, and 6, respectively, where the orientations of the disks are symmetric ($\theta _1=\theta _2$) during the motion. This is depicted in Fig. 2 (straight motion). Since the swimmer is symmetric with respect to the yz plane of the body frame, it will undergo a linear path without rotation. For each phase of the swimmer’s motion, its corresponding ODE is given in the Appendix A. Upon solving these ODEs, we can find the translational displacement of the swimmer $\Delta _{\text {sym}}$ as

$$\begin{aligned}{} & {} \Delta _{\text {sym}}=\left( \frac{48\pi ba\sin ^2{\theta _{\text {sym}}}}{(16a+3\pi b)(32a+9\pi b+16a\cos ^2{\theta _{\text {sym}}})}\right) \nonumber \\{} & {} \quad \left( l_{max}-l_{\text {sym}}\right) \end{aligned}$$

(15)

where

$$\begin{aligned} \theta _{\text {sym}}= & {} -\theta _{1,\text {min}}=-\theta _{2,\text {min}} \nonumber \\ \quad l_{\text {sym}}= & {} l_1=l_3\nonumber \\= & {} \frac{a}{5.4\pi b}[(32a+9\pi b)\ln {(\sec \theta _{\text {sym}}+\tan \theta _{\text {sym}})}\nonumber \\{} & {} \quad -12.8a\sin {\theta _{\text {sym}}}] \end{aligned}$$

(16)

for the case of $l_{\text {max}}\ge l_{\text {sym}}$. As mentioned in Sect. 2, $l_{\text {sym}}$ is the extended (contracted) length of the body link corresponding to the first (third) phase. As the disks and the sphere are not influenced by the perturbations caused by each other, the displacement during phases 1 and 3 is equal and in the opposite direction, which can be thought of as the latter is the time reversal of the former. Thus, the link extension (or contraction) $l_{sym}$, only contributes to changing the shape of the swimmer, while the translation occurs during the $l_{\text {max}}-l_{\text {sym}}$ portion of extension and contraction of the body link. Figure 3 shows $l_{\text {sym}}$ as a function of constraining angle $\theta _{\text {sym}}$ for some selected values of b/a. For a specific set of design parameters, $l_{\text {sym}}$ always increases as $\theta _{\text {sym}}$ rises, which is reflected in the figure. Furthermore, as $\theta _{\text {sym}}\rightarrow \pi /2$, $l_{\text {sym}}\rightarrow \infty$. Physically, the torque exerted on the disks decreases as $\theta _{\text {sym}}$ goes up, and in turn, much further extension of the body link is required for larger values of $\theta _{\text {sym}}$. According to the graph, any increase in b/a reduces $l_{\text {sym}}$. In fact, the sphere acts as an anchor for the disks; hence larger values of b/a give rise to an increase in the force exerted on the disks as the link expands.

Figure 4 shows $\Delta _{\text {sym}}/a$ as a function of possible values of $\theta _{\text {sym}}$, which keeps the condition $l_{\text {sym}}\le l_{\text {max}}$, for some selected values of $l_{\text {max}}/a$. It is clear that as the stroke length increases, the displacement of the swimmer increases too. More importantly, the dependency on $\theta _{\text {sym}}$ shows an optimum value for which the displacement reaches its maximum value. The value of $\theta _{\text {sym}}$ affects displacement in two ways: Firstly, the increase in $\theta _{\text {sym}}$ provides more difference in the resistance of disks during extension and contraction of the active link, which results in an increase in displacement of the swimmer. Secondly, the greater the value of $\theta _{\text {sym}}$, the larger $l_{\text {sym}}$ would be, as discussed about Fig. 3. This means a larger portion of the link would be dedicated to changing the shape of the disks without having any net displacement. As a result of these two opposing effects, there is indeed expected to be an optimal value of $\theta _{\text {sym}}$ for each assumed value of stroke length $l_{\text {max}}/a$.

As expected for a low Reynolds number swimmer, the expression for $\Delta _{\text {sym}}$ shows that the displacement of the swimmer in each cycle does not depend on the deformation rate ${\dot{l}}$. The mean translational velocity of the swimmer in the case of straight motion, $V_{\text {sym}}$, can be derived as

$$\begin{aligned}{} & {} V_{\text {sym}}=\left( \frac{48\pi ba\sin ^2{\theta _{\text {sym}}}}{(16a+3\pi b)(32a+9\pi b+16a\cos ^2{\theta _{\text {sym}}})}\right) \nonumber \\{} & {} \quad \left( \frac{l_{\text {max}}-l_{\text {sym}}}{\tau }\right) \end{aligned}$$

(17)

where $\tau$ is the time required for a complete cycle. The above expression can be compacted as $V_{\text {sym}}=\Delta _{\text {sym}}/\tau$.

3 2D curved motion: asymmetric constraining angles of disks

The translational displacement $\varvec{\Delta }=(\Delta _x,\Delta _y)$ and the change in orientation $\beta$ of the swimmer over the first cycle can be calculated by summing contributions $\varvec{\Delta }_i$ and $\beta _i$, respectively, correspond to the ith phase ($1\le i\le 6$) as

$$\begin{aligned}&\varvec{\Delta }=\int _{0}^{\tau } \varvec{V_{s}} \,dt=\sum _{j=1}^{6} \varvec{\Delta }_j \end{aligned}$$

(18)

$$\begin{aligned}&\beta =\int _{0}^{\tau } \dot{\varvec{\phi }} \,dt=\sum _{j=1}^{6} \beta _j \end{aligned}$$

(19)

Fig. 3

Dimensionless expansion or contraction length of the body link in the phases 1 and 3, $l_{\text {sym}}/a$ (Eq. 16), as a function of the constraining angle $\theta _{\text {sym}}$ (Eq. 15). Dotted (blue), dotted (red, marked with ’+’), dash-dotted (green), dash (purple), and solid (blue) lines correspond to $b/a=0.25, 0.5, 1, 2, 4$, respectively

Fig. 4

Dimensionless translational displacement $\Delta _{\text {sym}}/a$, as a function of the constraining angle $\theta _{\text {sym}}$ (Eq. 17). Solid (green), dash (red), and dash-dotted (blue) lines correspond to $l_{\text {max}}/a=4, 6, 8$, respectively

where $\tau$ is the time required for a complete cycle. We recall that the body-fixed coordinate system initially coincides with the laboratory frame. Figure 5 shows the trajectory and the orientation of the swimmer for a specific geometry of $g/a=15$, $h/a=10$, $b/a=2$, $\theta _{1,\text {min}}=-45^{\circ }$, $\theta _{2,\text {min}}=-60^{\circ }$, and the stroke length of $l_{\text {max}}/a=8$ during the first cycle. It can be seen that during the extension of the active link, the swimmer moves forward (in y direction), whereas it moves backward as the active link contracts. Since the disks’ orientations are different during expansion and contraction, the resultant translation is a forward movement (in y direction). The first and second phases of the motion are not affected by the stroke length $l_{\text {max}}/a$; hence, their contribution is an intrinsic property of the swimmer when it is fabricated ($\frac{d\varvec{\Delta _j}}{dl_{\text {max}}}=\frac{d\beta _j}{dl_{\text {max}}}=0$, $j=1,2$). Subsequently, at the beginning of the third phase, the body link has the constant extension length of $l=l_1+l_2$, and the corresponding body deformation $l_3 =l_{\text {max}}-(l_1+l_2)$ linearly depends on the stroke length $l_{\text {max}}$. During this phase, the swimmer rotates counter-clockwise, and the larger values of $l_{\text {max}}$ increase the magnitude of this rotation (we recall that $|\theta _{2,\text {min}} |\ge |\theta _{1,\text {min}} |$). While phase 6 does not contribute to the swimmer’s rotation, in the fourth and fifth phases, the swimmer experiences rotation. As phases 3, 4, and 5 depend on the stroke length $l_{\text {max}}$, we can alter this length to control the rotation of the swimmer. Figure 6 shows dimensionless translational displacements, $\Delta _x/a$, $\Delta _y/a$, and angular displacement $\beta$ of the swimmer as a function of $l_{\text {max}}$ for the same geometry as Fig. 5, and some selected values of $\theta _{2,\text {min}}$. Analogous to symmetric constraining angles of the disks, as $l_{\text {max}}/a$ increases, the swimmer achieves larger displacements in y direction. The nonzero values of $\Delta _x/a$ and $\beta$ are the results of the deviation of the swimmer’s constraining angles from its symmetrical configuration. Here larger values of $|\theta _{2,\text {min}} |$ correspond to more asymmetry in the shape of the swimmer, which increases the magnitude of these two quantities.

Fig. 5

Assuming a specific geometry of $g/a=15$, $h/a=10$, $b/a=2$, $\theta _{1,min}=-45^{\circ }$, $\theta _{2,min}=-60^{\circ }$, and $l_{max}/a=8$, the swimmer initially starts from the origin of the global frame, (0, 0) and $\phi =0$. a The trajectory of the swimmer in a cycle where x and y axes have different scales. b The evolution of the orientation of the swimmer as a function of the extension of the body link during a cycle. Solid and dash lines correspond to odd and even phases of the motion, respectively

Fig. 6

Translational (a  max and b) and angular (c) displacement of the swimmer as a function of stroke length, $l_{\text {max}}/a$, over one cycle, for a model with the same geometry as Fig. 5 ($g/a=15$, $h/a=10$, $b/a=2$, $\theta _{1,min}=-45^{\circ }$). d Dimensionless curvature of the trajectory as a function of the stroke length $\rho$. Solid, dashed, and dash-dotted lines correspond to $\theta _{2,min}=-60^{\circ }, -70^{\circ }, -75^{\circ }$, respectively

3.1 The trajectory of the swimmer over many cycles of motion

As we have shown in Appendix B, the noise-free trajectory of any swimmer undergoing multiple cyclic motions must be a circle. The center and radius of this circle are given in Appendix B, which only depend on the translational and angular displacement of the swimmer. In particular, the polar angle and magnitude of the translational displacement are needed in Eqs. B5 and B6. Assuming that the swimmer position, $x_c$, initially coincides with the origin of the global frame, the polar angle associated with the orientation of the translational displacement $\varvec{\Delta }(l_{\text {max}})$ can be obtained as $\arg (\varvec{\Delta })$. Considering small values of angular displacement, we can interpret this angle as a direction tangent to the circular trajectory. This angle, in general, differs from the orientation of the active link.

Using Eq. B6 from Appendix B, the radius of the swimmer’s trajectory, $\rho$, can be obtained as

$$\begin{aligned} \rho =\frac{\Vert \varvec{\Delta }\Vert }{2\sin {\beta /2}} \end{aligned}$$

(20)

In Fig. 6 (panel (d)), the curvature of the swimmer’s possible trajectories, $a/\rho$, is shown as a function of stroke length. The negative part of the curve indicates clockwise rotation, while the positive part corresponds to a counter-clockwise rotation of the swimmer. For $l_{\text {max}}/a\approx 5.46$, the curvature of the swimmer’s trajectory is zero, indicating that for a specific value of $l_{\text {max}}/a$, the swimmer has a linear trajectory. Figure 7 illustrates several possible trajectories of the swimmer performing a cyclic motion. According to this figure, for small values of stroke length, the swimmer’s movement is counter-clockwise along its circular trajectories, whereas for $l_{\textit{max}}/a>5.46$, the motion is clockwise. As it was interpreted from Fig. 6, for $l_{\text {max}}/a\approx 5.46$ the trajectory is a straight path. This straight path, in general, is not parallel to the direction of the active link (also y direction).

Fig. 7

Possible noise-free trajectories of the swimmer, which are circles. Geometrical parameters are $g/a=15$, $h/a=10$, $b/a=2$, $\theta _{1,\text {min}}=-45^{\circ }$ the same as Fig. 5. Each path (circle) can be followed by repeatedly performing expansion and contraction with a specific stroke length corresponding to the circle. The above trajectories are obtained by considering different values for the stroke length, $l_{\text {max}}/a$, wherein $3.5\le l_{\text {max}}/a\le 9$. Dotted (red) and dash-dotted (yellow) circles correspond to $l_{\text {max}}/a=3.5$ and $l_{\text {max}}/a=9$, respectively. Moreover, the dash (blue)line correspond to $l_{\text {max}}/a=5.46$

To reach any destination (outside of the two limiting circles of red and yellow colors), the swimmer can move along the circles, shown in Fig. 7, by performing cyclic motion with a specific choice of stroke length, $l_{\text {max}}/a$, corresponding to the desired circle. There is a specific choice of $l_{\text {max}}/a$ that leads to the straight motion of the swimmer, while below this value, the swimmer follows a circular trajectory counter-clockwise; when $l_{\text {max}}/a$ exceeds this value, the swimmer undergoes a clockwise one. Unlike the case of symmetric constraining angles, this straight path is not parallel to y axis. Motion along a straight path can be obtained for other sets of unequal constraining angles with various orientations and is not limited to this specific pair of constraining angles. This orientation can be defined as the polar angle of their displacement, $\varvec{\Delta }$, in the laboratory frame ($arg(\varvec{\Delta })$). In Fig. 8, orientation of straight path ($arg(\varvec{\Delta })$) is illustrated as a function of $|\theta _{2,\text {min}} |$, for three constant values of $\theta _{1,\text {min}}$. According to this figure, for small values of $|\theta _{1,\text {min}} |$, the straight path’s orientation can be significantly oblique toward the $-x$ direction.

Fig. 8

Straight path’s orientation (the angle between positive x direction and the path) as a function of constraining angle $\theta _{2,min}$ for three constant values of $\theta _{1,min}=-5^{\circ }, -10^{\circ }, -15^{\circ }$. The geometry of the swimmer is considered as Fig. 5 ($g/a=15$, $h/a=10$, $b/a=2$)

4 Concluding remarks

In this work, a novel scheme of a cargo container swimmer at low Reynolds number is introduced in which its propulsion is due to the activation of one telescopic link. This is an example of a strategy for relaxing the scallop theorem constraint. Although, here, the case of two passively revolving disks is considered, more generally, any two passively flapping elements with different hydrodynamic resistance in two perpendicular directions can be used. Some technical discussions about the operation condition of the swimmer are given to extend the potential capabilities of the presented approach in designing and fabricating swimmers with minimum active elements. The presented model can be used as a model for some biological elements such as Chlamydomonas and as a design scheme for synthetic swimmers.

Appendices

Appendix A ODEs for the case of straight motion

For the case of symmetric constraining angles, the governing ODEs can be derived upon substituting from Eqs. 2 and 3 into Eqs. 12–14 and solving the subsequent linear system of the equations. Considering each phase separately, the ODEs are calculated as:

For the first and third phases:

$$\begin{aligned}{} & {} \varvec{{\dot{\theta }}_1}= -{\dot{l}} \left( \frac{27b\pi \text {cos}(\theta )}{a(160a + 45\pi b - 64a\text {cos}^2(\theta ))}\right) {\hat{i}}_3 \end{aligned}$$

(A1)

$$\begin{aligned}{} & {} \varvec{v_O}={\dot{l}}\left( \frac{45b\pi }{96a + 45\pi b+ 64a\text {sin}^2(\theta ) }\right) {\hat{i}}_2 \end{aligned}$$

(A2)

For the second phase:

$$\begin{aligned} \varvec{v_O}={\dot{l}} \left( \frac{9b\pi }{32a + 9\pi b + 16a\text {cos}^2 (\theta _{1,\text {min}})}\right) {\hat{i}}_2 \end{aligned}$$

(A3)

For the fourth phase:

$$\begin{aligned} \varvec{v_O}={\dot{l}} \left( \frac{9b\pi }{32a + 9\pi b + 16a}\right) {\hat{i}}_2 \end{aligned}$$

(A4)

By integrating Eq. A1, expansion (contraction) length of the body link in the phase 1 (phase 3) can be found, which is denoted by $l_{\text {sym}}$ and given in Eq. 16. From the above equations, it is evident that only the second and fourth phases contribute to the swimmer’s displacement over each cycle, as also explained in Sect. 3.

Appendix B General description of the trajectory for an arbitrary cyclic motion of a swimmer in 2D

Here we consider the motion of a cyclic swimmer in the XY plane of the inertial frame XYZ, in which each cycle of motion leads to the resultant translation $\delta$ and rotation $\gamma$ as illustrated in Fig. 9.

Fig. 9

The trajectory of an arbitrary swimmer (green line) over two cycles (starting from point A and passing point B, which is the swimmer’s final position in the first cycle and the initial position for the second cycle, the swimmer reaches the eventual position at point C in the second cycle). The body-fixed coordinate system $E_{1}^AE_{2}^AE_{3}^A$ initially coincides with the laboratory frame XYZ

We will show that all initial and final positions of the swimmer in each cycle are concyclic. We consider an arbitrary cycle during the motion of the swimmer, initially starting from point A and reaching point B at the end of this cycle. We assume $\Theta$ to be the angle between $\overrightarrow{AB}$, the vector joining point A to point B, and the positive X axis. Without loss of generality, we assume that $E_{1}^AE_{2}^AE_{3}^A$ is the body-fixed frame initially coinciding with XYZ frame, and $E_{1}^BE_{2}^BE_{3}^B$ is the same body-fixed frame at the end of the first cycle at point B (Fig. 9). It can be shown that there is a point ${\varvec{o}}_c=(o_{c,1},o_{c,2})$ such that its position (mathematical representation) is the same in both the former and the latter frames (i.e., ${\varvec{o}}_c=(o_{c,1},o_{c,2})_{E_{1}^AE_{2}^AE_{3}^A}=(o_{c,1},o_{c,2})_{E_{1}^BE_{2}^BE_{3}^B}$). This point can be calculated as

$$\begin{aligned} {\varvec{o}}_c=\left( \frac{\delta \sin {(\Theta -\gamma /2)}}{2\sin {\gamma /2}}, \frac{\delta \cos {(\Theta -\gamma /2)}}{2\sin {\gamma /2}}\right) \end{aligned}$$

(B5)

As we obtained the point ${\varvec{o}}_c$ in an arbitrary cycle of the motion, this point has the same property for all the proceeding cycles of the swimmer; thus, it is the center of the circle passing through all the initial and final positions of the swimmer. Each cycle gives rise to the rotation of the body frame about point $\varvec{o_c}$ with angle $\gamma$. Thus, the positions of the swimmer at the end of each cycle are concyclic, with ${\varvec{o}}_c$ being the center of the circle. The radius of this circle $\rho$ can be derived as

$$\begin{aligned} \rho =\frac{\delta }{2\sin {\gamma /2}} \end{aligned}$$

(B6)

The system closes the circle after n cycles of motion, simply calculated as, $n=\lceil \frac{2\pi }{\gamma }\rceil$, where $\lceil x\rceil$ is the ceiling function mapping the least integer greater than or equal to x [40]. For small values of $\gamma$, the noise-free trajectory, analogous to Reference [33], is a circle.