1 Introduction

In practice, people are usually self-interested [1]; as indicated by the well-known prisoner’s dilemma (PD) game, profits earned by the defectors are higher than those obtained by the cooperators [2,3,4]. Hence, for an individual, defection seems to be the best option regardless of what the opponent does; while cooperators are inclined to be eliminated by natural selection. Nevertheless, in our daily life, cooperative behaviors widely exist and play important roles in the maintenance and prosperous of either the ancient past or modern society [5,6,7]. Thus, the emergence and maintenance of cooperative behaviors has attracted the interests of numerous scholars and endless efforts have been devoted into this era either theoretically or experimentally [8,9,10,11,12,13].

Among those studies, evolutionary game theory is developed as a simple and effective framework to study such problem [14,15,16,17,18,19,20,21,22,23,24]. In [8], the evolutionary game theory is introduced into complex network for the purpose of explaining cooperative behaviors in network population. Due to the network topology, compact clusters consisting of cooperators are inclined to be formed which play important roles in preventing the cooperators from being invaded by defectors. Along this line, even more scholars start to investigate this from different perspectives [25, 26]. Various mechanisms are proposed in order to promote the level of cooperation, such as, kin selection [27], direct reciprocity [28], group selection [29], indirect reciprocity [30], network reciprocity and spatial structure [31, 32]. Furthermore, the effects of various factors on cooperation are also thoroughly investigated, e.g., individual heterogeneity and willingness [33]. The evolution of cooperation under different strategy updating rules is also considered, being listed as learning and teaching mechanisms respectively [34,35,36,37,38,39]. Most of the afore-mentioned studies mainly focus on node-strategy in which a player applies the same strategy against all its neighbors [40,41,42,43,44,45,46,47,48].

In practice, we find that individuals are often inclined to apply different strategy and adjust their behaviors adaptively when interacting with different individuals. Scholars started to investigate the effect of interaction diversity on cooperation, which seems to be consistent with realistic cases, being referred to as edge-strategy for simplicity [49,50,51,52]. In [50], the authors proved that interactive diversity can promote the frequency of cooperation to a relatively high level by a large extent. While in [51], the authors claimed that this promotion effect is robust even if different factors, such as game metaphors, population types, payoff patterns and learning manners, are incorporated. Aiming to investigate the evolution of cooperation, the authors in [52] proposed two typical interaction patterns, being listed as interactive identity and interactive diversity respectively. Then, when interacting with different neighbors, the central player will adjust the strategy adaptively.

Here, we mainly devote our efforts into investigating the effects of varying the proportion of different updating rules on the frequency of cooperation under the interactive diversity scenario. The evolutionary dynamics of PD games are thoroughly studied. Here, two types of strategy updating rules are introduced into the proposed mechanism being listed as learning mechanism and teaching mechanism respectively [34]. Hence, the players are anticipated to be classified into two categories, i.e., Type-teaching and Type-learning, which are represented as Type-T and Type-L for short. As to the Type-T players, they are anticipated to share their strategies with corresponding neighbors; whereas, the Type-L players usually update their strategies by imitating those of their neighbors. We suppose that during the experimental trial, the type of certain player will remain forever once determined.

Overall, this manuscript is organized as follows: firstly, in the Model section, a detailed description is provided for the convenience of understanding the mechanism proposed here. Later, numerous simulations are conducted with sufficient discussions being provided. Finally, conclusions are given eventually.

2 Model

In this manuscript, the evolution process is conducted on the square lattice networks with periodic boundaries, while the size of the network equals to \(L\mathrm {\times }L\) (\(L\,=\,\)100–300 for the simulation conducted here). A player is assigned to each node, and we suppose there exists no empty nodes; thus, no position transition occurs. For each individual, it is anticipated to interact with its four neighbors. The strategies adopted by the central player against different neighbors vary due to the assumption of interactive diversity. For each player pair, two individuals are supposed to play the PD game; if interacting with different neighbors, the player is able to apply different strategies. Initially, the strategy adopted can be either cooperation (C) or defection (D) and they are anticipated to be evenly distributed on the square lattice network. For each player pair, both players will receive a reward of R if they are both cooperators. While they both get the punishment of P when choosing to defect simultaneously. Nevertheless, if two players apply different strategies against each other, the player who decides to adopt the strategy of cooperation will bear the sucker’s payoff S while the other player earns the highest payoff T. The PD game is supposed to meet the following requirement, i.e., \(T>R>P>S\), \(2R>S + P\); this will incur the well-known social dilemma of individual’s interest and collective ones. Here, the payoff matrix of the considered PD game is provided as:

$$\begin{aligned} M={\begin{array}{*{20}c} &{} {\begin{array}{*{20}c} C &{} D\\ \end{array} }\\ {\begin{array}{*{20}c} C\\ D\\ \end{array} } &{} \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1\\ b\\ \end{array} } &{} {\begin{array}{*{20}c} -0.5\\ 0\\ \end{array} }\\ \end{array} } \right) \\ \end{array} }. \end{aligned}$$

where b indicates the dilemma strength which varies between 1 and 2. As indicated by previous studies, such b is able to characterize relevant aspects of the PD game inherently.

As to the players, they are supposed to be divided into two categories, i.e., Type-T and Type-L. Thus, a parameter \(\alpha \) is defined to characterize such a division. We suppose, for a given parameter \(\alpha \), \(\alpha L^{{2}}\) players will belong to Type-L initially (for these players, they are supposed to choose the learning mechanism), while the rest belongs to Type-T (i.e., learning players). If \(\alpha =0\), all players are supposed to adopt the learning mechanism when updating process is necessary, whereas the teaching mechanisms will be applied if \(\alpha =1\). For the scenario with certain \({0<}\alpha <1\), both learning and teaching mechanisms coexist. Thus, the effects of applying different updating rules on the level of cooperation can be reflected by selecting different \(\alpha \). Here, the types of players remain once it is determined through the simulation process.

Here, we suppose that an individual x is chosen as the central player among all the players in the investigated lattice network. Thus, the number of elements in the neighboring set of the central player, i.e., \(\varPhi _{x}\), always equal to 4. Due to the assumption of interactive diversity, different strategy will be applied by the central player against the neighbor at different direction. For the strategy being applied against the counterpart at certain direction, it is randomly assigned initially, either cooperation or defection. Here, an individual y is chosen from the neighboring set of x for the purpose of easier understanding. We suppose that an interaction occurs between x and y, then a profit earned by player x can be determined being denoted as \(P_{xy}\). For the incorporated lattice network, the central player is anticipated to play games with all neighbors with separated strategies, and corresponding accumulated payoff, i.e., \(P_{x}\), can be derived by considering all the interactions. Thus, the accumulated payoff is calculated as:

$$\begin{aligned} P_{x}= \sum \nolimits _{y\in \varPhi _{x}}^k P_{xy} \end{aligned}$$
(1)

where k represents the number of neighbors for the central player x (for the square lattice network studied in this manuscript, \(k= 4\) for any player), while \(\phi _{x}\) represents the neighboring set of the central player x.

Fig. 1
figure 1

Illustration of the frequency of cooperators for scenarios with different parameter combination of b and \(\alpha \); experiments here are conducted on a \(L\times L\) square lattice network

Full size image
Fig. 2
figure 2

Illustration of the frequencies of cooperators for selected scenarios with \(\alpha = 0, 0.2, 0.5, 0.8, 1\); here, b varies between 0 and 1

Full size image

After calculating the payoffs of all players, the strategy updating process is anticipated to be conducted. For a selected central player, it is anticipated to update the strategies against all his/her neighbors. For instance, we take player x as the central player and the strategy pair needs to be refreshed against player y. Before updating corresponding strategy against a selected neighbor, a reference player is required, being indicated as reference r. Here, we suppose the probability of a neighbor y being selected as the reference equals to p; then the probability of any of the rest neighbors being chosen is obtained as (\({1-}p)\)/3. To be consistent with previous studies, p is set to be .919. Readers can refer to [50] for detailed information, the mechanism applied in this manuscript is similar. For the central player x and the selected reference r, corresponding payoffs being denoted as \(P_{x}\) and \(P_{r}\) can be determined according to formula (1). Later, the strategy updating process between player x and the neighbor y can be performed. If player x is a Type-L one, then the strategy applied by player x against its neighbor y will be updated by learning from the closest strategy of the reference. Otherwise, if player x is supposed to Type-T player, then the closest strategy possessed by the reference will be updated by imitating the strategy of player x. Corresponding probabilities can be calculated according to the well-known Fermi function [53]:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} W\left( s_{x}\leftarrow s_{r} \right) \!=\!\frac{1}{1+\mathrm {exp}[(P_{x}-P_{r})/K]} &{} s_{x} \hbox { belongs to Type-L}\\ \end{array} }\\ {\begin{array}{*{20}c} W\left( s_{r}\leftarrow s_{x} \right) \!=\!\frac{1}{1+\mathrm {exp}[(P_{r}-P_{x})/K]} &{} s_{x} \hbox { belongs to Type-T}\\ \end{array} }\\ \end{array} } \right. \end{aligned}$$
(2)

where K equals to 0.1 with 1/K representing the intensity of selection [54]. The updating process of strategy pair for player x and any one of its neighbors is similar. Hence, the strategy updating process against any of the other neighbors can be conducted accordingly.

The evolutionary process can be conducted through Monte Carlo (MC) simulation. Here, MC steps adopted in this manuscript equal to 5000. For the purse of ensuring accuracy, the final results are averaged over 20 times independently.

Fig. 3
figure 3

Illustrations of the evolutionary dynamics of cooperation at different Monto Carlo (MC) steps for several typical scenarios. a and b Represent the obtained frequencies of cooperation for scenarios of \(b = 1.2\) and 1.8 respectively

Full size image
Fig. 4
figure 4

Presentations of the obtained characteristic snapshots of players adopting different strategies for \(b = 1.2\). For a Type-L player, cooperators and defectors are denoted by yellow and cyan, respectively; whereas for a Type-T player, cooperators and defectors are denoted by red and blue respectively. Experiments here are conducted on the square lattice network. From top to bottom, the values of parameter \(\alpha \) equal to 0, 0.2, 0.8 and 1, respectively. From left to right, the presented snapshots are selected at different Monte Carlo (MC) steps, listed as 3, 30, 300 and 50000 respectively

Full size image
Fig. 5
figure 5

a and b Indicate the fractions of links with different strategy combinations in the stationary state for \(b = 1.2\) and 1.8 respectively. Here, possible connections are subdivided into four categories, i.e., CC, CD, DC and DD being represented by dark blue, green, yellow and red respectively

Full size image

3 Results analysis

In order to investigate the effects of varying the proportion of different updating rules on cooperation when interactive diversity is considered, we performed a number of simulations with sufficient discussions of the obtained results being provided in this section.

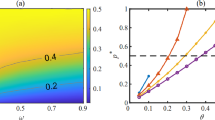
Firstly, we vary the value of parameter \(\alpha \) which indicates the possibility of certain player being either a Type-L player or a Type-T one for scenarios with different temptation. By performing sufficient simulations of scenarios with different parameter combinations of \(\alpha \) and b, corresponding frequencies of cooperation can be obtained accordingly as provided in Fig. 1. If \(\alpha =0\), then the scenario is equivalent to the case of the PD game with all the individuals being Type-L players. Whereas if \(\alpha =\) 1, the studied scenario is equivalent to the case of the PD game with all Type-T players. As presented in Fig. 1, for a fixed b (\(1<b < 1.75\)), we can find the fact that the frequency of cooperation starts to decrease first and then increases if \(\alpha \) is varying from 0 to 1. For a fixed b (\(1.75<b<2)\), the frequency of cooperation increases with the increase of \(\alpha \). For a relatively small \(\alpha \), for instance, \(\alpha <0.3\), the frequency of cooperation reduces gradually if b is increased from 1 to 2. Whereas for a relatively large \(\alpha \), the effect of varying b on the level of cooperation is neglectable; for instance, for \(\alpha >0.7\), corresponding value remains high.

In order to further understand the effect of varying \(\alpha \) on the frequency of cooperation clearly, simulation results for several selected scenarios (\(\alpha = 0, 0.2, 0.5, 0.8, 1\)) are presented in Fig. 2. As illustrated, the considered scenario is simplified as the traditional edge-strategy case if \(\alpha =0\); the level of cooperation reduced gradually with the increase of b and the cooperators diminishes when b approximately equals to 1.8. This is due to the fact that cooperation is inclined to diminish due to the large value of temptation to defect. Whereas with the introduction of Type-T players, the cooperators are able to survive and the effects of large b on cooperation seems to be weakened with the increase of \(\alpha \). Furthermore, the effect of increasing b on cooperation is neglectable if \(\alpha \) >0.8. For the scenario with all Type-T players, the cooperators dominate for any b between 1 and 2. The above discussions are consistent with the results being provided in Fig. 1. Hence, we can come to the conclusion that the updating rule of teaching plays an important role in promoting cooperation.

Later, a bunch of simulations are conducted for several scenarios with selected \(\alpha \) for two typical values of b (\(b = 1.2\) and 1.8) for an illustration. Corresponding results representing the evolutionary dynamics of cooperation over different MC time steps are provided in Fig. 3. Here, Fig. 3a and b indicate the obtained results for scenarios of \(b = 1.2\) and 1.8 respectively. For the experiments conducted here, \(\alpha \) equals to , 0.2, 0.5, 0.7 and 1 respectively.

As presented in Fig. 3a, for the studied scenario with \(b = 1.2\), the level of cooperation decreases first and then increases until a stationary value is arrived. Here, we can find that the level of cooperation decreases/increase slower for larger \(\alpha \) and the obtained stationary value is smaller for the scenario with larger \(\alpha \) if the parameter \(\alpha \) is relatively small (\(\alpha <0.5\)). However, we can find the fact that the proportion of cooperators is increasing gradually without reducing until the stationary value is obtained for scenarios with \(\alpha = 0.5, 0.7\) and 1. With the increase of the parameter \(\alpha \), a larger level of cooperation can be obtained, for instance, for \(\alpha = 1.\), almost all players adopt the strategy of cooperation and defectors seem to diminish eventually. As provided in Fig. 3b, for \(\alpha < 0.5\), the obtained frequencies of cooperation are decreasing gradually until the stationary values are derived. If \(\alpha = 0\), which corresponds to the scenario without Type-T players, all the players abandon the strategy of cooperation and choose to be defectors eventually. Whereas for \(\alpha \) > 0.5, the frequency of cooperation is increasing until a stationary value is obtained. If \(\alpha = 1\), which corresponds to the scenario without Type-L players, we can find that all the players are inclined to be cooperators eventually indicated by a cooperation level of 1. From these results, we can clearly come to the conclusion that even if the temptation to defect is relatively large, players start to adopt the strategy of cooperation with the introduction of Type-T players. With the increase of the proportion of Type-L players, more and more players are inclined to cooperate.

Aiming to understand the origin of observed phenomena extensively, characteristic snapshots of four types of strategies on the regular lattice network are further illustrated in Fig. 4 for different \(\alpha \) values. Here, the adopted values \(\alpha \) for the investigated scenarios equal to 0, 0.2, 0.8 and 1, respectively while b is assigned to be 1.2. Initially, the type of a player is determined according to the assigned parameter \(\alpha \) while corresponding strategy possessed by a player is randomly assigned. From left to right, the presented snapshots are selected at different Monte Carlo (MC) steps, listed as 3, 30, 300 and 50000 respectively. For a Type-L player, cooperators and defectors are denoted by yellow and cyan, respectively; whereas for a Type-T player, cooperators and defectors are denoted by red and blue respectively.

The provided subfigures (a1)–(a4) in Fig. 4 correspond to the obtained results for the scenario of \({\upalpha } = 0\); in such case, all the players are anticipated to adopt the Type-L mechanism while the cooperators are represented by yellow and players are inclined to learn from their neighbors. We can come to the conclusion that with the increase of MC step, the cooperators start to form some compact clusters which play important roles in helping the cooperators from being invaded by defectors. Moreover, these compact clusters expand and the defectors begin to be explored. Nevertheless, some compact clusters of defectors also exist in the stationary state which is helpful for the existence of defectors. This is consistent with the results in Fig. 2. As in Fig. 4b1–b4, though the number of Type-T players is relatively small, the defectors of Type-T are also capable of existing as defectors through forming compact clusters while the cooperators of Type-L and Type-T also form some compact clusters. Similarly, when \({\upalpha } = 0.8\), the fraction of Type-L is relatively small, the defectors still cannot totally be invaded by cooperators. In Fig. 4d1–d4, the defector will get less and less benefit and eventually be eliminated. Hence, Type-T is desirable for the promotion of cooperation.

Aiming to understand the origin of the above-observed phenomenon, the frequencies of different types of interaction chains indicating the strategy pairs between two players, i.e., CC, DD, CD and DC, are also calculated for different \(\alpha \) with corresponding results being presented in Fig. 5. Here, two typical scenarios with \(b = 1. 2\) and 1.8 are studied. For the above-mentioned four types of chains, CC(DD) indicates the case that two players adopt the strategy of cooperation simultaneously; while CD/DC represents the case that two players are applying different strategy against each other. The initial strategies of the players are randomly distributed; with the proceeding of the evolutionary process, a stationary state can be achieved. As presented in Fig. 5, the frequencies of the CD and DC links for both considered scenarios always equal to 0 approximately regardless of the value of \(\alpha \), this is due to the fact that CC and DC links are unbalanced and inclined to be broken easily. While for the frequency of CC link when \(b = 1.2\), it decreases first and then increases and the final value approximately equals to 1. Whereas the frequency of DD link follows an opposite trend, i.e., increases first and then decreases. As presented in Fig. 5b, the frequency of CC link keeps increasing with the increase of \(\alpha \) while the frequency of DD link keeps decreasing. This is consistent with the previous analysis, even if the temptation to defect is relatively large, the incorporation of Type-T players, the level of cooperation can be improved obviously.

4 Conclusion

Over in all, we mainly focus on the investigation of the effects of varying the proportion of different updating rules on the frequency of cooperation under interactive diversity in this manuscript. Here, a general framework indicating properties of interactive diversity is considered for the purpose of studying the evolutionary dynamics of edge-strategy. For the scenario of interactive diversity on the regular lattice network, each player has four neighbors and different strategies are anticipated to be applied against different neighbors when playing the PD games. As to the type of players, two categories are incorporated, being listed as Type-T and Type-L respectively. According to types of players, different updating rules are applied. Thus, the effects of varying the proportion of updating rules on the frequency of cooperation can be investigated thoroughly. Later, a bunch of simulations are conducted for scenarios of different parameters with sufficient analyses of the obtained results being provided. We find the fact that with the introduction of Type-T players, the frequency of cooperation can be improved apparently even if the temptation to defect is relatively large. We hope the insights in this manuscript is helpful in solving social dilemma.