1 Introduction

Amid the frequent climate problems and pandemic, cooperation is crucial for addressing these common issues, while social dilemmas are the biggest challenge for human cooperation [1,2,3]. In the field of management science, the important theoretical tool for describing social dilemmas is the social dilemma game, which mainly includes the prisoner’s dilemma game [4], snowdrift game [5], and public goods game [6].

Social dilemma problems have gradually received attention from scholars and have become an important research topic [7,8,9]. Nowak [10] and Olson [11] have both pointed out that it is theoretically impossible for collectives to spontaneously suppress the emergence of free riding behavior. However, cooperative behavior widely exists in the real world. To reveal the fundamental reasons for this theoretical and practical paradox, Nowak [12] summarized the five mechanisms: direct reciprocity, indirect reciprocity, intergroup selection, network reciprocity, and kin selection, and verified their effective role on promoting the emergence of cooperation behavior using evolutionary game theory. In addition, some studies have focused on the emergence and maintenance of group cooperation under uncertain environments. Wang et al. [13] found that Levy noise can promote the appearance of cooperation. Su et al. [14] and Donahue et al. [15] analyzed the diversity of games and abstracted the problem into the evolution of cooperation under multi-channel games and gave the conditions for promoting cooperation in social dilemma games through theoretical and simulation analysis.

The problem of cooperation in social dilemmas has traditionally been studied using the theoretical framework of the prisoner’s dilemma game, which focuses on pairwise interactions. As an important type of social dilemma game, public goods games for groups of interacting individuals are considered as a n-player version of prisoner’s dilemma game. Public goods games offer insights into how cooperation can emerge and be sustained within a larger group setting. Based on the research results of Nowak [12], many studies have investigated the mechanism of the emergence of cooperative behavior in the public goods game, mainly including punishment mechanisms [16,17,18], reward mechanisms [19,20,21], reputation mechanisms [22,23,24,25], and prepaid deposit mechanisms [26] [27,28,29,30]. With the deepening of research, Nowak et al. [31, 32] introduced population spatial structure into the study of public goods games and constructed a dynamic model framework for the spatial public goods game cooperative evolution system. Subsequently, the research focusses of the cooperative evolution of public goods games gradually shifted to the influence of population evolutionary characteristics such as uncertainty and heterogeneity on cooperation. Ashcroft et al. [33] analyzed the fixation probability of mutant individuals in a finite population environment with dynamic changes. Due to the invalid of simplification by considering additional ecological processes including oscillations in population size of predator and prey systems [34], periodic fluctuations and outbreaks of infectious diseases in humans [35], or chaotic dynamics under multispecies interactions [36], many studies begun to investigate the evolution of cooperation in public goods game with varying populations (see Table 1).

Table 1 Studies on public goods game with varying population size
Full size table

In recent years, the significance of preferences in understanding the dynamics of cooperation has gained increasing attention among researchers. Preferences can be defined as the choices that individuals favor when faced with various options. They are subjective in nature and influenced by individuals’ values, experiences, and social backgrounds. It is obvious that preferences play an important role in individuals’ behavior. To figure out how preference influence person’s behavior, many studies have systematically investigated the impact of preference on the dynamics of cooperation in social dilemma games [45,46,47,48,49]. The two of most widely discussed types of preferences are risk preference and fairness preference. However, in these studies, the focus is mainly on the evolution of cooperation in populations with homogeneous strategy selection preferences. This paper will consider the heterogeneity in individual strategy selection preferences in the public goods game.

Taken together, this paper will utilize a combination of analytical and simulation analysis methods to systematically reveal how the cooperation preference under stochastic strategy update rule affect the emergence and the maintenance of cooperation. This paper has two contributions. First, we consider the heterogeneous preference in the process of updating strategy. And this paper also considers two different types of mixed populations with fixed and fluctuating sizes.

This paper is structured as follows. Section 2 introduces the theoretical model. Section 3 investigates and discusses the evolution of cooperation in public goods game with preference-based stochastic strategy update rule. Section 4 concludes.

2 Theoretical Model

Carrying capacity constrains the development of populations [41]. In this paper, the basic reproductive capacity \({f}_{t}\) is used to characterize the impact of the carrying capacity on individual reproductive capacity, as shown in Eq. (1):

$${f}_{t}={e}^{\varepsilon +r(1-\frac{{n}_{t}}{K})}$$
(1)

In Eq. (1), \(K\) represents the carrying capacity of the evolutionary environment, and \({n}_{t}\ge 2\) represents the size of the population at time step\(t\). And \(\varepsilon \) means the individual’s reproductive capacity that is independent of the evolutionary environment. For any given value of \(K\) and\(r\), the higher the value of\(\varepsilon \), the greater of ability an individual has. Moreover, \(r\) represents the strength of influence of the size of population \({n}_{t}\) on the basic reproductive capacity\({f}_{t}\). For any given value of \(K\) and \(\varepsilon \), the higher the value of \(r\), the more \({n}_{t}\) will depress more influence on the basic reproductive capacity. It can be seen from Eq. (1) that when the population size is less than the carrying capacity (\({n}_{t}<K\)), we have\({f}_{t}>1\), which means that the population size can further increase. But when \({n}_{t}>K\), we have\({f}_{t}<1\), which means that the population size exceeds the carrying capacity, and further increase in population is constrained. Considering the non-exclusive living environment in the real world, this paper assumes that the basic reproductive capacity \({f}_{t}\) of all individuals is homogeneous.

In a public goods game, the strategy of individual \(i=1,\dots ,{n}_{t}\) can be represented as \({s}_{i}\left(t\right)\in S=\{\mathrm{0,1}\}\), where \({s}_{i}\left(t\right)=1\) indicates that individual \(i\) chooses the cooperation strategy (C), and \({s}_{i}\left(t\right)=0\) indicates the defection strategy (D). Individuals \(i\) who choose C strategy will contribute one unit of resource \({c}_{i}=1\) to the public goods pool, while individual \(i\) adopted D strategy contributes nothing \({c}_{i}=0\). The accumulated public goods resources in the pool will be multiplied by the return rate \(R\ge 2\) and then are distributed equally among all individuals. For simplicity, we divide the population \({\varvec{N}}=\{\mathrm{1,2},...,{n}_{t}\}\) into two subpopulations, the C subpopulation composed of cooperators \({i}_{C}(t)=\{i|{s}_{i}\left(t\right)=1,i=\mathrm{1,2},...,{n}_{t}\}\) and the D subpopulation composed of defectors \({i}_{D}(t)=\{i|{s}_{i}\left(t\right)=0,i=\mathrm{1,2},...,{n}_{t}\}\), where \({i}_{C}(t)\cup {i}_{D}(t)={\varvec{N}}\). Here, let \({x}_{t}=\sum_{i}{s}_{i}\left(t\right)\) be the size of the cooperative subpopulation, and \({y}_{t}={n}_{t}-{x}_{t}\) be the size of the defection subpopulation. Then, in the public goods game, the payoff of individual \(i\) at time step \(t\) can be written as \({\pi }_{i}(t)\), shown in Eq. (2):

$${\pi }_{i}\left(t\right)=R\frac{{x}_{t}}{{x}_{t}+{y}_{t}}-{c}_{i}=\left\{\begin{array}{c}Rp\left(t\right)-1, for \quad {s}_{i}\left(t\right)=1\\ Rp\left(t\right), {for \quad s}_{i}\left(t\right)=0\end{array}\right.$$
(2)

In Eq. (2), \(p\left(t\right)=\frac{{x}_{t}}{{x}_{t}+{y}_{t}}=\frac{{x}_{t}}{{n}_{t}}\) represents the proportion of cooperators. As \(p\left(t\right)>\frac{1}{2}\), cooperation is considered a successful evolutionary strategy; otherwise, defection is a successful evolutionary strategy.

This paper assumes that the reproductive capacity of individual \(i\) is jointly determined by the game payoff \({\pi }_{i}\left(t\right)\) and basic reproductive capacity \({f}_{t}\). At time step \(t\), the reproductive capacity of individual \(i\) is denoted as:

$${U}_{i}\left(t\right)=\left(1+\omega {\pi }_{i}\left(t\right)\right){f}_{t}$$
(3)

where \(\omega \) represents selection intensity. For \(\omega \)→0, weak selection is indicated, meaning that the reproductive capacity of individual \(i\) is weakly influenced by the public goods game. For \(\omega \)→1, strong selection is indicated, meaning that the reproductive capacity is strongly influenced by the game. From Eq. (3), for any individual \(i\in {i}_{C}(t)\), it holds that \({\pi }_{i}\left(t\right)={\pi }_{{\text{C}}}\left(t\right)\) and \({U}_{i}\left(t\right)={U}_{{\text{C}}}\left(t\right)\), and \({c}_{i}=1\). And for \(i\in {i}_{D}(t)\), we have \({\pi }_{i}\left(t\right)={\pi }_{{\text{D}}}\left(t\right)\) and \({U}_{i}\left(t\right)={U}_{{\text{D}}}\left(t\right)\), and \({c}_{i}=0\). Thus, the reproductive ability of cooperators is always less than or equal to that of defectors D, that is \({U}_{C}\left(t\right)\le {U}_{D}\left(t\right)\). This demonstrates that defectors have an evolutionary advantage in reproductive ability than cooperators. The public goods game under the constraint of carrying capacity is essentially still a typical public goods dilemma.

2.1 Evolution of cooperation in a fixed-size population

Based on the public goods game framework described above, we firstly construct a cooperative evolutionary dynamic model under the stochastic strategy update rule with preference in a fixed-size population. In a fixed-size population, the population size \({n}_{t}\) is constant, \({n}_{t}=n (n>2)\) for any time step \(t\). Fixed populations are common in real-life scenarios, such as organizations or collectives with a fixed number of positions. In a fixed-size population, the basic reproductive capacity of all individuals is homogeneous and constant. For simplicity, we assume that the basic reproductive capacity to be \({f}_{o}=1\).

After a round of the PGG, all individuals obtain benefits and then synchronously update their strategies by means of Wright–Fisher (WF) rule [50]. However, people often randomly choose strategies due to a lack of supporting information. Motivated by this reality, this paper introduces the stochastic strategy update (SSU) rule to characterize the strategy update process. Individuals follow the SSU rule with probability \(\mu (1>\mu >0)\) and the Wright–Fisher (WF) rule with probability \(1-\mu \). Moreover, this paper considers the heterogeneity of individual strategy preferences under the stochastic strategy update rule, where individuals have a preference \(\theta \) for D strategy and a preference \(\mu -\theta \) for C strategy. Thus, in a fixed-size population, the probability that \(k\) individuals choose the D strategy under the stochastic strategy update rule with preferences is \({b}_{\theta }\left({n}_{t},k\right)=\left(\genfrac{}{}{0pt}{}{{n}_{t}}{k}\right){\theta }^{k}{(1-\theta )}^{{n}_{t}-k}\), and the probability of choosing the C strategy is \({b}_{u-\theta }\left({n}_{t},k\right)=\left(\genfrac{}{}{0pt}{}{{x}_{t}}{k}\right){(u-\theta )}^{k}{(1-u+\theta )}^{{n}_{t}-k}\). Then, the transition probability \(P\left({x}_{t+1}|{x}_{t}\right)\) for the population from \({x}_{t}\) to \({x}_{t+1}\) can be written as Eq. (4):

$$ \begin{aligned} P(x_{t + 1} |x_{t} ) =&\, \sum\limits_{{{\text{z}}_{t + 1} = 0}}^{n} \left[P^{W} (z_{t + 1} |x_{t} ) \sum\limits_{{k = \max \left\{ {0,z_{t + 1} - x_{t + 1} } \right\}}}^{{\min \left\{ {z_{t + 1} ,x_{t + 1} } \right\}}} {b_{\theta } (z_{t + 1} ,k)} b_{\mu - \theta } (n - z_{t + 1} ,k + x_{t + 1} - z_{t + 1} )\right]\end{aligned} $$
(4)

In Eq. (4), \({P}^{W}\) represents the transition probability from the state \({x}_{t}\) to the state \({x}_{t+1}\) of a fixed population under the WF rule, which is shown in Eq. (5):

$$ P^{W} \left( {x_{t + 1} {|}x_{t} } \right) = \left( {\begin{array}{*{20}c} n \\ {x_{t + 1} } \\ \end{array} } \right)\left( {\frac{{x_{t} U_{t}^{C} }}{{x_{t} U_{t}^{C} + \left( {n - x_{t} } \right)U_{t}^{D} }}} \right)^{{x_{t + 1} }} \left( {\frac{{\left( {n - x_{t} } \right)U_{t}^{D} }}{{x_{t} U_{t}^{C} + \left( {n - x_{t} } \right)U_{t}^{D} }}} \right)^{{n - x_{t + 1} }} $$
(5)

From Eqs. (4) and (5), we can see that the stable state of the population must be a mixed state in which cooperators and defectors can coexist.

2.2 Evolution of cooperation in a fluctuating-size population

Another common type of populations is fluctuating-size population, such as villages with migration. In a fluctuating-size population, the change in population size is usually affected by the environment. The population state \(({x}_{t},{y}_{t})\) is characterized by the number of cooperators (\({x}_{t}\)) and defectors (\({y}_{t}\)). And the basic reproductive capacity of the population is given by \({f}_{t}={e}^{\varepsilon +r(1-\frac{{n}_{t}}{K})}\).

Under the WF rule, the transition probability from the state (\({x}_{t},{y}_{t}\)) to (\({x}_{t+1},{y}_{t+1}\)) in the fluctuating-size population can be represented by \({P}^{W}\left({x}_{t+1},{y}_{t+1}|{x}_{t},{y}_{t}\right)\), as shown in Eq. (6):

$$ P^{W} (x_{t + 1} ,y_{t + 1} |x_{t} ,y_{t} ) = \left( {\frac{{\left( {x_{t} U_{t}^{C} } \right)^{{x_{t + 1} }} e^{{ - x_{t} U_{t}^{C} }} }}{{x_{t + 1} !}}} \right)\left( {\frac{{\left( {y_{t} U_{t}^{D} } \right)^{{y_{t + 1} }} e^{{ - y_{t} U_{t}^{D} }} }}{{y_{t + 1} !}}} \right) $$
(6)

Based on Eq. (6), the transition probability from the state (\({x}_{t},{y}_{t}\)) at time step \(t\) to the state (\({x}_{t+1},{y}_{t+1}\)) at time step \(t+1\) in the fluctuating-size population is given by \(P\left({x}_{t+1},{y}_{t+1}|{x}_{t},{y}_{t}\right)\), as shown in Eq. (7):

$$ \begin{aligned} P\left( {x_{t + 1} ,y_{t + 1} {|}x_{t} ,y_{t} } \right) = &\,\mathop \sum \limits_{{z_{t + 1} = 0}}^{{n_{t + 1} }} \left[P^{W} (z_{t + 1} ,n_{t + 1} - z_{t + 1} |x_{t} ,y_{t} )\mathop \sum \limits_{{k = \max \left\{ {0,z_{t + 1} - x_{t + 1} } \right\}}}^{{\min \left\{ {z_{t + 1} ,x_{t + 1} } \right\}}}\right.\\ &\quad\times \left. b_{\theta } \left( {z_{t + 1} ,k} \right)b_{\mu - \theta } \left( {n_{t + 1} - z_{t + 1} ,k + x_{t + 1} - z_{t + 1} } \right)\vphantom{\mathop \sum \limits_{{k = \max \left\{ {0,z_{t + 1} - x_{t + 1} } \right\}}}^{{\min \{ {z_{t + 1} ,x_{t + 1} } \}}}}\right]\end{aligned}$$
(7)

Under the stochastic strategy update rule with preference, the evolutionary stable state (ESS) is dynamic rather than static in the evolutionary process. In the ESS, the numbers of cooperators and defectors fluctuate slightly around the state \(({x}^{*},{y}^{*})\), where \({x}^{*}\) represents the average size of the C subpopulation, and \({y}^{*}\) represents the average size of the D subpopulation [31]. Based on the characteristics of the evolutionarily stable state (ESS), the sizes of the C and D subpopulations at \(t\) and \(t+1\) satisfy Eq. (8) as shown below:

$$\begin{array}{c}{\rm E}_{\left({x}_{t},{y}_{t}\right)}\left[{x}_{t+1}\right]={x}^{*}\\ {\rm E}_{({x}_{t},{y}_{t})}\left[{y}_{t+1}\right]={y}^{*}\end{array}$$
(8)

From the theoretical model, Eq. (8) can be expanded into Eq. (9) as follows:

$$\begin{array}{c}{\rm E}_{\left({x}_{t},{y}_{t}\right)}\left[{x}_{t+1}\right]=\left(1-\theta \right){x}^{*}{U}_{C}^{*}+\left(\mu -\theta \right){y}^{*}{U}_{D}^{*}\\ {\rm E}_{\left({x}_{t},{y}_{t}\right)}\left[{y}_{t+1}\right]=\theta {x}^{*}{U}_{C}^{*}+\left(1-\mu +\theta \right){y}^{*}{U}_{D}^{*}\end{array}$$
(9)

According to Eqs. (8) and (9), (10) is derived as follows:

$$\begin{array}{c}{x}^{*}=\left(1-\theta \right){x}^{*}{U}_{C}^{*}+\left(\mu -\theta \right){y}^{*}{U}_{D}^{*}\\ {y}^{*}=\theta {x}^{*}{U}_{C}^{*}+(1-\mu +\theta ){y}^{*}{U}_{D}^{*}\end{array}$$
(10)

Based on the above theoretical model, it can be found that the stochastic strategy update rule with preference can alleviate the public goods dilemma where C strategy is dominant by D strategy to some extent. In the following part, we will further investigate the emergence and maintenance of cooperation under the stochastic strategy update rule with preference in two different types of populations.

3 Results

3.1 The dynamics of cooperation in the fixed-size population

To shed light on the impact of the stochastic strategy update rule with preference on cooperation, we initially delve into emergence and the maintenance of cooperation in the public goods game in the fixed-size population.

The state of the fixed-sized finite population in the ESS can be represented as \(({x}^{*},{y}^{*})=({x}^{*},n-{x}^{*})\), and the proportion of cooperators is denoted as \({p}^{*}=\frac{{x}^{*}}{n}\in \left(\mathrm{0,1}\right)\), shown as Eq. (11):

$${p}^{*}=\left(1-\theta \right){p}^{*}\left[1+\omega \left(R{p}^{*}-1\right)\right]+\left(\mu -\theta \right)\left(1-{p}^{*}\right)\left(1+\omega R{p}^{*}\right)$$
(11)

According to Eq. (11), let the function \({\varphi }_{1}\left({p}^{*}\right)=\left(1-\theta \right){p}^{*}\left[1+\omega \left(R{p}^{*}-1\right)\right]+\left(\mu -\theta \right)\left(1-{p}^{*}\right)\left(1+\omega R{p}^{*}\right)-{p}^{*}=0\). Since \(\mathrm{\varphi }\left(0\right)=\mu -\theta >0\) and \(\varphi \left(1\right)=-\theta (1+(R-1)\omega )<0\), and \({\varphi }{\prime}<0\), it is obvious that \(\varphi \left({p}^{*}\right)=0\) has a unique solution in the interval \((\mathrm{0,1})\), which is given by Eq. (12):

$${p}^{*}=\frac{\sqrt{R(\mu -\theta )+\theta -1+2\omega (\theta (2-R\mu -\mu )+{\mu }^{2}(R+1+\frac{1}{2\omega }))}+\omega (R(\mu -\theta )+\theta -1)-\mu }{2\omega (R\mu -1)}$$
(12)

In Eq. (12), we can observe that \({p}^{*}\) is determined jointly by \(\omega ,\;R,\;\mu \; {\text{and}}\; \theta\). If \({p}^{*}>\frac{1}{2}\), we have \(\theta \in (0,\frac{R\mu \omega +2\mu -\omega }{2\left(R\omega -\omega +2\right)})\), where \(\frac{R\mu \omega +2\mu -\omega }{2\left(R\omega -\omega +2\right)}>0\) and \(1\ge \mu >\frac{\omega }{R\omega +2}\). When \(\mu \in ({\mu }_{0},1]\), where \({u}_{0}=\frac{\omega }{R\omega +2}\), if \(\theta \in \left( {0,\frac{R\mu \omega + 2\mu - \omega }{{2\left( {R\omega - \omega + 2} \right)}}} \right)\), then we have \({p}^{*}>\frac{1}{2}\). Besides, according to Eq. (12), it is the smaller the \(\theta \), the larger the \({p}^{*}\).

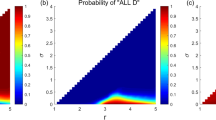
Based on the theoretical analysis results described above, we conducted simulations to further explore the dynamics of cooperation in the fixed-size population. The results of the simulations are shown in Fig. 1. Firstly, in Fig. 1a, for any given value of \(\mu \), the proportion of cooperators \({p}^{*}\) shows an upward trend as \(\omega \) increases from 0 to 1. Besides, when \(\omega \) is held constant, \({p}^{*}\) increases with increasing values of \(\mu \). These observations suggest that both an increase in \(\omega \) and \(\mu \) have a positive impact on the emergence of cooperation. Additionally, the presented results in Fig. 1b indicate that, given a fixed value of \(\mu \), increasing the value of \(\theta \) promotes the level of cooperation \({p}^{*}\). In fact, for certain values of \(\theta \), the proportion of cooperators \({p}^{*}\) can exceed \(\frac{1}{2}\) in the ESS, and cooperation becomes the dominant strategy in the fixed-size population.

Fig. 1
figure 1

a The proportion of cooperators \({p}^{*}\) across the parameters space in the fixed-size population. The color bar represents the level of \({p}^{*}\). b For given values of \(\mu \), the impact of increasing the value of \(\theta \) on \({p}^{*}\) in a fixed population

Full size image

Furthermore, we proceed with an investigation into the maintenance of cooperation in the fixed-size population. To evaluate the stability of cooperation, we examine the standard deviation of the frequency of cooperators in the ESS. This measure allows us to understand the performance of how it is maintained within the population. According to Eq. (9), the standard deviations of the C subpopulation \({\sigma }_{C}\) can be written as Eq. (13):

$${\sigma }_{C}=\sqrt{{\rm E}_{({x}_{t},{y}_{t})}{\left[{x}_{t+1}\right]}^{2}-{\left({\rm E}_{({x}_{t},{y}_{t})}\left[{x}_{t+1}\right]\right)}^{2}}=\sqrt{n{p}^{*}(1-{p}^{*})}$$
(13)

Then, the standard deviations of the D subpopulation \({\sigma }_{D}\) is given by Eq. (14):

$${\sigma }_{D}=\sqrt{{\rm E}_{({x}_{t},{y}_{t})}{\left[{y}_{t+1}\right]}^{2}-{\left({\rm E}_{({x}_{t},{y}_{t})}\left[{y}_{t+1}\right]\right)}^{2}}=\sqrt{n{p}^{*}(1-{p}^{*})}={\sigma }_{C}$$
(14)

The equations (Eqs. 13 and 14) indicate that \({\sigma }_{D}={\sigma }_{C}=\sqrt{n{p}^{*}(1-{p}^{*})}\) is influenced by the size of a fixed-size population. When comparing two populations with the same cooperation performance, it can be observed that a larger population size leads to higher fluctuation in the stable state. This implies that a larger population size may not be beneficial for the maintenance of cooperation. Additionally, from Eqs. (13) and (14), it can be inferred that in a fixed-size population, a greater difference in the sizes of the two subpopulations results in enhanced evolutionary stability. This suggests that when the sizes of the subpopulations differ significantly, it is more favorable for the long-term preservation of cooperation during the evolutionary process.

In Fig. 2, we provide empirical simulation results to illustrate the maintenance of cooperation in the fixed-size population. The presented results in Fig. 2a, c show that, in the ESS, the frequency of cooperators exhibits fluctuations over time around the equilibrium point, \({x}^{*}\). Specifically, in Fig. 2a, for \(\mu =0.1\) and \(\theta =0.05\), the frequency of cooperators exhibits the highest level of concentration among all four evolutionary scenarios, which showcases the best performance in the maintenance of cooperation. In fact, the discrepancy in the sizes of the two subpopulations is the highest for \(\mu =0.1\) and \(\theta =0.05\), which further verify the above-mentioned analysis results; that is, a greater discrepancy in the sizes of the two subpopulations leads to better performance in the evolutionary stability. Moreover, the presented results demonstrate that the conclusions drawn from Fig. 2a, c remain valid when examining Fig. 2b, d, which were obtained in a fixed population of \(K=n=5000\). This verifies the robustness with respect to changes in population size.

Fig. 2
figure 2

For K = 500, a the distribution of the frequency of cooperators in the ESS and c the evolutionary dynamics of C subpopulation in the fixed-size population. For K = 5000, b the distribution of the frequency of cooperators in the ESS and d the evolutionary dynamics of C subpopulation in the fixed-size population

Full size image

In the ESS, the sizes of two different subpopulations present dynamic changes over time rather than remaining constant. In Fig. 3, we present the dynamic of the C subpopulation in the ESS. We can observe the rise and fall of cooperation in Fig. 3. This is because that the preference leads to the fluctuation of population size and the stable state \({x}^{*}\) is the equilibrium that can guarantee either the C subpopulation or the D subpopulation a best payoff. Thus, we can observe the rise and fall of cooperation in the ESS.

Fig. 3
figure 3

The changing trend of the number of cooperators in the fixed-size population a between time step 4001 and 4201 and b between 5001 and 5201

Full size image

Overall, the above analysis provides systematic evidence of the emergence and maintenance of cooperation in the fluctuating-size population under the stochastic strategy update rule with preference. Firstly, an increase in either \(\omega \) or \(\mu \) positively affects the emergence of cooperation in a fixed-size population. In other words, promoting the preference for cooperation and increasing the selection strength are conducive to alleviating the public goods dilemma. However, in the fixed population, the maintenance of cooperation is controversial to the emergence of cooperation as cooperation becomes the dominant strategy.

3.2 The dynamics of cooperation in the fluctuating-size population

In a fluctuating-size population, the size \({n}_{t}={x}_{t}+{y}_{t}>2\) is dynamically changing over time. Without loss of the generality, the state of the fluctuating-size population is denoted as \(({x}^{*},{y}^{*})\), and the population size is \({n}^{*}={x}^{*}+{y}^{*}\). Then, in the ESS, the basic reproductive rate can be given by \({f}^*={e}^{\varepsilon +r(1-\frac{{n}^*}{K})}\) and \({p}^{*}\) can be calculated by Eq. (15):

$$ p^{*} = (1 - \theta )p^{*} \left[ {1 + \omega (Rp^{*} - 1)} \right]f^{*} + (\mu - \theta )(1 - p^{*} )(1 + \omega Rp^{*} )f^{*} $$
(15)

From Eq. (15), \({p}^{*}\) can be derived and is given by Eq. (16):

$$ p^{*} = \frac{{(1 - \theta )x^{*} U_{C}^{*} + (\mu - \theta )y^{*} U_{D}^{*} }}{{(1 - \theta )x^{*} U_{C}^{*} + (\mu - \theta )y^{*} U_{D}^{*} + \theta x^{*} U_{C}^{*} + (1 - \mu + \theta )y^{*} U_{D}^{*} }} = \frac{{(1 - \theta )p^{*} U_{C}^{*} + (\mu - \theta )(1 - p^{*} )U_{D}^{*} }}{{p^{*} U_{C}^{*} + (1 - p^{*} )U_{D}^{*} }} $$
(16)

Solving Eq. (16) yields the unique solution, as shown in Eq. (17):

$$ p^{*} = \frac{{\sqrt {R\left( {\mu - \theta } \right) + \theta - 1 + 2\omega \left( {\theta \left( {2 - R\mu - \mu } \right) + \mu^{2} \left( {R + 1 + \frac{1}{2\omega }} \right)} \right)} + \omega \left( {R\left( {\mu - \theta } \right) + \theta - 1} \right) - \mu }}{{2\omega \left( {R\mu - 1} \right)}} $$
(17)

We observe that Eq. (17) is identical to Eq. (12) suggesting that the conclusions drawn from Fig. 1 can also account for the emergence of cooperation in populations with fluctuating sizes. And the conditions under which cooperation thrives as a successful evolutionary strategy in fluctuating-size populations are equivalent to those in fixed-size populations.

Next, we further explore the maintenance of cooperation in the fluctuating-size population by using the standard deviation of the C subpopulation sizes in the ESS. Then, the variances of the cooperation and defection subpopulations can be calculated by Eq. (18):

$$\begin{array}{c}{\sigma }_{C}=\sqrt{{\rm E}_{\left({x}_{t},{y}_{t}\right)}{\left[{x}_{t+1}\right]}^{2}-{\left({\rm E}_{\left({x}_{t},{y}_{t}\right)}\left[{x}_{t+1}\right]\right)}^{2}}=\sqrt{{x}^{*}}\\ {\sigma }_{D}=\sqrt{{\rm E}_{({x}_{t},{y}_{t})}{\left[{y}_{t+1}\right]}^{2}-{\left({\rm E}_{({x}_{t},{y}_{t})}\left[{y}_{t+1}\right]\right)}^{2}}=\sqrt{{y}^{*}}\end{array}$$
(18)

According to Eq. (18), it can be observed that the maintenance of cooperation in a fluctuating-size population differs from that in a fixed-size population. To gain a better understanding of these differences, we conducted simulations and the results are depicted in Fig. 4. The presented results in Fig. 4a, c suggest that, within the same evolutionary environment, there is an unequal distribution of the frequency of cooperators and defectors in the ESS. Specifically, the higher the number of cooperators, the higher the variance, whereas the higher the number of defectors, the lower the variance. In addition, in Fig. 4b, d for K = 500, a similar observation can be made compared to Fig. 4a, c for K = 5000. This suggests that the evolutionary dynamics remain robust across different population sizes in the fluctuating-size population.

Fig. 4
figure 4

For K = 500, the distribution of a the frequency of cooperators and c the frequency of defectors in the ESS. For K = 5000, the distribution of b the frequency of cooperators and d the frequency of defectors in the ESS

Full size image

The above analysis indicates that the impact of the stochastic strategy update rule on the emergence of cooperation in the fluctuating-size population is consistent with that in the fixed-size population. Thus, in addition to promoting the preference for cooperation, increasing the selection strength is also conducive to alleviating the public goods dilemma not only in the fixed-size population but also in the fluctuating-size population. However, it can be observed in Fig. 5 that in the fluctuating-size population, the promotion of cooperation is controversial with the maintenance of cooperation in the C subpopulation.

Fig. 5
figure 5

From time step t = 3001 to t = 3101, the changing trend of the number of cooperators and the number of defectors in the fluctuating-size population

Full size image

4 Discussion

This paper mainly explores the impact of preference heterogeneity on the emergence and the maintenance of cooperation under the stochastic strategy update rules with preference. Firstly, two different types of population sizes, namely fluctuating and fixed sizes in fully mixed finite populations, were considered. In addition, this paper also considered the constraint of the carrying capacity of the populations on individual reproductive ability. Moreover, we build a theoretical model and conducted extensive simulations.

According to theoretical and simulations results, it is found that the preference for stochastic strategy selection has a significant influence on the emergence and maintenance of cooperation in the public goods game. Firstly, the way to promote the emergence of cooperation in the public goods game is basically the same in populations with fluctuating size and populations with fixed size. Specifically, promoting the preference for cooperation and increasing the selection strength are conducive to alleviating the public goods dilemma. In other words, if we want to reverse the public goods dilemma situation where the defection strategy dominates the public goods dilemma, we can adjust both parameters \(\mu \) and \(\omega \) and make the preference \(\theta \) satisfy the specific conditions. Secondly, the maintenance of cooperation in the ESS is another key indicator to evaluate the influence of the stochastic strategy update rule with preference on the public goods game. Based on the analysis results in Sect. 2.1 and 2.2, there is a significant difference in the maintenance of cooperation between the two different types of populations. In the fixed-size finite population, when the cooperative strategy is the evolutionary successful strategy of the population, increasing the cooperation preference can enhance the stability of the cooperative evolutionary dynamics, which is conducive to the maintenance of cooperation. In the fluctuating-size finite population, reducing the cooperation preference will reduce the stability of the cooperative evolutionary dynamics, which is not conducive to the maintenance of cooperation.

In summary, this paper obtains some conclusions that promote the emergence of cooperation and improve the stability of cooperative evolution. However, the research can be further expanded in the following aspects: (1) considering the coevolution of individual preferences and population states; (2) networked population structures; and (3) extending the strategy update rule to the Moran model.