Mathematical Modeling of an Analogue Self-Learning Neural Network Based on Memristive Elements Taking into Account Stochastic Switching Dynamics

Abstract

In this paper, we consider the issues of modeling an analog self-learning pulsed neural network based on memristive elements. One of the important properties of a memristor is the stochastic switching dynamics, which is mainly due to the stochastic processes of generation/recombination and the movement of ions (or oxygen vacancies) in a dielectric film under the effect of an electric field. The stochastic features are taken into account by adding a term responsible for the additive (Gaussian) noise to the memristor-state equation. The effect of noise on the functioning of an element is demonstrated using the dynamic model of a memristor as an example. The switching of a memristor from the high-resistance state to low-resistance state and vice versa is shown to occur from cycle to cycle in different ways, which is consistent with experimental data. We formulate a stochastic model that describes the hardware analog implementation of a pulsed neural network with memristive elements as synaptic weights and a learning mechanism based on the spike timing dependent plasticity (STDP) method. The operation of two neural networks consisting of one neuron with 64 synapses and two neurons with 128 synapses, respectively, is modeled. The recognition of 8 × 8 images is performed. The stochastic component in the memristor model is shown to have an effect on the fact that the templates from implementation to implementation are distributed among the neurons in different ways and the adaptation of weights (network training) occurs at different rates. In both cases, the network successfully learns to recognize the specified images.

INTRODUCTION

The issue of accelerating computations is relevant at any time. At first, manufacturers increased the processor frequency, then increased the number of cores in one processor, next adapted graphics processors for general computing, and now the transition from digital to analog computing seems promising since they perform computations orders of magnitude faster [1]. In the development of analog computing devices, a relatively new electrical element, a memristor [2, 3], which is a resistor whose conductivity depends on the total electric charge flowing through it, is often used. One of the ways to use these elements to speed up computations is to combine them into a matrix (crossbar), which allows effective implementation of the analog product of a matrix by a vector [4, 5]. Besides this, due to a certain similarity of the properties of these elements with the properties of biological synapses, it is possible to use memristors to create analog self-learning pulsed neural networks (PNNs) [6].

Pulsed neural networks are the third generation of neural networks. In this type of network, information is exchanged in the form of impulses, which is most consistent with the physiology of the biological brain. PNN training is based on local rules for changing weights. There are hardware implementations of a PNN based on semiconductor elements, in particular, the TrueNorth project [7]. Memristive elements are used both in PNNs and in deep neural networks [8]. However, error backpropagation algorithms, which are nonlocal in nature and have great computational complexity, are often used in this case.

There are a number of studies devoted to the implementation of a PNN based on memristors. In particular, the study [9] is aimed at developing experimental and theoretical approaches to finding effective learning rules. An approach to modeling neural networks based on the implementation of metal-oxide heterostructures with nonvolatile memory and multilevel resistive switching is presented in [10]. A learning protocol that is insensitive to the initial state of memristors, as well as to their differences within the same network, is experimentally demonstrated in [11].

PNN learning at the hardware level is usually based on the Hebb rule and synaptic plasticity. The spike timing dependent plasticity (STDP) method is used, according to which the change in the weights of neuron synapses depends on the time difference between the input and output pulses [12–14]. Those synaptic connections that cause neuron activation are strengthened while others are weakened. From the schematic viewpoint, the STDP method is implemented due to the 1T1-R crossbar architecture, in which each memristor corresponds to one transistor responsible for changing the conductivity, and the presence of feedback for each neuron with all synapses. A mathematical model of the PNN was proposed in [15]. The presence of such a model allows the selection of PNN parameters and the simulation of network operation in various modes.

According to experimental data on memristive elements, the nature of their functioning is partially stochastic [16]. As a rule, the process of switching a memristor from the low-resistance state to the high-resistance state and vice versa occurs from cycle to cycle in different ways [17]. In particular, this is associated with random processes occurring in the crystal lattice [18–20]. Mathematical models of memristors are usually formulated in the form of dynamic systems with respect to the memristor-state parameter, which characterizes the conductivity level of the element. In practice, the probabilistic behavior of elements can be taken into account using the stochastic-state equation instead of the deterministic one. One of the options for obtaining such an equation is to introduce an additive in the form of additive white (Gaussian) noise [21].

In this work, we study the effect of the stochastic properties of memristors on the operation of a neuromorphic network. Of practical interest is the issue of using the values of the network parameters determined using the deterministic model under the conditions of the stochastic dynamics of memristive elements. In other words, is it possible to perform network configuration only using a deterministic model? Besides, it is important to understand how the noise level will affect the learning rate and at what level of additive noise the neural network will not be able to function normally.

STOCHASTIC MEMRISTOR MODEL

Several groups of mathematical models of memristors can be distinguished: models of linear [22] and nonlinear drift [23], a model based on the Simmons barrier [24], models using special window functions to limit the state variable [25–27], and models taking into account the levels of voltages, at which the switching process begins in the form of threshold conditions [28–31].

An important feature of memristors is their stochastic behavior. From cycle to cycle, the switching of a memristor from the low-resistive state to the high-resistive state can occur in different ways [16, 17]. The nature of this behavior is associated with random processes occurring at the level of movement of oxygen vacancies in the dielectric film of a memristive element [18–20]. In [32, 33], the effect of noise on the switching process is considered from the general viewpoint of nonlinear relaxation phenomena in metastable systems under the influence of noise [32, 33].

In this work, stochastic features are taken into account by introducing a stochastic addition in the form of additive white (Gaussian) noise into the differential equation of the memristor state. This approach was successfully tested in [21].

We consider a model with a nonlinear voltage dependence. In general terms, the equation describing the memristor state with additive white noise can be represented as follows:

$$dx = af(x){{V}^{s}}dt + {{\eta }}dW,$$

where $x \in [0,\;1]$ is the state variable, $a$ is a constant determined by the material properties, $V$ is the current voltage value, $s$ is an odd integer, $f(x)$ is the window function used to approximate the nonlinear effects of ion drift and limit the boundaries, η is the coefficient characterizing the noise intensity, and $W$ is the Wiener process. The Biolek window function is often used [26]:

$$f(x,v) = \left\{ \begin{gathered} 1 - {{(x - 1)}^{{2p}}},\quad v \leqslant 0, \hfill \\ 1 - {{x}^{{2p}}},\quad v > 0. \hfill \\ \end{gathered} \right.$$

Here, we used the model of a memristor of this class [34] taking into account noise:

$$\begin{gathered} dx = \eta dW \\ \, + a \cdot {{V}^{s}}\left\{ \begin{gathered} \left[ {1 - {{{(1 - x)}}^{{2round\left( {\frac{b}{{|V| + c}}} \right)}}}} \right]dt,\quad V \leqslant - {{{v}}_{{{\text{thr}}}}}, \hfill \\ 0,\; - \,{{{v}}_{{{\text{thr}}}}} < V \leqslant {{{v}}_{{{\text{thr}}}}}, \hfill \\ \left[ {1 - {{{(x)}}^{{2round\left( {\frac{b}{{|V| + c}}} \right)}}}} \right]dt,\quad V > {{{v}}_{{{\text{thr}}}}}, \hfill \\ \end{gathered} \right. \\ \end{gathered} $$

(1)

$$I = {{x}^{n}}\beta \sinh ({{\alpha }_{M}}V) + \chi [\exp (\gamma V) - 1],\quad R = \frac{V}{I},$$

where $I$, $V$, and $R$ are the current values of current, voltage, and resistance; ${{{v}}_{{{\text{thr}}}}}$ is the threshold value of the activation voltage; $n$, β, α_M, χ, and γ are the adjustable parameters in the expression for the current, $round$ is the function of obtaining an integer result; and $b$ and $c$ are the adjustable coefficients of the basic equation.

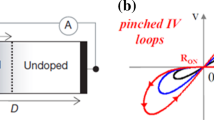
Memristor operation was modeled at the following pa-rameter values: $n = 5$, $\beta = 7.069 \times {{10}^{{ - 5}}}$ А, ${{{{\alpha }}}_{{\text{M}}}} = 1.8$ V^–1, $\chi = 1.946 \times {{10}^{{ - 4}}}$ А, ${{\gamma }} = 0.15$ V^–1, $a = 1$ V^–5, $s = 5$, $b = 15$ V, $c = 2$ V, ${{{v}}_{{{\text{thr}}}}} = 1$ V, $x(0) = 0$, and $V(t)$ is shown in Fig. 1a. Some of the values (${{{{\alpha }}}_{{\text{M}}}}$, ${{\gamma }}$, $a$, $s$, $b$, $c$, and ${{{v}}_{{{\text{thr}}}}}$) correspond to the values given in the previous study [34] while the part (${{\beta }}$, ${{\chi }}$) is selected to best fit the experimental data [34] on hafnium oxide (HfO₂) within the framework of the deterministic model (η = 0).

Fig. 1.

(a) Voltage versus time, and (b–d) I—V characteristics at a noise value of η = (b) 0.05, (c) 0.10, and (d) 0.15.

Figures 1b–1d show a comparison of the model current–voltage characteristic (I–V) at various noise values with the experimental curve from [34].

There are several random trajectories on the I—V characteristic plots, each of which corresponds to a certain switching cycle of the memristor. We note that the resulting spread in the I—V characteristics for various cycles is in agreement with the experimental data [16] for hafnium oxide.

The presence of noise in the memristor model leads to the fact that all parameters acquire stochastic properties. In particular, at η = 0.05, the estimate of the mathematical expectation of the minimal memristor resistance is $M[{{R}_{{{\text{on}}}}}] \approx 6.77$ kΩ and of the dispersion is $D[{{R}_{{{\text{on}}}}}] \approx 1$ kΩ². Other parameters such as the maximal resistance and switching voltage are less affected by additive noise. It is clear that at an increase in the noise value, the spread of the parameters will also increase.

Without loss of generality, we assume that the memristor model can be represented as two equations:

$$dx = {{F}_{X}}(x,\;V)dt + {{\eta }}dW,\quad R = {{F}_{R}}(x,\;V).$$

The first equation determines the dependence of the change rate of the memristor state on the applied voltage ($V$) and state ($x$) while the second one determines the value of the memristor resistance.

STOCHASTIC MATHEMATICAL MODEL OF THE NEUROMORPHIC NETWORK

The issues of modeling circuitry solutions of neuromorphic networks, including the use of the STDP learning method, are considered in [15, 35–39]. In this study, the STDP method is implemented using the 1T1R crossbar architecture and the presence of feedback in accordance with [15]. At the activation moment of neuron, two pulses of opposite sign arrive via the feedback channel with delays. If there is activity at the synapse and a positive feedback pulse arrives, then the resistance value of the corresponding memristor decreases, and if a negative feedback pulse arrives, the memristor resistance increases.

The circuitry model of a neuron represents a parallel RC circuit and an abstract pulse generator. When the value of the potential on the capacitor exceeds a certain threshold, its potential is reset, and the pulse generator produces an output signal and a feedback signal. Additionally, at the activation moment of a neuron, other neurons are suppressed (the potential accumulated by them is forcibly reduced in proportion to a certain coefficient).

The network is trained in the following way: at the initial moment, the synaptic weights are randomly initialized, and then, with equal probability, either arbitrary noise or predetermined templates are fed to the network input multiple times. Over time, the network adapts to template recognition. One learning epoch refers to the time during which a sample or random noise is displayed to the network. Template distribution among neurons occurs during the learning process.

A previously developed mathematical model of a neuromorphic network is presented in [15] without taking into account the stochastic dynamics of memristor switching. Taking into account the corresponding properties of memristive elements consists in replacing equations (3) in [15] with:

$$\begin{gathered} d{{x}_{{i,j}}} = \left\{ \begin{gathered} {{F}_{X}}({{x}_{{i,j}}},V_{{{\text{te}}}}^{j} - V_{{{\text{int}}}}^{j})dt + {{\eta }}d{{W}_{{i,j}}},V_{{\text{g}}}^{i}(t) > 0, \hfill \\ 0,V_{{\text{g}}}^{i}(t) = 0, \hfill \\ \end{gathered} \right. \\ {{R}_{{i,j}}} = {{F}_{R}}({{x}_{{i,j}}},V_{{{\text{te}}}}^{j} - V_{{{\text{int}}}}^{j}),\quad i = \overline {1,n} ,\quad j = \overline {1,m} , \\ \end{gathered} $$

where $n$ is the number of inputs, $m$ is the number of neurons, $V_{{\text{g}}}^{i}$ is the current value of the voltage at the ith input of the neural network, $V_{{{\text{te}}}}^{j}$ is the current value of the voltage in the feedback of the jth neuron, $V_{{{\text{i}}{\text{nt}}}}^{j}$ is the voltage at the capacitor of the jth neuron, ${{R}_{{i,j}}}$ is the resistance value of the memristor of the ith synapse of the jth neuron, ${{x}_{{i,j}}}$ is the state of the memristor of the ith synapse of the jth neuron, η is the coefficient characterizing the noise intensity, and ${{W}_{{i,\;j}}}$ is the Wiener process, which corresponds to the ith memristor of the jth neuron.

As a result of using stochastic equations of state for memristors, the entire model of the neuromorphic network also becomes stochastic.

We note that all memristors and neural networks in this study are modeled, and physical implementation is the subject of future research.

MATHEMATICAL MODELING OF A NEUROMORPHOUS NETWORK TAKING INTO ACCOUNT THE STOCHASTIC FEATURES OF MEMRISTIVE ELEMENTS

We consider a network consisting of one neuron ($m = 1$ and so the j index is further omitted) with 64 synapses. Parameter values: $n = 64$, ${{R}_{{{\text{int}}}}} = \;1\;{\text{k}}\Omega$, ${{C}_{{{\text{int}}}}} = 45\;\mu {\text{F}}$, $V_{{{\text{te}}}}^{ + } = 1.5\;{\text{V}}$, $V_{{{\text{te}}}}^{ - } = - 1.6\;{\text{V}}$, $V_{{{\text{te}}}}^{0}\, = \,10\;{\text{mV}}$, $V_{{{\text{out}}}}^{ + } = 2\;{\text{V}}$, ${{V}_{{{\text{th}}}}} = 3\;{\text{mV}}$, ${{{{\tau }}}_{r}} = 20\;{\text{ms}}$, ${{{{\tau }}}_{s}} = 2\;{\text{ms}}$, and ${{{{\tau }}}_{{{\text{out}}}}} = 10\;{\text{ms}}$. These values were obtained in [15] based on a deterministic model of a neuromorphic network. Parameters $V_{{{\text{te}}}}^{ + }$, $V_{{{\text{te}}}}^{ - }$, $V_{{{\text{te}}}}^{0}$, ${{{{\tau }}}_{r}}$, and ${{{{\tau }}}_{s}}$ determine the amplitudes, duration, and delay between pulses in the feedback, due to which learning according to the STDP method occurs.

In the simulation, at each epoch (equal to τ_r/2 s), the vector of input signals ${{{\mathbf{V}}}_{{\mathbf{g}}}}(t)$ corresponds to the recognized template (Fig. 2) or is set randomly (the vector elements have a discrete distribution: $V_{{\text{g}}}^{i} = 0$ V with a probability of $0.81$ and $V_{{\text{g}}}^{i} = 2$ V with a probability of $0.19$). For clarity, we write the ${{{\mathbf{V}}}_{{\mathbf{g}}}}$ vector corresponding to the template as a matrix:

$${{{\mathbf{V}}}_{{\mathbf{g}}}} = \left( \begin{gathered} {\text{0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{,}} \hfill \\ {\text{0}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 0}}{\text{,}} \hfill \\ {\text{0}}{\text{, 2}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 2}}{\text{, 0}}{\text{,}} \hfill \\ {\text{0}}{\text{, 2}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 2}}{\text{, 0}}{\text{,}} \hfill \\ {\text{0}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 0}}{\text{,}} \hfill \\ {\text{0}}{\text{, 0}}{\text{, 0}}{\text{, 2}}{\text{, 2}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{,}} \hfill \\ {\text{0}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 2}}{\text{, 0}}{\text{,}} \hfill \\ {\text{0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 0}}{\text{, 0}} \hfill \\ \end{gathered} \right){\text{V}}{\text{.}}$$

Fig. 2.

Recognizable template.

Figures 3 and 4 show the graphs of the behavior of the characteristic voltages of the neural network as a function of time. The upper graphs correspond to the zero value of the coefficient characterizing the noise intensity, i.e., to the actually deterministic memristor model, while the lower plots correspond to two different realizations at a value of η = 0.05. The dashed line shows what signal was fed to the input of the neural network at each specific epoch. A value of –1 represents noise, and a value of 0 represents a recognizable template. The dotted line with a dot reflects the voltage value on the capacitor of the neuron, and the solid gray thin line reflects the voltage value in the feedback. The solid thick line corresponds to the network-output voltage. As soon as the voltage at the capacitor reaches a certain threshold, the neuron is activated: a pulse at the output and a series of pulses in feedback appear.

Fig. 3.

Comparison of the behavior of the parameters of the neural network at the beginning of training.

Fig. 4.

Comparison of the behavior of the main parameters of the neural network at the end of training at η = 0 (upper graph) and 0.05 (lower graphs).

In all cases, the initial conditions and the learning process were fixed (the same sequence of values was fed to the input of the network). The graphs show that the network successfully learned while, due to the presence of a stochastic term in the memristor model, neuron activations occur with some random shifts in time. Figure 5 shows the process of changing the state variables of memristors for five different implementations. Here, we see that a stochastic addition to the memristor model leads to a different adaptation rate of the weights: in particular, the recognized pattern begins to be seen already from the 1500th epoch in the first implementation and only from the 2000th epoch in other implementations.

Fig. 5.

Comparison of changes in the weights in various implementations.

Fig. 6.

Recognizable templates.

Next, we consider the problem of recognizing two samples [15]. The parameters of the neuromorphic network model remain the same, except for ${{V}_{{{\text{th}}}}} = 4\;{\text{mV}}$. Since there is an interaction between neurons, the suppression coefficient of α = 0.1 is additionally set (at the activation moment of one neuron, the potential of the other neuron is reset in accordance with the suppression coefficient).

As earlier, the vector of input signals ${{{\mathbf{V}}}_{{\mathbf{g}}}}(t)$ in each epoch corresponds to the recognized patterns or is set randomly (the vector elements have a discrete distribution: $V_{{\text{g}}}^{i} = 0$ V with a probability of $0.8$ and $V_{{\text{g}}}^{i} = 2$ V with a probability of $0.2$).

Figures 7 and 8 show graphs of the voltage versus time at the beginning and at the end of the learning process for two different implementations. Figure 9 shows the change in the state variables of memristors for five implementations.

Fig. 7.

Comparison of the behavior of the main parameters of the neural network at the beginning of training in two different implementations.

Fig. 8.

Comparison of the behavior of the main parameters of the neural network at the end of training in two different implementations.

Fig. 9.

Comparison of changes in the weights of two neurons in various implementations.

The dotted line shows what was fed to the input of the neural network at each particular epoch. A value of –1 corresponds to noise, and a value of 0 corresponds to the first recognizable template, and a value of 1 corresponds to the second recognized template.

Here, we see that the templates were distributed among the neurons in different ways while the differences in the functioning of the network are insignificant: as in the previous example, there are small time shifts in the output pulses.

In all cases, the network successfully learned to recognize the specified images. However, the stochastic component in the memristor model influenced the fact that the templates from implementation to implementation are distributed among neurons in various ways and the adaptation of weights occurs at various rates.

DISCUSSION

As a result of simulating the operation of a neuromorphic network, it was found that the network successfully learned to recognize the specified templates at the parameter values selected within the framework of the deterministic model. This suggests that it is possible to configure the network without taking into account the stochastic nature of memristive elements. Additive noise first affects how the templates are distributed among neurons and, to a lesser extent, the delays in the output pulses.

The main characteristic of any neural network is accuracy. Usually, to evaluate it, a test dataset is fed into the network as input and the percentage of correct answers is determined. A distinctive feature of the network considered here is the presence of an internal state that changes during operation and, therefore, the classical testing approach is not strictly correct. In this regard, to estimate the accuracy, averaging over a certain time window was performed in the process of training the network: it was calculated how many times the network correctly responded to the input data. The used window size is 100 epochs. In addition, the question is whether the templates in the learning process can be randomly redistributed among neurons. Therefore, it is impossible to determine in advance which neuron will be responsible for which template before the learning process. To solve this issue, at each epoch, it is checked which neuron is most suitable for the template: the dot product between the input vector and the current vector of the synaptic-weight values of each neuron is maximized.

Figures 10 and 11 show the dependences of the accuracy on the epoch number for the two networks considered earlier. The curves corresponding to zero noise coefficient are actually obtained using the deterministic model. For nonzero values of the noise coefficient, the graphs show five different curves corresponding to different implementations. As can be seen, at a small value of η, the network in a number of implementations is trained faster than that in the absence of noise. However, at an increase in η, the learning process loses its stability and stops converging, as is evidenced by the strong scatter in the graphs at η = 0.25.

Fig. 10.

Dependence of recognition accuracy on the epoch number in the case of one sample.

Fig. 11.

Dependence of recognition accuracy on the epoch number in the case of two samples.

CONCLUSIONS

In the paper, we present the mathematical modeling of a self-learning neuromorphic network based on memristive elements, taking into account the stochasticity of the ongoing processes. A dynamic memristor model with additive noise was implemented. The I—V characteristics of hafnium oxide obtained as a result of simulation are in agreement with the experimental data. A complex stochastic mathematical model of pulsed neuromorphic network with a learning mechanism according to the STDP rule was formulated. Using the example of template recognition by neuromorphic networks with one and two neurons, the adaptation rate of network weights to recognized templates, as well as the template distribution over neurons, is shown to depend on the stochastic features of memristive elements. In this case, the network parameters can be configured without taking into account the stochastic dynamics of memristor switching. At a relatively low noise level, neural networks with parameters selected using a deterministic mathematical model are successfully trained to recognize specified templates.