INTRODUCTION

Nowadays, nanoplates are widely used in different industries. They are also used in medical instruments, measurement tools [1–5], aerospace equipment, energy storage systems such as capacitators [6–10], and detectors [11–13]. Therefore, it is important to investigate the dynamic behavior of nanoplates in magnetic fields. Subatomic effects or amber property can apply externally magnetic fields to nanostructures. If we put a conductive plate in a magnetic field, it deforms and an electromagnetic force affects its whole structure. Maxwell equations link between the electric and electromagnetic fields and the magnetic currents. Lorentz force also affects the structure of the plate. To analyze the vibration of a conductive nanoplate in a constant, one direction, in-plane magnetic field, continuum theories and thin plates theories as well as Maxwell equations and Lorentz force are applied.

Using experimental tests are not applicable to investigating the dynamic behavior of nanoplates since they are expensive and the control of their processes are difficult. Therefore, an analytical approach and the use of closed form solutions are of great importance and used by many researchers when investigating nanostructures.

Some theoretical studies have analyzed the behavior of nanoplates in magnetic fields. Wang et al. [14] investigated the effect of a longitudinal magnetic field on the diffusion of waves through a carbon nanotubes. To extract the related differential equation, they used a model of a thin plates and Lorentz force. Wang et al. [15] extracted differential equations for the vibration of nanoplates in a transverse magnetic field. Narendar et al. [16] experimentally studied the diffusion of waves through a single-layer carbon nanotube. Their results indicated that the velocity of bent frequencies increases when the power of the magnetic field grows. Therefore, non-local effects are significant in decreasing the velocity of waves, especially in low frequencies. Murmu et al. [17] investigated the vibration of a double-walled carbon nanotube in a longitudinal magnetic field. They used the non-local Euler–Bernoulli theory for beams when extracting their equations. Kiani [18] investigated the vibration of a double-walled carbon nanotube in a longitudinal magnetic field. He used the railly theory for beams, and used non-lattice methods for calculating displacement. Liang et al. [19] proposed a model for the frequency of the vibration of a beam in a magnetic field. They also conduct an experiment to investigate the vibration of a one side fixed support plate in a magnetic field. Moon and Pao [20] investigated buckling of plates in magnetic fields. They used the model developed for thin plates. Young and Pan [21] used an approach based on energy to investigate buckling and bending of thin plates in magnetic fields. They compared their analytical results with some experimental results.

Some studies tried to extract stress tensors for magneto-elastic materials in the presence of a magnetic fields [22, 23]. These studies also extract the strain-stress relationship for elastic plates. Murmu et al. [24] investigated the transverse vibration of graphene sheets in an in-plane magnetic field. They used the non-local Kirchhoff theory to conduct this investigation. They also discussed the frequency of simple support nanoplates in constant in-plane magnetic fields. Finally, Kiani [25] investigated the vibration of a conductive nanoplate in a constant in-plane magnetic field. He used the theories of plates and the Eringen’s non-local theory, and studied a rectangular plate with some simple boundary conditions.

The mechanical rules governing small-size problems are different from other mechanical rules governing problems in other sizes. Therefore, the results obtained from the field and consistivity equations will be reliable only after we modify our attitudes toward them. This is because the obtained results may depend strongly on the size of the problem. In contrast, compatibility equations are independent on the mechanical rules, the assumptions inherent in the kinematics deformation of structures, and the sizes of the problems. However, using these compatibility equations require the appropriate selection of boundary conditions. A wrong selection of boundary conditions leads to a wrong prediction of the behavior of the system. This is especially important in nano-size problems since it is hard to find the appropriate boundary conditions in these sizes. In response to this need, the quantum mechanics theory studies how mechanical theories are modified in small-size problems. In other words, these theories are used to revise field equations in small sizes. The non-local theory of elasticity and coupled stresses and strains can also contribute to revise the consistivity equations. Therefore, considering non-local effects are of great importance in small-size problems.

In this paper, the equations governing the movement of a nanoplate are obtained by using two approaches: an approach based on the energy conversion principle, and an approach that applies plates deformation theories and the equation describing Lorentz force. The purpose of using these equations is to investigate the vibration of the system. The results of these two approaches are obtained and compared with each other for a rectangular plate with simply support. In the first approach, the local equilibrium equations are used to calculate the distribution of stresses. Then, the energy conversion principle is applied to extract the integral equation describing the vibration of the system. Finally, we use the non-local Eringen’s theory to improve the equation by taking into account the non-local effects in calculating mid-plane curvatures. In the second approach, we extract a differential equation by using the Kirshoff’s theory for deformation of plates. Then, we use the equation presented in the references [14, 16] to calculate the volumetric force applied on the conductive nanoplate in a mid-plane magnetic field. The Eringen’s theory is also used to consider the non-local effects.

THE METHOD FOR EXTRACTING THE DIFFERENTIAL EQUATION FROM THE KIRSHOFF’S THEORY

In this section, based on the references [14, 16], we extract the equation calculating the electromagnetic force. According to these references, a constant magnetic field induces a volumetric force to all elements. The power of this force depends on the location vector of the element, the power of the applied magnetic field, and magnetic susceptibility of the nanoplate. This power is calculated as follows:

$${{f}_{m}} = \eta (~\nabla \times (~\nabla \times (~u \times {{H}_{0}})))\;{\kern 1pt} \times \;{\kern 1pt} ~{{H}_{0}},$$
(1)

where \(\eta \) is magnetic susceptibility of the nanoplate, \(u\) is the displacement vector of the elements, \({{H}_{0}}\) is the power of the applied constant field, and \(\nabla \) is the gradient operator. For the in-plane magnetic field, the loading can be considered as \({{H}_{0}} = ~{{H}_{x}}i + ~{{H}_{y}}j\). Also, we consider the displacement vector as \(u = ui + {v}j + wk\). Therefore, the transverse component of the volumetric force is calculated as follows:

$$\begin{gathered} {{f}_{{mz}}} = \eta (~{{w}_{,}}_{{xy}}{{H}_{y}} + {{w}_{{,yy}}}{{H}_{y}} \\ \, + {{w}_{,}}_{{zz}}{{H}_{y}} + {{u}_{{,xz}}}{{H}_{y}} + {{{v}}_{,}}_{{xz}}{{H}_{x}}){{H}_{y}} \\ \, - ~\eta (~{{u}_{{,yz}}}{{H}_{y}} - {{{v}}_{,}}_{{yz}}{{H}_{x}} - {{w}_{,}}_{{zz}}{{H}_{x}} \\ \, - {{w}_{,}}_{{xx}}{{H}_{x}} + {{w}_{,}}_{{yx}}{{H}_{y}}){{H}_{x}}. \\ \end{gathered} $$
(2)

Equation (2) should be simplified based on the theories of plates. Therefore, the displacement of the elements is considered as follows:

$$u = - z\frac{{\partial w}}{{\partial x}},$$
(3)
$${v} = - z\frac{{\partial w}}{{\partial y}},$$
(4)
$$w = {{w}_{0}}(x,y,t),$$
(5)

where \(w = {{w}_{0}}(x,y,t)\) is the mid-plane displacement. The mentioned idea for the deformation of plates is called the classic theory of plates or the Kirchhoff theory, which is applicable for thin plates. The following relation is applied for simplifying Eq. (2):

$$\begin{gathered} {{u}_{,}}_{{xz}} = - {{w}_{{,xx}}},~\quad {{{v}}_{,}}_{{xz}} = - {{w}_{,}}_{{xy}}, \\ {{u}_{,}}_{{yz}} = - {{w}_{{,xy}}},\quad {{{v}}_{,}}_{{yz}} = - {{w}_{{,yy}}}. \\ \end{gathered} $$
(6)

Therefore, the volumetric force is obtained as follows:

$${{f}_{{mz}}} = \eta (~{{w}_{,}}_{{yy}} - {{w}_{,}}_{{xx}}~)(~H_{y}^{2} - H_{x}^{2}).$$
(7)

Hence, the volumetric force applied to the Cartesian element of the volume of the plate is equal to \((~{{t}_{p}}{{f}_{{mz}}}~)(~dxdy~)\), where \({{t}_{p}}\) is the thickness of the nanoplate. By dividing this expression the area of the element that is adapted to the mid of the plane, the electromagnetic force applied to per unit of area is calculated as follows:

$${{F}_{{mz}}} = ~~{{t}_{p}}{{f}_{{mz}}}.$$
(8)

This force is used to investigating the transverse vibration of the plate. The frequencies related this vibration is called transverse or out-plane frequencies. Finally, based on the first order theory of plates, the Eringen’s non-local theory, and the D’Alembert’s effect, the transverse vibration of the conductive nanoplate within the elastic environment is described as follows:

$$\begin{gathered} D{{\nabla }^{4}}w = {{t}_{p}}~(~1 - ~\mu {{\nabla }^{2}}~) \\ \, \times [~\eta (~{{w}_{{,yy}}} - {{w}_{{,xx}}}~)(H_{y}^{2} - H_{x}^{2}) - \rho ~{{w}_{{,tt}}}], \\ \end{gathered} $$
(9)

where \(D\) is the stiffness constant of the plate, and \(\mu \) is the constant of the small size effect.

THE SOLUTION METHOD

By applying the Laplace operator in the non-local section of Eq. (9), the following equation is obtained:

$$\begin{gathered} D{{\nabla }^{4}}w = \eta ~{{t}_{p}}(~{{w}_{{,yy}}} - {{w}_{{,xx}}}~)(~H_{y}^{2} - H_{x}^{2}) \\ \, - ~\eta ~{{t}_{p}}\mu (~{{w}_{{,yyyy}}} - ~{{w}_{{,xxxx}}}~)(H_{y}^{2} - H_{x}^{2}) \\ \, - \rho {{t}_{p}}{{w}_{{,tt}}}\, + \rho {{t}_{p}}\mu (~{{w}_{{,xxtt}}}~\, + {{w}_{{,yytt}}}). \\ \end{gathered} $$
(10)

By assuming that the mid-plane displacement is described by the equation \(w = W(x,y)\sin \omega t\), Eq. (10) is rewritten as follows:

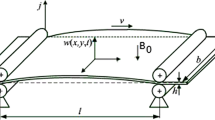
$$\begin{gathered} D{{\nabla }^{4}}W~ = \eta ~{{t}_{p}}(~ - {{W}_{{,xx}}}~)(~H_{y}^{2} - H_{x}^{2}) \\ \, - ~\eta ~{{t}_{p}}\mu (~{{W}_{{,yyyy}}} - ~{{W}_{{,xxxx}}}~)(~H_{y}^{2} - H_{x}^{2}~) \\ \, + \rho {{t}_{p}}{{\omega }^{2}}W - ~\rho {{t}_{p}}{{\omega }^{2}}\mu ~(~{{W}_{{,xx}}} + {{W}_{{,yy}}}). \\ \end{gathered} $$
(11)

A rectangular plate with the geometric structure of \(0 \leqslant x \leqslant a\), \(0 \leqslant y \leqslant b\) is considered. Also, we use the simply support boundary condition. The following equation is obtained:

$$W(x,y) = ~\mathop \sum \limits_{n = 1}^\infty \mathop \sum \limits_{m = 1}^\infty {{k}_{{mn}}}\sin \left( {~\frac{{n\pi x}}{a}~} \right)\sin \left( {\frac{{m\pi y}}{b}} \right).$$

By replacing Eq. (12) in Eq. (11), the following equation is obtained:

$$\begin{gathered} D\left[ {{{{\left( {~\frac{{n\pi }}{a}~} \right)}}^{4}} + 2{{{\left( {\frac{{n\pi }}{a}~} \right)}}^{2}}~{{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}} + ~{{{\left( {~\frac{{m\pi }}{b}~} \right)}}^{4}}~} \right] \\ = \eta {{t}_{p}}\left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} - ~{{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}}} \right]~(H_{y}^{2} - H_{x}^{2}) + \eta {{t}_{p}}\mu \\ \, \times \left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{4}} - {{{\left( {\frac{{m\pi }}{b}} \right)}}^{4}}} \right]~(H_{y}^{2} - H_{x}^{2}) + \rho {{t}_{p}}\omega _{{mn}}^{2}\mu \\ \times \left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}}} \right] + \rho {{t}_{p}}\omega _{{mn}}^{2}. \\ \end{gathered} $$
(13)

All naturally out-plane frequencies are obtained from Eq. (13).

THE METHOD FOR EXTRACTING THE DIFFERENTIAL EQUATION FROM THE FIRST ORDER THEORY OF SHE DEFORMATION

From Eq. (2) and the Mendelian deformation condition, the following equation is obtained:

$$\begin{gathered} {{f}_{{mz}}} = \eta (~{{w}_{{,xy}}}{{H}_{x}} + {{w}_{{,yy}}}{{H}_{y}} + ~{{\varphi }_{{x,x}}}{{H}_{y}} + ~{{\varphi }_{{y,x}}}{{H}_{x}}){{H}_{y}} \hfill \\ \, - \eta (~{{\varphi }_{{x,y}}}{{H}_{y}} - {{\varphi }_{{y,y}}}{{H}_{x}} - {{w}_{{,xx}}}{{H}_{x}} + {{w}_{{,yx}}}{{H}_{y}}){{H}_{x}}, \hfill \\ \end{gathered} $$
(14)

where \({{{{\varphi }}}_{x}}\) and \({{{{\varphi }}}_{y}}\) are the required functions for considering the suitable shear deformation. Since the magnetic field is not applied to the two directions simultaneously, Eq. (14) is simplified as follows:

$$\begin{gathered} {{f}_{{mz}}} = \eta ({{w}_{{,yy}}}{{H}_{y}} + ~{{\varphi }_{{,x,x}}}{{H}_{y}}){{H}_{y}} \\ \, + \eta (~{{\varphi }_{{y,y}}}{{H}_{x}} + {{w}_{,}}_{{xx}}{{H}_{x}}){{H}_{x}}. \\ \end{gathered} $$
(15)

We consider the non-local effects obtained by the Eringen’s theory. Therefore, the equation governing the vibration of the Mendelian plate is obtained as follows:

$$\begin{gathered} {{\nabla }^{4}}\left( {~w - \frac{\mu }{{{{k}_{s}}G{{t}_{p}}}}(~{{F}_{{mz}}} - \rho {{t}_{p}}{{w}_{{,tt}}})} \right) \\ = - \frac{{D + \mu {{k}_{s}}G{{t}_{p}}}}{{{{k}_{s}}G{{t}_{p}}D}}{{\nabla }^{2}}\left( {~{{F}_{{mz}}} - \rho {{t}_{p}}{{w}_{{,tt}}}~} \right) + \frac{1}{D}(~{{F}_{{mz}}} - \rho {{t}_{p}}{{w}_{{,tt}}}), \\ \end{gathered} $$
(16)
$$\begin{gathered} {{\nabla }^{4}}\left( {~w - \frac{{\eta \mu }}{{{{k}_{s}}G}}(~{{w}_{{,xx}}}H_{x}^{2} + {{w}_{{,yy}}}H_{y}^{2}) + \frac{\mu }{{{{k}_{s}}G}}\rho {{w}_{{,tt}}}~} \right) \\ - \frac{{\eta \mu }}{{{{k}_{s}}G}}{{\nabla }^{4}}(~{{\varphi }_{{x,x}}}H_{y}^{2}) - \frac{{\eta \mu }}{{{{k}_{s}}G}}{{\nabla }^{4}}(~{{\varphi }_{{y,y}}}H_{x}^{2})~~ \\ = - \frac{{D + \mu {{k}_{s}}G{{t}_{p}}}}{{{{k}_{s}}GD}}\eta {{\nabla }^{2}}(~{{w}_{{,xx}}}H_{x}^{2} + {{w}_{{,yy}}}H_{y}^{2}) \\ + \frac{{D + \mu {{k}_{s}}G{{t}_{p}}}}{{{{k}_{s}}GD}}{{\nabla }^{2}}(~\rho {{w}_{{,tt}}}~) - \frac{{D + \mu {{k}_{s}}G{{t}_{p}}}}{{{{k}_{s}}GD}}\eta {{\nabla }^{2}}(~{{\varphi }_{{x,x}}}H_{y}^{2}) \\ - \frac{{D + \mu {{k}_{s}}G{{t}_{p}}}}{{{{k}_{s}}GD}}\eta {{\nabla }^{2}}(~{{\varphi }_{{y,y}}}H_{x}^{2}) \\ + \frac{{\eta {{t}_{p}}}}{D}(~{{w}_{{,xx}}}H_{x}^{2} + {{w}_{{,yy}}}H_{y}^{2}) - \frac{{\rho {{t}_{p}}}}{D}{{w}_{{,tt}}} \\ + \frac{{\eta {{t}_{p}}}}{D}(~{{\varphi }_{{x,x}}}H_{y}^{2}) + \frac{{\eta {{t}_{p}}}}{D}(~{{\varphi }_{{y,y}}}H_{x}^{2}), \\ \end{gathered} $$
(17)

where \({{k}_{s}}\) is the shear revision constant. The functions \(w\), \({{\varphi }_{x}}\), and \({{\varphi }_{y}}\) are generally independent on each other. Therefore, Eq. (17) can be analyzed so that the terms in the two sides of the equation that are related to each function from \(w\), \({{\varphi }_{x}}\), and \({{\varphi }_{y}}\) are equal to each other independently. The following equation is obtained for calculating the naturally in-plane frequencies:

$$\begin{gathered} \left[ {\left( {~1 + \frac{{\eta \mu }}{{{{k}_{s}}G}}H_{x}^{2}{{{\left( {\frac{{n\pi }}{a}~} \right)}}^{2}} + \frac{{\eta \mu }}{{{{k}_{s}}G}}H_{y}^{2}{{{\left( {\frac{{m\pi }}{b}~} \right)}}^{2}} - \frac{{\mu {{\omega }^{2}}}}{{{{k}_{s}}G}}\rho ~} \right){{{\left( {~\frac{{n\pi }}{a}~} \right)}}^{4}}} \right. \\ \left. {\, + 2~{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}}~{{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}} + {{{\left( {~\frac{{m\pi }}{b}~} \right)}}^{4}}~} \right] \\ = \,\left( { - \frac{{D + \mu {{k}_{s}}G{{t}_{p}}}}{{{{k}_{s}}GD}}{\kern 1pt} \eta H_{x}^{2}{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}}\, - \,\frac{{D + \mu {{k}_{s}}G{{t}_{p}}}}{{{{k}_{s}}GD}}{\kern 1pt} \eta H_{y}^{2}{{{\left( {\frac{{m\pi }}{b}~} \right)}}^{2}}} \right. \\ \left. {\, + \frac{{D + \mu {{k}_{s}}G{{t}_{p}}}}{{{{k}_{s}}GD}}\rho {{\omega }^{2}}} \right)~\left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}}~} \right] - \frac{{\eta {{t}_{p}}}}{D}H_{x}^{2}{{\left( {~\frac{{n\pi }}{a}} \right)}^{2}} \\ - \frac{{\eta {{t}_{p}}}}{D}H_{y}^{2}{{\left( {\frac{{m\pi }}{b}~} \right)}^{2}} + \frac{{\rho {{\omega }^{2}}{{t}_{p}}}}{D}. \\ \end{gathered} $$
(18)

This equation calculates the naturally out-plane frequencies for the Mendelian plate.

EXTRACTING THE EQUATION BY LOCAL EQUILIBRIUM EQUATIONS AND THE ENERGY CONSERVATION PRINCIPLE

Due to their subatomic structure, materials are affected by their internal magnetic fields. If the net effects of these internal fields are not equal to zero, it is called that the material has the magnetic property. If a material has not a natural magnetic property, applying an external magnetic field can affect the movement of its electrons around the core and create an induced magnetic property, which is called magnetization. The relationship between such magnetization and the applied magnetic field is complex and depends strongly on the type of the material. However, a linear relationship is acceptable in most cases. The wastes related to this phenomenon through the movement can also be neglected. Such wastes are categorized into mechanical and magnetic wastes. Mechanical and viscosity frictions are the main mechanical wastes that can be neglected when investigating the problem. Magnetization irreversibility are the main magnetic wastes that can also be neglected. The supports are simply and their displacements are zero. Therefore, no energy can enter or exit the boundaries of the system. In this case, the main energies that affect movement of the nanoplate during its vibration are: the elastic potential energy, the kinematic energy, and the work conducted by the applied magnetic field. Hence, we write the energy conversion for the time interval of \(dt\) as follows:

$$\dot {E} = ~{{P}_{{n.c}}}.$$
(19)

The following approach is applied to calculate the energy rate. From Eq. (1) and the Kirshoff’s deformation assumption, the following equations are obtained:

$${{f}_{{mx}}} = - z\eta H_{y}^{2}({{w}_{{,xxx}}} + ~{{w}_{{,xyy}}}),$$
(20)
$${{f}_{{my}}} = - z\eta H_{x}^{2}({{w}_{{,yyy}}} + ~{{w}_{{,xxy}}}).$$
(21)

The local equilibrium equations are as follows:

$$\frac{{\partial {{\sigma }_{x}}}}{{\partial x}}~\; + \;~{{f}_{{mx}}} = 0,$$
(22)
$$\frac{{\partial {{\sigma }_{y}}}}{{\partial y}}~\; + ~\;{{f}_{{my}}} = 0,$$
(23)

Therefore, the distribution of the stresses due to magnetic loading is as follows:

$${{\sigma }_{{Bx}}} = z\eta H_{y}^{2}(~{{w}_{{,xx}}} + {{w}_{{,yy}}}~),$$
(24)
$${{\sigma }_{{By}}} = z\eta H_{x}^{2}(~{{w}_{{,xx}}} + {{w}_{{,yy}}}).$$
(25)

Hence, the following equations hold:

$${{M}_{{Bx}}} = \eta H_{y}^{2}\frac{{t_{p}^{3}}}{{12}}~(~{{w}_{{,xx}}} + {{w}_{{,yy}}}),$$
(26)
$${{M}_{{By}}} = \eta H_{x}^{2}\frac{{t_{p}^{3}}}{{12}}(~{{w}_{{,xx}}} + ~{{w}_{{,yy}}}).$$
(27)

Therefore, the elastic potential energy induced by applying the magnetic field is calculated as follows:

$$\begin{gathered} {{U}_{B}} = \frac{1}{2}\int {(~{{M}_{x}}{{\kappa }_{x}} + ~{{M}_{y}}{{\kappa }_{y}})dA} \\ = \eta \frac{{t_{p}^{3}}}{{24}}~\int {H_{y}^{2}w_{{,xx}}^{2} + H_{y}^{2}{{w}_{{,xx}}}{{w}_{{,yy}}}} \\ \, + H_{x}^{2}{{w}_{{,xx}}}{{w}_{{,yy}}} + ~H_{x}^{2}w_{{,yy}}^{2})dA. \\ \end{gathered} $$
(28)

Its rate is equal to:

$$\begin{gathered} {{({{U}_{B}})}_{{,t}}}~ = \eta \frac{{t_{p}^{3}}}{{24}}\int {\{ ~2~H_{y}^{2}{{w}_{{,xx}}}{{w}_{{,xxt}}} + (H_{y}^{2} + H_{x}^{2})} \\ \, \times (~{{w}_{{,xxt}}}{{w}_{{,yy}}} + {{w}_{{,xx}}}{{w}_{{,yyt}}}) + 2H_{x}^{2}{{w}_{{,yy}}}{{w}_{{,yyt}}}\} ~\int {dA} . \\ \end{gathered} $$
(29)

The other section of the elastic potential energy of the nanoplate is directly due to its deformation. Since we used the small-size deformation assumption, the elastic potential energy is added to the energy induced by magnetic loading. The small-size effects is considered when calculating the potential energy induced by magnetic loading. Therefore, the potential energy induced by the deformation is considered as follows:

$${{U}_{e}} = \frac{D}{2}\int {{{{({{\nabla }^{2}}w)}}^{2}}dA} ,$$
(30)
$${{({{U}_{e}})}_{{,t}}} = D\int {({{\nabla }^{2}}w){{{({{\nabla }^{2}}w)}}_{{,t}}}dA} .$$
(31)

The rate of the kinematic energy is as follows:

$$K = \frac{1}{2}\int {(~\rho {{t}_{p}}w_{{,t}}^{2})dA} ,$$
(32)
$$\dot {K} = \rho {{t}_{p}}\int {(~{{w}_{{,t}}}{{w}_{{,tt}}}~)dA} .$$
(33)

From another point of view, we can consider the power with which the magnetic field creates some energy for the system. Therefore, the work of the D’Alembert’s forces are calculated as follows:

$$\begin{gathered} {{P}_{{n.c}}} = \int {({{F}_{{mz}}}{{w}_{{,t}}}~)dA} \\ ~ = \int {\{ \eta {{t}_{p}}(~{{w}_{{,yy}}} - {{w}_{{,xx}}})(H_{y}^{2} - H_{x}^{2}){{w}_{{,t}}}\} dA} . \\ \end{gathered} $$
(34)

After replacing these equations into Eq. (19) and by considering the fact that all integrals are calculated based on midplane, the following equation is obtained:

$$\begin{gathered} \eta \frac{{t_{p}^{3}}}{{24}}\{ ~2~H_{y}^{2}{{w}_{{,xx}}}{{w}_{{,xxt}}} + (H_{y}^{2} + H_{x}^{2})(~{{w}_{{,xxt}}}{{w}_{{,yy}}} + {{w}_{{,xx}}}{{w}_{{,yyt}}}) \\ \, + 2H_{x}^{2}{{w}_{{,yy}}}{{w}_{{,yyt}}}\} + D({{\nabla }^{2}}w){{({{\nabla }^{2}}w)}_{{,t}}} + \rho {{t}_{p}}{{w}_{{,t}}}{{w}_{{,tt}}} \\ \, - \{ ~\eta {{t}_{p}}~(~{{w}_{{,yy}}} - {{w}_{{,xx}}}~)(~H_{y}^{2} - H_{x}^{2}~){{w}_{{,t}}}~\} = 0. \\ \end{gathered} $$
(35)

This equation is a result of Eq. (1). It is also based on the local equilibrium equations and the energy conservation principle. According to the solution approach presented in Section 3, the following equation is obtained for calculating the naturally out-plane frequencies:

$$\begin{gathered} \eta \frac{{t_{p}^{2}}}{{24}}\left\{ {2~H_{y}^{2}{{{\left( {\frac{{n\pi }}{a}} \right)}}^{4}} + 2(H_{y}^{2} + H_{x}^{2})} \right. \\ \times \left. {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}}{{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}} + 2H_{x}^{2}{{{\left( {\frac{{m\pi }}{b}} \right)}}^{4}}~} \right\}~ \\ + \frac{D}{{{{t}_{p}}}}~\left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}}} \right]~\left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}}} \right] \\ \, - \rho \omega _{{mn}}^{2} + \eta (~H_{y}^{2} - H_{x}^{2})\left( {~{{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}} - {{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}}} \right) = 0. \\ \end{gathered} $$
(36)

It is important to note that the Eringen’s non-local theory is not satisfied when extracting this equation. In other words, small-size effects are considered by using Eq. (1). If we want to satisfy the Eringen’s theory, the curvatures should also be calculated from the following equations:

$${{M}_{x}} - \mu {{\nabla }^{2}}{{M}_{x}} = D(~{{w}_{{,xx}}} + \vartheta {{w}_{{,yy}}}),$$
(37)
$${{M}_{y}} - \mu {{\nabla }^{2}}{{M}_{y}} = D(~{{w}_{{,yy}}} + \vartheta {{w}_{{,xx}}}).$$
(38)

By replacing Eqs. (26) and (27) into Eqs. (37) and (38), the following equations are obtained:

$${{w}_{{,xx}}} = - \eta \frac{{t_{p}^{3}}}{{12D({{\vartheta }^{2}} - 1)}}(~H_{y}^{2} - \vartheta H_{x}^{2}~)\{ ~{{\nabla }^{2}}w - \mu {{\nabla }^{4}}w\} ,$$
(39)
$${{w}_{{,yy}}} = - \eta \frac{{t_{p}^{3}}}{{12D({{\vartheta }^{2}} - 1)}}(~H_{x}^{2} - \vartheta H_{y}^{2})\{ ~{{\nabla }^{2}}w - \mu {{\nabla }^{4}}w\} .$$
(40)

Therefore, the rate of the elastic potential energy induced by applying the magnetic field is calculated as follows:

$$\begin{gathered} {{M}_{x}}{{\kappa }_{x}} + ~{{M}_{y}}{{\kappa }_{y}} = - \left( {~\eta \frac{{t_{p}^{3}}}{{12}}} \right)\left( {\eta \frac{{t_{p}^{3}}}{{12D({{\vartheta }^{2}} - 1)}}} \right) \\ \, \times [H_{x}^{4} + H_{y}^{4} - 2\vartheta H_{x}^{2}H_{y}^{2}](~{{\nabla }^{2}}w~)(~{{\nabla }^{2}}w - \mu {{\nabla }^{4}}w), \\ \end{gathered} $$
(41)
$$\begin{gathered} \frac{1}{2}{{({{M}_{x}}{{\kappa }_{x}} + ~{{M}_{y}}{{\kappa }_{y}})}_{{,t}}} = - \frac{1}{2}\left( {~\eta \frac{{t_{p}^{3}}}{{12}}} \right)\left( {\eta \frac{{t_{p}^{3}}}{{12D({{\vartheta }^{2}} - 1)}}} \right) \\ \, \times [H_{x}^{4} + H_{y}^{4} - 2\vartheta H_{x}^{2}H_{y}^{2}~] \\ \, \times \{ {{({{\nabla }^{2}}w)}_{{,t}}}({{\nabla }^{2}}w - \mu {{\nabla }^{4}}w) + ({{\nabla }^{2}}w){{({{\nabla }^{2}}w - \mu {{\nabla }^{4}}w)}_{{,t}}}\} . \\ \end{gathered} $$
(42)

The power of the applied magnetic field is calculated as follows:

$$\begin{gathered} (~{{w}_{{,xx}}} - {{w}_{{,yy}}}~) = - \left( {\eta \frac{{t_{p}^{3}}}{{12D({{\vartheta }^{2}} - 1)}}} \right) \\ \, \times [(1 + \vartheta )H_{y}^{2} - (1 + \vartheta )H_{x}^{2}]({{\nabla }^{2}}w - \mu {{\nabla }^{4}}w), \\ \end{gathered} $$
$$\begin{gathered} \eta {{t}_{p}}(H_{x}^{2} - H_{y}^{2})(~{{w}_{{,xx}}} - {{w}_{{,yy}}}){{w}_{{,t}}} \\ = - \eta {{t}_{p}}(~H_{x}^{2} - H_{y}^{2})\left( {\eta \frac{{t_{p}^{3}}}{{12D({{\vartheta }^{2}} - 1)}}} \right) \\ \, \times [(1 + \vartheta )H_{y}^{2} - (1 + \vartheta )H_{x}^{2}]({{\nabla }^{2}}w - \mu {{\nabla }^{4}}w){{w}_{{,t}}}. \\ \end{gathered} $$
(43)

We consider the nonlocal theory of elasticity for the work conducted by the D’Alembert’s forces. By using Eq. (19), the following equation is obtained:

$$\begin{gathered} - \frac{1}{2}\left( {~\eta \frac{{t_{p}^{3}}}{{12}}} \right)\left( {\eta \frac{{t_{p}^{3}}}{{12D({{\vartheta }^{2}} - 1)}}} \right)[H_{x}^{4} + H_{y}^{4} - 2\vartheta H_{x}^{2}H_{y}^{2}] \\ \times ~\{ ~{{({{\nabla }^{2}}w)}_{{,t}}}({{\nabla }^{2}}w - \mu {{\nabla }^{4}}w) + ({{\nabla }^{2}}w){{({{\nabla }^{2}}w - \mu {{\nabla }^{4}}w)}_{{,t}}}\} \\ + D({{\nabla }^{2}}w){{({{\nabla }^{2}}w)}_{{,t}}} + \rho {{t}_{p}}{{w}_{{,t}}}{{w}_{{,tt}}} - (\rho {{t}_{p}}{{\nabla }^{2}}{{w}_{{,tt}}}){{w}_{{,t}}} \\ \, + \eta {{t}_{p}}(H_{x}^{2} - H_{y}^{2})\left( {\eta \frac{{t_{p}^{3}}}{{12D({{\vartheta }^{2}} - 1)}}} \right) \\ \, \times [(1 + \vartheta )H_{y}^{2} - (1 + \vartheta )H_{x}^{2}]({{\nabla }^{2}}w - \mu {{\nabla }^{4}}w){{w}_{{,t}}} = 0. \\ \end{gathered} $$
(44)

The following equation is obtained for calculating the frequencies:

$$\begin{gathered} \left( {~\eta \frac{{t_{p}^{3}}}{{12}}} \right)\left( {\eta \frac{{t_{p}^{3}}}{{12D({{\vartheta }^{2}} - 1)}}} \right)[~H_{x}^{4} + H_{y}^{4} - 2\vartheta H_{x}^{2}H_{y}^{2}~] \\ \, \times \left\{ {~\left( {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}}} \right)} \right.\left\{ { - \left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}}} \right] - \mu } \right. \\ \left. {\left. { \times \left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{4}} + 2{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}}{{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{4}}} \right]} \right\}} \right\} \\ \, + D~\left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}}} \right]{{\left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} + \left( {\frac{{m\pi }}{b}} \right)} \right]}^{2}} \\ \, - \rho {{t}_{p}}\omega _{{mn}}^{2} - \rho {{t}_{p}}\omega _{{mn}}^{2}\mu \left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}}} \right] \\ \, + \eta {{t}_{p}}(~H_{x}^{2} - H_{y}^{2})\left( {\eta \frac{{t_{p}^{3}}}{{12D({{\vartheta }^{2}} - 1)}}} \right) \\ \, \times [(1 + \vartheta )H_{y}^{2} - (1 + \vartheta )H_{x}^{2}] \\ \, \times \left\{ { - ~\left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}}~} \right] - \mu } \right. \\ \times \left. {\left[ {{{{\left( {\frac{{n\pi }}{a}} \right)}}^{4}} + 2{{{\left( {\frac{{n\pi }}{a}} \right)}}^{2}}{{{\left( {\frac{{m\pi }}{b}} \right)}}^{2}} + {{{\left( {\frac{{m\pi }}{b}} \right)}}^{4}}} \right]} \right\} = 0. \\ \end{gathered} $$
(45)

RESULTS AND DISCUSSION

When we study small size problems, we face an important issue. The field and consistivity equations must be used so that it is acceptable as an engineering analysis, and there is also an acceptable accuracy. Based on this issue, different approaches are applied to analyze the mechanical behavior of nanoplates in a constant in-plane magnetic field. The energy conservation principle and the first low of Thermodynamics are fields equations and hold for all sizes. Therefore, using these two rules is a suitable approach for analyzing nano-size problems. We consider the following values for the parameters:

$$\begin{gathered} \rho = 2300\,~\frac{{{\text{kg}}}}{{{{{\text{m}}}^{{\text{3}}}}}},\quad {{H}_{x}} = 0,\quad \eta = 100,~ \\ {{H}_{y}} = 0.02~T,\quad D = 0.01\,{\text{N}}\;{\text{m}}{\text{,}}\quad ~{{k}_{s}} = 1.5,~ \\ \end{gathered} $$
(46)
$$\begin{gathered} G = 77~\,{\text{GPa}},\quad ~\mu = 0.3~\,{\text{m}},\quad a = b,\quad \\ {{t}_{p}} = 100~\,{\text{nm}},\quad ~\vartheta = 0.3. \\ \end{gathered} $$

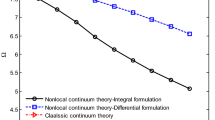
For these values, the frequencies \(\omega _{{01}}^{2}\) are calculated based on Eqs. (13) and (45), and are depicted in Tables 1–3.

Table 1. The estimated values of the frequencies from Eqs. (10) and (44) when \(a = 100\,{\text{nm}}\)
Full size table
Table 2. The estimated values of the frequencies from Eqs. (10) and (44) when \(a = 30\,{\text{nm}}\)
Full size table
Table 3. The estimated values of the frequencies from Eqs. (10) and (44) when \(a = 100\,{\text{nm}}\)
Full size table

CONCLUSIONS

Based on the outputs presented in Tables 1–3, it is concluded that:

1. When the length of the nanoplate or the power of the applied magnetic field increases, the estimated frequency decreases. This decrease is observable from both equations. However, Eq. (45) indicates higher decrease.

2. For magnetic powers less than 0.1 \(\sqrt {{\text{N}}\;{{{\text{m}}}^{{ - 2}}}} \), the predictions obtained from Eqs. (13) and (45) are very close to each other. Magnetic powers in the real world are usually less than 0.1 \(\sqrt {{\text{N}}\;{{{\text{m}}}^{{ - 2}}}} \). Therefore, the results obtained from Eqs. (13) and (45) are very close to each other for real-world magnetic fields.

Also, after investigating the results obtained from Eqs. (13) and (45) in magnetic powers more than 0.1 \(\sqrt {{\text{N}}\;{{{\text{m}}}^{{ - 2}}}} \), the following results are obtained.

3. When the power of the applied magnetic field increases, a viscosity property is created in the system. This property results in some wastes. Eq. (45) predicts this wastes in the magnetic field of 0.25 \(\sqrt {{\text{N}}\;{{{\text{m}}}^{{ - 2}}}} \). Also, this waste is independent on the length of the plate. Around this value, the nanoplate shows a complex behavior. In addition, the frequency shows high variation with respect to the variation in the power of the magnetic field. This behavior may be related to the small-size effects phenomenon, and introduces a quantum point of the system.

4. As the power of the field increases, the viscosity also highly increases. Therefore, an increase in the power of the magnetic field is not suitable from the point of view of the energy; if higher frequencies are needed, an increase in the length of the nanoplate is a suitable choice for decreasing energy wastes and increasing the frequency simultaneously.