Modeling the Structure of a Reinforcing Phase at Heat Treatment of Steel Products

Abstract

The article describes a new algorithm for predicting the structure of a reinforcing phase at heat treatment of high carbon steels. This approach is based on the construction of the distribution function of grains in their size for a set of regions in which the temperature gradient is sufficiently small. The proposed algorithm makes it possible to avoid calculating formation and growth of a single embryo and to proceed to modeling the structure in a relatively large cell, which can significantly reduce computational costs. To solve the problem of determining the distribution function of temperature fields, it is proposed to use a new approach based on integral heat transfer equations; this allows, on one hand, estimating the accuracy of calculations by the mismatch vector and, on the other hand, averaging thermophysical characteristics in a natural way and solving the problem on large-scale grid splits. Owing to the nonlinearity of the task and the need to use iterative procedures, integral equations provide the necessary conditions for their convergence. As a result of creating specialized software and carrying out a series of numerical calculations, it is possible to theoretically determine the necessary conditions for heat treatment for products made from steel of a particular grade: size and power of the heating inductor, the speed of its movement, the type of coolant and its feed rate, the depth of the hardened layer, etc.; as a result, this will make it possible to determine in advance the structure of the heat-treatable layer and reduce the total costs of experimental work.

INTRODUCTION

The processes of heat treatment of products made of steel and alloys that lead to the formation of a reinforcing phase in the process of eutectoid transformations can significantly increase the strength and wear resistance of operating surfaces, which is widely used in various industries and is one of the most common types of hardening. However, actually, the heat treatment regimes for this type of alloy, i.e., the cooling rate and exposure time at a certain temperature, as well as tempering of the hardened product to reduce the stresses arising during the heat treatment process, are often a subject of patenting and require performing a considerable amount of experimental work. Since the end of the 1990s, attempts have been made to theoretically predict the structure of the hardened layer obtained after heat treatment, depending on the steel grade and cooling conditions, in order to determine in advance the operating characteristics of the resulting product, which in turn will reduce total labor costs for experimental research.

For needs of a metallurgical company in Austria, the VAI-Q-Strip computer program was developed, in which the user can set the chemical composition of steel and thermomechanical conditions of rolling; the program allows calculating temperature conditions, austenite decomposition processes, and ferrite grain sizes, which allows one to predict mechanical properties of rolling [1]. Similar results are demonstrated by the Hot Strip Mill Model (HSSM) program model for forming the structure and properties of steels at hot rolling developed by the Integprocess Group, Inc., an American company, on instructions of the American Iron and Steel Institute. However, the main disadvantage of these programs is that they are based on a large number of known experimental data for so-called base grades and are not able to calculate mechanical properties for high carbon steels, including modern bainitic steels [1].

For adequate modeling of heat treatment processes, it is necessary, first, to be able to numerically calculate temperature fields in inhomogeneous media with varying thermophysical properties and moving heat sources (drains) (heat is generated during formation and growth of a nucleus). An important property of the algorithms used in this case should be the ability to assess the accuracy of the results obtained.

The second important condition is the use of the most appropriate model of formation and growth of nuclei of a new phase under conditions of varying temperature effect. This model should make it possible to calculate the grain size and total amount of ferrite and gamma phase in the total volume of the processed sample and in each part.

The third significant condition is the calculation of carbon concentration in the austenite phase, which changes owing to diffusion processes from the areas in which structural changes have occurred. If in any region the amount of carbon is insufficient, then the reinforcing phase does not form and here a ferrite zone remains. In the case of an excess of carbon, areas characteristic of cast irons will be released. For modeling these processes at each time step, it is necessary to solve numerically the diffusion equation with coefficients depending both on temperature and on carbon solubility in the austenitic matrix.

This paper presents a simplified computational model for formation of a reinforcing phase depending on temperature conditions under the assumption that the carbon concentration is sufficient for any area of the workpiece to form the gamma-prime phase.

METHODS FOR PREDICTING THE STRUCTURE OF THE REINFORCING PHASE

Attempts to use the model of formation of bainitic, pearlitic, and martensitic structures are presented in the literature depending on the temperature difference in the processed product by calculating temperatures [2] and using well-known diagrams [3] or simulating the processes of formation and growth of each individual nucleus of the carbide reinforcing phase [4]. Despite the fact that the latter approach does make it possible to model the structure of the reinforcing phase, its practical use is faced with the need to calculate too many nuclei—from tens of thousands to several million, given that their size is on the order of one micron or less (for example, Fig. 1 shows the structure of granular perlite [5] in carbon steels).

Fig. 1.

Microstructure of eutectoid steel: granular perlite.

For extended three-dimensional blanks, such calculations require the use of supercomputers, which makes it very difficult to perform calculations on the structure of steel for practical needs.

The integrated approach [6–12] allows one to naturally average thermophysical characteristics—heat capacity and thermal conductivity—for a heterogeneous mixture, which allows one to avoid consideration of individual nuclei and to use the mixture rule for calculation

$$G = (1 - \alpha ){{G}_{a}} + \alpha {{G}_{{{\text{reinf}}}}},$$

((1))

and use volume fractions of the reinforcing phase and austenite in averaging thermophysical characteristics of the current state of the material. Thus, for temperature calculations, it is necessary to be able to calculate at each moment the content (volume) of the reinforcing phase, or its concentration, in each section of the product being processed, which will allow one to use the mixture rule to determine the averaged thermal characteristics—thermal conductivity and heat capacity coefficients.

It is proposed to use the distribution function of the reinforcing phase along the radius of the grain (i.e., the volume of grains having a given radius) to calculate the structure of the reinforcing phase. Thus, using the known distribution function, one can find the most probable (or average) grain size of the reinforcing phase R_av, its total amount, and deviation from the mean (dispersion), which ultimately allows us to speak about the structure of the material of the product that is obtained as a result of its thermal treatment.

Figure 2 shows the nature of the distribution function of the reinforcing phase with respect to the grain size (grain radius), which, generally speaking, varies over time. The area under the graph of the function determines total volume of the reinforcing phase

$${{V_{{{\text{reinf}}}}^{{{\text{gen}}}}} \mathord{\left/ {\vphantom {{V_{{{\text{reinf}}}}^{{{\text{gen}}}}} V}} \right. \kern-0em} V} = \int\limits_0^{{{R}_{{\max }}}} {n(r){\text{d}}r} .$$

((2))

Fig. 2.

Distribution function of the reinforcing phase over the radius of grains.

In order to calculate the distribution function of the reinforcing phase with respect to the grain size, it is possible to use the distribution function that specifies the amount of grains also depending on their radius. Then the function of n(r) = V_reinf(r)/V can be found simply by multiplying their amount by the volume:

$$n(r) = {{4\pi } \mathord{\left/ {\vphantom {{4\pi } {3{{r}^{3}}N(r),}}} \right. \kern-0em} {3{{r}^{3}}N(r),}}$$

((3))

where N(r) is the number of grains of the reinforcing phase in a certain volume V having a given radius r. In turn, the function determining the number of grains of a given radius can be constructed if we know the probability of the emergence of new nuclei of the reinforcing phase and the growth rate of an individual nucleus. Figure 3 shows a graph reflecting the nature of the change in the dimensionless $(\bar {N}(r) = {{N(r)} \mathord{\left/ {\vphantom {{N(r)} {{{N}_{{\max }}}}}} \right. \kern-0em} {{{N}_{{\max }}}}})$ distribution function of the number of grains over radii constructed at different moments of time during isothermal cooling of the sample. At the beginning, for a certain rather long time, the rate of formation of a new phase, i.e., the number of nuclei produced per unit time in the selected volume V, constantly and slightly decreases, which is associated with the general small amount of the new reinforcing phase. Therefore, all that amount that was formed by a certain moment of time is known to us, and it remains only to calculate the radii of the grains at the next moment of time.

Fig. 3.

Nature of the change in the distribution function of the amount of nuclei of a new phase over their radii with time during isothermal exposure.

It is seen from Fig. 3 that over time a “shift” of the distribution function occurs in a certain sense that is caused by the growth of already existing grains and the emergence of new nuclei. At the final stage, the number of newly formed nuclei is minimal, which is associated with a large amount of the reinforcing phase formed in this selected volume, which naturally leads to a decrease in the total volume of austenite.

The above considerations make it possible to avoid a large number of calculations related to the calculation of the behavior of each individual nucleus and to proceed to the calculation of the distribution function of the reinforcing carbide phase according to the grain size at each moment of time under the conditions of thermal treatment. To do this, the following conditions must be met:

(1) The whole product must be broken into areas in which temperature gradient is close to zero in order to avoid the preferred direction of growth of nuclei (the model is designed to calculate the growth of the reinforcing phase for the case in which grains can be approximately considered as spherical).

(2) To construct the distribution function, it is necessary to use the dependence that determines the amount of nuclei formed depending on temperature per unit of time, i.e., the formation rate of new nuclei.

(3) It is also necessary to be able to calculate the growth rate of grains depending also on the current temperature.

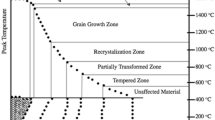
The conditions for choosing the mesh spacing for the calculation depend on the temperature distribution function and can be based on a preliminary general analysis of thermal treatment conditions (Fig. 4).

Fig. 4.

Choosing mesh spacing for prediction structure of surface layer during thermal treatment in the region of austenitic transition.

Despite the fact that the sizes of the selected cells are small enough and in actual calculations for dimensional parts can be on the order of one millimeter, this is incomparable with the sizes of grains, which have a size of ~1 μm (Fig. 1). In other words, with this approach, it is possible to increase the mesh step on each axis by ~10³ times (and, accordingly, reduce the computation time).

In order to obtain the dependence of the formation rate of new nuclei, one can use the following considerations: the formation of a new nucleus occurs owing to the selection of thermal energy in a selected region of space, has a probabilistic nature, and depends on the total volume of the austenite phase. Therefore, it is natural to assume that, to calculate the formation rate of new nuclei, the Gibbs distribution function can be used, in which the formation energy of a new nucleus of a critical radius R_cr and temperature difference providing transition of austenite to the gamma-prime phase is set

$$f(T) = A\exp ({{ - {{E}_{{{\text{cr}}}}}} \mathord{\left/ {\vphantom {{ - {{E}_{{{\text{cr}}}}}} k}} \right. \kern-0em} k}\left| {{{T}_{{{\text{aust}}}}} - T} \right|).$$

((4))

The behavior of this function depending on temperature is shown in Fig. 5, from which it follows that the parameter A has the meaning of the maximum value of nuclei which can be formed in the case of maximum temperature difference.

Fig. 5.

Behavior of the function of growth rate of new nuclei depending on current temperature.

It follows from this that, for a function determining the amount of new nuclei in the selected volume V, one can write the differential relation

$${{{\text{d}}N} \mathord{\left/ {\vphantom {{{\text{d}}N} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = A\exp ({{ - {{E}_{{{\text{cr}}}}}} \mathord{\left/ {\vphantom {{ - {{E}_{{{\text{cr}}}}}} k}} \right. \kern-0em} k}\left| {{{T}_{{{\text{aust}}}}} - T} \right|)(1 - {{{{V}_{{{\text{reinf}}}}}} \mathord{\left/ {\vphantom {{{{V}_{{{\text{reinf}}}}}} V}} \right. \kern-0em} V}).$$

((5))

In terms of a commonality in approach, the Gibbs distributions can also be applied to determine the growth function of grains of the reinforcing phase (change in their radii with time). For this, let us use the following provision: the grain growth is also caused by the formation of new nuclei, but not in the whole volume, but only on the grain surface. In other words, the grain surface initiates formation of nuclei of a critical size (with the same internal structure as a grain itself), resulting in an increase in its radius. Owing to the fact that, during the formation of a new nucleus, heat is evolved, which must be removed to ensure further growth of a grain, the following nuclei are formed mainly on the surface of the original grain and, because of the absence of a significant temperature gradient, provide a symmetrical grain growth uniformly in all directions. These arguments can be demonstrated with the help of the diagram shown in Fig. 6.

Fig. 6.

Grain growth of reinforcing phase based on model of initiation of this process by the grain surface itself.

The term grain initiation implies that the activation energy of a nucleus on the grain surface is much less than the activation energy of a nucleus in some other place. This model allows one to find the rate of change in the radius of a nucleus with time (under the condition that a grain surrounds a sufficient amount of the austenite phase)

$$\begin{gathered} \Delta {{V}_{{{\text{reinf}}}}} = (R(t + \Delta t) - R(t)){{S}_{{{\text{surface}}}}} \\ = \Delta R{{S}_{{{\text{surface}}}}} = {{4\pi } \mathord{\left/ {\vphantom {{4\pi } {3R_{{{\text{cr}}}}^{3}}}} \right. \kern-0em} {3R_{{{\text{cr}}}}^{3}}}\Delta N. \\ \end{gathered} $$

((6))

Assuming that in this case the formation rate of new nuclei is proportional to the Gibbs distribution function and the current surface area of a grain, we get

$${{{\text{d}}N} \mathord{\left/ {\vphantom {{{\text{d}}N} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = A{'}{\text{exp}}({{ - E_{{{\text{cr}}}}^{'}} \mathord{\left/ {\vphantom {{ - E_{{{\text{cr}}}}^{'}} k}} \right. \kern-0em} k}\left| {{{T}_{{{\text{aust}}}}} - T} \right|){{S}_{{{\text{surface}}}}}.$$

((7))

$${{dR} \mathord{\left/ {\vphantom {{dR} {dt}}} \right. \kern-0em} {dt}} = {{4\pi } \mathord{\left/ {\vphantom {{4\pi } {2R_{{{\text{cr}}}}^{3}A{'}{\text{exp}}}}} \right. \kern-0em} {2R_{{{\text{cr}}}}^{3}A{'}{\text{exp}}}}({{ - E_{{{\text{cr}}}}^{'}} \mathord{\left/ {\vphantom {{ - E_{{{\text{cr}}}}^{'}} k}} \right. \kern-0em} k}\left| {{{T}_{{{\text{aust}}}}} - T} \right|).$$

((8))

The obtained dependence (8) shows that the growth rate of a grain does not depend on its size and has the same appearance as the formation rate of new nuclei of a critical radius (5).

Figure 7 shows a sequence of diagrams reflecting the processes of change in the structure of the reinforcing phase made on the basis of the model described above. The shown sequence of states of the product material in a simplified form demonstrates quite adequate capabilities of the algorithm for predicting structural changes.

Fig. 7.

Modeling grain growth of reinforcing phase based on the proposed model:(a) initial stage, when several nuclei arise simultaneously; (b) final stage, in which growth of grains leads to almost complete filling entire volume.

NUMERICAL MODELING OF STRUCTURE FORMATION PROCESSES

The proposed model can be used for numerical modeling the processes of formation of the reinforcing phase in order to select the most appropriate heat treatment regimes for blanks of products from various alloys. Owing to the fact that, during the formation of a new phase, the thermophysical characteristics of the product material significantly change, to calculate temperature fields on each time layer, it is necessary to use an iterative procedure (Fig. 8).

Fig. 8.

Iterative algorithm for calculating the structure of reinforcing layer and current temperature distribution.

As is well known, iterative algorithms converge well in the case of bounded operators (which are not differential operators); therefore, for solving partial differential equations, which include the thermal conductivity equation, special algorithms that guarantee convergence of iterations must be used.

The author proposes to use for solving the problem of thermal conductivity (in the case of heat treatment) integral equations [9] whose solution from the very beginning is based on the convergence iterative procedure and which, in addition, allow estimating the accuracy of the obtained solution by the mismatch vector with the right parts. These equations can also be solved using an efficient paralleling procedure, which can even be organized on a graphics card of a personal computer or laptop [7].

CONCLUSIONS

The model of the formation of the reinforcing phase that is considered in the paper includes general provisions that are valid for most processes of phase or structural transformations, and, thus, it can be generalized to solve the problems of thermal treatment of products from heat-resistant nickel alloys, etc. Naturally, for the applied use of this method, it is necessary to conduct an additional comparative analysis of experimental data in order to determine a set of free parameters that are used to calculate the distribution function of the reinforcing phase with respect to the grain radius.

Together, the proposed model and the integral approach for numerical solution of the equations of thermal conductivity allows one to develop special software which can be used for preliminary selection of thermal treatment conditions of blanks made of high carbon steels in order to obtain a fine bainitic steel structure with both good strength and increased wear-resistant characteristics.

Development of such programs is especially relevant from the point of view of creating Russian software which further can be used at manufacturing enterprises or in design bureaus.