Introduction

The fundamental quantity to be determined by thermal analysis of welds is the temperature history, i.e., change in temperature with time, at each position on the weld cross section (Ref 1, 2). Given this quantity, observed weld microstructure and weld performance can be correlated with rates of temperature change during welding. In addition, mechanical response characteristics associated with residual strains within welds can be predicted using models for which temperature histories are input quantities. For weld thermal analysis in practice, i.e., the quantitative calculation of temperature histories for a given welding process, the direct-problem or first-principles approach for estimation of temperature histories entails solving the coupled transport equations using numerical methods based either on finite differences or finite volumes (Ref 3, 4). This approach has the advantage of providing insight concerning the relationship between weld characteristics and underlying physical processes, i.e., the nature of workpiece and energy source coupling. Another advantage of this approach is that for sufficiently controlled welding experiments, where weld meltpool morphology is simple, thermocouple measurements are available, and the direct model used for analysis is formulated in terms of small numbers of adjustable parameters, material properties can be determined. The procedure for determination of material properties would entail adjustment of model parameters to achieve agreement between predicted and measured temperature histories at thermocouple locations. The direct-problem approach, however, has many disadvantages for practical weld thermal analysis, which are as follows.

Models that are formulated in terms of basic theory, direct-problem-based models, are difficult to apply for quantitative weld analysis in that most material properties needed for this type of modeling are not available.

Weld meltpool morphologies can in general be extremely complex, e.g., martini glass, hour glass, and central bulge shapes, due to the wide variety and complexity of welding processes, e.g., hybrid welding processes. Direct-problem-based models are not structured to adopt as input detailed information concerning complex shapes of weld meltpools. That is to say, the detailed modeling of underlying physical processes resulting in complex meltpool morphologies is in practice not feasible.

A major “workhorse” for practical weld thermal analysis is the measurement of temperature histories at distributed locations on the workpiece surface using thermocouples. Direct-problem-based models are not structured to adopt thermocouple measurements as input, but rather only as verification of model output.

It is reasonable to assume that for a given set of welds, quantitative weld thermal analysis should utilize all available experimental measurements characterizing those welds. Direct-problem-based models are in general not structured for modeling “overdetermined-systems” (Ref 4), i.e., weld thermal analysis where relatively many experimental measurements are available, e.g., shape features of solidification boundaries and thermocouple measurements. Accordingly, with respect to input information for direct-problem-based modeling, experimental measurement can remain fallow or used only for model verification.

In contrast to the direct-problem approach, the inverse-problem approach (Ref 5-7) for weld thermal analysis, using parametric functions of minimal complexity, has many advantages for quantitative estimation of weld temperature histories (Ref 8-19). This approach entails calculation of temperature fields within the volume of the workpiece using parametric functions that are structured for convenient parameter adjustment with respect to detailed information obtained from measurements, such as solidification boundaries and thermocouple measurements. The concept of system representation using “minimally complex” parametric functions is related to that of system representation using linear combination of basis functions (Ref 4), which follows the analysis approach of signal processing, where analysis is in terms of the superposition of fundamental modes of system response (Ref 20). Following this approach, a system’s response, no matter how complex, is decomposed into a linear combination of component contributions whose formal structure are characteristic modes of that system. For example, in the case of signal processing of transmitted waves, e.g., electromagnetic or acoustic, the characteristic modes are sine and cosine functions, which represent in principle the simplest parameterization in terms of basis functions for inverse analysis. Similarly, in the case of inverse thermal analysis, the characteristic modes are the kernel and fourier series solutions to the heat conduction equation, representing the simplest parametrization in terms of basis functions (Ref 21). It follows that the inherent complexity of any numerical procedure for applying inverse models formulated in terms of linear combinations of basis functions should be significantly less than those for applying models based on first principles, i.e., transport equations, such as finite-element and finite volume procedures (Ref 3, 4). In addition to being physically consistent basis functions for parametric representation of weld temperature fields, the kernel and fourier series solutions to the heat conduction equation have general functional forms that are sufficiently flexible so as not to impose any form of model bias on calculated temperature histories. The mathematical foundation of inverse thermal analysis using linear combinations of basis functions is that of least-squares parameter optimization (Ref 4, 22, 23).

As discussed previously, inverse analysis compensates for lack of information concerning material properties and complex physical processes associated with energy source and workpiece coupling (Ref 24-29). For example, one goal of models formulated in terms of basic theory, for the case of deep-penetration welding, is simulation of the coupling of keyhole formation, melting, fluid flow in the weld meltpool and heat transfer from the solidification boundary into the heat effect zone (HAZ). It is important to note that with respect to practical analysis the purpose of modeling these influences, in particular, would be generation of the solidification boundary, the surface from which heat is transferred into the HAZ, which is the region of most probable weld failure, and difficult for inspection. Therefore, inverse models that adopt weld cross sections of solidification boundaries as “model input” should tend to compensate for lack of information concerning physical processes occurring within the melt pool. This reasoning also applies to physical processes occurring within the mushy zone. With respect to inverse analysis, measured solidification boundaries represent estimates of mushy-zone edges, which are at the solidus temperature.

There exists a fundamental aspect of inverse analysis methods that must be kept in mind. It follows that for inverse models, errors associated with experimental measurements, which are adopted as constraints, are encoded onto the optimized values of model parameters. Accordingly, quantitative inverse analyses should consider the sensitivity of calculated field quantities with respect to measurement errors that could be associated with constraint conditions.

Presented here is a case study inverse thermal analysis of structural steel deep-penetration welds. This analysis provides a parameterization of temperature histories for prediction of properties within the HAZ of welds for the regime considered. The present study applies an inverse thermal analysis procedure that uses volumetric constraint conditions on calculated three-dimensional solidification boundaries. These constraint conditions are such that two-dimensional projections of calculated solidification boundaries are constrained to fall within measured solidification cross-section boundaries. For the present study, which considers deep-penetration welds of structural steel, inverse thermal analysis includes prediction of temperature histories at experimentally estimated HAZ edges. The parametric temperature histories presented in the study can be adopted for inverse thermal analysis of welds corresponding to other process parameters or welding processes whose process conditions are within similar regimes. Finally, the results of this study can contribute to a parameter space for inverse thermal analysis, which contains a wide range of parameters corresponding to different welding processes, process conditions, and different types of metals and their alloys.

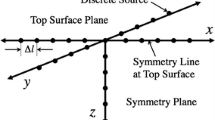
The formal structure of the inverse analysis approach applied in this study is that of parametric model representation of the temperature field in terms of numerical-analytical basis functions (Ref 24-29). The basis functions are termed numerical-analytical because they consist of numerical integrals of analytic functions over time. The conceptual foundation of this approach was introduced by Ref 30, and provides a general reduction of model complexity for purposes of weld thermal analysis. Reduction of model complexity is achieved by adopting numerical-analytical models for either the heat source or temperature field (or both) in combination with numerical methods. Among notable studies applying this approach are Ref 2, 31-34. The inverse analysis approach applied here has been used (Ref 35) for construction of a parameter space relating welding process parameters, e.g., current and welding speed, to weld efficiency for keyhole plasma arc welding. Similarly, the present study contributes to a parameter space relating shapes of weld solidification boundaries, or shapes of any specified boundaries within the weld, to weld temperature histories, as well as to weld process parameters. An aspect of the inverse analysis methodology applied here, which permits convenient adjustment of parameters, is use of discrete volumetric source distributions. These source distributions, consisting of a finite number of point sources distributed in three dimensions, are conveniently adjustable with respect to location and source strength for calculation of temperature fields on and exterior to specified isothermal boundaries, e.g., solidification boundaries (see Ref 24-29). The use of discrete source distributions in this study, which are within three dimensions (i.e., volumetric), is formally equivalent to the Myhr-Grong method (Ref 32), which typically employs discrete source distributions within two-dimensional planes transverse to the relative motion of heat source and workpiece. References 36, 37, and reference therein, demonstrate the use of discrete source distributions for numerical modeling of transport phenomena associated with welding processes.

The organization of the subject areas presented is as follows. First, a brief description of the general procedure for inverse analysis of heat deposition processes is presented. Second, results of inverse thermal analyses of structural steel deep-penetration welds are presented. These results provide a quantitative parametric representation of temperature histories for these welds and for any welds associated with similar welding process conditions. Third, a discussion is presented concerning aspects of the inverse analysis procedure. Finally, a conclusion is given.

Inverse Analysis Procedure

Following the inverse analysis approach, a parametric model provides a means for the inclusion of information concerning the physical characteristics of a given energy deposition process. A physically consistent parametric representation of temperature fields for heat deposition during welding of plate structures is given by

$$T(\hat{x},t) = T_{\text{A}} + \sum\limits_{k = 1}^{{N_{k} }} {\sum\limits_{n = 1}^{{N_{t} }} {C(\hat{x}_{k} )G\left( {\hat{x},\hat{x}_{k} ,\kappa ,n \Delta t,V} \right)} }$$
(1)

and

$$T(\hat{x}_{n}^{c} ,t_{n}^{c} ) = T_{n}^{c} ,$$
(2)

where

$$\begin{aligned} G\left( {\hat{x},\hat{x}_{k} ,t,\kappa ,V} \right) = & \frac{1}{t}\exp \left[ { - \frac{{(x - x_{k} - Vt)^{2} + (y - y_{k} )^{2} }}{4\kappa t}} \right] \\ & \times \left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{\kappa m^{2} {{\pi }}^{2} t}}{{l^{2} }}} \right]\cos \left[ {\frac{{m{{\pi }}z}}{l}} \right]\cos \left[ {\frac{{m{{\pi }}z_{k} }}{l}} \right]} } \right\} \\ \end{aligned}$$
(3)

and

$$C(\hat{x}) = \sum\limits_{k = 1}^{{N_{k} }} {Q(\hat{x}_{k} ){t{\delta }}(\hat{x} - \hat{x}_{k} } ),$$
(4)

where \(Q(\hat{x}_{k} )\) is the value of the discrete source function at location \(\hat{x}_{k}\). The quantities \(\kappa\), V, and l are the thermal diffusivity, welding speed, and plate thickness, respectively. The constraint conditions defined by Eq 2, which represent input for the model defined by Eq 1-4, are imposed on the temperature field by minimization of the objective function defined by

$$Z_{T} = \sum\limits_{{n{ = }1}}^{N} {w_{n} \left( {T(\hat{x}_{n}^{c} ,t_{n}^{c} ) - T_{n}^{c} } \right)}^{2},$$
(5)

where \(T_{n}^{c}\) is the target temperature for position \(\hat{x}_{n}^{c} \, = \,(x_{n}^{c} ,y_{n}^{c} ,z_{n}^{c} )\). The quantities \(w_{n}\) (n = 1,…,N) are weight coefficients that specify relative levels of influence associated with constraint conditions \(T_{n}^{c}\). The output quantity of the model defined by Eq 1-4 is the three-dimensional temperature field \(T(\hat{x},t)\) spanning the entire volume of the workpiece.

The procedure for inverse thermal analysis defined by Eq 1-5 entails adjustment of the parameters \(C(\hat{x}_{k} )\), \(\hat{x}_{k},\) and \(\varDelta t\). The parametric model combines numerical integration with optimization of linear combinations of numerical-analytical basis functions, which include fundamental solutions to the heat conduction equation and their Fourier series representation (Ref 21). In particular, Eq 1 defines a discrete numerical integration over time, where the time step \(\varDelta t\) is specified according to the average energy deposited during the time \(\varDelta t\), for transition of the temperature field to steady state. It should be noted that the formulation of the inverse analysis methodology defined by Eq 1-5 is equipped with a mathematical structure that satisfies all boundary conditions associated with welding of plate structures (see Ref 24-29 for further discussion).

In addition to the parameters defined with respect to Eq 1-5, the parametric model applied for inverse analysis includes a length scale parameter l S, where in general l S < l defined by Eq 3, for specification of the spatial scale of the calculated temperature field with respect to which parameters are adjusted. This length scale parameter provides for inclusion of more details of shape features of measured solidification boundaries to be adopted as constraint conditions. Inverse analyses using this parameter are given in Ref 29. However, for the analyses that follow, the two length parameters, i.e., the plate thickness l and the depth l S of the specified region of the temperature field to be calculated, are taken to be the same.

Case Study Analysis of Steel Welds

In this section, results of inverse thermal analyses of structural steel deep-penetration welds are described, which correspond to different weld process conditions and associated process-control parameters. The significance of the inverse-problem approach for these analyses is that the nature of the coupling of the energy source to the workpiece, which is a function of beam power and process-control parameters, is in principle difficult to specify relative to analysis based on the direct-problem approach. Previous studies considered inverse thermal analysis of steel welds using different types of constraint conditions (Ref 25, 26). A series of studies (Ref 28, 29) considered inverse thermal analysis of welds using multiple constraint conditions, where both solidification and estimated phase-transformation boundaries were adopted as constraint conditions. In particular, welds of CP-Ti and a Ti-6Al-4V were considered, where weld-cross-section measurements of both solidification and estimated \({{\alpha }} - {{\beta }}\) phase-transformation boundaries were adopted as constraint conditions on the calculated temperature field. For those studies, motivation for adopting \({{\alpha }} - {{\beta }}\) phase transformation boundaries as constraint conditions was that in practice, for welds of Ti and its alloys, one can associate (approximately) this boundary with the observed edge of the HAZ, and accordingly, specify an isothermal boundary of known temperature. The present study uses experimentally estimated solidification boundaries for assigning volumetric constraints (see Eq 2) on the calculated temperature fields. As discussed in Ref 27, for regions within the workpiece not close to the energy source, reasonable estimates of temperature-field values, at specified locations, are sufficient for imposing constraint conditions.

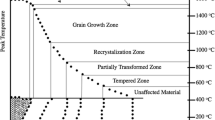
For steel welds, especially those of structural steel, the HAZ consists by various regions whose microstructures have been well characterized (see Ref 1). These regions are described schematically in Fig. 1. Referring to this figure, it should be noted that, for inverse thermal analysis of structural steel welds, one should be able to associate the observed edge of the HAZ with a range of temperatures characteristic of that region of the weld (see Fig. 1).

Fig. 1
figure 1

Schematic representation of different regions within the HAZ for steel welds and approximate location of experimentally observable HAZ edge

Full size image

The structural steel deep-penetration welds, whose inverse analysis is presented here, consist of laser and laser-GTA hybrid welds (Ref 38, 39). The analyses presented here entail calculation of the steady-state temperature field for a specified range of sizes and shapes of inner surface boundaries \(S_{i}\) defined by the solidification boundary, and experimentally observed estimates of the HAZ edge. The shapes of these boundaries are determined experimentally by analysis of transverse weld cross sections showing microstructure revealing solidification and estimated HAZ-edge boundaries. For calculations of the temperature field, which adopt solidification boundaries as constraints, the parameter values assumed are \(\kappa\) = 5.88 × 10−6 m2 s−1, T M = 1503.0 °C. As discussed previously (Ref 25, 27), reasonable estimates of \(\kappa\) and T M are sufficient for inverse analysis. This assumption is sufficient, within reasonable estimates, in that the set of parameters \(C(\hat{x}_{k} )\), k = 1,…,N k , and \(\kappa\) are not uniquely determined by inverse analysis. Thus, changing estimated values of \(\kappa\) would require different values of \(C(\hat{x}_{k} )\) in order to satisfy specified constraint conditions associated with T M. With respect to inverse analysis, the interpretation of \(\kappa\) as both an estimated material property and adjustable parameter is emphasized within the following.

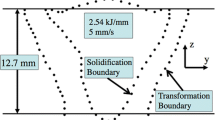
The goal of the present analysis is determination of a set of parameters that can serve as initial estimates for parameter adjustment with respect to deep-penetration welds of steels, whose process parameters are within similar regimes. Parameter adjustment with respect to other welds, which assume the results of this study as initial estimates, would adopt \(\kappa\) and T M as adjustable parameters, as well as the discrete source function \(C\left( {\hat{x}_{k} } \right)\). Values of the workpiece thickness l and welding speed V defined in Eq 3 are given in the figures below. The upstream boundary constraints on the temperature field, T c  = T M for (y c , z c ) defined in Eq 2, are given in Tables 1, 2, 3, and 4 for the solidification boundaries. Given in Tables 5, 6, 7, and 8 are values of the discrete source function that have been calculated according to the constraint conditions and weld specifications given in Tables 1, 2, 3, and 4. The relative location of each discrete source is specified according to indexing scheme shown in Fig. 2. Shown in Fig. 3 to 22 are experimentally measured transverse weld cross sections of solidification and HAZ-edge boundaries (Ref 38, 39), and different planer slices of the steady-state temperature field that have been calculated according to the constraint conditions given in Tables 1, 2, 3, and 4 for the solidification boundary. Referring to the planar slices of the calculated temperature fields shown in these figures, it can be seen that all boundary conditions are satisfied, namely the condition \(T(\hat{x},t) = T_{\text{M}}\) at the solidification boundary, and \(\nabla T \cdot \hat{n} = 0\) at surface boundaries, where \(\hat{n}\) is normal to the surface.

Table 1 Experimentally measured estimates of locations (y c ,z c ) on solidification and transformation boundaries, which are on transverse cross section of Weld 1
Full size table
Table 2 Experimentally measured estimates of locations (y c ,z c ) on solidification and transformation boundaries, which are on transverse cross section of Weld 2
Full size table
Table 3 Experimentally measured estimates of locations (y c ,z c ) on solidification and transformation boundaries, which are on transverse cross section of Weld 3
Full size table
Table 4 Experimentally measured estimates of locations (y c ,z c ) of solidification and transformation boundaries, which are on transverse cross section of Weld 4
Full size table
Table 5 Volumetric source function \(C\left( {\hat{x}_{k} } \right)\) calculated according to solidification-boundary constraint conditions given in Table 1, where Δl = (2.4/60) mm, x k  = y k  = 0.0 for k = 1 to 12 and z k  = 1 for k = 13 to 20 (WELD 1)
Full size table
Table 6 Volumetric source function \(C\left( {\hat{x}_{k} } \right)\) calculated according to solidification-boundary constraint conditions given in Table 2, where Δl = (2.4/60) mm, x k  = y k  = 0.0 for k = 1 to 12 and z k  = 1 for k = 13 to 20 (Weld 2)
Full size table
Table 7 Volumetric source function \(C\left( {\hat{x}_{k} } \right)\) calculated according to solidification-boundary constraint conditions given in Table 3, where Δl = (2.4/60) mm, x k  = y k  = 0.0 for k = 1 to 12 and z k  = 1 for k = 13 to 20 (Weld 3)
Full size table
Table 8 Volumetric source function \(C\left( {\hat{x}_{k} } \right)\) calculated according to solidification-boundary constraint conditions given in Table 4, where Δl = (2.4/60) mm, x k  = y k  = 0.0 for k = 1 to 12 and z k  = 1 for k = 13 to 20 (Weld 4)
Full size table
Fig. 2
figure 2

Indexing scheme for relative locations of discrete sources, k = 1,…,N k

Full size image
Fig. 3
figure 3

Experimentally measured transverse weld cross sections of solidification and HAZ-edge boundaries for steel laser weld (laser power: 4500 W) (Weld 1)

Full size image
Fig. 4
figure 4

Two-dimensional slices, at half workpiece top surface and longitudinal cross section at symmetry plane, of three-dimensional temperature field (°C) calculated using cross-section information given in Table 1 for solidification boundary (Weld 1)

Full size image
Fig. 5
figure 5

Temperature history (°C) of transverse cross section of weld calculated using cross-section information given in Table 1 for solidification boundary, where grid size equals (7.0/60) mm and V = 8.5 mm/s (Weld 1)

Full size image
Fig. 6
figure 6

Two-dimensional slices, at half workpiece top surface and longitudinal cross section at symmetry plane, of three-dimensional temperature field (°C) at estimated HAZ-edge boundary calculated using constraints defined by Eq 2, and given in Table 1 for solidification boundary (Weld 1)

Full size image
Fig. 7
figure 7

Temperature history (°C) at estimated HAZ-edge boundary of transverse cross section of weld calculated using constraints defined by Eq 2, and given in Table 1 for solidification boundary, where grid size equals (7.0/60) mm and V = 8.5 mm/s (Weld 1)

Full size image
Fig. 8
figure 8

Experimentally measured transverse weld cross sections of solidification and HAZ-edge boundaries for steel laser-GTA hybrid weld (laser power: 4500 W, arc voltage and current: 123 V and 190 A, respectively) (Weld 2)

Full size image
Fig. 9
figure 9

Two-dimensional slices, at half workpiece top surface and longitudinal cross section at symmetry plane, of three-dimensional temperature field (°C) calculated using cross-section information given in Table 2 for solidification boundary (Weld 2)

Full size image
Fig. 10
figure 10

Temperature history (°C) of transverse cross section of weld calculated using cross-section information given in Table 2 for solidification boundary, where grid size equals (7.0/60) mm and V = 8.5 mm/s (Weld 2)

Full size image
Fig. 11
figure 11

Two-dimensional slices, at half workpiece top surface and longitudinal cross section at symmetry plane, of three-dimensional temperature field (°C) at estimated HAZ-edge boundary calculated using constraints defined by Eq 2, and given in Table 2 for solidification boundary (Weld 2)

Full size image
Fig. 12
figure 12

Temperature history (°C) at estimated HAZ-edge boundary of transverse cross section of weld calculated using constraints defined by Eq 2, and given in Table 2 for solidification boundary, where grid size equals (8.5/60) mm and V = 8.5 mm/s (Weld 2)

Full size image
Fig. 13
figure 13

Experimentally measured transverse weld cross sections of solidification and HAZ-edge boundaries for steel laser weld (laser power: 4000 W) (Weld 3)

Full size image
Fig. 14
figure 14

Two-dimensional slices, at half workpiece top surface and longitudinal cross section at symmetry plane, of three-dimensional temperature field (°C) calculated using cross-section information given in Table 3 for solidification boundary (Weld 3)

Full size image
Fig. 15
figure 15

Temperature history (°C) of transverse cross section of weld calculated using cross-section information given in Table 3 for solidification boundary, where grid size equals (5.0/60) mm and V = 16.9 cm/s (Weld 3)

Full size image
Fig. 16
figure 16

Two-dimensional slices, at half workpiece top surface and longitudinal cross section at symmetry plane, of three-dimensional temperature field (°C) at estimated HAZ-edge boundary calculated using constraints defined by Eq 2, and given in Table 3 for solidification boundary (Weld 3)

Full size image
Fig. 17
figure 17

Temperature history (°C) at estimated HAZ-edge boundary of transverse cross section of weld calculated using constraints defined by Eq 2, and given in Table 3 for solidification boundary, where grid size equals (5.0/60) mm and V = 16.9 cm/s (Weld 3)

Full size image
Fig. 18
figure 18

Experimentally measured transverse weld cross sections of solidification and transformation boundaries for steel laser-GTA hybrid weld (laser power: 4000 W, arc voltage and current: 20 V and 165 A, respectively) (Weld 4)

Full size image
Fig. 19
figure 19

Two-dimensional slices, at half workpiece top surface and longitudinal cross section at symmetry plane, of three-dimensional temperature field (°C) calculated using cross-section information given in Table 4 for solidification boundary (Weld 4)

Full size image
Fig. 20
figure 20

Temperature history (°C) of transverse cross section of weld calculated using cross-section information given in Table 4 for solidification boundary, where grid size equals (5.0/60) mm and V = 16.9 cm/s (Weld 4)

Full size image
Fig. 21
figure 21

Two-dimensional slices, at half workpiece top surface and longitudinal cross section at symmetry plane, of three-dimensional temperature field (°C) at estimated HAZ-edge boundary calculated using constraints defined by Eq 2, and given in Table 4 for solidification boundary (Weld 4)

Full size image
Fig. 22
figure 22

Temperature history (°C) at estimated HAZ-edge boundary of transverse cross section of weld calculated using constraints defined by Eq 2 given in Table 4 for solidification boundary, where grid size equals (5.0/60) mm and V = 16.9 cm/s (Weld 4)

Full size image

Discussion

The inverse analysis procedure entails calculating a three-dimensional solidification boundary using experimentally measured constraint conditions, and the temperature field consistent with the isothermal surface associated with that boundary. The resulting three-dimensional temperature field permits calculation of temperature histories as a function of transverse position within the cross section of the weld. Shown in Fig. 4, 9, 14, and 19 are two-dimensional slices of the calculated three-dimensional temperature field obtained using the constraint conditions given in Tables 1, 2, 3, and 4 for the measured solidification boundary, which are parallel to the relative motion of laser or laser-GTA source and workpiece. Shown in Fig. 5, 10, 15, and 20 are two-dimensional slices of this three-dimensional temperature field that are perpendicular to the relative motion of laser or laser-GTA source and workpiece. Referring to these figures, it should be noted that t = 0 has been assigned arbitrarily to a two-dimensional slice at the leading edge of the solidification boundary. Accordingly, shown in Fig. 5, 10, 15, and 20 is passage with time of the calculated three-dimensional solidification boundaries through experimentally measured transverse cross sections of these boundaries, which are indicated by sparse dotted contours. For the planar slices of the calculated temperature field shown in Fig. 4, 5, 9, 10, 14, 15, 19, and 20, the weld meltpool and regions having temperatures below melting are indicated by uniform black and banded gray scale, respectively. Referring to the calculated temperature fields shown in these figures, the constraint conditions on the calculated three-dimensional solidification boundaries are such that projections of all their two-dimensional transverse slices, as a function of time, are consistent with the experimentally measured transverse cross sections of these boundaries.

Shown in Fig. 6, 11, 16, and 21 are two-dimensional slices of the calculated three-dimensional temperature field at estimated HAZ-edge boundaries obtained using the constraint conditions defined by Eq 2, and given in Tables 1, 2, 3, and 4 for the solidification boundary, which are parallel to the relative motion of laser or laser-GTA source and workpiece. Shown in Fig. 7, 12, 17, and 22 are two-dimensional slices of this three-dimensional temperature field that are perpendicular to the relative motion of laser or laser-GTA source and workpiece. Again, referring to these figures, it should be noted that t = 0 has been assigned arbitrarily to a two-dimensional slice at the leading edges of the isothermal boundaries. Accordingly, shown in Fig. 7, 12, 17, and 22 is passage with time of the calculated three-dimensional isothermal boundaries through experimentally measured transverse cross sections of the estimated HAZ-edge boundaries, which are indicated by sparse dotted contours. For the planar slices of the calculated temperature field shown in Fig. 6, 7, 11, 12, 16, 17, 21, and 22, regions having temperatures below and above calculated isothermal boundaries at estimated HAZ edges are indicated by uniform black and banded gray scale, respectively. Referring to the calculated temperature fields shown in these figures, it can be seen that the predicted temperature histories at cross-section locations close to the experimentally estimated HAZ edge are within a range of temperatures characteristic of that for steels (see Fig. 1). These results show reasonable consistency between model input, solidification cross-section measurements, and model output, predicted temperature histories close to the HAZ edge. As discussed above, a fundamental aspect of inverse analysis methods is that errors associated with experimental measurements, which are adopted as constraints, are encoded onto the optimized values of model parameters. Therefore, the predicted temperature histories at the HAZ edges are expected to have errors due to the fact that, in practice, it is difficult to measure solidification and HAZ-edge boundaries for steels. In particular, metallographic analysis of weld cross sections (Ref 40), using etchants, must consider the finite thickness of the mushy zone adjacent to the solidus isotherm, as well as the many different crystallographic zones in proximity of the HAZ edge (see Fig. 1), which in principle may not be well defined. It is interesting to note, however, that the inverse analysis procedure provides a consistency check with respect to experimental procedures for measurements of solidification and HAZ boundaries, for a given steel weld.

The results of this study can be adopted for more efficient inverse thermal analysis of other types of stainless steel welds. This follows in that parameter optimization can be made more efficient using initial estimates of the parameter values, which require only fine adjustment with respect to constraint conditions. Model-parameter optimization for welds, whose process parameters are within similar regimes to those for which model-parameter values have been determined previously (e.g., parameters \(C(\hat{x}_{k} )\), \(\hat{x}_{k}\), \(\varDelta t\) \(\kappa,\) and T M for the parametric model defined by Eq 1-4), can adopt these values as initial estimates for subsequent fine adjustment. In addition, although the thermal diffusivity \(\kappa\) and melt temperature T M of steels may vary, this variation is not over a wide range of values. This is the case in general for different types of metals and their alloys. It follows that parameter optimization for a specific type of steel weld, which uses initial estimates of parameter values corresponding to different types of steel welds, can adopt \(\kappa\) and T M as adjustable parameters, as well as other model parameters, e.g., \(C(\hat{x}_{k} )\), \(\hat{x}_{k}\), \(\varDelta t\). Accordingly, the parametric temperature histories constructed according to Tables 1, 2, 3, and 4 can contribute to a parameter space containing a sufficient range of parameters corresponding to different welding processes, process conditions, and different types of metals and their alloys. It follows that, given a sufficient accumulation of parameterized temperature histories, spanning a wide range of process conditions, further investigation should concern determination of an optimal structure for such a parameter space.

Finally, it should be noted that using measurements of solidification boundaries as constraint conditions is formally equivalent to using thermocouple measurements for this purpose. This follows in that thermocouple measurements can be associated with points on three-dimensional isothermal surfaces. For example, the maximum value of a weld temperature history measured by thermocouple on the surface of a workpiece can be associated with a three-dimensional isothermal surface whose temperature equals that value. This three-dimensional isothermal surface can be adopted as a volumetric constraint on the calculated temperature field following the same procedure applied in this study. As emphasized in previous studies, the temperature fields extending over the top and bottom surfaces of the workpiece represent conveniently available data to be used for inverse analysis, and are typically measured using thermocouples. In the case of relatively large welding speeds, the use of thermocouple measurements may require an additional adjustable parameter associated with thermocouple time delay.

Conclusion

A specific objective of this report is to further examine, for the case of structural steel welds, the concept of using experimentally measured temperature-field constraints for inverse thermal analysis (Ref 24-29). A general objective of this report is to describe a quantitative inverse thermal analysis of structural steel deep-penetration welds corresponding to various weld process parameters and to construct numerical-analytical basis functions that can be used by weld analyst to calculated weld temperature histories, which are for welding processes associated with similar process conditions. This report contributes to the continuing evolution of a parametric representation of the temperature field T (\(\hat{x}\), t, \(\kappa\), V, S i , l) for inverse thermal analysis of welds associated with different types of metals, their alloys, and weld process conditions. The weld temperature histories obtained by inverse analysis could in practice be used to predict solid-state phase transitions and mechanical response characteristics.