1 INTRODUCTION

The development of the production of materials and structures operated under conditions of the unsteady interaction of different physical kinds of fields has attracted the attention of scientists working in this and related fields. They were increasingly attracted to models of the mechanics of coupled fields and, in particular, models of mechanodiffusion. High-intensity technological processes (explosion welding, production of silicon on an insulator, electric spark and laser processing of materials, etc.) also require taking into account the coupling of mechanical and diffusion fields in the material.

Recently, a large number of works have been published, which are related to studying the effects of the interaction between mechanical and diffusion fields. Thus, a fairly rigorous mathematical theory of mechanodiffusion has been formed, based on phenomenological approaches and models of thermodynamics and continuum mechanics [1–3].

Questions related to the direct solution of problems of unsteady coupled mechanodiffusion, with the exception of a few individual works, have been developed mainly since the mid-1990s. An analysis of the existing publications shows that, in terms of solving the corresponding initial boundary value problems, models in the rectangular Cartesian coordinate system have been most comprehensively studied. There are relatively few works on solving problems of mechanodiffusion in cylindrical and spherical coordinate systems, and we can single out [4–18] among them.

On the one hand, the main difficulty in solving unsteady problems is the problem of inverting the Laplace transform. In the listed works, it is solved mainly using the Durbin method and its modifications [5–9, 13–15], quadrature formulas based on the use of orthogonal polynomials or Riemann sums [10, 11, 15], or using various numerical methods [12, 18]. At the same time, the images obtained when solving specific problems are so cumbersome that it is not always possible to practically check the possibility of using a particular method to find their originals.

On the other hand, when solving problems in curvilinear coordinate systems, it is important to find a system of eigenfunctions that are the solution to the corresponding Sturm–Liouville problem. As applied to related problems of mechanodiffusion, this issue has not been discussed in well-known scientific papers to date. However, using the example of problems in a rectangular Cartesian coordinate system, it was shown that the Sturm–Liouville problem can be solved only for a certain class of boundary conditions [19]. Thus, the method of separating variables in mechanodiffusion problems has a limited scope.

To solve the problem posed, the method of equivalent boundary conditions [19, 20] is used, which allows us to express the solution of a problem with arbitrary boundary conditions in terms of known solutions of problems with boundary conditions of a special form. This approach makes it possible to significantly expand the class of problems to be solved and was tested in modeling mechanodiffusion processes in a solid orthotropic cylinder [20].

2 PROBLEM STATEMENT

A hollow orthotropic multicomponent cylinder is considered, which is under the action of an unsteady pressure uniformly distributed over the inner and outer surfaces. The mathematical formulation of the problem includes a linearized equation of motion of a hollow cylinder, the law of mass conservation in local form, and N linearized equations of the mass transfer. The statement is closed by the boundary conditions corresponding to the given surface disturbances (a dot in the suffix denotes the derivative with respect to time and a dash denotes the derivative with respect to the coordinate) [20, 21]

$$\begin{gathered} \ddot {u} = u{\kern 1pt} ''\; + \frac{{u{\kern 1pt} '}}{r} - \frac{u}{{{{r}^{2}}}} - \sum\limits_{j = 1}^N {{{\alpha }_{j}}\eta _{j}^{'}} ,\quad {{\eta }_{{N + 1}}} = - \sum\limits_{q = 1}^N {{{\eta }_{q}}} , \\ {{{\dot {\eta }}}_{q}} + {{t}_{q}}{{{\ddot {\eta }}}_{q}} = - {{\Lambda }_{q}}\left( {u{\kern 1pt} '''\; + \frac{{2u{\kern 1pt} ''}}{r} - \frac{{u{\kern 1pt} '}}{{{{r}^{2}}}} + \frac{u}{{{{r}^{3}}}}} \right) + {{D}_{q}}\left( {\eta _{q}^{{''}} + \frac{{\eta _{q}^{'}}}{r}} \right), \\ \end{gathered} $$
(1)
$$\begin{gathered} {{\left. {\left( {u{\kern 1pt} '\; + {{c}_{{12}}}\frac{u}{r} - \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{\eta }_{j}}} } \right){\kern 1pt} } \right|}_{{r = 1}}} = f_{{11}}^{*}(\tau ),\quad {{\left. {\left( {u{\kern 1pt} '\; + {{c}_{{12}}}\frac{u}{r} - {\kern 1pt} \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{\eta }_{j}}} } \right){\kern 1pt} } \right|}_{{r = {{R}_{1}}}}} = f_{{12}}^{*}(\tau ), \\ {{\left. {{{\eta }_{q}}} \right|}_{{r = 1}}} = {{f}_{{q + 1,1}}}(\tau ),\quad {{\left. {{{\eta }_{q}}} \right|}_{{r = {{R}_{1}}}}} = {{f}_{{q + 1,2}}}(\tau ). \\ \end{gathered} $$
(2)

Assuming that the cylinder is initially in an undisturbed state, the initial conditions are assumed to be zero.

All the values in (1) and (2) are dimensionless. Their relationship with dimensional analogs is given by the following equalities:

$$\begin{gathered} u = \frac{{{{u}_{r}}}}{{{{r}_{2}}}},\quad \tau = \frac{{Ct}}{{{{r}_{2}}}},\quad {{C}^{2}} = \frac{{{{C}_{{1111}}}}}{\rho },\quad {{t}_{q}} = \frac{{C{{\tau }^{{(q)}}}}}{{{{r}_{2}}}},\quad {{c}_{{12}}} = \frac{{{{C}_{{1122}}}}}{{{{C}_{{1111}}}}}, \\ {{R}_{1}} = \frac{{{{r}_{1}}}}{{{{r}_{2}}}},\quad r = \frac{{r{\kern 1pt} ^*}}{{{{r}_{2}}}},\quad {{\alpha }_{q}} = \frac{{\alpha _{{11}}^{{(q)}}}}{{{{c}_{{11}}}}},\quad {{D}_{q}} = \frac{{D_{{11}}^{{(q)}}}}{{C{{r}_{2}}}},\quad {{\Lambda }_{q}} = \frac{{{{m}^{{(q)}}}\alpha _{{11}}^{{(q)}}D_{{11}}^{{(q)}}n_{0}^{{(q)}}}}{{\rho C{{r}_{2}}R{{T}_{0}}}}, \\ \end{gathered} $$
(3)

where t is time; \({{u}_{r}}\) is the radial component of the displacement vector; \(r{\kern 1pt} *\) is the radial coordinate; \({{r}_{1}}\) is the inner radius of the cylinder; \({{r}_{2}}\) is the outer radius of the cylinder; \({{\eta }_{q}} = {{n}^{{(q)}}} - n_{0}^{{(q)}}\) is the increment in the concentration of a substance; \({{n}^{{(q)}}}\) and \(n_{0}^{{(q)}}\) are the current and initial concentrations of the qth substance in the composition of a multicomponent medium; \({{m}^{{(q)}}}\) is the molar mass of the qth substance in the composition of a multicomponent medium; \({{C}_{{ijkl}}}\) are the components of the tensor of elastic constants; ρ is the density of the medium; \(\alpha _{{ij}}^{{(q)}}\) are the components of the tensor of diffusion constants characterizing the deformations arising due to diffusion; \(D_{{ij}}^{{(q)}}\) are the components of the diffusion tensor; R is the universal gas constant; \({{T}_{0}}\) is the temperature of a continuous medium; and \({{\tau }^{{(q)}}}\) is the relaxation time of diffusion flows.

To solve the problem posed, the method of equivalent boundary conditions is used, according to which an auxiliary problem is first solved with boundary conditions of the following form [20]:

$$\begin{gathered} {{\left. {\left( {u{\kern 1pt} '\; + \frac{u}{r} - \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{\eta }_{j}}} } \right){\kern 1pt} } \right|}_{{r = 1}}} = f_{{11}}^{*}(\tau ),\quad {{\left. {\left( {u{\kern 1pt} '\; + \frac{u}{r} - \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{\eta }_{j}}} } \right)} \right|}_{{r = {{R}_{1}}}}} = f_{{12}}^{*}(\tau ), \\ {{\left. {{{\eta }_{q}}} \right|}_{{r = 1}}} = {{f}_{{q + 1,1}}}(\tau ),\quad {{\left. {{{\eta }_{q}}} \right|}_{{r = {{R}_{1}}}}} = {{f}_{{q + 1,2}}}(\tau ). \\ \end{gathered} $$
(4)

Here, functions \(f_{{1l}}^{*}(\tau )\) \((l = 1,2)\) are to be determined. The solution of the auxiliary problem (1) and (4) is sought in the form

$$\left\{ \begin{gathered} u(r,\tau ) \\ {{\eta }_{q}}(r,\tau ) \\ \end{gathered} \right\} = \sum\limits_{l = 1}^2 {\int\limits_0^\tau {\left\{ \begin{gathered} {{G}_{{11l}}}(r,\tau - t) \\ {{G}_{{q + 1,1l}}}(r,\tau - t) \\ \end{gathered} \right\}f_{{1l}}^{*}(t)dt} } + \sum\limits_{l = 1}^2 {\sum\limits_{m = 2}^{N + 1} {\int\limits_0^\tau {\left\{ \begin{gathered} {{G}_{{1ml}}}(r,\tau - t) \\ {{G}_{{q + 1,ml}}}(r,\tau - t) \\ \end{gathered} \right\}{{f}_{{ml}}}(t)dt} } } ,$$
(5)

where \({{G}_{{nml}}}(r,\tau )\) \(\left( {\forall n,m = \overline {1,N + 1} } \right)\) are the surface Green functions, which are solutions of the following problems of the initial boundary value:

$$\begin{gathered} \left( {G_{{1ml}}^{{''}} + \frac{{G_{{1ml}}^{'}}}{r} - \frac{{{{G}_{{1ml}}}}}{{{{r}^{2}}}}} \right) - \sum\limits_{j = 1}^N {{{\alpha }_{j}}G_{{j + 1,ml}}^{'}} = {{{\ddot {G}}}_{{1ml}}}, \\ - {{\Lambda }_{q}}\left( {G_{{1ml}}^{{'''}} + \frac{{2G_{{1ml}}^{{''}}}}{r} - \frac{{G_{{1ml}}^{'}}}{{{{r}^{2}}}} + \frac{{{{G}_{{1ml}}}}}{{{{r}^{3}}}}} \right) + {{D}_{q}}\left( {G_{{q + 1,ml}}^{{''}} + \frac{{G_{{q + 1,ml}}^{'}}}{r}} \right) = {{{\dot {G}}}_{{q + 1,ml}}} + {{t}_{q}}{{{\ddot {G}}}_{{q + 1,ml}}}; \\ \end{gathered} $$
(6)
$$\begin{gathered} {{\left. {\left( {G_{{1ml}}^{'} + \frac{1}{r}{{G}_{{1ml}}} - \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{G}_{{j + 1,ml}}}} } \right){\kern 1pt} } \right|}_{{r = 1}}} = {{\delta }_{{1m}}}{{\delta }_{{1l}}}\delta (\tau ),\quad {{\left. {{{G}_{{q + 1,ml}}}{\kern 1pt} } \right|}_{{r = 1}}} = {{\delta }_{{q + 1,m}}}{{\delta }_{{1l}}}\delta (\tau ), \\ {{\left. {\left( {G_{{1ml}}^{'} + \frac{1}{r}{{G}_{{1ml}}} - \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{G}_{{j + 1,ml}}}} } \right){\kern 1pt} } \right|}_{{r = {{R}_{1}}}}} = {{\delta }_{{1m}}}{{\delta }_{{2l}}}\delta (\tau ),\quad {{\left. {{{G}_{{q + 1,ml}}}} \right|}_{{r = {{R}_{1}}}}} = {{\delta }_{{q + 1,m}}}{{\delta }_{{2l}}}\delta (\tau ), \\ {{\left. {{{G}_{{1ml}}}} \right|}_{{\tau = 0}}} = {{\left. {{{{\dot {G}}}_{{1ml}}}} \right|}_{{\tau = 0}}} = {{\left. {{{G}_{{q + 1,ml}}}} \right|}_{{\tau = 0}}} = {{\left. {{{{\dot {G}}}_{{q + 1,ml}}}} \right|}_{{\tau = 0}}} = 0. \\ \end{gathered} $$
(7)

Here, \({{\delta }_{{ij}}}\) is the Kronecker symbol and \(\delta (\tau )\) is the Dirac delta function.

3 STURM–LIOUVILLE PROBLEM

The solution of the auxiliary problem is sought in the form of series in terms of eigenfunctions of the elastic-diffusion operator. To formulate the corresponding Sturm–Liouville problem, we use the Fourier variable separation method. In other words, the solution of problem (6) with homogeneous boundary conditions corresponding to (7) will be sought in the form

$${{G}_{1}}(r,\tau ) = V(r)W(\tau ),\quad {{G}_{{q + 1}}}(r,\tau ) = {{\Phi }_{q}}(r)\Psi (\tau ).$$
(8)

Here, the second and third indices in the notation of Green’s functions are omitted for brevity, because zero boundary conditions are considered. In addition, to simplify the calculations, we will assume that there are no relaxation effects (\({{t}_{q}}\) = 0) and the material is two-component (N = 1). For brevity, we will also omit the notation of index q, denoting the number of the component of the substance.

Substitution of equalities (8) into the system of equations (6) leads to the following relations:

$$\frac{{\ddot {W}(t)}}{{W(t)}} = \gamma ,\quad \frac{{\dot {\Psi }(t)}}{{\Psi (t)}} = {{\gamma }^{2}}\omega ,\quad \frac{{\Psi (t)}}{{W(t)}} = p = {\text{const}};$$
(9)
$$\begin{gathered} V{\kern 1pt} ''(r) + \frac{{V{\kern 1pt} '(r)}}{r} - \frac{{V(r)}}{{{{r}^{2}}}} - p\alpha \Phi {\kern 1pt} '(r) = {{\gamma }^{2}}V(r), \\ D\left( {\Phi {\kern 1pt} ''(r) + \frac{{\Phi '(r)}}{r}} \right) - \frac{{{{\Lambda }_{q}}}}{p}\left( {V{\kern 1pt} '''(r) + \frac{{2V{\kern 1pt} ''(r)}}{r} - \frac{{V{\kern 1pt} '(r)}}{{{{r}^{2}}}} + \frac{{V(r)}}{{{{r}^{3}}}}} \right) = {{\gamma }^{2}}\omega \Phi (r), \\ \end{gathered} $$
(10)

where \(\gamma \), \(\omega \), and \(p\) are constants.

The solution of system (10) in the ring \({{R}_{1}} \leqslant r \leqslant 1\) is sought in the following form:

$$V(r) = {{V}^{{(1)}}}{{J}_{1}}(\nu r) + {{V}^{{(2)}}}{{Y}_{1}}(\nu r),\quad \Phi (r) = {{\Phi }^{{(1)}}}{{J}_{0}}(\nu r) + {{\Phi }^{{(2)}}}{{Y}_{0}}(\nu r),$$
(11)

where \({{J}_{\mu }}(z)\) is the Bessel function of the first kind of order \(\mu \) and \({{Y}_{\mu }}(z)\) is the Bessel function of the second kind (Neumann function) of order \(\mu \) [22].

Substituting (11) into (10) and taking into account the properties of the Bessel functions [22], we arrive at the following systems of linear algebraic equations (\(l = 1,2\)):

$$({{\nu }^{2}} - {{\gamma }^{2}}){{V}^{{(l)}}} - p\nu \alpha {{\Phi }^{{(l)}}} = 0,\quad - {\kern 1pt} \frac{\Lambda }{p}{{V}^{{(l)}}} + (D{{\nu }^{2}} - {{\gamma }^{2}}\omega ){{\Phi }^{{(l)}}} = 0.$$
(12)

Equating the determinants of these systems to zero, we arrive at a single characteristic equation

$$({{\nu }^{2}} - {{\gamma }^{2}})(D{{\nu }^{2}} - {{\gamma }^{2}}\omega ) - {{\nu }^{4}}\alpha \Lambda = 0,$$

whose roots are determined by the formulas

$$\begin{gathered} {{\nu }_{1}} = \gamma \sqrt {\frac{{D - \omega - \sqrt {{{{(D - \omega )}}^{2}} - 4\omega (D - \alpha \Lambda )} }}{{2D}}} ,\quad {{\nu }_{3}} = - {{\nu }_{1}}, \\ {{\nu }_{2}} = \gamma \sqrt {\frac{{D - \omega + \sqrt {{{{(D - \omega )}}^{2}} - 4\omega (D - \alpha \Lambda )} }}{{2D}}} \quad {{\nu }_{4}} = - {{\nu }_{2}}. \\ \end{gathered} $$
(13)

These quantities, like the characteristic equation, do not depend on the parameter p, therefore, without loss of generality, we further assume \(p = 1\).

Moving to the first two equalities in (9), we have

$$\ddot {W}(t) - {{\gamma }^{2}}W(t) = 0,\quad \dot {\Psi }(t) - {{\gamma }^{2}}\omega \Psi (t) = 0.$$

The solution of these equations has the form [23]

$$W(\tau ) = {{C}_{1}}{{e}^{{\gamma \tau }}} + {{C}_{2}}{{e}^{{ - \gamma \tau }}},\quad \Psi (\tau ) = C{{e}^{{{{\omega }^{2}}\gamma \tau }}}.$$

For the simultaneous fulfillment of these equalities, it is necessary to set ω = ±1/γ. However, one of the constants \({{C}_{1}}\) or \({{C}_{2}}\) must be zero, i.e.,

$$\omega = {{\gamma }^{{ - 1}}}\quad \Rightarrow \quad {{C}_{2}} = 0,\quad \gamma C = {{C}_{1}}\quad {\text{or}}\quad \omega = - {{\gamma }^{{ - 1}}}\quad \Rightarrow \quad {{C}_{1}} = 0,\quad \gamma C = - {{C}_{2}}.$$

We use the first chain of equalities. Substituting these values into (13), we obtain

$$\begin{gathered} {{\nu }_{l}} = \gamma {{{\tilde {A}}}_{l}},\quad {{{\tilde {A}}}_{3}} = - {{{\tilde {A}}}_{1}},\quad {{{\tilde {A}}}_{4}} = - {{{\tilde {A}}}_{2}}, \\ {{{\tilde {A}}}_{1}} = \sqrt {\frac{{\gamma D - 1 + \sqrt {{{{(\gamma D - 1)}}^{2}}{\kern 1pt} - 4\gamma (D - \alpha \Lambda )} }}{{2\gamma D}}} ,\quad {{{\tilde {A}}}_{2}} = \sqrt {\frac{{\gamma D - 1 - \sqrt {{{{(\gamma D - 1)}}^{2}} - 4\gamma (D - \alpha \Lambda )} }}{{2\gamma D}}} . \\ \end{gathered} $$

Thus, taking into account the properties of even and odd Bessel functions \({{J}_{\mu }}(z)\) and \({{Y}_{\mu }}(z)\), the general solution of system (10) is written as follows:

$$\begin{gathered} V(r) = \sum\limits_{j = 1}^2 {\left[ {V_{j}^{{(1)}}{{J}_{1}}(\gamma {{{\tilde {A}}}_{j}}r) + V_{j}^{{(2)}}{{Y}_{1}}(\gamma {{{\tilde {A}}}_{j}}r)} \right]} , \\ \Phi (r) = \sum\limits_{j = 1}^2 {\left[ {\Phi _{j}^{{(1)}}{{J}_{0}}(\gamma {{{\tilde {A}}}_{j}}r) + \Phi _{j}^{{(2)}}{{Y}_{0}}(\gamma {{{\tilde {A}}}_{j}}r)} \right]} . \\ \end{gathered} $$
(14)

The remaining constants \(V_{j}^{{(l)}}\) and \(\Phi _{j}^{{(l)}}\) are found from the boundary conditions. In this case, taking into account equalities (12)

$$\Phi _{j}^{{(l)}} = \frac{{{{\gamma }^{2}} - \nu _{j}^{2}}}{{{{\nu }_{j}}\alpha }}V_{j}^{{(l)}}.$$

In accordance with the problem statement, the functions in (14) must satisfy the following boundary conditions:

$${{\left. {\left( {V{\kern 1pt} '\; + V{\text{/}}r - \alpha \Phi } \right)} \right|}_{{r = {{R}_{1}}}}} = 0,\quad {{\left. {\left( {V{\kern 1pt} '\; + V{\text{/}}r - \alpha \Phi } \right)} \right|}_{{r = 1}}}{\kern 1pt} = 0,\quad {{\left. \Phi \right|}_{{r = {{R}_{1}}}}} = 0,\quad {{\left. \Phi \right|}_{{r = 1}}} = 0,$$
(15)

Substituting (14) into (15), we arrive at a system of linear algebraic equations with respect to \(V_{l}^{{(1)}}\) and \(V_{l}^{{(2)}}\):

$$\begin{gathered} \sum\limits_{l = 1}^2 {{{\varepsilon }_{l}}\left[ {V_{l}^{{(1)}}{{J}_{0}}({{\nu }_{l}}) + V_{l}^{{(2)}}{{Y}_{0}}({{\nu }_{l}})} \right]} = 0,\quad \sum\limits_{l = 1}^2 {({{\nu }_{l}} - {{\varepsilon }_{l}})\left[ {V_{l}^{{(1)}}{{J}_{0}}({{\nu }_{l}}) + V_{l}^{{(2)}}{{Y}_{0}}({{\nu }_{l}})} \right]} = 0, \\ \sum\limits_{l = 1}^2 {{{\varepsilon }_{l}}\left[ {V_{l}^{{(1)}}{{J}_{0}}({{\nu }_{l}}{{R}_{1}}) + V_{l}^{{(2)}}{{Y}_{0}}({{\nu }_{l}}{{R}_{1}})} \right]} = 0, \\ \sum\limits_{l = 1}^2 {({{\nu }_{l}} - {{\varepsilon }_{l}})\left[ {V_{l}^{{(1)}}{{J}_{0}}({{\nu }_{l}}{{R}_{1}}) + V_{l}^{{(2)}}{{Y}_{0}}({{\nu }_{l}}{{R}_{1}})} \right]} = 0,\quad {{\varepsilon }_{l}} = ({{\gamma }^{2}} - \nu _{l}^{2}){\text{/}}{{\nu }_{l}}. \\ \end{gathered} $$
(16)

The matrix of this system is reduced to the form

$$\left( {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&{{{Y}_{0}}({{\nu }_{2}}){\text{/}}{{J}_{0}}({{\nu }_{2}})} \\ 0&0&1&0 \\ 0&0&0&{{{Y}_{0}}({{\nu }_{2}}{{R}_{1}}){{J}_{0}}({{\nu }_{2}}) - {{Y}_{0}}({{\nu }_{2}}){{J}_{0}}({{\nu }_{2}}{{R}_{1}})} \end{array}} \right).$$

Hence it follows that the fulfillment of the following equality is a necessary condition for the existence of a nonzero solution to system (16):

$${{Y}_{0}}({{\lambda }_{n}}){{J}_{0}}({{\lambda }_{n}}{{R}_{1}}) - {{J}_{0}}({{\lambda }_{n}}){{Y}_{0}}({{\lambda }_{n}}{{R}_{1}}) = 0.$$

Then \(V_{1}^{{(1)}} = 0\) and \(V_{1}^{{(2)}} = 0\), and for the remaining unknowns

$$V_{2}^{{(1)}} = - \frac{{{{Y}_{0}}({{\nu }_{2}})}}{{{{J}_{0}}({{\nu }_{2}})}}V_{2}^{{(2)}},\quad V_{2}^{{(2)}} \in \mathbb{R}.$$

Substituting into (14), we obtain

$$\begin{gathered} V(r) = \sum\limits_{n = 1}^\infty {{{{v}}_{n}}{{\Psi }_{1}}({{\lambda }_{n}}r)} ,\quad {{\Psi }_{1}}({{\lambda }_{n}}r) = {{Y}_{0}}({{\lambda }_{n}}){{J}_{1}}({{\lambda }_{n}}r) - {{J}_{0}}({{\lambda }_{n}}){{Y}_{1}}({{\lambda }_{n}}r), \\ \Phi (r) = \sum\limits_{n = 1}^\infty {{{\varphi }_{n}}{{\Psi }_{0}}({{\lambda }_{n}}r)} ,\quad {{\Psi }_{0}}({{\lambda }_{n}}r) = {{Y}_{0}}({{\lambda }_{n}}){{J}_{0}}({{\lambda }_{n}}r) - {{J}_{0}}({{\lambda }_{n}}){{Y}_{0}}({{\lambda }_{n}}r), \\ \end{gathered} $$
(17)

where \({{\lambda }_{n}}\) are the roots of the equation

$${{\Psi }_{0}}({{\lambda }_{n}}{{R}_{1}}) = {{Y}_{0}}({{\lambda }_{n}}){{J}_{0}}({{\lambda }_{n}}{{R}_{1}}) - {{J}_{0}}({{\lambda }_{n}}){{Y}_{0}}({{\lambda }_{n}}{{R}_{1}}) = 0.$$
(18)

The constructions used remain valid in the case of more complex models for multicomponent media (\(N \geqslant 1\)) and taking into account the relaxation effects (\({{t}_{q}} \ne 0\)). For example, when \({{t}_{q}} \ne 0\) and N = 1, only the second equality in (9) changes, which is written as

$$\frac{{\dot {\Psi }(t) + {{t}_{q}}\ddot {\Psi }(t)}}{{\Psi (t)}} = {{\gamma }^{2}}\omega \quad (q = 1).$$

In this case, system (10) does not change and the representation of its solution in form (11) is preserved. Therefore, further in a similar way, we obtain the result in form (14), with the only difference that the coefficients \(\gamma {{\tilde {A}}_{j}}\) will differ from those obtained with \({{t}_{q}} = 0\) and N = 1. Thus, the solution of the Sturm–Liouville problem in this case also has form (17) and (18). The result obtained is generalized for N > 1.

4 REPRESENTATION OF SOLUTIONS AS SERIES IN EIGENFUNCTIONS

In accordance with the results obtained in the previous subsection, we consider the following series (\(\alpha = 0,\;1\)):

$$f(r) = \sum\limits_{n = 1}^\infty {{{f}_{n}}{{\Psi }_{\alpha }}({{\lambda }_{n}}r)} ,\quad {{f}_{n}} = \frac{1}{{{{{\left\| {{{\Psi }_{\alpha }}({{\lambda }_{n}}r)} \right\|}}^{2}}}}\int\limits_{{{R}_{1}}}^1 {rf(r){{\Psi }_{\alpha }}({{\lambda }_{n}}r)dr,} $$
(19)

where the quantities \({{\left\| {{{\Psi }_{\alpha }}({{\lambda }_{n}}r)} \right\|}^{2}}\) are defined in this way:

$${{\left\| {{{\Psi }_{\alpha }}({{\lambda }_{n}}r)} \right\|}^{2}} = \int\limits_{{{R}_{1}}}^1 {r{{\Psi }_{\alpha }}({{\lambda }_{n}}r){{\Psi }_{\alpha }}({{\lambda }_{n}}r)dr} .$$

Using the well-known equality [25]

$$\int {z{{Z}_{\nu }}(\lambda z){{S}_{\nu }}(\mu z)dz} = \frac{{\mu z{{Z}_{\nu }}(\lambda z){{S}_{{\nu - 1}}}(\mu z) - \lambda z{{Z}_{{\nu - 1}}}(\lambda z){{S}_{\nu }}(\mu z)}}{{{{\lambda }^{2}} - {{\mu }^{2}}}},$$

where any of the functions \({{J}_{\nu }}\) or \({{Y}_{\nu }}\) serve as \({{Z}_{\nu }}\) and \({{S}_{\nu }}\), and \(\lambda \) and \(\mu \) are arbitrary numbers, it is not difficult to obtain a similar relation for the functions introduced in the previous paragraph:

$$\int {r{{\Psi }_{\alpha }}(\lambda r){{\Psi }_{\alpha }}(\mu r)dr} = \frac{{\mu r{{\Psi }_{\alpha }}(\lambda r){{\Psi }_{{\alpha - 1}}}(\mu r) - \lambda r{{\Psi }_{{\alpha - 1}}}(\lambda r){{\Psi }_{\alpha }}(\mu r)}}{{{{\lambda }^{2}} - {{\mu }^{2}}}}.$$
(20)

We assume \(\lambda \) satisfies Eq. (18), i.e., \({{\Psi }_{0}}(\lambda {{R}_{1}}) = 0\). In this case, it follows from (17) that

$${{\Psi }_{0}}(\lambda ) = {{Y}_{0}}({{\lambda }_{n}}){{J}_{0}}({{\lambda }_{n}}) - {{J}_{0}}({{\lambda }_{n}}){{Y}_{0}}({{\lambda }_{n}}) \equiv 0.$$

Then, using equality (20) and following [24], we have

$$\int\limits_{{{R}_{1}}}^1 {r{{\Psi }_{1}}(\lambda r){{\Psi }_{1}}(\lambda r)dr} = \mathop {\lim }\limits_{\mu \to \lambda } \frac{{\mu {{R}_{1}}{{\Psi }_{1}}(\lambda {{R}_{1}}){{\Psi }_{0}}(\mu {{R}_{1}}) - \mu {{\Psi }_{1}}(\lambda ){{\Psi }_{0}}(\mu )}}{{{{\mu }^{2}} - {{\lambda }^{2}}}}$$
$$ = \mathop {\lim }\limits_{\mu \to \lambda } \frac{{{{R}_{1}}{{\Psi }_{1}}(\lambda {{R}_{1}}){{\Psi }_{0}}(\mu {{R}_{1}}) - {{\Psi }_{1}}(\lambda ){{\Psi }_{0}}(\mu ) + \mu R_{1}^{2}{{\Psi }_{1}}(\lambda {{R}_{1}})\Psi _{0}^{'}(\mu {{R}_{1}}) - \mu {{\Psi }_{1}}(\lambda ){{\Psi }_{0}}(\mu )}}{{2\mu }}$$
$$ = \frac{1}{2}\left[ {R_{1}^{2}{{\Psi }_{1}}(\lambda {{R}_{1}})\Psi _{0}^{'}(\lambda {{R}_{1}}) - {{\Psi }_{1}}(\lambda ){{\Psi }_{0}}(\lambda )} \right] = \frac{1}{2}{{\left[ {{{\Psi }_{1}}(\lambda )} \right]}^{2}} - \frac{{R_{1}^{2}}}{2}{{\left[ {{{\Psi }_{1}}(\lambda {{R}_{1}})} \right]}^{2}},$$

and likewise

$$\int\limits_{{{R}_{1}}}^1 {r{{\Psi }_{0}}(\lambda r){{\Psi }_{0}}(\lambda r)dr} = \frac{1}{2}{{\left[ {{{\Psi }_{1}}(\lambda )} \right]}^{2}} - \frac{{R_{1}^{2}}}{2}{{\left[ {{{\Psi }_{1}}(\lambda {{R}_{1}})} \right]}^{2}}.$$

Here, L’Hospital’s rule is used to calculate the limits.

Thus, we arrive at the following result:

$$\int\limits_{{{R}_{1}}}^1 {r{{\Psi }_{\alpha }}({{\lambda }_{n}}r){{\Psi }_{\alpha }}({{\lambda }_{k}}r)dr} = \left\{ \begin{gathered} 0,\quad n \ne k, \hfill \\ \Psi ({{\lambda }_{n}}),\quad k = n; \hfill \\ \end{gathered} \right.$$
(21)
$$\Psi ({{\lambda }_{n}}) = {{\left\| {{{\Psi }_{\alpha }}({{\lambda }_{n}}r)} \right\|}^{2}} = \frac{1}{2}{{\left[ {{{\Psi }_{1}}({{\lambda }_{n}})} \right]}^{2}} - \frac{{R_{1}^{2}}}{2}{{\left[ {{{\Psi }_{1}}({{\lambda }_{n}}{{R}_{1}})} \right]}^{2}}\quad (\alpha = 0,\;1),$$
(22)

which means that the functions \({{\Psi }_{\alpha }}({{\lambda }_{n}}r)\) are orthogonal on the interval \({{R}_{1}} \leqslant r \leqslant 1\) in the sense of the scalar product defined by the equality

$$(f,g) = \int\limits_{{{R}_{1}}}^1 {rf(r)g(r)dr} .$$

By analogy with the technique described in [20], the following formulas are proved for the transformation of the differential operators in Eq. (6):

$$\int\limits_{{{R}_{1}}}^1 {r\left( {G_{{1ml}}^{'}(r,\tau ) + {{{{G}_{{1ml}}}(r,\tau )} \mathord{\left/ {\vphantom {{{{G}_{{1ml}}}(r,\tau )} r}} \right. \kern-0em} r}} \right){{\Psi }_{0}}({{\lambda }_{n}}r)dr} = {{\lambda }_{n}}\Psi ({{\lambda }_{n}})G_{{1ml}}^{H}({{\lambda }_{n}},\tau );$$
(23)
$$\int\limits_{{{R}_{1}}}^1 {rG_{{q + 1,ml}}^{'}(r,\tau ){{\Psi }_{1}}({{\lambda }_{n}}r)dr} = \left. {r{{\Psi }_{1}}({{\lambda }_{n}}r){{G}_{{q + 1,ml}}}(r,\tau )} \right|_{{{{R}_{1}}}}^{1} - {{\lambda }_{n}}\Psi ({{\lambda }_{n}})G_{{q + 1,ml}}^{H}({{\lambda }_{n}},\tau );$$
(24)
$$\begin{gathered} \int\limits_{{{R}_{1}}}^1 {\left( {G_{{1ml}}^{{''}}(r,\tau ) + {{G_{{1ml}}^{'}(r,\tau )} \mathord{\left/ {\vphantom {{G_{{1ml}}^{'}(r,\tau )} r}} \right. \kern-0em} r} - {{{{{{{G}_{{1ml}}}(r,\tau )} \mathord{\left/ {\vphantom {{{{G}_{{1ml}}}(r,\tau )} r}} \right. \kern-0em} r}}}^{2}}} \right){{\Psi }_{1}}({{\lambda }_{n}}r)rdr} \\ = \left. {r\left( {G_{{1ml}}^{'}(r,\tau ) + {{{{G}_{{1ml}}}(r,\tau )} \mathord{\left/ {\vphantom {{{{G}_{{1ml}}}(r,\tau )} r}} \right. \kern-0em} r}} \right){{\Psi }_{1}}({{\lambda }_{n}}r)} \right|_{{{{R}_{1}}}}^{1} - \lambda _{n}^{2}\Psi ({{\lambda }_{n}})G_{{1ml}}^{H}({{\lambda }_{n}},\tau ); \\ \end{gathered} $$
(25)
$$\begin{gathered} \int\limits_{{{R}_{1}}}^1 {\left( {G_{{q + 1,ml}}^{{''}}(r,\tau ) + {{G_{{q + 1,ml}}^{'}(r,\tau )} \mathord{\left/ {\vphantom {{G_{{q + 1,ml}}^{'}(r,\tau )} r}} \right. \kern-0em} r}} \right){{\Psi }_{0}}({{\lambda }_{n}}r)rdr} \\ = \left. {{{\lambda }_{n}}r{{\Psi }_{1}}({{\lambda }_{n}}r){{G}_{{q + 1,ml}}}(r,\tau )} \right|_{{{{R}_{1}}}}^{1} - \lambda _{n}^{2}\Psi ({{\lambda }_{n}})G_{{q + 1,ml}}^{H}({{\lambda }_{n}},\tau ); \\ \end{gathered} $$
(26)
$$\begin{gathered} \int\limits_{{{R}_{1}}}^1 {\left( {G_{{1ml}}^{{'''}}(r,{\kern 1pt} \tau ) + {{2G_{{1ml}}^{{''}}(r,{\kern 1pt} \tau )} \mathord{\left/ {\vphantom {{2G_{{1ml}}^{{''}}(r,{\kern 1pt} \tau )} r}} \right. \kern-0em} r} - {{G_{{1ml}}^{'}(r,\tau )} \mathord{\left/ {\vphantom {{G_{{1ml}}^{'}(r,\tau )} {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}} + {{{{G}_{{1ml}}}(r,\tau )} \mathord{\left/ {\vphantom {{{{G}_{{1ml}}}(r,\tau )} {{{r}^{3}}}}} \right. \kern-0em} {{{r}^{3}}}}} \right){{\Psi }_{0}}({{\lambda }_{n}}r)rdr} \\ = {{\lambda }_{n}}\left. {r\left( {G_{{1ml}}^{'}(r,\tau ) + {{{{G}_{{1ml}}}(r,\tau )} \mathord{\left/ {\vphantom {{{{G}_{{1ml}}}(r,\tau )} r}} \right. \kern-0em} r}} \right){{\Psi }_{1}}({{\lambda }_{n}}r)} \right|_{{{{R}_{1}}}}^{1} - \lambda _{n}^{3}\Psi ({{\lambda }_{n}})G_{{1ml}}^{H}({{\lambda }_{n}},\tau ), \\ \end{gathered} $$
(27)

where

$$\begin{gathered} \left\{ \begin{gathered} {{G}_{{1ml}}}(r,\tau ) \\ {{G}_{{q + 1,ml}}}(r,\tau ) \\ \end{gathered} \right\} = \sum\limits_{n = 1}^\infty {\left\{ \begin{gathered} G_{{1ml}}^{H}\left( {{{\lambda }_{n}},\tau } \right){{\Psi }_{1}}\left( {{{\lambda }_{n}}r} \right) \\ G_{{q + 1,ml}}^{H}\left( {{{\lambda }_{n}},\tau } \right){{\Psi }_{0}}\left( {{{\lambda }_{n}}r} \right) \\ \end{gathered} \right\}} , \\ \left\{ \begin{gathered} G_{{1ml}}^{H}({{\lambda }_{n}},\tau ) \\ G_{{q + 1,ml}}^{H}({{\lambda }_{n}},\tau ) \\ \end{gathered} \right\} = \frac{1}{{\Psi ({{\lambda }_{n}})}}\int\limits_{{{R}_{1}}}^1 {r\left\{ \begin{gathered} {{G}_{{1ml}}}(r,\tau ){{\Psi }_{1}}({{\lambda }_{n}}r) \\ {{G}_{{q + 1,ml}}}(r,\tau ){{\Psi }_{0}}({{\lambda }_{n}}r) \\ \end{gathered} \right\}dr} , \\ {{\Psi }_{\alpha }}({{\lambda }_{n}}r) = {{Y}_{0}}({{\lambda }_{n}}{{R}_{2}}){{J}_{\alpha }}({{\lambda }_{n}}r) - {{J}_{0}}({{\lambda }_{n}}{{R}_{2}}){{Y}_{\alpha }}({{\lambda }_{n}}r)\quad (\alpha = 0,1). \\ \end{gathered} $$
(28)

5 ALGORITHM OF THE SOLUTION

As noted, the main problem (1) and (2) is solved in two stages. First, the Green functions for the auxiliary problem (1) and (4) are found. To do this, the Laplace transform in time is applied to problem (6) and (7), after which the desired functions are presented in the form of series (28). As a result, problem (6) and (7) using formulas (23)–(27) is reduced to a system of linear algebraic equations with respect to \(G_{{kml}}^{{LH}}({{\lambda }_{n}},s)\) (index \(L\) denotes the Laplace transform and \(s\) is the Laplace transform parameter):

$${{k}_{1}}({{\lambda }_{n}},s)G_{{1ml}}^{{LH}}({{\lambda }_{n}},s) - {{\lambda }_{n}}\sum\limits_{j = 1}^N {{{\alpha }_{j}}G_{{j + 1,ml}}^{{LH}}({{\lambda }_{n}},s)} = \frac{{{{\delta }_{{1m}}}}}{{\Psi ({{\lambda }_{n}})}}{{\Phi }_{l}}({{\lambda }_{n}}),$$
$$ - {{\Lambda }_{q}}\lambda _{n}^{3}G_{{1ml}}^{{LH}}({{\lambda }_{n}},s) + {{k}_{{q + 1}}}({{\lambda }_{n}},s)G_{{q + 1,ml}}^{{LH}}({{\lambda }_{n}},s)$$
$$ = - \frac{{{{\lambda }_{n}}{{\Lambda }_{q}}}}{{\Psi ({{\lambda }_{n}})}}\left( {{{\delta }_{{1m}}} + \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{\delta }_{{j + 1,m}}}} - \frac{{{{D}_{q}}}}{{{{\Lambda }_{q}}}}{{\delta }_{{q + 1,m}}}} \right){{\Phi }_{l}}({{\lambda }_{n}}),$$
(29)
$${{k}_{1}}({{\lambda }_{n}},s) = \lambda _{n}^{2} + {{s}^{2}},\quad {{k}_{{q + 1}}}({{\lambda }_{n}},s) = {{D}_{q}}\lambda _{n}^{2} + s + {{t}_{q}}{{s}^{2}},$$
$${{\Phi }_{l}}({{\lambda }_{n}}) = {{\Psi }_{1}}({{\lambda }_{n}}){{\delta }_{{1l}}} - {{R}_{1}}{{\Psi }_{1}}({{\lambda }_{n}}{{R}_{1}}){{\delta }_{{2l}}}.$$

The solution of system (29) is found by successive elimination of unknowns

$$\begin{gathered} G_{{q + 1,p + 1,l}}^{{LH}}({{\lambda }_{n}},s) = \frac{{{{P}_{{q + 1,p + 1,l}}}({{\lambda }_{n}},s)}}{{\Psi ({{\lambda }_{n}}){{Q}_{q}}({{\lambda }_{n}},s)}} - \frac{{{{\lambda }_{n}}({{\Lambda }_{q}}{{\alpha }_{p}} - {{D}_{q}}{{\delta }_{{pq}}}){{\Phi }_{l}}({{\lambda }_{n}})}}{{\Psi ({{\lambda }_{n}}){{k}_{{q + 1}}}({{\lambda }_{n}},s)}}, \\ \left\{ {\begin{array}{*{20}{c}} {G_{{11l}}^{{LH}}({{\lambda }_{n}},s)} \\ {G_{{1,q + 1,l}}^{{LH}}({{\lambda }_{n}},s)} \end{array}} \right\} = \frac{1}{{\Psi ({{\lambda }_{n}})P({{\lambda }_{n}},s)}}\left\{ {\begin{array}{*{20}{c}} {{{P}_{{11l}}}({{\lambda }_{n}},s)} \\ {{{P}_{{1,q + 1,l}}}({{\lambda }_{n}},s)} \end{array}} \right\}, \\ G_{{q + 1,1l}}^{{LH}}({{\lambda }_{n}},s) = \frac{{{{P}_{{q + 1,1l}}}({{\lambda }_{n}},s)}}{{\Psi ({{\lambda }_{n}}){{Q}_{q}}({{\lambda }_{n}},s)}} - \frac{{{{\lambda }_{n}}{{\Lambda }_{q}}{{\Phi }_{l}}({{\lambda }_{n}})}}{{\Psi ({{\lambda }_{n}}){{k}_{{q + 1}}}({{\lambda }_{n}},s)}}. \\ \end{gathered} $$
(30)

Here, \(P({{\lambda }_{n}},s)\), \({{P}_{{mkl}}}({{\lambda }_{n}},s)\), and \(Q({{\lambda }_{n}},s)\) are polynomials from s, which are defined as follows:

$$P({{\lambda }_{n}},s) = {{k}_{1}}({{\lambda }_{n}},s)\Pi ({{\lambda }_{n}},s) - \lambda _{n}^{4}{\kern 1pt} \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{\Lambda }_{j}}{{\Pi }_{j}}({{\lambda }_{n}},s)} ,\quad Q({{\lambda }_{n}},s) = {{k}_{{q + 1}}}({{\lambda }_{n}},s)P({{\lambda }_{n}},s),$$
$${{P}_{{11l}}}({{\lambda }_{n}},s) = - {{\Delta }_{l}}\left[ {\Pi ({{\lambda }_{n}},s) - \lambda _{n}^{2}{\kern 1pt} \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{\Lambda }_{j}}{{\Pi }_{j}}({{\lambda }_{n}},s)} } \right],$$
$${{P}_{{q + 1,kl}}}({{\lambda }_{n}},s) = - {{\Lambda }_{q}}\lambda _{n}^{3}{{P}_{{1kl}}}({{\lambda }_{n}},s),$$
$${{P}_{{1,q + 1,l}}}({{\lambda }_{n}},s) = - \lambda _{n}^{2}{{\alpha }_{q}}{{\Delta }_{l}}\left[ {{{D}_{q}}{{\Pi }_{q}}({{\lambda }_{n}},s) - \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{\Lambda }_{j}}{{\Pi }_{j}}({{\lambda }_{n}},s)} } \right],$$
$${{\Delta }_{{ln}}} = \left\{ \begin{gathered} - {{\Psi }_{1}}({{\lambda }_{n}}),\quad l = 1 \hfill \\ {{R}_{1}}{{\Psi }_{1}}({{\lambda }_{n}}{{R}_{1}}),\quad l = 2, \hfill \\ \end{gathered} \right.$$
$$\Pi ({{\lambda }_{n}},s) = \prod\limits_{j = 1}^N {{{k}_{{j + 1}}}({{\lambda }_{n}},s)} ,\quad {{\Pi }_{j}}({{\lambda }_{n}},s) = \prod\limits_{k = 1,k \ne j}^N {{{k}_{{k + 1}}}({{\lambda }_{n}},s)} .$$

The transition to the space of originals in formulas (30) is carried out with the help of residues and tables of operational calculus [25]

$$G_{{1kl}}^{H}({{\lambda }_{n}},\tau ) = \frac{1}{{\Psi ({{\lambda }_{n}})}}\sum\limits_{m = 1}^{2N + 2} {A_{{1kl}}^{{(m)}}} {{\operatorname{e} }^{{{{s}_{{mn}}}\tau }}},\quad A_{{1kl}}^{{(m)}} = \frac{{{{P}_{{1kl}}}({{\lambda }_{n}},{{s}_{{mn}}})}}{{P{\kern 1pt} '({{\lambda }_{n}},{{s}_{{mn}}})}},\quad A_{{q + 1,kl}}^{{(m)}} = \frac{{{{P}_{{q + 1,kl}}}({{\lambda }_{n}},{{s}_{{mn}}})}}{{Q{\kern 1pt} '({{\lambda }_{n}},{{s}_{{mn}}})}},$$
$$G_{{q + 1,1l}}^{H}({{\lambda }_{n}},\tau ) = \frac{1}{{\Psi ({{\lambda }_{n}})}}\left[ {\sum\limits_{j = 1}^2 {\frac{{{{\Delta }_{{ln}}}{{\lambda }_{n}}{{\Lambda }_{q}}{{\operatorname{e} }^{{{{\xi }_{{jqn}}}\tau }}}}}{{k_{{q + 1}}^{'}({{\lambda }_{n}},{{\xi }_{{jqn}}})}}} + \sum\limits_{m = 1}^{2N + 4} {A_{{q + 1,1l}}^{{(m)}}{{\operatorname{e} }^{{{{s}_{{mn}}}\tau }}}} } \right],$$
(31)
$$G_{{q{\kern 1pt} + 1,p + 1,l}}^{H}({{\lambda }_{n}},\tau ) = \frac{1}{{\Psi ({{\lambda }_{n}})}}\left[ {\sum\limits_{m = 1}^{2N + 4} {A_{{q + 1,p + 1,l}}^{{(m)}}{{{\text{e}}}^{{{{s}_{{mn}}}\tau }}}} + \sum\limits_{j = 1}^2 {\frac{{{{\Delta }_{{ln}}}{{\lambda }_{n}}({{\Lambda }_{q}}{{\alpha }_{p}} - {{D}_{q}}{{\delta }_{{pq}}}){{{\text{e}}}^{{{{\xi }_{{jqn}}}\tau }}}}}{{k_{{q + 1}}^{'}({{\lambda }_{n}},{{\xi }_{{jqn}}})}}} } \right],$$

where the prime denotes the derivative with respect to parameter \(s\), \({{s}_{{mn}}}\) are the zeros of the polynomial \(P({{\lambda }_{n}},s)\), and \({{\xi }_{{jqn}}}\) are the zeros of the polynomial \({{k}_{{q + 1}}}({{\lambda }_{n}},s)\) determined by the formulas

$${{\xi }_{{1qn}}} = \frac{{ - 1 - \sqrt {1 - 4{{t}_{q}}{{D}_{q}}\lambda _{n}^{2}} }}{{2{{t}_{q}}}},\quad {{\xi }_{{2qn}}} = \frac{{ - 1 + \sqrt {1 - 4{{t}_{q}}{{D}_{q}}\lambda _{n}^{2}} }}{{2{{t}_{q}}}}.$$

The solution of the auxiliary problem must satisfy the boundary conditions (2). Substituting (5) into (2) and integrating by parts in the terms containing \(f_{{1l}}^{*}\), we arrive at a system of equations connecting the right-hand sides of boundary conditions (2) and (4):

$$\int\limits_0^\tau {{{A}_{{11}}}(\tau - t)\frac{{\partial f_{{11}}^{*}(t)}}{{\partial t}}dt} + \int\limits_0^\tau {{{A}_{{12}}}(\tau - t)\frac{{\partial f_{{12}}^{*}(t)}}{{\partial t}}dt} = {{F}_{1}}(\tau ),\quad {{A}_{{ij}}}(\tau ) = {{\delta }_{{ij}}} + \int\limits_0^\tau {{{a}_{{ij}}}(\xi )} d\xi ,$$
$$\int\limits_0^\tau {{{A}_{{21}}}(\tau - t)\frac{{\partial f_{{11}}^{*}(t)}}{{\partial t}}dt} + \int\limits_0^\tau {{{A}_{{22}}}(\tau - t)\frac{{\partial f_{{12}}^{*}(t)}}{{\partial t}}dt} = {{F}_{2}}(\tau ),$$
$$\begin{gathered} {{a}_{{11}}}(\tau - t) = ({{c}_{{12}}} - 1){{G}_{{111}}}(1,\tau - t),\quad {{a}_{{12}}}(\tau - t) = ({{c}_{{12}}} - 1){{G}_{{112}}}(1,\tau - t), \\ {{a}_{{21}}}(\tau - t) = ({{c}_{{12}}} - 1){{G}_{{111}}}({{R}_{1}},\tau - t),\quad {{a}_{{22}}}(\tau - t) = ({{c}_{{12}}} - 1){{G}_{{112}}}({{R}_{1}},\tau - t), \\ \end{gathered} $$
(32)
$${{F}_{1}}(\tau ) = {{f}_{{11}}}(\tau ) - ({{c}_{{12}}} - 1)\sum\limits_{l = 1}^2 {\sum\limits_{m = 2}^{N + 1} {\int\limits_0^\tau {{{G}_{{1ml}}}(1,\tau - t){{f}_{{ml}}}(t)dt} } } ,$$
$${{F}_{2}}(\tau ) = {{f}_{{12}}}(\tau ) - \frac{{{{c}_{{12}}} - 1}}{{{{R}_{1}}}}\sum\limits_{l = 1}^2 {\sum\limits_{m = 2}^{N + 1} {\int\limits_0^\tau {{{G}_{{1ml}}}({{R}_{1}},\tau - t){{f}_{{ml}}}(t)dt} } } .$$

The numerical solution of system (32), found using the quadrature formula of the average rectangles, has the following form (\(h\) is the splitting step and \({{N}_{\tau }}\) is the number of split points):

$$\begin{gathered} y_{1}^{{(m - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}} = \frac{{{{b}_{1}}{\rm A}_{{22}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}} - {{b}_{2}}{\rm A}_{{12}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}}}{{{\rm A}_{{11}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}{\rm A}_{{22}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}} - {\rm A}_{{12}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}{\rm A}_{{21}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}}},\quad y_{2}^{{(m - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}} = \frac{{{{b}_{2}}{\rm A}_{{11}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}} - {{b}_{1}}{\rm A}_{{21}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}}}{{{\rm A}_{{11}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}{\rm A}_{{22}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}} - {\rm A}_{{12}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}{\rm A}_{{21}}^{{({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}}}, \\ y_{l}^{{(m)}}{\kern 1pt} = \frac{{\partial f_{{1l}}^{*}({{\tau }_{m}})}}{{\partial \tau }},\quad {\rm A}_{{ij}}^{{(m)}}{\kern 1pt} = {{A}_{{ij}}}({{\tau }_{m}}),\quad {{\tau }_{m}} = mh,\quad {{\tau }_{{m - 1/2}}} = \left( {m - \frac{1}{2}} \right)h\quad (m = \overline {0,{{N}_{\tau }}} ), \\ {{b}_{i}} = \frac{1}{h}\left( {{{\varphi }_{i}}({{\tau }_{m}}) - hS_{{i11}}^{{(m - 1/2)}} - hS_{{i22}}^{{(m - 1/2)}}} \right),\quad S_{{ijl}}^{{(m - 1/2)}} = \sum\limits_{k = 1}^{m - 1} {{\rm A}_{{ij}}^{{(m - k + 1/2)}}y_{l}^{{(k - 1/2)}}} . \\ \end{gathered} $$
(33)

Now the solution to the original problem (1) and (2) is obtained by numerically calculating the convolutions (5) of Green’s functions (31) with the functions determined by formulas (33):

$$\begin{gathered} u(r,{{\tau }_{i}}) = \sum\limits_{l = 1}^2 {\left[ {h\sum\limits_{m = 1}^i {G_{{11l}}^{*}(r,{{\tau }_{{i - m + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}})y_{l}^{{(m - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}} + \sum\limits_{m = 2}^{N + 1} {\int\limits_0^{{{\tau }_{i}}} {{{G}_{{1ml}}}(r,{{\tau }_{i}} - t){{f}_{{ml}}}(t)dt} } } \right]} , \\ {{\eta }_{q}}(r,{{\tau }_{i}}) = \sum\limits_{l = 1}^2 {\left[ {h\sum\limits_{m = 1}^i {G_{{q + 1,1l}}^{*}(r,{{\tau }_{{i - m + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}})y_{l}^{{(m - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}} + \sum\limits_{m = 2}^{N + 1} {\int\limits_0^\tau {{{G}_{{q + 1,ml}}}(r,{{\tau }_{i}} - t){{f}_{{ml}}}(t)dt} } } \right]} , \\ G_{{mkl}}^{*}(r,\tau ) = \int\limits_0^\tau {{{G}_{{mkl}}}(r,t)dt} . \\ \end{gathered} $$
(34)

6 CALCULATION EXAMPLE

As an example, we consider a three-component cylinder (N = 2, independent components zinc 1.0% and copper 4.5%, which diffuse into duralumin) [26]:

$${{C}_{{12}}} = 6.93 \times {{10}^{{10}}}\;{\text{N/}}{{{\text{m}}}^{2}},\quad {{C}_{{66}}} = 2.56 \times {{10}^{{10}}}\;{\text{N/}}{{{\text{m}}}^{2}},\quad {{T}_{0}} = 700\;{\text{K}},\quad \rho = 2700\;{\text{kg/}}{{{\text{m}}}^{3}},$$
$${{r}_{1}} = 0.7 \times {{10}^{{ - 3}}}\;{\text{m}},\quad \alpha _{1}^{{(1)}} = 6.55 \times {{10}^{7}}\;{\text{J/}}{{{\text{m}}}^{3}},\quad \alpha _{1}^{{(2)}} = 6.14 \times {{10}^{7}}\;{\text{J/}}{{{\text{m}}}^{3}},$$
$${{m}^{{(1)}}} = 0.065\;{\text{kg/mol}},\quad {{m}^{{(2)}}} = 0.064\;{\text{kg/mol}},$$
$$D_{1}^{{(1)}} = 2.62 \times {{10}^{{ - 12}}}\;{{{\text{m}}}^{2}}{\text{/s}},\quad D_{1}^{{(2)}} = 2.89 \times {{10}^{{ - 15}}}\;{{{\text{m}}}^{2}}{\text{/s}},\quad n_{0}^{{(1)}} = 0.01,\quad n_{0}^{{(2)}} = 0.045,\quad {{r}_{2}} = 0.1 \times {{10}^{{ - 2}}}\;{\text{m}}.$$

We assume for the calculation in the boundary conditions (2)

$${{f}_{{11}}}(\tau ) = {{f}_{{12}}}(\tau ) = H(\tau ),\quad {{f}_{{q + 1,1}}}(\tau ) = {{f}_{{q + 1,2}}}(\tau ) = 0.$$

By formulas (33) we calculate \(\partial f_{{1l}}^{*}{\text{/}}\partial \tau \) in the nodes \({{\tau }_{m}}\). Then we find a solution to the original problem using (34).

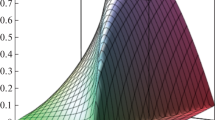
The calculation results are shown in Figs. 1–3. For the calculation, 20 terms of the Fourier series and \({{N}_{\tau }} = 40\) partition points in the numerical solution of Eqs. (32) are used. A further increase in these parameters by a factor of two leads to a result that differs from the result obtained by no more than 1%.

Fig. 1.
figure 1

Movements \(u(r,\tau )\).

Full size image
Fig. 2.
figure 2

Increment of zinc concentration \({{\eta }_{1}}(r,\tau )\).

Full size image
Fig. 3.
figure 3

Radial stresses \({{\sigma }_{r}}(r,\tau )\).

Full size image

Figure 1 shows the space-time distribution of the displacement field inside the cylinder. Figure 2 shows the change in the increase in the concentration of the first component (zinc), which is initiated by the mechanical loads applied to the surfaces of the cylinder.

The numerical calculations show that in the model under consideration, the effect of the mass transfer on the field of displacements and stresses is very small and the graphs of the solutions of the elastic-diffusion problem and the elastic problem (at \(\alpha _{1}^{{(q)}} = 0\)) are exactly the same.

This agrees with the results obtained earlier [27, 28], where it is noted that the effect of diffusion on the mechanical field begins to manifest itself as a small phase shift only after a certain time interval has elapsed, which is several orders of magnitude longer than the one considered here.

7 CONCLUSIONS

A model is proposed and an algorithm is developed for solving an unsteady problem for an orthotropic hollow multicomponent homogeneous cylinder under the action of a uniformly distributed external pressure. The interaction of mechanical and diffusion fields in a hollow orthotropic cylinder is studied on the example of a three-component material. The results obtained qualitatively coincide with the results of the experimental studies [29], where it is noted that the interaction of mechanical and diffusion fields begins to manifest itself most significantly only under plastic deformations and is insignificant in the region of elastic deformations.

However, it follows from formulas (31) that the magnitude of the diffusion field is directly proportional to the magnitude \({{\Lambda }_{q}}\), which in turn is proportional to the product αqDq; i.e., the greater the values of the diffusion coefficients Dq and diffusion constants αq, characterizing the volumetric change due to the mass transfer, the stronger the effect of field coupling is manifested. For most known alloys, these values do not differ much from those given in the calculation example. However, there are no fundamental restrictions on the possibility of creating materials that are more sensitive to mechanodiffusion effects. Thus, the proposed model makes it possible to study the interaction of physical fields in continuous media and evaluate the effect of the coupling of fields on the stress-strain state of structures and their individual elements.