1 MOROZOV–SOLOVYOV EQUATIONS FOR A PLASMA AT REST

For a plasma at rest (ions at rest), the general system of hydrodynamic equations for a two-component ideal plasma for the stationary case in the traditional notation looks like this [1–3]:

$$\operatorname{div} n{{{\mathbf{V}}}_{e}} = 0,\quad {{m}_{e}}n({{{\mathbf{V}}}_{e}},\nabla {{{\mathbf{V}}}_{e}}) = - \nabla {{p}_{e}} - en\left( {{\mathbf{E}} + \frac{1}{c}[{{{\mathbf{V}}}_{e}},{\mathbf{B}}]} \right),\quad 0 = - \nabla {{p}_{i}} + en{\mathbf{E}},$$
$$({{{\mathbf{V}}}_{e}},{{s}_{e}}) = 0,\quad {{p}_{e}} = p{}_{e}(n,{{s}_{e}}),\quad {{p}_{i}} = p{}_{i}(n),$$
$$\operatorname{curl} {\mathbf{B}} = - \frac{{4\pi }}{c}en{{{\mathbf{V}}}_{e}},\quad \operatorname{div} {\mathbf{B}} = 0,\quad {\mathbf{E}} = - \nabla \Phi .$$

Here \(e,\;{{m}_{e}},\;n\), and \({{{\mathbf{V}}}_{e}}\) are the charge, mass, density, and electron velocity; E and B are the electric and magnetic fields; \({{p}_{e}}\) and \({{p}_{i}}\) are the pressure of electrons and ions, respectively.

Under the conditions of axial symmetry, this system can be written in a more comprehensible form by introducing two flow functions [1, 2]. For this, two functions are introduced in the standard way: the flux function \(\Psi (r,z)\) and the full current function \(J(r,z)\):

$${{B}_{r}} = - \frac{1}{{2\pi r}}\frac{{\partial \Psi }}{{\partial z}},\quad {{B}_{z}} = \frac{1}{{2\pi r}}\frac{{\partial \Psi }}{{\partial r}},\quad {{B}_{\varphi }} = - \frac{{2J}}{{cr}},$$
$${{j}_{r}} = - \frac{1}{{2\pi r}}\frac{{\partial J}}{{\partial z}},\quad {{j}_{z}} = \frac{1}{{2\pi r}}\frac{{\partial J}}{{\partial r}},\quad {{j}_{\varphi }} = - \frac{c}{{8{{\pi }^{2}}r}}\Delta {\kern 1pt} ^*{\kern 1pt} \Psi ,{\text{ }}$$
$$\Delta {\kern 1pt} ^*{\kern 1pt} \Psi = \frac{{{{\partial }^{2}}\Psi }}{{\partial {{r}^{2}}}} - \frac{1}{r}\frac{{\partial \Psi }}{{\partial r}} + \frac{{{{\partial }^{2}}\Psi }}{{\partial {{z}^{2}}}}.$$

Due to the symmetry conditions, we have the integrals of motion:

$$F(J) = ({{m}_{e}}{\text{/}}2){\mathbf{V}}_{e}^{2} - e\Phi + {{m}_{e}}{{W}_{e}}$$
(1)

—energy integral (Bernoulli integral) of electrons (no dissipation),

$$K(J) = r{{m}_{e}}{{V}_{{e,\varphi }}} - \frac{1}{{2\pi }}\frac{e}{c}(\Psi + \pi {{r}^{2}}{{H}_{z}})$$
(2)

—and integral of the angular momentum of electrons (axial symmetry). Here \({{H}_{z}} = \operatorname{const} \) is the longitudinal magnetic field (it appears if an external field is added to the equations of motion \({\mathbf{H}} = (0,0,{{H}_{z}})\)).

In these terms, the Morozov–Solovyov equations (MS equations) have the form

$$\begin{gathered} \frac{{c{{m}_{e}}}}{{8{{\pi }^{2}}e}}\Delta {\kern 1pt} ^*{\kern 1pt} \Psi - n\left[ {\frac{1}{{2\pi }}\frac{e}{c}(\Psi + \pi {{r}^{2}}{{H}_{z}}) + K(J)} \right] = 0, \\ \frac{{{{m}_{e}}}}{{4{{\pi }^{2}}{{e}^{2}}}}\left[ {\frac{\partial }{{\partial z}}\left( {\frac{1}{{rn}}\frac{{\partial J}}{{\partial z}}} \right) + \frac{\partial }{{\partial r}}\left( {\frac{1}{{rn}}\frac{{\partial J}}{{\partial r}}} \right)} \right] \\ = \frac{1}{{\pi {{c}^{2}}}}\frac{J}{r} + rn\left( {\frac{{dF}}{{dJ}} - {{m}_{e}}{{T}_{e}}\frac{{d{{s}_{e}}}}{{dJ}}} \right) + \frac{{{{j}_{\varphi }}}}{e}\frac{{dK}}{{dJ}}. \\ \end{gathered} $$
(3)

Thus, the solution of the equations of stationary configurations depends on three arbitrary functions \(K(J),F(J)\), and \({{s}_{e}}(J)\) (where \({{s}_{e}}(J)\) is the entropy of electrons).

For the case of ideal electron and ion gases (we consider the constant polytropes \(\gamma \) to be equal for electrons and ions), we have

$${{W}_{e}}(n,J) = \frac{\gamma }{{(\gamma - 1){{m}_{e}}}}{\kern 1pt} {{G}_{e}}(J){{n}^{{\gamma - 1}}},\quad {{W}_{i}}(n) = \frac{\gamma }{{(\gamma - 1){{m}_{i}}}}{{G}_{i}}{{n}^{{\gamma - 1}}},\quad {{G}_{i}} = \operatorname{const} .$$
(4)

Bernoulli’s law (1) gives an algebraic equation for finding the concentration. If (for simplicity \(\gamma = 3\)), this equation becomes biquadratic and we obtain an explicit expression for the concentration:

$$\begin{gathered} {{n}^{2}} = \frac{{Q \pm {{{\left( {{{Q}^{2}} - \frac{{3{{m}_{e}}}}{{4{{\pi }^{2}}{{e}^{2}}{{r}^{2}}}}({{G}_{i}} + {{G}_{e}}(J)){{{(\nabla J)}}^{2}}} \right)}}^{{1/2}}}}}{{3({{G}_{i}} + {{G}_{e}}(J))}}, \\ Q = F(J) - \frac{1}{{2{{m}_{e}}{{r}^{2}}}}{{\left( {\frac{1}{{2\pi }}\frac{e}{c}\Psi + K + \frac{{{{r}^{2}}}}{2}\frac{e}{c}{{H}_{z}}} \right)}^{2}}. \\ \end{gathered} $$
(5)

Thus, the MS equations (in contrast to the Grad–Shafranov equation) make it possible to determine the absolute values of the density of the confining plasma. It was shown in [4] that in the range of parameters corresponding to the + sign (dense plasma), the system is elliptical, and for the sign − (rarefied plasma) it is hyperbolic. We will consider here only the elliptical case: the + sign in formula (5).

In [5, 6], an original approach to study the equilibrium flows of a plasma containing several types of particles, and in particular, a two-component (electrons and ions) plasma, was proposed. This approach is used to study equilibrium configurations in systems with a reversed field (RF) and in compact tori (spheromak). The approach proposed by  Morozov and Solovyov, can also be used to study such systems.

2 BOUNDARY VALUE PROBLEM FOR A TOROIDAL TRAP

We consider an axisymmetric toroidal chamber with an elongated Z cross-section shape. This area was obtained as follows: in the plane \((r,z)\), an isosceles triangle is built, with the apex at the point \(({{r}_{{\max }}},0)\) and base parallel to the z axis passing through the point \(({{r}_{{\min }}},0)\). Then three internal angles of the triangle are smoothed by arcs of circles, whose centers lie on the bisectors of the same angles.

The following conditions are imposed on the boundary of the region:

$$J \equiv {{J}_{0}},\quad \Psi \equiv {{\Psi }_{0}}.$$
(6)

The value of J0 is equal to the current in the external toroidal winding. Value Ψ0 is equal to the magnetic field flux through the central hole of the torus. The lines \(J = \operatorname{const} \) are electron streamlines in the plane \((r,z)\). The lines Ψ = const are the magnetic field lines in the plane \((r,z)\). For the convenience of the numerical solution, we will use new units of measurement, using the characteristic physical parameters included in the formulation of the problem. The unit of length will be the distance between the z axis and chamber \({{L}_{0}}\). The magnetic field will be measured in units \({{B}_{0}} = 2{{J}_{0}}{\kern 1pt} /{\kern 1pt} c{{L}_{0}}\). The units of density and temperature are formed from the known characteristic values of the given functions \(F(J) = {{F}_{0}}f(J{\kern 1pt} /{\kern 1pt} {{J}_{0}})\), \({{G}_{e}}(J)\) = \({{G}_{{e0}}}g(J{\kern 1pt} /{\kern 1pt} {{J}_{0}})\), \(K(J) = {{K}_{0}}k(J{\text{/}}{{J}_{0}})\), i.e.,

$${{T}_{{e0}}} = {{F}_{0}}{\text{/}}{{k}_{{\text{B}}}},\quad n_{0}^{2} = {{k}_{{\text{B}}}}{{T}_{{e0}}}{\text{/}}{{G}_{{e0}}},\quad {{T}_{{i0}}} = n_{0}^{2}{{G}_{{i0}}}{\text{/}}{{k}_{{\text{B}}}},$$

where \({{k}_{{\text{B}}}}\) is Boltzmann’s constant.

In the new units, conditions (6) take the form

$$J = 1,\quad \Psi = {{{{B}_{{p0}}}} \mathord{\left/ {\vphantom {{{{B}_{{p0}}}} {{{B}_{0}}}}} \right. \kern-0em} {{{B}_{0}}}} = \delta ,\quad {{B}_{{p0}}} = {{{{\Psi }_{0}}} \mathord{\left/ {\vphantom {{{{\Psi }_{0}}} {(2\pi L_{0}^{2})}}} \right. \kern-0em} {(2\pi L_{0}^{2})}},$$
(7)

and relations (1) and (2) will be written in the following form:

$$f(J) = \frac{{{{\xi }^{2}}}}{\beta }\frac{{{{{\mathbf{j}}}^{2}}}}{{{{n}^{2}}}} + \frac{3}{2}(\eta + g(J)){{n}^{2}},\;\;{\text{the Bernoulli integral}},$$
(8)
$$\alpha k(J) = - {{\xi }^{2}}\frac{{r{{j}_{\varphi }}}}{n} - \Psi - \frac{{{{r}^{2}}}}{2}{{h}_{z}} = 0,\;\;{\text{the moment integral}},$$
(9)

and the MS equations (3) (\(\Psi = rA\))

$$\begin{gathered} {{\xi }^{2}}\left( {\frac{{{{\partial }^{2}}A}}{{\partial {{z}^{2}}}} + \frac{\partial }{{\partial r}}\left( {\frac{1}{r}\frac{{\partial rA}}{{\partial r}}} \right)} \right) = \frac{n}{r}\left( {rA + \alpha k(J) + \frac{{{{r}^{2}}}}{2}{{h}_{z}}} \right), \\ {{\xi }^{2}}\left[ {\frac{\partial }{{\partial z}}\left( {\frac{1}{{rn}}\frac{{\partial J}}{{\partial z}}} \right) + \frac{\partial }{{\partial r}}\left( {\frac{1}{{rn}}\frac{{\partial J}}{{\partial r}}} \right)} \right] - \frac{J}{r} = \frac{\beta }{2}rn\left( {\frac{{df}}{{dJ}} - \frac{1}{2}{{n}^{2}}\frac{{dg(J)}}{{dJ}}} \right) + \alpha {{j}_{\varphi }}\frac{{dk}}{{dJ}}. \\ \end{gathered} $$
(10)

The formula for density (5)

$$\begin{gathered} q = f(J) - \frac{1}{{{{\xi }^{2}}\beta {{r}^{2}}}}{{\left( {\Psi + \alpha k(J) + \frac{{{{r}^{2}}}}{2}{{h}_{z}}} \right)}^{2}}, \\ {{n}^{2}} = \frac{{q + \sqrt {{{q}^{2}} - 6\frac{{{{\xi }^{2}}}}{{\beta {{r}^{2}}}}(\eta + g(J)){{{(\nabla J)}}^{2}}} }}{{3(\eta + g(J))}}. \\ \end{gathered} $$
(11)

The following dimensionless parameters appeared in the problem:

$$\begin{gathered} {{\xi }^{2}} = \frac{{{{c}^{2}}{{m}_{e}}{{m}_{i}}}}{{4\pi {{e}^{2}}L_{0}^{2}{{n}_{0}}({{m}_{e}} + {{m}_{i}})}} = \frac{{{{c}^{2}}{{m}_{e}}}}{{4\pi {{e}^{2}}L_{0}^{2}{{n}_{0}}}},\quad \beta = \frac{{8\pi {{k}_{B}}{{n}_{0}}{{T}_{{e0}}}}}{{B_{0}^{2}}},\quad \eta = \frac{{{{T}_{{i0}}}}}{{{{T}_{{e0}}}}}, \\ \alpha = \frac{{{{c}^{2}}{{K}_{0}}}}{{2e{{L}_{0}}{{J}_{0}}}} = \frac{c}{e}\frac{{{{K}_{0}}}}{{{{B}_{0}}L_{0}^{2}}},\quad \delta = \frac{{{{B}_{{p0}}}}}{{{{B}_{0}}}},\quad {{h}_{z}} = \frac{{{{H}_{z}}}}{{{{B}_{0}}}}. \\ \end{gathered} $$
(12)

Among the dimensionless parameters, the parameter \({{\xi }^{2}}\) is particularly important. It was shown in [4] that the Grad–Shafranov equation is obtained from the MS equations in the limit \({{\xi }^{2}} \ll 1\). However, since this parameter is included singularly (it occurs at higher derivatives), the Grad–Shafranov equations are not only a limiting case but also a degenerate case of the MS equations. It is important to note that the small parameter \(\mu = {{m}_{e}}{\text{/}}{{m}_{i}}\) is not included in the problem at all.

It is easy to obtain the necessary condition for the existence of a solution to a boundary value problem for the MS equations. For the density to be positive, it is necessary for value q in (11) to be always positive. However, it is known and easy to calculate it at any point on the boundary of the region: for example, at the point \(({{r}_{{\min }}},0)\). Then we get

$${{\xi }^{2}}\beta > {{(\alpha + \delta + (r_{{\min }}^{2}{\text{/}}2){{h}_{z}})}^{2}}{\text{/}}r_{{\min }}^{2},$$
(13)

a very easily verifiable necessary condition for the existence of a solution to a boundary value problem. In the real existing traps, the parameter \({{\xi }^{2}}\) takes on a rather small value. In this case, it can be seen that, other things being equal, it is more difficult to satisfy this condition the smaller \({{r}_{{\min }}}\), i.e., the smaller the distance from the chamber to the z axis.

The following dependences for the function-parameters were used in the calculations:

$$f(J) \equiv 1 + {{d}_{f}}{{(1 - J)}^{2}},\quad g(J) \equiv 1 + {{d}_{g}}{{(1 - J)}^{2}},\quad k(J) = 1 + {{d}_{k}}{{(1 - J)}^{2}}.$$
(14)

What these three functions can be in real systems remains an open question.

In [7], calculations were carried out for a classical chamber with a circular cross section and with constant function parameters \({{d}_{f}} = {{d}_{g}} = {{d}_{k}} = 0\). In this case, the right side of the second of equations (10) is identically equal to zero. Here we consider a more general case (14). By changing the signs and values of coefficients (14) (in this case, of course, the conditions \(f(J) > 0\), \(g(J) > 0\)) it is possible to qualitatively simulate all significantly different cases of the behavior of these functions.

3 NUMERICAL RESULTS

The boundary value problem (6) and (10) is a complex nonlinear problem for an elliptic system of second-order equations. It contains many numeric parameters (12) and three parameter functions \(f(J)\), \(g(J)\), and \(k(J)\).

The parameters of the existing (and those that had existed) toroidal magnetic traps (geometric dimensions, fields, and currents) can vary greatly. There are numerous theoretical and experimental studies on them [8, 9]. In this study, no precise reference to a particular facility or its parameters was made, although the main geometrical parameters correspond to the two operating JET and JT60 tokamaks [7]. The main aim of the calculations is (as in [7]) the desire to make sure that the complete MS equations (10) have solutions in which plasma is confined; i.e., such solutions in which the plasma pressure is maximum in the central region of the chamber and takes much lower values near its entire boundary.

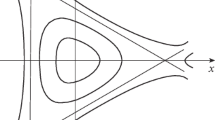
The main desired functions are the functions \(J\) and \(\Psi \). Figure 1 shows the lines of the function level \(J(r,z)\), \(\Psi (r,z)\), and \({{P}_{e}}(r,z)\), as well as the electric field in the plane \((r,z)\) at

$$\begin{gathered} {{\xi }^{2}} = 0.02,\quad \beta = 126,\quad \alpha = 1,\quad \delta = 0.06,\quad \eta = 0.05,\quad {{h}_{z}} = 1.5, \\ {{d}_{f}} = 2.0,\quad {{d}_{g}} = 2.25,\quad {{d}_{k}} = 2.5. \\ \end{gathered} $$
(15)
Fig. 1.
figure 1

Distribution over the chamber cross section: (a) total current functions J(r, z), (b) magnetic flux functions Ψ(r, z), (c) pressure Pe(r, z), (d) poloidal electric field.

Full size image

All values of the calculation parameters (15), except for the values df, dg, and dk, do not change further. Since ξ2 is sufficiently small, the pattern of the level lines \(\Psi \) is close to the level lines \({{P}_{e}}\). There is a well-defined area of increased pressure (hence, temperature and density). At the boundary of the chamber, the pressure is lower by a factor of about 20 than the pressure in the central part. The electric field has a potential well in the center and keeps the ions. Figure 2 shows the patterns of the distribution of the toroidal components of the magnetic field \({{B}_{\varphi }}\) and current \({{j}_{\varphi }}\).

Fig. 2.
figure 2

(a) Azimuth magnetic field level lines Bφ; (b) azimuthal electric current jφ; (c) pressure distribution \({{P}_{e}}(r,z)\) at z = 0; (d) distribution \({{\beta }_{{{\text{loc}}}}} = 8\pi {{P}_{e}}(r,z){\text{/}}{{B}_{\varphi }}(r,z)\) at z = 0.

Full size image

The field decreases with distance from the axis, and the current (in absolute value) is maximum at the center and sharply decreases towards the chamber’s boundaries. Figure 2c shows a one-dimensional graph of the pressure changes in the middle section of the chamber (z = 0) and the graph of the local value of \({{\beta }_{{{\text{loc}}}}} = 8\pi {{P}_{e}}{\text{/}}B_{\varphi }^{2}\). In the area of compression, \({{\beta }_{{{\text{loc}}}}} \approx 10\), and on the border, \({{\beta }_{{{\text{loc}}}}} \leqslant 0.1\). Thus, a set of parameters is indicated for which the solution of the MS equations has a canonical form.

This picture is not always available. For example, we will show two variants of calculations, when the overall picture of the solution looks different. Figures 3a and 3b show the level lines \(J(r,z)\) and \(\Psi (r,z)\) at \({{d}_{f}} = 0\), \({{d}_{g}} = 0.5\), and \({{d}_{k}} = 0.3\).

Fig. 3.
figure 3

Distribution over the chamber cross section: (a) total current functions \(J(r,z)\), (b) magnetic flux functions \(\Psi (r,z)\) at \({{d}_{f}} = 0\), \({{d}_{g}} = 0.5\), \({{d}_{k}} = 0.3\). Chamber cross section distribution: (c) total current functions \(J(r,z)\), (d) magnetic flux functions \(\Psi (r,z)\) at \({{d}_{f}} = 0\), \({{d}_{g}} = 2.5\), \({{d}_{k}} = - 0.2\).

Full size image

The pattern of electron current lines has changed significantly, while the picture of the magnetic field has not changed qualitatively. Figures 3c and 3d show the level lines \(J(r,z)\) and \(\Psi (r,z)\) at \({{d}_{f}} = 0\), \({{d}_{g}} = 2.5\), and \({{d}_{k}} = - 0.2\). The pattern of electron streamlines has become even more complex. However, note that the pressure distribution in these two cases remained close to the previous one and the plasma compression is again of the order of 20.

The numerical solution of the problem was carried out by the second-order finite element method on a triangular grid. Triangulation was carried out using the AFM method (moving front method). The corresponding linear problems were solved either by the minimum discrepancy method or by the conjugate gradient method.

4 CONCLUSIONS

This paper presents a brief derivation of the MS equations for a plasma with ions at rest and presents the first results of a numerical study of a boundary value problem for toroidal traps with an elongated Z cross section shape. For the first time, the MS equations are used in their most general form. The parameters of the problem are indicated for which the solutions of these equations give a physically well-interpreted picture of the distribution of the main quantities. More complex cases of electron component flows are briefly considered. The main conclusion drawn is that the MS equations provide much more information about the properties of equilibrium configurations than the Grad–Shafranov equation; thus, these equations can be used to obtain new, interesting results in the study of equilibrium configurations in various plasma traps.