INTRODUCTION

In research papers on various programs of controlled nuclear fusion (CNF), considerable attention has been drawn to studies of the confinement of a dense and hot plasma by the magnetic field. The aim of the study is to specify the physical conditions under which plasma configurations, which are not in contact with the case and elements of its design confining the trap, may exist for the time necessary for a theoretically possible synthesis reaction. This time far exceeds the characteristic times of fast plasma processes; therefore, the desired configuration of the plasma and magnetic field can be considered to be in equilibrium. Our paper refers to a series of works on the mathematical simulation of the equilibrium magnetoplasma configurations in the approximation of continuum mechanics, i.e., magnetic gas dynamics.

In plasma facilities involved in CNF, the toroidal-shaped traps are widespread in which the ends of the plasma column are closed on each other and are thus free from the need to contact any details. These include the well-known tokamak and stellarator, as well as traps in which conductors with the electric current producing a magnetic “skeleton” of the configuration are immersed inside the plasma volume but not in contact with it. These traps were proposed by A.I. Morozov and were called Galatheas [1]. The studies of plasma and field configurations in the traps, strictly speaking, should take into account their geometry, i.e., in this case, the toroidal one. However, this significantly complicates the mathematical apparatus used. Suffice it to say that in axisymmetric problems in a circular torus, the natural coordinates are polar coordinates in the \((z,r)\) plane centered on the magnetic axis of the torus. The corresponding problems are discussed in some approximations in [2]. The simplified theoretical studies of the toroidal configurations are based on replacing them with cylindrical analogues, i.e., with tori with an infinite radius, which is acceptable for solving basic qualitative problems about the properties of equilibrium configurations and their stability. We can get acquainted with the state of the art in the field with examples of configurations in Z-pinches, cylinders with a helical field, etc., e.g., with the help of reviews [3–6] with a bibliography of the works of the corresponding period. Among the recent theoretical and computational works related mainly to tokamaks, we can name, e.g., the articles [7–9] and the sources cited there. The simplest example of a Galathea trap is a Galathea Belt [10]. Numerical models and calculations of equilibrium configurations in it are studied in detail in an analog straightened into a cylinder [11]. The mathematical model of the toroidal configuration in the “Belt” and the first results of the calculations and their comparison with the cylindrical version of the trap are presented in [12, 13].

In this paper, the Belt model is refined toward a more visual interpretation of the results. In addition, an attempt was made to address the issue of differences in the equilibrium configurations in a cylinder and torus in a more general form, avoiding specific details of the Belt and even the entire class of Galathea traps. For this purpose, the simplest and most well-known example of a trap was chosen, a plasma cylinder with a current (Z-pinch) and its toroidal version, which actually underlies the modern tokamaks. Plasma configurations in a cylinder of a circular cross section are one-dimensional and differ in the variants of a given distribution of the electric current density along the radius. The configurations in the torus at any cross section can have only axial symmetry; i.e., they are two-dimensional. For simplicity, it is more convenient to consider them in square sections in order to remain in the system of cylindrical coordinates \((z,r)\) without introducing the more complex ones mentioned above. For this reason, we considered an intermediate instance, a straight cylinder of a square cross section with two-dimensional plasma and field configurations in it. As a result of the calculations, the geometrical forms of the configurations deformed on bending to the torus were obtained for two series of the current distributions in the Z-pinch that characterize their quantitative parameters. All the studied configuration variants solve the boundary value problems with a two-dimensional Grad-Shafranov equation [2, 14, 15]. The numerical solutions are obtained by an iterative relaxation method and, in this sense, are diffusionally stable, which is in a way associated with the traditionally understood MHD stability according to [16–18]. The Galathea-Belt calculations showed that the cylindrical configurations are more stable than toroidal ones; i.e., at the same current value in the conductors, the magnetic field in the cylinder is able to hold the plasma with the higher pressure values.

1 MATHEMATICAL EQUILIBRIUM MODELS

Mathematical models of plasma configurations held by a magnetic field in a state of equilibrium deal with the distribution of three quantities in the studied region of space: pressure p, magnetic field strength H, and electric current density j. In general, they should satisfy the three plasma statics equations [2, 17, 18]:

$$\nabla p = \frac{1}{c}{\mathbf{j}} \times {\mathbf{H}},\,\,\,\,\frac{c}{{4\pi }}{\mathbf{j}} = {\text{rot}}{\mathbf{H}},\,\,\,\,{\text{div}}{\mathbf{H}} = 0.$$
((1.1))

In the two-dimensional models of the configurations with symmetry, they are reduced to a single scalar equation for the magnetic flux function. In studies of axisymmetric \(\left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial \varphi }}} \right. \kern-0em} {\partial \varphi }} \equiv 0} \right)\) configurations, it is called the Grad-Shafranov equation [2, 6, 7, 14–18]

$$\Delta {\text{*}}\Psi + 4\pi {{r}^{2}}\frac{{dp}}{{d{\kern 1pt} {\Psi }}} + {{\left( {\frac{{4\pi }}{c}} \right)}^{2}}I\frac{{dI}}{{d{\Psi }}} = 0,$$
((1.2))

where \(\Delta {\text{*}}\Psi = r\frac{\partial }{{\partial r}}\left( {\frac{1}{r}\frac{{\partial \Psi }}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}\Psi }}{{\partial {{z}^{2}}}}\), \({{H}_{r}} = - \frac{1}{r}\frac{{\partial \Psi }}{{\partial z}}\), \({{H}_{z}} = \frac{1}{r}\frac{{\partial \Psi }}{{\partial r}}\), \(I = \frac{c}{{4\pi }}r{{H}_{\varphi }}\).

Its planar variety corresponds to the cylindrical coordinates with planar symmetry \(\left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0em} {\partial z}} \equiv 0} \right)\)

$$\Delta \Psi + 4\pi \frac{{dp}}{{d{\kern 1pt} {\Psi }}} + {{\left( {\frac{{4\pi }}{c}} \right)}^{2}}I\frac{{dI}}{{d{\Psi }}} = 0,$$
((1.3))

where \({{H}_{x}} = \frac{{\partial \Psi }}{{\partial y}}\), \({{H}_{y}} = - \frac{{\partial \Psi }}{{\partial x}}\), \(I = \frac{c}{{4\pi }}{{H}_{z}}\).

A model of a specific configuration is produced by solving a boundary value problem with one of these equations in a given region with the given boundary conditions. In addition, two \(p({\Psi })\) and \(I({\Psi })\) functions are required, which describe the pressure and poloidal electric current distribution between magnetic surfaces Ψ = const, corresponding to the assumed or desired information about the studied configuration.

Together with the toroidal and cylindrical traps, in which the plasma and field equilibrium is described by two-dimensional Eqs. (1.2) and (1.3), the simplest form of the trap, the Z-pinch, is considered, i.e., a circular cylinder with the axial current jz and the azimuthal magnetic field Hφ uniform in coordinates \((z,\varphi )\) [4]. The configurations in it are one-dimensional, and Eqs. (1.1) in polar coordinates have the form

$$\frac{{dp}}{{dr}} = - \frac{1}{c}jH;\,\,\,\,j = \frac{c}{{4\pi }}\frac{{dHr}}{{rdr}},$$
((1.4))

where \(H = {{H}_{\varphi }}\), \(~j = {{j}_{z}}\). By setting one of the unknown functions, e.g., j = j(r), it is easy to obtain the remaining two ones by integrating Eqs. (1.4). The need for the Grad-Shafranov equation is eliminated here, but formally it is valid in the form

$$\frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{d\Psi }}{{dr}}} \right) + 4\pi \frac{{dp}}{{d{\Psi }}} = 0,$$
((1.5))

since \(I({\Psi }) \equiv 0\). The magnetic flux function Ψ and the dependence \(p({\Psi })\) are associated with the solution of Eqs. (1.4) by the obvious relation (see Section 2 for details)

$$H = - \frac{{d{\Psi }}}{{dr}};\,\,\,\,\frac{{dp}}{{d{\Psi }}} = {{\frac{{dp}}{{dr}}} \mathord{\left/ {\vphantom {{\frac{{dp}}{{dr}}} {\frac{{d{\kern 1pt} {\Psi }}}{{dr}}}}} \right. \kern-0em} {\frac{{d{\kern 1pt} {\Psi }}}{{dr}}}} = {{ - \frac{{dp}}{{dr}}} \mathord{\left/ {\vphantom {{ - \frac{{dp}}{{dr}}} {H(r)}}} \right. \kern-0em} {H(r)}}.$$
((1.6))

It is easier and more convenient to compare the equilibrium plasma configurations in the Z-pinch and its toroidal analog by the example of a straight column and torus with a square cross section, since it would be natural to move from cylindrical coordinates to a circular cross section of a torus (z, r) to polar ones (ρ, ω) in the plane φ = const,

$$z = \rho {\text{cos}}\omega ;\,\,\,\,r = {{r}_{0}} + \rho {\text{sin}}\omega ,$$

which would complicate the mathematical apparatus of the model [2]. Therefore, the equilibrium problems mentioned above are considered in square cross sections, respectively, \(\left| x \right| < R\), \(\left| y \right| < R\) and \(\left| z \right| < R\), \(\left| {r - {{r}_{0}}} \right| < R\), where \({{r}_{0}}\) is the main radius of the torus, and R is the radius of the cross sections of the column and torus which are initially assumed to be circular. The models in both cases are two-dimensional unlike the circular column and are built based on the boundary-value problems with equations of the Grad-Shafranov type (1.2) or (1.3), in which \(I({\Psi }) \equiv 0\), and the dependence \(p({\Psi })\) is taken from the one-dimensional problem in the circular pinch obtained from the given one-dimensional current density j(r) using formulas (1.4) and (1.6).

The study of the Galathea Belt with two parallel conductors begun in [12, 13] is continued by the comparative analysis of toroidal and cylindrical Galathean traps. Here, the same Eqs. (1.2) and (1.3) are used, in which I(Ψ) ≡ 0, and the function p(Ψ) is not monotonic with the maximum at a singular point of the field on the axis of the cylinder or on the magnetic axis of the torus, e.g.,

$$p = ~{{p}_{0}}{\text{exp}}\left( { - {{{\left( {\frac{{{\Psi } - {{{\Psi }}_{0}}}}{q}} \right)}}^{2}}} \right),$$
((1.7))

where \({{{\Psi }}_{0}} = {\Psi (0,0)}\) in the cylinder and \({{{\Psi }}_{0}} = {{\max }_{r}}{\Psi (}r{\text{,0)}}\) in the torus.

The parameter Ψ0 is selected in the process of solving problems such that it is equal to the value of the solution Ψ at the singular point mentioned above. The parameter q makes it possible to adjust the transverse size of the plasma configuration around this point [6, 17, 18].

The electric current in the conductors is represented by an additional term \({{4\pi r{{j}^{{{\text{ex}}}}}} \mathord{\left/ {\vphantom {{4\pi r{{j}^{{{\text{ex}}}}}} c}} \right. \kern-0em} c}\) in Eq. (1.2) for the torus

$${{j}^{{{\text{ex}}}}}(z,r) = \mathop \sum \limits_{k = 1}^2 {{j}_{0}}{\text{exp}}\left( { - \frac{{{{{(r - {{r}_{0}})}}^{2}} + {{{(z - {{z}_{k}})}}^{2}}~}}{{r_{c}^{2}}}} \right),$$
((1.8))

where \({{z}_{1}} = {{z}_{0}}\); \({{z}_{2}} = - {{z}_{0}}\) are coordinates of the centers of the conductors’ cross sections by the plane \(\varphi = const\); and \({{r}_{c}}\) is the conditional radius of conductors. A similar term in Eq. (1.3) for a cylinder is \({{4\pi {{j}^{{{\text{ex}}}}}} \mathord{\left/ {\vphantom {{4\pi {{j}^{{{\text{ex}}}}}} c}} \right. \kern-0em} c}\), where

$${{j}^{{{\text{ex}}}}}(x,y) = \mathop \sum \limits_{k = 1}^2 {{j}_{0}}{\text{exp}}\left( { - \frac{{{{{(x - {{x}_{k}})}}^{2}} + {{y}^{2}}~}}{{r_{c}^{2}}}} \right),$$
((1.9))

\({{x}_{1}} = {{x}_{0}}\), and \({{x}_{2}} = - {{x}_{0}}\). The coefficient \({{j}_{0}}\) is chosen such that the integral

$$\iint {{{j}^{{{\text{ex}}}}}drdz = {{J}_{c}},}$$
((1.10))

taken around each conductor, was equal to the given \({{J}_{c}}\) value of the electric current in it.

The boundaries of the squares given above are assumed to be nontransparent to the magnetic field \({{H}_{n}} = 0\), where n is the direction of the normal to the boundary. Hence the boundary condition Ψ = const follows, and this constant can be set to zero, i.e.,

$${{{\Psi }}_{\Gamma }} = 0.$$
((1.11))

The numerical solution of the problems posed is carried out in dimensionless variables ; i.e., all variables are assigned to units of measurement composed of the dimensional parameters of the problem. In pinch problems, this is the radius of the circular pinch or half of the side of the square R and the electric current J flowing through the cross section of the column. In plane problems with Eq. (1.3), the units of measurement are

$${{(x,y)}_{u}} = {{r}_{u}} = R;\,\,\,\,{{H}_{u}} = \frac{{2J}}{{c{{r}_{u}}}};\,\,\,\,{{\Psi }_{u}} = {{H}_{u}}{{r}_{u}};\,\,\,\,{{j}_{u}} = \frac{c}{{4\pi }}\frac{{{{H}_{u}}}}{{{{r}_{u}}}};\,\,\,\,{{p}_{u}} = \frac{{H_{u}^{2}}}{{4\pi }}.$$
((1.12))

The parameter q in (1.7) should obviously be related to the unit \({{\Psi }_{u}}\). In toroidal problems, the function \(\Psi \) differs from the azimuthal component of the vector potential H by the factor r; consequently, the unity \({{\Psi }_{u}}\) should contain an additional factor of length compared to Eq. (1.12). Comparing Eqs. (1.2) and (1.3), it is easy to see that the functions \(\Psi \) and I in the toroidal problems, they increase as they become more distant from the symmetry axis together with the radius r, therefore their units should contain an additional factor of the length dimension. Here there are two obvious possibilities. If \({{\Psi }_{u}} = {{H}_{u}}r_{u}^{2}\), the dimensionless \(\Psi \) value will increase proportionally to the main radius \({{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {{{r}_{u}}}}} \right. \kern-0em} {{{r}_{u}}}}\), and this should be borne in mind in the discussion of the physical meaning of the calculation results [12]. A better choice of this multiplier is the value of the main torus radius \({{r}_{0}}\), at which the dimensionless \(\Psi \) values do not increase with the radius and at large \({{r}_{0}}\) values approach their plane analogs. In this work, it is assumed

$${{\Psi }_{u}} = {{H}_{u}}{{r}_{u}}{{r}_{0}},$$
((1.13))

and the remaining units coincide with Eq. (1.12).

In the Galathea-Belt problems in a cylinder or square torus, the unit of length is half the distance between the centers of the conductors

$${{r}_{u}} = {{x}_{0}} = {{z}_{0}},$$
((1.14))

and the other units are composed of \({{r}_{u}}\) and J according to Eqs. (1.12) and (1.13), where \(J = {{J}_{c}}\) is the given current in each of the conductors immersed in the plasma.

In the problems considered in this paper (\(I({\Psi }) \equiv 0\)), the Grad-Shafranov equation in dimensionless variables has the form

$$\Delta {\text{*}}\Psi + {{\left( {{r \mathord{\left/ {\vphantom {r {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}} \right)}^{2}}\frac{{dp}}{{d{\kern 1pt} {\Psi }}} + \frac{r}{{{{r}_{0}}}}{{j}^{{{\text{ex}}}}}(r,z) = 0.$$
((1.15))

The boundary value problem in the torus is set in the region \(\left| {r - {{r}_{0}}} \right| < R\), \(\left| z \right| < R\) with the boundary condition \({{{\Psi }}_{\Gamma }} = 0\).

In the toroidal cord problems, R = 1 and \({{j}^{{{\text{ex}}}}}\) = 0, while \(p({\Psi })\) is determined by solving a one-dimensional Z-pinch problem in a circle (1.6).

In problems on the Galathea-Belt, \({{z}_{0}} = 1\) and R = 2, and the \(p({\Psi })\) and \({{j}^{{{\text{ex}}}}}\) functions are set by formulas (1.7) and (1.8). The parameter \({{\Psi }_{0}}\) is determined by an additional condition: it is equal to the value of the desired \(\Psi \) function on the magnetic axis of the torus, i.e., in the singular point of the axis z = 0, where it has a local maximum

$${{{\Psi }}_{0}} = \mathop {\max }\limits_r {\Psi (}r,0).$$
((1.16))

In the cylindrical analogs of the same problems, the role of Eq. (1.15) is played by

$$\Delta \Psi + \frac{{dp}}{{d{\Psi }}} + {{j}^{{{\text{ex}}}}}(x,y) = 0.$$
((1.17))

The region of the solution \(\left| x \right| < R\), \(\left| y \right| < R\), the function \({{j}_{{{\text{ex}}}}}\) is set by the formula (1.9); \(p(\Psi )\) and the boundary conditions are the same.

In the straightened Galathea-Belt \({{x}_{0}} = 1\), \(p({\Psi })\) is defined in the same way as above, with the difference that the singular point is in the center of the square, i.e.,

$${{{\Psi }}_{0}} = {\Psi }\left( {0,0} \right).$$
((1.18))

In the plasma cylinder problem, R = 1 and \({{j}^{{{\text{ex}}}}}\) = 0, while \(p(\Psi )\) is taken from the one-dimensional Z-pinch problem.

We note that the problems in the (x, y) plane are symmetric with respect to the coordinate axes and in the cross section of the torus by the (z, r) plane—with respect to the r axis—consequently, it suffices to solve them accordingly in the quarter x > 0, y > 0 and in the half z > 0 of the considered regions, placing the boundary symmetry conditions on the axes.

The problems are solved numerically by the iterative relaxation method: in difference analogs of equations of the type

$$\frac{{\partial \Psi }}{{\partial t}} = \Delta \Psi + g(\Psi ).$$
((1.19))

The nonlinear term \(g(\Psi )\) is taken from the previous iteration (the “time”-step), and the alternating direction method is applied to the linear equation on the next layer [18–20]. Convergence to the equilibrium solution takes place under certain conditions, since the coefficients of the equation and the boundary conditions do not depend on “time” t.

2 EQUILIBRIUM CONFIGURATIONS IN PLASMA TORI AND CYLINDERS

One-dimensional problems of equilibrium magnetoplasma configurations in a straight column of a circular cross section with the current in the axial direction use the dimensionless varieties of Eqs. (1.4)

$${{dp} \mathord{\left/ {\vphantom {{dp} {dr}}} \right. \kern-0em} {dr}} = - jH;\,\,\,\,j = {{dHr} \mathord{\left/ {\vphantom {{dHr} {rdr}}} \right. \kern-0em} {rdr}}$$
((2.1))

in a circle of radius R = 1. The specific configuration is determined by the distribution of the electric current j(r). We set it in the form

$$j = {{j}_{0}}f(r),\,\,\,\,{{j}_{0}} = {{\left( {\int\limits_0^1 {f(r)rdr} } \right)}^{{ - 1}}},$$
((2.2))

where the dimensionless parameter \({{j}_{0}}\) provides the following equality in the dimensional quantities

$$\iint\limits_{\left| r \right| < R} {j(r)rdrd\varphi = J}$$
((2.3))

with the given values of the column radius R and the current value J in it. The magnetic field H(r) and pressure p(r) are determined by integrating from (2.1):

$$H(r) = \frac{{{{j}_{0}}}}{r}\int\limits_0^r {f(\xi )\xi d} \xi ;\,\,\,\,p(r) = {{p}_{\Gamma }} + \int\limits_r^1 {j(\xi )H(\xi )d\xi } ,$$
((2.4))

where the integration constant \({{p}_{\Gamma }}\), the pressure at the column boundary, does not affect the solution of the problem. Further it is assumed that \({{p}_{\Gamma }} = 0\); i.e., in fact, the results of calculations should be attributed to the difference \(p - {{p}_{\Gamma }}\).

Introducing the magnetic flux function \(\Psi \) by \(H = - {{d\Psi } \mathord{\left/ {\vphantom {{d\Psi } {dr}}} \right. \kern-0em} {dr}}\), we obtain from Eqs. (2.1) and (2.4) a one-dimensional version of an equation of the Grad-Shafranov type (1.5):

$$\frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{d\Psi }}{{dr}}} \right) + \frac{{dp}}{{d{\Psi }}} = 0,$$
((2.5))

in which

$$p(\Psi ) = p(r(\Psi ));\,\,\,\,\frac{{dp}}{{d\Psi }} = {{\frac{{dp}}{{dr}}} \mathord{\left/ {\vphantom {{\frac{{dp}}{{dr}}} {\frac{{d\Psi }}{{dr}}}}} \right. \kern-0em} {\frac{{d\Psi }}{{dr}}}} = - {{\frac{{dp}}{{dr}}} \mathord{\left/ {\vphantom {{\frac{{dp}}{{dr}}} {H = j(r(}}} \right. \kern-0em} {H = j(r(}}\Psi )).$$
((2.6))

Here, \(r = r(\Psi )\) is the inverse function with respect to \(\Psi (r) = - \int_1^r {H(\xi )d\xi } \).

Two series of problems are considered. In the first one \(f(r) = 1 - k{{r}^{2}}\), i.e.,

$$j(r) = \frac{4}{{2 - k}}(1 - k{{r}^{2}}),\,\,\,\,0 \leqslant k \leqslant 1$$
((2.7))

is a “parabolic” current with the maximum on the axis of the column. When the parameter k changes from 0 to 1, the current changes from constant to a maximally convex one along the coordinate r. In this series

$$H(r) = \frac{{2r}}{{2 - k}}\left( {1 - \frac{k}{2}{{r}^{2}}} \right);\,\,\,\,\Psi (r) = \frac{{1 - {{r}^{2}}}}{{2 - k}}\left( {1 - \frac{k}{4}(1 + {{r}^{2}})} \right);$$
$$p(r) = \frac{{4(1 - {{r}^{2}})}}{{{{{(2 - k)}}^{2}}}}\left( {1 - k\left( {\frac{3}{4} - \frac{k}{6}} \right)(1 + {{r}^{2}}) + \frac{{{{k}^{2}}}}{6}{{r}^{4}}} \right).$$

Hence dependence \(p(\Psi )\) follows

$$\begin{gathered} p(\Psi ) = \frac{{2(2 - k)}}{{3k}}{{\left( {\frac{{4k{\Psi }}}{{2 - k}} + 1} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} - \frac{1}{k}\left( {\frac{{4k{\Psi }}}{{2 - k}} + 1} \right) + \frac{{2k - 1}}{{3k}}; \\ \frac{{dp}}{{d{\kern 1pt} {\Psi }}} = j = 4\left( {\sqrt {\frac{{4k{\Psi }}}{{2 - k}} + 1} - \frac{1}{{2 - k}}} \right), \\ \end{gathered} $$
((2.8))

which is natural to use in two-dimensional problems of direct and toroidal columns of a square section.

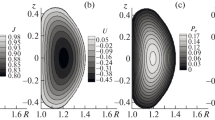
An example of the calculation of the field and plasma configurations in the cylinder and torus and their comparison with each other are shown in Fig. 1. The parameter k = 0.9 is selected close to the right-hand end of the considered range, and the main torus radius (dimensionless) \({{r}_{0}} = 1\) is the minimum possible for the current nonuniformity and the toroidal trap to be manifested in the most noticeable way. Here, firstly, it is clear that, as expected, the configurations in the square and circular cylinder are topologically the same. They differ in the values of the poloidal magnetic flux \({{{\Psi }}_{{\max }}}\), pressure \({{p}_{{\max }}}\), and electric current \({{j}_{{\max }}}\), which are higher in a square than in a circle in accordance with the difference of their areas. Secondly, the toroidal configurations are deformed in comparison with the cylindrical ones: the magnetic axis is displaced from the center by \(\delta r = 0.48.\) The maximum \({{{\Psi }}_{{\max }}}\) and \({{p}_{{\max }}}\) values in the torus are higher than in the cylinder, which is consistent with the fact that the configuration became smaller as a result of the above-mentioned deformation.

Fig. 1.
figure 1

Magnetic field and pressure in cylindrical (a) and toroidal (b) plasma cords with maximum of electric current in center: r0 = 1; k = 0.9.

Full size image

The dependence of the characteristics of the equilibrium magnetoplasma configurations on the parameter \({{r}_{0}}\) is presented in Table 1 for two values of the parameter k. It follows from them that at the increase in the main torus radius, their properties approach those of the cylindrical ones. As a result of the calculations, this qualitatively obvious result acquires quantitative estimates. A comparison of Tables 1a and 1b shows that only the radius of the torus \({{r}_{0}}\) mainly affects the displacement of the magnetic axis δr, and the magnetic flux \({{{\Psi }}_{{\max }}}\) and pressure \({{p}_{{\max }}}\) also depend on the nonuniformity of the current along the radius.

Table 1.   Parameters of toroidal and cylindrical configurations with maximum current in center at (a) k = 0.9 and (b) k = 0.5
Full size table

The second series of calculations was carried out with the currents maximal at the boundary of the plasma column, namely, \(f(r) = {{r}^{N}}\):

$$j(r) = (N + 2){{r}^{N}},\,\,\,\,N \geqslant 0.$$
((2.9))

As the exponent N increases, the current density is redistributed from constant at N = 0 towards the column boundary and in the limit at \(N \to \infty \) becomes “skinned,” i.e., concentrated only on the boundary. It follows from Eq. (2.9) that

$$\begin{gathered} H(r) = {{r}^{{N + 1}}};\,\,\,\,\Psi (r) = \frac{{1 - {{r}^{{N + 2}}}}}{{N + 2}}; \\ p(r) = \frac{{N + 2}}{{2(N + 1)}}\left( {1 - {{r}^{{2(N + 1)}}}} \right); \\ p\left( {\Psi } \right) = \frac{{N + 2}}{{2(N + 1)}}\left( {1 - {{{(1 - (N + 2)\Psi )}}^{{\frac{{2(N + 1)}}{{N + 2}}}}}} \right); \\ \frac{{dp}}{{d{\kern 1pt} {\Psi }}} = (N + 2){{\left( {1 - (N + 2)\Psi } \right)}^{{{N \mathord{\left/ {\vphantom {N {(N + 2)}}} \right. \kern-0em} {(N + 2)}}}}}. \\ \end{gathered} $$
((2.10))

The calculations of the configurations of this series are illustrated by an example in Fig. 2 with a relatively moderate (N = 2) increase in the current from the center to the boundary and the minimum possible radius of the torus \({{r}_{0}} = 1\). Here, the configurations occupy the region surrounding the magnetic axis, with almost constant values of the magnetic flux function and pressure and almost no electric current, surrounded by a belt of their intense transition to the given values at the boundary. The configuration in the torus is deformed and shifted towards the outer boundary. Unlike the previous series, the magnetic flux \({{{\Psi }}_{{\max }}}\) and the maximum pressure \({{p}_{{\max }}}\) in both configurations almost coincide with their values in the circular cylinder; i.e., their characteristic volume coincides. With the growth of the exponent N, this volume increases. The \({{{\Psi }}_{{\max }}}\) and \({{p}_{{\max }}}\) values in it decrease according to formulas (2.10) and the transition belt near the boundary is narrowed. The displacement of the magnetic axis δr decreases, obviously, with the increase in the radius \({{r}_{0}}\), as well as with the increase in the factor N, which is illustrated in Table 2.

Fig. 2.
figure 2

Magnetic field and pressure in cylindrical (a) and toroidal (b) plasma cords with electric current maximum at boundary: \({{r}_{0}} = 1\); N = 2.

Full size image
Table 2.   Magnetic axis displacement \(\delta r\) in toroidal and cylindrical configurations with maximum current at boundary at (a) N = 2 and (b) N = 5
Full size table

The solutions of all variants of the problems of both the mentioned series are obtained in the calculations by the relaxation method. It follows that the considered equilibrium configurations are stable with respect to perturbations of the same dimension, i.e., two-dimensional perturbations of the magnetic flux. This stability, called diffusional, is evident in the problems of the second series, where \(g{\text{'}}(\Psi ) < 0\) and the differential operator of a linearized problem with an equation of the Grad-Shafranov type (1.19)

$$L[u] \equiv - \Delta u - g{\text{'}}(\Psi )u;\,\,\,\,{{\left. u \right|}_{\Gamma }} = 0$$
((2.11))

is positive definite [6, 17, 18]. In the problems of the first series, the result is not trivial, since \(g{\text{'}}(\Psi ) > 0\) at all k > 0. Moreover, at k = 1, just as in any other pinch problems in which \(j = {{dp} \mathord{\left/ {\vphantom {{dp} {d\Psi }}} \right. \kern-0em} {d\Psi }} = 0\) at the boundary r = 1, the solution obtained in the calculations is not unique: along with the solution found, the problem has a trivial solution Ψ ≡ 0. The nontrivial solution turned out to be diffusion-stable, to which any nonzero initial distribution \(\Psi \) is attracted during the relaxation process.

The result obtained is of interest because it is a necessary condition for the traditional MHD stability of the considered equilibrium configurations: the latter requires the diffusive stability of a family of two-dimensional problems, which together cover all the possible three-dimensional perturbations [16–18].

3 EQUILIBRIUM CONFIGURATIONS IN A GALATHEA-BELT

The models of the equilibrium magnetoplasma configurations in the cylindrical and toroidal varieties of the Galathea-Belt trap use boundary value problems with equations of the Grad-Shafranov type (1.17) and (1.15) in square regions \(\left| x \right| < R\), \(\left| y \right| < R\) and \(\left| {r - {{r}_{0}}} \right| < R\), \(\left| z \right| < R\), respectively, with the boundary condition . The currents in conductors with centers \(({{x}_{k}} = \pm 1,\)\(y = 0)\) and \((r = {{r}_{0}},{{z}_{k}} = \pm 1)\) are presented by functions (1.9) and (1.8). The function \(p(\Psi )\) has form (1.7), where the parameter \({{\Psi }_{0}}\) is selected according to the formulas (1.18) and (1.16) such that the value of the desired function was \(\Psi = {{\Psi }_{0}}\) at the singular point of the magnetic field on the magnetic axis of the system.

An example of one of the variants of the calculations with the parameter values R = 2; \({{r}_{c}} = 0.2;\)\(q = 0.2;\)\({{p}_{0}} = 0.75\); and \({{r}_{0}} = 2\) is presented in Fig. 3 by the magnetic lines \(\Psi - {{\Psi }_{0}} = const\) and isobars \(p = const\). The configuration in a straight cylinder is a curvilinear quadrilateral with the sides, which are convex inward, and thin slips encircling the conductors with the current. The characteristic features of the toroidal configuration are manifested in the most noticeable way in the torus of the minimum possible radius \({{r}_{0}} = 2\). Just as in the case mentioned above, the configuration is topologically equivalent to the cylindrical one but it is deformed: it has lost its symmetry about the center of the square and is shifted towards the outer boundary. The magnetic axis is displaced from the center of the square by \(\delta r = 0.52\). The parameter \({{\Psi }_{0}}\), characterizing the poloidal magnetic flux between the separatrix of the field and the outer boundary, is decreased compared with the cylindrical configuration.

Fig. 3.
figure 3

Magnetic field and pressure in cylindrical (a) and toroidal (b) Galathea-Belt: \({{r}_{0}} = 2\); \({{p}_{0}} = 0.75\).

Full size image

The diffusive stability of the configurations under consideration, i.e., convergence of the iterative process of the solution of the problems, takes place at the constraint on \({{p}_{0}}\), the maximum dimensionless pressure in the center of the configuration and on the magnetic field separatrix passing through it

$${{p}_{0}} < p_{0}^{{{\text{cr}}}}.$$
((3.1))

In terms of the mathematical apparatus of the problems, condition (3.1) corresponds to the positive definiteness of the differential operator of the linearized problem (2.11). It ensures the existence, uniqueness, and diffusive stability of the solutions of problems with semilinear elliptic differential equations, on which a wide class of mathematical models of the interaction of reaction and diffusion processes [11, 12, 17, 18] are based. Apparently, the physical meaning of restriction (3.1) is that the magnetic field of the given current \({{J}_{c}}\) in the conductors can keep the plasma in the trap of the given size R, which is only of limited pressure.

In toroidal traps, constraint (3.1) holds, but it is reinforced (\(p_{0}^{{{\text{cr}}}}\) decreases) when the torus radius \({{r}_{0}}\) becomes smaller, i.e., on the increase in the curvature of the trap in the azimuthal direction. This result is presented in Table 3. It clarifies a similar situation in [12, 13], where the units of measure \({{\Psi }_{u}}\) and q are less successfully chosen (1.12), and the increase in \(\Psi \) proportional to the radius \({{r}_{0}}\) is not correlated with a constant parameter value q, i.e., the decrease in \(p_{0}^{{{\text{cr}}}}\) [12, 13] with the increase in \({{r}_{0}}\) due to the compression of the configuration in the direction transverse to the magnetic field.

Table 3.   Critical pressure values \(p_{0}^{{{\text{cr}}}}\) in toroidal and cylindrical Galathea-Belt configurations
Full size table

The dependence of the quantitative characteristics of the configurations, the displacement δr and the parameter \({{\Psi }_{0}}\), which is responsible for the magnetic flux, on the torus radius \({{r}_{0}}\) is shown in Table 4 for three different pressure values \({{p}_{0}}\). The analysis of this dependence and the comparison of the toroidal configurations with the cylindrical one (\({{r}_{0}} = \infty \)) makes it possible to make the following conclusion. At any values \({{r}_{0}} \geqslant 2\), the equilibrium plasma and field configurations may exist in the traps at any maximum pressure values not exceeding \(p_{0}^{{{\text{cr}}}}\) given in Table 3. The solutions of the boundary value problems under condition (3.1) are unique and diffusion-stable. It follows from Table 4 that on increasing the plasma pressure \({{p}_{0}}\) the displacement δr of the magnetic axis and the magnetic flux value \({{\Psi }_{0}}\) between the separatrix of the field and the outer boundary increase. The differences between the toroidal and cylindrical configurations are noticeably blurred as the torus radius \({{r}_{0}}\) increases: the \({{\Psi }_{0}}\) values nearly coincide at \({{r}_{0}} \geqslant 6\), and the displacement is measured in percentage units at \({{r}_{0}} \geqslant 8\).

Table 4.   Parameters of toroidal and cylindrical configurations in Galathea-Belt at (a) \({{p}_{0}} = 0.5\), (b) \({{p}_{0}} = 0.75\), (c) \({{p}_{0}} = 1\)
Full size table

CONCLUSIONS

This work presents the mathematical models of the plasma MHD equilibrium in typical examples of toroidal magnetic traps and their analogs straightened into a cylinder. A comparative analysis of the quantitative characteristics of the plasma configurations in the torus and cylinder is given.