Identification of a Production Function with Age Limit for Production Capacities

Abstract

The microlevel dynamics of the age-limited production capacities differentiated by the moments of creation set the macrolevel production function. The microdescription is based on the hypothesis of the capacity loss at a constant rate and constant number of jobs from the moment of the creation of the production unit to its closure, when the age limit is exceeded. An analytical expression for the endogenous production function with the given maximum age of the capacities is obtained in characteristic exponential growth modes with the constant share of new capacities. A transient growth mode with varying incremental capital intensity of new capacities is considered. The production function’s parameters can be determined even with significant variations of the new capacity’s share in the total capacity, which occurred in the Russian economy. For this purpose, the initial microeconomic model of the production capacity’s dynamics is used in the numerical calculations of the production function. The parameters are estimated indirectly based on a comparison of the results of the calculations by the model with the statistical data over 1970–2017. The obtained value of the average age limit of capacities A = 25 for the Russian economy explains the vanishing of cost inflation in 2017. The identification of the endogenous production function parameters also show that the value of the average incremental capital intensity for the entire Russian economy decreased significantly from 1970 to 2017. The decrease is explained by the increase in the share of the primary industry in the output.

1 INTRODUCTION

The age limit of production capacities is included in the production function’s parameters [1]. A classical production function is identified by time series of output and production factors. The aggregate production function depends on the external parameters of the model; its identification is a complicated problem that can be solved using high-speed calculations [2].

In this paper, a concise derivation of the analytical expression of the aggregate production function is presented with the consideration of the age limit of the capacities [1] for the typical growth modes. In contrast to [1], we use a new equation for the dynamics of the incremental capital–output ratio. In [1, 3, 4], the results of identification of the new production function for some countries are presented. Since the Russian economy was not in the typical mode of growth in 1970–2017, the numerical methods are applied to identify the production function using the initial microdescription of the capacity dynamics. The results and the procedure of identification of the production function are presented and the economic interpretation is given.

The problem of obtaining the aggregate production function by the initial distribution of the production potential of firms in the industry was first formulated by H. Houthakker [5]. He showed that the Cobb—Douglas production function was obtained from the Pareto distribution at the microlevel. In [6], the reverse operation of obtaining the initial distribution for the classical CES production function was considered. The concept of production capacity (the greatest possible output) was introduced by L. Johansen [7], who applied it instead of the capital concept to build production functions of certain industries in Norway and Sweden [8].

A.A. Petrov and I.G. Pospelov systematically applied production functions aggregated over the capacity distribution in the economic macromodels [9]. In [10], A.A. Shananin investigated the aggregate production functions of many variables and revealed the unambiguity of the production and profit functions. In [11], a new class of aggregate production functions was obtained for the capacity decreasing at a constant rate and fixed number of jobs.

Another direction of the studies of the aggregate production functions employs capital as the production factor. In [12], the form of the production function at the macrolevel was derived from the distribution of ideas at the microlevel. In [13], the level of the general factor productivity of the production function depended on the special shock distribution at the microlevel, which resulted in the creation of jobs and job losses. In [14], it was shown that the technology menu [12] was a special case of the support set concept, and the relation between production functions and technology menus was clarified. The “ideas’ model” generates the CES function.

These two directions provide equivalent results as long as the capital-output ratio does not vary. In this paper, the capital–output ratio varies, which makes our approach considerably different from the other direction.

2 PRODUCTION FUNCTIONS REPRESENTABLE BY THE PRODUCTION CAPACITY DISTRIBUTION OVER TECHNOLOGIES

This paper is a natural continuation of [11]. Here we recall the basic results of [11] and specify the applications.

Hypothesis 0.At each time moment t, the number of jobs at the production unit is fixed from the time$\tau \leqslant t$of its creation, and the production capacity$m(t,\tau )$decreases at the constant rate$\mu > 0$.

According to Hypothesis 0, the capacity $m(t,\tau ) = J(\tau )\exp ( - \mu (t - \tau ))$ decreases, and the labor input $\lambda (t,\tau ) = \nu (\tau )\exp (\mu (t - \tau ))$ increases. Here $J(\tau )$ is the initial capacity and $\nu (\tau )$ is the initial labor input at the time of creation $\tau$.

2.1 Aggregate Production Function

In the case of Hypothesis 0, the production function [9] $f(t,x) = {{Y(t)} \mathord{\left/ {\vphantom {{Y(t)} {M(t)}}} \right. \kern-0em} {M(t)}}$ (the aggregate capacity utilization) on balanced growth path can be written as [11]

$$f(t,x) = 1 - {{\left[ {1 - \left( {1 - \varepsilon - {\mu \mathord{\left/ {\vphantom {\mu \sigma }} \right. \kern-0em} \sigma }} \right){x \mathord{\left/ {\vphantom {x {\nu (t)}}} \right. \kern-0em} {\nu (t)}}} \right]}^{{\left( {1 - \varepsilon - {\mu \mathord{\left/ {\vphantom {\mu \sigma }} \right. \kern-0em} \sigma }} \right)}}},$$

(1)

where $\varepsilon \geqslant 0$ is the pace of the technological progress, the minimum labor input is

$${{d\nu } \mathord{\left/ {\vphantom {{d\nu } {dt}}} \right. \kern-0em} {dt}} = - \varepsilon \sigma (t)\nu (t),\,\,\,\,\nu (0) = {{\nu }_{0}},$$

(2)

and the share of new capacities $\sigma (t) = {{J(t)} \mathord{\left/ {\vphantom {{J(t)} {M(t)}}} \right. \kern-0em} {M(t)}}$ on balanced growth path, Y(t) $J(t),{\text{ }}M(t)\sim \exp (\gamma t)$, is constant: $\sigma = {\text{const}}{\text{.}}$ In a closed economy,

$$Y(t) = C(t) + bJ(t),$$

(3)

where $b$ is the incremental capital–output ratio and $C(t)$ is the consumption. Therefore, on balanced growth path, $C(t)\sim \exp (\gamma t)$ if $b = {\text{const}}$.

2.2 The Problem of Indirect Identification of the Economic Model

Let $N$ the external parameters be set on a hypercube with dimension $N$: ${{{\mathbf{a}}}^{ - }} \leqslant {\mathbf{a}} \leqslant {{{\mathbf{a}}}^{ + }}.$ Let some macroparameters have the statistical analogs: $X_{i}^{{{\text{stat}}}}(t),$$t = {{t}_{0}},...,{{t}_{n}},i = 1,...,M.$ The Theil inequality index is used as the criterion of closeness of the calculated and the statistical time series:

$${{T}_{i}} = \sqrt {{{\left( {\sum\limits_{t = {{t}_{0}}}^{{{t}_{n}}} {{{{\left( {{{X}_{i}}(t) - X_{i}^{{{\text{stat}}}}(t)} \right)}}^{2}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{t = {{t}_{0}}}^{{{t}_{n}}} {{{{\left( {{{X}_{i}}(t) - X_{i}^{{{\text{stat}}}}(t)} \right)}}^{2}}} } \right)} {\left( {\sum\limits_{t = {{t}_{0}}}^{{{t}_{n}}} {{{{\left( {{{X}_{i}}(t)} \right)}}^{2}} + {{{\left( {X_{i}^{{{\text{stat}}}}(t)} \right)}}^{2}}{\kern 1pt} } } \right)}}} \right. \kern-0em} {\left( {\sum\limits_{t = {{t}_{0}}}^{{{t}_{n}}} {{{{\left( {{{X}_{i}}(t)} \right)}}^{2}} + {{{\left( {X_{i}^{{{\text{stat}}}}(t)} \right)}}^{2}}{\kern 1pt} } } \right)}}} .$$

(4)

The convolution of the criteria of closeness (4) can be written as

$$S = \prod\limits_{i = 1}^M {\left( {1 - {{T}_{i}}} \right)} \to \mathop {\max }\limits_{{{{\mathbf{a}}}^{ - }} \leqslant {\mathbf{a}} \leqslant {{{\mathbf{a}}}^{ + }}} .$$

2.3 Forecast Made at the End of 2006 about the Crisis of 2008 in the Russian Economy

The model with the production capacities differentiated by the creation time suggests that the growth of the economy after the crisis of 1998 was related to the old capacity utilization. At the end of 2006, the problem of identifying a Ramsay type dynamic economic model [15] was considered. As a result of the solution of this problem [15, p. 98] we could predict a crisis in 2008. Had there been an immediate response to this forecast, it would have been possible to avoid the drop in GDP that ocurred in 2009 and the subsequent stagnation through transition to growth by creating new and more efficient capacities.

3 DYNAMICS OF AGE-LIMITED PRODUCTION CAPACITIES

Now, in contrast to Hypothesis 0, we assume that the production capacities have a certain age limit $A(t) < \infty$, after which they are not used. This is a natural limitation on the calculations.

Hypothesis 1. The number of jobs at a producing unit remains constant from its creation time $\tau \leqslant t$ to its closure time $\tau + A(t),$ where $A(t)$ is the maximum age of the capacities, and the production capacity $m(t,\tau )$ decreases at the constant rate $\mu > 0$.

Then the aggregate capacity $M(t) = \int_{t - A(t)}^t J (\tau )\exp ( - \mu (t - \tau ))d\tau$ is described by the following differential-difference equation:

$${{dM(t)} \mathord{\left/ {\vphantom {{dM(t)} {dt}}} \right. \kern-0em} {dt}} = J(t) - \mu M(t) - (1 - {{dA(t)} \mathord{\left/ {\vphantom {{dA(t)} {dt}}} \right. \kern-0em} {dt}})J(t - A(t))\exp ( - \mu A(t)),$$

(5)

where the variation rate of the capacity age limit is bounded from above: ${{A(t)} \mathord{\left/ {\vphantom {{A(t)} {dt}}} \right. \kern-0em} {dt}} \leqslant 1$, since the capacities withdrawn are not returned.

The production function is set implicitly [1] subject to the optimal utilization of the capacities by labor forces $L(t)$, starting from the most efficient age at zero years to the age of $\theta (t,L(t)) \leqslant A(t)$:

$$Y(t) = \int\limits_{t - \theta (t,L(t))}^t J (\tau )\exp ( - \mu (t - \tau ))d\tau ,\,\,\,\,L(t) = \int\limits_{t - \theta (t,L(t))}^t \nu (\tau )J(\tau )d\tau .$$

(6)

4 PRODUCTION FUNCTION WITH THE AGE LIMIT $A = {\text{const}}$

Here the statements of [1, p. 146–148] are reformulated.

4.1 The Capacity Growth Rate $\gamma$’s Relationship with Parameters $\sigma$, $\mu$, and $A$

Lemma 1 follows directly from the equation for the aggregate capacity (5):

Lemma 1.If the capacity age limit is set at $A = {\text{const}} > 0$and the aggregate capacity$M(t)$grows at the constant rate$\gamma$, while the share of new capacities$\sigma$is constant,

$$M(t) = {{M}_{0}}\exp \left( {\gamma t} \right),\,\,\,\,\sigma = {{J(t)} \mathord{\left/ {\vphantom {{J(t)} {M(t)}}} \right. \kern-0em} {M(t)}} = {\text{const}},$$

then the growth rate of the aggregate capacity$\gamma$is determined by the relation

$$\gamma = \varphi (\sigma ,A) - \mu ,$$

(7)

where$\varphi (\sigma ,A)$is the single real solution

$$1 - {\varphi \mathord{\left/ {\vphantom {\varphi \sigma }} \right. \kern-0em} \sigma } = {\text{exp}}( - \varphi A)$$

(8)

over the interval$\varphi \in (0,\sigma )$subject to the existence of the solution$A > {1 \mathord{\left/ {\vphantom {1 \sigma }} \right. \kern-0em} \sigma }$.

4.2 Production Function with Balanced Growth

Based on Lemma 1, the following theorem can be formulated

Theorem 1.We assume the mode of balanced growth with the rate$\gamma$

$$M(t) = {{M}_{0}}\exp (\gamma t),\,\,\,\,Y(t) = {{Y}_{0}}\exp (\gamma t),\,\,\,\,J(t) = {{J}_{0}}\exp (\gamma t),\,\,\,\,C(t) = {{C}_{0}}\exp (\gamma t)$$

(9)

meeting the following conditions in a closed economy (3):

(a) Hypothesis 1 about the fixed number of jobs and a decrease in capacity at the rate of$\mu$to a certain agelimit$A(t)$is true;

(b) the capacity’s maximum age limit is fixed at$A(t) = A = {\text{const}}$;

(c) the incremental capital–output ratio is fixed$b(t) = b = {\text{const}}$;

(d) the minimum labor input$\nu (t)$decreases due to thetechnological progress according to(2): ${{d\nu (t)} \mathord{\left/ {\vphantom {{d\nu (t)} {dt}}} \right. \kern-0em} {dt}} = - \varepsilon \sigma (t)\nu (t)$.

Then the following statements are true:

(1) the share of new capacities is constant:$\sigma (t) = {{J(t)} \mathord{\left/ {\vphantom {{J(t)} {M(t)}}} \right. \kern-0em} {M(t)}} = \sigma = {\text{const}}$;

(2) the aggregate production capacity dynamics (5) with balanced growth (9) sets the relationship between the growth rate$\gamma$and the production function parameters$\sigma ,\mu \,\,{\text{and}}\,\,A$as the implicit function$\gamma = \gamma (\sigma ,\mu ,A)$of these parameters (7) and (8);

(3) relations (6) provide the following expression of the production function$Y(t) = M(t){\text{ }}f(t,x)$:

$$f(t,x) = \left\{ {1 - {{{\left[ {1 - \left( {{\gamma \mathord{\left/ {\vphantom {\gamma \sigma }} \right. \kern-0em} \sigma } - \varepsilon } \right){x \mathord{\left/ {\vphantom {x {\nu (t)}}} \right. \kern-0em} {\nu (t)}}} \right]}}^{{{{(\gamma + \mu )} \mathord{\left/ {\vphantom {{(\gamma + \mu )} {(\gamma - \varepsilon \sigma )}}} \right. \kern-0em} {(\gamma - \varepsilon \sigma )}}}}}} \right\}{\sigma \mathord{\left/ {\vphantom {\sigma {\left( {\gamma + \mu } \right)}}} \right. \kern-0em} {\left( {\gamma + \mu } \right)}},$$

(10)

(4) the ratio between the average and the minimum labor inputs of the capacities is constant:${x \mathord{\left/ {\vphantom {x {\nu (t)}}} \right. \kern-0em} {\nu (t)}} = {{L(t)} \mathord{\left/ {\vphantom {{L(t)} {\left( {M(t)\nu (t)} \right)}}} \right. \kern-0em} {\left( {M(t)\nu (t)} \right)}} = {\text{const}}.$

According to Theorem 1, the production function contains parameters $\mu ,\varepsilon ,\sigma ,A\,\,{\text{and}}\,\,\nu (t)$, and the transcendental equation (8) and equality (7) are used to determine $\gamma$ via $\mu ,\sigma \,\,{\text{and}}\,\,A$. Excluding $\sigma = {{(\gamma + \mu )} \mathord{\left/ {\vphantom {{(\gamma + \mu )} {(1 - \exp ( - (\gamma + \mu )A))}}} \right. \kern-0em} {(1 - \exp ( - (\gamma + \mu )A))}}$ from (7) and (8) and substituting into (10), we obtain the form suitable for investigating Solow’s golden rule of growth [11].

4.3 Link to the Production Function Obtained Earlier

The following two corollaries of Theorem 1 are true.

Corollary 1.The new production function with balanced growth (10), (7), and (8), while taking into consideration the maximum age limitation A of the capacities and the fixed incremental capital–output ratio b, at$A \to \infty$, provides the production function with unlimited age capacities (1).

Corollary 2.With balanced growthat rate$\gamma$ (9), fixed incremental capital–output ratio b, and the given maximum capacity age A, the number of people employed in the labor force in the economy$L(t)$due to the technological progress (2), according to statement 4 of Theorem 1, grows at a lower rate$\eta = \gamma - \varepsilon \sigma$than the other volume macroeconomic indices; moreover, the average employment level grows at the rate of$\xi = \varepsilon \sigma$, $L(t) = {{L}_{0}}\exp \left( {(\gamma - \varepsilon \sigma )t} \right),~~c(t) = {{C(t)} \mathord{\left/ {\vphantom {{C(t)} {L(t)}}} \right. \kern-0em} {L(t)}} = {{c}_{0}}\exp \left( {\varepsilon \sigma t} \right).$

4.4 Transient Production Function with the Decreasing Incremental Capital–Output Ratio $b(t)$

The parameters of the studied model were identified in [1, 3, 4], and it was mentioned that the mode of growth was typical of many countries with the variable incremental capital–output ratio $b(t)$. This is also true for the Russian economy of 1970–2017.

According to the numerical experiments [4], the dynamics of the macroeconomic indices illustrate the statistics better if we assume that the rate of variation of the incremental capital–output ratio $b(t)$ is proportional to the share of new capacities $\sigma (t)$; i.e., the form of the $b(t)$ variation is similar to that of the minimum capital–output ratio $\nu (t)$ variation according to (2):

$${{db(t)} \mathord{\left/ {\vphantom {{db(t)} {dt}}} \right. \kern-0em} {dt}} = - \beta \sigma (t)b(t),\,\,\,\,b(0) = {{b}_{0}}.$$

(11)

Based on statement 3 from [1, p. 147, 148] and Lemma 1, subject to $b(t)$ varying according to (11), we formulate a new theorem.

Theorem 2.We assume that in the closed economy (3) with the varying capital–output ratio$Y(t) = C(t) + b(t)J(t)$, in the mode of growth of the aggregate capacity and GDP at the rate of$\gamma$,

$$M(t) = {{M}_{0}}\exp (\gamma t),\,\,\,\,Y(t) = {{Y}_{0}}\exp (\gamma t),$$

(12)

the following conditions are met:

(a) the incremental capital–output ratio$b(t)$decreases according to (11) at the rate of$\beta \sigma (t)$, where$\beta = {\text{const}} > 0$;

(b) the share of new capacities is fixed,

$$\sigma (t) = {{J(t)} \mathord{\left/ {\vphantom {{J(t)} {M(t)}}} \right. \kern-0em} {M(t)}} = \sigma = {\text{const}}{\text{,}}$$

(13)

(c) Hypothesis 1 about the fixed number of jobs and the capacity decrease at the rate of$\mu$until reaching its age limit$A(t)$is true;

(d) the maximum capacity age is fixed:$A(t) = A = {\text{const}}$;

(e)the minimum labor input$\nu (t)$decreases due to the technological progress according toEq. (2).

Then the following statements are true:

(1) the production function$f(t,x)$(aggregate capacity utilization) in the transient mode (12), (11), and (13) has the form of (10), (7), and (8);

(2) the ratio between the average and the minimum labor inputs is${x \mathord{\left/ {\vphantom {x {\nu (t)}}} \right. \kern-0em} {\nu (t)}} = {\text{const}}$;

(3) the rate of growth of the number of people employed in the labor force in the economy is$\eta = \gamma - \varepsilon \sigma$;

(4) the share of consumption in the output${{C(t)} \mathord{\left/ {\vphantom {{C(t)} {Y(t)}}} \right. \kern-0em} {Y(t)}}$grows, and the share of savings${{b(t)J(t))} \mathord{\left/ {\vphantom {{b(t)J(t))} {Y(t)}}} \right. \kern-0em} {Y(t)}}$decreases; here the average consumption$c(t)$ = ${{C(t)} \mathord{\left/ {\vphantom {{C(t)} {L(t)}}} \right. \kern-0em} {L(t)}}$grows at a rate exceeding its value under balancedgrowth$\varepsilon \sigma$.

5 RESULTS OF IDENTIFICATION OF THE PRODUCTION FUNCTION

The analytical expression of the production function is obtained for two typical modes of growth. Transient conditions are usual for the Russian economy. We identify the production function parameters by the Russian data for 1970–2017 based on the initial micromodel and assuming the variability of the share of new capacities $\sigma (t)$ in the aggregate capacity. In this way, we can determine the values of the parameters, which are typical for the Russian economy, of this production function.

5.1 Condition of Average Capacity Utilization

By definition, output does not exceed production capacity. Let us consider GDP as the total output within the single-sector model. We assume that the following inequality is true for each year t

$$Y(t) = \int\limits_{t - X(t)}^t J (t)\exp ( - \mu (t - \tau ))d\tau \leqslant \int\limits_{t - A}^t J (t)\exp ( - \mu (t - \tau ))d\tau = M(t),$$

where $X(t)$ is the maximum age of the capacity utilization in year t and A is the age limit of the capacities, which is assumed fixed.

In [16], it was shown that the spare capacities are about 30% of the real economy. Taking into consideration the transient nature of the processes that occur in the Russian economy, we assume that the average capacity utilization is at the level of 60% here.

5.2 Results of Identification of the Model Parameters

The modification $N_{L}^{{}}$ of the Theil criterion $T_{L}^{{}}$ was used for the indirect identification of the parameters as the criterion of closeness of the statistical time series $L_{s}^{{}}(t)$ and the time series calculated by the $L(t)$ model of employment in the economy according to the Russian data in 1970–2017:

$${{N}_{L}} = 1 - T_{L}^{2} = {{2\left( {\sum\limits_{t = {{t}_{0}}}^{{{t}_{n}}} {L(t){{L}_{s}}(t)} } \right)} \mathord{\left/ {\vphantom {{2\left( {\sum\limits_{t = {{t}_{0}}}^{{{t}_{n}}} {L(t){{L}_{s}}(t)} } \right)} {\left( {\sum\limits_{t = {{t}_{0}}}^{{{t}_{n}}} {{{L}^{2}}(t) + L_{s}^{2}(t)} } \right)}}} \right. \kern-0em} {\left( {\sum\limits_{t = {{t}_{0}}}^{{{t}_{n}}} {{{L}^{2}}(t) + L_{s}^{2}(t)} } \right)}} \to \mathop {\max }\limits_{{{{\mathbf{a}}}^{ - }} \leqslant {\mathbf{a}} \leqslant {{{\mathbf{a}}}^{ + }}} .$$

(14)

This modification significantly accelerates the parallel calculation [2] by excluding the square root calculation. The required parameters a in (14) are ${{b}_{0}},\beta ,\mu ,{{\nu }_{0}},\varepsilon ,A\,\,{\text{and}}\,\,{{\gamma }_{0}}$. The best value of criterion $N_{L}^{{}} = 0.9283$ is attained at the following values of the parameters: $b_{0}^{{}} = 5.598$ yr, $\beta = 0.430,$$\mu = 0.03155$ yr^–1, $\nu _{0}^{{}} = 2.512$ people yr/RUR1M, 2010, $\varepsilon = 0.3465,$$A = 25$ yr, and ${{\gamma }_{0}} = 0.05$ yr^–1, so that the estimation of the initial distribution of the production capacities is $m({{t}_{0}},\tau ) = J({{t}_{0}})\exp ( - 0.05({{t}_{0}} - \tau )),$ where $0 \leqslant {{t}_{0}} - \tau \leqslant A$ is the age.

5.3 Macroeconomic Indices of the Identification

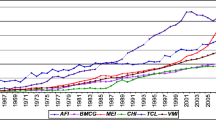
In Fig. 1, the quality of model identification by the closeness of the simulated and the statistical time series is estimated for employment in the economy $L(t)$. The variation fluctuations are related to the model’s rigidity.

Fig. 1.

Calculation of employment by model L_mod and the statistical data on employment in the economy L stat in 1970–2017.

In Fig. 2, the estimation of the average age of production capacities avrAge and the maximum age of their utilization mxAge are presented. The latter is calculated based on the condition that the capacities are utilized by labor forces starting from the youngest age (with better labor efficiency) until the exhaustion of the labor resources. In reality, all the considered capacities are partially utilized, and conversion to new capacities is slow.

Fig. 2.

Calculation of the capacity’s average age avrAge and the maximum age of its utilization mxAge in 1970–2017.

In Fig. 3, the dynamics of the production function $f(t,x)$ (utilization of the aggregate capacity) and the share of savings in the GDP in 1970–2017 are shown. Apparently, the share of savings in the GDP in the post-Soviet era decreased almost by a factor of three, and utilization of the available capacities halved by the mid-1990s before recovering to the usual level of 60 to 70%.

Fig. 3.

Utilization of production capacity $f(x)$ and the share of savings in GDP ${{b(t)J(t)} \mathord{\left/ {\vphantom {{b(t)J(t)} {Y(t)}}} \right. \kern-0em} {Y(t)}}$ in 1970–2017.

As shown in Fig. 4, the dynamics of the share of new capacities $\sigma (t)$ in the aggregate capacity in comparison with the fixed rate $\mu$ of the capacities decreased due to wear. In the mid-1990s, the share $\sigma (t)$ was lower than $\mu$, so that it did not provide for the recovery of even the capacity’s physical wear.

Fig. 4.

Share of new capacities in the total capacity σ and the rate of the decline of capacity μ in 1970–2017.

In Fig. 5, the dynamical decrease in the incremental capital–output ratio $b(t)$ in 1970–2017 due to the increase in the share of primary industries is shown.

Fig. 5.

Incremental capital–output ratio b in 1970–2017.

In Fig. 6, the model estimations of the dynamics of the least labor intensivity $\nu$ and the average labor intensivity of the utilized capacities $\lambda$ are shown.

Fig. 6.

Lowest labor intensity ν and the average labor intensity λ in 1970–2017.

5.4 Microeconomic Indices of Identification

In Fig. 7, the distribution of production capacities $m(t,\tau )$ over their creation times $\tau$ for the typical years t = 1991, 1997, 2008, 2010, 2015, and 2017 is presented. The production capacities in these graphs are measured in trillions of rubles in 2010. The fully utilized capacities are marked in black and the spare capacities, in white. In the real economy and spare capacities are available at all moments of their creation [16]. At t = 1991, the share of new capacities reduced. Further, as shown in the curve for t = 1997, this reduction continued. After 1998, the utilization of old capacities ceased to decrease. The curve for t = 2008 shows the same old capacities utilized, which were utilized at t = 1997. At t = 2008, the capacity utilization reached saturation. Then it started to decline; see t = 2010, 2015, and 2017. In the real economy, spare capacities are partially used, so they influence the cost inflation. The curves for t = 2015 and 2017 show that the thick tail of capacities disappeared in 2017; therefore, since then, cost inflation practically ceased.

Fig. 7.

Distribution of production capacities $m(t,\tau )$ over the years that they were created τ (in trillions of rubles, 2010) in the years t = 1991, 1997, 2008, 2010, 2015, and 2017.

6 CONCLUSIONS

Here we present some interesting economic conclusions from the results of identifying the parameters of the production function, which were obtained by the high-speed cluster calculations. The conclusions were primarily based on the main result of identification that the average maximum age A of capacities is 25 years in Russia (investment age is A + 1 = 26 years).

(1) The cost inflation caused by the increase in the labor intensity of old capacities ended in 2017 (1991 + 26 = 2017). The old capacities were decommissioned, and cost inflation died out with them.

(2) In order to support the low level of inflation that is necessary to correct structural imbalances, the minimum salary can be raised, thus reducing the death rate of the population and increasing demand for domestic products. It is possible to increase budget expenditure.

(3) Further growth without a high rate of inflation is possible only through investments in new capacities; it is unprofitable to utilize old capacities.

(4) Scientific knowledge will be in demand for starting up production capacities with new technologies.

(5) Money creation can promote growth because inflation is limited.

(6) It is necessary to train staff to utilize new production assets.

(7) The transition to balanced growth path within the economic policy requires targeting (providing the necessary minimum of) the share of new production capacities σ, which, according to Corollary 2 of Theorem 1, is related to the economic growth rate $\gamma = \varepsilon \sigma + \eta$, where η is the rate of the increase in employment in the economy. Having substituted the above-mentioned results of identification, we obtain the minimum necessary growth rate γ = 0.049. It means that the economy will need relevant state investments, for example in infrastructure, for several years until the private investments in the economy grow stronger.

Secondly, the age limit of the capacities is an additional control tool, and the conclusions stated above are true under the conditions that it is constant in Russia. In order to achieve a higher growth rate in the Russian economy, the average age limit of the production capacities should be decreased by adequate measures.

APPENDIX A

Proof of Theorem 1. Statement 1 follows directly from (9). In order to prove Statement 2 (another formulation of Lemma 1), it is sufficient to divide (5) by $M(t)$, to find the derivative of $M(t)$ in the obtained equation according to (9), and to use Statement 1. The expression of production function (10) in Statement 3 directly follows from the substitution of the constant share of the new capacity $\sigma$ into relations (6). Under balanced growth (9), the values $M(t)$ and $Y(t)$ grow at a constant rate; therefore $f(t,x) = {\text{const}}$ and Statement 4 follows from (10), which completes the proof of Theorem 1.

Proof of Theorem 2. According to Lemma 1, the growth rate $\gamma$ (7) is determined by relation (8). Equation (8) has a unique positive solution if the derivative of the left-hand side of this equation is greater than the derivative of the right-hand side at $\varphi = 0$, which satisfies the condition $A > {1 \mathord{\left/ {\vphantom {1 \sigma }} \right. \kern-0em} \sigma }$ of Lemma 1. Statement 1 is proved by substituting (7) and (8) into the parametric expression for the production function (6). Finally, we obtain relation (10). Statement 2 follows from the definition of the production function $Y(t) = M(t)f(t,x)$ and equalities (10) and (12). Statement 3 follows from Statement 2, condition (13), and Eq. (2) describing the dynamics of the lowest labor intensity. In order to prove Statement 4, we take into consideration that it follows from condition (13) that the growth rate of the new capacities $J(t)$ coincides with the growth rate of the aggregate capacity $M(t)$, and then, according to (11) and (12), the share of savings in relation to the output decreases, ${{b(t)J(t)} \mathord{\left/ {\vphantom {{b(t)J(t)} {Y(t)}}} \right. \kern-0em} {Y(t)}} = ({{{{b}_{0}}{{J}_{0}}} \mathord{\left/ {\vphantom {{{{b}_{0}}{{J}_{0}}} {{{Y}_{0}}}}} \right. \kern-0em} {{{Y}_{0}}}})\exp ( - \beta \sigma t)$, and consequently, the share of consumption ${{C(t)} \mathord{\left/ {\vphantom {{C(t)} {Y(t)}}} \right. \kern-0em} {Y(t)}} = 1 - {{b(t)J(t)} \mathord{\left/ {\vphantom {{b(t)J(t)} {Y(t)}}} \right. \kern-0em} {Y(t)}}$ increases. According to Statement 2, the average consumption in the transient mode is determined by the relation

$$c(t) = \left( {f({x \mathord{\left/ {\vphantom {x {\nu (t)}}} \right. \kern-0em} {\nu (t)}}) - \sigma {{b}_{0}}\exp \left( { - \beta \sigma t} \right)} \right){{\nu (t)} \mathord{\left/ {\vphantom {{\nu (t)} {\left( {{{\nu }_{0}}x} \right)}}} \right. \kern-0em} {\left( {{{\nu }_{0}}x} \right)}}\exp \left( {\varepsilon \sigma t} \right),$$

i.e., the average consumption in the transition mode (at ${x \mathord{\left/ {\vphantom {x {\nu (t)}}} \right. \kern-0em} {\nu (t)}} = {\text{const}}$) grows faster than in the balanced growth mode (9). This completes the proof of Theorem 2.