Keywords

1 Introduction

The golden rule of capital accumulation is well known in mathematical economics and it is included in standard courses on economic growth [1, 2]. The solution to this problem has been considered in many works, see, for example, [3,4,5]. The golden rule of capital accumulation establishes a condition under which the capital-labor ratio (capital stock per worker) maximizes average consumption (consumption per worker) in a steady state of economic growth. In a simple model without scientific and technological progress, the golden rule boils down to the fact that the marginal productivity of capital is equal to the sum of the population growth rate and the rate of capital degradation.

A clear mathematical formulation of the problem of optimal economic growth for the simplest dynamic economic model, taking into account restrictions on control, is presented, for example, in [6]. In addition, it is possible to solve the control synthesis problem, i.e. find an explicit expression of the dependence of the optimal control on the state of the system (phase coordinate) [6]. The latter allows to formulate a universal golden rule [6] for choosing the optimal level of consumption depending on the current level of capital-labor ratio, valid for all time points and for all not too large initial levels of capital-labor ratio. On the contrary, here the golden rule is not considered for the entire optimal trajectory of movement, but only for those areas where the optimal control does not take boundary values and for characteristic growth pathes. However, this problem is considered here not only for the standard Cobb-Douglas production function, but in the main for a new endogenous production function. This allows us to get new effects that have an economic applied character.

In the extreme case, if the savings are zero, all the income is consumed, which cancels the investment as well as the replacement of the capital which wears out. In the long run, when capital is fully consumed, income is reduced to almost zero. The same is true for consumption: an excessive preference for short-term consumption is to the detriment of future generations. If the savings are equal the full income, all these revenues could go to investment but consumption is zero and there is no incentive to invest. Growth is zero, too. Excessive foresight does not benefit future generations either. Between these two extremes, there is (at least) a level of savings that maximizes average growth, allowing the growth of regular and identical consumption for all generations (intergenerational solidarity). According to [4], the only way to reach this optimum is to set the real interest rate at a value equal to population growth. Indeed, if we can adjust the marginal productivity rate of capital to the population growth rate, we can also adjust the savings rate to the share of profit in the national income.

Formally writing, the nation wants to maximize intertemporal utility

$$ \int _0^{\infty } e^{-\delta t} u(c_t)dt,$$

where \(u(c_ {t})\) is the instant utility of consumption and \(\delta \) is the subjective rate of time discount. If K is capital, L is labor and Y is output of production, then \(k=K/L\) is the ratio of capital to labor, \(f(k)=Y/L\) is the homogeneous of degree one production function. The evolution of consumption depends on the differential equation

$$ \dot{k}=f(k)-nk-c,$$

where \(c=C/L\) is the per capita consumption, \(n=\dot{L}/L\) is the growth rate of the population, and the point above a variable is the derivative over time. The current value of the Hamiltonian has the form

$$H=u(c_t)+\chi \left( f(k)-nk-c\right) ,$$

where \(\chi \) is the constant auxiliary variable. After substituting this variable under first-order conditions, we find

$$\left( {u^{\prime \prime }(c)}/{u^{\prime }(c)}\right) {\dot{c}}=\delta +n-f^{\prime }(k).$$

Really, \(\partial H/\partial c_t = \partial u/\partial c_t - \chi =0\), \(\dot{\chi }=\chi \delta -\partial H/\partial k =\chi (\delta -f^{\prime }(k)+n)\), so \(\chi =u^{\prime }(c)\), and \(\dot{\chi }=u^{\prime \prime }(c)\dot{c}\). For stationary equilibrium we have \(\dot{c} = 0\) and then

$$f^{\prime }(k^{*})=\delta +n.$$

With this modified golden rule, the ratio of capital to labor will be smaller because of the impatience of the society represented by the discount rate of time.

Further, in the work, we will not take into account the discount rate, but instead of this we will take into account technological progress, and also move on from considering capital to considering production capacity.

In [7], on the basis of aggregating the original micro-description of production, a new class of production functions was obtained. Such a production function, along with other parameters, contains directly the growth rate of the economy, which makes the task of finding optimal accumulation more interesting, even in the absence of scientific and technological progress. The production function [7] shows the dependence of output on production factors, which are total labor and total production capacity. Production capacity is the highest possible output. For the transition from the capital to the production capacity, the capital intensity is used.

Works [8, 9] give numerical representations of the endogenous production function of type [7], which, along with the growth rate of the economy and the rate of degradation of capacities, contains the maximum age of production capacity. Thus, the production capacity leaves the production process, not only due to its degradation but also due to its dismantling when exceeding the maximum age (due to its obsolescence).

In the description of the golden rule, we move from the variable capital-labor ratio to the average labor intensity of capacities.

2 Solow Model in Terms of Capacity and Labor Intensity

Here we express the Solow model of economic growth [3] in terms of the Houthak-ker–Johansen model [7, 10, 11]: Y(t)—total output (GDP), M(t)—total production capacity (maximum possible output), L(t)—the number of workers (it is proportional to population), \(\nu (t)\)—the smallest labor intensity (labor input rate per unit of product, that is the number of workers per one unit of output). The last one characterizes technical progress. In these variables, we assume that a production function sets the dependence of output (GDP) Y(t) on the total production capacity (in units of output) M(t) and total effective labor, taking into account its efficiency (in units of output it is the ratio of workers to the smallest labor intensity), \(L(t)/\nu (t)\). Technological progress that enters in this way is known as Harrod-neutral or labor-augmenting [2]. Note, that in this formulation, the use of a homogeneous production function of the first degree does not cause problems with the units of measurement. For example, for the Cobb–Douglas production function \(Y=M^{\alpha } (L/\nu )^{\beta }\) with \(\alpha +\beta =1\), we have the units of the output \([Y] = [Y]^{\alpha } [Y]^{1-\alpha }=[Y]\).

For a homogeneous production function \(Y(t) = F(M(t), L(t)/\nu (t))\) one of two variables can be taken out in order to obtain an intensive form of production function F, function f of one variable. In our case, it is more convenient to take out the total production capacity, then

$$\begin{aligned} Y(t) = M(t) f(x), x=\frac{L(t)}{\nu (t)M(t)} \end{aligned}$$
(1)

and the production function in intensive form has the meaning of the function of loading the total capacity. If the output does not exceed the maximum possible output, \(Y(t) \le M(t)\) (the production capacity overload is not allowed), then \( f(x) \le 1\). For example, for the Cobb–Douglas production function the function of capacity loading \(f(x)=x(t)^{\beta }\), where \(\beta \) is output elasticity of labor.

In a closed economy, the output Y(t) is divided into the consumption C(t) and the capital accumulation of bJ(t):

$$\begin{aligned} Y(t) = bJ (t) + C (t). \end{aligned}$$
(2)

In (2) \( b> 0 \) is the coefficient of incremental capital-output ratio, it shows how much capital-forming products need to be purchased to create one unit of capacity. The value of J(t) is the volume of newly created capacity.

If we use the usual dynamics of total production capacity, then

$$\begin{aligned} \dot{M}(t) {\mathop {=}\limits ^{\mathrm {def}}} \frac{dM(t)}{dt}=J(t)-\mu M(t), \end{aligned}$$
(3)

where \(\mu >0\) is a depreciation rate of capacity.

A rate s of capital accumulation: \( bJ (t) = sY (t) \). Then we have \(J(t)=sf(x)M(t)/b\) and from (3) the tempo of the total production capacity is equal

$$\begin{aligned} \frac{\dot{M}(t)}{M(t)}=\frac{s}{b}f(x)-\mu . \end{aligned}$$
(4)

From the other side, if

$$\begin{aligned} \frac{\dot{L}(t)}{L(t)}=n, -\dot{\nu }(t)/\nu (t)=g, \end{aligned}$$
(5)

where n is the population growth rate, g is the rate of fall of the lowest labor intensity (rate of growth for the level of technology), then from (1) and (5) we have \(M=L/(x \nu )\) and

$$\begin{aligned} \frac{\dot{M}(t)}{M(t)}=n+g-\frac{\dot{x}(t)}{x(t)}. \end{aligned}$$
(6)

The main interest of the model is the dynamics of average labor intensity of the total capacity in relative units with respect to the smallest labor intensity x, the effective labor per unit of capacity stock. In accordance of (4), (6) its behavior over time is given by the next analogy of the key equation of the Solow model in terms of x:

$$\begin{aligned} \frac{\dot{x}(t)}{x(t)}=n+g+\mu -sf(x)/b. \end{aligned}$$
(7)

Stationarity condition is \(\dot{x}(t)=0\), so from here in steady-state

$$\begin{aligned} sf(x) = b(n+g+\mu ). \end{aligned}$$
(8)

If we denote \(\dot{M}(t)/M(t)=\gamma \), then from (6) we obtain that the steady state growth rate is expressed by the relation

$$\begin{aligned} \gamma =n+g. \end{aligned}$$
(9)
Fig. 1.
figure 1

The golden rule saving rate \(s_{gold}=0.35\) for the Cobb–Douglas production function \(f(x)=x^{\beta }\). The vertical axis shows the steady-state of consumption per effective person \(c^{*}\) correspond to each saving rate \(s\in (0,1)\). The curve \(c^{**}\) is obtained under the condition \(f(x)\le 1.\)

Full size image

Labor productivity in relative units \(y {\mathop {=}\limits ^{\mathrm {def}}} \nu (t)Y(t)/L(t) = f(x)/x\). Then the growth rate of labor productivity in relative units is

$$\begin{aligned} \frac{\dot{y}(t)}{y(t)}=\dot{x}(t)\left( \frac{f^{\prime }(x)}{f(x)} - \frac{1}{x(t)}\right) . \end{aligned}$$
(10)

Consumption per effective labor has the form

$$\begin{aligned} c {\mathop {=}\limits ^{\mathrm {def}}} \frac{\nu (t) C(t)}{L(t)} = \frac{f(x)-sf(x)}{x}. \end{aligned}$$
(11)

In steady-state (8) we obtain

$$\begin{aligned} c(x)=\frac{f(x) - b(n+g+\mu )}{x}. \end{aligned}$$
(12)

In accordance with (8) \(x=x(s)\), so that \(c=c(s)\), and from (12) we have

$$\begin{aligned} c^{\prime }_{s}=\left( x f^{\prime }(x) - f(x)+ b(n+g+\mu )\right) \frac{x^{\prime }_{s}}{x^2}. \end{aligned}$$
(13)

So that in terms of \(x=x_{gold}\) the Solow model golden rule be

$$\begin{aligned} x f^{\prime }(x) - f(x)+ b(n+g+\mu ) = 0. \end{aligned}$$
(14)

For the Cobb–Douglas production function \(f(x)=x^{\beta }\) we have from (8) \(sx^{\beta }=b(n+g+\mu )\), and from (14) \((1-\beta )x^{\beta }=b(n+g+\mu )\). So that, \(s=1-\beta =\alpha =\epsilon _M\), where \(\epsilon _M\) is the total output elasticity by total capacity M.

Figure 1 presents the relation between steady-state consumption per effective labor \(c^{*}\) and saving rate s that is implied by (12). The steady-state \(x^*(s)\) is from the condition (8). For the Cobb–Douglas production function \(x^*(s)=(b(n+g+\mu )/s)^{1/\beta }\). Here in Fig. 1 we use \(\beta =0.65\) and the values of the model parameters obtained on the base of statistical data 1970–2017 for the Russian economy [8]: \(b=1.1\), \(n=0.01124\), \(g=0.038115\), \(\mu =0.03155\).

3 An Exogenous Production Function

An exogenous production function for production capacities with limited age was constructed in [8]. The economic system consists of separate production units. The production unit is characterized by the technology used and the capacity—the maximum possible product output per unit of time. The production technology is fully determined by the labor intensity—the norm of the cost of human labor for the production of a unit of product. The production capabilities of such an economic system are described by the value M(t, H) of the total capacity of production units whose technology is \(\lambda \in H \subset R_+^1\).

The production capacity dynamics on micro-level is described by the hypothesis proposed in [7,8,9]. Production capacity decreases due to aging and the number of working places on it is fixed since the creation of this capacity up to reaching age limit A(t).

Hypothesis 1: The number of workplaces in the production unit remains unchanged for each time moment t from the time moment of its creation \(\tau \le t\) until the time moment of its liquidation \(\theta =\tau +A(\theta ) \ge t\) , where A(t) is the age limit of the production capacities, and the production capacity \(m(t,\tau )\) decreases with a constant rate \(\mu >0\).

If the capacities of new production units are created continuously with a speed J(t) and all have the same labor input \(\nu (t)\), which does not increase with time, then the measure M(t, H) has a continuous density \(m (t, \lambda )\), which varies according to a first-order partial differential equation [7]:

$$\begin{aligned} \frac{\partial m(t,\lambda )}{\partial t}=-2\mu m(t,\lambda )-\mu \lambda \frac{\partial m(t,\lambda )}{\partial \lambda } \end{aligned}$$
(15)

with boundary condition

$$\begin{aligned} m(t,\nu )=\frac{J(t)}{\left( \mu \nu (t)-d\nu /dt\right) }. \end{aligned}$$
(16)
Fig. 2.
figure 2

Estimation of the distribution of production capacities of the Russian economy by age (vintage capacity) in 2018, at constant prices 2010. The years of investment are plotted on the horizontal axis.

Full size image

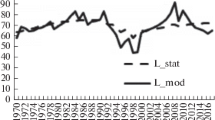
Figure 2 shows the vintage production capacity in 2018. Production capacity measures the maximum output at constant prices of 2010. For the evaluation the capacity, we used the parameters of the micro-description of the model for changes in production capacity. It was assumed that the least laboriousness decreases with the rate \( g (t) = - \dot{\nu }/\nu = \epsilon \sigma (t) \), and the capital intensity coefficient for new capacities also decreases due to increasing of the share of primary industries in the issue, \(\dot{b}/b=- \zeta \sigma (t)\), where \(\sigma =J(t)/M(t)\). Parameter identification was made by comparing the calculated and statistical time series for output and labor according to the data of 1970–2017: \(b(1970)=5.598\), \(\zeta =0.430\), \(\nu (1970)=2.512\), \(\epsilon =0.3465\), \(A=25\). Parameter estimation methodology is described in more detail in [8, 9].

The expression for the production function is more convenient to derive on the basis of a micro-description of the dynamics of production capacity in the variables \( t, \tau \). The initial capacity is \(m(t,t)=J(t)\). Then \(m(t,\tau )=J(\tau )exp(-\mu (t-\tau ))\). This reduction in capacity requires, in order to maintain the number of workplaces, an appropriate increase in labor intensity \(\lambda (t,\tau )=\nu (\tau )exp(\mu (t-\tau ))\), where \(\nu (\tau )\) is the labor intensity on the production unit at moment of its creation \(\tau \). At every time moment t the investors choose the best technology with the smallest amount of labor \(\nu (t)\). This lowest labor intensity is decreased with time due to technological progress with the rate \(g(t)>0\). The total capacity is

$$\begin{aligned} M(t)=\int _{t-A(t)}^{t} J(\tau )e^{-\mu (t-\tau )}d\tau . \end{aligned}$$
(17)

Assuming the total effective labor \(L(t)/\nu (t)\) is used in optimal way starting from the new production capacity with best technology \(\nu (t)\) up to production capacity with age \(\theta (x)\le A\). Then the production function is determined by the next system of two equations:

$$\begin{aligned} f(x)= \int _{t-\theta (x)}^{t} \frac{M(\tau )}{M(t)}\sigma (\tau )e^{-\mu (t-\tau )}d\tau , \end{aligned}$$
(18)
$$\begin{aligned} x= \int _{t-\theta (x)}^{t} \frac{M(\tau )}{M(t)} \frac{\nu (\tau )}{\nu (t)} \sigma (\tau ) d\tau , \end{aligned}$$
(19)

where instead of the differential Eq. (3) for total production capacity M(t) in this case we have the next differential-difference equation for the total capacity M(t) in the intensive variables with the fixed age limit A. It has the form [8]:

$$\begin{aligned} \frac{dM(t)}{dt}=\left( \sigma (t)-\mu \right) M(t)-\sigma (t-A)M(t-A)e^{-\mu A}, \end{aligned}$$
(20)

where \(\sigma (t)\) is the ratio of new capacities to total capacity, \(\sigma (t)=J(t)/M(t)\).

If the ratio \(\sigma (t)\) is constant and total production capacity grows with constant rate

$$\begin{aligned} \sigma (t)=\frac{J(t)}{M(t)}=\sigma , \frac{\dot{M}(t)}{M(t)}=\gamma , \end{aligned}$$
(21)

we can find an exogenous production function.

Based on Proposition 1 from [8], taking into account our notation (1) for x and (5) for g, the following theorem can be formulated.

Theorem 1

Let in a closed economy (2) on a balanced growth path with the rate \(\gamma ,\)

$$M(t)=M_0 e^{\gamma t}, Y(t)=Y_0 e^{\gamma t}, J(t)=J_0 e^{\gamma t}, C(t)=C_0 e^{\gamma t},$$

the following conditions are met:

  1. (a)

    it is true the hypothesis 1 about a fixed number of workplaces and a drop in production capacity at a rate \(\mu \) up to a certain age limit A;

  2. (b)

    it is fixed the maximum age of the production capacities, \(A(t)=A=const\);

  3. (c)

    it is fixed the ratio of incremental capital intensity, \(b(t)=b=const\);

  4. (d)

    it is reduced the least labor intensiveness due to scientific and technical progress in accordance with (5), \(\dot{\nu }(t)/\nu (t)=-g\).

Then the following statements are true:

  1. (1)

    the share of new capacity is fixed: \(\sigma (t)=J(t)/M(t)=\sigma =const\);

  2. (2)

    the dynamics of total production capacity (20) on balanced growth path sets the relationship between the growth rate of economy (21) \(\gamma =\varphi (\sigma , \mu , A) - \mu \) and an implicit function \(\varphi \) of this parameters \(\sigma \), \(\mu \), A by equation

    $$\begin{aligned} \varphi = \sigma (1-e^{-\varphi A}); \end{aligned}$$
    (22)
  3. (3)

    relation (22) gives the following expression for the production function

    $$\begin{aligned} f(x)=\frac{\sigma }{\varphi }\left\{ 1-\left[ 1-\frac{(\varphi -\mu -g)}{\sigma } x\right] ^{\varphi /(\varphi -\mu -g)}\right\} , \end{aligned}$$
    (23)

    where \(\mu \) is the depreciation rate of production capacities, and g is the rate (5) of technological progress;

  4. (4)

    the ratio of the average labor intensity of the production capacities to the least labor intensity is constant: \(x=L(t)/(\nu (t)M(t))=const\).

Proof

It follows directly from the relations (18), (19) for the production function under the conditions (a)–(d) specified in the theorem.

Indeed, on the balanced growth path (BGP) \(\sigma =J(t)/M(t)=J_0/M_0=const\), so the statement (1) is satisfied.

Then, from \(\sigma =const\), \(A=const\), and condition of BGP \(M(t-A)/M(t)=exp(-\gamma A)\) the Eq. (20) gives \(\gamma =-\mu +\sigma (1-exp(-(\gamma +\mu )A))\). By virtue of the notation \(\varphi =\gamma +\mu \), we obtain the relation (22), so the statement (2) is satisfied.

Since on BGP \(M(\tau )/M(t)=exp(-\gamma (t-\tau ))\), so from (18), \(\varphi =\gamma +\mu \), and \(\sigma =const\) we have \(f(x)=(1-exp(-\varphi \theta (x)))\sigma /\varphi \). From (19) considering condition d), \(\nu (\tau )/\nu (t)=exp(g(t-\tau ))\), we have \(x=(1-exp(-(\varphi -\mu -g) \theta (x)))\sigma /(\varphi -\mu -g)\). Excluding from these relations for f and x the value \(exp(-\theta (x))\) we have (23). So, the statement (3) is satisfied.

The statement (4) is satisfied because on BSP we have \(f(x)=Y(t)/M(t)=M_0/Y_0=const\), so \(x=const\).

Now, by elimination the term \(\sigma \) from (22), (23), \(\sigma =\varphi /\left( 1-e^{-\varphi A}\right) \), and using (9),

$$\begin{aligned} \varphi =n+g+\mu , \end{aligned}$$
(24)

we have the next form of the production function in steady-state

$$\begin{aligned} f(x,A)=\frac{1}{(1-e^{-\varphi A})}\left\{ 1-\left[ 1-\frac{n}{\varphi }(1-e^{-\varphi A}) x\right] ^{\varphi /n}\right\} . \end{aligned}$$
(25)

Changes in the average labor intensity x and in the age limit of capacities A change the level of loading f(x, A) of the total capacity.

4 Golden Rule for the Endogenous Production Function

In the model under consideration the total production capacity dynamics (20) differs from the usual Eq. (3), so that we should change the Eq. (4) on the next one:

$$\begin{aligned} \frac{\dot{M}(t)}{M(t)}=\frac{1}{b}sf(x,A)\left( 1-e^{-\varphi A}\right) -\mu . \end{aligned}$$
(26)

In accordance of (26), (6) the effective labor per unit of capacity stock x, the key equation of our model will be

$$\begin{aligned} \frac{\dot{x}(t)}{x(t)}=\varphi - \frac{1}{b} s f(x,A)\left( 1-e^{-\varphi A}\right) . \end{aligned}$$
(27)

So, the dynamics of average labor intensity of the total capacity x depends of the age limit of capacities A.

Instead of (8) in steady-state (\(\dot{x}(t)=0\)) we have

$$\begin{aligned} sf(x,A) = \frac{b\varphi }{\left( 1-e^{-\varphi A}\right) }. \end{aligned}$$
(28)

For the consumption per effective labor (11) in steady-state (28) instead of (12) we have

$$\begin{aligned} c(x,A)=\frac{1}{x}\left( f(x,A) - \frac{b\varphi }{\left( 1-e^{-\varphi A}\right) }\right) . \end{aligned}$$
(29)

Then

$$\begin{aligned} c_{s}^{\prime } = \left\{ \frac{f_{x}^{\prime }}{x}-\frac{f(x,A)-b\varphi /\left( 1-e^{-\varphi A}\right) }{x^{2}} \right\} x_{s}^{\prime }. \end{aligned}$$
(30)

So, the model under consideration golden rule in terms of \(x=x_{gold}\) is

$$\begin{aligned} \left[ x f_{x}^{\prime }(x,A) - f(x,A)\right] \left( 1-e^{-\varphi A}\right) + b\varphi = 0, \end{aligned}$$
(31)

where due to (24) \(\varphi =\gamma +\mu =n+g+\mu \).

For our production function (25) we have

$$\begin{aligned} f_{x}^{\prime } = \left[ 1-\frac{n}{\varphi }(1-e^{-\varphi A}) x\right] ^{-1+\varphi /n}. \end{aligned}$$
(32)

and from (28) and (31)

$$\begin{aligned} s_{gold} = \frac{b\varphi }{1- \left[ 1-zn/\varphi \right] ^{\varphi /n}}, \end{aligned}$$
(33)

where

$$\begin{aligned} z {\mathop {=}\limits ^{\mathrm {def}}} (1-e^{-\varphi A})x_{gold} \end{aligned}$$
(34)

is a root of the transcendental equation

$$\begin{aligned} 1 - \frac{z}{(1-zn/\varphi )}=(1-b\varphi )(1-z n/\varphi )^{\varphi /n}. \end{aligned}$$
(35)

For the endogenous production function (25) from (31)–(33) we have

$$\begin{aligned} s^{*} = 1 - \frac{(1-b\varphi )z^{*}}{b\varphi +(1 - b n)z^{*}}. \end{aligned}$$
(36)
Fig. 3.
figure 3

The golden rule saving rate \(s_{gold}=0.67\) for the exogenous production function f(x, A). The vertical axis shows the steady-state of consumption per effective person \(c^{*}\) correspond to each saving rate \(s\in (0,1)\).

Full size image

From (28), (31) we have the next algorithm for calculating the curve \(c=c (s)\) for the production function in a stable-stage:

$$\begin{aligned} z = \frac{\varphi }{n}\left[ 1-\left( 1-\frac{b\varphi }{s}\right) ^{n/\varphi }\right] , \end{aligned}$$
(37)
$$\begin{aligned} B {\mathop {=}\limits ^{\mathrm {def}}} \left( 1-e^{-\varphi A}\right) f(x,A)=1-\left( 1-\frac{n}{\varphi } z\right) ^{\varphi /n}, \end{aligned}$$
(38)
$$\begin{aligned} c= \frac{1}{z}(B-b\varphi ). \end{aligned}$$
(39)

The age limit A value explicitly affects the value of \(x_{gold}\) due to the formula (34). The value A is not explicitly included in the expression for the steady-state consumption per effective labor \(c^*\) due to (37)–(39):

$$\begin{aligned} c^* = \frac{n b (1/s - 1)}{1 - (1 - b\varphi /s)^{n/\varphi }}. \end{aligned}$$
(40)

The dependence of the steady-state consumption per effective person \(c^{*}\) (40) on A exists since \(\varphi =\varphi (\sigma ,A)\) in accordance with (22).

Figure 3 presents the relation between steady-state consumption per effective labor \(c^{*}\) and saving rate s that is implied by (29). The steady-state \(x^*(s)\) is from the condition (28). Here in Fig. 3 we use the values for parameters of the current Russian economy (in particular, see above Sect. 3): \(b=1.1\), \(n=0.01124\), \(g=0.038115\), \(\mu =0.03155\).

5 Conclusions and Implication

The introduction provides a brief reference to the literature on the problem of the golden rule saving rate.

The second section shows that the Houthakker–Johansen model notation [10, 11] is suitable for describing classical problems, in particular, the problem of golden rule saving rate. At the same time, the concept of the production function in the model has a clear economic meaning of capacity utilization, and the variables have a decent dimension: either dimensionless or have dimension per unit of time.

The third section presents the endogenous production function, in which the Houthakker–Johansen model manifests itself well. Here production function is based on the distribution of production capacity for technology. In the end, the production function is presented in the stationary mode parameters.

In the fourth section, formulas for calculating the golden growth for this endogenous production function are obtained. As it turned out, the age limit of capacities does not affect the steady-state consumption per effective labor, but it affects the value of the effective labor per unit of the total capacity.

It can be concluded that the presentation of the golden rule for the exogenous production function can be used in education courses for students of classical mathematical economics. It gives food for thought about the current state of the economy.

Phelps in his Nobel lecture [12] gives an overview of works that take into account the realities of the modern economy. As an example, he points out his own models that take these realities into account, or at least remove some of the limitations of the neoclassical approach. In the model of exogenous production function presented here, an example of a departure from neoclassical principles is also given. In particular, the production function built here takes into account structural changes, and its analytical form is valid under certain conditions. In the numerical experiments with the model it is possible to use the micro-description of production sector. This saves the proposed mathematical description for the stages of the production cycle of the economy, in which there are sharp changes in the structure of production capacities.