Constructing a Limiter Based on Averaging the Solutions for the Discontinuous Galerkin Method

Abstract

The Galerkin method with discontinuous basis functions has proved to be effect in solving hyperbolic systems of equations numerically. However, to ensure the solution yielded by this method is monotonic, a smoothing operator is required to be used, especially if the solution contains strong discontinuities. In this paper, a well-proven smoothing operator based on a WENO reconstruction and a smoothing operator of a new type based on averaging the solutions that takes into account the rate of change of the solution and the rate of change of its derivatives is considered. The effect of these limiters in solving a series of test problems is compared. The application of the proposed smoothing operator is shown to be as good as the action of a WENO limiter, in some cases even exceeding it in the accuracy of the resulting solution, which is confirmed by the numerical studies.

1 INTRODUCTION

The Galerkin method with discontinuous basis functions [1], which is characterized by a high order of accuracy on smooth solutions, is widely applied to solve gas dynamics problems. We know that to ensure the monotonicity of the solution yielded by this method, the so-called slope limiters or limiters are required to be introduced, especially if the solution has strong discontinuities. However, limiters may have a negative effect on the accuracy of the resulting solution [2–4]. Therefore, it is still a topical issue to preserve the order of accuracy of the solution and ensure the solution is monotonic.

The classical Cockburn limiter [1] is the most widely used one. This limiter is easy to implement in a multidimensional case on grids of an arbitrary structure. However, it reduces the accuracy of the resulting solution. Various approaches to resolve this issue have been recently developed. One of the approaches to create a limiter of a high order of accuracy is proposed in the works of Krivodonova [5]. However, this limiter works well only on structured grids. Another approach to creating a high-order limiter is to use a WENO limiter [6–10].

In this work, we consider the well-proven [6] smoothing operator based on a WENO reconstruction and the smoothing operator of a new type that takes into account the rate of change of the solution and the rate of change of its derivatives. The ideas used in constructing these limiters can be easily moved to a multidimensional case and grids of an arbitrary structure and do not decrease the order of the scheme theoretically.

2 DESCRIPTION OF THE DISCONTINUOUS GALERKIN METHOD FOR EULER EQUATIONS

Consider the Euler equation written in the conservative form

$${{\partial }_{t}}{\mathbf{U}} + \nabla \cdot {\mathbf{F}}({\mathbf{U}}) = 0$$

((1))

with the addition of the appropriate initial boundary conditions, whose form depends on the particular problem and will be made more specific below.

The conservative variables U and components of the flow function F(U) are given as

$${\mathbf{U}} = \left\{ \begin{gathered} \rho \hfill \\ \rho u \hfill \\ E \hfill \\ \end{gathered} \right\},\,\,\,\,{{{\mathbf{F}}}_{x}}\left( {\mathbf{U}} \right) = \left\{ \begin{gathered} \rho u \hfill \\ \rho {{u}^{2}} + p \hfill \\ (E + p)u \hfill \\ \end{gathered} \right\},$$

((2))

where ρ is the density of the liquid, u is the speed, p is the pressure, $\varepsilon$ is specific internal energy, and $E = \rho (\varepsilon + {{{{u}^{2}}} \mathord{\left/ {\vphantom {{{{u}^{2}}} 2}} \right. \kern-0em} 2})$ is the total energy per unit volume.

To find the pressure p, we use the state equation of the ideal gas

$$p = (\gamma - 1)\rho \varepsilon ,$$

where γ is the adiabatic index.

To apply the discontinuous Galerkin method, we cover the segment where we search for the solution by the grid $0 = {{x}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \leqslant {{x}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} \leqslant ... \leqslant {{x}_{{N + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = L$ with the step $\Delta {{x}_{i}}$$= ({{x}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - {{x}_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}})$.

In each interval ${{x}_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \leqslant x \leqslant {{x}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, we search for the approximate solution of the system of equations (1) as the projection of the vector of the conservative variables $U = (\rho ,\rho u,E)$ onto the space of polynomials P(х) of power n in the basis $\left\{ {{{\phi }_{k}}(x)} \right\}$ with the time-dependent coefficients. Then, the solutions have the form

$${{U}_{h}}(x,t) = \sum\limits_{k = 0}^n {{{U}_{k}}(t){{\phi }_{k}}(x)} ,$$

((3))

where n is the degree of polynomials and ${{\phi }_{k}}(x)$ is the respective basis function.

The discontinuous Galerkin method searches for the approximate solution of system (1) as the solution to the following system [1]

$$\begin{gathered} \int\limits_{{{I}_{i}}} {{{\partial }_{t}}{{U}_{h}}(x,t){{\phi }_{k}}(x)dx - \int\limits_{{{I}_{i}}} {F({{U}_{h}}(x,t)){{\partial }_{x}}{{\phi }_{k}}(x)dx} } \\ + \,\,{{F}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\phi }_{k}}(x_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{l}) - {{F}_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\phi }_{k}}(x_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{r}) = 0, \\ \end{gathered} $$

((4))

where i = 1, …, N, k = 0, 1, 2. In (4), ${{U}_{h}}(x,t) = \left( \begin{gathered} {{\rho }_{h}}(x,t) \hfill \\ \rho {{u}_{h}}(x,t) \hfill \\ {{E}_{h}}(x,t) \hfill \\ \end{gathered} \right)$ is the vector of the solution, ${{\phi }_{k}}(x_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{l})$, ${{\phi }_{k}}(x_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{r})$ is the basis function with the number k on the interval I_i calculated at the points ${{x}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, ${{x}_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, and ${{F}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},{{F}_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, which are discrete flows that are monotonic functions of two variables

$${{F}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \Phi ({{U}_{h}}(x_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{l},t),{{U}_{h}}(x_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{r},t)),\,\,\,\,{{F}_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \Phi ({{U}_{h}}(x_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{l},t),{{U}_{h}}(x_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{r},t)),$$

such that the fitting condition

$$\Phi ({{U}_{h}}(x_{i}^{{}},t),{{U}_{h}}(x_{i}^{{}},t)) = F({{U}_{h}}(x_{i}^{{}},t))$$

holds for them.

In this work, we used the Rusanov–Lax–Friedrichs flows (5) [11, 12] and the Godunov flow [13] as a numerical flow.

$$\begin{gathered} \Phi ({{U}_{h}}(x_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{l},t),{{U}_{h}}(x_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{r},t)) \\ = \frac{1}{2}\left( {F({{U}_{h}}(x_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{l},t)) + F({{U}_{h}}(x_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{r},t)) - A({{U}_{h}}(x_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{r},t) - {{U}_{h}}(x_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{l},t))} \right), \\ A = \mathop {\max }\limits_i \left( {\left| {u_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{l}} \right| + c_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{l},\left| {u_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{r}} \right| + c_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{r}} \right), \\ \end{gathered} $$

((5))

where ${{u}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ is the speed and ${{c}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ is the speed of sound.

2.1 Constructing the WENO Reconstruction Based Limiter for the Discontinuous Galerkin Method

We know that to ensure the solution yielded by the discontinuous Galerkin method is monotonic, we need to introduce the so-called slope limiters or limiters, especially if the solution has strong discontinuities. A limiter is an operator acting on the function of the approximate solution on each interval ${{x}_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},{{x}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$. According to [1], we use $\Lambda {{\Pi }_{h}}u$ to designate the action of this operator on the function u.

In [6], a limiter for the discontinuous Galerkin method (DGM) is proposed based on a WENO reconstruction, allows preserving the high level of accuracy of the method and does not distort the solution profile. We follow this work to describe the limiting WENO procedure for DGM.

At the first stage, we need to find the faulty cells, i.e., the cells that may require limiting.

At the next stage, the numerical solution is replaced by the reconstructed one in the faulty cells, with the polynomials yielded during reconstruction preserving the original integral average value in the cell and the high order of accuracy, while being less subject to oscillations.

To find the faulty cells, we use the TVBminmod limiter [6]. We designate the average value of the solution u in the cell by

$${{\bar {u}}_{j}} = \frac{1}{{\Delta {{x}_{j}}}}\int\limits_{{{I}_{j}}} {udx} .$$

We also designate

$${{\tilde {u}}_{j}} = u_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ - } - {{\bar {u}}_{j}},\,\,\,\,{{\tilde {\tilde {u}}}_{j}} = {{\bar {u}}_{j}} - u_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ + },$$

where ${{\tilde {u}}_{j}}$ and ${{\tilde {\tilde {u}}}_{j}}$ are transformed either by the classical minmod limiter

$$\begin{gathered} \tilde {u}_{j}^{{\bmod }} = \min \bmod \left( {{{{\tilde {u}}}_{j}},{{\Delta }_{ + }}{{{\bar {u}}}_{j}},{{\Delta }_{ - }}{{{\bar {u}}}_{j}}} \right),\,\,\,\,\tilde {\tilde {u}}_{j}^{{\bmod }} = \min \bmod \left( {{{{\tilde {\tilde {u}}}}_{j}},{{\Delta }_{ + }}{{{\bar {u}}}_{j}},{{\Delta }_{ - }}{{{\bar {u}}}_{j}}} \right), \\ {{\Delta }_{ + }}{{{\bar {u}}}_{j}} = {{{\bar {u}}}_{{j + 1}}} - {{{\bar {u}}}_{j}},\,\,\,\,{{\Delta }_{ - }}{{{\bar {u}}}_{j}} = {{{\bar {u}}}_{j}} - {{{\bar {u}}}_{{j - 1}}}, \\ \end{gathered} $$

where the minmod function is specified in (6) or via the transformed TVBminmod function (7)

$$\min \,\bmod ({{a}_{1}},...,{{a}_{K}}) = \left\{ \begin{gathered} \operatorname{sgn} ({{a}_{1}})\mathop {\min }\limits_{1 \leqslant j \leqslant K} \left| {{{a}_{j}}} \right|\,\,{\text{if}}\,\,\operatorname{sgn} ({{a}_{1}}) = \operatorname{sgn} ({{a}_{2}}) = ... = \operatorname{sgn} ({{a}_{K}}), \hfill \\ 0,\,\,\,\,{\text{otherwise,}} \hfill \\ \end{gathered} \right.$$

((6))

$$\tilde {m}({{a}_{1}},...,{{a}_{K}}) = \left\{ \begin{gathered} {{a}_{1}}\,\,{\text{if}}\,\,\left| {{{a}_{1}}} \right| \leqslant M{{h}^{2}}, \hfill \\ \min \,mod({{a}_{1}},...,{{a}_{K}}),\,\,\,\,{\text{otherwise,}} \hfill \\ \end{gathered} \right.$$

((7))

where the parameter М is chosen according to the solution of the problem. To find the faulty cells, we assume that if one of the minmod functions has worked, i.e., it has returned values different from the first argument, the cell will be marked faulty.

2.2 Constructing New Polynomials on Faulty Cells Using the WENO Limiter

The principal idea of the WENO limiter is that we construct a new polynomial on a faulty cell that is a convex combination of the original polynomial and the polynomials on the adjacent cells with the necessary corrections to preserve the integral average in the cell.

We assume that we need to limit the solution in the cell ${{I}_{j}}$. We use ${{P}_{1}}$ to designate the polynomial reconstructed on this cell, and we use ${{P}_{0}}$ and ${{P}_{2}}$ to designate the polynomials on the cells to the left $({{I}_{{j - 1}}})$ and right $({{I}_{{j + 1}}})$ of ${{I}_{j}}$, respectively.

To preserve the integral average value ${{\bar {P}}_{1}}$ at the current cell, we perform the transformations

$${{\tilde {P}}_{0}}(x) = {{P}_{0}}(x) - {{\bar {P}}_{0}} + {{\bar {P}}_{1}},\,\,\,\,{{\tilde {P}}_{2}}(x) = {{P}_{2}}(x) - {{\bar {P}}_{2}} + {{\bar {P}}_{1}},$$

where

$${{\bar {P}}_{0}} = \frac{1}{{\Delta x}}\int\limits_{{{I}_{j}}} {{{P}_{0}}(x)dx} ,\,\,\,\,{{\bar {P}}_{1}} = \frac{1}{{\Delta x}}\int\limits_{{{I}_{j}}} {{{P}_{1}}(x)dx} ,\,\,\,\,{{\bar {P}}_{2}} = \frac{1}{{\Delta x}}\int\limits_{{{I}_{j}}} {{{P}_{2}}(x)dx} .$$

Then, the transformed polynomial will appear as follows,

$$P_{1}^{{{\text{new}}}}(x) = {{\omega }_{0}}{{\tilde {P}}_{0}}(x) + {{\omega }_{1}}{{P}_{1}}(x) + {{\omega }_{2}}{{\tilde {P}}_{2}}(x),$$

((8))

and the integral average and the order of accuracy of the new polynomial $\bar {P}_{1}^{{{\text{new}}}}(x)$ coincide with the initial ones for ${{\bar {P}}_{1}}(x)$ if ${{\omega }_{0}} + {{\omega }_{1}} + {{\omega }_{2}} = 1$.

We can calculate the normalized weights by the formulas

$${{\omega }_{l}} = {{{{{\bar {\omega }}}_{l}}} \mathord{\left/ {\vphantom {{{{{\bar {\omega }}}_{l}}} {\sum\limits_{k = 0}^2 {{{{\bar {\omega }}}_{k}}} }}} \right. \kern-0em} {\sum\limits_{k = 0}^2 {{{{\bar {\omega }}}_{k}}} }},$$

where ${{\bar {\omega }}_{l}}$ are nonnormalized nonlinear weight functions of the linear weights ${{\gamma }_{l}}$ and the so-called smoothness indicators ${{\beta }_{l}}$

$${{\bar {\omega }}_{l}} = \frac{{{{\gamma }_{l}}}}{{{{{(\varepsilon + {{\beta }_{l}})}}^{r}}}},\,\,\,\,{{\beta }_{l}} = \sum\limits_{s = 1}^n {\int\limits_{{{I}_{j}}} {\Delta x_{j}^{{2s - 1}}} } {{\left( {\frac{{{{\partial }^{s}}}}{{\partial {{x}^{s}}}}{{P}_{l}}(x)} \right)}^{2}}dx,\,\,\,\,l = 0,1,2,$$

where n is the order of the polynomial. In all the calculations, $\varepsilon = {{10}^{{ - 6}}}$, r = 2.

The linear weights can be chosen to be any positive numbers, with their sum equaling 1. Since the central cell is most frequently the best one for the smooth solution, then according to [6], we give the highest linear weight to it, i.e., ${{\gamma }_{1}} \gg {{\gamma }_{0}},$${{\gamma }_{1}} \gg {{\gamma }_{2}}$. In the calculations below, we use the coefficients given in the original work—${{\gamma }_{0}} = 0.001,$${{\gamma }_{1}} = 0.998,$ and ${{\gamma }_{2}} = 0.001$.

2.3 Constructing the Limiter Based on Averaging the Solution for the Discontinuous Galerkin Method

In this work, we propose a different approach to construct the limiter. We consider a new polynomial

$$P_{j}^{{sm}} = \bar {P}_{j}^{{}} + P_{j}^{0}\left( {1 - \max ({{\alpha }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},{{\alpha }_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}})} \right),\,\,\,\,P_{j}^{0} = P_{j}^{{}} - \bar {P}_{j}^{{}}.$$

((9))

We need to choose the criterion for choosing the coefficients ${{\alpha }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},{{\alpha }_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$.

First, we consider the order of deviation of the neighboring polynomials from the arithmetic average of their integral average values. As one of the coefficients, we take

$$\begin{gathered} {{\mu }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \frac{{\int\limits_{{{x}_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}^{{{x}_{{j + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} {{{{({{P}_{j}} - {{P}_{{j + 1}}})}}^{2}}dx} }}{{\left( {\int\limits_{{{x}_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}^{{{x}_{{j + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} {{{{({{P}_{j}} - P_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{{\text{av}}}})}}^{2}}dx + \int\limits_{{{x}_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}^{{{x}_{{j + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} {{{{({{P}_{{j + 1}}} - P_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{{\text{av}}}})}}^{2}}dx} } } \right)}}, \\ P_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{{\text{av}}}} = \frac{{{{{\bar {P}}}_{j}} + {{{\bar {P}}}_{{j + 1}}}}}{2}. \\ \end{gathered} $$

((10))

This coefficient does not reduce the order of the obtained polynomial.

Note that

$$\frac{{{{\partial }^{k}}{{P}_{j}}}}{{\partial {{x}^{k}}}}({{x}_{j}}) = {{\gamma }_{k}}u_{k}^{j},\,\,\,\,\frac{{{{\partial }^{k}}{{P}_{{j + 1}}}}}{{\partial {{x}^{k}}}}({{x}_{{j + 1}}}) = {{\gamma }_{k}}u_{k}^{{j + 1}},\,\,\,\,k = 1,n,$$

((11))

in the discontinuous Galerkin method, where ${{x}_{j}}$ is the center of the cell ${{I}_{j}}$. The constants ${{\gamma }_{k}}$ depend on the choice of the basis in the discontinuous Galerkin method.

Note that it follows from equalities (11) that

$$\frac{\partial }{{\partial x}}\left( {\frac{\partial }{{\partial t}}\frac{{{{\partial }^{{k - 1}}}P}}{{\partial {{x}^{{k - 1}}}}}} \right)({{x}_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}) = \frac{1}{{\Delta x}}\left( {\frac{\partial }{{\partial t}}\frac{{{{\partial }^{{k - 1}}}{{P}_{{j + 1}}}}}{{\partial {{x}^{{k - 1}}}}}({{x}_{{j + 1}}}) - \frac{\partial }{{\partial t}}\frac{{{{\partial }^{{k - 1}}}{{P}_{j}}}}{{\partial {{x}^{{k - 1}}}}}({{x}_{j}})} \right).$$

However, we can specify the time derivatives $\frac{\partial }{{\partial t}}\frac{{{{\partial }^{{k - 1}}}P}}{{\partial {{x}^{{k - 1}}}}}({{x}_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}})$ as

$$\frac{\partial }{{\partial t}}\frac{{{{\partial }^{k}}P}}{{\partial {{x}^{k}}}}({{x}_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}) = \frac{1}{2}\left( {\frac{\partial }{{\partial t}}\frac{{{{\partial }^{k}}{{P}_{{j + 1}}}}}{{\partial {{x}^{k}}}}({{x}_{{j + 1}}}) + \frac{\partial }{{\partial t}}\frac{{{{\partial }^{k}}{{P}_{j}}}}{{\partial {{x}^{k}}}}({{x}_{j}})} \right).$$

Thus, we can specify coefficient ${{\beta }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ (12) via the rate of change of the solution and its derivatives

$${{\beta }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \sum\limits_{s = 1}^k {\left| {\frac{{\frac{1}{{\Delta x}}\left( {\frac{\partial }{{\partial t}}{\kern 1pt} \frac{{{{\partial }^{{s - 1}}}{{P}_{{j{\kern 1pt} + 1}}}({{x}_{{j{\kern 1pt} + 1}}})}}{{\partial {{x}^{{s - 1}}}}} - \frac{\partial }{{\partial t}}{\kern 1pt} \frac{{{{\partial }^{{s - 1}}}{{P}_{j}}({{x}_{j}})}}{{\partial {{x}^{{s{\kern 1pt} - 1}}}}}} \right) - \frac{1}{2}\left( {\frac{\partial }{{\partial t}}{\kern 1pt} \frac{{{{\partial }^{s}}{{P}_{{j{\kern 1pt} + 1}}}({{x}_{{j + 1}}})}}{{\partial {{x}^{s}}}} + \frac{\partial }{{\partial t}}{\kern 1pt} \frac{{{{\partial }^{s}}{{P}_{j}}{\kern 1pt} ({{x}_{j}})}}{{\partial {{x}^{s}}}}} \right)}}{{\frac{1}{{\Delta x}}\left( {\frac{\partial }{{\partial t}}{\kern 1pt} \frac{{{{\partial }^{{s - 1}}}{{P}_{{j{\kern 1pt} + 1}}}({{x}_{{j{\kern 1pt} + 1}}})}}{{\partial {{x}^{{s{\kern 1pt} - 1}}}}} - \frac{\partial }{{\partial t}}{\kern 1pt} \frac{{{{\partial }^{{s - 1}}}{{P}_{j}}({{x}_{j}})}}{{\partial {{x}^{{s{\kern 1pt} - 1}}}}}} \right) + \frac{1}{2}\left( {\frac{\partial }{{\partial t}}{\kern 1pt} \frac{{{{\partial }^{s}}{{P}_{{j{\kern 1pt} + 1}}}({{x}_{{j + 1}}})}}{{\partial {{x}^{s}}}} + \frac{\partial }{{\partial t}}{\kern 1pt} \frac{{{{\partial }^{s}}{{P}_{j}}({{x}_{j}})}}{{\partial {{x}^{s}}}}} \right)}}} \right|} .$$

((12))

We compose the coefficient

$${{\alpha }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{\mu }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\beta }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\frac{{{{c}_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\Delta t}}{{\Delta x}},$$

((13))

proportional to the time step but still preserving the dimensionality.

The coefficient includes the multiplier ${1 \mathord{\left/ {\vphantom {1 {\Delta x}}} \right. \kern-0em} {\Delta x}}$, which can theoretically reduce the accuracy of the solution; therefore, if we replace it by the multiplier ${{{{\rho }_{1}}} \mathord{\left/ {\vphantom {{{{\rho }_{1}}} {\bar {\rho }}}} \right. \kern-0em} {\bar {\rho }}}$, where ${{\rho }_{h}}(x) = \sum\nolimits_{k = 0}^n {{{\rho }_{k}}(x)} {\kern 1pt} {{\phi }_{k}}(x)$ is density (1), $\bar {\rho }$ is the integral average, and ${{\rho }_{1}}$ is the first derivative ${{\rho }_{h}}(x)$, we can theoretically preserve the order of accuracy of the scheme

$${{\alpha }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{\mu }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\beta }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\frac{{{{c}_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\Delta t}}{{{{\bar {\rho }} \mathord{\left/ {\vphantom {{\bar {\rho }} {{{\rho }_{1}}}}} \right. \kern-0em} {{{\rho }_{1}}}}}}.$$

((14))

3 STUDYING THE ORDER OF ACCURACY OF THE METHOD

To study how the limiter influences the order of accuracy of the discontinuous Galerkin method, we consider the problem described in detail in [2]. As the initial data, we use a simple wave with constant entropy ${p \mathord{\left/ {\vphantom {p {{{\rho }^{\gamma }}}}} \right. \kern-0em} {{{\rho }^{\gamma }}}}$ and constant Riemann invariant ${{R}^{ + }} = u + \frac{2}{{\gamma - 1}}c$.

We determined the orders of accuracy Od of the method involved in the norm L²

$${{\left\| {U{\text{*}} - {{U}^{T}}} \right\|}_{{{{L}^{2}}}}} = {{\left( {\int\limits_{ - 1}^1 {{{{\left( {U{\text{*}} - {{U}^{T}}} \right)}}^{2}}} } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$$

((15))

$$Od = {{\log }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\frac{{{{{\left\| {{{U}_{h}} - {{U}^{T}}} \right\|}}_{{{{L}^{2}}}}}}}{{{{{\left\| {{{U}_{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}}}} - {{U}^{T}}} \right\|}}_{{{{L}^{2}}}}}}}$$

((16))

as of the instant T = 0.07. Table 1 gives errors (15) and order of accuracy (16) of the solution obtained by the discontinuous Galerkin method without using the limiting functions (the first series of calculations, rows 1–4), using the WENO limiter (rows 5–8), using the limiter based on averaging the solution with coefficient (13) proportional to ${{{{\rho }_{1}}} \mathord{\left/ {\vphantom {{{{\rho }_{1}}} {\bar {\rho }}}} \right. \kern-0em} {\bar {\rho }}}$ (rows 9–12), and using the same limiter with coefficient (13) proportional to ${1 \mathord{\left/ {\vphantom {1 {\Delta x}}} \right. \kern-0em} {\Delta x}}$ (rows 13–16).

Table 1

${{L}^{2}}$					T = 0.07
		n = 1		n = 2
	N	error	order	error	order
	500	7.81e−04		3.82e−05
	1000	1.63e−04	2.25	3.66e−06	3.38
	2000	2.93e−05	2.48	4.14e−07	3.14
	4000	5.32e−06	2.46	4.97e−08	3.05
WENO
	500	7.83e−04		2.77e−04
	1000	1.63e−04	2.25	4.74e−05	2.54
	2000	2.93e−05	2.48	4.65e−07	6.67
	4000	5.34e−06	2.45	4.97e-08	3.22
$k\sim {{{{\rho }_{1}}} \mathord{\left/ {\vphantom {{{{\rho }_{1}}} {\bar {\rho }}}} \right. \kern-0em} {\bar {\rho }}}$
	500	7.81e−04		3.83e−05
	1000	1.63e−04	2.25	3.66e−06	3.38
	2000	2.93e−05	2.48	4.14e−07	3.14
	4000	5.32e−06	2.46	4.97e−08	3.05
$k\sim \Delta x$
	500	7.81e−04		4.05e−05
	1000	1.63e−04	2.25	3.67e−06	3.46
	2000	2.93e−05	2.48	4.14e−07	3.14
	4000	5.32e−06	2.46	4.97e−08	3.05

Table 1 shows that none of the limiters studied reduced the accuracy of the scheme. However, the WENO limiter for quadratic polynomials n = 2 is not monotonic when determining the accuracy of the solution (rows 5–8). This can also be seen when solving other problems [6]. When we use the limiter based on averaging the solution, unlike the WENO limiter, we do not observe any deterioration of the accuracy of the solution on large grids.

4 NUMERICAL EXPERIMENTS

We consider a series of test one-dimensional nonstationary gas dynamics problems [14–21]. Despite their simple statements, these problems reflect all the peculiarities of gas-dynamic flows. Table 2 shows the initial distribution of the density, speed, and pressure.

Table 2

Problem number	Values of gas-dynamic parameters on left			Values of gas-dynamic parameters on right			Calculation time
	$\rho$	$u$	$p$	$\rho$	$u$	$p$
1	1	0	1	0.125	0	0.1	2.0
2	0.445	0.698	3.528	0.5	0	0.571	1.3
3	1	0	1	0.02	0	0.02	0.15
4	3.857	0.920	10.333	1	3.55	1	0.09
5	1	−2	0.4	1	2	0.4	0.15
6	3.857143	2.629369	10.3333	1 + 0.2 sin (5x)	0	1	1.8

Problem 1 (Sod’s problem). Breakdown of discontinuity results in a shock wave moving to the low-pressure area, an expansion fan expanding into the high-pressure area, and a contact discontinuity (Fig. 1). In Figs. 1–5, the solid thin line corresponds to the exact solution.

Fig. 1.

Density profiles in Problem 1 (points) when using (a) averaging solution with coefficient $k\sim \Delta x,$М = 6; (b) WENO limiter М = 6.

Fig. 2.

Density profiles in Problem 2 (points) when using (a) averaging solution with coefficient $k\sim \Delta x,$М = 20; (b) WENO limiter М = 20.

Fig. 3.

Density profiles in Problem 3 (points) when using (a) averaging solution with coefficient $k\sim \Delta x,$М = 300; (b) WENO limiter М = 1000.

Fig. 4.

Density profiles in Problem 4 (points) when using (a) averaging solution with coefficient $k\sim \Delta x,$М = 5000; (b) WENO limiter М = 5000.

Fig. 5.

Internal energy profiles in Problem 5 (points) when using (a) averaging solution with coefficient $k\sim \Delta x,$М = 30; (b) WENO limiter М = 30.

Problem 2 (Lax’s problem). In this problem, we have the same configuration of the solution as in Sod’s problem, which consists of a shock wave, a contact discontinuity with larger differences in gas-dynamic parameters than in the previous problem and, unlike Sod’s problem, a less intensive expansion fan (Fig. 2).

Problem 3 (Supersonic shock tube). The configuration of the solution to this problem is similar to the two previous ones. There arises a shock wave, an expansion fan, and a contact discontinuity. However, the solution of this problem allows evaluating the operation of computational schemes in the arising areas of supersonic flows (Fig. 3).

Problem 4 (Mach 3 problem). The solution is a contact discontinuity and two expansion waves (Fig. 4).

Problem 5 (Einfeldt problem). The solving process yields two symmetric expansion fans propagating into opposite directions and a stationary contact discontinuity (Fig. 5).

Problem 6 (Shock entropy wave interaction) is an interaction of a shock wave with entropy perturbation. The Mach number of the shock wave moving along the axis X is M = 3.5. After the shock wave passes, a complex flow is formed behind the front, where a series of shock waves of a smaller amplitude is formed with time (Fig. 6). In Fig. 6, the solid thin line corresponds to the numerical solution obtained on the grid with the step $\Delta {\kern 1pt} x = 5 \times {{10}^{{ - 3}}}$.

Fig. 6.

Density profiles in Problem 6 (points) when using averaging solution with coefficient $k\sim \Delta x,$ (a) М = 0.01; (b) М = 100; when using WENO limiter (c) М = 0.01; (d) М = 100.

Problem 7 (Woodward-Colella blast waves). This problem is a model of the interaction of two shock waves and is a common test to check whether numerical methods for solving gas dynamics problems work. At the initial instant, the density $\rho = 1$, the speed u = 0, and the pressure is distributed as follows: p = 10³ for $0 \leqslant x \leqslant 0.1$, $p$ = 10⁻² for $0.1 \leqslant x \leqslant 0.9$, and p = 10² for $0.9 \leqslant x \leqslant 1$. The calculation time is t = 0.038 (Fig. 7). In Fig. 7, the solid thin line corresponds to the numerical solution obtained on the grid with the step $\Delta {\kern 1pt} x = 6.25 \times {{10}^{{ - 5}}}$.

Fig. 7.

Density profiles in Problem 7 (points) when using averaging solution with coefficient $k\sim \Delta x,$ (a) М = 0.01; (b) М = 200; when using WENO limiter (c) М = 0.01; (d) М = 200.

In problems 1, 2, and 6, the calculation area is $- 5 \leqslant x \leqslant 5$, while it is $0 \leqslant x \leqslant 1$ in problems 3, 4, and 5. The discontinuity point is ${{x}_{0}} = 0$ in problems 1 and 2, ${{x}_{0}} = 0.5$ in problems 3, 4, and 5, and ${{x}_{0}} = - 4$ in problem 6. We performed calculations for problems 1–5 on a 100-cell grid; for problem 6, on a 200-cell grid; and for problem 7, on a 400-cell grid. In all the calculations, we assumed the gas to be ideal with the adiabatic index $\gamma = 1,4$.

To determine faulty cells, we need to specify the parameter М in the TVB-minmod limiter. We performed the first series of calculations with the parameter М = 0.01. This parameter superfluously determines the cells that require limiting. Our next step was to determine the critical value of the parameter М so that its further increase did not affect the limiting quality; i.e., the calculation could be performed without the limiter.

When solving problems 1–5 using the piecewise linear basis functions, we cannot unambiguously see the advantages of one of the limiters we study. However, when solving more complicated problems 6 and 7, the limiter based on averaging yields better results. When we move to quadratic basis functions, we see a better solution profile when applying the limiter based on averaging with the coefficient $k\sim \Delta {\kern 1pt} x$ compared to using the same limiter with the coefficient $k\sim {{{{\rho }_{1}}} \mathord{\left/ {\vphantom {{{{\rho }_{1}}} {\bar {\rho }}}} \right. \kern-0em} {\bar {\rho }}}$ or the WENO limiter. In [22], we showed that in some cases the coefficient $k\sim {{{{\rho }_{1}}} \mathord{\left/ {\vphantom {{{{\rho }_{1}}} {\bar {\rho }}}} \right. \kern-0em} {\bar {\rho }}}$ makes the limiter more dissipative when the quadratic functions are used.

The next series of calculations was to determine the critical value of the parameter М. Thus, as the parameter М increases, although we can naturally see more distinct profiles in the domains of the discontinuities of the solutions in all problems, there are also some oscillations.

Problems 4 and 5 turned out to be the most difficult to solve numerically. Both represent the breakdown of a gas-dynamic discontinuity in the form of a contact discontinuity and two expansion waves. When solving problem 4, we obtained the best results using the WENO-type limiter on linear basis functions; for the quadratic basis functions, the change in the parameter М did not improve the results significantly.

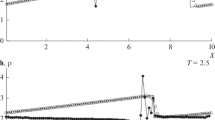
Problem 5 deserves our separate attention. We know that it is frequently used for testing numerical methods, the accuracy of the representation of the domain of the contact discontinuity being one of the indicators of a smoothly operating scheme. Almost in all the calculations, we can see a nonphysical spike of the internal energy. We considered several numerical schemes to solve this problem (Fig. 8). We give the series of calculations performed by the Godunov first-order scheme and the discontinuous Galerkin third-order method with the quadratic basis functions and using the “torque” limiter [2–5] (Fig. 9a).

Fig. 8.

Internal energy profiles in Problem 5 (points), number of cells is 500. (a) DGM, n = 2, Godunov flow, torque limiter (b) Godunov’s scheme, n = 0.

Fig. 9.

Internal energy profiles in Problem 5 (points) with pseudoheat conductivity taken into account. (a) Torque limiter; n = 2; (b) Godunov’s scheme, n = 0.

By adding pseudoheat conductivity to the numerical approximation of flow (5), we have a significant decrease in the emission of the entropy (Fig. 9).

We pay attention to how initial data are given. In this problem, the discontinuity point ${{x}_{0}} = 0.5$ is at the boundary between the cells. The speed u = −0.2 in the domain to the left of the discontinuity point $x \leqslant {{x}_{0}}$, while it is u = 0.2 in the domain to the right of it. We choose the grid so that the point ${{x}_{0}} = 0.5$ is inside the cell and by approximating the speed in this cell, we have u = 0. We can clearly see in Fig. 10 that there is practically no spike in the entropy.

Fig. 10.

Internal energy profiles in Problem 5 (points), number of cells is 501. (a) Torque limiter n = 2; (b) Godunov’s scheme, n = 0.

Fig. 11.

Internal energy profiles in Problem 5 (points), number of cells is 500. (a) Torque limiter n = 2; (b) Godunov’s scheme, n = 0.

Doing the same and approximating the speed discontinuity in two cells, we manage to obtain the solution that corresponds to the physical one (Fig. 11). Note that in this case adding the numerical scheme with the summand corresponding to the pseudoheat conductivity did not yield any further improvement in the results. Thus, we found that the defect arising in the numerical solution to problem 5 is due to the way the initial data are given, as well as to the choice of the numerical scheme.

Figure 12 shows the results of the calculations of problem 5 with the corrected profile of the initial speed. The graphs show that we managed to qualitatively improve the result, with the limiters based on averaging yielding a smoother solution profile.

Fig. 12.

Internal energy profiles in Problem 5, number of cells is 50 000. (a) Godunov’s scheme, n = 0 (black points on solid line); Torque limiter, n = 2 (white points on solid line); (b) WENO (solid thick line); $k \sim \Delta {\kern 1pt} x$ (white points).

5 CONCLUSIONS

The numerical results have shown that when solving problems by the discontinuous Galerkin method, both the WENO-type limiter and limiter based on averaging allow obtaining a high order of accuracy on smooth solutions and distinct, nonoscillating profiles on shock waves given the right choice of the respective constant used to determine the faulty cells. Moreover, both limiters are sufficiently easy to implement and generalize onto multidimensional unstructured grids.