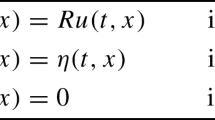1. INTRODUCTION

The finite element approximation of optimal control problems has been extensively studied in the literature. It is impossible to give even a very brief review here. See [2, 5, 15, 22] and [16, 17] for elliptic control problems and parabolic control problems, respectively.

Although the finite element method has successfully simulated a lot of optimal control problems, it fails to solve a certain class of optimal control problems, in which the objective function contains not only the primal state variable, but also its gradients. Mixed finite element methods will be the best choice because both the scalar variable and the flux variable can be approximated to the same accuracy using such methods. Some results on a priori error estimates and superconvergence of Raviart–Thomas mixed finite element methods for elliptic and parabolic optimal control problems can be found in [3, 4, 6, 21]. In [3, 4], Chen used the postprocessing projection operator, which was defined by Meyer and Rösch [15] to prove quadratic superconvergence of control by mixed finite element methods. In [9], Guo, Fu, and Zhang discussed a splitting positive definite mixed finite element method for the elliptic optimal control problem and derived a priori error estimates.

Many real applications, such as heat conduction control for materials with memory, population dynamics control, wave control, and control in elastic-plastic mechanics, necessitate consideration of optimal control problems governed by elliptic integral equations, parabolic integro-differential equations, and hyperbolic integro-differential equations. In [2], the authors analyzed Galerkin finite element discretizations for a class of constrained optimal control problems that are governed by the Fredholm integral and integro-differential equations. In [19], Shen et al. derived equivalent a posteriori error estimates with lower and upper bounds for a finite element approximation of a constrained optimal control problem governed by a parabolic integro-differential equation. In [10], Hou considered an \(H^1\)-Galerkin mixed finite element approximation of linear parabolic integro-differential optimal control problems and obtained a priori error estimates. In [11], Hou obtained a priori error estimates of Raviart–Thomas mixed finite element methods for optimal control problems governed by hyperbolic integro-differential equations. To the best of the author’s knowledge, in the literature there are no papers on splitting positive definite mixed finite element approximations for hyperbolic integro-differential optimal control problems.

Splitting positive definite mixed finite element methods were first proposed in [23] to solve miscible displacement of compressible flow in porous media. As compared with the standard mixed finite element methods, this technique has the following advantages: the Ladyzhenskaya–Babushka–Brezzi (LBB) consistency condition for finite element spaces is not necessary and the original problems can be split into two independent symmetric positive definite sub-schemes. The superconvergence of fully discrete splitting positive definite mixed finite element methods for hyperbolic equations was studied in [20]. A priori error estimates of splitting positive definite mixed finite element methods for hyperbolic and elliptic optimal control problems can be found in [14,24] and [9], respectively.

In this paper, we will discuss a priori error estimates and superconvergence of splitting positive definite mixed finite element approximations for pseudo-hyperbolic integro-differential optimal control problems. Of interest to us are the following optimal control problems, which are widely encountered in reaction diffusion and nerve conduction processes:

$$\min\limits_{u \in K\subset U}\Bigg\{\frac{1}{2}\int\limits_0^T\bigg(\|\boldsymbol{p}-\boldsymbol{p}_d\|^2+\|y-y_d\|^2+\| u\|^2\bigg)dt\Bigg\} ,\ {(1.1)}$$
$$y_{tt}-\mathrm{div\,}\boldsymbol{p}-\mathrm{div\,}\boldsymbol{p}_t+\int\limits_0^{t}\mathrm{div\,}\boldsymbol{p}(s)ds=f+ u,\ \ \ x\in \Omega,\ \ t \in J,\ {(1.2)}$$
$$\boldsymbol{p}=\nabla y,\ \ \ x\in \Omega,\ \ t\in J,\ {(1.3)}$$
$$\nabla y\cdot \boldsymbol{n}=0,\ \ \ x\in{\partial \Omega},\ \ t\in J,\ {(1.4)}$$
$$y(x,0)=y_0(x),\ \ \ x\in \Omega,\ {(1.5)}$$
$$y_t(x,0)=y_1(x),\ \ \ x\in \Omega,\ {(1.6)}$$

where \(\Omega\subset{\mathbf{R}^2}\) is a polygonal domain, \(J=[0,T]\), and \(\boldsymbol{n}\) is the outward normal on \(\partial \Omega\). Let \(K\) be a closed convex set in \(U=L^2(J;L^2(\Omega))\), \(f\) and \(y_{d}\in L^{2}(J;L^{2}(\Omega))\), \(\boldsymbol{p}_{d}\in L^{2}(J;(L^{2}(\Omega))^2)\), and \(y_{0}\) and \(y_1\in H^{1}(\Omega)\). The set \(K\) is defined as follows:

$$K=\left\{u\in U: \int\limits_0^{T} \int\limits_\Omega u\,dx\,dt\geq 0\right\}.\ {(1.7)}$$

In this paper, we adopt the standard notations of \(W^{m,p}(\Omega)\) for Sobolev spaces on \(\Omega\) with a norm \(\|\cdot\|_{m,p}\) given by \(\| v \|_{m,p}^{p}=\sum\limits_{|\alpha|\leq m}\| D^\alpha v\|_{L^{p}(\Omega)}^{p}\) and a semi-norm \(|\cdot|_{m,p}\) given by \(| v|_{m,p}^{p}=\sum\limits_{|\alpha|= m}\| D^\alpha v\|_{L^{p}(\Omega)}^{p}\). We set \(W_0^{m,p}(\Omega)=\{v\in W^{m,p}(\Omega): v|_{\partial \Omega}=0\}\). For \(p=2\), we denote as follows:\(H^m(\Omega)=W^{m,2}(\Omega)\), \(H_0^m(\Omega)=W_0^{m,2}(\Omega)\), \(\|\cdot\|_{m}=\|\cdot\|_{m,2}\), and \(\|\cdot\|=\|\cdot\|_{0,2}\).

Let \(L^s(J;W^{m,p}(\Omega))\) be the Banach space for all \(L^s\) integrable functions from \(J\) into \(W^{m,p}(\Omega)\) with the norm \(\|v\|_{L^s(J;W^{m,p}(\Omega))}=\Big(\int\limits_0^T||v| |_{W^{m,p}(\Omega)}^sdt\Big)^{1/s}\) for \(s\in [1,\infty)\) and the standard modification for \(s=\infty\). For simplicity of presentation, we denote \(\| v\|_{L^s(J;W^{m,p}(\Omega))}\) by \(\| v\|_{L^s(W^{m,p})}\). The spaces \(H^1(J;W^{m,p}(\Omega))\) can be defined similarly. In addition, \(C\) denotes a general positive constant independent of \(h\), where \(h\) is the spatial mesh step.

This paper is organized as follows. In Section 2, we construct a splitting positive definite mixed finite element scheme for optimal control problem (1.1)–(1.6) and give equivalent optimality conditions. The main results of this paper are stated in Section 3 and 4. In Section 3 we introduce some useful intermediate variables and give a priori error estimates for the control variable, state variables, and co-state variables. In Section 4, we derive the superconvergence properties for all the variables. Then, using the postprocessing method, we obtain the superconvergence result for the control variable.

2. MIXED METHODS FOR OPTIMAL CONTROL PROBLEMS

In this section, we will construct a splitting positive definite mixed finite element scheme for control problem (1.1)–(1.6). To this end, we take the state spaces \(\boldsymbol{L}=H^{2}(J;\boldsymbol{V})\) and \(\boldsymbol{W}=H^{2}(J;W)\), where \(\boldsymbol{V}\) and \(W\) are defined as follows:

$$\boldsymbol{V}=H_{0}(\mathrm{div\,};\Omega)=\left\{\boldsymbol{v}\in (L^2(\Omega))^2\mid \mathrm{div\,}\boldsymbol{v}\in L^2(\Omega),\boldsymbol{v}\cdot \boldsymbol{n}|_{\partial \Omega}=0\right\}, \quad W=L^2(\Omega).\ {(2.1)}$$

The Hilbert space \(\boldsymbol{V}\) is equipped with the following norm:

$$\|\boldsymbol{v}\|_{H(\mathrm{div\,};\Omega)}=\left(\|\boldsymbol{v}\|_{0,\Omega}^2+\|\mathrm{div\,} \boldsymbol{v}\|_{0,\Omega}^2\right)^{1/2}.$$

A mixed weak form of (1.2) and (1.3) can be given as follows:

$$(\boldsymbol{p},\boldsymbol{v})=-(y,\mathrm{div\,}\boldsymbol{v})\ \ \forall\, \boldsymbol{v}\in \boldsymbol{V},\ {(2.2)}$$
$$(y_{tt},w)-(\mathrm{div\,}\boldsymbol{p},w)-(\mathrm{div\,}\boldsymbol{p}_t,w)+\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}(s),w)ds=(f+u,w)\ \ \forall\, w\in W,\ {(2.3)}$$

where \((\cdot,\cdot)\) is the inner product \(L^{2}(\Omega)\).

Similarly to [9], taking \(w=\mathrm{div\,}\boldsymbol{v}\) in (2.3) and differentiating (2.2) with respect to \(t\), we obtain

$$(\boldsymbol{p}_{tt},\boldsymbol{v})+(\mathrm{div\,}\boldsymbol{p},\mathrm{div\,}\boldsymbol{v})+(\mathrm{div\,}\boldsymbol{p}_t,\mathrm{div\,}\boldsymbol{v})-\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}(s),\mathrm{div\,}\boldsymbol{v})ds=-(f+u,\mathrm{div\,}\boldsymbol{v})\ \ \forall\, \boldsymbol{v}\in \boldsymbol{V}.\ {(2.4)}$$

Now, we recast (1.1)–(1.6) as the following weak form: find \((\boldsymbol{p},y,u)\in \boldsymbol{L}\times \boldsymbol{W}\times K\) such that

$$\min\limits_{u \in K\subset U}\Bigg\{\frac{1}{2}\int\limits_0^T\bigg(\|\boldsymbol{p}-\boldsymbol{p}_d\|^2+\|y-y_d\|^2+\| u\|^2\bigg)dt\Bigg\} ,\ {(2.5)}$$
$$(\boldsymbol{p}_{tt},\boldsymbol{v})+(\mathrm{div\,}\boldsymbol{p},\mathrm{div\,}\boldsymbol{v})+(\mathrm{div\,}\boldsymbol{p}_t,\mathrm{div\,}\boldsymbol{v})-\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}(s),\mathrm{div\,}\boldsymbol{v})ds =-(f+u,\mathrm{div\,}\boldsymbol{v})\ \ \forall\, \boldsymbol{v}\in \boldsymbol{V}, \ {(2.6)}$$
$$\boldsymbol{p}(x,0)=\nabla y_0(x),\ {(2.7)}$$
$$\boldsymbol{p}_t(x,0)=\nabla y_1(x),\ {(2.8)}$$
$$(y_{tt},w)-(\mathrm{div\,}\boldsymbol{p},w)-(\mathrm{div\,}\boldsymbol{p}_t,w)+\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}(s),w)ds =(f+u,w)\ \ \forall\, w\in W,\ {(2.9)}$$
$$y(x,0)=y_0(x),\ {(2.10)}$$
$$y_t(x,0)=y_1(x).\ {(2.11)}$$

Since the objective functional is convex, it follows from [13] that optimal control problem (2.5)–(2.11) has a unique solution \((\boldsymbol{p},y,u)\) and a triplet \((\boldsymbol{p},y,u)\) is a solution of (2.5)–(2.11) if and only if there is a co-state \((\boldsymbol{q},z)\in \boldsymbol{L}\times \boldsymbol{W}\) such that \((\boldsymbol{p},y,\boldsymbol{q},z,u)\) satisfies the following optimality conditions:

$$(\boldsymbol{p}_{tt},\boldsymbol{v})+(\mathrm{div\,}\boldsymbol{p},\mathrm{div\,}\boldsymbol{v})+(\mathrm{div\,}\boldsymbol{p}_t,\mathrm{div\,}\boldsymbol{v})-\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}(s),\mathrm{div\,}\boldsymbol{v})ds =-(f+u,\mathrm{div\,}\boldsymbol{v})\ \ \forall\, \boldsymbol{v}\in \boldsymbol{V}, \ {(2.12)}$$
$$\boldsymbol{p}(x,0)=\nabla y_0(x),\ {(2.13)}$$
$$\boldsymbol{p}_t(x,0)=\nabla y_1(x),\ {(2.14)}$$
$$(y_{tt},w)-(\mathrm{div\,}\boldsymbol{p},w)-(\mathrm{div\,}\boldsymbol{p}_t,w)+\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}(s),w)ds =(f+u,w)\ \ \forall\, w\in W,\ {(2.15)}$$
$$y(x,0)=y_0(x),\ {(2.16)}$$
$$y_t(x,0)=y_1(x),\ {(2.17)}$$
$$(z_{tt},w)=(y-y_d,w)\ \ \forall\, w\in W,\ {(2.18)}$$
$$z(x,T)=0,\ {(2.19)}$$
$$z_t(x,T)=0,\ {(2.20)}$$
$$(\boldsymbol{q}_{tt},\boldsymbol{v})+(\mathrm{div\,}\boldsymbol{q},\mathrm{div\,}\boldsymbol{v})-(\mathrm{div\,}\boldsymbol{q}_t,\mathrm{div\,}\boldsymbol{v})-\int\limits_t^T(\mathrm{div\,}\boldsymbol{q}(s),\mathrm{div\,}\boldsymbol{v})ds$$
$$= (z,\mathrm{div\,}\boldsymbol{v})-\int\limits_t^T(z(s),\mathrm{div\,}\boldsymbol{v})ds-(z_t,\mathrm{div\,}\boldsymbol{v}) +(\boldsymbol{p}-\boldsymbol{p}_d,\boldsymbol{v})\ \ \forall\, \boldsymbol{v}\in \boldsymbol{V}, \ {(2.21)}$$
$$\boldsymbol{q}(x,T)=0,\ {(2.22)}$$
$$\boldsymbol{q}_t(x,T)=0,\ {(2.23)}$$
$$\int\limits_0^T(u-\mathrm{div\,}\boldsymbol{q}+z,\tilde{u}-u)dt\geq 0 \ \ \forall\, \tilde{u} \in K.\ {(2.24)}$$

Inequality (2.24) can be expressed as follows:

$$u=\max\{0,\overline {z-\mathrm{div\,}\boldsymbol{q}}\}-(z-\mathrm{div\,}\boldsymbol{q}), \ {(2.25)}$$

where \(\overline{z-\mathrm{div\,}\boldsymbol{q}}= \frac{\int\limits_0^{T} \int\limits_\Omega (z-\mathrm{div\,}\boldsymbol{q})\,dx\,dt}{\int\limits_0^{T} \int\limits_\Omega1dxdt}\).

Let \({\mathcal T}_{h}\) denote a regular rectangulation of the domain \(\Omega\), \(h_{\tau}\) be the diameter of \(\tau\), and \(h= \max\limits_{\tau \in {\mathcal {T}}_{h}}h_{\tau}\). Let \(\boldsymbol{V}_h\times W_h\subset \boldsymbol{V}\times W\) denote the lowest order Raviart–Thomas mixed finite element space [18], namely,

$$\boldsymbol{V}_h:=\{ \boldsymbol{v}_h\in \boldsymbol{V}:\forall \, \tau\in {\mathcal {T}}_h, \boldsymbol{v}_h|_{\tau}\in Q_{1,0}(\tau)\times Q_{0,1}(\tau)\}, \ {(2.26)}$$
$$W_h:=\{ w_h\in W:\forall \, \tau\in {\mathcal {T}}_h, w_h|_{\tau}\in Q_{0,0}(\tau)\},\ {(2.27)}$$

where \(Q_{m,n}(\tau)\) indicates the space of polynomials of degree no more than \(m\) and \(n\) in \(x\) and \(y\) on \(\tau\), respectively. Moreover, we set \(K_h=U_h\cap K\), where \(U_h=L^2(J;W_h)\).

Before the mixed finite element scheme is presented, we introduce two operators. Firstly, we define the standard \(L^2(\Omega)\)-projection [7] \(P_h:\ W\rightarrow W_h\), which satisfies the following conditions for any \(\phi \in W\):

$$(P_h\phi-\phi, w_{h})=0 \ \ \forall \ w_{h}\in W_{h}, \ {(2.28)}$$
$$\|\phi-P_h\phi\|_{-s,r}\leq Ch^{1+s}\|\phi\|_{1,r},\ \ s=0,1,\ \ 2\leq r \leq \infty, \ \ \forall\, \phi\in W^{1,r}(\Omega).\ {(2.29)}$$

Next, recall the Fortin projection (see [1] and [7]) \(\Pi_h:\ \boldsymbol{V} \rightarrow \boldsymbol{V}_h\), which satisfies the following conditions for any \(\boldsymbol{q}\in \boldsymbol{V}\):

$$(\mathrm{div\,}(\Pi_h\boldsymbol{q}-\boldsymbol{q}),w_{h})=0\quad \forall\, w_{h}\in W_h,\ {(2.30)}$$
$$\|\boldsymbol{q}-\Pi_h\boldsymbol{q}\|_{0,\rho}\leq Ch\|\boldsymbol{q}\|_{1,\rho},\quad 2\leq \rho\leq \infty, \ \ \forall\, \boldsymbol{q} \in (W^{1,\rho}(\Omega))^{2}, \ {(2.31)}$$
$$\|\mathrm{div\,}(\boldsymbol{q}-\Pi_h\boldsymbol{q})\|\leq Ch\|\mathrm{div\,} \boldsymbol{q}\|_{1}\quad \forall\, \mathrm{div\,}\boldsymbol{q} \in H^{1}(\Omega). \ {(2.32)}$$

Now, we can construct the splitting positive definite mixed finite element approximation for problem (1.1)–(1.6): find \((\boldsymbol{p}_h,y_h,u_h)\in H^2(J;\boldsymbol{V}_h)\times H^2(J;W_h)\times K_h\) such that

$$\min\limits_{u_h \in K_h\subset U_h}\Bigg\{\frac{1}{2}\int\limits_0^T\bigg(\|\boldsymbol{p}_h-\boldsymbol{p}_d\|^2+\|y_h-y_d\|^2+\|u_h\|^2\bigg)dt\Bigg\}, \ {(2.33)}$$
$$(\boldsymbol{p}_{htt},\boldsymbol{v}_h)+(\mathrm{div\,}\boldsymbol{p}_{h},\mathrm{div\,}\boldsymbol{v}_h)+(\mathrm{div\,}\boldsymbol{p}_{ht},\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}_h(s),\mathrm{div\,}\boldsymbol{v}_h)ds$$
$$=-(f+u_h,\mathrm{div\,}\boldsymbol{v}_h)\ \ \forall\, \boldsymbol{v}_h\in \boldsymbol{V}_h, \ {(2.34)}$$
$$\boldsymbol{p}_h(x,0)=\Pi_h\nabla y_{0}(x),\ {(2.35)}$$
$$\boldsymbol{p}_{ht}(x,0)=\Pi_h\nabla y_{1}(x),\ {(2.36)}$$
$$(y_{htt},w_h)-(\mathrm{div\,}\boldsymbol{p}_h,w_h)-(\mathrm{div\,}\boldsymbol{p}_{ht},w_h)+\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}_h(s),w_h)ds =(f+u_h,w_h)\ \ \forall\, w_h\in W_h,\ {(2.37)}$$
$$y_h(x,0)=P_hy_{0}(x),\ {(2.38)}$$
$$y_{ht}(x,0)=P_hy_{1}(x).\ {(2.39)}$$

Similar to the continuous case, optimal control problem (2.33)–(2.39) has a unique solution \((\boldsymbol{p}_h,y_h,u_h)\), and a triplet \((\boldsymbol{p}_h,y_h,u_h)\) is the solution of (2.33)–(2.39) if and only if there is a co-state \((\boldsymbol{q}_h,z_h)\in H^2(J;\boldsymbol{V}_h)\times H^2(J;W_h)\) such that \((\boldsymbol{p}_h,y_h,\boldsymbol{q}_h,z_h,u_h)\) satisfies the following optimality conditions:

$$(\boldsymbol{p}_{htt},\boldsymbol{v}_h)+(\mathrm{div\,}\boldsymbol{p}_{h},\mathrm{div\,}\boldsymbol{v}_h)+(\mathrm{div\,}\boldsymbol{p}_{ht},\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}_h(s),\mathrm{div\,}\boldsymbol{v}_h)ds$$
$$=-(f+u_h,\mathrm{div\,}\boldsymbol{v}_h)\ \ \forall\, \boldsymbol{v}_h\in \boldsymbol{V}_h, \ {(2.40)}$$
$$\boldsymbol{p}_h(x,0)=\Pi_h\nabla y_{0}(x),\ {(2.41)}$$
$$\boldsymbol{p}_{ht}(x,0)=\Pi_h\nabla y_{1}(x),\ {(2.42)}$$
$$(y_{htt},w_h)-(\mathrm{div\,}\boldsymbol{p}_h,w_h)-(\mathrm{div\,}\boldsymbol{p}_{ht},w_h)+\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}_h(s),w_h)ds$$
$$=(f+u_h,w_h)\ \ \forall\, w_h\in W_h,\ {(2.43)}$$
$$y_h(x,0)=P_hy_{0}(x),\ {(2.44)}$$
$$y_{ht}(x,0)=P_hy_{1}(x),\ {(2.45)}$$
$$(z_{htt},w_h)=(y_h-y_d,w_h)\ \ \forall\, w_h\in W_h ,\ {(2.46)}$$
$$z_h(x,T)=0,\ {(2.47)}$$
$$z_{ht}(x,T)=0,\ {(2.48)}$$
$$(\boldsymbol{q}_{htt},\boldsymbol{v}_h)+(\mathrm{div\,}\boldsymbol{q}_{h},\mathrm{div\,}\boldsymbol{v}_h)-(\mathrm{div\,}\boldsymbol{q}_{ht},\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_t^T(\mathrm{div\,}\boldsymbol{q}_h(s),\mathrm{div\,}\boldsymbol{v}_h)ds$$
$$=(z_h,\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_t^T(z_h(s),\mathrm{div\,}\boldsymbol{v}_h)ds -(z_{ht},\mathrm{div\,}\boldsymbol{v}_h)+(\boldsymbol{p}_h-\boldsymbol{p}_d,\boldsymbol{v}_h)\ \ \forall\, \boldsymbol{v}_h\in \boldsymbol{V}_h,\ {(2.49)}$$
$$\boldsymbol{q}_h(x,T)=0,\ {(2.50)}$$
$$\boldsymbol{q}_{ht}(x,T)=0,\ {(2.51)}$$
$$\int\limits_0^T(u_h-\mathrm{div\,}\boldsymbol{q}_h+z_h,\tilde{u}_h-u_h)dt\geq 0 \ \ \forall\, \tilde{u}_h \in K_h.\ {(2.52)}$$

Similarly, inequality (2.52) can be rewritten as follows:

$$u_h=\max\{0,\overline {z_h-\mathrm{div\,}\boldsymbol{q}_h}\}-(z_h-\mathrm{div\,}\boldsymbol{q}_h),\ {(2.53)}$$

where \(\overline{z_h-\mathrm{div\,}\boldsymbol{q}_h}= \frac{\int\limits_0^{T} \int\limits_\Omega (z_h-\mathrm{div\,}\boldsymbol{q}_h)\,dx\,dt}{\int\limits_0^{T} \int\limits_\Omega1\,dx\,dt}\).

3. A PRIORI ERROR ESTIMATES

In this section, we introduce some intermediate variables and derive a priori error estimates. First, for any \(\tilde{u}\in K\), let us define a discrete state solution \((\boldsymbol{p}_h(\tilde{u}),y_h(\tilde{u}),\boldsymbol{q}_h(\tilde{u}),z_h(\tilde{u}))\) with \(\tilde{u}\) that satisfies the following conditions:

$$(\boldsymbol{p}_{htt}(\tilde{u}),\boldsymbol{v}_h)+(\mathrm{div\,}\boldsymbol{p}_{h}(\tilde{u}),\mathrm{div\,}\boldsymbol{v}_h)+(\mathrm{div\,}\boldsymbol{p}_{ht}(\tilde{u}),\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}_h(\tilde{u})(s),\mathrm{div\,}\boldsymbol{v}_h)ds$$
$$=-(f+\tilde{u},\mathrm{div\,}\boldsymbol{v}_h)\ \ \forall\, \boldsymbol{v}_h\in \boldsymbol{V}_h,\ {(3.1)}$$
$$\boldsymbol{p}_h(\tilde{u})(x,0)=\Pi_h\nabla y_{0}(x),\ {(3.2)}$$
$$\boldsymbol{p}_{ht}(\tilde{u})(x,0)=\Pi_h\nabla y_{1}(x),\ {(3.3)}$$
$$(y_{htt}(\tilde{u}),w_h)-(\mathrm{div\,}\boldsymbol{p}_h(\tilde{u}),w_h)-(\mathrm{div\,}\boldsymbol{p}_{ht}(\tilde{u}),w_h)+\int\limits_0^t(\mathrm{div\,}\boldsymbol{p}_h(\tilde{u})(s),w_h)ds$$
$$=(f+\tilde{u},w_h)\ \ \forall\, w_h\in W_h,\ {(3.4)}$$
$$y_h(\tilde{u})(x,0)=P_hy_{0}(x),\ {(3.5)}$$
$$y_{ht}(\tilde{u})(x,0)=P_hy_{1}(x),\ {(3.6)}$$
$$(z_{htt}(\tilde{u}),w_h)=(y_h(\tilde{u})-y_d,w_h)\ \ \forall\, w_h\in W_h ,\ {(3.7)}$$
$$z_h(\tilde{u})(x,T)=0,\ {(3.8)}$$
$$z_{ht}(\tilde{u})(x,T)=0,\ {(3.9)}$$
$$(\boldsymbol{q}_{htt}(\tilde{u}),\boldsymbol{v}_h)+(\mathrm{div\,}\boldsymbol{q}_{h}(\tilde{u}),\mathrm{div\,}\boldsymbol{v}_h)-(\mathrm{div\,}\boldsymbol{q}_{ht}(\tilde{u}),\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_t^T(\mathrm{div\,}\boldsymbol{q}_h(\tilde{u})(s),\mathrm{div\,}\boldsymbol{v}_h)ds$$
$$=(z_h(\tilde{u}),\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_t^T(z_h(\tilde{u})(s),\mathrm{div\,}\boldsymbol{v}_h)ds$$
$$-(z_{ht}(\tilde{u}),\mathrm{div\,}\boldsymbol{v}_h)+(\boldsymbol{p}_h(\tilde{u})-\boldsymbol{p}_d,\boldsymbol{v}_h)\ \ \forall\, \boldsymbol{v}_h\in \boldsymbol{V}_h,\ {(3.10)}$$
$$\boldsymbol{q}_h(\tilde{u})(x,T)=0,\ {(3.11)}$$
$$\boldsymbol{q}_{ht}(\tilde{u})(x,T)=0.\ {(3.12)}$$

As we defined before, the exact solution and its approximation can be written in the following way:

$$(\boldsymbol{p},y,\boldsymbol{q},z)=(\boldsymbol{p}(u), y(u),\boldsymbol{q}(u), z(u)),$$
$$(\boldsymbol{p}_h, y_h, \boldsymbol{q}_h, z_h)=(\boldsymbol{p}_h(u_h),y_h(u_h),\boldsymbol{q}_h(u_h),z_h(u_h)).$$

Lemma 3.1.Let\((\boldsymbol{p}, y, \boldsymbol{q}, z)\)be a solution of\((2.12)\)–\((2.24)\)and\((\boldsymbol{p}_h(u), y_h(u), \boldsymbol{q}_h(u), z_h(u))\)be a solution of\((3.1)\)–\((3.12)\)at\({\tilde{u}}=u\).Assume that\(y\), \(\boldsymbol{p}\), \(\boldsymbol{q}\),and\(z\)have enough regularity for our purpose; then we have

$$\|y-y_{h}(u)\|_{L^{\infty}(L^2)}+\|\boldsymbol{p}-\boldsymbol{p}_h(u)\|_{L^{\infty}(L^2)}+\|\mathrm{div\,}(\boldsymbol{p}-\boldsymbol{p}_h(u))\|_{L^{\infty}(L^2)}\leq Ch,\ {(3.13)}$$
$$\|z-z_{h}(u)\|_{L^{\infty}(L^2)}+\|\boldsymbol{q}-\boldsymbol{q}_h(u)\|_{L^{\infty}(L^2)}+\|\mathrm{div\,}(\boldsymbol{q}-\boldsymbol{q}_h(u))\|_{L^{\infty}(L^2)}\leq Ch.\ {(3.14)}$$

Proof. Let

$$\rho_1=\Pi_h\boldsymbol{p}-\boldsymbol{p}_h(u),\quad \rho_2=\boldsymbol{p}-\Pi_h\boldsymbol{p},\quad \rho_3=y-P_hy,\quad \rho_4=P_hy-y_{h}(u),$$
$$\rho_5=\Pi_h\boldsymbol{q}-\boldsymbol{q}_h(u),\quad \rho_6=\boldsymbol{q}-\Pi_h\boldsymbol{q},\quad \rho_7=z-P_hz,\quad \rho_8=P_hz-z_{h}(u).$$

From (2.12)–(2.23) and (3.1)–(3.12), with the aid of (2.28) and (2.30) for any \(w_h\in W_h\) and \(\boldsymbol{v}_h\in \boldsymbol{V}_h\), we have the following error equations:

$$(\rho_{2tt}+\rho_{1tt},\boldsymbol{v}_h)+(\mathrm{div\,} \rho_{1},\mathrm{div\,}\boldsymbol{v}_h)+(\mathrm{div\,} \rho_{1t},\mathrm{div\,}\boldsymbol{v}_h) -\int\limits_0^t(\mathrm{div\,} \rho_{1}(s),\mathrm{div\,}\boldsymbol{v}_h)ds=0, \ {(3.15)}$$
$$(\rho_{4tt},w_h)-(\mathrm{div\,} \rho_{1},w_h)-(\mathrm{div\,} \rho_{1t},w_h)+\int\limits_0^t(\mathrm{div\,} \rho_1(s),w_h)ds=0, \ {(3.16)}$$
$$(\rho_{8tt},w_h)=(\rho_{4},w_h),\ {(3.17)}$$
$$(\rho_{6tt}+\rho_{5tt},\boldsymbol{v}_h)+(\mathrm{div\,} \rho_{5},\mathrm{div\,}\boldsymbol{v}_h)-(\mathrm{div\,} \rho_{5t},\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_t^T(\mathrm{div\,} \rho_{5}(s),\mathrm{div\,}\boldsymbol{v}_h)ds$$
$$=(\rho_{8},\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_t^T(\rho_{8}(s),\mathrm{div\,}\boldsymbol{v}_h)ds-(\rho_{8t},\mathrm{div\,}\boldsymbol{v}_h)+(\rho_{2}+\rho_{1},\boldsymbol{v}_h).\ {(3.18)}$$

Taking \(\boldsymbol{v}_h=\rho_{1t}\) in (3.15) and using the Cauchy inequality, we have

$$\frac{1}{2}\frac{d}{dt}(\|\rho_{1t}\|^2+\|\mathrm{div\,} \rho_{1}\|^2)+\|\mathrm{div\,} \rho_{1t}\|^2 \leq C(\|\rho_{2tt}\|^2+\|\rho_{1t}\|^2)+C\int\limits_{0}^{t}\|\mathrm{div\,}\rho_{1}(s)\|^2ds.\ {(3.19)}$$

Integrating (3.19) from 0 to \(t\) and using the relation \(\rho_1(0)=\rho_{1t}(0)=0\), Gronwall’s lemma, and (2.31), we get

$$\|\rho_{1t}\|_{L^{\infty}(L^2)}^2+\|\mathrm{div\,} \rho_{1}\|_{L^{\infty}(L^2)}^2+\|\mathrm{div\,} \rho_{1t}\|_{L^{2}(L^2)}^2 \leq Ch^2\|\boldsymbol{p}_{tt}\|_{L^{2}(H^1)}^2. \ {(3.20)}$$

Note that \(\rho_1=\int\limits_0^t \rho_{1t}(s)ds\). Then we have

$$\|\rho_{1}\|^2\leq C\int\limits_{0}^{t}\|\rho_{1t}(s)\|^2ds. \ {(3.21)}$$

From (3.20) and (3.21), we get

$$\|\rho_{1}\|_{L^{\infty}(L^2)}+\|\rho_{1t}\|_{L^{\infty}(L^2)} +\|\mathrm{div\,}\rho_{1}\|_{L^{\infty}(L^2)}+\|\mathrm{div\,}\rho_{1t}\|_{L^{2}(L^2)}\leq Ch\|\boldsymbol{p}_{tt}\|_{L^{2}(H^1)}. \ {(3.22)}$$

Taking \(w_h=\rho_{4t}\) in (3.16) and using the Cauchy inequality, we have

$$\frac{1}{2}\frac{d}{dt}\|\rho_{4t}\|^2\leq C(\|\mathrm{div\,} \rho_{1}\|^2+\|\rho_{4t}\|^2+\|\mathrm{div\,} \rho_{1t}\|^2)+ C\int\limits_{0}^{t}\|\mathrm{div\,}\rho_{1}(s)\|^2ds. \ {(3.23)}$$

Integrating (3.23) from 0 to \(t\), using the relation \(\rho_4(0)=\rho_{4t}(0)=0\), Gronwall’s lemma, and (3.22), we get

$$\|\rho_{4t}\|_{L^{\infty}(L^2)}^2\leq Ch^2\|\boldsymbol{p}_{tt}\|_{L^{2}(H^1)}^2. \ {(3.24)}$$

Since \(\rho_4=\int\limits_0^t \rho_{4t}(s)ds\), we have

$$\|\rho_{4}\|^2\leq C\int\limits_{0}^{t}\|\rho_{4t}(s)\|^2ds. \ {(3.25)}$$

It follows from (3.24) and (3.25) that

$$\|\rho_{4}\|_{L^{\infty}(L^2)}+\|\rho_{4t}\|_{L^{\infty}(L^2)}\leq Ch\|\boldsymbol{p}_{tt}\|_{L^{2}(H^1)}.\ {(3.26)}$$

Selecting \(w_h=-\rho_{8t}\) in (3.17) and using the Cauchy inequality, we have

$$-\frac{1}{2}\frac{d}{dt}\|\rho_{8t}\|^2\leq C\|\rho_{4}\|^2+C\|\rho_{8t}\|^2.\ {(3.27)}$$

Integrating (3.27) from \(t\) to \(T\), using the relation \(\rho_8(T)=\rho_{8t}(T)=0\), \(\rho_8=-\int\limits_t^T \rho_{8t}(s)ds\), Gronwall’s lemma, and (3.26), we get

$$\|\rho_{8}\|_{L^{\infty}(L^2)}+\|\rho_{8t}\|_{L^{\infty}(L^2)}\leq Ch\|\boldsymbol{p}_{tt}\|_{L^{2}(H^1)}.\ {(3.28)}$$

Taking \(\boldsymbol{v}_h=-\rho_{5t}\) in (3.18) and using the Cauchy inequality, we have

$$-\frac{1}{2}\frac{d}{dt}(\|\rho_{5t}\|^2+\|\mathrm{div\,} \rho_{5}\|^2)+\|\mathrm{div\,} \rho_{5t}\|^2$$
$$\leq C(\|\rho_{6tt}\|^2+\|\rho_{5t}\|^2+\|\rho_{8t}\|^2+\|\rho_{8}\|^2 +\|\rho_{1}\|^2+\|\rho_{2}\|^2) +C\int\limits_{t}^{T}(\|\mathrm{div\,}\rho_{5}(s)\|^2+\|\rho_{8}(s)\|^2)ds.\ {(3.29)}$$

Integrating (3.29) from \(t\) to \(T\), using the relations \(\rho_5(T)=\rho_{5t}(T)=0\) and \(\rho_5=-\int\limits_t^T \rho_{5t}(s)ds\), Gronwall’s lemma, (3.22), (3.28), and (2.31), we get

$$\|\rho_{5}\|_{L^{\infty}(L^2)}+\|\rho_{5t}\|_{L^{\infty}(L^2)} +\|\mathrm{div\,}\rho_{5}\|_{L^{\infty}(L^2)}\leq Ch(\|\boldsymbol{p}_{tt}\|_{L^{2}(H^1)}+\|\boldsymbol{q}_{tt}\|_{L^{2}(H^1)}+\|\boldsymbol{p}\|_{L^{2}(H^1)}).\ {(3.30)}$$

Combining (3.22), (3.26), (3.28), (3.30), (2.29), (2.31), (2.32), and the triangle inequality, we complete the proof of the lemma.\(\Box\)

Set \(\beta_1=\boldsymbol{p}_h(u)-\boldsymbol{p}_h\), \(\beta_2=y_h(u)-y_h\), \(\beta_3=\boldsymbol{q}_h(u)-\boldsymbol{q}_h\), and \(\beta_4=z_h(u)-z_h\). From (3.1)–(3.12) and (2.40)–(2.51), for any \(w_h\in W_h\) and \(\boldsymbol{v}_h\in \boldsymbol{V}_h\), we get

$$(\beta_{1tt},\boldsymbol{v}_h)+(\mathrm{div\,} \beta_1,\mathrm{div\,}\boldsymbol{v}_h)+(\mathrm{div\,} \beta_{1t},\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_0^t(\mathrm{div\,} \beta_1(s),\mathrm{div\,}\boldsymbol{v}_h)ds=-(u-u_h,\mathrm{div\,}\boldsymbol{v}_h),\ {(3.31)}$$
$$(\beta_{2tt},w_h)-(\mathrm{div\,} \beta_1,w_h)-(\mathrm{div\,} \beta_{1t},w_h)+\int\limits_0^t(\mathrm{div\,} \beta_1(s),w_h)ds=(u-u_h,w_h),\ {(3.32)}$$
$$(\beta_{4tt},w_h)=(\beta_2,w_h),\ {(3.33)}$$
$$(\beta_{3tt},\boldsymbol{v}_h)+(\mathrm{div\,} \beta_3,\mathrm{div\,}\boldsymbol{v}_h)-(\mathrm{div\,} \beta_{3t},\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_t^T(\mathrm{div\,} \beta_{3t}(s),\mathrm{div\,}\boldsymbol{v}_h)ds$$
$$=(\beta_4,\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_t^T(\beta_4(s),\mathrm{div\,}\boldsymbol{v}_h)ds-(\beta_{4t},\mathrm{div\,}\boldsymbol{v}_h)+(\beta_1,\boldsymbol{v}_h).\ {(3.34)}$$

Using the stability analysis of Lemma 3.1, we have

Lemma 3.2.Let\((\boldsymbol{p}_h, y_h, \boldsymbol{q}_h, z_h)\)and\((\boldsymbol{p}_h(u), y_h(u), \boldsymbol{q}_h(u), z_h(u))\)be discrete solutions of\((3.1)\)–\((3.12)\)at\({\tilde{u}}=u_h\)and\({\tilde{u}}=u\),respectively. Then we have

$$\|y_h-y_h(u)\|_{L^{\infty}(L^2)}+\|\boldsymbol{p}_h-\boldsymbol{p}_h(u)\|_{L^{\infty}(L^2)}\leq C\|u-u_h\|_{L^{2}(L^2)}, \ {(3.35)}$$
$$\|z_h-z_h(u)\|_{L^{\infty}(L^2)}+\|\boldsymbol{q}_h-\boldsymbol{q}_h(u)\|_{L^{\infty}(L^2)}\leq C\|u-u_h\|_{L^{2}(L^2)}, \ {(3.36)}$$
$$\| \mathrm{div}(\boldsymbol{p}_h-\boldsymbol{p}_h(u))\|_{L^{\infty}(L^2)}+\|\mathrm{div}(\boldsymbol{q}_h-\boldsymbol{q}_h(u))\|_{L^{\infty}(L^2)}\leq C\|u-u_h\|_{L^{2}(L^2)}. \ {(3.37)}$$

Lemma 3.3.Let\(u\)be a solution of\((2.12)\)–\((2.24)\)and\(u_h\)be a solution of\((2.40)\)–\((2.52)\).Then

$$\int\limits_0^T(\mathrm{div\,} \boldsymbol{q}_{h}(u)-\mathrm{div\,} \boldsymbol{q}_{h}-(z_{h}(u)-z_{h}),u-u_h)dt\leq 0.\ {(3.38)}$$

Proof. Take \(\boldsymbol{v}_h=\beta_3\) in (3.31), \(w_h=\beta_4\) in (3.32), \(\boldsymbol{v}_h=-\beta_1\) in (3.34), and \(w_h=-\beta_2\) in (3.33), respectively. Then integrating the four resulting equations from 0 to \(T\), we notice that

$$\beta_{1}(0)=\beta_{1t}(0)=\beta_{3}(T)= \beta_{3t}(T)=0,$$
$$\beta_{2}(0)=\beta_{2t}(0)=\beta_{4}(T)=\beta_{4t}(T)=0,$$
$$\int\limits_0^T\int\limits_{0}^{t}(\mathrm{div\,} \beta_1(s),\mathrm{div\,} \beta_3)\,ds\,dt=\int\limits_0^T\int\limits_{t}^{T}(\mathrm{div\,} \beta_{3}(s),\mathrm{div\,} \beta_1)\,ds\,dt,$$

and

$$\int\limits_0^T\int\limits_{0}^{t}(\mathrm{div\,} \beta_1(s),\beta_4)\,ds\,dt=\int\limits_0^T\int\limits_{t}^{T} (\beta_{4}(s),\mathrm{div\,} \beta_1)\,ds\,dt,$$

Then we find that

$$\int\limits_0^T(\mathrm{div\,} \boldsymbol{q}_h(u)-\mathrm{div\,} \boldsymbol{q}_h-(z_{h}(u)-z_{h}),u-u_h)dt=-\|\beta_1 \|_{L^2(L^2)}^2-\|\beta_2\|_{L^2(L^2)}^2,\ {(3.39)}$$

which gives (3.38).\(\Box\)

Lemma 3.4.Let\(u\)be a solution of\((2.12)\)–\((2.24)\)and\(u_h\)be a solution of\((2.40)\)–\((2.52)\).Then

$$\| u-u_h\|_{L^{2}(L^2)}\leq Ch.\ {(3.40)}$$

Proof. It follows from (2.24), (2.28), and (2.52) that

$$\begin{array}{lll} \| u-u_h\|_{L^{2}(L^2)}^2&=& \displaystyle \int\limits_{0}^{T}( u-u_h, u-u_h)\,dt \\ & =& \displaystyle \int\limits_{0}^{T}\!\!\big(u{-}\mathrm{div\,}\boldsymbol{q}{+}z, u{-}u_h\big)\,dt{+}\int\limits_{0}^{T}\!\!\big(\mathrm{div\,}(\boldsymbol{q}{-}\boldsymbol{q}_h(u)){+}z_h(u){-}z,u{-}u_h\big)\,dt \\ && + \displaystyle \int\limits_{0}^{T}\big(\mathrm{div\,}(\boldsymbol{q}_h(u)-\boldsymbol{q}_h)-(z_h(u)-z_h),u-u_h\big)\,dt \\ && - \displaystyle \int\limits_{0}^{T}\big(u_h-\mathrm{div\,}\boldsymbol{q}_h+z_h, u-P_hu\big)\,dt-\int\limits_{0}^{T}\big(u_h-\mathrm{div\,}\boldsymbol{q}_h+z_h, P_hu-u_h\big)\,dt \\ & \leq& \displaystyle \int\limits_{0}^{T}\big(\mathrm{div\,}(\boldsymbol{q}-\boldsymbol{q}_h(u))+z_h(u)-z, u-u_h\big)\,dt \\ && + \displaystyle \int\limits_{0}^{T}\big(\mathrm{div\,}(\boldsymbol{q}_h(u)-\boldsymbol{q}_h)-(z_h(u)-z_h),u-u_h\big)\,dt. \end{array} \ {(3.41)}$$

Using the Cauchy inequality, we see that

$$\int\limits_{0}^{T}(\mathrm{div\,}(\boldsymbol{q}-\boldsymbol{q}_h(u))+z_h(u)-z, u-u_h)dt$$
$$\leq \|\mathrm{div\,}(\boldsymbol{q}-\boldsymbol{q}_h(u))\|_{L^{2}(L^2)}^2+\|z_h(u)-z\|_{L^{2}(L^2)}^2 +\frac{1}{2}\|u-u_h\|_{L^{2}(L^2)}^2.\ {(3.42)}$$

Then (3.40) can be proved using (3.41), (3.42), and Lemmas 3.1 and 3.3.\(\Box\)

Using Lemmas 3.1, 3.2, and 3.4, and the triangle inequality, we get the following theorem.

Theorem 3.1.Let\((\boldsymbol{p},y,\boldsymbol{q},z,u)\)and\((\boldsymbol{p}_{h},y_{h},\boldsymbol{q}_{h},z_{h},u_{h})\)be solutions of\((2.12)\)–\((2.24)\)and\((2.40)\)–\((2.52)\),respectively. Assume that\(y\), \(\boldsymbol{p}\), \(\boldsymbol{q}\),and\(z\)have enough regularity for our purpose. Then we have

$$\|y-y_{h}\|_{L^{\infty}(L^2)}+\|\boldsymbol{p}-\boldsymbol{p}_h\|_{L^{\infty}(L^2)}+\|\mathrm{div\,}(\boldsymbol{p}-\boldsymbol{p}_h)\|_{L^{\infty}(L^2)}\leq Ch,\ {(3.43)}$$
$$\|z-z_{h}\|_{L^{\infty}(L^2)}+\|\boldsymbol{q}-\boldsymbol{q}_h\|_{L^{\infty}(L^2)}+\|\mathrm{div\,}(\boldsymbol{q}-\boldsymbol{q}_h)\|_{L^{\infty}(L^2)}\leq Ch.\ {(3.44)}$$

4. SUPERCONVERGENCE

In this section, we will derive the superconvergence result for the control variable.

Lemma 4.1.Let\((\boldsymbol{p}_h(P_hu), y_h(P_hu), \boldsymbol{q}_h(P_hu), z_h(P_hu))\)and\((\boldsymbol{p}_h(u), y_h(u), \boldsymbol{q}_h(u), z_h(u))\)be a discrete solution of\((3.1)\)–\((3.12)\)at\(\tilde{u}=P_hu\)and\(\tilde{u}=u\),Then we have

$$\|y_h(P_hu)-y_h(u)\|_{L^{\infty}(L^2)}+\|\boldsymbol{p}_h(P_hu)-\boldsymbol{p}_h(u)\|_{L^{\infty}(L^2)}=0,\ {(4.1)}$$
$$\|z_h(P_hu)-z_h(u)\|_{L^{\infty}(L^2)}+\|\boldsymbol{q}_h(P_hu)-\boldsymbol{q}_h(u)\|_{L^{\infty}(L^2)}=0,\ {(4.2)}$$
$$\|\mathrm{div}(\boldsymbol{p}_h(P_hu)-\boldsymbol{p}_h(u))\|_{L^{\infty}(L^2)}+\|\mathrm{div}(\boldsymbol{q}_h(P_hu)-\boldsymbol{q}_h(u))\|_{L^{\infty}(L^2)}=0.\ {(4.3)}$$

Proof. Set \(e_1=\boldsymbol{p}_h(P_hu)-\boldsymbol{p}_h(u)\), \(e_2=y_h(P_hu)-y_h(u)\), \(e_3=\boldsymbol{q}_h(P_hu)-\boldsymbol{q}_h(u)\), and \(e_4=z_h(P_hu)-z_h(u)\). From (3.1)–(3.12), for any \(\boldsymbol{v}_h\in \boldsymbol{V}_h\) and \(w_h\in W_h\), we get

$$(e_{1tt},\boldsymbol{v}_h)+(\mathrm{div\,} e_1,\mathrm{div\,}\boldsymbol{v}_h)+(\mathrm{div\,} e_{1t},\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_0^t(\mathrm{div\,} e_1(s),\mathrm{div\,}\boldsymbol{v}_h)ds=-(P_hu-u,\mathrm{div\,}\boldsymbol{v}_h), \ {(4.4)}$$
$$(e_{2tt},w_h)-(\mathrm{div\,} e_1,w_h)-(\mathrm{div\,} e_{1t},w_h)+\int\limits_0^t(\mathrm{div\,} e_1(s),w_h)ds=(P_hu-u,w_h), \ {(4.5)}$$
$$(e_{4tt},w_h)=(e_2,w_h),\ {(4.6)}$$
$$(e_{3tt},\boldsymbol{v}_h)+(\mathrm{div\,} e_3,\mathrm{div\,}\boldsymbol{v}_h)-(\mathrm{div\,} e_{3t},\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_t^T(\mathrm{div\,} e_{3t}(s),\mathrm{div\,}\boldsymbol{v}_h)ds$$
$$=(e_4,\mathrm{div\,}\boldsymbol{v}_h)-\int\limits_t^T(e_4(s),\mathrm{div\,}\boldsymbol{v}_h)ds-(e_{4t},\mathrm{div\,}\boldsymbol{v}_h)+(e_1,\boldsymbol{v}_h). \ {(4.7)}$$

Note that \((P_hu-u, w_{h})=0\) and \((P_hu-u, \mathrm{div\,}\boldsymbol{v}_h)=0\). Then using the stability analysis of Lemma 3.1, we complete the proof of the lemma.\(\Box\)

Lemma 4.2.Let\((\boldsymbol{p}, y, \boldsymbol{q}, z)\)be a solution of\((2.12)\)–\((2.23)\)and\((\boldsymbol{p}_h(u), y_h(u), \boldsymbol{q}_h(u), z_h(u))\)be a solution\((3.1)\)–\((3.12)\)at\({\tilde{u}}=u\).Assume that\(y\), \(\boldsymbol{p}\), \(\boldsymbol{q}\),and\(z\)have enough regularity for our purpose. Then

$$\|P_hy-y_{h}(u)\|_{L^{\infty}(L^2)}+\|\Pi_h\boldsymbol{p}-\boldsymbol{p}_h(u)\|_{L^{\infty}(L^2)}\leq Ch^2,\ {(4.8)}$$
$$\|P_hz-z_{h}(u)\|_{L^{\infty}(L^2)}+\|\Pi_h\boldsymbol{q}-\boldsymbol{q}_h(u)\|_{L^{\infty}(L^2)}\leq Ch^2,\ {(4.9)}$$
$$\|\mathrm{div\,}(\Pi_h\boldsymbol{p}-\boldsymbol{p}_h(u))\|_{L^{2}(L^2)}+\|\mathrm{div\,}(\Pi_h\boldsymbol{q}-\boldsymbol{q}_h(u))\|_{L^{2}(L^2)}\leq Ch^2. \ {(4.10)}$$

Proof. From [8] we know that for any \(\boldsymbol{p}\in \boldsymbol{V}\) and \(\boldsymbol{v}_h\in \boldsymbol{V}_h\)

$$(\boldsymbol{p}-\Pi_h\boldsymbol{p},\boldsymbol{v}_{h})\leq Ch^2(\|\boldsymbol{p}\|_2\|\boldsymbol{v}_{h}\|+\|\boldsymbol{p}\|_1\|\mathrm{div\,} \boldsymbol{v}_{h}\|).\ {(4.11)}$$

Using the same estimates as in Lemma 3.1, we complete the proof of the lemma.\(\Box\)

Lemma 4.3.Let\(u\)be a solution of\((2.12)\)–\((2.24)\)and\(u_h\)be a solution of\((2.40)\)–\((2.52)\).Then

$$\int\limits_0^T(\mathrm{div\,} \boldsymbol{q}_{h}(P_hu)-\mathrm{div\,} \boldsymbol{q}_{h}-(z_{h}(P_hu)-z_{h}),P_hu-u_h)dt\leq 0.\ {(4.12)}$$

Proof. Let

$$\alpha_1=\boldsymbol{p}_h(P_hu)-\boldsymbol{p}_h,\quad \alpha_2=y_h(P_hu)-y_h, \quad \alpha_3=\boldsymbol{q}_h(P_hu)-\boldsymbol{q}_h,\quad \alpha_4=z_h(P_hu)-z_h.$$

Similarly to Lemma 3.3, we find that

$$\int\limits_0^T(\mathrm{div\,} \boldsymbol{q}_h(P_hu)-\mathrm{div\,} \boldsymbol{q}_h-(z_{h}(P_hu)-z_{h}),P_hu-u_h)dt=-\|\alpha_1\|_{L^2(L^2)}^2 -\|\alpha_2\|_{L^2(L^2)}^2,\ {(4.13)}$$

which gives (4.12).\(\Box\)

Lemma 4.4.Let\(u\)be a solution of\((2.12)\)–\((2.24)\)and\(u_h\)be a solution of\((2.40)\)–\((2.52)\).Assume that all the conditions in Lemmas \(4.1\)–\(4.3\)are valid. Then we have

$$\|P_{h}u-u_h\|_{L^{2}(L^2)}\leq Ch^2.\ {(4.14)}$$

Proof. Taking \(\tilde{u}=u_h\) in (2.24) and \(\tilde{u}_h=P_hu\) in (2.52), we have

$$\int\limits_0^T(u_h-\mathrm{div\,}\boldsymbol{q}_h+z_h-u+\mathrm{div\,}\boldsymbol{q}-z,P_hu-u_h)dt+\int\limits_0^T(u-\mathrm{div\,}\boldsymbol{q}+z,P_hu-u)dt\geq 0.\ {(4.15)}$$

According to (4.15), (2.28), and (2.30), we have

$$\begin{array}{lll} \|P_hu-u_{h}\|_{L^{2}(L^{2})}^{2}&=& \displaystyle \int\limits_{0}^{T}(P_hu-u_{h},P_hu-u_{h})\,dt \\ &=& \displaystyle \int\limits_{0}^{T}(P_hu-u,P_hu-u_{h})\,dt+\int\limits_{0}^{T}(z_h-z-\mathrm{div\,}\boldsymbol{q}_h+\mathrm{div\,}\boldsymbol{q},P_hu-u_{h})\,dt \\ & & + \displaystyle \int\limits_{0}^{T}(-\mathrm{div\,}\boldsymbol{q}+\mathrm{div\,}\boldsymbol{q}_h+u+z-u_h-z_h,P_hu-u_{h})\,dt \\ &\leq& \displaystyle \int\limits_{0}^{T}(P_hu-u,P_hu-u_{h})\,dt+\int\limits_{0}^{T}(z_h-z-\mathrm{div\,}\boldsymbol{q}_h+\mathrm{div\,}\boldsymbol{q},P_hu-u_{h})\,dt \\ && + \displaystyle \int\limits_{0}^{T}(u-\mathrm{div\,}\, \boldsymbol{q}+z,P_hu-u)\,dt \\ &=& \displaystyle \int\limits_{0}^{T}(\mathrm{div\,}(\Pi_h\boldsymbol{q}-\boldsymbol{q}_h(u))-(P_hz-z_h(u)),P_hu-u_h)\,dt \\ && + \displaystyle \int\limits_{0}^{T}(\mathrm{div\,}(\boldsymbol{q}_h(u)-\boldsymbol{q}_h(P_hu))-(z_h(u)-z_h(P_hu)),P_hu-u_h)\,dt \\ && + \displaystyle \int\limits_{0}^{T}(\mathrm{div\,}(\boldsymbol{q}_h(P_hu)-\boldsymbol{q}_h)-(z_h(P_hu)-z_h),P_hu-u_h)\,dt \\ && + \displaystyle \int\limits_{0}^{T}(u-\mathrm{div\,} \boldsymbol{q}+z,P_hu-u)\,dt \\ &=:&I_{1}+I_{2}+I_{3}+I_{4}. \end{array} \ {(4.16)}$$

Using the Cauchy inequality and Lemmas 4.1 and 4.2, we have

$$I_{1}\leq C(\|\mathrm{div\,}(\Pi_h\boldsymbol{q}-\boldsymbol{q}_h(u))\|_{L^{2}(L^{2})}^{2}+\|P_hz-z_h(u)\|_{L^{2}(L^{2})}^{2}) +\frac{1}{3}\|P_hu-u_h\|_{L^{2}(L^{2})}^{2}\ {(4.17)}$$

and

$$I_{2}=0.\ {(4.18)}$$

Using (2.25), we find that

$$I_{4}=\max\{0,\overline {z-\mathrm{div\,}\boldsymbol{q}}\}\cdot \int\limits_0^{T} \int\limits_\Omega(P_hu-u)dxdt=0.\ {(4.19)}$$

Combining (4.16)–(4.19) with (4.12), we complete the proof of the lemma.\(\Box\)

Similarly to Lemma 3.2, we have

Lemma 4.5.Let\((\boldsymbol{p}_h(P_hu),y_h(P_hu),\boldsymbol{q}_h(P_hu),z_h(P_hu))\)and\((\boldsymbol{p}_h,y_h,\boldsymbol{q}_h,z_h)\)be solutions of\((3.1)\)–\((3.12)\)at\(\tilde{u}=P_hu\)and\(\tilde{u}=u_h\),respectively. Then

$$\|y_h(P_hu)-y_h\|_{L^{\infty}(L^2)}+\|\boldsymbol{p}_h(P_hu)-\boldsymbol{p}_h\|_{L^{\infty}(L^2)}\leq\|P_{h}u-u_h\|_{L^{2}(L^2)}, \ {(4.20)}$$
$$\|z_h(P_hu)-z_h\|_{L^{\infty}(L^2)}+\|\boldsymbol{q}_h(P_hu)-\boldsymbol{q}_h\|_{L^{\infty}(L^2)}\leq\|P_{h}u-u_h\|_{L^{2}(L^2)}, \ {(4.21)}$$
$$\| \mathrm{div}(\boldsymbol{p}_h(P_hu)-\boldsymbol{p}_h)\|_{L^{\infty}(L^2)}+\|\mathrm{div}(\boldsymbol{q}_h(P_hu)-\boldsymbol{q}_h)\|_{L^{\infty}(L^2)}\leq\|P_{h}u-u_h\|_{L^{2}(L^2)}. \ {(4.22)}$$

Combining Lemmas 4.1–4.5 and the triangle inequality, we have the following lemma.

Lemma 4.6.Let\((\boldsymbol{p}, y, \boldsymbol{q}, z)\)be a solution of\((2.12)\)–\((2.24)\)and\((\boldsymbol{p}_h, y_h, \boldsymbol{q}_h, z_h)\)be a solution of\((2.40)\)–\((2.52)\).Assume that all the conditions in Lemmas \(4.1\)–\(4.5\)hold. Then

$$\|P_hy-y_{h}\|_{L^{\infty}(L^2)}+\|\Pi_h\boldsymbol{p}-\boldsymbol{p}_h\|_{L^{\infty}(L^2)}\leq Ch^2,\ {(4.23)}$$
$$\|P_hz-z_{h}\|_{L^{\infty}(L^2)}+\|\Pi_h\boldsymbol{q}-\boldsymbol{q}_h\|_{L^{\infty}(L^2)}\leq Ch^2,\ {(4.24)}$$
$$\|\mathrm{div\,}(\Pi_h\boldsymbol{p}-\boldsymbol{p}_h)\|_{L^{\infty}(L^2)}+\|\mathrm{div\,}(\Pi_h\boldsymbol{q}-\boldsymbol{q}_h)\|_{L^{\infty}(L^2)}\leq Ch^2. \ {(4.25)}$$

In order to improve the global accuracy of the approximation, let us firstly construct the recovery operator \(G_h\). Let \(G_h\nu\) be a continuous piecewise linear function (without zero boundary constraint). The nodal values of \(G_h\nu\) are defined by the least-squares argument on the element patches surrounding the nodes; see details in the definition of \(R_h\) in [12].

Now we can derive the following superconvergence result for the control variable.

Theorem 4.1.Let\(u\)and\(u_h\)be solutions of\((2.12)\)–\((2.24)\)and\((2.40)\)–\((2.52)\),respectively. Assume that all the conditions in Lemmas \(4.1\)–\(4.5\)hold. Then

$$\|u-G_{h}u_h\|_{L^{2}(L^2)}\leq Ch^2.\ {(4.26)}$$

Proof. Note that

$$\|u-G_{h}u_h\| \leq \|u-G_{h}u\|+\|G_{h}u-G_{h}P_hu\|+\|G_{h}P_hu-G_{h}u_h\|.\ {(4.27)}$$

According to [12, Lemma 4.2], we have

$$\|u-G_{h}u\|\leq Ch^2.\ {(4.28)}$$

Using the definition of \(G_{h}\), we have

$$G_{h}u=G_{h}P_hu,\ {(4.29)}$$
$$\|G_{h}P_hu-G_{h}u_h\|\leq \|P_hu-u_h\|.\ {(4.30)}$$

Combining (4.27)–(4.30) with Lemma 4.4, we complete the proof of the theorem.\(\Box\)

5. CONCLUSIONS

In this paper, we investigate a priori error estimates and superconvergence of splitting positive definite mixed finite element methods for optimal control problems (1.1)–(1.6). Our theoretical results of semidiscrete splitting positive definite mixed finite element approximation for pseudo-hyperbolic integro-differential control problems seem to be new.

In the next work, we will discuss a posteriori error estimates. Moreover, we will consider fully discrete splitting positive definite mixed finite element methods for parabolic and hyperbolic integro-differential optimal control problems.