Adhesion Mechanics. Estimation of Contact-Layer Parameters

Abstract

The adhesion interaction between an adhesive and a substrate was estimated on the basis of the notion about an anisotropic layer as a contact layer between an adhesive and a substrate. One possible method of estimating the contact-layer parameters, such as shear modulus G*, thickness h*, and true shear strength τ_ad of the adhesion bond between an adhesive and a substrate, was proposed. The experimental and theoretical (analytical) dependences of the average adhesion strength on the gluing length and the glue (adhesive) layer thickness were used in the shear microtests of a joint of “overlap” type. A comparison of theoretical results with experimental data demonstrated that theoretical results were in good agreement with experimental data.

When estimating the quality of adhesion interaction between a glue (adhesive) and a substrate, i.e., a material to be glued, it is possible in an experiment to measure only the destructing load and the gluing surface area. The result of dividing the destructing load by the gluing surface area is usually called the “adhesion strength,” i.e., for shear τ_ad or normal tear-off. However, such adhesion strength proves to be strongly dependent on the gluing length and other geometric parameters of a tested specimen. This dependence is caused by a nonuniform distribution of stresses over the gluing surface area. The so-called “precise solution” in elasticity theory leads to a singularity (infinity) of tangent stresses at the corner points of an adhesion joint, i.e., in the areas where they are equal to zero. This means that the solution is incorrect and the Cauchy problem has not been solved. Moreover, such a result makes it impossible to introduce any physically clear criterion of destruction in an adhesive joint. For this reason, a theory is needed that would allow calculation of a nonuniform distribution of stresses over a gluing area and strictly satisfy the boundary conditions. Moreover, a direct comparison of theoretical calculations with experimental dependences is desirable. One such theory is that of adhesion mechanics [1–3], which is used here and based on the idea that it is needed to characterize the contact interaction by the contact anisotropic layer alongside with the continuity of stress and displacement vectors at the boundary of gluing.

The theory contains three parameters—contact-layer shear modulus G*, contact-layer thickness h*, and the true adhesive strength, e.g., for shear τ_ad of normal tear-off. The latter definition is understood to mean a characteristic that is independent of the geometric parameters of an adhesive joint model, but reflects the strength of bonding between this pair of materials, i.e., an adhesive and a substrate. This parameter is incorporated into the theory as a gluing-destruction criterion, which may be considered as an achievement of this theory, as the proposed approach has enabled the strict solution of the Cauchy problem with satisfaction of all the initial equations and boundary conditions and excluded singularity at the corner points of models. In paper [1], the precise problem solution by the contact layer method was compared with the approximate so-called “one-dimensional solution.” It has turned out that the deviation between these solutions is less than 10%. For this reason, “one-dimensional” solutions are used here to determine the contact-layer parameters. They are remarkable in that they can be found in a reviewable analytical form. This has provided the possibility to derive the dependences of the average adhesion strength on different model parameters, including geometric ones. This average strength, as already mentioned, is the only experimentally measurable parameter available for us. In addition, as usual, assuming that our solution is true and taking two or three points from an experimental dependence, we find two or three of the parameters that are necessary in the theory. Here, two or three points and parameters are not occasionally mentioned. In the case of one-dimensional solutions, two contact-layer parameters are always joined into the single parameter representing the ratio of the shear modulus of a contact layer to its thickness G*/h*. This ratio is called the “adhesive interaction intensity” or, put differently, the “contact-layer rigidity.” This is acceptable and convenient in practice. However, researchers sometimes need all three contact-layer parameters. Let us remember that shear modulus G* is related with the Young modulus of an orthotropic medium, i.e., a contact layer, by the simple equation G* = E*/2.

The results [1] of solving the theoretical problems of adhesion mechanics in one- and two-dimensional formulations give some grounds to believe that, to perform the qualitative and quantitative analysis of the mechanical behavior of adhesion models, it is possible to confine consideration only to the solutions of one-dimensional problems in one or another method of testing and compare them with the results of experimental studies. Let us remember that, when estimating the quality of an adhesion joint, we are able to determine only the average adhesion strength as a ratio of the destructing load to the gluing surface area in one or another method of testing. This means that theory must provide the possibility to isolate this parameter in it for further comparison with experiment, desirably, in an analytical form. As has been clarified, only the solutions of adhesion-mechanics problems in the one-dimensional formulation are able to satisfy this requirement.

The basic equations of a one-dimensional problem can be derived by means of limit transitions from the equations obtained in the previous section for a planar case. This has been done in the paper [1]. The divergence from the complete solution was nearly 10%. Here, we solve the problem in one-dimensional formulation for the method of shear testing on an adhesion joint of “overlap” type by using one of the basic assumptions for a contact layer, i.e., such that its thickness is small enough to derive the equations immediately for the one-dimensional model.

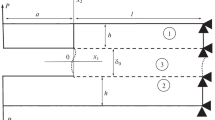
First of all, we study the shear behavior (perpendicularly to the plane of Fig. 1) of a one-dimensional model composed of n one-dimensional plates (rods), which have thickness b and represent layers of substrates and adhesives joint to each other by means of contact layers (Fig. 1).

Fig. 1.

Fragment of a multilayer plate element with acting inner forces and stresses (one-dimensional problem).

The equilibrium condition for kth element dx of a one-dimensional rod is

$$\begin{array}{*{20}{l}} { - {{\tau }_{k}}b{\text{d}}x - {{N}_{k}}b + {{\tau }_{{k + 1}}}b{\text{d}}x + \left[ {({\text{d}}{{N}_{k}}{\text{/d}}x){\text{d}}x} \right]b = {\text{ }}0.} \end{array}$$

Here, τ_k is the tangent stresses in the kth contact layer, b is the model width, N_k = σ_xkh_k is the force per unit model width (b = 1), σ_xk is the normal stress acting in a cross section of the kth rod, and h_k is the kth rod thickness. Whence we obtain the differential equation of equilibrium for an element of the kth rod,

$${{\tau }_{k}} - {{\tau }_{{k + 1}}} = {\text{d}}{{N}_{k}}{\text{/d}}x,\,\,\,\,k = 0,1,2, \ldots ,n.$$

(1)

If there are no tangent stresses applied to the surfaces of edge rods 0 and n of a multilayer model (see Fig. 1), τ₀ = t_{k + 1} = 0.

The overall deformation of the kth rod along axis 0x (see Fig. 1) is composed of elastic deformation e_k and generalized deformation ε_qk, which is still understood to mean the thermal, chemical, and moisture deformations or their sums; i.e.,

$${{\varepsilon }_{{xk}}} = {{N}_{k}}{\text{/}}{{h}_{k}}{{E}_{k}} + {{\varepsilon }_{{qk}}}.$$

(2)

The deformation is related with the displacement of kth rod medium (here, cross section) elements u_k of the along axis x (Fig. 2) by the Cauchy equation

$${{\varepsilon }_{{xk}}} = {\text{d}}{{u}_{k}}{\text{/d}}x.$$

(3)

Fig. 2.

Scheme of displacements along axis x for the elements of a layered system: h_k is the contact-layer thickness.

Because the thickness of the contact layer working for shear along the rod surface is small, it is possible to assume that the displacements in kth contact layer $u_{k}^{*}$ vary by the linear law (see Fig. 2)

$$\begin{gathered} u_{k}^{*} = {{a}_{k}} + {{c}_{k}}y;\,\,\,\,\sum\limits_{i = 0}^{k - 1} {\left( {{{h}_{i}} + h_{i}^{*}} \right) \leqslant y \leqslant } \sum\limits_{i = 0}^{k - 1} {\left( {{{h}_{i}} + h_{i}^{*}} \right) + h_{k}^{*}} , \\ h_{0}^{*} = 0;\,\,\,\,k = 0,1,2, \ldots ,n. \\ \end{gathered} $$

(4)

At the interlayer boundaries, the displacements of particles composing the layers must be continuous; i.e.,

$$\begin{gathered} \sum\limits_{i = 0}^{k - 1} {\left( {{{h}_{i}} + h_{i}^{*}} \right)} ;\,\,\,\,u_{k}^{*} = {{u}_{{k - 1}}}; \\ y = \sum\limits_{i = 0}^{k - 1} {\left( {{{h}_{i}} + h_{i}^{*}} \right) + h_{k}^{*}} ;\,\,\,\,u_{k}^{*} = {{u}_{k}}. \\ \end{gathered} $$

(5)

Whence we obtain that

$$\begin{gathered} {{c}_{k}} = \frac{{{{u}_{k}} - {{u}_{{k - 1}}}}}{{h_{k}^{*}}}; \\ {{a}_{k}} = \frac{{\left[ {\sum\limits_{i = 0}^{k - 1} {\left( {{{h}_{i}} + h_{i}^{*}} \right) + h_{k}^{*}} } \right]{{u}_{{k - 1}}} + \left[ {\sum\limits_{i = 0}^{k - 1} {\left( {{{h}_{i}} + h_{i}^{*}} \right)} } \right]{{u}_{k}}}}{{h_{k}^{*}}}. \\ \end{gathered} $$

(6)

The asterisk denotes the parameters of contact layers (see Fig. 1).

The shear deformations in a contact layer are

$${{\varepsilon }_{{xy,k}}} = \partial {{u}_{k}}{\text{/}}\partial y.$$

(7)

From Eqs. (4)–(7), we find that

$${{\varepsilon }_{{xy,k}}} = {{c}_{k}} = ({{u}_{k}} - {{u}_{{k - 1}}}){\text{/}}h_{k}^{*}.$$

(8)

The shear deformations of an elastic contact layer are related with the shear stresses by the Hooke’s law as

$${{\varepsilon }_{{xy,k}}} = {{e}_{{xy,k}}} = {{\tau }_{k}}{\text{/}}G_{k}^{*}.$$

(9)

As a result of substitutions and rearrangements, we obtain

$$\begin{gathered} {{{\text{d}}{{\tau }_{k}}} \mathord{\left/ {\vphantom {{{\text{d}}{{\tau }_{k}}} {{\text{d}}x}}} \right. \kern-0em} {{\text{d}}x}} = {{G_{k}^{*}} \mathord{\left/ {\vphantom {{G_{k}^{*}} {h_{k}^{*}}}} \right. \kern-0em} {h_{k}^{*}}}\left[ {{{{{N}_{k}}} \mathord{\left/ {\vphantom {{{{N}_{k}}} {\left( {{{h}_{k}}{{E}_{k}}} \right)}}} \right. \kern-0em} {\left( {{{h}_{k}}{{E}_{k}}} \right)}}} \right. \\ - \left. {{{{{N}_{{k - 1}}}} \mathord{\left/ {\vphantom {{{{N}_{{k - 1}}}} {\left( {{{h}_{{k - 1}}}{{E}_{{k - 1}}}} \right)}}} \right. \kern-0em} {\left( {{{h}_{{k - 1}}}{{E}_{{k - 1}}}} \right)}} + {{\varepsilon }_{{q,k}}} - {{\varepsilon }_{{q,k - 1}}}} \right]. \\ \end{gathered} $$

(10)

Differentiating Eq. (1) with respect to x and excluding the derivatives of tangent stresses by means of Eq. (10), we obtain the system of equations for the sought functions N_k(x):

$$\begin{gathered} \frac{{{{{\text{d}}}^{2}}{{N}_{k}}}}{{{\text{d}}{{x}^{2}}}} - \left( {\frac{{G_{k}^{*}}}{{h_{k}^{*}{{h}_{k}}{{E}_{k}}}} + \frac{{G_{{k + 1}}^{*}}}{{h_{{k + 1}}^{*}{{h}_{k}}{{E}_{k}}}}} \right){{N}_{k}} \\ + \,\,\frac{{G_{k}^{*}}}{{h_{k}^{*}{{h}_{{k - 1}}}{{E}_{{k - 1}}}}}{{N}_{{k - 1}}} + \frac{{G_{{k + 1}}^{*}}}{{h_{k}^{*}{{h}_{{k + 1}}}{{E}_{{k + 1}}}}}{{N}_{{k + 1}}} \\ + \,\,\frac{{G_{{k + 1}}^{*}}}{{h_{{k + 1}}^{*}}}\left( {{{\varepsilon }_{{q,k + 1}}} - {{\varepsilon }_{{q,k}}}} \right) - \frac{{G_{k}^{*}}}{{h_{k}^{*}}}\left( {{{\varepsilon }_{{q,k}}} - {{\varepsilon }_{{q,k - 1}}}} \right) = 0. \\ \end{gathered} $$

(11)

For the layers 0 and n, we obtain, respectively,

$$\begin{gathered} {{{\text{d}}}^{2}}{{N}_{0}}{\text{/}}d{{x}^{2}} - \left( {G_{1}^{*}{\text{/}}h_{1}^{*}} \right)\left[ {{{N}_{0}}{\text{/}}\left( {{{h}_{0}}{{E}_{0}}} \right)} \right. \\ - \,\,{{N}_{1}}{\text{/}}\left( {{{h}_{1}}{{E}_{1}}} \right) - \left. {({{\varepsilon }_{{q,1}}} - {{\varepsilon }_{{q,0}}})} \right] = 0; \\ {{{\text{d}}}^{2}}{{N}_{n}}{\text{/d}}{{x}^{2}} - \left( {G_{1}^{*}{\text{/}}h_{1}^{*}} \right)\left[ {{{N}_{n}}{\text{/}}\left( {{{h}_{n}}{{E}_{n}}} \right)} \right. \\ - {{N}_{{n = 1}}}{\text{/}}\left( {{{h}_{{n - 1}}}{{E}_{{n - 1}}}} \right) - \left. {({{\varepsilon }_{{q,n}}} - {{\varepsilon }_{{q,n - 1}}})} \right] = 0. \\ \end{gathered} $$

(12)

The systems of Eqs. (11) and (12) contain n + 1 equations for finding n + 1 unknowns N_k. The solution of this system at specified boundary conditions for N_k at x = ±l/2 presents no principal difficulties.

EFFECT OF THE GEOMETRIC AND PHYSICAL PARAMETERS OF AN OVERLAP JOINT OF PLATES ON THE SHEAR STRENGTH

In the previous section, equations and boundary conditions were derived for a system composed of many layers that differ in properties. Here, it is sufficient to confine consideration to the basic model, which is widely applied in the shear tests of adhesion overlap joints. It is usually composed of two identical glued rods 0 and 2 with an adhesive (glue) layer between them. The loading patterns used for such a model are illustrated in Fig. 3. It is widely applied to determine the shear strength in the gluing of metallic, wooden, and other plates and as a model of fiber-reinforced composites. In the equations from the previous section, it should be set that E₀ = E₂, h₀ = h₂, ε_q0 = ε_q2, α_t0 = α_t2, g₁ = g₂ = g = G*/h*, and h* = $h_{1}^{*}$ = $h_{2}^{*}$.

Fig. 3.

Loading patterns for an overlap joint of plates: 0 and 2 are two different (in the general case) glued materials (substrates) spaced apart by a glue (adhesive) layer.

In this case, Eqs. (11) and (12) for loading patterns I, III, and IV (see Fig. 3) will take the form

$$\begin{gathered} {{{\text{d}}}^{2}}{{N}_{0}}{\text{/d}}{{x}^{2}} + g( - {{k}_{0}}{{N}_{0}} + {{k}_{1}}{{N}_{1}} + {{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q0}}}) = {\text{ }}0; \\ {{{\text{d}}}^{2}}{{N}_{2}}{\text{/d}}{{x}^{2}} + g( - {{k}_{0}}{{N}_{2}} + {{k}_{1}}{{N}_{1}} + {{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q0}}}) = {\text{ }}0; \\ {{N}_{0}} + {{N}_{1}} + {{N}_{2}} = P{\text{/}}b. \\ \end{gathered} $$

(13)

For pattern II, the last equation has the form N₀ + N₁ + N₂ = 0, and, for variant IV, parameter P is replaced by –P. Let us introduce the substitution

$$\varphi = {{N}_{0}} + {{N}_{1}};\,\,\,\,f = {{N}_{0}} - {{N}_{1}},$$

(14)

to result in the system

$$\begin{gathered} \varphi {\kern 1pt} '' - ({{k}_{0}} + 2{{k}_{1}})g\varphi + 2{{k}_{1}}P{\text{/}}b + 2g({{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q0}}}) = 0; \\ f{\kern 1pt} '' - g{{k}_{0}}{\text{ }}f = 0. \\ \end{gathered} $$

(15)

For loading pattern II, the first equation in Eqs. (15) has no term with P/b.

A particular solution of heterogeneous equation (15) will be

$${{\varphi }_{r}} = 2({{k}_{1}}P{\text{/}}(b + {{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q0}}}){\text{/}}({{k}_{0}} + 2{{k}_{1}}).$$

(16)

The solutions of system (15) will be written as

$$\begin{gathered} \varphi = {{A}_{1}}{\kern 1pt} \sinh {\kern 1pt} {{\omega }_{1}}x + {{B}_{1}}{\kern 1pt} \cosh {\kern 1pt} {{\omega }_{1}}x + {{\varphi }_{r}}; \\ f = {{A}_{2}}{\kern 1pt} \sinh {\kern 1pt} {{\omega }_{2}}x + {{B}_{2}}{\kern 1pt} \cosh {\kern 1pt} {{\omega }_{2}}x. \\ \end{gathered} $$

(17)

The boundary conditions for all the variants are quite evident. Here, let us confine our consideration to the most widely used variant of testing I (see Fig. 3):

$$\begin{gathered} x = l{\text{/}}2{\kern 1pt} :\,\,\,\,{{N}_{0}} = 0;\,\,\,\,{{N}_{1}} = 0;\,\,\,\,{{N}_{2}} = P{\text{/}}b; \\ \varphi = P{\text{/}}B;\,\,\,\,f = - P{\text{/}}b; \\ x = - \frac{l}{2}{\kern 1pt} :\,\,\,\,{{N}_{0}} = \frac{P}{b};\,\,\,\,{{N}_{1}} = 0;\,\,\,\,{{N}_{2}} = 0; \\ \varphi = \frac{P}{B};\,\,\,\,f = \frac{P}{b}. \\ \end{gathered} $$

(18)

Substituting Eqs. (17) into the boundary conditions, we find the constants A₁, …, B₂. Tangent stresses τ₁ and τ₂ can be found from Eq. (1). As a result, we have for pattern I that

$$\begin{gathered} {{N}_{0}} = {{\sigma }_{0}}{{h}_{0}} = \frac{{\varphi + f}}{2} = \frac{P}{{2b}} \\ \times \,\,\left( {\frac{{{{k}_{0}}}}{{{{k}_{0}} + 2{{k}_{1}}}}\frac{{\cosh {\kern 1pt} {{\omega }_{1}}x}}{{\cosh {\kern 1pt} {{\nu }_{1}}}} - \frac{{\sinh {\kern 1pt} {{\omega }_{2}}x}}{{\sinh {\kern 1pt} {{\nu }_{2}}}} + \frac{{2{{k}_{1}}}}{{{{k}_{0}} + 2{{k}_{1}}}}} \right) + \frac{{{{\varphi }_{T}}}}{2}; \\ \end{gathered} $$

$$\begin{gathered} {{N}_{2}} = {{\sigma }_{2}}{{h}_{0}} = \frac{{\varphi - f}}{2} = \frac{P}{{2b}} \\ \times \,\,\left( {\frac{{{{k}_{0}}}}{{{{k}_{0}} + 2{{k}_{1}}}}\frac{{\cosh {\kern 1pt} {{\omega }_{1}}x}}{{\cosh {\kern 1pt} {{\nu }_{1}}}} + \frac{{\sinh {\kern 1pt} {{\omega }_{2}}x}}{{\sinh {{\nu }_{2}}}} + \frac{{2{{k}_{1}}}}{{{{k}_{0}} + 2{{k}_{1}}}}} \right) + \frac{{{{\varphi }_{T}}}}{2}; \\ {{N}_{1}} = {{\sigma }_{1}}{{h}_{1}} = \frac{P}{b} - ({{N}_{0}} + {{N}_{1}}) = \frac{P}{{2b}}\frac{{{{k}_{0}}}}{{{{k}_{0}} + 2{{k}_{1}}}} \\ \times \,\,\left( {1 - \frac{{\cosh {\kern 1pt} {{\omega }_{1}}x}}{{\cosh {\kern 1pt} {{\nu }_{1}}}}} \right) - {{\varphi }_{T}}; \\ {{\tau }_{1}}(x) = - \frac{{{\text{d}}{{N}_{0}}}}{{dx}} = \frac{P}{{2b}} \\ \times \,\,\left( { - {{\omega }_{1}}\frac{{{{k}_{0}}}}{{{{k}_{0}} + 2{{k}_{1}}}}\frac{{\sinh {\kern 1pt} {{\omega }_{1}}x}}{{\sinh {{\nu }_{1}}}} + {{\omega }_{2}}\frac{{\cosh {\kern 1pt} {{\omega }_{2}}x}}{{\cosh {\kern 1pt} {{\nu }_{2}}}}} \right) + {{\tau }_{T}}; \\ {{\tau }_{2}}(x) = - \frac{{d{{N}_{2}}}}{{dx}} = {{\tau }_{1}}( - x). \\ \end{gathered} $$

(19)

The notations used in Eqs. (19) are

$$\begin{gathered} \omega _{1}^{2} = ({{k}_{0}} + 2{{k}_{1}})g;\,\,\,\,\omega _{2}^{2} = {{k}_{0}}g;\,\,\,\,{{\nu }_{1}} = {{\omega }_{1}}l{\text{/}}2; \\ {{\nu }_{2}} = {{\omega }_{2}}l{\text{/}}2;\,\,\,\,{{\varphi }_{T}} = \frac{{2({{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q0}}})}}{{{{k}_{0}} + 2{{k}_{1}}}}\left( {1 - \frac{{\cosh {\kern 1pt} {{\omega }_{1}}x}}{{\cosh {\kern 1pt} {{\nu }_{1}}}}} \right); \\ {{\tau }_{T}} = \frac{{{\text{d}}{{\varphi }_{T}}}}{{2dx}} = \frac{{{{\omega }_{1}}({{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q0}}})}}{{{{k}_{0}} + 2{{k}_{1}}}}\left( {\frac{{\sinh {\kern 1pt} {{\omega }_{1}}x}}{{\cosh {\kern 1pt} {{\nu }_{1}}}}} \right) \\ = \,\,{{\tau }_{{1T}}}(x) = - {{\tau }_{{2T}}}(x) = {{\tau }_{{2T}}}( - x). \\ \end{gathered} $$

(20)

Let us consider one of the most frequently encountered cases, in which the curing of a glue (adhesive) is performed at an increased temperature (the stresses appearing under curing are neglected) and the tests of a model are carried out at normal temperature in the regime of shear under tension (pattern I). This means that ϑ = ΔT = T_test – T₀ < 0 and P > 0. Then, ε_q1 – ε_q2 = (α₁ – α₀)ϑ.

As a rule, the linear expansion coefficient of a polymer adhesive is higher than for a substrate, i.e., α₁ > α₀, and, for this reason, (α₁ – α₀)ϑ < 0. For convenience, let us write τ₁(x) in Eqs. (19) in the form of two summands, of which the first reflects the effect of force P and the second characterizes the effect of the temperature; i.e.,

$$\begin{gathered} {{\tau }_{1}}(x) = {{\tau }_{{1P}}}(x) + {{\tau }_{{1T}}}(x) \\ = \frac{P}{{2b}}\left( { - {{\omega }_{1}}\frac{{{{k}_{0}}}}{{{{k}_{0}} + 2{{k}_{1}}}}\frac{{\sinh {\kern 1pt} {{\omega }_{1}}x}}{{\cosh {\kern 1pt} {{\nu }_{1}}}} + {{\omega }_{2}}\frac{{\cosh {\kern 1pt} {{\omega }_{2}}x}}{{\sinh {\kern 1pt} {{\nu }_{2}}}}} \right) \\ + \,\,({{\alpha }_{1}} - {{\alpha }_{0}})\vartheta \frac{{{{\omega }_{1}}}}{{{{k}_{0}} + 2{{k}_{1}}}}\left( {\frac{{\sinh {\kern 1pt} {{\omega }_{1}}x}}{{\cosh {\kern 1pt} {{\nu }_{1}}}}} \right); \\ ( - l{\text{/}}2 \leqslant x \leqslant l{\text{/}}2). \\ \end{gathered} $$

(21)

The second summand in the right brackets is positive at all x, and the first summand is positive only at x < 0. The temperature term is also positive at x < 0. This means that τ₁(x) attains a maximum at x = –1/2 and τ₂(x) = τ₁(–x) at x = l/2, i.e., in the area where tensile forces P are applied. The distribution of τ₁(x) is exemplified in Fig. 4. The calculations were performed by using the following parameters: g = G*/h* = 29 600 MPa/mm, l = 20 mm, E₀ = 2 × 10⁴ MPa, E₁ = 6 × 10³ MPa, h₀ = h₂ = 2 mm, h₁ = 0.2 mm, α₁ = 8 × 10^–5 K^–1, α₁ = 1 × 10^–5 K^–1, ΔT = –100 K, and P/2b = 59 N/mm.

Fig. 4.

Example for the distribution of tangent stresses along the gluing length ξ = 2x/L (Eq. (21)) in an overlap joint under loading according to pattern I (see Fig. 3).

For further analysis and comparison with experimental data, it is necessary first of all to determine the criterion of model destruction under shear. Let us assume that the destruction of a model under shear occurs at the moment when maximum τ₁(x) attains a certain critical value τ_ad, which is called the “adhesion strength” of a model under shear. It should also be taken into account that, as known, the integral characteristic of a model, i.e., the average tangent stress equal to the ratio of destructing load P_b to gluing surface area bl: $\bar {\tau }$ = τ_av = P_b/bl, is usually determined in experiments.

Based on Eqs. (21), the effect of the geometric and physical parameters of a model and an experiment on this average characteristic measured in experiments will be analyzed. For this purpose, let us determine τ_max = τ₁(–l/2) to equate it to τ_ad and further express τ as

$$\begin{gathered} \bar {\tau } = {{\tau }_{1}}\left( { - \frac{l}{2}} \right) = {{\tau }_{2}}\left( {\frac{l}{2}} \right) \\ = \bar {\tau }{{\left( {\frac{{{{\nu }_{1}}{{k}_{0}}}}{{{{k}_{0}} + 2{{k}_{1}}}}\tanh {\kern 1pt} {{\nu }_{1}} + {{\nu }_{2}}{\kern 1pt} \coth {\kern 1pt} {{\nu }_{2}}} \right)}_{{\max }}} \\ - \,\,2({{\alpha }_{1}} - {{\alpha }_{0}})\vartheta \frac{{{{\nu }_{1}}\tanh {\kern 1pt} {{\nu }_{1}}}}{{l({{k}_{0}} + 2{{k}_{1}})}}. \\ \end{gathered} $$

(22)

From Eq. (22), we derive the expression for the average value of $\bar {\tau }$ as

$$\begin{gathered} \bar {\tau } = \frac{{{{P}_{b}}}}{{bl}} = \frac{{{{\tau }_{{{\text{ad}}}}}({{k}_{0}} + 2{{k}_{1}}) + 2({{\alpha }_{1}} - {{\alpha }_{0}})\vartheta {{\nu }_{1}}\tanh {\kern 1pt} {{\nu }_{1}}{\text{/}}l}}{{{{\nu }_{1}}{{K}_{0}}\tanh {\kern 1pt} {{\nu }_{1}} + {{\nu }_{2}}({{k}_{0}} + 2{{k}_{1}})\coth {\kern 1pt} {{\nu }_{2}}}}; \\ \nu _{1}^{2} = ({{k}_{0}} + 2{{k}_{1}})g{{l}^{2}}{\text{/}}4;\,\,\,\,\nu _{2}^{2} = {{k}_{0}}g{{l}^{2}}{\text{/}}4; \\ g = G\text{*}{\text{/}}h\text{*};\,\,\,\,{{k}_{0}} = 1{\text{/}}({{E}_{0}}{{h}_{0}});\,\,\,\,{{k}_{1}} = 1{\text{/}}({{E}_{1}}{{h}_{1}}). \\ \end{gathered} $$

(23)

DEPENDENCE OF $\bar {\tau }$ ON THE LENGTH OF A GLUED JOINT

In Eqs. (23), ν₁ and ν₂ linearly grow with an increase in the length l, function tanh ν₁ smoothly ascends from zero to q, and the limit of ν₁tanh ν₁ = ν₂/tanh ν₂ is equal to 1 at l → 0. For this reason, the limit of the denominator of $\bar {\tau }$ in Eqs. (23) is equal to k₀ + 2k₁ at l → 0 and ∞ at l → ∞. The corresponding limits of the temperature term are equal to 0 (zero). Whence,

$$\mathop {\lim }\limits_{l \to 0} \bar {\tau } = {{\tau }_{{{\text{ad}}}}},\,\,\,\,\mathop {\lim }\limits_{l \to \infty } \bar {\tau } = 0.$$

(24)

Hence, it follows from Eqs. (23) that value $\bar {\tau }$ measured experimentally must vary from τ_ad to zero, when the gluing length is changed from zero to infinity. The last limit means that, beginning from a certain length, destructing load P_b is almost independent or very weakly depends on the gluing length. The plot of change in $\bar {\tau }$ with the gluing length is shown in Fig. 5a.

Fig. 5.

Theoretical dependences of the average adhesion strength $\bar {\tau }$ in the shear tests of an overlap joint on different parameters, such as (a) gluing length, (b, c) adhesive-layer thickness, (d) substrate rigidity, and (e–k) temperature of tests.

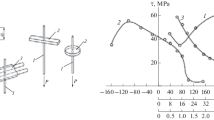
The experimental dependences of $\bar {\tau }$ on different parameters are plotted in Fig. 6. Of them, curve 4 reflects the dependence on the gluing length and is identical to the theoretical dependence shown in Fig. 5a. This curve was measured on specially prepared specimens of layered reinforced plastics, in which every monolayer (lamina) was preliminarily cut across as shown in Fig. 7. In such specimens, the possible bending of glued layers, which would create tearing stresses at the boundary of gluing, are almost excluded.

Fig. 6.

Experimental results of shear tests for an overlap joint of plates: (1) destructing load P_b vs. the glued-joint thickness h_g for a steel–Araldite filled epoxy glue system [6, pp. 245–259]; (2, 3) $\bar {\tau }$ vs. temperature of tests, the substrate is aluminum, and the adhesive is epoxy polyamide and filled EPTs-1 glues, respectively [7]; and (4) $\bar {\tau }$ vs. gluing length for an glass–epoxide joint [1].

Fig. 7.

Reinforced plastic specimen for interlayer shear tests. Preliminary cuts are marked with vertical strokes [1–3].

The first limit in Eqs. (24) opens opportunities for estimating the “true” strength of bonding in a given adhesive–substrate pair as a value independent of the geometry of a specimen as

$${{\tau }_{{{\text{ad}}}}} = \mathop {\lim }\limits_{S \to 0} {{P}_{b}}{\text{/}}S,$$

(25)

where S is the gluing surface area.

DEPENDENCE OF $\bar {\tau }$ ON THE ADHESIVE THICKNESS

The adhesive-layer thickness is composed of thickness of contact layers h* and thickness of a polymer (adhesive) layer h₁; i.e., h_g = 2h* + h₁. Hence, initially, when h₁ = 0, thickness h_g is increased due to growth in the contact-layer thickness from zero to a certain ultimate value $h_{{\max }}^{*}$. Thereafter, h₁ starts to grow from zero to infinity. At the first stage (h₁ = 0), Eq. (23) takes the simple form

$$\bar {\tau } = {{\tau }_{{{\text{ad}}}}}(\tanh {\kern 1pt} {{\nu }_{2}}){\text{/}}{{\nu }_{2}}.$$

(26)

Whence it follows that, when h* grows from zero to $h_{{\max }}^{*}$, $\bar {\tau }$ increases from zero to a certain finite value ${{\bar {\tau }}_{k}}$, which may become equal to τ_ad at small ν₂. Thereafter, when h₁ grows from zero to infinity, $\bar {\tau }$ decreases from ${{\bar {\tau }}_{k}}$ to the value

$${{\bar {\tau }}_{{\min }}} = \frac{{l{{k}_{0}}{{\tau }_{{{\text{ad}}}}} + 2({{\alpha }_{1}} - {{\alpha }_{0}})\vartheta {{\nu }_{2}}\tanh {\kern 1pt} {\kern 1pt} {{\nu }_{2}}}}{{l{{k}_{0}}{{\nu }_{2}}(\tanh {\kern 1pt} {\kern 1pt} {{\nu }_{2}} + \cosh {\kern 1pt} {{\nu }_{2}})}},$$

(27)

as k₁ → 0 and ν₁ → ν₂.

If the temperature term of Eq. (23) at certain h₁ proves to be such that the denominator itself in Eq. (23) will be equal to zero, the lower limit of $\bar {\tau }$ will be zero. The destruction of a model with a further increase in h₁ will occur due to temperature stresses without applying force P. For this reason, the dependence of $\bar {\tau }$ on h_g may be of two possible types (Figs. 5b, 5c). The experimental data on the dependence of $\bar {\tau }$ on h_g from the paper [2] are shown in Fig. 6 (curve 1). They qualitatively illustrate the correctness of theoretical conclusions for the gluing of steel bars filled with Araldite epoxy glue as an example. If the effect of temperature is neglected in Eq. (23), the limit of $\bar {\tau }$ at h₁ → ∞ will be

$$\bar {\tau }_{{\min }}^{0} = \frac{{{{\tau }_{{{\text{ad}}}}}\tanh {\kern 1pt} {{\nu }_{2}}}}{{{{\nu }_{2}}\left[ {1 + {{{\left( {\tanh {\kern 1pt} {{\nu }_{2}}} \right)}}^{2}}} \right]}}$$

(28)

instead of Eq. (27). The square brackets in Eq. (28) contain a that which is higher than unity, but lower than 2. Therefore, $\bar {\tau }_{{\min }}^{0}$ in Eq. (28) is lower than $\bar {\tau }$ from Eq. (26) at h* = $h_{{\max }}^{*}$. This means that $\bar {\tau }$ will decrease with an increase in the adhesive-layer thickness from $h_{{\max }}^{*}$ to h_g = $h_{{\max }}^{*}$ at h₁ → ∞. Hence, an extremal character of the dependence of $\bar {\tau }$ on h_g is explained by the selection of this model, i.e., by the fact that the existence of contact layers and an active polymer layer is taken into account. Temperature stresses are promotive for a more appreciable decrease in $\bar {\tau }$ with an increase in h_g.

DEPENDENCE OF $\bar {\tau }$ ON THE RIGIDITY OF A SUBSTRATE

Rigidity of a substrate 1/k₀ = E₀h₀ can be varied by changing either its thickness h₀ or Young modulus E₀ (keeping all the other model parameters unchanged). When E₀ is increased from zero to infinity, parameters ν₁ and ν₂ are varied within the ranges ∞ > ν₁ ≥ $\nu _{1}^{*}$ = $(l{\text{/}}2)\sqrt {2g{{k}_{1}}}$, ∞ > ν₂ ≥ 0.

Then, using Eq. (23), we find the possible interval of change in $\bar {\tau }$ with an increase in the rigidity from zero to infinity:

$$0 \leqslant \bar {\tau } \leqslant {{\tau }_{{{\text{ad}}}}} + {{\left[ {({{\alpha }_{1}} - {{\alpha }_{0}})\vartheta \nu _{1}^{*}} \right]} \mathord{\left/ {\vphantom {{\left[ {({{\alpha }_{1}} - {{\alpha }_{0}})\vartheta \nu _{1}^{*}} \right]} {{{k}_{l}}l}}} \right. \kern-0em} {{{k}_{l}}l}}.$$

(29)

The regularity derived from Eqs. (23) and (29) for the change of $\bar {\tau }$ with an increase in E₀H₀ is shown in Fig. 5d.

Based on Eq. (29), it is possible to imagine a method for estimating the “true” adhesion strength τ_ad. For this purpose, it is necessary to use thick bars (with high h₀) as a substrate and join them together with a thin glue layer for 1/k₁ to tend to zero. In this case, the second summand in Eq. (29) will almost be equal to zero, and $\bar {\tau }$ measured in the experiment will become close to τ_ad.

EXPERIMENTAL

The model is schematized in Fig. 8. The rounded edges of steel plates essentially reduce the effect of bending, and the glued joint works only for shear. To determine the dependence of average adhesion strength $\bar {\tau }$ on adhesive gluing length h_k, the glued surfaces of specimens were brought to the 12th class of treatment quality. In the latter case of treatment, the precision of measuring the gluing thickness is 1 μm. Steel plates were glued together by using K-115 low-shrinkage cold cured epoxy compound with polyethylene polyamine as a hardener. The destruction of specimens had an adhesion character.

Fig. 8.

Scheme of a specimen for shear tests: h is the substrate thickness, h_k = h₁ + 2h* is the overall glue layer thickness composed of the thicknesses of adhesive (1) as such and two thicknesses of contact layers (2) 2h*, l is the glue-layer length, and P is the tensile force at two edges of a specimen.

The performed studies have demonstrated that average adhesion strength $\bar {\tau }$ measured in shear tests is a function of the geometric and physical parameters of a substrate, a polymer adhesive, a contact layer, and experiments (e.g., the temperature). In this case of cold curing without thermal treatment with negligible chemical shrinkage in the glue compound, $\bar {\tau }$ can be expressed as

$$\begin{gathered} \bar {\tau } = \frac{{{{\tau }_{{{\text{ad}}}}}({{E}_{1}}{{h}_{1}} + 2{{E}_{0}}{{h}_{0}})}}{{{{E}_{1}}{{h}_{1}}{{\nu }_{1}}\tanh {\kern 1pt} {{\nu }_{1}} + \left( {{{E}_{1}}{{h}_{1}} + 2{{E}_{0}}{{h}_{0}}} \right){{\nu }_{2}}\coth {\kern 1pt} {{\nu }_{2}}}}; \\ \nu _{1}^{2} = \frac{{{{l}^{2}}}}{4}\left( {\frac{1}{{{{E}_{0}}{{h}_{0}}}} + \frac{2}{{{{E}_{1}}{{h}_{1}}}}} \right)\frac{{G\text{*}}}{{h\text{*}}};\,\,\,\,\nu _{2}^{2} = \frac{{{{l}^{2}}}}{4}\left( {\frac{1}{{{{E}_{0}}{{h}_{0}}}}} \right)\frac{{G\text{*}}}{{h\text{*}}}, \\ {{\tau }_{{{\text{ad}}}}} = \lim (\mathop {{{P}_{b}}}\limits_{l \to 0} {\text{/}}bl), \\ \end{gathered} $$

(30)

where E₀ and E₁ are the Young moduli of an adhesive and a substrate, G* is the shear modulus of a contact layer, h* is the contact layer thickness, h_k = $2h\text{*} + \,\,{{h}_{1}}$; h_k is the overall thickness of a glued joint, h₁ is the adhesive-layer thickness without consideration for the contact-layer thickness, τ_ad is the adhesion-bond strength under shear, P_b is the load (destructing force under shear), and l is the gluing length (see Fig. 8).

The above-performed theoretical study and analysis of Eq. (30) show that dependence $\bar {\tau }({{h}_{k}})$ has an extremal character and the value of h* can be determined on the abscissa of $\bar {\tau }({{h}_{k}})$. Such a theoretical preposition has provided a basis for the design of experiments and the interpretation of their results. Experimental dependence $\bar {\tau }({{h}_{k}})$ is shown in Fig. 9 (curve 1). Due to a number of methodological difficulties, a glued joint with a thickness of less than 7.8 μm has not been experimentally created. For this reason, it is impossible to establish the contact-layer thickness by immediate experiment without an extremum in the curve $\bar {\tau }({{h}_{k}})$. However, it should be pointed out that we have $\bar {\tau }$ = 0 at h_k = 0 and, therefore, it is possible to confidently conclude that an extremum is located between points h_k = 0 and h_k = 7.8 μm (the dashed part of curve 1 in Fig. 9).

Fig. 9.

Experimental data on adhesion strength under shear $\bar {\tau }$ of a K-115 steel–epoxy compound joint vs. (1) adhesive-layer thickness and (2) gluing length.

To determine G*/h* from the experimental results by Eq. (30), the following method was used. Equation (30) contains two unknowns G*/h* and τ_ad, and the other parameters can be easily found from independent experiments. The analysis of Eq. (30) and experiments evidence that one of the most influential parameters in $\bar {\tau }$ is gluing length l. If we have two pairs of values (${{\bar {\tau }}_{1}}$, l₁) and (${{\bar {\tau }}_{2}}$, l₂) from experimental dependence $\bar {\tau }(l)$, it is possible to determine G*/h* and τ_ad. The experimental values of the pair (${{\bar {\tau }}_{1}}$, l₁) and (${{\bar {\tau }}_{2}}$, l₂) can be determined from dependence $\bar {\tau }(l)$ shown as curve 2 in Fig. 9. It is possible to exclude τ_ad from Eq. (30). Then,

$$\begin{gathered} {{A}_{1}}{{{\bar {\tau }}}_{1}} = {{A}_{2}}{{{\bar {\tau }}}_{2}};\,\,\,\,{{A}_{1}} = {{E}_{1}}{{h}_{1}}\nu _{1}^{{(1)}}\tanh {\kern 1pt} \nu _{1}^{{(1)}} \\ + \,\,\left( {{{E}_{1}}{{h}_{1}} + 2{{E}_{0}}{{h}_{0}}} \right)\nu _{2}^{{(1)}}\coth {\kern 1pt} \nu _{2}^{{(1)}}; \\ {{A}_{2}} = {{E}_{1}}{{h}_{1}}\nu _{1}^{{(2)}}\tanh {\kern 1pt} \nu _{1}^{{(2)}} + \left( {{{E}_{1}}{{h}_{1}} + 2{{E}_{0}}{{h}_{0}}} \right)\nu _{2}^{{(2)}}\coth {\kern 1pt} \nu _{2}^{{(2)}}. \\ \end{gathered} $$

(31)

The values of $\nu _{1}^{{(i)}}$ and $\nu _{2}^{{(i)}}$ (i = 1, 2) must be determined in compliance with l₁ and l₂ from experimental dependence $\bar {\tau }$(l).

The value of G*/h* is determined from Eq. (31) by the graphic method, the essence of which is to determine the intersection point corresponding to the sought value of G*/h* for the functions A₁${{\bar {\tau }}_{1}}$ and A₂${{\bar {\tau }}_{2}}$ by specifying different G*/h*.

For the accepted model, we have the following initial data: Е₀ = 10⁵ MPa (steel), E₁ = 3000 MPa (K-115 epoxy glue), h₀ = 7 mm, h₁ = 0.18 mm. Using curve 2 in Fig. 9, we determine that l₁ = 3 mm, l₁ = 10 mm, ${{\bar {\tau }}_{1}}$ = 35.4 MPa, and ${{\bar {\tau }}_{1}}$ = 17.5 MPs. The graphical solution of Eq. (31) yields G*/h* = 29.6 × 10⁴ MPa/mm.

To calculate the stresses in the adhesion joint of this pair, it is sufficient to know the value of G*/h*.

In practice, researchers are usually interested in the numerical values of the thickness of shear modulus of a contact layer. In our experiments, similar data cannot be immediately determined; however, if one of values G* and h* is known, the other can be easily determined. Based on the described experiments, it is only possible to estimate the ultimate value of h*. Let us admit that, in the limit case, the shear modulus of a contact layer is equal to shear modulus of a polymer G_p, which is experimentally determined on polymer casts. In this case, the ultimate value of h* can be easily determined. The shear modulus of epoxy polymer from compound K-115 is G_p = 1150 MPa, whereas the ultimate value of h* will be 3.8 μm, i.e., is within the range of experimentally presumable values from curve 1 in Fig. 9, as the gluing thickness, as already mentioned, incorporates two contact-layer thicknesses and the polymer thickness and, if the value of h* is correctly determined, the condition 2h* + h₁ = h_k must be met. It follows from our experiments that, in the limit case, 2h* = 7.6 μm; i.e., the mentioned condition is met.

Based on the above-obtained results, it is possible to expect that gluing will be composed exclusively of the contact layer at h* < 7.8 μm.

CONCLUSIONS

Hence, based on the computational method and experimental data, it is possible to estimate the order of magnitude for the rigidity G*/h* of the contact layer and its thickness h* in the adhesion joint of the polyepoxide–steel system. The found rigidity (adhesion interaction intensity) provides quantitative estimation, in particular, for the maximum stress equal to true adhesion bond strength τ_ad for a given adhesive–substrate pair. It has been noted earlier that τ_ad is determined by the limit of P_b/S at S → 0 or by two experimental points from Eq. (31). Thus, using the limit transition from curve 2 in Fig. 9, we fine true adhesion strength τ_ad = 40 MPa.

Using Eq. (4), it is possible to determine τ_ad for any pairs of values belonging to curve 2 (Fig. 9) from the dependence ($\bar {\tau }$, l):

$$\begin{gathered} {{\tau }_{{{\text{ad}}}}} \\ = \bar {\tau }\left( {\frac{{\left( {{{E}_{1}}{{h}_{1}} + 2{{E}_{0}}{{h}_{0}}} \right)}}{{{{E}_{1}}{{h}_{1}}{{\nu }_{1}}\tanh {\kern 1pt} {{\nu }_{1}} + \left( {{{E}_{1}}{{h}_{1}} + 2{{E}_{0}}{{h}_{0}}} \right){{\nu }_{2}}\coth {\kern 1pt} {{\nu }_{2}}}}} \right). \\ \end{gathered} $$

(32)

Calculation is performed by using the above-given numerical data at fixed $\bar {\tau }$ and l, e.g., $\bar {\tau }$ = 35 MPa at l = 3 mm and the already-known value G*/h* = 29.6 × 10⁴ MPa/mm. Using Eq. (30), coefficients ν₁ and ν₂ are estimated as 0.289 and 0.689, respectively. Theoretical τ_ad calculated by Eq. (32) is equal to 40.7 MPa, and, using $\bar {\tau }$ at l = 10 mm, we obtain τ_ad = 41 MPa; i.e., τ_ad determined with consideration for the contact layer is nearly constant, independent of the gluing length, and close to the above determined ultimate value of 40 MPa.

If τ_ad is calculated by a different method, e.g., from the solution of A.L. Rabinovich [4], i.e.,

$$\begin{gathered} {{\tau }_{{{\text{ad}}}}} = {{\tau }_{{\max }}} = \frac{{\bar {\tau }\omega }}{{\tanh {\kern 1pt} \omega }};\,\,\,\,\omega = \frac{{\alpha {{l}^{2}}}}{2}; \\ {{\alpha }^{2}} = {{G}_{p}}{\text{/}}({{E}_{0}}{{h}_{0}}{{h}_{1}}), \\ \end{gathered} $$

(33)

we result in τ_ad = 35 MPa at l = 3 mm and τ_ad = 18.8 MPa at l = 10 mm. The calculation by Eq. (33) was performed at the same above-given values of E₀, h₀, h₁, l, and G_p = 1150 MPa. Hence, the estimation of τ_ad by Eq. (33) gives a wide spread, whereas constant τ_ad estimated by the proposed theory (Eqs. (31) and (32)) as almost independent of the geometry of a specimen gives some grounds to consider it as a true strength characteristic, i.e., the adhesion strength under shear for a given discrete model (adhesion pair).