Expansion and Collapse of a Bubble Near a Cylindrical Protuberance on a Plane Wall

Abstract

Expansion and collapse of a bubble near a cylindrical protuberance on a plane rigid wall are considered in the regime with the formation of a wall-directed cumulative liquid jet in the stage of collapse. The end face of the cylindrical protuberance is plane and parallel to the wall. The attention is directed to investigating the influence of the radius and height of the cylindrical protuberance on the shape and velocity of the cumulative jet tip and the pressure in the bubble at the moment of impact of the jet onto the bubble surface part closest to the wall. These parameters are of interest in view of the destructive potential of cavitation. The study is performed numerically by the boundary element method. It is found that as the protuberance radius grows, both the cumulative jet tip velocity and the pressure in the bubble at the moment of impact first monotonically increase to some extreme values and then also monotonically decrease. Unlike that, with the rising protuberance height, the velocity of the cumulative jet tip monotonically increases, whereas the pressure in the bubble first non-monotonically increases with formation of two local maxima and then monotonically decreases to a limit value corresponding to the protuberance with the infinite height.

1 INTRODUCTION

The study of the features of bubble dynamics near the rigid surfaces of solids is of interest for prevention of the harmful consequences of the mechanical action of cavitation [1, 2] as well as for its useful applications [3]. To date, main attention was directed to the investigation of the bubble dynamics near a plane wall, in particular, its dependence on the initial bubble shape [4, 5], the distance between the bubble and the wall [6–9], the presence of other bubbles [10, 11], the amplitude and frequency of the acoustic excitation [12–14], etc. Along with that much attention was given to the investigation of the bubble dynamics near curved walls [15–19]. But not much is known about the influence of local convexities and concavities on a plane wall. The present work considers the dependence of the bubble dynamics on a local roughness on a plane wall in the form of a single cylindrical protuberance, the end face of which is plane and parallel to the wall. It is devoted to studying the influence of the radius of the protuberance and its height on the shape and the speed of the cumulative liquid jet tip and the pressure in the bubble at the moment of the impact of the cumulative jet on the bubble surface part nearest to the wall, which is important for the estimate of the destructive potential of cavitation [20–23]. The study is performed by the boundary element method with the fundamental solution for an unbounded domain [24].

2 PROBLEM STATEMENT

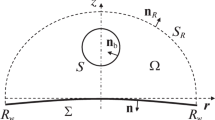
The expansion and collapse of a gas bubble in a liquid near a cylindrical protuberance on a plane rigid wall are considered (Fig. 1). The problem is axisymmetrical, the symmetry axis $z$, which is the axis of symmetry of the protuberance, passes through the bubble center. The origin of the cylindrical coordinates $r,\ z$ is located on the end face of the cylindrical protuberance.

Fig. 1

Bubble near a cylindrical protuberance on a plane rigid wall: $d$ is the distance between the initial position of the bubble center and the end face of the protuberance, $h$ is the height of the protuberance, $R_{cyl}$ is the radius of the protuberance.

Initially (at the time moment $t=0$) the bubble is spherical, the liquid pressure is $p_{L}=1$ bar, the bubble is in the phase of expansion. At this moment the bubble radius is $R=0.1$ mm, the pressure in the bubble is $p_{b}=37.765$ bar, the velocity of the radial expansion is $dR/dt=103.7$ m/s, the distance from the bubble center to the end face of the cylindrical protuberance is $d=R_{m}$, where $R_{m}$ is the bubble radius at the end of bubble expansion without a wall. With time the bubble first expands to some maximum volume and then collapses. In the course of collapse, a wall-directed cumulative liquid jet arises on the bubble surface (possibility of appearance of such jets was mentioned in [20, 21]). At some moment, which is denoted below as $t_{c}$, the jet impacts on the bubble surface part closest to the wall.

The study is directed to the investigation of the dependence of the bubble dynamics on the radius $R_{cyl}$ and the height $h$ of the cylindrical protuberance. Main attention is paid to the bubble shape, the speed of the cumulative jet and the pressure inside the bubble at the moment $t_{c}$ of the impact of this jet onto the bubble surface part nearest to the wall. These characteristics to a large extent determine the wall load, which is of practical interest. The study is performed by the boundary element method, in which the liquid is treated as incompressible. At the place of impact of the cumulative jet onto the bubble surface part nearest to the wall, shock pulses can occur. For their adequate simulation and, therefore, for the adequate description of the bubble collapse at $t>t_{c}$, it is necessary to take into account the liquid compressibility. Since it is ignored in the boundary element method, the bubble collapse is considered in the present work only till the moment of the cumulative jet impact onto the bubble surface part nearest to the wall $(t_{c})$.

3 MATHEMATICAL MODEL AND NUMERICAL TECHNIQUE

It is assumed that the liquid is incompressible, its motion is potential, and the pressure in the bubble is uniform. The liquid flow is governed by the equations

$$\Delta\Phi=0,\quad\Phi_{t}+\frac{1}{2}(\nabla\Phi)^{2}+\frac{p-p_{L}}{\rho_{L}}=0,$$

(1)

where $\Phi$ is the velocity potential, $\rho_{L}$ is the liquid density ($\rho_{L}=1000$ kg/m${}^{3}$). The pressure in the bubble $p_{b}$ changes adiabatically $p_{b}=p_{b0}(V_{0}/V)^{\kappa},$ where $V_{0},V$ are the initial and current bubble volumes, $\kappa$ is the specific heats ratio ($\kappa=1.4$), $p_{b0}$ is the initial pressure in the bubble.

The following boundary conditions are set on the bubble surface

$$p^{+}=p_{b}-2\sigma H,\quad d\mathbf{r}_{b}/dt=\mathbf{u}$$

(2)

and on the wall

$$\mathbf{u}\cdot\mathbf{n}=0,$$

(3)

where $p^{+}$ is the liquid pressure on the bubble surface, $\sigma$ is the surface tension ($\sigma=0.073$ kg/s${}^{2}$), $H$ is the mean curvature, $\mathbf{r}_{b}$ is the position vector, $\mathbf{u}=\nabla\Phi$ is the velocity, $\mathbf{n}$ is the normal to the wall.

Equations (1)–(3) are solved by a numerical technique [24] based on the boundary element method with the fundamental solution for an unbounded domain. The no-penetration condition (3) on the wall is satisfied numerically, for which purpose the profile of the wall surface in its axial section is divided into cells. In doing so, the unbounded liquid domain on the wall is replaced with a sufficiently distant artificial boundary.

4 BUBBLE DYNAMICS NEAR A WALL

The following non-dimensional quantities with an asterisk are used below:

$$d^{*}=d/R_{m},\quad h^{*}=h/R_{m},\quad R^{*}=R/R_{m},\quad p^{*}=p/p_{L},$$

$$v^{*}=|\mathbf{u}|/(p_{L}/\rho_{L})^{1/2},\quad t^{*}=t/[R_{m}/(\rho_{L}/p_{L})^{1/2}].$$

The influence of the radius and height of the cylindrical protuberance is considered in the ranges $0<R_{cyl}^{*}<\infty$ and $0\leq h^{*}<\infty$ with the initial distance from the bubble center to the protuberance end face $d^{*}=1$.

4.1 Bubble Dynamics Near a Plane Wall without a Protuberance

Figure 2 illustrates the main features of the bubble deformation near a plane wall without a protuberance in the cases with $d^{*}=1$ and $1.5$.

Fig. 2

Change of the bubble shape during the bubble expansion (dashed lines) and collapse (solid lines) near a plane wall without a cylindrical protuberance for (a) $d^{*}=1$ and (b) $d^{*}=1.5$.

Figure 2 shows that in the presented cases just a single point makes an initial area of the cumulative jet tip impact. The presence of a wall close to the bubble leads to that the bubble surface part nearest to the wall becomes somewhat flattened at the moment of the maximum expansion (the moment of the collapse beginning) $t_{m}^{*}$. With growing distance between the bubble and the wall the flattening decreases. At some moment $t_{c}^{*}$, the cumulative jet impacts onto the bubble surface part closest to the wall. In the variants given in Fig. 2, the jet tip velocity $v_{jc}^{*}$ and the pressure in the bubble $p_{bc}^{*}$ at the impact moment $t^{*}_{c}$ are $v_{jc}^{*}=8.30$ and $p_{bc}^{*}=0.89$ for $d^{*}=1$ (Fig. 2a) and $v_{jc}^{*}=10.37$ and $p_{bc}^{*}=12.57$ for $d^{*}=1.5$ (Fig. 2b).

4.2 Influence of the Radius of a Cylindrical Protuberance on a Plane Wall

Figure 3 shows the influence of a cylindrical protuberance on a plane wall on the dynamics of a bubble during its expansion and collapse till the moment $t_{c}^{*}$ of the cumulative jet impact onto the bubble surface part closest to the wall. It can be concluded by comparing Fig. 3 with Fig. 2 that the presence of a cylindrical protuberance on a wall most significantly influences the shape of the bubble at the end of expansion and during the subsequent collapse. In particular, one can see that at the moment of maximum expansion the bubble surface part closest to the wall is more flattened in the presence of the protuberance than without it. With the protuberance the radial size of the bubble surface part closest to the wall is reduced more significantly. In the absence of the protuberance, the impact begins with the collision of the jet tip center with the center of the bubble surface part closest to the wall. By contrast, in the presence of the protuberance the impact begins with circular contact of the jet and the bubble surface part closest to the wall. In other words, the initial impact area in the case with the protuberance is a ring rather than a single point as in the case without it. As a result, a gas cavity occurs between the jet tip and the central zone of the bubble surface part closest to the wall. And this is very important since the presence of such a cavity can significantly intensify the shock pulse appearing in the liquid due to the impact, and therefore significantly increase the pulse action on the wall.

Fig. 3

Change of the bubble shape during the bubble expansion (dashed lines) and collapse (solid lines) near a plane wall with a cylindrical protuberance for $R_{cyl}^{*}=0.35$ and $h^{*}=0.5$.

Figure 4 shows the influence of the protuberance radius on the bubble shape at the moment $t_{c}^{*}$ of the cumulative liquid jet impact onto the lower part of the bubble surface. It follows from Fig. 4 that for $R_{cyl}^{*}<0.05$ and $R_{cyl}^{*}>1.5$ the bubble shapes at moment $t_{c}^{*}$ are only slightly different from those given in Figs. 2b and 2a, respectively, for a plane wall without a protuberance. With growing $R_{cyl}^{*}$ in the interval between 0.05 and 1.5, the curvature radii of the jet tip and the lower part of the bubble surface in the vicinity of the symmetry axis first come closer, so that at $R_{cyl}^{*}\approx 0.2$ the initial impact region is a bowl-shaped surface around the symmetry axis rather than just a single point. In the interval $0.2<R_{cyl}^{*}<0.3$, the lower part of the bubble surface becomes more and more curved as compared to the impacting jet tip. As a result, the jet impact becomes initially annular, and a gas cavity is formed between the jet tip and the lower part of the bubble surface (this feature was mentioned above when discussing Fig. 3). In the interval of $R_{cyl}^{*}$ from 0.3 to 0.425, the difference in the curvature of the lower part of the bubble surface and the impacting jet tip gradually decreases. As a result, the annular initial impact region is gradually transformed back into a bowl-shaped one, as it is at $R_{cyl}^{*}=0.2$. With further growth in $R_{cyl}^{*}$, the curvature of the lower part of the bubble surface decreases, so that the beginning of the impact is transformed into a shape similar to that in the case with $R_{cyl}^{*}\approx 0.05$.

Fig. 4

Profiles of the wall and the bubble at the moment of the liquid jet impact onto the lower part of the bubble surface (solid lines) and fragments of the lower part of the bubble surface at the moment of maximum bubble expansion (dotted lines) for $d^{*}=1$, $h^{*}=0.5$ and a number of $R_{cyl}^{*}$ values.

Figure 5 shows the protuberance radius effect on the jet tip speed and the pressure in the bubble at the moment $t_{c}^{*}$ of the jet impact onto the lower part of the bubble surface. It is seen that the influence of $R_{cyl}^{*}$ on the speed $v_{jc}^{*}$ is significantly less than on the pressure $p_{bc}^{*}$. Along with that, the speed $v_{jc}^{*}$ and the pressure $p_{bc}^{*}$ with growing $R_{cyl}^{*}$ both at first monotonically increase from their values corresponding to the purely plane wall at $d^{*}=1.5$ (Fig. 2b), and then monotonically decrease to their values corresponding to the purely plane wall at $d^{*}=1$ (Fig. 2a). The major changes in $p^{*}_{bc}$ take place in the interval $0.125<R_{cyl}^{*}<0.75$. The maximum values of $v^{*}_{jc}$ and $p_{bc}^{*}$ are attained at $R_{cyl}^{*}\approx 0.75$ and $R_{cyl}^{*}\approx 0.425$, respectively.

Fig. 5

Dependencies of the jet tip speed $v_{jc}^{*}$ and the pressure in the bubble $p_{bc}^{*}$ at the moment $t_{c}^{*}$ of the jet impact onto the lower part of the bubble surface on the radius $R_{cyl}^{*}$ of the cylindrical protuberance on the wall for $d^{*}=1$ and $h^{*}=0.5$. Dots on the right and left sides indicate the corresponding values in the cases of a plane wall without a protuberance at $d^{*}=1$ and $d^{*}=1.5$, respectively.

4.3 Influence of the Height of a Cylindrical Protuberance on a Plane Wall

Figure 6 shows the influence of the height $h^{*}$ of the cylindrical protuberance on the wall on the bubble shape at the moment $t_{c}^{*}$ of the cumulative liquid jet impact onto the lower part of the bubble surface. It follows from Fig. 6 that as $h^{*}$ increases in the interval between 0.1 and 0.4, the difference in the curvature radii of the jet tip and the lower part of the bubble surface in the vicinity of the symmetry axis decreases, so that at $h^{*}\approx 0.4$ the initial area of impact transforms into a bowl-shaped surface around the symmetry axis (as it in Fig. 4 at $R_{cyl}^{*}=0.425$). In the interval $0.5<h^{*}<1.8$, the lower part of the bubble surface becomes increasingly sharper as compared to the impacting jet tip. As a result, the beginning of impact becomes annular and a gas cavity appears between the jet tip and the lower part of the bubble surface (as it in Fig. 4 at $R_{cyl}^{*}=0.3$). With further increase of $h^{*}$, the cavity size decreases and then the cavity disappears, while a convexity directed to the jet tip (counter jet) arises at the lower part of the bubble surface in the vicinity of the symmetry axis. With an even further increase in $h^{*}$, the counter jet becomes more pronounced. It should be noted that with growing $h^{*}$, the distance between the central area of the lower part of the bubble surface and the end face of the protuberance at the moment of the cumulative jet impact $t^{*}_{c}$ increases.

Fig. 6

Profiles of the bubble and a part of the wall at the moment of the liquid jet impact onto the lower part of the bubble (solid lines) and fragments of the lower part of the bubble surface at the moment of the maximum bubble expansion (dotted lines) for $d^{*}=1$, $R_{cyl}^{*}=0.35$ and a number of $h^{*}$ values.

Figure 7 shows the protuberance hight effect on the jet tip speed and the pressure in the bubble at the moment $t_{c}^{*}$ of the jet impact onto the lower part of the bubble surface. It is seen that with rising $h^{*}$, the speed $v_{jc}^{*}$ monotonically increases, whereas the change of the pressure $p_{bc}^{*}$ is essentially non-monotonic. With growing $h^{*}$, the value of the pressure first increases to $p_{bc}^{*}\approx 67$ at $h^{*}\approx 0.5$, then slightly decreases to $p_{bc}^{*}\approx 60$ at $h^{*}\approx 0.75$, after that strongly increases to $p_{bc}^{*}\approx 207$ at $h^{*}\approx 1.8$, and then again decreases to its limit at $h^{*}\rightarrow\infty$.

Fig. 7

Dependencies of the jet tip speed $v_{jc}^{*}$ and the pressure in the bubble $p_{bc}^{*}$ at the moment $t_{c}^{*}$ of the jet impact onto the lower part of the bubble surface on the height $h^{*}$ of the cylindrical protuberance on the wall for $d^{*}=1$ and $R_{cyl}^{*}=0.35$. Dots on the left side indicate the corresponding values in the case of a plane wall without a protuberance at $d^{*}=1$.

5 CONCLUSIONS

The influence of the height and radius of a cylindrical protuberance on a plane wall on the shape and speed of the cumulative jet and the pressure in the bubble at the moment of its collapse at which the jet impacts onto the bubble surface part closest to the wall has been studied. The study is performed by the boundary element method. It has been found that as the protuberance radius grows, both the cumulative jet tip speed and the pressure in the bubble at the moment of the impact first monotonically increase to some extreme values and then also monotonically decrease. Unlike that, with the rising protuberance height, the cumulative jet speed monotonically increases, whereas the pressure in the bubble first non-monotically increases with formation of two local maxima and then monotinically decreases to a limit value corresponding to the protuberance with the infinite height. The second local maximum is significantly higher than the first one.