1 INTRODUCTION

Knowledge of the features of the dynamics of bubbles near the surfaces of rigid bodies is of great importance in such applications as underwater explosions [1, 2], cavitation erosion [3, 4], ultrasonic cleaning of rigid surfaces [5], various methods of treatment in medicine [6], etc. Numerous theoretical [7–11] and experimental [12–14] studies show that the geometry and law of motion of bodies significantly affect the features of the interaction of bubbles with the surfaces of the bodies. The most common algorithms used for the numerical simulation of the bubble dynamics in the cases with small influence of the liquid viscosity and compressibility are based on the boundary element method. For a bubble near a flat rigid surface (wall), such an algorithm was first proposed in [15] and then developed in a number of later works [16–18]. Its efficiency is due to the use of a fundamental solution for a half-space in which the no-penetration condition are satisfied automatically, which eliminates the need to introduce unknowns at the nodes on the wall surface. A similar approach was also applied to curved rigid walls [19, 20], where the corresponding fundamental solutions obtained by the image method was utilized. However, in many practical situations, the geometry of the wall (body surface) because of its micro-roughness can be very complex, so that finding a fundamental solution that satisfies the condition of no-penetration on the body surface is a very difficult and perhaps even impossible task. In such cases, one can use the fundamental solution for an unbounded domain, and the no-penetration condition on a wall can be satisfied numerically at a number of grid nodes on the wall. The main problem in this case is the non-closed surface of the wall. In the numerical algorithm, the infinite liquid domain of the problem is replaced by a finite computational one with an artificial boundary, and the validity of the numerical solution is estimated by increasing the size of the domain [21–23]. In this paper, the efficiency of one of the algorithms that implements this approach is investigated.

2 PROBLEM STATEMENT

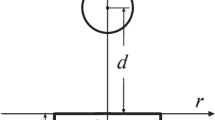
The modeling of the axisymmetric dynamics of a gas bubble near a curved rigid wall by the boundary element method using the fundamental solution for an unbounded region is considered. In such a case, the no-penetration condition on the wall is satisfied numerically. To this end, the contour of the wall in its axial section, like the contour of the bubble surface, is divided into cells. In doing so, the unbounded area of the wall is replaced by a finite area with an artificial boundary of the radius \(r=R_{w}\), where \(r\) is the distance to the axis of symmetry. Main attention of the study is directed to the dependence of the numerical solution on the radius of the computational domain on the wall \(R_{w}\), the number of cells \(N_{un}\) when the domain is partitioned uniformly, and the number of cells \(N\) when it is partitioned non-uniformly with condensation toward the axis of symmetry according to geometric progression. The study is carried out for problems of the collapse of a bubble near a flat wall and of the expansion and subsequent collapse of a bubble near the concave and convex walls. The surface of the curved walls is determined by the equation [19, 20]

$$f(r,z)=d_{2}[\xi^{2}(z+\xi h)+(1-\xi^{2})d_{1}]-(h-z)d_{1}=0,$$
(1)

where \(z\) is the axial coordinate of the cylindrical coordinate system \(r\), \(z\) with the origin at the point of the wall located on the symmetry axis of the problem, \(d_{1}=\{r^{2}+(z+\xi h)^{2}\}^{1/2}\), \(d_{2}=\{r^{2}+(h-z)^{2}\}^{1/2}\), \(h\) is the distance from the wall to the center of the bubble along the axis of symmetry \(z\), \(\xi\) is a parameter defining the curvature of the wall (the wall is convex for 0 <\(\xi\)<1, concave for \(\xi\) > 1 and flat for \(\xi=1\)). The curvature of the wall at the origin is \(3(\xi-1)/(4\xi)\). The dependence \(z=z(r)\) for the wall points is determined from the ODE \(dz/dr=-f_{r}/f_{z}\) with \(z(0)=0\), where \(f_{r}\), \(f_{z}\) are the corresponding partial derivatives. To evaluate the efficiency of the algorithm based on the fundamental solution for an unbounded domain, its results are compared with those calculated using the fundamental solution for the corresponding half-spaces. The numerical solution to the problem of the dynamics of a bubble near a flat wall using a fundamental solution for a half-space is found by a well-known method presented in [15–17], and the solutions to the problems of the dynamics of a bubble near the concave and convex walls are taken from [19].

3 FEATURES OF THE NUMERICAL TECHNIQUE BASED ON THE FUNDAMENTAL SOLUTION FOR UNBOUNDED DOMAIN

Fig. 1 shows the computational domain \(\Omega\), bounded by the wall \(\Sigma\) and some spherical surface \(S_{R}\) with the radidial co-ordinate Rw of the point of its intersection with the wall. It is assumed that with an increase in the size of the computational domain (the value of \(R_{w}\)), the values of the potential in the considered part of the computational domain \(\Omega\) will tend to their limiting values [21–23]. Thus, a series of calculations is needed to determine the value of \(R_{w}\), at which its further increase has little effect on the problem solution. The integral over the sphere \(S_{R}\) tends to zero at \(R_{w}\to\infty\) [24] and therefore it is not included in the integral equation. In this case, the integral equation for the velocity potential can be written as [24]

$$\int\limits_{S\bigcup\Sigma}\left(G\frac{\partial\phi}{\partial n}(x^{\prime})-\phi(x^{\prime})\frac{\partial G}{\partial n^{\prime}}\right)ds^{\prime}=c(x)\phi(x),$$
(2)

where \(G(x,x^{\prime})=1/(4\pi|x-x^{\prime}|)\) is the fundamental solution (Green’s function) for the unbounded domain, \(c\)(\(x\))=1 for \(x\in\Omega\), \(c\)(\(x\))=0.5 \(x\in S\cup\Sigma\).

Fig. 1
figure 1

Computational domain \(\Omega\) : \(S\) is the bubble surface, \(\Sigma\) is the curved wall with the center at \(r=0\), \(z=0\), \(S_{R}\) is the sphere with the center at \(r=0\), \(z=0\), \(R_{w}\) is the radius of the wall section by the sphere \(S_{R}\).

Full size image

In the numerical solution of (2) by BEM, a grid of nodes is introduced on the surfaces of the bubble and the wall (0 \(\leq r\leq R_{w}\)), while the values to be determined at the nodes on the bubble surface are those of the normal velocity under given values of the velocity potential. Similar values to be determined at the nodes on the wall are the values of the potential under the zero normal speed (i.e., the no-penetration condition ). The diagonal elements of the system of linear equations written for the nodes on the wall are set equal to 0.5, while for the nodes on the bubble surface they are determined by the formula [25]

$$c(x)=1+\int\limits_{S}\left(\frac{\partial G(x,x^{\prime})}{\partial n}\right)ds$$

which is sometimes called as 4\(\pi\) rule [26].

4 RESULTS

In all the problems considered below, the liquid pressure is \(p_{\infty}=1\) bar, the bubble is filled with gas with the adiabatic exponent \(\gamma=1.4\), the initial distance from the bubble center to the wall along the symmetry axis is 1.2\(R_{0}\), the bubble contour in its axial section is covered by a uniform mesh with the cell number \(N_{b}=200\). In the case of non-uniform partition of the wall contour in its axial section, a mesh is used with condensation to the axis of symmetry, the arc coordinates of which form a geometric progression with the denominator of the progression equal to \(q=(s_{w}/s)^{1/(N-1)}\) , where \(s=\pi R_{0}/N_{b}\) is the size of the element near the axis of symmetry, \(s_{w}\) is the length of the arc of the wall from the axis of symmetry to the point with the radial coordinate \(R_{w}\).

4.1 Collapse of a Bubble Near a Flat Wall

In a liquid at rest, bounded by a motionless flat wall, there is a stationary gas spherical bubble with a radius of \(R_{0}=1\) mm. At the initial moment of time \(t=0\), the pressure in the bubble instantly decreases to \(p_{b0}=0.238p_{\infty}\). As a result of the difference between the pressures in the liquid and the bubble, the latter begins to collapse.

The evolution of the surface of the bubble during its collapse is illustrated in Fig. 2a, which shows the results of calculations using the method [17] based on the fundamental solution for the half-space. It can be seen that during the collapse, a cumulative liquid jet directed to the wall is formed on the bubble surface part more distant from the wall. At some instant \(t_{c}\), the jet hits the bubble surface part closest to the wall. As a result, an intense pressure pulse (or even a shock wave) can form in the liquid, which in practice determines one of the mechanisms of cavitation damage. The numerical solution obtained using the fundamental solution for the half-space by the method of [17] plays the role of a reference solution in the present work. Fig. 2b shows the results of calculations by the method of this work for the boundary of the computational domain on the wall with \(R_{w}=10R_{0}\) with its uniform partition into \(N_{un}=200\) cells (note that a subsequent increase in \(R_{w}\) and \(N_{un}\) does not lead to noticeable changes in the contours shown in Fig. 2b). It can be seen that the contours of the bubble in Fig. 2b are in excellent agreement with the corresponding contours in Fig. 2a.

Fig. 2
figure 2

Collapse of a bubble near a flat wall: evolution of the bubble surface derived by BEM using fundamental solutions for (a) the unlimited domain and (b) the half-space.

Full size image
Fig. 3
figure 3

Collapse of a bubble near a flat wall, calculated by the method of the present work: the numerical convergence (a, c, e) of the bubble profile at the time \(t_{c}\) and (b, d, f) of the velocity of the upper pole of the bubble in the final stage of collapse (a, b) with increasing the radius of the computational domain on the wall, (c, d) with refining the uniform partition of the computational domain on the wall and (e, f) with refining the non-uniform partition of the computational domain on the wall. In (b, d, f), dots indicate the moment instant \(t_{c}\) at which the jet hits the bubble surface part closest to the wall, t and vz0 are in m/s and \(\mu\)s, respectively.

Full size image

Figure 3 shows the features of the convergence of the numerical solution according to the method of the present work with growing the radius \(R_{w}\) of the computational domain on the wall (at \(N_{un}=20R_{w}/R_{0}\)), the number of the grid cells \(N_{un}\) in the uniform partition of this area (at \(R_{w}=20R_{0}\)), and the number of the grid cells \(N\) in its non-uniform partition (at \(R_{w}=20R_{0}\)). The convergence of the bubble shape at the time \(t_{c}\) and the velocity of the upper pole of the bubble in the final stage of the collapse is quite clear. In particular, graphical convergence is achieved for \(R_{w}\approx\)20 \(R_{0}\), \(N_{un}\approx\) 100, and \(N\approx\) 25, respectively. It should be noted that the characteristics presented in Fig. 3, calculated for these values of \(R_{w}\) , \(N_{un}\) or \(N\), and the corresponding characteristics of the reference numerical solution graphically coincide.

4.2 Expansion and Collapse of a Bubble Near a Concave Wall

In liquid at rest, bounded by a motionless concave wall defined by (1) with \(\xi=3\), there is a motionless spherical gas bubble with a radius of \(R_{0}=0.157\) mm. At \(t=0\), the pressure in the bubble instantly increases to \(p_{b0}=100p_{\infty}\). As a result, the bubble first expands and then collapses. With these parameters, the maximum bubble radius in the absence of a wall is \(R_{max}\approx 1\) mm.

Fig. 4
figure 4

Expansion and collapse of a bubble near a concave wall: evolution of the bubble surface in the phase of its collapse according to the results of (a) [19] and (b) the present work.

Full size image

The evolution of the bubble surface at the phase of collapse is presented in Fig. 4a, which shows the results taken from [19]. They were obtained using the fundamental solution for the corresponding half-space. It can be seen that here, as in the case of bubble collapse near a flat wall, a cumulative jet is also formed on the bubble surface part more distant from the wall. At some moment \(t_{c}\) this jet hits the bubble surface part closest to the wall. At the same time, the jet characteristics (e.g., the shape and the velocity that are important for applications) are here appreciably different from those in the case of a flat wall. Figure 4b shows the results of calculations by the method of the present work for the computational domain on the wall with \(R_{w}=10R_{0}\) and its uniform partition (\(N_{un}=200\)). It can be seen that the bubble contours in Fig. 4b are in excellent agreement with those in Fig. 4a.

Fig. 5
figure 5

Same as in Fig. 3, but for expansion and subsequent collapse of a bubble near a concave wall with \(\xi=3\).

Full size image

Figure 5, like Fig. 3, demonstrates the features of the convergence of the numerical solution in terms of the bubble shape at the moment \(t_{c}\) and the velocity of the upper pole of the bubble in the final stage of collapse with an increase in the radius \(R_{w}\) (at \(N_{un}=20R_{w}/R_{0}\)) and the cell numbers \(N_{un}\) and \(N\) (at \(R_{w}=20R_{0}\)). The results show that the graphical convergence of the characteristics shown in Fig. 5 is achieved at \(R_{w}\approx\) 20\(R_{0}\), \(N_{un}\approx\) 200 and \(N\approx\) 100, respectively.

4.3 Expansion and Collapse of a Bubble Near a Convex Wall

The problem considered in this section differs from that in the previous one only in that here the wall is convex with \(\xi=0.3\).

Fig. 6
figure 6

Same as in Fig. 4, but for a convex wall.

Full size image

The evolution of the bubble surface in the phase of collapse is illustrated in Fig. 6a, which shows the results from [19], obtained using the fundamental solution for the corresponding half-space. As in the cases of bubble collapse near the flat and concave walls, one can see here the formation and development of a cumulative jet directed toward the wall. At the same time, this case of a convex wall differs from the cases of flat and concave walls not only by the characteristics of the jet (shape, velocity), but also by the geometry of the bubble surface part closest to the wall. In particular, here, by the time \(t_{c}\), it bends toward the jet. Figure 6b shows the results of calculations by the method of the present work for the computational domain boundary with \(R_{w}=10R_{0}\) and its uniform partition (\(N_{un}=200\)). It can be seen that the contours of the bubble in Fig. 6b are in excellent agreement with those in Fig. 6a.

Figure 7, like Fig. 5, illustrates the features of the convergence of the numerical solution with an increase in the radial co-ordinate of the computational domain \(R_{w}\) (at \(N_{un}=20R_{w}/R_{0}\)), the cell numbers \(N_{un}\) and \(N\) (at \(R_{w}=20R_{0}\)). Calculations show that the graphical convergence of the characteristics presented in Fig. 7 is nearly achieved at \(R_{w}\approx\) 20 \(R_{0}\), \(N_{un}\approx\) 200, and \(N\approx\) 100, respectively. It is interesting to note that, as in the case of the concave wall, with increasing the number \(N\) of non-uniform partition of the wall, the bubble profile shifts up to its limiting position, while with rising the number \(N_{un}\) of its uniform partition, the bubble profile shifts down to its limiting position.

Fig. 7
figure 7

Same as in Fig. 3, 5, but for a convex wall.

Full size image

5 CONCLUSIONS

The study of the efficiency of modeling of the axisymmetric dynamics of a gas bubble near a curved wall by the boundary element method using the fundamental solution of the Laplace equation for an unbounded domain was carried out. For this purpose, the problems of bubble collapse near a flat wall and the expansion and subsequent collapse of a bubble near concave and convex walls were considered. The results obtained were compared with those derived using fundamental solutions for the regions bounded by the considered walls. Good agreement was obtained. The presented results demonstrate the convergence of the numerical solution with an increase in the size of the computational domain on the wall, the cell number in uniform partition of the wall contour and in its non-uniform partition with condensation to the axis of symmetry according to geometric progression. It is shown that the non-uniform partition of the flat wall contour requires a significantly smaller number of nodes than its uniform partition does. For the curved walls, this effect is less appreciable. It should be noted that the choice of a special form of the fundamental solution, which satisfies the no-penetration condition, allows one to reduce the computation time by about a factor of \((N_{b}+N)^{2}/N_{b}^{2}\). Unfortunately, such solutions cannot always be constructed for complex wall geometry of the wall.