Evaluation of Absolute Permeability in Heterogeneous and Anisotropic Porous Media Using the Lattice Boltzmann Simulations

Abstract

This paper presents a systematical study of the effect of porosity, pore-level heterogeneity and anisotropy on the absolute permeability of digital images of porous media. The main goal is to develop an analytical formula that estimates permeability as a function of these three parameters at once. Permeability is assessed based on numerical simulations using the lattice Boltzmann equations. Digital models of porous media are generated by a combined method consisting of Monte-Carlo and quartet structure generation set (QSGS) algorithms. Increase in heterogeneity negatively affects permeability. With an increase in porosity, the effect of heterogeneity on flow properties decreases. There was a linear decrease in permeability during the transition between favorable and unfavorable anisotropy. The influence of anisotropy is most pronounced in samples with high porosity and monotonically reduces with decreasing porosity. Heterogeneity negatively influences on the sensitivity of flow properties to changes in anisotropy and independent on porosity.

1 INTRODUCTION

Single-phase flows in porous media occur in many scientific and engineering disciplines, such as underground hydromechanics, oil and gas engineering, hydrology and hydrogeology, medicine, and chemical engineering. One technology for measuring transport properties, such as absolute permeability, involves performing laboratory flow experiments, which are laborious, time consuming and expensive. For this reason, an alternative method for assessing flow characteristics is to use analytical dependences that relate permeability to other characteristics of a porous medium (porosity, specific surface area of pore channels). The development of a universal formula that makes it possible to predict the transport properties of porous materials with high quality and accuracy is a matter of great fundamental and practical importance and an urgent research area.

One of the main and widely used formulas is the Kozeny–Carman equation, which connects porosity $m$ and absolute permeability $k$ as follows [1, 2]:

$$k=\frac{1}{C_{KC}\tau^{2}}\frac{m^{3}}{S^{2}_{V}},$$

(1)

where $S_{V}$ is the specific surface area, $\tau$ is the tortuosity, and $C_{KC}$ is the Kozeny–Carman constant. This formula was developed on the basis of the simplest capillary bundle model and also does not explicitly take into account heterogeneity and anisotropy of the pore structure. Its applicability is limited and the accuracy is insufficient [3]. These disadvantages stimulate the improvement of this formula and the derivation of new equations.

In recent decades, this problem has been intensively studied, resulting in the development of various relationships. A group of articles has been published in which the flow properties of ordered and arbitrary structures were studied. Gebart [4] developed an analytical equation for homogeneous media with quadratic and hexagonal arrangements of circular fibers: $k=R_{f}^{2}C_{G}(\sqrt{\frac{1-m_{c}}{1-m}}-1)^{5/2}$, where $R_{f}$ is the fiber radius, $m_{c}$ is the threshold porosity, and $C_{G}$ is the fitting parameter. Eshghinejadfard et al. [5] and Ebrahimi Khabbazi et al. [6] investigated the flow properties of body- and face-centered cubes and have developed the relationship for the Kozeny–Carman constant. Koponen et al. [7] studied flows in media with square obstacles and offered using the effective porosity $m^{eff}$ instead of the full porosity in the Kozeny–Carman equation. Rumpf and Gupte [8] obtained an empirical relationship for the sphere packing models: $k=0.178d^{2}m^{5.5}$ ($d$ is the grain diameter). This formula shows high deviations for structures with low and high porosity.

The above ratios for arbitrary structures can be useful for a rough assessment of their flow properties. The main disadvantage of these relationships is that they do not take into account the heterogeneity and, moreover, the anisotropy of the pore space. So far, there are several studies in which the influence of anisotropy and heterogeneity on the flow properties is investigated mainly qualitatively, but a numerical description of the revealed effects is not performed. To the best of our knowledge, no such systematic quantitative researches have been conducted.

A group of papers reported a significant effect of heterogeneity on tortuosity and permeability. It was found in [9, 10] that ‘‘permeability of a random medium is lower than the permeability of a regularly ordered medium with the same porosity‘‘. In [11], in the study of samples with different structures and the same porosity, large deviations of tortuosity from the average value were found, which decreased with increasing porosity. The effect of square particles locations in soils was considered in [12], but the arrangement of particles and their possible movements were limited and not arbitrary in this study.

An attempt to numerically describe the effect of heterogeneity and anisotropy on permeability and tortuosity was made in [13]. According to the published results, no clear correlation was found between the flow properties and porous media characteristics. Moreover, the influence of anisotropy has not been studied for structures with various porosity and heterogeneity. The permeability of heterogeneous and anisotropic shales was assessed in [14]. On the graphs presented in this work, one can note the correlation, but, unfortunately, it is not evaluated numerically and the results are not systematized to the end. There are other high-quality studies on this issue [15–17], but they are also obviously not enough.

Today, numerical experiments performed on digital models of porous media have become a widely used method for studying their properties or pore-scale processes. Digital models can be represented by X-ray computed tomography (CT) images of natural samples [18] as well as artificially generated structures [13–16, 19]. There are various algorithms for generating porous media. The most commonly used methods are quartet structure generation set (QSGS) [13–15, 20], random distribution of obstacles [19, 20], and Monte-Carlo [21, 22]. Unlike X-ray CT models, artificial structures are more suitable for studying flow properties, since the methods mentioned above can control the characteristics of a porous medium (porosity, specific surface area, heterogeneity, anisotropy). Digital models also allow one to quantify their heterogeneity and anisotropy through image processing [14], which is extremely difficult to do on real samples.

The findings of this paper are based on the numerical simulations of single-phase flows in porous structures using the lattice Boltzmann equations (abbreviated as LBEs) [23]. LBEs have become a powerful tool for pore-scale simulations and, as far as we know, used most often in comparison with the Navier-Stokes equations [24] and the pore network model [25]. The attractiveness of the LBEs involves simple boundary conditions on obstacles (the ‘‘bounce back‘‘ rule) and an easy numerical scheme, a short duration of one iterative time step, and good adaptation to GPGPU and OpenMP technologies. The accuracy of Single-relaxation time (SRT) and Multi-relaxation time (MRT) collision models within LBEs was investigated in [26, 27]. Unlike the SRT model, the results obtained with the MRT model are independent of viscosity. In addition, when testing these models on a planar Poiseuille flow, the accuracy of the MRT model is much higher.

In our previous paper [21], we found the numerical effect of heterogeneity on the absolute permeability and tortuosity of isotropic structures. An analytical formula was obtained that predicts permeability and tortuosity in the dependence of porosity and heterogeneity. Unfortunately, the results of this paper are limited since they are valid only for isotropic porous media.

To overcome this disadvantage, the scope of the present paper is to systematically study the effect of porosity, pore-level heterogeneity and anisotropy on absolute permeability. The value of the results lies in the identified effect of anisotropy on permeability in media with different heterogeneity and porosity. The target of our investigation is an analytical formula that estimates permeability as a function of porosity, heterogeneity, and anisotropy and determines the advantage of the results.

2 METHODS

2.1 Mathematical Model

This article uses LBEs with an MRT collision model to simulate pore-scale single phase flows.

In the LBEs, the fluid flow is regarded as the dynamics of an ensemble of particles with a given finite number of possible velocities. The flow domain in the standard case is a grid with square or cubic cells forming a lattice. During a time step $\Delta t$, particles, without interacting with each other, can make one act of displacement between adjacent nodes. Possible directions for particle movements are described using two-dimensional D2Q9 model [23]: ${\mathbf{e}}_{1}=c\cdot(0,0)$, ${\mathbf{e}}_{2}=c\cdot(1,0)$, ${\mathbf{e}}_{3}=c\cdot(0,1)$, ${\mathbf{e}}_{4}=c\cdot(-1,0)$, ${\mathbf{e}}_{5}=c\cdot(0,-1)$, ${\mathbf{e}}_{6}=c\cdot(1,1)$, ${\mathbf{e}}_{7}=c\cdot(-1,1)$, ${\mathbf{e}}_{8}=c\cdot(-1,-1)$, and ${\mathbf{e}}_{9}=c\cdot(1,-1)$, where $c=\Delta l/\Delta t$ is the lattice speed.

The state of the system at each grid node is described using one-particle distribution functions $f({\mathbf{r}},{\mathbf{u}},t)$. The functions $f({\mathbf{r}},{\mathbf{u}},t)$ are presented as a set of distribution functions $f_{i}$, where $i=1,\dots,9$ indicates the direction of particle movement in the D2Q9 model. The function $f_{i}$ characterizes a part of the particles moving in the $i$-th direction.

The dynamics of the particle ensemble is described in several stages. The first stage is a streaming step. At this stage, during $\Delta t$, the particles move to neighboring nodes in possible directions for D2Q9. The second stage deals with the collision process of particles, as a result of which the distribution function tends to an equilibrium state. The evolution of $f_{i}$ in time and space is described by Eq. (2):

$$f_{i}({\mathbf{r}}+{\mathbf{e}}_{i}\Delta t,t+\Delta t)=f_{i}({\mathbf{r}},t)+\Omega_{i}({\mathbf{r}},t)$$

(2)

where $\Omega_{i}({\textbf{r}},t)$ is a collision operator. The macroscopic fluid variables, namely the density and velocity, are obtained by Eqs. (3) and (4):

$$\rho_{i}({\mathbf{r}},t)=\sum_{i=1}^{9}f_{i}({\mathbf{r}},t),$$

(3)

$${\mathbf{u}}({\mathbf{r}},t)=\frac{1}{\rho}\sum_{i=1}^{9}{\mathbf{e}}_{i}f_{i}({\mathbf{r}},t).$$

(4)

The pressure $p$ is associated with the fluid density according to the following relationship: $p=\rho c^{2}/3$. The relaxation parameter $T$ controls the kinematic viscosity $\mu$ as follows: $\mu=(\frac{2T-1}{6})\frac{{\Delta l}^{2}}{\Delta t}$. $T$ cannot take values less than 0.5, because negative values of fluid viscosity are not physical. As $T$ increases, the viscous properties of the fluid also grow. Based on the reported ranges of the relaxation parameter [4, 26], the simulations are performed at $T=1$.

The MRT collision operator [28] is described by

$$\Omega_{i}=-{\mathbf{M}}^{-1}{\mathbf{S}}(m_{i}-m_{i}^{eq}).$$

(5)

In Eq. (5), $m_{i}=\sum_{i=1}^{9}{\mathbf{M}}_{ik}f_{k}$ .The view of matrix ${\mathbf{M}}$ and the formulas for the calculation of in the D2Q9 model are given in [26]. The components of the diagonal matrix ${\mathbf{S}}$ in Eq. (5) are described in [27].

Kinematic viscosity $\mu=10^{-6}$ m${}^{2}$/s and density $\rho$ = 1000 kg/m${}^{3}$. At the initial time, the pore space is completely filled with fluid. A fluid with the same properties is injected through one of the sides and is selected through the opposite side. The flow occurs at a constant pressure drop $\Delta P=$50 Pa between the input and output boundaries. The boundary conditions on the input and output sections are realized by Zou and He relationships [29]. The external borders of the sample are impermeable. On the internal and external impermeable boundaries, the ‘‘bounce-back‘‘ conditions are applied [24].

2.2 Porous Media Properties

In this paper, the numerical simulations are carried out in artificially generated two-dimensional models of granular porous media. To create digital images, a specially developed combined method was applied, consisting of QSGS and Monte-Carlo algorithms. In contrast to the random location algorithm used in [19, 21], QSGS enables us to generate porous morphological features very similar to the real pore structure [20]. QSGS is also suitable for controlling pore space anisotropy, which is difficult when using obstacles of a given shape.

Most porous materials have a unique structure at the pore level. In our study, the characteristics of the pore space are described numerically using two parameters: disorder, which is used to assess heterogeneity, and anisotropy. These values are calculated by processing digital images of the porous medium.

The disorder parameter $H$ is a corrected standard deviation of local porosity:

$$H=\sum_{i=1}^{N}\sqrt{\frac{(\varphi_{i}^{\alpha}-\varphi)^{2}}{N-1}}$$

[22], where $\varphi$ is the average sample porosity, $\varphi_{i}^{\alpha}$ is the local porosity calculated in the $i$th unit cell, and $N$ is the number of cells.

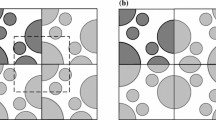
Depending on the meshing, uniform square or cubic lattices [22] and Voronoi diagram [21] are distinguished. Fig. 1 shows the isotropic porous structures different heterogeneities.

Fig. 1

Porous structures with different disorders generated by combined QSGS and Monte-Carlo algorithms: (a) $H=0.055$; (b) $H=0.105$; (c) $H=0.179$; (d) $H=0.246$.

When reviewing the literature [13, 14], we have identified a general approach to the numerical estimation of anisotropy. The parameter describing anisotropy will be called ‘‘anisotropy‘‘ and denoted by $A$. This characteristic is defined as the ratio of the sum of the pore height $n_{y}$ to the sum of the pore width $n_{x}$: $A=n_{y}/n_{x}$. To calculate $n_{y}$ and $n_{x}$, all pore sizes $h_{i}$ and $w_{i}$ are measured in each cross section perpendicular to the OX and OY axes, respectively: $n_{y}=\sum_{i=1}^{P}h_{i}$, $n_{x}=\sum_{i=1}^{P}w_{i}$, where $P$ is the number of pores. Without losing the generality of this approach, $n_{y}$ and $n_{x}$ can be swapped when evaluating $A$. Anisotropic porous media with different $m$ and $H$ are shown in Fig. 2.

Fig. 2

Porous media with different porosity ($m$), disorder ($H$), and anisotropy ($A$).

3 RESULTS AND DISCUSSION

3.1 Evaluation of Permeability and Tortuosity

In this section, we aim to identify and numerically evaluate the effect of anisotropy and heterogeneity on the transport properties of porous media with different porosities. The study will be carried out in two stages. At the first stage, we investigate how heterogeneity affects permeability and tortuosity in isotropic porous media with different porosities. Then, by adding an anisotropy factor, we study the effect of anisotropy in samples having different heterogeneity and porosity.

The components of absolute permeability tensor are measured using Darcy’s law: $k_{ii}=\frac{Q_{i}\eta L_{i}}{S\Delta P}$, where $i$ indicates flow direction ($x$ or $y$), $Q_{i}$ is the flow rate through the outlet section perpendicular to the $i$th direction, $S$ is the length of the outlet boundary, $\Delta P$ is the pressure drop between the inlet and outlet boundaries, $L_{i}$ is the length of the sample in the $i$th direction, and $\eta$ is the dynamic viscosity. When calculating the absolute permeability at constant $\Delta P$, $Q_{i}$ corresponds to the steady state flow rate.

For isotropic structures, the results will be presented only for the $k_{xx}$ component. Subscript $xx$ will be omitted. Macroscopic tortuosity is determined as the ratio of the average of the actual path lengths to the system length in the direction of the macroscopic flow [5, 10, 11] and is estimated using the following relationship:

$$\tau=\frac{\sum_{i,j}\sqrt{u_{x}^{2}(i,j)+u_{y}^{2}(i,j)}}{\sum_{i,j}u_{x}(i,j)},$$

(6)

where $u_{x}$ and $u_{y}$ are the velocity components of the flow field, and $(i,j)$ indicates the node number.

3.2 Isotropic Heterogeneous Porous Media

Before we begin to study anisotropic porous media, it is necessary to define the heterogeneity effect and develop the relationship between disorder and transport properties for isotropic media. To determine only the effect of disorder, a series of numerical simulations was carried out on a group of samples with the same porosity and close values of the specific surface length, but with various pore structures. Specific surface length $S_{V}$ is calculated as the ratio of the solid phase perimeter to the sample area. The study was performed for 8 values of porosity in the range from 0.435 to 0.741. The number of porous structures generated for one porosity value is about 75–100. The limitation of the minimum porosity is associated with a large number of impermeable porous structures at $H>0.15$ with a further decrease in porosity.

The results for tortuosity and permeability are shown in Fig. 3. To avoid effects not related to porosity and specific surface length, all further results for absolute permeability are shown in dimensionless form: $k^{*}=10^{12}k\frac{S_{V}^{2}}{m^{3}}$, where $k$ is a result of the numerical simulations. According to shown data, an increase in porosity causes a decrease in the average tortuosity for a group of samples with the same porosity (Fig. 3a).

Fig. 3

Effect of disorder on tortuosity (a) and dimensionless permeability (b) for samples with different porosities. The solid curves are the result of fitting using Eq. (7) for tortuosity and Eq. (8) for permeability.

A clear influence of disorder on tortuosity and permeability was found. The revealed effect is stronger in media with low porosity and decreases monotonically with an increase in porosity. At $m=0.436$, the drop in permeability with increasing heterogeneity reaches 3 times, while at $m=0.635$ it is only 25%.

The numerical results obtained for a group of samples with the same porosity were fitted using linear dependences (solid lines in Fig. 3):

$$\tau(m,H)=\alpha(m)+\beta(m)(H-H^{0}),$$

(7)

$$k^{*}(m,H)=\gamma(m)+\delta(m)(H-H^{0}).$$

(8)

Coefficients $\alpha$ and $\gamma$ in the Eqs. (7) and (8) depend on porosity and determine the permeability and tortuosity for $H=H^{0}$. Coefficients $\beta$ and $\delta$ in the Eqs. (7) and (8) define the slopes of the curves and indicate the sensitivity of permeability and tortuosity to change in disorder at different porosities, respectively. $H^{0}=0.04$ is the minimum disorder. This initial value corresponds to samples with an ordered arrangement of cores of the growing solid phase. Index 1 in Eq. (8) indicates the first approach for assessing permeability.

For $m\leq 0.585$, the offered dependences approximate the results of numerical simulations with an R-squared exceeding 0.64 for tortuosity (Fig. 3a) and 0.83 for permeability (Fig. 3b). A decrease in the R-squared for $m>0.585$ is associated with a weakened of the effect of disorder on tortuosity and disorder.

The dependences of the fitting parameters $\alpha$ and $\beta$ (Eq. (7) for tortuosity) as well as $\gamma$ and $\delta$ (Eq. (8) for permeability) on porosity are illustrated in Figs. 4a and 4b, respectively. As shown, each of the four parameters obeys a linear law with high $R^{2}>0.93$. When approximating, the following relationships were derived: $\alpha(m)=1.558-0.553m$; $\beta(m)=1.402-1.683m$; $\gamma(m)=-0.763+0.814m$; $\delta(m)=-0.062+0.372m$. After substituting these formulas into Eqs. (7) and (8), we propose new dependences for tortuosity and permeability:

$$\tau(m,H)=1.558-0.533m+(1.402-1.683m)(H-0.04),$$

(9)

$$k^{*}(m,H)=-0.062+0.372m+(0.814m-0.763)(H-0.04).$$

(10)

In contrast to the previously developed relationships [4–8], Eqs. (9) and (10) have the advantage of numerically predicting tortuosity and permeability in porous structures with different heterogeneities.

Fig. 4

Dependences of the fitting parameters on porosity: (a) $\alpha$ and $\beta$ from Eq. (7) and (b) $\gamma$ and $\delta$ from Eq. (8).

3.3 Anisotropic Heterogeneous Porous Media

In this section, we complicate our research by adding an anisotropy factor. Unlike papers [13, 14], where the influence of anisotropy was investigated for porous structures with random heterogeneity, we present a systematic study of the effect of anisotropy on transport properties of porous media having various and known porosity and heterogeneity. In other words, we want to find out how porosity and disorder affect the sensitivity of permeability to changes in anisotropy. Thus, if the effect will be clearly identified, the goal is to derive a dependency of permeability on three parameters at once.

If the parameter $A$ is used in the form described in Section 2.3.2, the anisotropy can be considered favorable for the flow driven along the OX axis if $A<1$, and unfavorable for $A>1$ (see Fig. 2). In our study, the upper limit of anisotropy is 1.6–1.7. This value is justified by the appearance of very low-permeable and impermeable structures with a further increase in anisotropy (especially for models with low porosity). The same maximum was also used in [14] when studying shales. The lower limit of anisotropy is 0.4–0.5. Based on Fig. 2a, which illustrates a structure with a pronounced anisotropy, we believe that the introduced lower limit is sufficient.

To study the effect of anisotropy, only the $k_{xx}$ component of the absolute permeability tensor is evaluated. If we obtain the analytical dependency of $k_{xx}$ on the characteristics of the pore space, then the $k_{yy}$ component can be estimated using the same relationship, but, obviously, for the inverse $A$.

To study the influence of porosity, disorder and anisotropy, a series of numerical simulations was carried out for samples with 8 porosity values ranging from 0.395 to 0.74. For each porosity, 5–6 groups of samples were generated. Each group has the same disorder and different anisotropy.

The results for $m=$ 0.395, 0.485, 0.585, and 0.635 are shown in Fig. 5. For each porosity, data for 3 different disorders are presented. We also examined porous media with low $m=0.395$ for $H<0.16$, which were not considered in the previous section, in order to specifically demonstrate low permeability at $A\approx 1$.

Fig. 5

Effect of anisotropy on dimensionless permeability $k^{*}$ for samples with different porosities and disorders: $m=$ (a) 0.395, (b) 0.485, (c) 0.585, (d) 0.635. The solid curves are the result of approximation using Eq. (11).

In Fig. 5, we found the expected monotonic decrease in transport properties when transition from favorable ($A<1$) to unfavorable ($A>1$) anisotropy. As shown, as the disorder increases, the $k^{*}$ values shift towards lower values. The negative effect of disorder on permeability was clearly identified in the previous section when studying isotopic structures (Fig. 3b). Continuing the analysis of the obtained numerical data, it can be found that the sensitivity to changes in anisotropy is strongest in media with low heterogeneity ($H\approx 0.05$). The effect of anisotropy decreases with increasing disorder.

To describe this effect numerically and to identify such a possible impact of porosity, the data were fitted using a linear dependency:

$$k^{*}(m,H,A)={\alpha}_{1}(m,H)+{\alpha}_{2}(m,H)(A-A^{0}).$$

(11)

Fit lines are shown by solid curves in Fig. 5. $A^{0}=1$ in the Eq. (11) indicates isotropic porous structures. The first term ${\alpha}_{1}(m,H)$ characterizes the permeability in isotropic porous media. We will not evaluate this fitting parameter and can set that ${\alpha}_{1}(m,H)=k(m,H)$, where $k$ is calculated using Eq. (10). The second term in the Eq. (11) describes the effect of anisotropy. The coefficient ${\alpha}_{2}$ indicates the slope of the fitting lines in Fig. 5, which, in fact, determines the impact of porosity and heterogeneity. Thus, in order to obtain the final formula, the goal now is to develop a relationship for ${\alpha}_{2}$.

The calculated slope coefficients ${\alpha}_{2}$ are shown in Fig. 6. Each set of points plotted for samples with the same porosity was approximated using the following linear equation:

$${\alpha}_{2}(m,H)={\lambda}_{1}(m)+{\lambda}_{2}(m)(H-0.04).$$

(12)

Fig. 6

The dependency of the parameter ${\alpha}_{2}$ on disorder, illustrated for groups of samples with different porosities. The colored solid curves are the result of approximation using the Eq. (12).

The R-squared for each curve is greater than 0.90. Several effects have been identified. First, the influence of anisotropy is most pronounced in samples with high porosity and monotonically reduces with decreasing porosity. This effect is reflected in Fig. 6. Coefficient ${\lambda}_{1}$ in the Eq. (12) determines ${\alpha}_{2}$ at the initial $H=0.04$ and, in fact, determines the average effect of anisotropy for samples with the same porosity. The dependency of ${\lambda}_{1}$ on porosity is shown in Fig. 7a. We have selected the linear fitting function that most accurately describes coefficients ${\lambda}_{1}$ with $R^{2}=0.99$: ${\lambda}_{1}(m)=0.05-0.352m$.

Fig. 7

Dependences of the parameters ${\lambda}_{1}$ (a) and ${\lambda}_{2}$ (b) from the Eq. (12) on porosity. The line on the left figure is a fitting line: ${\lambda}_{1}(m)=0.05-0.352m$. The black solid line on the right figure is equal to 0.41 and shows the value averaged over all ${\lambda}_{2}$.

Secondly, the slopes of the curves, which are numerically described by the coefficients ${\lambda}_{2}$ in the Eq. (12), as seen in Fig. 6, are practically identical for groups of samples with different porosities. This feature means that the disorder effect can be considered as independent on porosity. The estimated ${\lambda}_{2}$ for different $m$ are shown in Fig. 7b. The absence of a pronounced effect of porosity allows us to use the average value ${\lambda}_{2}=0.41$, shown by black solid line in Fig. 7b. According to the obtained data, the maximum deviations of ${\lambda}_{2}$ from the mean value do not exceed 12%. As a result, Eq. (12) has the form

$${\alpha}_{2}(m,H)=0.05-0.352m+0.41(H-0.04).$$

(13)

Substituting Eqs. (10) and (13) into Eq. (11), we can present an analytical formula that predicts the absolute permeability in porous media with different porosity, heterogeneity and anisotropy:

$$k^{*}(m,H,A)=-0.062+0.372m+(0.814m-0.763)(H-0.04)$$

$${}+[0.05-0.352m+0.41(H-0.04)](A-1).$$

(14)

The resulting relationship Eq. (14) is a complex nonlinear function that depends on three variables at once. This equation was developed on the basis of stepwise approximations of numerical data. To be confident in the accuracy and reliability of the results obtained by the Eq. (14), the developed formula should be validated by performing numerical simulations on a huge number of porous structures with various combinations of porosity, disorder, and anisotropy.

For validation, 8 groups of samples were generated with the same porosity ranging from 0.45 to 0.71. For each porosity, about 200 pore structures were generated with various combinations of heterogeneity and anisotropy. Thus, about 1600 samples were tested.

The discrepancy between the numerical and analytical data is estimated using the error $\Delta$ (in percents), which is calculated using following equation: $\Delta=100(k_{num}^{*}-k_{analyt}^{*})/k_{analyt}^{*}$. In this formula, $k_{analyt}^{*}$ are analytical data evaluated by Eq. (14), and $k_{num}^{*}$ are numerical results. The results show that almost all error values are within 30%. For over than 77% of samples, $\Delta$ is in the range [–15% $\div$ 15%], which can be considered a satisfactory deviation. Errors modules above 30 percent were extremely rare. The Eq. (14) predicts slightly underestimated data when compared with numerical results. $\Delta>0$ was obtained for 61% of the samples.

4 CONCLUSIONS

This paper presents a systematic study of the effect of heterogeneity, anisotropy and porosity on the transport properties of porous media. The main findings of this paper are formulated below.

• 1. For isotropic structures, a significant effect of heterogeneity and porosity on the absolute permeability and tortuosity was obtained. An increase in disorder negatively affects transport properties. With an increase in porosity, the effect of disorder on the transport properties decreases.

• 2. For anisotropic structures, a linear decrease in permeability was found during the transition between favorable ($A<1$) and unfavorable ($A>1$) anisotropy. The influence of anisotropy is most pronounced in samples with high porosity and monotonically reduces with decreasing porosity. Heterogeneity negatively affects the sensitivity of the flow properties to changes in anisotropy and can be considered independent on porosity.

• 3. Based on the stepwise approximations of numerical results, an analytical equation was developed that predicts permeability depending on porosity, disorder and anisotropy. The derived relationship was successfully validated on a huge number of porous structures (about 1600 samples). It was found that the discrepancy between the analytical and numerical data for 77% of the tested samples is in the range [$-15\%\div 15\%$]. The maximum error is within 30%.