INTRODUCTION

At the present developmental stage of natural sciences with the rapidly expanding capabilities of the latest technologies, of particular importance are disciplines that have arisen at the junction of several areas of knowledge, such as nanophotonics and nanoplasmonics. In particular, nanostructured composite media are widely used in biological and medical applications. This is due to the interesting optical properties of metal–dielectric spherical nanoparticles associated with plasmon resonance. In the modern scientific terminology, these are called core–shell particles. Interest in the theoretical study of metal–dielectric core–shell nanoparticles is confirmed by the large number of publications on this subject in scientific journals [1–7].

Calculation of layered spherical nanoparticles with two or more layers in the shell refines experimental data. At the same time, progress achieved in nanostructure manufacturing technology makes it possible to create nanocomposite structures with complex inclusions, consisting of a core and several shell layers. The resonance fields in them vary widely and are controlled by the particle structure, which bodes well for their practical application [8–10]. Various combined materials for manufacturing complex nanoparticles and various changes in shell and core thickness make it possible to obtain particles with predetermined properties.

The present article derives the polarizability formula of a layered particle with one shell; for this, the theory proposed in [11] was used. The advantage of this calculation method is that it can be generalized to a case differing from quasistatics; method is applicable to spherical structures with an arbitrary number of shells surrounding the core. A far as the author knows, the paper also presents for the first time a formula obtained for the polarizability of a particle with a two-layer shell.

THEORETICAL STUDY OF THE OPTICAL PROPERTIES OF A MULTILAYER NANOPARTICLE

Let us solve the quasistatic problem in the case of a layered medium. In spherical symmetry, this is a sphere with a shell. In the electric field of an incident wave, a metal nanoparticle is polarized. The field of the scattered wave in the case of dipole resonance is a dipole field with the moment [12]

$$p = {{\alpha }_{1}}{{E}_{0}},$$
(1)

where E0 is the external field strength and α1 the polarizability of a particle. Here, the dipole orientation is assumed to be parallel to the direction of the electric field strength, since the polarization of the sphere is induced by the field. Let us find the expression that determines this value. For this, we write the formula derived in [11] for the field strength of the wave scattered by the particle:

$${{E}_{1}} = {{Y}_{1}}(\theta ,\varphi ){{A}_{0}}\frac{{\exp ( - a(r))}}{r}\frac{{\sin {{{(\tilde {a}(d))}}^{2}}}}{{\sin {{{(a(d))}}^{2}}}},$$
(2)

where \(r\) is the radial coordinate, \({{A}_{0}}\) – is the amplitude, \(d\) – bis the sphere’s radius, \({{Y}_{1}}({\theta },{\varphi })\) – is the angular part of the wavefunction of the dipole harmonic [10, 13], and a(r) is the phase function of the spherical wave determined by the equation [11]:

$$\frac{1}{{{{H}_{{\theta }}}(r,{\theta },z)}}\frac{{\partial {{H}_{{\theta }}}(r,{\theta },z)}}{{\partial r}} = \sqrt {\frac{{{{{\varepsilon }}_{2}}}}{{{{{\varepsilon }}_{1}}}}} {\text{cot}}(a(r)),$$
(3)

where \({{H}_{{\theta }}}(r,{\theta },z)\) is the azimuthal component of the magnetic field of the wave. The relationship between two phase functions determined by equality (3) in two adjacent regions of a piecewise-homogeneous medium with spherical symmetry (dielectric constants of the media \({{{\varepsilon }}_{1}}~\)and \({{{\varepsilon }}_{2}}\)) at their boundary with radius d is given by the formula

$$(\tilde {a}(d)) = \sqrt {\frac{{{{{\varepsilon }}_{2}}}}{{{{{\varepsilon }}_{1}}}}} {\text{cot}}(a(d)).$$
(4)

The last factor in the expression for field (2), taking into account (4), can be represented as

$$\frac{{\sin {{{(\tilde {a}(d))}}^{2}}}}{{\sin {{{(a(d))}}^{2}}}} = \frac{{{\text{cot}}{{{(a(d))}}^{2}} + 1}}{{\frac{{{{{\varepsilon }}_{2}}}}{{{{{\varepsilon }}_{1}}}}{\text{cot}}{{{(a(d))}}^{2}} + 1}},$$
(5)

where \({{{\varepsilon }}_{1}},{{{\varepsilon }}_{2}}\) – is the dielectric constant of the sphere and its medium, respectively. According to formula [11], for the quasistatic approximation (k0d\( \ll \) 1, where k0 = ω/c, ω is the frequency of the electromagnetic wave), the cotangent of the dipole harmonic phase function \(~{\text{cot}}(a(d))\) at the particle boundary is \(\sqrt 2 \). Since the polarizability of a particle corresponds to plasmon resonance, the cotangent of the phase function at the particle boundary is \(\sqrt {\frac{{{{{\varepsilon }}_{2}}}}{{{{{\varepsilon }}_{1}}}}} \). Summarizing, taking into account (2) and (5), we arrive at the result

$${{E}_{1}} = {{Y}_{1}}(\theta ,\varphi ){{A}_{0}}\frac{{\exp ( - a(r))}}{r}\frac{{({{{\varepsilon }}_{2}} - {{{\varepsilon }}_{1}})}}{{({{{\varepsilon }}_{1}} + 2{{{\varepsilon }}_{2}})}}.$$
(6)

Let us decompose the initial wave into spherical harmonics [10, 13]. Only the dipole harmonic in the expansion of the incident wave enters into the resonance; therefore, \({{E}_{{0~}}}\) can approximately be represented as

$${{E}_{{0~}}} = {{Y}_{1}}({\theta },{\varphi }){{A}_{0}}\frac{{\exp ( - a(r))}}{r}.$$
(7)

The dipole field is [12]

Hence, taking into account (1), (6), (7), we obtain the polarizability of the particle:

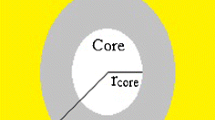
$${{{\alpha }}_{1}} = \frac{{({{{\varepsilon }}_{2}} - {{{\varepsilon }}_{1}})}}{{({{{\varepsilon }}_{1}} + 2{{{\varepsilon }}_{2}})}}{{d}^{3}}.$$
(8)

Determining the polarizability of a core–shell particle is a bit more complicated (Fig. 1a). The field strength of the eigenmode at the particle boundary in this case is

$$\begin{gathered} {{E}_{{2~}}} = {{Y}_{1}}({\theta },{\varphi }){{A}_{0}} \\ \, \times \;\,\frac{{2\sin (a(r))}}{r}~\frac{{{\text{cot}}{{{(a(d))}}^{2}} + 1}}{{\frac{{{{{\varepsilon }}_{2}}}}{{{{{\varepsilon }}_{1}}}}{\text{cot}}{{{(a(d))}}^{2}} + 1}}~\frac{{{\text{cot}}{{{(a({{d}_{1}}))}}^{2}} + 1}}{{\frac{{{{{\varepsilon }}_{3}}}}{{{{{\varepsilon }}_{2}}}}{\text{cot}}{{{(a({{d}_{1}}))}}^{2}} + 1}}, \\ \end{gathered} $$
(9)

where \(r\) is the radial coordinate, \({{d}_{1}}\) is the outer radius of the particle, \(~{{{\varepsilon }}_{2}}\) is the dielectric constant of the shell, and \({{{\varepsilon }}_{3}}\) is the dielectric constant of the medium around a complex particle. Hence, using the expressions obtained in [11] for at the second interface between the media in the particle, we conclude that the polarizability of the outer sphere in the field of a wave scattered by the inner sphere, like any wave of dipole harmonic, is

$${{{\alpha }}_{2}} = \frac{{({{{\varepsilon }}_{3}} - {{{\varepsilon }}_{2}})}}{{({{{\varepsilon }}_{2}} + 2{{{\varepsilon }}_{3}})}}d_{1}^{3}.$$
(10)
Fig. 1.
figure 1

(Color online) Schematic representation of spherical particle with single- (a) and two-layer (b) shell.

Full size image

Since the particle is polarized in the field penetrating inside it, the polarizability of a complex particle is equal to the ratio of the sum of the polarizabilities of the spheres, its components, to the transmittance of the field inside the particle. The latter is equal to the ratio of the fields inside and outside the particle near the interface. When the direction of wave propagation changes, the transverse field component also changes to the opposite direction; taking this into account and comparing the real parts of the field strengths determined by formulas (6) and (7), we arrive at the expression for the field transmittance

$$t = 1 + \frac{{2{{\alpha }_{1}}{{\alpha }_{2}}}}{{{{d}_{1}}^{6}}}.$$
(11)

Writing the ratio and summing the terms, as well as using Eqs. (8)–(11), we write the result as an expression containing the dielectric constants of the three media:

$$\begin{gathered} {{{\alpha }}_{{12}}} = {{d}_{1}}^{3} \\ \times \;{\kern 1pt} \frac{{({{{\varepsilon }}_{3}} - {{{\varepsilon }}_{2}})({{{\varepsilon }}_{1}} + 2{{{\varepsilon }}_{2}}) + {{{\left( {\frac{d}{{{{d}_{1}}}}} \right)}}^{3}}({{{\varepsilon }}_{2}} - {{{\varepsilon }}_{1}}){{\;}}({{{\varepsilon }}_{2}} + 2{{{\varepsilon }}_{3}})}}{{({{{\varepsilon }}_{1}} + 2{{{\varepsilon }}_{2}}){{\;}}({{{\varepsilon }}_{2}} + 2{{{\varepsilon }}_{3}}) + 2{{{\left( {\frac{d}{{{{d}_{1}}}}} \right)}}^{3}}({{{\varepsilon }}_{2}} - {{{\varepsilon }}_{1}})\left( {{{{\varepsilon }}_{3}} - {{{\varepsilon }}_{2}}} \right)}}. \\ \end{gathered} $$
(12)

This is a well-known and widely applied result obtained in [14] using the Maxwell–Garnett rule for calculating the effective dielectric constant [15]. This formula was derived in a different way in monograph [13]. The equality of the numerator and denominator in expression (12) to zero determines the invisibility and resonance polarization, respectively. If the polarizability of a particle is zero, it does not contribute to the scattered field and does not absorb the external wave energy; therefore, the scattering and absorption cross sections of the particle are zero and there is no external wave scattering. This makes it impossible to detect the position of the particle; i.e., the particle is invisible. The opposite effect occurs in the case of resonance. The external wave field increases without limitation. This allows metallic nanoparticles to be used in medical applications, since this effect is responsible for the giant field amplification in the Raman scattering of light by molecules [16, 17]. This calculation method can also be applied to core–shell particles with more than three layers. For this, we need to write the electric field formula for a three-layer particle under plasmon resonance conditions:

$$\begin{gathered} {{E}_{{3~}}} = {{Y}_{1}}({\theta },{\varphi }){{A}_{0}}\frac{{2\sin (a(r))}}{r} \\ \times \;{\kern 1pt} \frac{{{\text{cot}}{{{(a(d))}}^{2}} + 1}}{{\frac{{{{{\varepsilon }}_{2}}}}{{{{{\varepsilon }}_{1}}}}{\text{cot}}{{{(a(d))}}^{2}} + 1}}~\frac{{{\text{cot}}{{{(a({{d}_{1}}))}}^{2}} + 1}}{{\frac{{{{{\varepsilon }}_{3}}}}{{{{{\varepsilon }}_{2}}}}{\text{cot}}{{{(a({{d}_{1}}))}}^{2}} + 1}}~\frac{{{\text{cot}}{{{(a({{d}_{2}}))}}^{2}} + 1}}{{\frac{{{{{\varepsilon }}_{4}}}}{{{{{\varepsilon }}_{3}}}}{\text{cot}}{{{(a({{d}_{2}}))}}^{2}} + 1}},~ \\ \end{gathered} $$
(13)

where \(r\) is the radial coordinate, \({{d}_{1}}\) is the radius of the inner shell, \({{d}_{2}}\) is the outer radius of the particle, \(~{{{\varepsilon }}_{2}}\) is the dielectric constant of the inner shell, \({{{\varepsilon }}_{3}}\) is the dielectric constant of the outer shell, and \({{{\varepsilon }}_{4}}\) is dielectric constant of the medium surrounding a complex particle (Fig. 1b).

In the quasistatic approximation, we must set the cotangent in the numerator of the last factor equal to \(i\sqrt {\frac{{{{{\varepsilon }}_{4}}}}{{{{{\varepsilon }}_{3}}}}} \), and in the denominator, \(\sqrt 2 \), we write the expression for the polarizability of the outer sphere in the field of dipole spherical harmonics

$${{{\alpha }}_{3}} = \frac{{({{{\varepsilon }}_{4}} - {{{\varepsilon }}_{3}})}}{{({{{\varepsilon }}_{3}} + 2{{{\varepsilon }}_{4}})}}d_{2}^{3}.$$
(14)

The expression for the polarizability of a complex particle, as above, is written via the transmittance of the field inside the particle, determined by formulas (1) and (13). The final result, taking into account formulas (13), (14), has the form

$$\begin{gathered} {{{\alpha }}_{{123}}} = {{d}_{2}}^{3}\frac{{{{{\left( {\frac{{{{d}_{1}}}}{{{{d}_{2}}}}} \right)}}^{3}}\left[ {({{{\varepsilon }}_{3}} - {{{\varepsilon }}_{2}})({{{\varepsilon }}_{1}} + 2{{{\varepsilon }}_{2}}) + {{{\left( {\frac{d}{{{{d}_{1}}}}} \right)}}^{3}}({{{\varepsilon }}_{2}} - {{{\varepsilon }}_{1}}){{\;}}({{{\varepsilon }}_{2}} + 2{{{\varepsilon }}_{3}})} \right]({{{\varepsilon }}_{3}} + 2{{{\varepsilon }}_{4}})}}{{({{{\varepsilon }}_{1}} + 2{{{\varepsilon }}_{2}}){{\;}}({{{\varepsilon }}_{2}} + 2{{{\varepsilon }}_{3}})({{{\varepsilon }}_{3}} + 2{{{\varepsilon }}_{4}}) + 2{{{\left( {\frac{d}{{{{d}_{2}}}}} \right)}}^{3}}{{{\left( {\frac{{{{d}_{1}}}}{{{{d}_{2}}}}} \right)}}^{3}}({{{\varepsilon }}_{2}} - {{{\varepsilon }}_{1}})({{{\varepsilon }}_{3}} - {{{\varepsilon }}_{2}})({{{\varepsilon }}_{4}} - {{{\varepsilon }}_{3}})}} \\ \, + {{d}_{2}}^{3}\frac{{({{{\varepsilon }}_{1}} + 2{{{\varepsilon }}_{2}}){{\;}}({{{\varepsilon }}_{2}} + 2{{{\varepsilon }}_{3}})({{{\varepsilon }}_{4}} - {{{\varepsilon }}_{3}})}}{{({{{\varepsilon }}_{1}} + 2{{{\varepsilon }}_{2}}){{\;}}({{{\varepsilon }}_{2}} + 2{{{\varepsilon }}_{3}})({{{\varepsilon }}_{3}} + 2{{{\varepsilon }}_{4}}) + 2{{{\left( {\frac{d}{{{{d}_{2}}}}} \right)}}^{3}}{{{\left( {\frac{{{{d}_{1}}}}{{{{d}_{2}}}}} \right)}}^{3}}({{{\varepsilon }}_{2}} - {{{\varepsilon }}_{1}})({{{\varepsilon }}_{3}} - {{{\varepsilon }}_{2}})({{{\varepsilon }}_{4}} - {{{\varepsilon }}_{3}})}}. \\ \end{gathered} $$
(15)

The resulting formula can be used to calculate the resonance conditions for particles with a double shell. This tool can be used to predict the optical plasmon resonance properties of metal–dielectric nanoparticles and, accordingly, to design nanostructured composite media. In this case, the resonance frequencies of radiation, which is amplified by scattering by these media, depend on the structure and material composition of the particles; in the case of particles with a double shell, they are located in a very wide range. Since the calculation method can be applied to particles with an arbitrary number of layers in the shell, almost any frequency range of visible and infrared radiation can be used for theoretical research.

Let us consider this conclusion with the example of particles with a double shell. Using the obtained formulas, we can easy calculate the absorption cross section of nanoparticles with a shell. The relationship between this quantity and the polarizability of a particle is determined by the equality [10]

$${\sigma } = {{k}_{0}}\sqrt {{{{\varepsilon }}_{{{\text{out}}}}}} {\text{Im}}\alpha ,$$
(16)

where σ is the particle absorption cross section, α is the polarizability of the particle, εout is the dielectric constant of the external medium in which the particle is placed.

Figure 2a plots the dependence of the absorption cross section of a particle on the scattered if the particle has a gold core and an optically dense shell. In this calculation using formulas (12) and (16), the ratio of the outer and inner radii of the shell varies in the range (0, 5). Resonances span the spectrum from about 0.16 to 0.24 µm. Varying the ratio of the shell radii in this calculation in the range (5, 40), we arrive at the dependence plotted in Fig. 2b. Clearly, in this case, the resonances are located in a narrow region of the spectrum corresponding to a wavelength of 0.65 μm. Changing the shell’s dielectric constant and the core radius does not significantly change the width and position of the resonance regions in the spectrum of the scattered wave.

Fig. 2.
figure 2

Dependence of absorption cross section (σ) on wavelength of radiation (λ) scattered by single-shell nanoparticles having the following material and geometric parameters: ε2 = 12, ε3 = 5, ε1 = εm, where εm is the dielectric constant of gold (ωpl = 9 eV is the plasma frequency, τ = 13 fs is the electron relaxation time), d = 1, d1 = xd, x varies from 0 to 5 (a) and from 5 to 40 (b); numerals on graph correspond to x values.

Full size image

The ratio of the radius of the core and the shell closest to it was varied with a ratio of the external radius of a complex particle to the radius of the boundary of two shell layers 1 (Fig. 3a) and 3 (Fig. 3b). Two features of the graphs are noteworthy: first, the regions of the spectrum where there is no resonance in a particle with one shell are overlapped by resonance, and second, the absorption cross section maximum is 1000 times greater than Fig. 2.

Fig. 3.
figure 3

Dependence of absorption cross section (σ) on wavelength of radiation (λ) scattered by double-shell nanoparticles having the following material and geometric parameters: ε2 = 12, ε4 = 5, ε3 = ε1 = εm, where εm is the dielectric constant of  gold  (ωpl = 9 eV is  the plasma frequency, τ = 13 fs is the electron relaxation time), d1/d2= 1 (a), d1/d2= 1/3 (b), d = 1, d1= xd, x varies from 0 to 40; numerals on graph correspond to x values.

Full size image

Summing up the graphical analysis of formulas (12), (15), (16), we can conclude that the use of nanoparticles with a double shell significantly broadens the possible spectrum of resonance frequencies of the scattered wave. Such nanoparticles lead to a sharp increase in the field enhancement effect, which useful in gigantic Raman scattering.

CONCLUSIONS

A method is considered for calculating the polarizability of spherical core–shell nanoparticles with an arbitrary number of layers in the shell. For the first time, the polarizability formula for particles with a double shell is derived. This formula, as well as the expression for the polarizability of particles with a more complex composition, also accessible for the above calculation method, makes it possible to predict the optical plasmon resonance properties of metal–dielectric nanoparticles.