EFFECTIVE INTERFERENCE MECHANISM FOR CONDUCTIVITY CONTROL IN MOLECULAR ELECTRONICS

Abstract—We study structural models of molecular quantum conductors, the transport properties of which can be effectively controlled by modified interference-based tunneling transmission through the electric field of the gate.

INTRODUCTION

Today, traditional microelectronics faces a number of significant problems that hinder the increased performance of computing systems in addition to decreased size. One reason for this is the limitation on the transistor switching rate due to the impossibility of reducing the supply voltage while maintaining an acceptable switching steepness (in traditional field effect transistors, the current cannot increase by more than ten times with an increase in gate voltage by 60 mV at room temperature). Therefore, devices with lower supply voltages and a greater steepness of the subthreshold characteristic are actively being developed instead of traditional silicon transistors. Studies on tunneling field-effect transistors [1], field-effect transistors with a “negative gate capacitance” [2], and switches based on spin-orbital coupling [3] are particularly noteworthy.

Since the 1970s [4], the possibility of using individual molecules as active electronics elements captured the interest of scientists. To date, significant progress has been made in the theoretical description and, in particular, experimental implementation of single-molecule controlled conductors [5]. The most effective conductivity control for individual molecules is the phenomenon of quantum interference. However, frequently, one controls the destructive quantum interference (DQI), which significantly reduces the current through the molecule, i.e., “turns off” the transistor, by electrochemical effects [6, 7] that is unsuitable for creating scalable integrated circuits. DQI can also be controlled by shifting the spectrum of the molecule in the gate field [8, 9]. In this case, the gate potential determines the position of the energy of zero tunnel transparency of the conductor and can practically “block” the conductivity of the molecule when this energy coincides with the Fermi level. However, the switching slope of such devices is limited, like in traditional field-effect transistors, so the supply voltage cannot be significantly reduced at room temperature [10]. The characteristics of advanced results in the practical implementation of such devices have not yet surpassed traditional transistors [11]. In [12], a four-level model of a transistor with a significant switching slope was theoretically considered, which was interpreted by the authors as a consequence of DQI due to tunneling through a highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO).

In [13], a new interference mechanism for controlling the conductivity of quantum molecular conductors was proposed. It is based on the resonance coalescence effect [14] at an exceptional point of an open quantum system formed by a molecular conductor and electrodes, accompanied by a DQI with a gate controlled degeneracy of eigenstates of different parities. In [13], a general model was considered that takes into account two levels that can become degenerate. In this work, we study the general appearance of the structure of interference molecular transistors in which the effect of resonance coalescence is possible and, as a result, which are capable of efficient switching by an external inhomogeneous gate field. It is shown that the model [12] is a special case of the general mechanism described in [13], and models with similar switching properties are also considered.

THEORETICAL MODEL

Let us consider the application of the general approach developed in [13] to the description of the system proposed in [12] as a quantum interference transistor. As was shown in [12], DQI can take place in the system schematically shown in Fig. 1a if the tunnel matrix elements ${{J}_{i}}$ between the side anchor groups and the HOMO and LUMO of the central molecule are the same: ${{J}_{i}} = J$. In such a system, there are two degenerate states if the HOMO and LUMO energies are symmetric with respect to ${{\varepsilon }_{0}}$, i.e. if ${{\varepsilon }_{{{\text{LUMO}}}}} = {{\varepsilon }_{0}} + \Delta$ and ${{\varepsilon }_{{{\text{HOMO}}}}} = {{\varepsilon }_{0}} - \Delta$. These degenerate states have energy ${{\varepsilon }_{0}}$, and the corresponding symmetric and antisymmetric wavefunctions can be calculated from the Hamiltonian ${{\hat {H}}_{0}}$ of the isolated system [12]:

$${{\hat {H}}_{0}} = \left( {\begin{array}{*{20}{c}} {{{\varepsilon }_{0}}}&J&J&0 \\ J&{{{\varepsilon }_{{{\text{LUMO}}}}}}&0&J \\ J&0&{{{\varepsilon }_{{{\text{HOMO}}}}}}&J \\ 0&J&J&{{{\varepsilon }_{0}}} \end{array}} \right).$$

(1)

Fig. 1.

General view of model of four-level system in tight-binding basis in HOMO–LUMO representation (a); general view of model in site representation (b); three  topologies of  structure  undergoing  DQI and resonance coalescence (c–e). In case (e) ${{\tau }_{2}} = \frac{{{{\tau }_{1}}}}{{{\text{|}}{{\varepsilon }_{1}} - {{\varepsilon }_{2}}{\text{|}}}}[\sqrt {{{{({{\varepsilon }_{1}} - {{\varepsilon }_{2}})}}^{2}} + 4{{\tau }^{2}}} - 2\tau ]$.

Model (1) has a mixed atomic orbital character. The electronic states of the anchor groups interacting with the electrodes are described in the basis of atomic orbitals, while the atomic structure of the molecule is not specified, but the presence of two orbitals with given tunneling matrix elements is postulated. A more general formalism [13] makes it possible to decipher this structure and determine the relationship between the parameters of the Hamiltonian and microscopic atomic characteristics.

The normalized symmetric ${\text{|}}s\rangle$ and antisymmetric ${\text{|}}a\rangle$ degenerate states have the following wavefunctions (in the same basis as ${{\hat {H}}_{0}}$):

$$\begin{gathered} {\text{|}}s\rangle = \frac{1}{{\sqrt {2{{\Delta }^{2}} + 8{{J}^{2}}} }}{{(\Delta , - 2J,2J,\Delta )}^{\dag }}, \\ {\text{|}}a\rangle = \frac{1}{{\sqrt 2 }}{{(1,0,0, - 1)}^{\dag }}. \\ \end{gathered} $$

(2)

In the basis of on-site localized states, interaction with contacts in the wideband approximation [15] can be described by the following vectors:

$$\begin{gathered} {{({\mathbf{u}}_{L}^{{{\text{site}}}})}^{\dag }} = (\sqrt \Gamma ,0,0,0), \\ {{({\mathbf{u}}_{R}^{{{\text{site}}}})}^{\dag }} = (0,0,0,\sqrt \Gamma ). \\ \end{gathered} $$

(3)

Here, at the i_th vector position ${\mathbf{u}}_{{L(R)}}^{{{\text{site}}}}$ is a tunnel matrix element between the i_th state of the system and the left (right) electrode. Therefore, in the basis of states ${\text{|}}s\rangle$ and ${\text{|}}a\rangle$, the interaction with the contacts can be written as

$${\mathbf{u}}_{{L,R}}^{{sa}} = \left( {\begin{array}{*{20}{c}} {\frac{\Delta }{{\sqrt {2{{\Delta }^{2}} + 8{{J}^{2}}} }}}&{ - \frac{{\sqrt 2 J}}{{\sqrt {{{\Delta }^{2}} + 4{{J}^{2}}} }}}&{\frac{{\sqrt 2 J}}{{\sqrt {{{\Delta }^{2}} + 4{{J}^{2}}} }}}&{\frac{\Delta }{{\sqrt {2{{\Delta }^{2}} + 8{{J}^{2}}} }}} \\ {\frac{1}{{\sqrt 2 }}}&0&0&{ - \frac{1}{{\sqrt 2 }}} \end{array}} \right){\mathbf{u}}_{{L,R}}^{{{\text{site}}}} = \sqrt \Gamma \left( {\begin{array}{*{20}{c}} {\frac{\Delta }{{\sqrt {2{{\Delta }^{2}} + 8{{J}^{2}}} }}} \\ { \pm \frac{1}{{\sqrt 2 }}} \end{array}} \right).$$

(4)

Thus, each of the states ${\text{|}}s\rangle$ and ${\text{|}}a\rangle$ has a coupling with both the left and right contacts, which allows tunneling of carriers through both states. Moreover, due to the different sign of the matrix coupling elements in (4) for the ${\text{|}}s\rangle$- and ${\text{|}}a\rangle$-states, DQI of these contributions is attained. As is seen from expression (2), the states that determine the behavior of the transmission coefficient of the system are localized mainly on the anchor groups. The corresponding amplitudes with an increase in energy split between the HOMO and LUMO tend to constant values. Thus, it is the degenerate states of the side anchor groups that determine the nontrivial evolution of the transmission coefficient, in contrast to the DQI mechanism proposed in [12] due to tunneling through the HOMO and LUMO.

Let the gate potential shift the spectrum of the central molecule by $V$, i.e., ${{\varepsilon }_{{{\text{LUMO}}}}} = {{\varepsilon }_{0}} + \Delta + V$ and ${{\varepsilon }_{{{\text{HOMO}}}}} = {{\varepsilon }_{0}} - \Delta + ~V$. Moreover, the degeneracy of states ${\text{|}}s\rangle$ and ${\text{|}}a\rangle$ is removed: ε_s = ε₀ + $4V{{J}^{2}}{{({{\Delta }^{2}} + 4{{J}^{2}})}^{{ - 1}}}$ and ${{\varepsilon }_{a}} = {{\varepsilon }_{0}}$. Stationary current through such a system, taking into account the contribution only from states ${\text{|}}s\rangle$ and ${\text{|}}a\rangle$, can be calculated using the standard Landauer–Buttiker formula:

$$I = \frac{e}{h}\int {T(E)[{{f}_{L}}(E) - {{f}_{R}}(E)]dE} ,$$

(5)

where $T(E)$ is the probability of tunneling through a quantum conductor, which can be written in a standard form [16]:

$$T(E) = 4\operatorname{Tr} [{{\hat {\Gamma }}_{R}}{{\hat {G}}^{r}}{{\hat {\Gamma }}_{L}}{{\hat {G}}^{a}}].$$

(6)

Here, ${{\hat {G}}^{{a,r}}}$ is the advanced and retarded Green functions of the system, taking into account only the states ${\text{|}}s\rangle$ and ${\text{|}}a\rangle$; ${{\hat {\Gamma }}_{{L(R)}}} = {\mathbf{u}}_{{L(R)}}^{{sa}}{{({\mathbf{u}}_{{L(R)}}^{{sa}})}^{\dag }}$ is the anti-Hermitian component of the contact self-energy. Using relations (2) and (4), we can write the transmittance of the system in a form common to any two-terminal quantum conductor [17]:

$$T(E) = \frac{{{\text{|}}P(E){{{\text{|}}}^{2}}}}{{{\text{|}}P(E){{{\text{|}}}^{2}} + \,\,{\text{|}}Q(E){{{\text{|}}}^{2}}}},$$

(7)

with $P(E) = 4\Gamma {{J}^{2}}{{({{\Delta }^{2}} + 4{{J}^{2}})}^{{ - 1}}}(E - {{\varepsilon }_{0}} - V)$ and Q(E) = $\det (E\hat {I} - {{\hat {H}}_{{{\text{aux}}}}})$, where

$${{\hat {H}}_{{{\text{aux}}}}} = \left( {\begin{array}{*{20}{c}} {{{\varepsilon }_{0}} + \frac{{4{{J}^{2}}V}}{{{{\Delta }^{2}} + 4{{J}^{2}}}}}&{\frac{{i\Delta \Gamma }}{{\sqrt {{{\Delta }^{2}} + 4{{J}^{2}}} }}} \\ {\frac{{i\Delta \Gamma }}{{\sqrt {{{\Delta }^{2}} + 4{{J}^{2}}} }}}&{{{\varepsilon }_{0}}} \end{array}} \right).$$

(8)

According to expression (7), the real zeros of the function $P(E)$ correspond to zero transparency, and the reals zeros of the functions $Q(E)$, to perfect (unity) transparency. For $V = 0$, Hamiltonian (8) describes tunneling through a system with two degenerate levels. Thus, the four-level model (1) [12] is effectively reduced to two-level [13].

Since the zeros of function $Q(E)$ are determined by the eigenvalues of auxiliary non-Hermitian Hamiltonian (8), the exceptional point of this Hamiltonian taking place at ${\text{|}}V{\text{|}} = {{V}_{{EP}}} = \frac{{\Delta \Gamma }}{{2{{J}^{2}}}}\sqrt {{{\Delta }^{2}} + 4{{J}^{2}}}$ corresponds to the coalescence of resonances in this system [17]. Moreover, if ${\text{|}}V{\text{|}} < {{V}_{{EP}}}$, the peaks of the tunneling transparency (near the energies of levels ${\text{|}}s\rangle$ and ${\text{|}}a\rangle$) will be less than unity and the minimum amplitude ${{T}_{{{\text{peak}}}}}$ they reach for $V = 0$, when the symmetric and antisymmetric states are degenerate. It is easy to calculate that

$${{T}_{{{\text{peak}}}}} = \frac{{4{{J}^{4}}}}{{{{{({{\Delta }^{2}} + 2{{J}^{2}})}}^{2}}}}.$$

(9)

For $J \ll \Delta$, we have ${{T}_{{{\text{peak}}}}} \approx \frac{{4{{J}^{4}}}}{{{{\Delta }^{4}}}}$, which exactly corresponds to the result [12], a key feature of which is the possibility of significant reduction of ${{T}_{{{\text{peak}}}}}$ and, accordingly, an increase in the ratio of currents in open and closed states with an increase of $\Delta {\text{/}}J$ ratio.

EXAMPLES OF FOUR-LEVEL STRUCTURES

The general formalism of [13] makes it possible to explicitly construct specific microscopic realizations of model [12], having determined the relationship between the parameters of Hamiltonian (1) and the geometry and microscopic characteristics of the molecule and anchor groups.

Four-site models. The simplest way to describe the LUMO and HOMO of a central molecule in the site representation is to consider the structure, the most general form of which is shown in Fig. 1b. The requirement of equality of all hopping integrals ${{J}_{i}}$ in the diagonal basis of the central molecule leads to only three possible configurations:

$$\tau \ne 0,\quad {{\tau }_{1}} = {{\tau }_{3}} = 0,\quad {{\tau }_{2}} = {{\tau }_{4}} \ne 0\quad {\text{and}}\quad {{\varepsilon }_{1}} = {{\varepsilon }_{2}},$$

$$\tau = 0,\quad {{\tau }_{1}} = {{\tau }_{2}} = {{\tau }_{3}} = {{\tau }_{4}} \ne 0\quad {\text{and}}\quad {{\varepsilon }_{1}} \ne {{\varepsilon }_{2}},$$

$$\begin{gathered} \tau \ne 0,\quad {{\tau }_{1}} = {{\tau }_{3}} \ne 0,\quad {{\varepsilon }_{1}} \ne {{\varepsilon }_{2}} \\ {\text{and}}\quad {{\tau }_{2}} = {{\tau }_{4}} = \frac{{{{\tau }_{1}}}}{{{\text{|}}{{\varepsilon }_{1}} - {{\varepsilon }_{2}}{\text{|}}}}[\sqrt {{{{({{\varepsilon }_{1}} - {{\varepsilon }_{2}})}}^{2}} + 4{{\tau }^{2}}} - 2\tau ]. \\ \end{gathered} $$

Here, all parameters are considered to be real. The first configuration is the Hückel model for the trimethylenemethane diradical, which was considered in detail in [13]. The structures corresponding to the given configurations are shown in Figs. 1c–1e. All these structures can be brought into a highly symmetric configuration with a pair of degenerate states. In particular, degenerate states in the first system take place for ${{\varepsilon }_{1}} = {{\varepsilon }_{0}}$, and in the second and third for $({{\varepsilon }_{1}} + {{\varepsilon }_{2}}){\text{/}}2 = {{\varepsilon }_{0}}$.

Since these structures are described by the general model formulated in the previous section, their most important property, the minimum achievable tunneling transparency, is described by expression (9) for $J = {{\tau }_{1}}{\text{/}}\sqrt 2$ and $\Delta = \tau$ for the first structure, $J = {{\tau }_{1}}$ and  $\Delta = {\text{|}}{{\varepsilon }_{1}} - {{\varepsilon }_{2}}{\text{|/}}2$ for the second, and J = $\frac{{{{\tau }_{1}}}}{{{\text{|}}{{\varepsilon }_{1}} - {{\varepsilon }_{2}}{\text{|}}}}\sqrt {{{{({{\varepsilon }_{1}} - {{\varepsilon }_{2}})}}^{2}} + 4{{\tau }^{2}} - 2\tau \sqrt {{{{({{\varepsilon }_{1}} - {{\varepsilon }_{2}})}}^{2}} + 4{{\tau }^{2}}} }$ and Δ = $\frac{1}{2}\sqrt {{{{({{\varepsilon }_{1}} - {{\varepsilon }_{2}})}}^{2}} + 4{{\tau }^{2}}}$ for the third. The evolution of the transmission coefficient for these structures is shown in Figs. 2a–2c, and the spectra of the transmission coefficient in the case of degeneracy of the eigenstates are shown in Figs. 2d–2f. Clearly, the peak values of the transmission coefficients in this case agree very well with the estimate obtained from expression (9).

Fig. 2.

(Color online) Transmission control in four-level system. Evolution of transmittance spectrum with change in energy of central molecule (a–c) for structures shown in Figs. 1a–1c, respectively; parameters: ${{\varepsilon }_{0}} = 0$ and ${{\tau }_{1}} = 20\Gamma$ are the same for all cases, $\tau = 20\Gamma$ (a), ${{\varepsilon }_{1}} - {{\varepsilon }_{2}} = 40\Gamma$ (b), and ${{\varepsilon }_{1}} - {{\varepsilon }_{2}} = \tau = 20\Gamma$ (c). Solid lines—unity transmittance; dashed lines—zero transmittance. The resonance coalescence is indicated by bold dot. The worst transmittance spectra of these structures (d–f). Dashed lines—estimate in accordance with expression (9). Evolution of transmission spectrum for structure similar to that shown in Fig. 1c, but with ${{\tau }_{2}} = \frac{{{{\tau }_{1}}{\text{|}}{{\varepsilon }_{1}} - {{\varepsilon }_{2}}{\text{|}}}}{{2\tau }}$ (g); parameters: ${{\varepsilon }_{0}} = 0$ and ${{\varepsilon }_{1}} - {{\varepsilon }_{2}} = \tau = {{\tau }_{1}} = 20\Gamma$. The worst transmittance spectrum of this structure (h).

It is important to note that a decrease in transparency by the same mechanism is possible in the case of a four-site system in which effective jumps ${{J}_{i}}$ between the anchor side groups and the central molecule are not necessarily equal to each other (Fig. 1a), which was not noted in [12]. It is easy to establish that degenerate states in such a system take place for a continuous set of parameters ${{J}_{i}}$ (and not just the specific situation with all ${{J}_{i}}$ equal to each other). As an example, let us consider a structure of the form, like in Fig. 1e. Studying the properties of the eigenvalues of its Hamiltonian, we can conclude that this structure has degenerate states with energy ${{\varepsilon }_{0}}$ if the following condition is met:

$$\begin{gathered} 2\left( {1 + \frac{{\tau _{2}^{2}}}{{\tau _{1}^{2}}}} \right)\left( {{{\varepsilon }_{0}} - \frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{2}} \right) \\ \, - ({{\varepsilon }_{1}} - {{\varepsilon }_{2}})\left( {1 - \frac{{\tau _{2}^{2}}}{{\tau _{1}^{2}}}} \right) + 4\frac{{\tau {{\tau }_{2}}}}{{{{\tau }_{1}}}} = 0. \\ \end{gathered} $$

(10)

It is easy to verify that this structure with ${{\varepsilon }_{1}} + {{\varepsilon }_{2}} = 2{{\varepsilon }_{0}}$ and ${{\tau }_{2}} = \frac{{{{\tau }_{1}}}}{{{\text{|}}{{\varepsilon }_{1}} - {{\varepsilon }_{2}}{\text{|}}}}[\sqrt {{{{({{\varepsilon }_{1}} - {{\varepsilon }_{2}})}}^{2}} + 4{{\tau }^{2}}} - 2\tau ]$ satisfies condition (10). However, there are many other configurations that lead to degeneration of levels. For example, let us consider the case ${{\varepsilon }_{2}} = {{\varepsilon }_{0}}$ and ${{\tau }_{2}} = \frac{{{{\tau }_{1}}{\text{|}}{{\varepsilon }_{1}} - {{\varepsilon }_{2}}{\text{|}}}}{{2\tau }}$, which clearly satisfies (10). By diagonalizing the Hamiltonian of the central part of the system, we can conclude that in this structure ${{J}_{1}} = {{J}_{3}} = {{J}_{ + }}$ and ${{J}_{2}} = {{J}_{4}} = {{J}_{ - }}$, where

$$\begin{gathered} {{J}_{ \pm }} = \frac{{{{\tau }_{1}}}}{{2\sqrt 2 \tau }} \\ \, \times \sqrt {4{{\tau }^{2}} + {{{({{\varepsilon }_{1}} - {{\varepsilon }_{2}})}}^{2}} \pm ({{\varepsilon }_{1}} - {{\varepsilon }_{2}})\sqrt {4{{\tau }^{2}} + {{{({{\varepsilon }_{1}} - {{\varepsilon }_{2}})}}^{2}}} } . \\ \end{gathered} $$

(11)

Obviously, ${{J}_{ + }} \ne {{J}_{ - }}$. Nevertheless, the resonances coalesce, and an antiresonance forms (Fig. 2g). Figure 2h shows the spectrum of the smallest transmittance of the system, the peak values of which also agree well with estimate (9).

Three-site model. The scheme of a structure showing coalescence of resonances and the formation of DQI in Fig. 1a requires at least four states involved in the tunneling process. However, the nature of this phenomenon, as shown in [13], more likely imposes restrictions on the symmetry of the system than on its specific configuration. For a system to have at least one pair of degenerate levels, its symmetry group must have an irreducible representation of at least two dimensions [18]. No two-site system can satisfy this condition, but a three-site system can. Let us consider the three-site structure shown in Fig. 3a, with the following Hamiltonian:

$${{\hat {H}}_{0}} = \left( {\begin{array}{*{20}{c}} {{{\varepsilon }_{0}}}&\tau &\tau \\ \tau &{{{\varepsilon }_{1}}}&\tau \\ \tau &\tau &{{{\varepsilon }_{0}}} \end{array}} \right).$$

(12)

For ${{\varepsilon }_{1}} = {{\varepsilon }_{0}}$, the system has triangular symmetry, which group has an irreducible two-dimensional representation. In this case, there are two degenerate states with energy ${{\varepsilon }_{0}} - \tau$. The corresponding symmetric and antisymmetric states can be written in the same basis as Hamiltonian (12):

$$\begin{gathered} {\text{|}}s\rangle = \frac{1}{{\sqrt 6 }}{{(1, - 2,1)}^{\dag }}, \\ {\text{|}}a\rangle = \frac{1}{{\sqrt 2 }}{{(1,0, - 1)}^{\dag }}. \\ \end{gathered} $$

(13)

Fig. 3.

(Color online) Schematic representation of three-site structure (a). Evolution of transmittance spectrum of a system with change of on-sete energy ${{\varepsilon }_{1}}$ (${{\varepsilon }_{0}} = \tau = 10\Gamma$). Solid lines—unity transmittance; dashed lines—zero transmittance. Resonance coalescence is indicated by bold dot (b). Worst transmittance spectrum with maximum estimate ${{T}_{{{\text{peak}}}}} = \frac{1}{4}$ (c).

Following [13], it is easy to verify that the minimum amplitude of the peaks of tunnel transparency in this system is equal to ${{T}_{{{\text{peak}}}}} = \frac{1}{4}$ and cannot be reduced by any change in parameters. Figure 1b shows the evolution of the transmittance spectrum of this system, calculated in the wideband approximation. Clearly, it has the same behavior as in the case of four-level structures (Fig. 2).

INTERFERENCE TRANSPORT IN MORE COMPLEX SYSTEMS

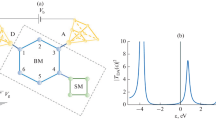
Since the physical mechanism of the described switching of system conductivity is based only on a pair of degenerate states with different parity, the hybrid four-state orbital structure proposed in [12] is not universal. In fact, the Hückel models of some molecular conductors, e.g., from disjoint diradicals, cannot be reduced to such a structure. In [13], in particular, a divinylcyclobutadiene model was studied. In this paper, we consider another example of a disjoint diradical: tetramethyleneethane (TME) [19] (Fig. 4a).

Fig. 4.

(Color online) Interference transport in TME. Structural model of diradical configuration of TME (a). TME carbon skeleton in form of graph for the Hückel model (b). Evolution of transmittance spectrum with change of on-site energy ${{\varepsilon }_{1}}$ for $\tau = 10\Gamma$. Solid lines—unity transmittance; dashed llines—zero transmittance. Resonance coalescence is indicated by bold dot (c). Worst transmittance spectrum for ${{\varepsilon }_{1}} = {{\varepsilon }_{0}}$ in logarithmic scale (d).

In the Hückel model, the Hamiltonian of electrons at the p-orbital of carbon atoms in TME can be written as

$${{\hat {H}}_{0}} = \left( {\begin{array}{*{20}{c}} {{{\varepsilon }_{0}}}&0&\tau &0&0&0 \\ 0&{{{\varepsilon }_{1}}}&\tau &0&0&0 \\ \tau &\tau &{{{\varepsilon }_{1}}}&\tau &0&0 \\ 0&0&\tau &{{{\varepsilon }_{1}}}&\tau &\tau \\ 0&0&0&\tau &{{{\varepsilon }_{1}}}&0 \\ 0&0&0&\tau &0&{{{\varepsilon }_{0}}} \end{array}} \right),$$

(14)

and the coupling with the electrodes in the wideband approximation, as

$$\begin{gathered} {{{\mathbf{u}}}_{L}} = {{(\sqrt \Gamma ,0,0,0,0,0)}^{\dag }}, \\ {{{\mathbf{u}}}_{L}} = {{(0,0,0,0,0,\sqrt \Gamma )}^{\dag }}. \\ \end{gathered} $$

(15)

It is important to note that the symmetry operation in this system is not a mirror reflection, but a 180° rotation around the axis perpendicular to the plane of the molecule and passing through its center. For ${{\varepsilon }_{1}} = {{\varepsilon }_{0}}$ this system has degenerate states with energy ${{\varepsilon }_{0}}$, among which it is possible to distinguish even ${\text{|}}s\rangle$ and odd ${\text{|}}a\rangle$ combinations with respect to the symmetry operation:

$$\begin{gathered} {\text{|}}s\rangle = \frac{1}{2}{{(1, - 1,0,0, - 1,1)}^{\dag }}, \\ {\text{|}}a\rangle = \frac{1}{2}{{(1, - 1,0,0,1, - 1)}^{\dag }}. \\ \end{gathered} $$

(16)

The transmittance of this system can be calculated by general formula (6). Figure 4c shows the evolution of the transmittance spectrum with a change in ${{\varepsilon }_{1}}$; Fig. 4d, the worst transmittance spectrum, corresponding to the degenerate case for ${{\varepsilon }_{1}} = {{\varepsilon }_{0}}$. Since the molecule in question is a disjoint diradical, in the two-level approximation (states ${\text{|}}s\rangle$ and ${\text{|}}a\rangle$) in the degenerate case, tunneling is completely absent (${{T}_{{{\text{peak}}}}} = 0$). In a real system, transparency is nonzero only due to contributions of states remote by energy.

CONCLUSIONS

Based on the example of a number of molecular structures with different geometries, we have demonstrated the universal nature of the previously proposed mechanism for a sharp change in tunneling transparency near an exceptional point of an open quantum system formed by a molecule and electrodes [13]. In fact, we are dealing with a quantum phase transition in the crossover mode, which can be initiated by a weak external potential, and results in a substantial decrease in the supply voltage and, accordingly, power consumption. In all the examples considered, the leading role in the switching mechanism is played by (almost) degenerate levels near the Fermi level. Such levels are absent in linear molecules and are present only in nonsimply connected configurations, which is directly related to the interference nature of the considered mechanism. There is no doubt that, in addition to the molecules described in this article and in [13], there are many others, in particular, belonging to the family of diradicals [20], which have similar switching characteristics. Study of the properties of such molecules and molecular structures in the makeup of a device is an urgent and important task in modern molecular nanoelectronics. The possibility of practical implementation of logical integrated circuits based on similar molecular structures is largely determined by the capabilities of planar technology. According to modern forecasts (ITRS 2.0, Imec), successful lithography with atomic accuracy is expected at the beginning of the next decade, which will make the transition to active elements of integrated circuits based on molecular structures highly probable.