1 INTRODUCTION

According to recent research, the phenomenon of accelerated expansion of the universe has been considered more significant and interesting subject in the modern generation of cosmology and astrophysics [1, 2]. Cosmological constant has been introduced [3, 4] in order to understand this concept. This interesting expansion phenomenon is governed by the Einstein theory of relativity and classical dynamics of solar objects. However, the relativity theory shows some constraints, since within the theoretical framework some significant issues are not addressed properly like dark energy, dark matter, initial singularity, late-time cosmic acceleration and flatness problems. The theory of relativity describes the cosmological behavior and ideas in weak reign, while a few modifications are needed to show the strong fields in the frame of cosmic expansion of universe. As an alternative to general relativity, different gravitational modified theories have been presented in the recent decades. Some alternative models of gravity are proposed which are believed to be a real cause of this accelerating expansion of the universe. Capozziello [5] explained that modified theories of gravity are assumed as an extensive tool to present the mysterious behavior of dark energy and late time cosmic issues. One of the simplest and well known modifications of general theory of relativity is f(R) theory of gravity proposed by Buchdahl [6] by changing Ricci scalar R term with an arbitrary function f(R). The role of modified gravitational theories has important significance in exploring the evolutionary aspects of the universe [7]. These theories of gravity are considered as an alternative to resolve the enigmatic nature of the universe which is the main cause of the accelerated expansion of universe [8, 9].

Another theory which has attained prominence in the recent years is modified Gauss–Bonnet gravity, also recognized as f(\(\mathcal{G}\)) gravity [10–12]. The reconstruction techniques for f(\(\mathcal{G}\)) gravity have been developed by Nojiri and Odintsov [13] and also it was illustrated that how the cosmological sequence of matter dominance, deceleration-acceleration transition and acceleration era may emerge by using such theory of modified gravity. Felice and Tsujikawa [14] studied the solar system constraints on cosmologically viable f(\(\mathcal{G}\)) gravity models and also observed that these models were responsible for late-time cosmic acceleration. The phase space analysis for viable v models and the conditions on their cosmological viability have been explored by Zhou et al. [15]. The role of Gauss–Bonnet term in the late time accelerated phases of the universe was discussed by Sharif and Fatima [16].

In astrophysics, the compact stars generally originate due to the gravitational collapse of the massive stars. The resulting outcome of this gravitational collapse depends upon the mass of the star. Compact stars include white dwarfs, neutron stars and black holes. The physical features of stars comprises the relation between the interior pressure and gravitational force which results into an equilibrium state, known as hydrostatic equilibrium structures. This phenomenon has great significance in studying the interior structure of the stars. The solutions for isotropic stars in general relativity are described by Tolman–Oppenheimer–Volkoff (TOV) equations [17–19]. Neutron star model based on a stringy inspired Gauss–Bonnet gravity has been explored using TOV equations by Momeni and Myrzakulov [20]. Several authors [21–29] have employed the TOV approach to examine the interior structure of the compact objects. TOV equations represent the relationship between the pressure, mass and energy density of a particular star. These TOV equations show that how the pressure and energy density are affected with respect to mass of the compact star. For compact stars particularly for the neutron stars, the interior pressure equivalent to the gravitational pressure is actually the pressure that is being evinced from degeneracy of fermions. The relativistic approach in general relativity by considering the set of TOV equations for the nonrotating spherically symmetric hydrostatic equilibrium, is given as

$$\begin{gathered} \frac{{dp}}{{dr}} = - G\frac{{(\rho {{c}^{2}} + p)(m{{c}^{2}} + 4\pi {{r}^{3}})}}{{{{r}^{2}}{{c}^{4}} - 2Gm{{c}^{2}}r}}{\text{,}} \\ \frac{{dm}}{{dr}} = 4\pi \rho {{r}^{2}}, \\ \end{gathered} $$
((1))

where p, ρ being the radial pressure and energy density respectively and m represents the stellar mass of the star, these all are dependent on the radial coordinate r. For the compact star at the boundary r = R, the total stellar mass of the star is computed as

$$M(R) = \int\limits_0^R {4\pi {{r}^{2}}\rho dr.} $$
((2))

In order to solve above coupled equations, a suitable choice of equations of state (EoS) plays an important role which exhibits the connection between pressure and energy density. The equilibrium configurations of neutron as well as quark stars have been studied by Moraes et al. [30] with different forms of EoS and it has been observed that the maximum mass could cross the observational limits. The possible existence of neutron stars with high central densities and larger masses than general relativity has been pointed out in the context of modified theories of gravity [31–33].

The development of TOV equations for different modified gravity models have great contribution for better understanding and examining the nature of compact stars structures and matter at high densities [34–37]. In particular, the study of TOV equations in modified f(R) gravity have very interesting consequences [38–41]. Artyom and collaborators [35] investigated quark star models with realistic EoS in non-perturbative f(R) gravity and found the mass-radius relationship. The structure of neutron star have been studied by Deliduman et al. [42] in f(R) = R + βRμνRμν gravity with perturbative approach and the mass-radius relations are observed for the six different EoS parameters. In fact, the study of compact stars has gained most attention in modified theories of gravity and a reasonable amount of work related to neutron stars have been a strong subject of discussion [43–45]. Astashenok et al. [34] investigated modified TOV equations and the possible existence of neutron stars with strong magnetic fields in the context of the extended theories of gravity. For this purpose the authors considered generalized form of the Einstein theory consisting of the Gauss-Bonnet invariant term and further they compared the results with f(R) gravity. Recently the charged compact structures in modified Gauss–Bonnet gravity have been discussed by Ilyas [46].

In this paper, we aim to investigate the TOV equations in the frame of f(\(\mathcal{G}\)) gravity. For this purpose, we derive the full system of equations of motion for a spherically symmetric static spacetime with perfect fluid. In particular, the hydrostatic equilibrium equations have been developed and the profiles of energy density, pressure and mass of stars are investigated through two different equations of state models. Moreover, the physical attributes of the compact objects have been discussed in detail for the different values of model parameter. The paper is organized as follows: A brief discussion of the modified theory f(\(\mathcal{G}\)) gravity with its field equations and fundamental formulation has been presented in Section 2. In Section 3, we investigate the physical features of the neutron and quark strange stars by using two different EoS. Last section, is based on the conclusive remarks of the results.

2 MODIFIED FIELD EQUATIONS OF f(\(\mathcal{G}\)) GRAVITY

The most general action for modified Gauss–Bonnet gravity is [47]

$$S = \int {{{d}^{4}}x\sqrt { - g} \left[ {\frac{R}{{2{{\kappa }^{2}}}} + f(\mathcal{G})} \right] + {{S}_{m}},} $$
((3))

where R is Ricci scalar, κ2 = 8πG is coupling constant and Sm is the matter Lagrangian. Varying the action (3) with respect to metric tensor, the modified field equations

$$\begin{gathered} {{R}_{{\mu \nu }}} - \frac{1}{2}R{{g}_{{\mu \nu }}} + 8\left[ {{{R}_{{\mu \rho \nu \sigma }}} + {{R}_{{\rho \nu }}}{{g}_{{\sigma \mu }}} - {{R}_{{\rho \sigma }}}{{g}_{{\nu \mu }}}_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}} \right. \\ \,\left. { - {{R}_{{\mu \nu }}}{{g}_{{\sigma \rho }}} + {{R}_{{\mu \sigma }}}{{g}_{{\nu \rho }}} + \frac{R}{2}({{g}_{{\mu \nu }}}{{g}_{{\sigma \rho }}} - {{g}_{{\mu \sigma }}}{{g}_{{\nu \rho }}})} \right] \\ \, \times {{\nabla }^{\rho }}{{\nabla }^{\sigma }}{{g}_{\mathcal{G}}} + (\mathcal{G}{{f}_{\mathcal{G}}} - f){{g}_{{\mu \nu }}} = {{\kappa }^{2}}{{T}_{{\mu \nu }}}, \\ \end{gathered} $$
((4))

where subscript \(\mathcal{G}\) in \({{f}_{\mathcal{G}}}\) represents derivative of f(\(\mathcal{G}\)) with respect to \(\mathcal{G}\) while Rμν and Rμρνσ are the Ricci and Riemann tensors, respectively. The Gauss–Bonnet term \(\mathcal{G}\) is defined as

$$\mathcal{G} = {{R}^{2}} - 4{{R}_{{\mu \nu }}}{{R}^{{\mu \nu }}} + {{R}_{{\mu \nu \sigma \rho }}}{{R}^{{\mu \nu \sigma \rho }}}.$$
((5))

We take the signature for the Riemannian metric as (+, –, –, –). Covariant derivative and Riemann tensor are denoted by ∇μVν = ∂μVν – \(\Gamma _{{\mu \nu }}^{\lambda }\)Vλ and \(R_{{\mu \nu \rho }}^{\sigma }\) = ∂ν\(\Gamma _{{\mu \rho }}^{\sigma }\) – ∂ρ\(\Gamma _{{\mu \nu }}^{\sigma }\) + \(\Gamma _{{\mu \rho }}^{\omega }\Gamma _{{\mu \nu }}^{\sigma }\) – \(\Gamma _{{\mu \nu }}^{\omega }\Gamma _{{\omega \rho }}^{\sigma }\) respectively. Let us consider the spherically symmetric metric

$$d{{s}^{2}} = {{e}^{{\nu (r)}}}d{{t}^{2}} - {{e}^{{\lambda (r)}}}d{{r}^{2}} - {{r}^{2}}(d{{\theta }^{2}} + {{\sin }^{2}}\theta d{{\phi }^{2}}),$$
((6))

where ν and λ being some arbitrary function of r. For the spacetime (6), the components of Einstein tensor Gαβ read

$$\begin{gathered} {{G}_{{11}}} = \frac{{{{e}^{{\nu - \lambda }}}}}{{{{r}^{2}}}}(\lambda 'r + {{e}^{\lambda }} - 1), \\ {{G}_{{22}}} = \frac{1}{{{{r}^{2}}}}(\nu 'r - {{e}^{\lambda }} + 1), \\ \end{gathered} $$
((7))
$${{G}_{{33}}} = \frac{{r{{e}^{{ - \lambda }}}}}{4}( - \nu '\lambda 'r + \nu {{'}^{2}}r + 2\nu ''r - 2\lambda ' + 2\nu '),$$
((8))

where “ ' ” denotes the radial derivative. Using Eqs. (4) and (7), (8), tt and rr components of the field equations are

$$\begin{gathered} \frac{1}{{{{r}^{2}}}}(\lambda 'r + {{e}^{\lambda }} - 1) - 8{{e}^{{ - \lambda }}}({{f}_{{\mathcal{G}\mathcal{G}\mathcal{G}}}}\mathcal{G}{{'}^{2}} + {{f}_{{\mathcal{G}\mathcal{G}}}}\mathcal{G}'')\left( {\frac{{1 - {{e}^{\lambda }}}}{{{{r}^{2}}}}} \right) \\ \, + (\mathcal{G}{{f}_{\mathcal{G}}} - f){{e}^{{ - \lambda }}} - 4{{e}^{\lambda }}(\lambda '\mathcal{G}'{{f}_{{\mathcal{G}\mathcal{G}}}})\left( {\frac{{{{e}^{\lambda }} - 3}}{{{{r}^{2}}}}} \right) = {{\kappa }^{2}}\rho {{e}^{\lambda }}, \\ \end{gathered} $$
((9))
$$\begin{gathered} \frac{1}{{{{r}^{2}}}}(\nu 'r - {{e}^{\lambda }} + 1) - 4{{e}^{{ - \lambda }}}\nu '\mathcal{G}'{{f}_{{\mathcal{G}\mathcal{G}}}}\left( {\frac{{{{e}^{\lambda }} - 3}}{{{{r}^{2}}}}} \right) \\ \, - (\mathcal{G}{{f}_{\mathcal{G}}} - f){{e}^{\lambda }} = {{\kappa }^{2}}p{{e}^{\lambda }}. \\ \end{gathered} $$
((10))

The Gauss–Bonnet invariant and the conservation equation for the spherically symmetric space time (6) turn out to be

$$\begin{gathered} \mathcal{G} = \frac{{2{{e}^{{ - \lambda }}}}}{{{{r}^{2}}}}(\nu '\lambda ' + \nu {{'}^{2}}{{e}^{{ - \lambda }}} \\ \, - 3\nu '\lambda '{{e}^{{ - \lambda }}} - 2\nu '' - \nu {{'}^{2}} + 2\nu ''{{e}^{{ - \lambda }}}), \\ \end{gathered} $$
((11))
$$\frac{{dp}}{{dr}} + \frac{{\nu '}}{2}(p + \rho ) = 0.$$
((12))

The gravitational mass m of a spherical star with inner radius r may be related by the equation e–λ = (1 – 2m/r). Thus writing Eqs. (9) and (10) in terms of \(\frac{{dp}}{{dr}}\), \(\frac{{dm}}{{dr}}\), ρ and after some manipulations, we obtain the corresponding TOV equations

$$\begin{gathered} \frac{2}{{{{r}^{2}}}}\frac{{dm}}{{dr}} + 8{{\left[ {1 - \frac{{2m}}{r}} \right]}^{2}}\left[ {\frac{{\frac{{2m}}{{{{r}^{3}}}}}}{{1 - \frac{{2m}}{r}}}} \right][{{f}_{{\mathcal{G}\mathcal{G}\mathcal{G}}}}\mathcal{G}{{'}^{2}} + {{f}_{{\mathcal{G}\mathcal{G}}}}\mathcal{G}''] \\ \, + 4\left[ {\frac{{2m}}{{{{r}^{5}}}}\left( {1\, - \,\frac{r}{m}\frac{{dm}}{{dr}}} \right)( - 2r\, + \,6m)} \right]\mathcal{G}'{{f}_{{\mathcal{G}\mathcal{G}}}}\, + \,(\mathcal{G}{{f}_{\mathcal{G}}}\, - \,f)\, = \,8\pi \rho , \\ \end{gathered} $$
((13))
$$\begin{gathered} - \frac{2}{{{{r}^{2}}}}\left( {\frac{{r - 2m}}{{p + \rho }}} \right)\frac{{dp}}{{dr}}\left[ {1 + \frac{4}{{{{r}^{2}}}}(2r - 6m)\mathcal{G}'{{f}_{{\mathcal{G}\mathcal{G}}}}} \right] \\ \, - \frac{{2m}}{{{{r}^{3}}}} - (\mathcal{G}{{f}_{\mathcal{G}}} - f) = 8\pi p. \\ \end{gathered} $$
((14))

We will use these equations to further analyze the neutron and quark stars. Now we consider f(\(\mathcal{G}\)) = α\({{\mathcal{G}}^{n}}\), where f(\(\mathcal{G}\)) being an analytic function of the Gauss–Bonnet invariant term \(\mathcal{G}\) [12]. Here we particulary choose n = 2 for the sake of simplicity and two dimensional graphical analysis. Now manipulating Eqs. (13) and (14) together

$$\frac{{d\rho }}{{dr}} = \frac{{{{r}^{2}}(p + \rho )}}{{2(r - 2m)\left( {1 + \frac{{8\alpha (2r - 6m)\mathcal{G}'}}{{{{r}^{2}}}}} \right)}}$$
$$ \times \left[ {\frac{{ - 2m}}{{{{r}^{3}}}} - 8\pi (p + \rho ) + \frac{2}{{{{r}^{2}}}}{{{\frac{{dm}}{{dr}}}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} \right.$$
((15))
$$\left. { + \frac{{(16\alpha m)( - 2r\, + \,6m)\mathcal{G}'\left( {1\, - \,\frac{{r\frac{{dm}}{{dr}}}}{m}} \right)}}{{{{r}^{5}}}}\, + \,\frac{{32\alpha m\left( {1\, - \,\frac{{2m}}{r}} \right)\mathcal{G}''r}}{{{{r}^{3}}}}} \right].$$

2.1 Boundary Conditions

We are interested to integrate the differential Eq. (15) to find the physical characteristics of the hydrostatic equilibrium of the compact stars. We define some specific boundary conditions starting at the center of the star:

$$m(0) = 0,\quad \rho (0) = {{\rho }_{c}},\quad p(0) = {{p}_{c}}.$$
((16))

The solutions at the surface of the compact stars (r = R) are computed with the specific condition p(R) = 0 such that the interior spacetime of star is matched smoothly with Schwarzschild solution. The metric potentials of interior and exterior spacetime are connected through eν(R) = \(\frac{1}{{{{e}^{\lambda }}(R)}}\) = 1 – \(\frac{{2M}}{R}\), with M represents the stellar mass of the compact star.

2.2 Equation of State Models

The structure and the formation of a neutron star totally depends on the EoS parameter which forms the connection between pressure and energy density inside the star [48]. After defining the EoS, the differential Eq. (15) can be computed for unknown functions m, p, and ρ. Moreover, EoS will be useful to reduce one unknown and help in integrating process. The two well known EoS (Polytropic and MIT bag model) have been considered to observe the equilibrium structures of compact stars in f(\(\mathcal{G}\)) theory of gravity. The work by Tooper [49] may be a valuable example where he used polytropic EoS to study neutron stars. Thus to study using polytropic EoS p = ωρ5/3, Eq. (15) takes the form

$$\frac{5}{3}{{\rho }^{{2/3}}}\omega \frac{{d\rho }}{{dr}} = \frac{{{{r}^{2}}({{\rho }^{{5/3}}}\omega + \rho )}}{{2(r - 2m)\left( {1 + \frac{{8\alpha (2r - 6m)\mathcal{G}'}}{{{{r}^{2}}}}} \right)}}$$
$$ \times \left[ {\frac{{ - 2m}}{{{{r}^{3}}}} - 8\pi ({{\rho }^{{5/3}}}\omega + \rho ) + \frac{2}{{{{r}^{2}}}}{{{\frac{{dm}}{{dr}}}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} \right.$$
((17))
$$\left. { + \frac{{(16\alpha m)( - 2r\, + \,6m)\mathcal{G}'\left( {1\, - \,\frac{{r\frac{{dm}}{{dr}}}}{m}} \right)}}{{{{r}^{5}}}}\, + \,\frac{{32\alpha m\left( {1\, - \,\frac{{2m}}{r}} \right)\mathcal{G}''r}}{{{{r}^{3}}}}} \right].$$

Here we assume ω = 1.4745 × 10–3 (fm3/MeV)2/3 [50, 51]. The choice of MIT bag model p = a(ρ – 4b) is considered to be more appropriate, while studying the strange quark matter [52]. For massive quark stars, we may choose parameter a = 0.28, with ms = 250 MeV [53]. The parameter b is called bag constant and for this work we consider b = 60 MeV/fm3.

$$a\frac{{d\rho }}{{dr}} = \frac{{{{r}^{2}}(a(\rho - 4b) + \rho )}}{{2(r - 2m)\left( {1 + \frac{{8\alpha (2r - 6m)\mathcal{G}'}}{{{{r}^{2}}}}} \right)}}$$
$$ \times \left[ {\frac{{ - 2m}}{{{{r}^{3}}}} - 8\pi (a(\rho - 4b) + \rho ) + \frac{2}{{{{r}^{2}}}}{{{\frac{{dm}}{{dr}}}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} \right.$$
((18))
$$\left. { + \frac{{(16\alpha m)( - 2r\, + \,6m)\mathcal{G}'\left( {1\, - \,\frac{{r\frac{{dm}}{{dr}}}}{m}} \right)}}{{{{r}^{5}}}}\, + \,\frac{{32\alpha m\left( {1\, - \,\frac{{2m}}{r}} \right)\mathcal{G}''r}}{{{{r}^{3}}}}} \right].$$

3 NEUTRON AND STRANGE STARS IN f(\(\mathcal{G}\)) GRAVITY

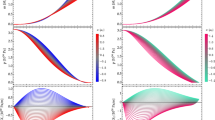
Equations (17) and (18) are highly nonlinear differential equations and it seems difficult to find a solution through analytical method. Here we prefer the Runge–Kutta 4th order method and use the boundary conditions for different values of α to investigate the three important physical aspects of the compact stars i.e. energy density ρ, pressure p and the normalized stellar mass m/\({{M}_{ \odot }}\). The graphical behavior of energy density and pressure for the neutron and strange quark stars is shown in Figs. 1 and 2. It cab be easily observed from these graphs that as r → 0 then energy density attains the maximum value. The graphs in Fig. 2 depicts that as r increases, the radial pressure for the neutron and strange quark stars decreases. Moreover, pressure approaches to zero on the boundary. Observations from both density and pressure profiles indicates the high compactness of the stars for power law f(\(\mathcal{G}\)) gravity model. The graph in Fig. 3 shows a directly proportional relation between mass and radial coordinate which is exactly according to usual patterns of mass-radius relationship for compact stars. It is observed that the stellar mass of the neutron and quark stars almost shows opposite behavior with the increasing values of α.

Fig. 1.
figure 1

(Color online) The energy density profiles for neutron and strange quark stars for some different values of parameter α are shown in (a) and (b), respectively. The value of the central energy density has been assumed as 900 MeV/fm3.

Full size image
Fig. 2.
figure 2

(Color online) The pressure profiles against the radial coordinate for neutron and strange quark stars are presented in (a) and (b), respectively for some different parametric values of α.

Full size image
Fig. 3.
figure 3

(Color online) The masses normalized with the solar masses against radial coordinate for the neutron stars are presented in (a) and for strange quark stars, in (b), for some different parametric values of α.

Full size image

4 CONCLUDING REMARKS

The main focus of this work is to investigate the physical aspects of the compact structures in f(\(\mathcal{G}\)) gravity. For this purpose, we have considered generalized TOV equation in f(\(\mathcal{G}\)). Moreover, the polytropic EoS (p = ωρ5/3) for neutron stars and the MIT bag model EoS (p = a(ρ – 4b)) for strange quark stars are used to investigate the generalized TOV equation. Due to the highly nonlinear and difficult nature of corresponding differential equations, we prefer numerical methods and use suitable boundary conditions for different values of α. The physical and geometrical aspects of these EoS for different parametric values of a have been examined. The model parameter α plays an important role in evolution of compact structures in f(\(\mathcal{G}\)). For f(\(\mathcal{G}\)) = α\({{\mathcal{G}}^{2}}\) gravity model, the behavior of energy density ρ, pressure p and the normalized stellar mass m/\({{M}_{ \odot }}\) has been shown in Figs. 1–3. It is clear from the graphs as the radial coordinate r → 0, the value of energy density attains the maximum value, which shows the compactness of the star. Also, the radial pressure for the neutron and strange quark stars decreases as r increases and approaches to zero on the boundary. Moreover, it is also observed that the stellar mass of the neutron and quark stars almost shows opposite behavior with the increasing values of α. The increasing behavior of the stellar mass of the compact subjects is due to the model parameter α, which plays an important role in this frame of reference. In general, we can say that the effect caused by the model parameter term is very analogous to that caused by the pressure or an extra electric charge in the configurations of neutron and strange stars in general relativity [50–55]. However, it is important to point out that the mass-radius relation shows a directly proportional relation which represents the physical attributes of the compact structures. The findings of this work are same as already available in literature [30, 56]. Furthermore, the mass-radius relation illustrate that by adopting the cubic f(R) gravity corrections, the maximal mass of neutron stars can be achieved [34]. In principle, the possibility of massive neutron stars M > 4\({{M}_{ \odot }}\) having radius 12–15 km in modified gravity is possible. Thus in our case, existence of the stable stars with high central densities seems realistic by considering the quadratic f(\(\mathcal{G}\)) gravity corrections.