1 INTRODUCTION

A study of physical behavior as well as different evolutionary stages of stellar objects is one of the most intriguing issues in relativistic astrophysics. The factors like condensation of gaseous material and self-gravitation play a vital role in the structure formation and evolution of celestial bodies. The internal constitution of these objects is well described by an equation of state (EoS). Eddington [1] explored that gas in a star could be made to obey a polytropic relation between its pressure and density for a particular choice of temperature distribution. He named those star models as polytropic stars that provide a crude approximation to more realistic stellar models. Since then, the modeling of compact objects via polytropic EoS captivated the attention of many researchers.

The structure of polytropes is represented by Lane–Emden equation which is the coupling of non-linear differential equations (hydrostatic equilibrium equation and mass conservation equation). Tooper [2] was the pioneer to study the isotropic relativistic spherical systems with polytropic EoS and obtained numerical solution of structure equations. He also discussed gravitational collapse of massive star as a mechanism to produce large amount of energy. Thirukkanesh and Ragel [3] found a class of exact solutions for static polytropic sphere and checked their physical features expected in a realistic stellar model. Herrera and Barreto [4] studied the isotropic as well as anisotropic spherically symmetric relativistic polytropes and obtained numerical solution of structure equations describing polytropes. Herrera et al. [5] constructed anisotropic conformally flat polytropes with spherical symmetry and checked their viability through energy conditions. Azam et al. [6] explored polytropic charged sphere with generalized polytropic EoS and found that stability of models is enhanced as the compactness parameter is decreased.

Recent observational data in modern cosmology disclosed that our universe is experiencing an accelerated expansion which is believed due to the mysterious form of energy known as dark energy. Some theoretical results revealed that dark energy might be described by the cosmological constant (also interpreted as the vacuum energy density) which is characterized by repulsive pressure. These observations gained attention to the study of astrophysical objects with cosmological constant. Zubairi et al. [7] obtained solutions of the Einstein field equations for spherically symmetric mass distributions with cosmological constant. They also studied the structure of non-spherical compact objects and evaluated stellar properties (mass, radius, pressure and density) for these objects.

Böhmer and Harko [8] examined the instability of spherically symmetric matter distribution in the presence of cosmological constant. They concluded that a large cosmological constant increases the value of critical adiabatic index. Hossein [9] discussed the formation of anisotropic compact stars from cosmological constant and found that the developed model is valid for any compact star. Stuchlík et al. [10] investigated the role of cosmological constant on spherically symmetric polytropes with perfect fluid and analyzed physical features of polytropic sphere. They found that repulsive cosmological constant has a relevant effect on polytropes when the length scale is comparable with cosmological constant.

The spherically symmetric static solutions of the Einstein field equations are well-known staples in general relativity but the cylindrically symmetric static solutions are less familiar. A study of non-spherical self-gravitating systems gained much significance after cylindrical gravitational wave solution of Einstein field equations. Since then many authors attempted to find the cylindrical solutions as well as the physical properties of stellar models in the context of cylindrical symmetry. Scheel et al. [11] examined stability of cylindrical polytropes and concluded that they are stable in contrast with spherical polytropes. Herrera et al. [12] examined cylindrically symmetric self-gravitating fluids and found that matter quantities have significant influence on the dynamics of cylindrically symmetric matter distribution. Abbas et al. [13] studied the formation of anisotropic cylindrical compact objects with cosmological constant and checked their regularity conditions as well as stability. We formulated the anisotropic polytropic cylindrical models through conformal flatness and found an increasing behavior of model compactness [14]. Azam et al. [15] presented the general formalism for charged anisotropic cylindrical polytrope and found that one of the developed models is physically acceptable.

This paper explores isotropic cylindrical polytropes in the presence of cosmological constant. The plan of the paper is as follows. In the next section, we discuss matter distribution satisfying two cases of polytropic EoS for cylindrically symmetric spacetime to construct structure equations which help to study physical characteristics of polytropes and then investigate the resulting models numerically. The energy conditions for the developed models are also investigated. In Section 3, we analyze the stability of polytropic models through cracking. Finally, we conclude our main findings in the last section.

2 FLUID DISTRIBUTION AND STRUCTURE EQUATIONS

We formulate general relativistic equations governing the equilibrium state of cylindrically symmetric matter distribution satisfying polytropic EoS. The line element representing static cylindrical symmetry is given as [16]

$$d{{s}^{2}} = - {{A}^{2}}(r)d{{t}^{2}} + {{B}^{2}}(r)d{{r}^{2}} + {{C}^{2}}(r)d{{\phi }^{2}} + d{{z}^{2}}.$$
((1))

The fluid inside this configuration is assumed to be perfect fluid bounded by hypersurface Σ so that rΣ = const. The energy-momentum tensor for such matter distribution is given as

$${{T}_{{\alpha \beta }}} = (\rho + P){{V}_{\alpha }}{{V}_{\beta }} + P{{g}_{{\alpha \beta }}},$$
((2))

where ρ, P, and Vα are the energy density, isotropic pressure, and four-velocity, respectively. In comoving coordinates, the four-velocity is defined as

$${{V}_{\alpha }} = - A\delta _{\alpha }^{0} \Rightarrow {{V}_{\alpha }}{{V}^{\alpha }} = - 1.$$

The corresponding field equations (Rαβ – \(\frac{1}{2}\)Rgαβ + Λgαβ = 8πTαβ) turn out to be

$$8\pi \rho + \Lambda = \frac{1}{{{{B}^{2}}}}\left( {\frac{{B'C'}}{{BC}} - \frac{{C''}}{C}} \right),\quad 8\pi P - \Lambda = \frac{1}{{{{B}^{2}}}}\left( {\frac{{A'C'}}{{AC}}} \right),$$
$$8\pi P - \Lambda = \frac{1}{{{{B}^{2}}}}\left( {\frac{{A''}}{A} - \frac{{A'B'}}{{AB}}} \right),$$
$$8\pi P - \Lambda = \frac{1}{{{{B}^{2}}}}\left( {\frac{{A''}}{A} - \frac{{A'B'}}{{AB}} - \frac{{B'C'}}{{BC}} + \frac{{A'C'}}{{AC}} + \frac{{C''}}{C}} \right),$$

where prime denotes differentiation with respect to r while Λ is the cosmological constant. We take C(r) = r as our Schwarzschild coordinate. Consequently, the field equations reduce to the following form

$$8\pi \rho + \Lambda = \frac{1}{{r{{B}^{2}}}}\left( {\frac{{B'}}{B}} \right),$$
((3))
$$8\pi P - \Lambda = \frac{1}{{r{{B}^{2}}}}\left( {\frac{{A'}}{A}} \right),$$
((4))
$$8\pi P - \Lambda = \frac{1}{{{{B}^{2}}}}\left( {\frac{{A''}}{A} - \frac{{A'B'}}{{AB}}} \right),$$
((5))
$$8\pi P - \Lambda = \frac{1}{{{{B}^{2}}}}\left( {\frac{{A''}}{A} - \frac{{A'B'}}{{AB}} - \frac{1}{r}\left( {\frac{{B'}}{B} + \frac{{A'}}{A}} \right)} \right).$$
((6))

Thorne [17] defined C-energy for cylindrical spacetimes as

$$m = \frac{1}{8}(1 - {{l}^{{ - 2}}}{{\nabla }^{\alpha }}\tilde {r}{{\nabla }_{\alpha }}\tilde {r}),$$

with

$${{\bar {\rho }}^{2}} = {{\zeta }_{{(1)a}}}\zeta _{{(1)}}^{a},\quad {{l}^{2}} = {{\zeta }_{{(2)a}}}\zeta _{{(2)}}^{a},\quad \bar {r} = \bar {\rho }l,$$

here \(\bar {\rho }\), l, and \(\bar {r}\) are the circumference radius, specific length and areal radius, respectively, and ζ(1) = \(\frac{\partial }{{\partial \phi }}\), ζ(2) = \(\frac{\partial }{{\partial z}}\) are Killing vectors for cylindrical system. The C-energy for our line element takes the form

$$m(r) = \frac{1}{8}\left( {1 - \frac{1}{{{{B}^{2}}}}} \right).$$
((7))

The conservation law, \(T_{{\beta ;\alpha }}^{\alpha }\) = 0, yields

$$P' + \frac{{A'}}{A}(\rho + P) = 0.$$
((8))

Using Eqs.(4) and (7), we obtain

$$\frac{{A'}}{A} = \frac{{8\pi rP - r\Lambda }}{{1 - 8m}}.$$

where

$$m = 2\pi \int\limits_0^r {r\rho dr} $$
((9))

representing the total mass inside the cylindrical compact object. Consequently, Eq. (8) becomes

$$P' + \frac{{8\pi rP - r\Lambda }}{{1 - 8m}}(\rho + P) = 0.$$
((10))

The matter distribution is found to be realistic if it satisfies certain conditions known as energy conditions. For isotropic fluid configuration, these conditions are

$$\begin{gathered} ({\text{i}})\,\rho \geqslant 0,\quad ({\text{ii}})\,\rho + P \geqslant 0,\quad ({\text{iii}})\,\rho - P \geqslant 0, \\ ({\text{iv}})\,\rho + 3P \geqslant 0. \\ \end{gathered} $$
((11))

Next, we consider that stellar object satisfying two cases of polytropic EoS and formulate the structure equations.

2.1 Case 1

In this case, we consider

$$P = k\rho _{0}^{\gamma } = k\rho _{0}^{{1 + \frac{1}{n}}},\quad \rho - {{\rho }_{0}} = nP,$$
((12))

here γ, k, and n indicate polytropic exponent, constant and index, respectively, while ρ0 is the baryonic density. We introduce some new variables

$$\begin{gathered} \alpha = \frac{{{{P}_{c}}}}{{{{\rho }_{c}}}},\quad \Phi _{0}^{n}(\xi ) = \frac{{{{\rho }_{0}}(r)}}{{{{\rho }_{{0c}}}}},\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} = \sqrt {\frac{{4\pi {{\rho }_{c}}}}{{\alpha (n + 1)}}} , \\ \lambda = \frac{\Lambda }{{8\pi {{\rho }_{c}}}} = \frac{{{{\rho }_{{{\text{vac}}}}}}}{{8\pi {{\rho }_{c}}}}, \\ r = \frac{\xi }{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }},\quad {v}(\xi ) = \frac{{m(r){{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}^{3}}}}{{4\pi {{\rho }_{c}}}}. \\ \end{gathered} $$
((13))

Here, ρ0c, ρc, and Pc indicate the central values of baryonic as well as total energy density and pressure, respectively, and ρvac denotes the vacuum energy density. The terms ξ, λ, Φ0(ξ), \({v}\)(ξ) are dimensionless radial coordinate, cosmological constant, density and mass parameters, respectively, while \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} \) is constant with dimensions of length–1. The value of Λ is measured to be 1.3 × 10–56 cm–2 and the related vacuum energy density is 10–29 g/cm3 [10]. Using Eq. (13) in (10) and (9), we have

$$\begin{gathered} \frac{{d{{\Phi }_{0}}}}{{dx}} + 2{\tilde{\overset{\smile}{A}}{}^{2}}x\Phi _{0}^{n}(\Phi _{0}^{n}(1 - n\alpha + n\alpha {{\Phi }_{0}}) - \lambda ) \\ \, \times (1 - n\alpha + \alpha (n + 1){{\Phi }_{0}})\left( {1 - \frac{{8\alpha (n + 1){v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}} \right) = 0, \\ \end{gathered} $$
((14))
$$\frac{{d{v}}}{{dx}} - \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} {\tilde{\overset{\smile}{A}}{}^{2}}x\Phi _{0}^{n}}}{2}(1 - n\alpha + n\alpha {{\Phi }_{0}}) = 0,$$
((15))

where x = ξ/\(\tilde{\overset{\smile}{A}} \), \(\tilde{\overset{\smile}{A}}\) = rΣ\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} \). The above equation represents the internal structure of cylindrical compact object. Differentiating Eq. (14) with respect to x and then using (15), we obtain

$$\frac{{(1 - n\alpha + (1 + n)\alpha {{\Phi }_{0}})(\Phi _{0}^{n}(1 - n\alpha + n\alpha {{\Phi }_{0}}) - \lambda )}}{{1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}}}\left[ {\frac{{2\Phi _{0}^{n}}}{{1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}}} + 8(1 + n)} \right.$$
$$\left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\, \times \alpha {\tilde {\overset{\smile}{A}}{}^{2}}{{x}^{2}}\Phi _{0}^{{2n}}(1 - n\alpha + n\alpha {{\Phi }_{0}}) + 2nx\Phi _{0}^{{n - 1}}\frac{{d{{\Phi }_{0}}}}{{dx}}} \right] + \frac{{2x\Phi _{0}^{n}}}{{1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}}}$$
((16))
$$\, \times [n\Phi _{0}^{{n - 1}}{{(1 - n\alpha + \alpha (n + 1){{\Phi }_{0}})}^{2}} + \alpha (n + 1)(\Phi _{0}^{2}(1 - n\alpha + n\alpha {{\Phi }_{0}}))]\frac{{d{{\Phi }_{0}}}}{{dx}} + {\tilde{\overset{\smile}{A}}{}^{-2}}\frac{{{{d}^{2}}{{\Phi }_{0}}}}{{d{{x}^{2}}}} = 0.$$

This equation is termed as Lane–Emden equation describing polytrope in hydrostatic equilibrium. The energy conditions in this case yield

$$\begin{gathered} ({\text{i}})\,1 - n\alpha + n\alpha {{\Phi }_{0}} \geqslant 0,\quad ({\text{ii}})\,1 - n\alpha + \alpha (n + 1){{\Phi }_{0}} \geqslant 0, \\ ({\text{iii}})\,1 - n\alpha + \alpha (n - 1){{\Phi }_{0}} \geqslant 0,\quad ({\text{iv}})\,1 - n\alpha + \alpha (n + 3){{\Phi }_{0}} \geqslant 0. \\ \end{gathered} $$
((17))

We note that Eqs. (14) and (15) represent a system of two differential equations in two unknowns (Φ0 and \({v}\)). We solve these equations numerically with the initial conditions

$${v}(0) = 0,\quad {{\Phi }_{0}}(0) = 1.$$
((18))

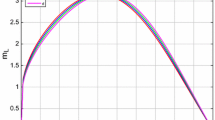
Figure 1 shows the solution of Eqs. (14) and (15) for zero as well as nonzero cosmological constant. The left graph indicates the viable behavior of Φ0, i.e., it must be positive inside the object and decreases as one moves away from the center of star. Moreover, Φ0 falls off more quickly for λ = 0. The right plot demonstrates the behavior of dimensionless mass function \({v}\). We observe that \({v}\) has larger values for larger λ indicating that the increase in λ yields more compact models. The energy conditions are plotted in Fig. 2 for zero as well as non-zero cosmological constant showing that all the energy bounds are satisfied for different values of λ.

Fig. 1.
figure 1

(Color online) Plots for Φ0 (a) and \({v}\) (b) versus x for λ = 0 (1), λ = 0.3 (2), and λ = 0.7 (3) with n = 1.5, α = 0.2.

Full size image
Fig. 2.
figure 2

(Color online) Plots for energy conditions versus x for λ = 0 (1), λ = 0.3 (2), and λ = 0.7 (3) with n = 1.5, α = 0.2.

Full size image

2.2 Case 2

Here, we consider the case

$$p = k{{\rho }^{\gamma }} = k{{\rho }^{{1 + \frac{1}{n}}}},\quad \rho {{\left( {1 - K\rho _{0}^{{\frac{1}{n}}}} \right)}^{n}} = {{\rho }_{0}},$$
((19))

with ρ(r) = ρcΦn(ξ). In this case, the structure equations lead to

$$\begin{gathered} \frac{{d\Phi }}{{dx}} + 2{\tilde{\overset{\smile}{A}}{}^{2}}x(\Phi _{{}}^{n}(\Phi _{{}}^{n} - \lambda )(1 + \alpha \Phi ) \\ \times \left( {1 - \frac{{8\alpha (n + 1){v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}} \right) = 0, \\ \end{gathered} $$
((20))
$$\frac{{d{v}}}{{dx}} - \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} {\tilde{\overset{\smile}{A}}{}^{2}}x{{\Phi }^{n}}}}{2} = 0.$$
((21))

Again, following the same procedure as in case 1, the Lane–Emden equation in this case turns out to be

$$\begin{gathered} \frac{{(1\, + \,\alpha \Phi )({{\Phi }^{n}}\, - \,\lambda )}}{{1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}}}\left[ {2{{\Phi }^{n}}\left( {1\, + \,\frac{{nx\frac{{d\Phi }}{{dx}}}}{\Phi }} \right)\, + \,\frac{{8(1\, + \,n)\alpha {\tilde {\overset{\smile}{A}}{}^{2}}{{x}^{2}}{{\Phi }^{{2n}}}}}{{1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}}}} \right] \\ + \frac{{2x{{\Phi }^{n}}}}{{1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}}}[n{{\Phi }^{{n - 1}}}(1 + \alpha \Phi ) \\ \, + \alpha ({{\Phi }^{n}} - \lambda )]\frac{{d\Phi }}{{dx}} + {\tilde {\overset{\smile}{A}}{}^{-2}}\frac{{{{d}^{2}}\Phi }}{{d{{x}^{2}}}} = 0. \\ \end{gathered} $$
((22))

The energy bounds for this case are

$$\begin{gathered} ({\text{i}})\,{{\Phi }^{n}} \geqslant 0,\quad ({\text{ii}})\,1 + \alpha \Phi \geqslant 0, \\ ({\text{iii}})\,1 - \alpha \Phi \geqslant 0,\quad ({\text{iv}})\,1 + 3\alpha \Phi \geqslant 0. \\ \end{gathered} $$
((23))

In this case, we solve Eqs. (20) and (21) and obtain Φ as well as \({v}\) as shown in Fig. 3. It is found that the behavior of both Φ and \({v}\) is same as obtained in case 1. Also, the energy conditions are satisfied in this case (Fig. 4).

Fig. 3.
figure 3

(Color online) Plots for Φ (a) and \({v}\) (b) versus x for λ = 0 (1), λ = 0.3 (2), and λ = 0.7 (3) with n = 1.5, α = 0.2.

Full size image
Fig. 4.
figure 4

(Color online) Plots for energy conditions in case 2 versus x for λ = 0 (1), λ = 0.3 (2), and λ = 0.7 (3) with n = 1.5, α = 0.2.

Full size image

3 CRACKING IN POLYTROPES

A relativistic stellar model is worthless if it is not stable against fluctuations in its matter variables, e.g., pressure and energy density. This small disturbance destroys the equilibrium state of these heavenly bodies leading to different fascinating phenomena such as collapse, expansion, cracking and overturning. Cracking and overturning of self-gravitating objects correspond to the appearance of radial forces with different signs within matter distribution [19]. When the radial force is directed inward in the interior of compact object and reverses its sign at some point (cracking point), cracking occurs while overturning is produced for reverse situation. This idea does not refer to the collapse or expansion of matter configuration but its tendency to split at a particular point within the fluid. We analyze the stability of cylindrical polytropes models through cracking. For this purpose, the force distribution function is defined as

$$R = \frac{{dP}}{{dr}} + \frac{{8\pi rP - r\Lambda }}{{1 - 8m}}(\rho + P).$$
((24))

We take out the system from equilibrium state by perturbing energy density as well as pressure via polytropic parameters in each case.

3.1 Case 1

Firstly, we perturb the polytropic constant, i.e., k → \(\tilde {k}\) = k + δk, consequently, the energy density and pressure are perturbed as

$$\tilde {P} = hP,\quad \tilde {\rho } = {{\rho }_{0}} + nhP,$$
((25))

where h = \(\frac{{\tilde {k}}}{k}\) and tilde indicates the perturbed quantity. Inserting these perturbed parameters in Eq. (24), we have

$$\begin{gathered} \tilde {R} = {{\rho }_{c}}\Phi _{0}^{n}\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} h\alpha (n + 1){{{\frac{{d{{\Phi }_{0}}}}{{d\xi }}}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}} \right. \\ \left. { + \frac{{8\pi \xi {{\rho }_{c}}(\alpha {{\Phi }_{0}} - \lambda )}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} \left( {1 - \frac{{8\alpha (n + 1){\tilde {v}}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}} \right)}}(1 - n\alpha + \alpha (n + 1)h{{\Phi }_{0}})} \right], \\ \end{gathered} $$

representing the disturbed state of the system. Using the relation \(\hat {\tilde {R}}\) = \(\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}{{4\pi \rho _{c}^{2}}}\tilde {R}\), the above equation turns out to be

$$\begin{gathered} \hat {\tilde {R}} = h\Phi _{0}^{n}\alpha (n + 1)\frac{{d{{\Phi }_{0}}}}{{d\xi }} + \frac{{2\xi \Phi _{0}^{n}(\alpha {{\Phi }_{0}} - \lambda )}}{{1 - \frac{{8\alpha (n + 1){\tilde {v}}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}}} \\ \, \times (1 - n\alpha + \alpha (n + 1)h{{\Phi }_{0}}). \\ \end{gathered} $$
((26))

Now expanding the function \(\hat {\tilde {R}}\) by using Taylor’s expansion, we obtain

$$\begin{gathered} \delta \hat {R} = \hat {\tilde {R}}(\xi ,1 + h,{v} + \delta {v}) \\ = \hat {\tilde {R}}(\xi ,1,{v}) + {{\left. {\frac{{\partial \hat {\tilde {R}}}}{{\partial h}}} \right|}_{{h = 1,{\tilde {v}} = {v}}}}\delta h + {{\left. {\frac{{\partial \hat {\tilde {R}}}}{{\partial {\tilde {v}}}}} \right|}_{{h = 1,{\tilde {v}} = {v}}}}\delta {v}{.} \\ \end{gathered} $$
((27))

Since the system is at equilibrium in the unperturbed state, so \(\hat {\tilde {R}}\)(ξ, 1, \({v}\)) = 0. From Eq. (26), we evaluate

$$\begin{gathered} {{\left. {\frac{{\partial \hat {\tilde {R}}}}{{\partial h}}} \right|}_{{h = 1,{\tilde {v}} = {v}}}} = \frac{{2\alpha \xi \Phi _{0}^{{1 + n}}}}{{1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}}}[(n + 1)(\alpha {{\Phi }_{0}} - \lambda ) \\ \, + (1 - n\alpha + (1 + n)\alpha {{\Phi }_{0}})] + \Phi _{0}^{n}\frac{{d{{\Phi }_{0}}}}{{d\xi }}m \\ \end{gathered} $$
((28))
$$\begin{gathered} {{\left. {\frac{{\partial \hat {\tilde {R}}}}{{\partial {\tilde {v}}}}} \right|}_{{h = 1,{\tilde {v}} = {v}}}} \\ = \frac{{16(1 + n)\alpha \xi \Phi _{0}^{n}( - \lambda + \alpha {{\Phi }_{0}})(1 - n\alpha + (1 + n)\alpha {{\Phi }_{0}})}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} {{{\left( {1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}} \right)}}^{2}}}}. \\ \end{gathered} $$
((29))

Moreover, the mass function in this case yields

$$\delta {v} = \frac{{\partial {v}}}{{\partial h}}\delta h = \frac{{n\alpha \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}{2}{{f}_{1}}(\xi )\delta h,$$
((30))

where f1(ξ) = \(\int_0^\xi {\hat {\xi }} \Phi _{0}^{{n + 1}}\)d\(\hat {\xi }\). Substituting Eqs. (28)–(30) in (27), the force function turns out to be

$$\begin{gathered} \delta {{{\hat {R}}}_{1}} = \delta h\Phi _{0}^{n}\left( {\frac{{2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} (1 + n)\alpha \xi {{\Phi }_{0}}( - \lambda + \alpha {{\Phi }_{0}})}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} - 8(1 + n)\alpha {v}}} + \frac{{2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} \alpha \xi {{\Phi }_{0}}(1 - n\alpha + (1 + n)\alpha {{\Phi }_{0}})}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} - 8(1 + n)\alpha {v}}}} \right. \\ \left. { + \frac{{8{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}^{2}}n(1 + n){{\alpha }^{2}}\xi {{f}_{1}}(\xi )( - \lambda + \alpha {{\Phi }_{0}})(1 - n\alpha + h(1 + n)\alpha {{\Phi }_{0}})}}{{{{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} - 8(1 + n)\alpha {v})}}^{2}}}} + \frac{{d{{\Phi }_{0}}}}{{d\xi }}} \right). \\ \end{gathered} $$

Using the variable ξ = x\({\tilde {\overset{\smile}{A}}}\), the above equation yields

$$\begin{gathered} \delta {{{\hat {R}}}_{1}} = \delta h\Phi _{0}^{n}\left( {\frac{{2(1 + n)x{\tilde {\overset{\smile}{A}}}\alpha {{\Phi }_{0}}(\alpha {{\Phi }_{0}} - \lambda )}}{{1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}}} + \frac{{2x{\tilde {\overset{\smile}{A}}}\alpha {{\Phi }_{0}}(1 - n\alpha + (1 + n)\alpha {{\Phi }_{0}})}}{{1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}}}} \right. \\ \left. { + \frac{{8n(1 + n)x{\tilde {\overset{\smile}{A}}}{{\alpha }^{2}}{{f}_{1}}(x)(\alpha {{\Phi }_{0}} - \lambda )(1 - n\alpha + h(1 + n)\alpha {{\Phi }_{0}})}}{{{{{\left( {1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}} \right)}}^{2}}}} + \frac{{\frac{{d{{\Phi }_{0}}}}{{dx}}}}{\tilde {\overset{\smile}{A}}}} \right). \\ \end{gathered} $$
((31))

In order to observe cracking, we plot this force distribution function by fixing polytropic index, the parameter α and varying cosmological constant as shown in left plot (Fig. 5). It is found that cylindrical polytropes remain stable for all choices of parameters n, α, and λ.

Fig. 5.
figure 5

(Color online) Plots for δ\({{\hat {R}}_{1}}\) (a) and δ\({{\hat {R}}_{2}}\) (b) versus x for λ = 0 (1), λ = 0.3 (2), and λ = 0.7 (3) with n = 1.5, α = 0.2.

Full size image

Secondly, we introduce the perturbations in polytropes via polytropic index (n → \(\tilde {n}\) = n + δn) yielding

$$\begin{gathered} \delta {{{\hat {R}}}_{2}} = \frac{{2x{\tilde {\overset{\smile}{A}}}{{\rho }_{c}}\Phi _{0}^{n}( - \lambda + \alpha \Phi _{0}^{{1 + n}})}}{{{{{\left( {1 - \frac{{8(1 + n)\alpha {v}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}} \right)}}^{2}}}} \\ \, \times \left( {\frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} - 8(1 + n)\alpha {v})((1 - n\alpha )\ln {{\Phi }_{0}} + \alpha {{\Phi }_{0}})}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}} \right. \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}\, + 4(1 + n)x{\tilde {\overset{\smile}{A}}{}^2}\alpha {{f}_{2}}(x)(1 - n\alpha + n\alpha {{\Phi }_{0}})} \right)\delta h, \\ \end{gathered} $$
((32))

where f2(x) = \(\int_0^x {\hat {x}} \)ΦnlnΦ0d\(\hat {x}\). This force function is plotted for different values of cosmological constant as shown in right plot (Fig. 5). It is observed that the compact object remains stable for all choices of parameters when n is perturbed.

3.2 Case 2

Firstly, we perturb the polytropic constant, i.e., k → \(\tilde {k}\) = k + δk, consequently, the energy density and pressure are perturbed as

$$\tilde {P} = hP,\quad \tilde {\rho } = \frac{{{{\rho }_{0}}}}{{{{{(1 + hk\rho _{0}^{{1/n}})}}^{n}}}},$$
((33))

where h = \(\frac{{\tilde {k}}}{k}\) and tilde indicates the perturbed quantity. Using the above equation, the perturbed energy density takes the form

$$\tilde {\rho } = \rho + nP(1 - h),$$

where we have used h = 1 + δh. Inserting these perturbed parameters in Eq. (24), we have

$$\begin{gathered} \tilde {R} = h\alpha {{\rho }_{c}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} (n + 1){{\Phi }^{n}}\frac{{d\Phi }}{{d\xi }} \\ \, + \frac{{8\pi \xi \alpha {{\rho }_{c}}{{\Phi }^{{n + 1}}} - 8\pi {{\rho }_{c}}\lambda }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} - 8\alpha (n + 1){v}}}\{ {{\rho }_{c}}{{\Phi }^{n}}[1 + \alpha \{ n + h(1 - n)\} \Phi ]\} , \\ \end{gathered} $$

representing the disturbed state of the system. Using the dimensionless variable \(\hat {\tilde {R}}\) = \(\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}{{4\pi \rho _{c}^{2}}}\tilde {R}\), the above equation turns out to be

$$\begin{gathered} \hat {\tilde {R}} = h{{\Phi }^{n}}\frac{{d\Phi }}{{d\xi }} + \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}{{4\pi {{\rho }_{c}}}}\left\{ {\frac{{8\pi \xi \alpha {{\rho }_{c}}{{\Phi }^{{n + 1}}} - 8\pi {{\rho }_{c}}\lambda }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} - 8\alpha (n + 1){v}}}} \right\} \\ \, \times ({{\rho }_{c}}{{\Phi }^{n}}[1 + \alpha \{ n + h(1 - n)\} \Phi ]). \\ \end{gathered} $$

Using Taylor’s expansion, we obtain

$$\begin{gathered} \delta {{{\hat {R}}}_{3}} = \left[ {\frac{{{{\Phi }^{n}}}}{\tilde {\overset{\smile}{A}}}\frac{{d\Phi }}{{dx}}} \right. \\ + \left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} \alpha (n + 1)\Phi - 4n\alpha {{f}_{3}}(x)\left( {\frac{{1 + \alpha \Phi }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} - 8\alpha (n + 1){v}}}} \right)} \right\} \\ \left. { \times \left( {\frac{{8\pi \alpha {{\rho }_{c}}x{\tilde {\overset{\smile}{A}}}{{\Phi }^{n}} - 8\pi {{\rho }_{c}}\lambda {\tilde {\overset{\smile}{A}}}x}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} - 8\alpha (n + 1){v}}}} \right)} \right]\delta h, \\ \end{gathered} $$
((34))

where f3(x) = \(\int_0^x {\hat {x}} \)Φn+ 1d\(\hat {x}\). In order to observe cracking, we plot this force distribution function by fixing polytropic index, the parameter a and varying cosmological constant as shown in first plot (Fig. 6). It is found that cylindrical polytropes remain stable for all choices of parameters n, α, and λ.

Fig. 6.
figure 6

(Color online) Plots for δ\({{\hat {R}}_{3}}\) (a, c) and δ\({{\hat {R}}_{4}}\) (b, d) versus x for λ = 0 (1), λ = 0.3 (2), and λ = 0.7 (3) with n = 1.5, α = 0.2.

Full size image

Secondly, we introduce the perturbations in polytropes via polytropic index (n → \(\tilde {n}\) = n + δn) yielding

$$\begin{gathered} \delta {{{\hat {R}}}_{4}} = \left[ {\left( {\frac{{{{\Phi }^{n}}\ln \Phi }}{\tilde {\overset{\smile}{A}}}\frac{{d\Phi }}{{dx}} + 2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} (1 + \alpha \Phi )\left\{ {\frac{{({\tilde {\overset{\smile}{A}}}x\alpha {{\Phi }^{{n + 1}}} - {\tilde {\overset{\smile}{A}}}x\lambda )(1 + \ln \Phi ){{\Phi }^{n}}}}{{{\tilde {\overset{\smile}{A}}} - 8\alpha (n + 1)\user1{v}}}} \right.} \right.} \right. \\ \left. {\left. {\left. { + \frac{{8\alpha ({\tilde {\overset{\smile}{A}}}x\alpha {{\Phi }^{{n + 1}}} - \lambda {\tilde {\overset{\smile}{A}}}x)}}{{{{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} - 8\alpha (n + 1)\user1{v})}}^{2}}}}} \right\}} \right) + 32\pi {{\rho }_{c}}{{\Phi }^{n}}(1 + \alpha \Phi )\left\{ {\frac{{({\tilde {\overset{\smile}{A}}}x\alpha {{\Phi }^{{n + 1}}} - \lambda {\tilde {\overset{\smile}{A}}}x)}}{{{{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} - 8\alpha (n + 1)\user1{v})}}^{2}}}}} \right\}{{f}_{4}}(x)} \right]\delta n, \\ \end{gathered} $$
((35))

where f4(x) = \(\int_0^x {\hat {x}} \)ΦnlnΦd\(\hat {x}\). This force function is plotted for different values of cosmological constant as shown in right plot of first row as well as second row of Fig. 6. It is observed that the polytropic model experiences cracking as we increase the value of λ, i.e., the presence of cosmological constant leads to unstable models when n is perturbed.

4 FINAL REMARKS

Self-gravitating compact objects belong to an important class of those astronomical bodies whose study become vital in recent era. In this paper, we have studied the general relativistic polytropic compact object with isotropic matter distribution for cylindrically symmetric spacetime in the presence of cosmological constant. We have taken Schwarzschild radial coordinate for our geometry and explored the field equations. Two non-linear ordinary differential equations describing the internal structure of compact object are formulated for two cases of polytropic EoS. Similar to the polytropic sphere, the polytropic cylinder is characterized by three dimensionless parameters, i.e., the polytropic index (n), the relativistic parameter (α) reflecting the role of relativistic effects in its structure and the cosmological constant manifesting the role of vacuum energy density. We have solved the structure equations numerically and found that mass function is monotonically increasing. In the presence of cosmological constant, it grows faster as compared to that in the absence of λ. The physical viability of resulting models is investigated through energy conditions and found that the developed models meet all the energy bounds for both zero and non-zero values of cosmological constant.

The stability analysis of stellar models is very important to check their physical viability. We have used the idea of cracking and take out system from equilibrium state through perturbations. We have perturbed the energy density and pressure of the system in two ways. We have perturbed polytropic constant as well as polytropic index and constructed the force distribution functions δ\({{\hat {R}}_{1}}\) and δ\({{\hat {R}}_{2}}\) describing total radial forces in case 1, respectively. We have found that the resulting models are stable towards perturbations for all choices of n, α, and λ while the models in case 2 are stable only for perturbed polytropic constant. For anisotropic spherical polytropes, cracking and overturning occur when the energy density as well as local anisotropy of the system are perturbed through polytropic constant and index [20] whereas the isotropic cylindrically symmetric fluid configuration with cosmological constant leads to stable models with perturbed polytropic constant in both cases.