1 INTRODUCTION

Now it is no doubt, that different astrophysical object have magnetic fields. There are observational confirmations of the magnetism of the Sun, planets, stars, galaxies and another celestial bodies [1]. It is also quite reasonable to assume the magnetic fields on the accretion discs surrounding black holes, neutron stars and white dwarfs [2]. The magnetic field can be divided to two different components [3, 4]. The first one is associated with the magnetic field which is connected with the turbulent motions and it has the typical length scale comparable with turbulent cells. The second component is the result of the averaging the magnetic field on such spatial lengths and it is has the regular structures which can be associated with the whole objects [5]. This component is much more interesting from the point of view of different physical processes and possible observational tests.

The generation of the large-scale magnetic fields is usually described by the dynamo mechanism [6]. It is based on joint action of the alpha-effect, which characterizes the structure of the turbulent motions, and the differential rotation (it is connected with the difference between the angular velocities for different parts of the object). They compete with the turbulent diffusion which can suppress the dynamo process. So, the dynamo is a threshold phenomenon which can take place only if the parameters which describe it are higher than some critical values.

The regular magnetic field evolution is described by the Steenbeck–Krause–Rädler equation [7]. It is quite difficult to be solved both analytically and numerically. So it is quite useful to take some approximations which can make possible the asymptotical analysis and facilitate the numerical solution. Usually there are different models which are connected with the specific features of the objects, especially their geometrical shape [8].

We are mostly interested in the magnetic field generation in the disc objects. They can be associated with the galaxies and accretion discs. Usually the no-\(z\) approximation is used for such objects [9, 10]. It takes into account that the magnetic field mainly lies in the disc plane. So, the vertical component of the magnetic field can be neglected, and the partial derivative of it can be taken from the solenoidality condition. Also, the \(z\)-derivatives of the plane components of the magnetic field can be replaced by the algebraic expressions. It is quite useful for lots of galaxy objects.

Unfortunately, if we describe the discs which large half-thickness, the no-\(z\) approximation will give some mistakes. So, it is necessary to use the models which take into account the vertical structure of the magnetic field [11–13]. Firstly, such model has been used for the outer rings of galaxies [14–16]. Also it can be taken for the objects, where the vertical length scales are comparable with the radial ones.

Here we give the estimates of the magnetic field evolution for these two different models of the magnetic field generation and compare the results. We also give the numerical solutions of the magnetic field for such cases.

2 BASIC EQUATIONS

The magnetic field in the disc can be presented as:

$$\vec {H} = \vec {B} + \vec {b};$$

where \(\vec {b}\) is the small-scale field and \(\vec {B} = \left\langle {\vec {H}} \right\rangle \) is the large-scale one (the averaging is connected with the turbulent cells). As for the velocity of the motions of the medium we can take a similar formulae:

$${\vec {v}} = \vec {V} + \vec {u};$$

where \(\vec {V} = \left\langle {{\vec {v}}} \right\rangle \) and \(\vec {u}\) is the small-scale velocity.

The regular magnetic field is described by the Steenbeck–Krause–Rädler equation [7]:

$$\frac{{\partial \vec {B}}}{{\partial t}} = \vec {\nabla } \times (\alpha \vec {B}) + \vec {\nabla } \times (V \times \vec {B}) + \eta {{\vec {\nabla }}^{2}}\vec {B};$$

where \(\eta \) is the turbulent diffusivity coefficient, and \(\alpha \) characterizes the vorticity of the small-scale motions:

$$\alpha = - \frac{\tau }{3}\left\langle {\vec {u} \cdot \vec {\nabla } \times \vec {u}} \right\rangle ;$$

where \(\tau \) is the typical timescale of the turbulent motions.

3 NO-z MODEL

If we use the no-\(z\) approximation for the magnetic field, the magnetic field can be described by the following model [17]:

$$\vec {B}(r,z,t) = \vec {B}(r,0,t)\cos\left( {\frac{{\pi z}}{{2h}}} \right).$$

The field is mainly connected with the radial component of the magnetic field \({{B}_{r}}\) and the angular one \({{B}_{\varphi }}\). The partial derivatives of the magnetic field can be changed by the following expressions [17]:

$$\frac{{{{\partial }^{2}}\vec {B}(r,z,t)}}{{\partial {{z}^{2}}}} = - \frac{{{{\pi }^{2}}\vec {B}(r,z,t)}}{{4{{h}^{2}}}}.$$

For alpha-effect it is possible to take the following model:

$$\alpha = \alpha (z) = {{\alpha }_{0}}\frac{z}{h},$$

where \({{\alpha }_{0}}\) is the typical value of the alpha-effect (it is often proportional to the angular velocity \(\Omega \) of the disc).

If we rewrite the equation for the components of the magnetic fields, we will obtain:

$$\frac{{\partial {{B}_{r}}}}{{\partial t}} = - {{R}_{\alpha }}{{B}_{\varphi }} - \frac{{{{\pi }^{2}}{{B}_{r}}}}{4} + {{\lambda }^{2}}\left( {\frac{{{{\partial }^{2}}{{B}_{r}}}}{{\partial {{r}^{2}}}} + \frac{{\partial {{B}_{r}}}}{{r\partial r}} - \frac{{{{B}_{r}}}}{{{{r}^{2}}}}} \right);$$
$$\frac{{\partial {{B}_{\varphi }}}}{{\partial t}} = - {{R}_{\omega }}{{B}_{r}} - \frac{{{{\pi }^{2}}{{B}_{\varphi }}}}{4} + {{\lambda }^{2}}\left( {\frac{{{{\partial }^{2}}{{B}_{\varphi }}}}{{\partial {{r}^{2}}}} + \frac{{\partial {{B}_{\varphi }}}}{{r\partial r}} - \frac{{{{B}_{\varphi }}}}{{{{r}^{2}}}}} \right).$$

Here we use the dimensionless units [9]. The distances are measured in units of \(R\) and the times are measured in units of \(\tfrac{{{{h}^{2}}}}{\eta }\). Here \(\lambda = \tfrac{h}{R}\) shows the dissipation in the disc plane, \({{R}_{\alpha }} = \tfrac{{{{\alpha }_{0}}\eta }}{h}\) describes the alpha-effect and \({{R}_{\omega }} = \tfrac{{{{h}^{2}}r\Omega {\kern 1pt} '(r)}}{\eta }\) describes the differential rotation.

To estimate the magnetic field evolution, it is useful to take the local approximation [18]. It is connected with the value \(\lambda = 0\) which corresponds to the zero dissipation in the disc plane:

$$\frac{{d{{B}_{r}}}}{{dt}} = - {{R}_{\alpha }}{{B}_{\varphi }} - \frac{{{{\pi }^{2}}{{B}_{r}}}}{4};$$
$$\frac{{d{{B}_{\varphi }}}}{{dt}} = - {{R}_{\omega }}{{B}_{r}} - \frac{{{{\pi }^{2}}{{B}_{\varphi }}}}{4}.$$

If we assume that the exponential growth according to the law:

$${{B}_{{r,\varphi }}} = {{B}_{{0r,\varphi }}}\exp(\gamma t);$$

we shall have the result:

$$\gamma = - \frac{{{{\pi }^{2}}}}{4} \pm \sqrt D ;$$

where \(D = \left| {{{R}_{\alpha }}{{R}_{\omega }}} \right|\) is the so-called dynamo number. We can see, that the growth rate \(\gamma \) can be positive only if:

$$D > {{D}_{{{\text{cr}}}}};$$

where \({{D}_{{{\text{cr}}}}}\) is the critical dynamo number:

$${{D}_{{{\text{cr}}}}} = \frac{{{{\pi }^{4}}}}{{16}} \approx 6.$$

It is also interesting to study the full model, solving the equations in partial derivatives. To do that, we can use the boundary conditions:

$${{\left. {{{B}_{r}}} \right|}_{{r = 0}}} = {{\left. {{{B}_{r}}} \right|}_{{r = 1}}} = {{\left. {{{B}_{\varphi }}} \right|}_{{r = 0}}} = {{\left. {{{B}_{\varphi }}} \right|}_{{r = 1}}} = 0;$$

and initial condition:

$${{\left. {{{B}_{r}}} \right|}_{{t = 0}}} = 0;$$
$${{\left. {{{B}_{\varphi }}} \right|}_{{t = 0}}} = {{B}_{0}}\sin(\pi r).$$

The approximate model shows that the azimuthal component of the magnetic field is proportional to the Bessel function [19]:

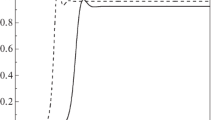
$${{B}_{\varphi }} \sim {{B}_{0}}{{J}_{1}}\left( {\frac{{5\pi r}}{4}} \right)\exp\left( {t( - \frac{{{{\pi }^{2}}}}{4} + \sqrt D + \frac{{{{\lambda }^{2}}{{\pi }^{2}}}}{{16}}} \right).$$

The results for different values of the dynamo numbers are given on Figs. 1, 2.

Fig. 1.
figure 1

No-\(z\) approximation: numerical calculations for the time evolution of the magnetic field. Different lines correspond to different values of the parameter \(D\): the solid line—\(D = 5\), the dotted line—\(D = 50\), the dashed line—\(D = 100\).

Full size image
Fig. 2.
figure 2

No-\(z\) approximation: comparison of the radial profiles of the azimuthal magnetic field obtained using analytical approximation and numerical calculation. The solid line corresponds to the approximate equation expressed in terms of the Bessel function; the dotted line—to the numerical calculation. \(D = 50\), \(t = 1\), \(\lambda = 0.025\), \({{B}_{0}} = 0.01\).

Full size image

4 rz-MODEL

If we take into account the vertical structure of the magnetic field, it is quite convenient to present the magnetic field using the following combination:

$$\vec {B} = B{{\vec {e}}_{\varphi }} + \vec {\nabla } \times (A{{\vec {e}}_{\varphi }}),$$

where \(B\) is the azimuthal component of the magnetic field and \(A\) is the azimuthal component of the vector potential of the magnetic field.

If we rewrite the Steenbeck–Krause–Rädler equations, we shall obtain [16, 20]:

$$\begin{gathered} \frac{{\partial A}}{{\partial t}} = {{R}_{\alpha }}zB + {{\lambda }^{2}}\left( {\frac{{{{\partial }^{2}}A}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}A}}{{\partial {{r}^{2}}}} + \frac{{\partial A}}{{r\partial r}} - \frac{A}{{{{r}^{2}}}}} \right), \\ \frac{{\partial B}}{{\partial t}} = - {{R}_{\omega }}A + {{\lambda }^{2}}\left( {\frac{{{{\partial }^{2}}B}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}B}}{{\partial {{r}^{2}}}} + \frac{{\partial B}}{{r\partial r}} - \frac{B}{{{{r}^{2}}}}} \right), \\ \end{gathered} $$
(1)

where \({{R}_{\omega }} < 0\) so \(D = - {{R}_{\alpha }}{{R}_{\omega }}\),

$${{R}_{\omega }}\frac{{\partial A}}{{\partial z}} = \frac{\pi }{{2\lambda }}{{R}_{\omega }}{{R}_{A}}(r){{T}_{A}}(t){{Z}_{B}}(z).$$

Expanding the function \(f(z) = z\cos\left( {\tfrac{{\pi z}}{{2\lambda }}} \right)\) in series of \({{g}_{n}} = \sin\left( {\tfrac{{\pi nz}}{{2\lambda }}} \right)\), in the first order, we obtain

$$f(z) \approx C\sin\left( {\frac{{\pi z}}{{2\lambda }}} \right),$$
(2)

where

$$C\, = \,\frac{1}{{2\lambda }}\int\limits_{ - 2\lambda }^{2\lambda } \,f(z)\sin\left( {\frac{{\pi z}}{{2\lambda }}} \right)dz\, = \,\frac{{2\lambda }}{{{{\pi }^{2}}}}\int\limits_{ - \pi }^\pi \,y\cos y\sin ydy\, = \,\frac{{ - \lambda }}{\pi }.$$

Then, we have the following system of equations:

$$\begin{gathered} {{R}_{A}}T_{A}^{'} \approx \left( { - \frac{\lambda }{\pi }{{R}_{\alpha }}} \right){{R}_{B}}{{T}_{B}} - \frac{{{{\pi }^{2}}}}{4}{{R}_{A}}{{T}_{A}} \\ + \;{{\lambda }^{2}}\left( {\frac{{{{d}^{2}}{{R}_{A}}}}{{d{{r}^{2}}}}{{T}_{A}} + \frac{1}{r}\frac{{d{{R}_{A}}}}{{dr}}{{T}_{A}} - \frac{1}{{{{r}^{2}}}}{{R}_{A}}{{T}_{A}}} \right), \\ {{R}_{B}}T_{B}^{'} \approx \left( { - \frac{\pi }{{2\lambda }}{{R}_{\omega }}} \right){{R}_{A}}{{T}_{A}} - \frac{{{{\pi }^{2}}}}{4}{{R}_{B}}{{T}_{B}} \\ + \;{{\lambda }^{2}}\left( {\frac{{{{d}^{2}}{{R}_{B}}}}{{d{{r}^{2}}}}{{T}_{B}} + \frac{1}{r}\frac{{d{{R}_{B}}}}{{dr}}{{T}_{B}} - \frac{1}{{{{r}^{2}}}}{{R}_{B}}{{T}_{B}}} \right). \\ \end{gathered} $$
(3)

The final expression for the approximation:

$$B \sim {{B}_{0}}{{J}_{1}}\left( {\frac{{5\pi r}}{4}} \right)\exp\left[ {t\left( { - \frac{{{{\pi }^{2}}}}{4} + \sqrt {\frac{D}{2}} + \frac{{{{\lambda }^{2}}{{\pi }^{2}}}}{{16}}} \right)} \right].$$
(4)

The results are shown on Figs. 3, 4. The numerical calculation shows that the real critical dynamo number is close to this value (\({{D}_{{{\text{cr}}}}} \approx 13\)).

Fig. 3.
figure 3

\(rz\)-model: numerical calculations for the time evolution of the magnetic field. Different lines correspond to different values of the parameter \(D\): the solid line—\(D = 5\), the dotted line—\(D = 50\), the dashed line—\(D = 100\).

Full size image
Fig. 4.
figure 4

\(rz\)-model: comparison of the radial profiles of the azimuthal magnetic field obtained using analytical approximation and numerical calculation. The solid line corresponds to the approximate equation expressed in terms of the Bessel function; the dotted line—to the numerical calculation. \(D = 50\), \(t = 1\), \(z = 0\), \(\lambda = 0.025\), \({{B}_{0}} = 0.01\).

Full size image

5 CONCLUSIONS

We have analyzed the magnetic field growth in the discs using two different models. The first one is connected with the no-\(z\) approximation which takes into account that the disc is quite thin. The \(rz\)-model describes also the vertical structure of the magnetic field, which is more complicated [20]. It was obtained that the critical dynamo number for this model is different, and the typical growth rate is different, too. Also it can be shown that the magnetic field can have the dypolar symmetry. This model can be used both for the galactic dynamo and for the dynamo in accretion discs.