1. INTRODUCTION

Sandwich structures occupy an important place in the manufacture of composite parts. They are present in practically all fields of application. These structures are fabricated by gluing or welding two thin skins on a lighter-weight core with weaker mechanical characteristics, which maintains spacing between the skins and transfers mechanical loads by shear from one skin to the other. Such a structure has very high strength/mass and stiffness/mass ratios in bending. There are various models of sandwich structures. The most recognized and widely used one is a sandwich structure with three homogeneous layers (core and face sheets). A growing trend is the introduction of advanced composite materials in the manufacture of sandwich plates. The incorporation of FG and sandwich structures in the construction sectors has increased considerably to overcome the problem of conventional structures and materials related to their low resistance to high temperatures [1–3]. We find in the literature sandwich plates with faces made of functionally graded material (FGM) and an isotropic core [4–6] or with homogeneous face sheets and an FG core [6–9].

Numerous studies of sandwich panels with FGM face sheets have been made with regard to their use in the design of engineered structures. Analysis of the thermal buckling response of sandwich plates with two FGM faces and a homogeneous central core was presented in [5] using the theory of sinusoidal shear strain. Natarajan and Ganapathi [10] analyzed the static bending and vibrational response of two types of FGM sandwich plates composed of homogeneous face sheets with an FGM core and FGM face sheets with a homogeneous hard core. The analysis was performed using a model of higher-order shear deformation theory (HSDT) and a QUAD-8 shear flexible element. A higher-order theory of shear deformation by thickness stretching was applied by Neves et al. [11] to analyze various behaviors of two FG sandwich models. An analytical model for the response analysis of FG sandwich structures with an isotropic middle layer was proposed by Thai et al. [12] with taking into account the boundary conditions. The dynamic and static behaviors of 2D FG and isotropic sandwich structures were studied by Nguyen et al. [13] for fully FG plates and two sandwich models, one with an FG core and the other with FGM skins. Akavci [14] presented a new theory of quasi-3D shear and normal deformation of plates with a hyperbolic warping function for various responses (stability, static, dynamic) using FG sandwich plates with an FG core or FG face sheets.

Thermomechanical behavior is due to the combination of mechanical and thermal loads simultaneously. This type of loading is common in structures used in the aircraft, ship building, marine industries, automotive and civil engineering, and it is necessary to examine their responses under such loading conditions. There are few works that study the bending behavior of graded sandwich structures under various types of load (mechanical/thermal). Zenkour and Alghamdi [15] investigated the flexural behavior of 2D graded sandwich structures with a ceramic core and FG skins subjected to thermomechanical loads. Wang and Shen [16] studied the nonlinear behavior (buckling, vibration, bending) of an FG sandwich subjected to thermal environment and resting on an elastic foundation.

Some authors are also interested in crack and fracture problems in the structures. For example, Hirannaiah et al. [17] investigated the thermomechanical dynamic response and stability of imperfect FG sandwich plates with geometric discontinuity and physical neutral surface. Kanu et al. [18] discussed the effect of fracture on the mechanical behavior of FG structures and materials. Based on the finite element method, Abbas and Razavi [19] examined the thermoelastic response of a fiber-reinforced anisotropic material by considering a crack problem. Petrova and Schmauder [20] modeled and studied the thermomechanical fracture of an FG structure taking into account multiple crack interaction. Abouelregal et al. [21] proposed a generalized heat equation for a temperature-dependent nonsimple thermoelastic cylinder with including the Caputo–Fabrizio fractional derivative. Based on an extension of the Fourier approach, the Atangana–Baleanu operator, and a novel nonlocal single core, Atta [22] investigated a thermoelastic medium with a spherical cavity within the framework of partial elastic thermal diffusion theory. Based on the Hermite–Ritz method and classical beam theory, Jena et al. [23] studied the effect of the presence of an elastic substrate on the vibrational characteristics of an imperfect FG beam, taking into account the small scale effect via bi-Helmholtz nonlocal elasticity. Many studies are devoted to the investigation of the thermal and thermomechanical response [24, 25].

The development of different theories to predict the behavior of FG structures has increased because of their wide use in the field of engineering structures. There are several plate theories developed to analyze FG materials. The classical model (classical plate theory (CPT)) is an extension of the Kirchhoff–Love hypothesis for slender and thin isotropic structures [26–28]. However, it cannot be applied for short and thick FG structures as it takes no account of the shear effect. The second model proposed by Reissner–Mindlin is called the first-order shear deformation theory (FSDT). The accuracy of its solutions depends heavily on the prediction of the best estimates for the shear correction factors to correct uniform shear stresses across the entire thickness of the structure [29–32]. The CPT and FSDT theories were shown to be inadequate for computing accurate solutions of FG plates. Another option is the refined higher-order shear deformation theory (HSDT) [33–40]. This model does not need any correction factors and can more accurately predict the behavior of moderate and thick FG plates. However, a larger number of unknown variables in the displacement field in HSDT leads to higher computational costs.

Here we develop a combined four-variable integral model with the aim to reduce the number of unknown variables and computational cost, to obtain accurate results, and to process several types of FG sandwich plates. The thermomechanical bending response of 2D FG sandwich structures is investigated analytically using the model.

The proposed combined exponential-cubic-sinusoidal integral shear deformation theory contains

only four variable functions, and therefore its governing equations are reduced compared to other similar solutions. The model takes into account the transverse shear deformation effect in a parabolic manner along the thickness direction and satisfies the stress-free boundary conditions on nonplate surfaces without any requirement for shear correction factors. The equations of stability are derived from the virtual work principle. Navier’s technique is applied to obtain the closed form. The numerical values of displacements and stresses obtained with the current theory are verified and compared with various existing solutions. Finally, the effects of certain parameters, such as the load type (transversal and thermal), volume fraction, thermal load, layer-to-thickness ratio and other dimensions, on the sandwich structure response are studied.

2. MATHEMATICAL MODELING

2.1. FG Sandwich Geometry

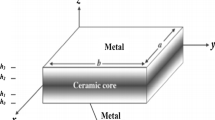
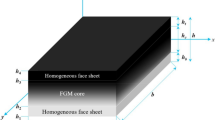
In this work, various uniform sandwich plates are considered. The geometry and dimensions are presented in Fig. 1. The plate is made of Ti-6A1-4V/ZrO2 (metal/ceramic) and contains three layers, which are either homogeneous or functionally graded, as presented in Sect. 5.

Fig. 1.
figure 1

Geometry of a three-layered FG sandwich plate.

Full size image

2.1.1. FG Face Sheets

The properties (E, ν and α) of the face sheet layers are calculated as [41, 42]:

$${E^{(1,3)}} = {E_{\rm{m}}} + ({E_{\rm{c}}} - {E_{\rm{m}}}){V^{(1,3)}},\;{\alpha ^{(1,3)}} = {\alpha _{\rm{m}}} + ({\alpha _{\rm{c}}} - {\alpha _{\rm{m}}}){V^{(1,3)}}$$
((1))

with

$${V^{(1)}} = {\left( {{{z - {h_0}} \over {{h_1} - {h_0}}}} \right)^{{p_{{\rm{fs}}}}}},\;z \in [{h_0},\;{h_1}],\;{V^{(3)}} = {\left( {{{z - {h_3}} \over {{h_2} - {h_3}}}} \right)^{{p_{{\rm{fs}}}}}},\;z \in [{h_2},\;{h_3}].$$
((2))

The subscripts c and m correspond to the used ceramic or metal material. The exponent pfs is the gradient index, and V(1,3) is the volume fraction of the 1st and 3rd layers.

2.1.2. FG Core

In contrast to the face sheet properties, the properties of the FG core vary as exponential function:

$${E^{(2)}} = {E_{\rm{m}}}\exp \left( {\ln \left( {{{{E_{\rm{c}}}} \over {{E_{\rm{m}}}}}} \right){V^{(2)}}} \right),\;{V^{(2)}} = {\left( {{{2|z|} \over {{h_2} - {h_1}}}} \right)^{{p_{{\rm{core}}}}}},\;z \in [{h_1},\;{h_2}],$$
((3))

where pcore is the core gradient index.

The thickness ratios of the three layers of FG sandwich plates are summarized in Table 1.

Table 1. Estimates of parameters h0, h1, h2 and h3 for different FG sandwich plates
Full size table

2.2. Kinematics

It is assumed that the straight section is perpendicular to the neutral axis, but loses its perpendicularity and flatness after deformation according to the conventional HSDT theories. The displacement field of HSDT contains five unknown variables and is given as follows [43]:

$$u(x,y,z) = {u_0}(x,y) - z{{\partial {w_0}(x,y)} \over {\partial x}} + f(z){\varphi _x}(x,y),$$
$$v(x,y,z) = {v_0}(x,y) - z{{\partial {w_0}(x,y)} \over {\partial y}} + f(z){\varphi _y}(x,y),$$
((4))
$$w(x,y,z) = {w_0}(x,y),$$

where u0, v0, w0, φx, φy are the five unknown displacement functions of the mid-plane of the plate.

Unlike the analytical theory used for thin structures which neglects the transverse shear effect as the classical theory and unlike the FSDT that assumes constant shear stresses across the thickness and the HSDT theories containing a larger number of variables, the developed model based on the section that loses its perpendicularity and flatness after deformation gives a parabolic variation of transverse shear stresses through the thickness, ensures their equality to zero on the upper and lower surfaces without requiring any correction factors, and contains only four unknown variables. By changing

$${\varphi _x} = {\zeta _1}\int {\theta (x,y){\rm{ d}}x} \;{\rm{and}}\;{\varphi _y} = {\zeta _2}\int {\theta (x,y){\rm{ d}}y} ,$$

the integral displacement fields can be simplified as follows:

$${u(x,y,z) = {u_0}}(x,y) - z{{\partial {w_0}} \over {\partial x}} + {\zeta _1}f(z)\int {\theta (x,y){\rm{d}}x} ,$$
$${v(x,y,z) = {v_0}}(x,y) - z{{\partial {w_0}} \over {\partial y}} + {\zeta _2}f(z)\int {\theta (x,y){\rm{d}}y,} $$
((5))
$$w(x,y,z) = {w_0}(x,y).$$

The constants ζ1 and ζ2 depend on the geometry.

In the current study, the shape functions f(z) take a combined form (exponential-cubic-trigonometric) and satisfy the stress-free boundary conditions, with

$$f(z) = z\left( {{e^{{{ - 2{z^2}} \mathord{\left/ {\vphantom {{ - 2{z^2}} {{h^2}}}} \right. \kern-\nulldelimiterspace} {{h^2}}}}} + \left( {1 - {4 \over 3}{{\left( {{z \over h}} \right)}^2}} \right) - {h \over {\pi z}}\sin \left( {{{\pi z} \over h}} \right)} \right),$$
((6))
$$g(z) = 1 + {e^{{{ - 2{z^2}} \mathord{\left/ {\vphantom {{ - 2{z^2}} {{h^2}}}} \right. \kern-\nulldelimiterspace} {{h^2}}}}} - {{4{z^2}{e^{{{ - 2{z^2}} \mathord{\left/ {\vphantom {{ - 2{z^2}} {{h^2}}}} \right. \kern-\nulldelimiterspace} {{h^2}}}}}} \over {{h^2}}} - 4{\left( {{z \over h}} \right)^2} - \cos \left( {{{\pi z} \over h}} \right).$$

By deriving the displacement field, we obtain the strain field as

((7))

where

((8))

and g(z) is given as follows:

$$g(z) = {{{\rm{d}}f(z)} \over {{\rm{d}}z}}.$$
((9))

The integrals appearing in the above expressions must be solved by a Navier-type solution and can be expressed as

$${\partial \over {\partial y}}\int {\theta {\rm{d}}x = \chi {{{\partial ^2}\theta } \over {\partial x\partial y}},\;{\partial \over {\partial x}}\int {\theta {\rm{d}}y = \psi {{{\partial ^2}\theta } \over {\partial x\partial y}},} } \;\int {\theta {\rm{d}}x = \chi {{\partial \theta } \over {\partial x}},\;\int {\theta {\rm{d}}y = \psi {{\partial \theta } \over {\partial y}}} } ,$$
((10))

with

$$\chi = - {1 \over {{\alpha ^2}}},\;\psi = - {1 \over {{\beta ^2}}},\;{\zeta _1} = {\alpha ^2},\;{\zeta _2} = {\beta ^2}.$$
((11))

2.3. Constitutive Equations

The stress–strain relationships can be expressed as

((12))

where εx, εy, γxy, γxz, γyz and σx, σy, τxy, τxz, τyz are the strain and stress components, respectively.

The elastic constants of the nth layer are

$$C_{11}^{(n)} = C_{22}^{(n)} = {{{E^{(n)}}(z)} \over {1 - {\nu ^{(n)}}^2}},\;{C_{12}} = {{\nu {E^{(n)}}(z)} \over {1 - {\nu ^{(n)}}^2}},\;C_{44}^{(n)} = C_{55}^{(n)} = C_{66}^{(n)} = {{{E^{(n)}}(z)} \over {2(1 + {\nu ^{(n)}})}}.$$
((13))

3. GOVERNING EQUATIONS

The virtual work principle [44–46] is applied for a static thermomechanical problem of an FG sandwich plate:

$$\delta U + \delta V = 0.$$
((14))

After replacing the virtual strain energy δU and the virtual work δV done by applied forces in the above equation, the principle of virtual work takes the following form:

$$\int\limits_A {[{N_x}\delta \varepsilon _x^0} + {N_y}\delta \varepsilon _y^0 + {N_{xy}}\delta \gamma _{xy}^0 + M_x^{\rm{b}}\delta k_x^{\rm{b}} + M_y^{\rm{b}}\delta k_y^{\rm{b}} + M_{xy}^{\rm{b}}\delta k_{xy}^{\rm{b}} + M_x^{\rm{s}}\delta k_x^{\rm{s}}$$
$$ + M_y^{\rm{s}}\delta k_y^{\rm{s}} + M_{xy}^{\rm{s}}\delta k_{xy}^{\rm{s}} + S_{yz}^{\rm{s}}\delta \gamma _{yz}^0 + S_{xz}^{\rm{s}}\delta \gamma _{xz}^0]{\rm{d}}\Omega - \int\limits_\Omega {qw{\rm{d}}\Omega } = 0,$$
((15))

where the stress resultants N, M and S are defined as

((16))
$$(S_{xz}^{\rm{s}},\;S_{yz}^{\rm{s}}) = \sum\limits_{n = 1}^3 {\int\limits_{{h_{n - 1}}}^{{h_n}} {{{({\tau _{xz}},\;{\tau _{yz}})}^{(n)}}g(z)\;{\rm{d}}z,} } $$

where the top and bottom z coordinates of the nth layer are hn and hn–1, and Ω is the top surface.

The static governing equations of the system can be obtained based on the virtual work cited in the above equation as

$$\delta {u_0}:{{\partial {N_x}} \over {\partial x}} + {{\partial {N_{xy}}} \over {\partial y}} = 0,$$
$$\delta {v_0}:{{\partial {N_{xy}}} \over {\partial x}} + {{\partial {N_y}} \over {\partial y}} = 0,$$
$$\delta {w_0}:{{{\partial ^2}M_x^{\rm{b}}} \over {\partial {x^2}}} + 2{{{\partial ^2}M_{xy}^{\rm{b}}} \over {\partial x\partial y}} + {{{\partial ^2}M_y^{\rm{b}}} \over {\partial {y^2}}} + q = 0,$$
((17))
$$\delta \theta : - {\zeta _1}M_x^{\rm{s}} - {\zeta _2}M_y^{\rm{s}} - (\chi {\zeta _1} + \psi {\zeta _2}){{{\partial ^2}M_{xy}^{\rm{s}}} \over {{\partial _x}{\partial _y}}} + \chi {\zeta _1}{{\partial S_{xz}^{\rm{s}}} \over {\partial {x^2}}} + \psi {\zeta _2}{{\partial S_{yz}^{\rm{s}}} \over {\partial y}} = 0.$$

The resultants N, M and S can be computed by substituting Eqs. (8), (9) and (13) into Eqs. (17) as follows:

((18))

where

$$N = {\{ {N_x},\;{N_y},\;{N_{xy}}\} ^t},\;{M^{\rm{b}}} = {\{ M_x^{\rm{b}},\;M_y^{\rm{b}},\;M_{xy}^{\rm{b}}\} ^t},$$
$${M^{\rm{s}}} = {\{ M_x^{\rm{s}},\;M_y^{\rm{s}},\;M_{xy}^{\rm{s}}\} ^t},\;{N^T} = {\{ N_x^T,\;N_y^T,\;0\} ^t},$$
$${M^{{\rm{b}}T}} = {\{ M_x^{{\rm{b}}T},\;M_y^{{\rm{b}}T},\;0\} ^t},\;{M^{{\rm{s}}T}} = {\{ M_x^{{\rm{s}}T},\;M_y^{{\rm{s}}T},\;0\} ^t},$$
((19))
$${\varepsilon ^{(0)}} = {\{ \varepsilon _x^{(0)}{\rm{, }}\varepsilon _y^{(0)}{\rm{, }}\gamma _{xy}^{(0)}\} ^T},\;{k^{\rm{b}}} = {\{ k_x^{\rm{b}}{\rm{, }}k_y^{\rm{b}}{\rm{, }}k_{xy}^{\rm{b}}\} ^T},\;{k^{\rm{s}}} = {\{ k_x^{\rm{s}}{\rm{, }}k_y^{\rm{s}}{\rm{,}}\;k_{xy}^{\rm{s}}\} ^T}$$

with

((20))

and

$$({A_{22}},\;{B_{22}},\;{D_{22}},\;B_{22}^{\rm{s}},\;D_{22}^{\rm{s}},\;H_{22}^{\rm{s}}) = ({A_{11}},\;{B_{11}},\;{D_{11}},\;B_{11}^{\rm{s}},\;D_{11}^{\rm{s}},\;H_{11}^{\rm{s}}),$$
$$A_{44}^{\rm{s}} = A_{55}^{\rm{s}} = \sum\limits_{n = 1}^3 {\int\limits_{{h_{n - 1}}}^{{h_n}} {{{{E^{(n)}}(z)} \over {2(1 + \nu )}}{{[g(z)]}^2}{\rm{d}}z} } .$$
((21))

The stress and moment resultants due to thermal loading (NxT, NyT, MxbT, MybT, MxsT and MysT) are defined by

((22))

The through-thickness variation of temperature T(x, y, z) [30–33] can be expressed in a generalized form as

$$T(x,y,z) = {T_1}(x,y) + {z \over h}{T_2}(x,y) + {{f(z)} \over h}{T_3}(x,y),$$
((23))

where T1, z/hT2, and f(z)/hT3 are the uniform, linear and nonlinear variation of temperature load through the thickness, with

((24))

4. CLOSED-FORM SOLUTIONS

The analytical solution used here to solve Eq. (17) is the Navier solution given by [47–51]:

((25))

with α = mπ/a and β = nπ/b.

The chosen solution ensures the boundary condition

$${N_x} = M_x^{\rm{b}} = M_x^{\rm{s}} = {v_0} = {w_0} = {{\partial \theta } \over {\partial y}} = 0\;{\rm{at}}\;x = 0,\;a,$$
((26))
$${N_y} = M_y^{\rm{b}} = M_y^{\rm{s}} = {u_0} = {w_0} = {{\partial \theta } \over {\partial x}} = 0\;{\rm{at}}\;x = 0,\;b.$$

The bi-sinusoidal load can be given as

$$q(x,\;y) = {q_0}\sin \left( {{{m\pi x} \over a}} \right)\sin \left( {{{n\pi y} \over b}} \right).$$
((27))

The final solution of the system can be obtained by substituting Eqs. (19), (20) and (22) into Eqs. (18) and the subsequent results into Eqs. (17):

$$[\Re ]\{ \Delta \} = \{ P\} ,$$
((28))

where \([\Re ],\) {Δ} and {P} are the stiffness matrix, displacement and force vectors given by

$${\Re _{11}} = {A_{11}}{\alpha ^2} + {A_{66}}{\beta ^2},$$
$${\Re _{12}} = \alpha \beta ({A_{12}} + {A_{66}}),$$
$${\Re _{13}} = ({B_{12}} + 2{B_{66}})\alpha {\beta ^2} + {B_{11}}{\beta ^3},$$
$${\Re _{14}} = - ({C_{11}}{\zeta _1} + {C_{12}}{\zeta _2})\alpha - {C_{66}}(\chi {\zeta _1} + \psi {\zeta _2})\alpha {\beta ^2},$$
$${\Re _{22}} = {A_{22}}{\beta ^2} + {A_{66}}{\alpha ^2},$$
$${\Re _{23}} = - {B_{22}}{\beta ^3} - (2{B_{66}} + {B_{12}}){\alpha ^2}\beta ,$$
((29))
$${\Re _{24}} = - ({C_{12}}{\zeta _1} + {C_{22}}{\zeta _2})\beta + {C_{66}}(\chi {\zeta _1} + \psi {\zeta _2}){\alpha ^2}\beta ,$$
$${\Re _{33}} = {D_{11}}{\alpha ^4} + {D_{22}}{\beta ^4} + 2(2{D_{66}} + {D_{12}}){\alpha ^2}{\beta ^2},$$
$${\Re _{34}} = 2{F_{66}}(\chi {\zeta _1} + \psi {\zeta _2}){\alpha ^2}{\beta ^2} + {\zeta _2}({F_{12}}{\alpha ^2} + {F_{22}}{\alpha ^2}) + {\zeta _1}({F_{11}}{\alpha ^2} + {F_{12}}{\beta ^2}),$$
$${\Re _{44}} = {H_{11}}\zeta _1^2 + {H_{22}}\zeta _2^2 + 2{H_{12}}{\zeta _1}{\zeta _2} + {H_{66}}{(\chi {\zeta _1} + \psi {\zeta _2})^2}{\alpha ^2}{\beta ^2} + A_{55}^s\zeta _1^2{\chi ^2}{\alpha ^2} + A_{44}^s\zeta _2^2{\psi ^2}{\beta ^2}$$

and

$$\{ {P_1}\} = \alpha ({A^T}{t_1} + {B^T}{t_2} + {}^a{B_T}{t_3}),$$
$$\{ {P_2}\} = \beta ({A^T}{t_1} + {B^T}{t_2} + {}^a{B_T}{t_3}),$$
((30))
$$\{ {P_3}\} = - {q_0} - h({\alpha ^2} + {\beta ^2})({B^T}{t_1} + {D^T}{t_2} + {}^a{D_T}{t_3}),$$
$$\{ {P_4}\} = - 2h({C^T}{t_1} + {F^T}{t_2} + {}^a{F_T}{t_3}),$$

in which

$$\{ {A^T},{B^T},{D^T}\} = \sum\limits_{n = 1}^3 {\int\limits_{{h_{n - 1}}}^{{h_n}} {{{{E^{(n)}}(z)} \over {1 - {\nu ^{(n)}}^2}}} } (1 + {\nu ^{(n)}}){\alpha ^{(n)}}\{ 1,\bar z,{\bar z^2}\} {\rm{d}}z,$$
$$\{ {}^a{B_T},{}^a{D_T}\} = \sum\limits_{n = 1}^3 {\int\limits_{{h_{n - 1}}}^{{h_n}} {{{{E^{(n)}}(z)} \over {1 - {\nu ^{(n)}}^2}}} } (1 + {\nu ^{(n)}})\bar f(z){\alpha ^{(n)}}\{ 1,\bar z\} {\rm{d}}z,$$
((31))
$$\{ {C^T},{F^T},{}^a{F_T}\} = \sum\limits_{n = 1}^3 {\int\limits_{{h_{n - 1}}}^{{h_n}} {{{{E^{(n)}}(z)} \over {1 - {\nu ^{(n)}}^2}}} } (1 + {\nu ^{(n)}}){\alpha ^{(n)}}\bar f{(z)^{(n)}}\{ 1,\bar z,\bar f(z)\} {\rm{d}}z,$$

where

$$\bar z = {z \over h},\;\bar f(z) = {{f(z)} \over h}.$$
((32))

5. NUMERICAL RESULTS

In this section, the materials used in the FG sandwich plate are ZrO2 ceramics: Young’s modulus Ec = 117.0 GPa, thermal expansion coefficient αc = 7.11 × 10–6/K and Poison’s ratio ν = 0.3, and Ti-6A1-4V metal: Young’s modulus Em = 66.2 GPa, thermal expansion coefficient αm = 10.3 × 10 –6/K and Poison’s ratio ν = 0.3. In order to verify the proposed model, various results are presented, discussed and compared with those found in the published literature. The dimensionless form of the deflection and stresses is given by

$$\bar w = {{{{10}^3}} \over {{{{q_0}{a^4}} \mathord{\left/ {\vphantom {{{q_0}{a^4}} {({E_0}{h^3}) + {{{{10}^3}{\alpha _0}{t_2}{a^2}} \mathord{\left/ {\vphantom {{{{10}^3}{\alpha _0}{t_2}{a^2}} h}} \right. \kern-\nulldelimiterspace} h}}}} \right. \kern-\nulldelimiterspace} {({E_0}{h^3}) + {{{{10}^3}{\alpha _0}{t_2}{a^2}} \mathord{\left/ {\vphantom {{{{10}^3}{\alpha _0}{t_2}{a^2}} h}} \right. \kern-\nulldelimiterspace} h}}}}}w\left( {{a \over 2},{b \over 2}} \right),$$
$${\bar \sigma _x} = {{10} \over {{{{{{q_0}{a^2}} \mathord{\left/ {\vphantom {{{q_0}{a^2}} {{h^2} + {{10{E_0}{\alpha _0}{t_2}{a^2}} \mathord{\left/ {\vphantom {{10{E_0}{\alpha _0}{t_2}{a^2}} h}} \right. \kern-\nulldelimiterspace} h}}}} \right. \kern-\nulldelimiterspace} {{h^2} + {{10{E_0}{\alpha _0}{t_2}{a^2}} \mathord{\left/ {\vphantom {{10{E_0}{\alpha _0}{t_2}{a^2}} h}} \right. \kern-\nulldelimiterspace} h}}}}^2}}}{\sigma _x}\left( {{a \over 2},{b \over 2},z} \right),$$
$${\bar \tau _{xy}} = {1 \over {{{{q_0}a} \mathord{\left/ {\vphantom {{{q_0}a} {h + {{{E_0}{\alpha _0}{t_2}a} \mathord{\left/ {\vphantom {{{E_0}{\alpha _0}{t_2}a} {(10h)}}} \right. \kern-\nulldelimiterspace} {(10h)}}}}} \right. \kern-\nulldelimiterspace} {h + {{{E_0}{\alpha _0}{t_2}a} \mathord{\left/ {\vphantom {{{E_0}{\alpha _0}{t_2}a} {(10h)}}} \right. \kern-\nulldelimiterspace} {(10h)}}}}}}{\tau _{xy}}(0,0,z),$$
((33))
$${\bar \tau _{xz}} = {1 \over {{{{q_0}a} \mathord{\left/ {\vphantom {{{q_0}a} {h + {{{E_0}{\alpha _0}{t_2}a} \mathord{\left/ {\vphantom {{{E_0}{\alpha _0}{t_2}a} {(10h)}}} \right. \kern-\nulldelimiterspace} {(10h)}}}}} \right. \kern-\nulldelimiterspace} {h + {{{E_0}{\alpha _0}{t_2}a} \mathord{\left/ {\vphantom {{{E_0}{\alpha _0}{t_2}a} {(10h)}}} \right. \kern-\nulldelimiterspace} {(10h)}}}}}}{\tau _{xz}}\left( {0,\;{b \over 2},\;z} \right),$$

where q0 = 100 Pa, a/h = 10, t1 = 0, and t2 = t3 = 100 K, E0 = 1 GPa, α0 = 10–6/K.

For the validation of the current model based on undetermined integral HSDT theory, the obtained results for the axial stress and central deflection are checked and compared with the existing model [15] based on sinusoidal and first-order shear deformation theory. The validation results in Table 2 are obtained for layer thickness ratios of 1-1-1 and 2-1-2 and the face sheet gradient indices 1, 2, 3, 4 and 5. It is clearly seen that the model results are in excellent agreement with the results obtained in [15] with the model of sinusoidal shear deformation plate theory. The difference between the FSDT theory (Reissner–Mindlin model) and the current model is due to the uniform shear stress distribution across the thickness assumed by the FSDT model. We can also conclude that the 1-1-1 sandwich plate gives smaller values of the central deflection because the core layer is most rigid and occupies a third of the total thickness of the structure.

Table 2. Validation of the dimensionless central transverse displacement and axial stresses of an FG sandwich plate with an isotropic core under thermomechanical loading
Full size table

Table 3 presents the results for the dimensionless central deflection and stresses along the x axis as functions of the layer thickness and the face sheet gradient index pfs. Three models considered are 1-1-1, 1-2-1, and 2-1-2. The results indicate that the lower value of nondimensional transverse displacement \(\bar w\) is observed for the 1-2-1 sandwich structure, because the core is rich in ceramics (pcore = 1) and its thickness is twice as much as that of the face sheet. It is also seen that the nondimensional axial stress is in inverse relation to the face sheet gradient index, because the structure becomes rich in metal while the central deflection increases. The most rigid sandwich plate is 1-1-1 with a smaller value of central deflection. A higher value of nondimensional axial stress is obtained for the 1-2-1 FG sandwich plate.

Table 3. Nondimensional central transverse displacement and axial stresses of a sandwich structure with three FG layers under thermomechanical loading
Full size table

Figure 2 plots the distribution of the dimensionless central transverse displacement along the x axis and the dimensionless axial, in-plane and shear stresses across the plate thickness. The plate has homogeneous upper and lower face sheets and an FGM core. Since the FGM core is symmetrical, the axial and in-plane stresses become zero at the center line, while the value of transverse shear stress \(\bar \tau \)xz is maximum at this point. It can be seen from the plotted curves that an increase in the core gradient index leads to an increase in the dimensionless axial \(\bar \sigma \)x, transverse \(\bar \tau \)xz and in-plane \(\bar \tau \)xy shear stresses in the intermediate core layer. It is remarkable that the results are almost the same for the homogeneous face sheets independently of the pcore values. The dimensionless deflection is slightly influenced by the core material index because the face sheets are more rigid with a thickness twice as much as that of the core (1-1-1).

Fig. 2.
figure 2

Effect of the core gradient index pcore on the flexural characteristics of a sandwich structure with identical layer thicknesses under thermomechanical loading, pfs = 0 (color online).

Full size image

Figure 3 plots the transverse central displacement and stress variations versus the face sheet gradient index of the FG sandwich structure subjected to both thermal and mechanical loading. The results indicate that the nondimensional central deflection increases with increasing face sheet gradient index pfs, because the face sheets become rich in metal. The transverse \(\bar \tau \)xz and in-plane \(\bar \tau \)xy shear stresses increase with increasing face sheet gradient index at the surface and at the center line, respectively. Contrariwise, the axial stress is in inverse relation to the gradient index pfs at the upper and lower faces of the FG structure. The present model gives a parabolic form of transverse shear stresses along the thickness direction. It can be concluded that the transverse \(\bar \tau \)xz, axial \(\bar \sigma \)x and in-plane \(\bar \tau \)xy stresses are symmetrical about the center line because the scheme of the structure is symmetrical.

Fig. 3.
figure 3

Effect of the face sheet gradient index pfs on the displacement \(\bar w\) and stresses \(\bar \sigma \)x, \(\bar \tau \)xy and \(\bar \tau \)xz of the 1-1-1 sandwich structure subjected to thermomechanical loading, pcore = 1 (color online).

Full size image

Figure 4 illustrates the effect of thermal load on the displacement \(\bar w\) and stress \(\bar \sigma \)x, \(\bar \tau \)xy and \(\bar \tau \)xz distribution along the transverse direction of the FG sandwich structure under thermomechanical loading. It can be seen from the graphic results that all stress curves show a nonlinear distribution along the z axis (material gradient direction). An increase in temperature t3 leads to an increase in the dimensionless values of axial \(\bar \sigma \)x and in-plane \(\bar \tau \)xy stresses. However, the distribution of the transverse shear stress \(\bar \tau \)xz is in direct relation to the nonlinear thermal parameter t3, indicating that the temperature rise has an impact on the flexural characteristics of the 1-1-1 FG sandwich plates. We can conclude again that the stresses are symmetrical because the material properties vary symmetrically about the center line.

Fig. 4.
figure 4

Influence of the nonlinear thermal parameter t3 on the displacement \(\bar w\) and stresses \(\bar \sigma \)x, \(\bar \tau \)xy and \(\bar \tau \)xz of the 1-1-1 sandwich structure under thermomechanical loading, q0 = 100, t2 = 100 (color online).

Full size image

6. CONCLUSIONS

The bending response of a uniform FG sandwich plate subjected to combined thermomechanical loading was investigated using a combined analytical exponential-cubic-sinusoidal integral HSDT theory. The flexural characteristics such as displacements and stresses were determined by solving governing differential equations derived from Hamilton’s principle. The validity of the proposed model was checked, and an excellent accuracy of the results and reduced computational time were achieved. The obtained results led to some important conclusions:

– The central deflection value is in direct relation to the face sheet gradient index because the index increases as the structure becomes rich in metal.

– The stresses along the thickness direction are nonlinear.

– The dimensionless axial and in-plane stresses are in inverse relation to the temperature parameter.

– An increase in the ceramic core thickness leads to a decrease in the deflection values because ceramics is more rigid.

Finally, it is necessary to account for the transverse shear effect, thermal load, material gradient variation and layer thickness in the sandwich structure calculation in order to correctly predict the structure dimensions in civil and mechanical engineering. To overcome the limitations of the current model, we can extend and improve the current formulation by including the thickness stretching effect in the calculation. The model can also be used for others materials, as shown in [51–59].