1. INTRODUCTION

In recent years, the enhanced quality properties of nanomaterials have caught the attention of numerous researchers. The significance of size effects becomes pronounced as structures reach very small dimensions, as evidenced by atomistic modeling and experimental studies. Consequently, the size effect plays a crucial role in shaping the mechanical behavior of micro- and nanostructures. There is a notable current trend within the scientific community towards exploring the mechanical behavior of structures using nanoscale elements. Given the substantial interest of a growing number of researchers in employing nanoscale beams and plates, it becomes imperative to acquire comprehensive knowledge about the size-dependent behavior of these diminutive elements. As a result, nonlocal continuum theories were developed to elucidate small-scale effects when investigating the mechanical characteristics of nanodevices. Eringen [1] proposed the first nonlocal theory, called nonlocal elasticity theory, which relates the stress state in a desired point not only to the strain of this particular point but also to the strain of all adjacent points. This theory was employed by an abundant range of authors, and it is worth demonstrating some of the previous works gaining nonlocal elasticity during their study on the mechanical response of nanobeams or nanoplates. Evaluations of the contact problem of functionally graded materials via various analytical and numerical methods were exposed by Yaylacı et al. [2–14]. Wang et al. [15] analyzed the wave dispersion characteristics of nanoplates within nonlocal elasticity. The studies conducted by Ebrahimi et al. [16–19] are notable for the dynamic analysis of nanomaterials via size effects. Eltaher et al. [20] described the vibrational properties of nanobeams in the framework of the finite element method and Euler–Bernoulli beam theory. The bending vibration analysis of nanobeams was performed by Ghadiri and Shafiei [21] using the differential quadrature method. A few years later, researchers figured out that nonlocal elasticity theory was not powerful enough to completely estimate the behavior of small structures [22]. In other words, the stiffness-hardening behavior of nanostructures was neglected in nonlocal elasticity and only the stiffness-softening effect was included. This stimulated the development of a new nonlocal theory, called nonlocal strain gradient theory, to rectify the mentioned deficiency. Li and Hu [23] presented nonlocal strain gradient theory to highlight size effects while studying the buckling response of nanobeams. Examination of the thermomechanical buckling properties of orthotropic nanoplates was performed by Farajpour et al. [24] in the framework of nonlocal strain gradient theory. The constitutive equation of classical continuum mechanics does not consider size effects [25–34]. This makes it difficult to accurately describe thermal and mechanical engineering properties of nanomaterials. Continuum mechanics was used to address this issue as an alternative to small-scale investigations and molecular dynamics simulations. Narendar and Gopalakrishnan [35] dealt with surface effects on the wave propagation behavior of a nanoplate. Impact and reaction of thermal stresses on various functionally graded materials were discussed by Tounsi et al. [36–45] within different computational theories.

Graphene sheets possess some advantageous over other small structures made of different materials, such as higher elastic potential [46] and larger thermal conductivity [47]. According to the above information, it is necessary to obtain detailed results on the mechanical response of these types of nanostructures. Thus, Murmu and Pradhan [48] tried to show the dynamic response of embedded monolayer graphene sheets employing Eringen’s nonlocal theory. Ansari and Rouhi [49] presented an atomistic finite element model for vibration and axial buckling analysis of monolayer graphene sheets. Size-dependent mechanical characteristics of propagating waves in graphene sheets were exactly studied by Arash et al. [50] within nonlocal elasticity. Furthermore, magnetomechanical vibration and stability analysis of monolayer graphene sheets rested on the viscoelastic foundation is the issue of another research performed by Ghorbanpour Arani et al. [51]. Xiao et al. [52] presented nonlocal strain gradient theory to examine the wave propagation behavior of viscoelastic monolayer graphene sheets.

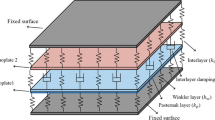
The literature survey reveals that wave propagation characteristics of a graphene sheet on the viscoelastic medium under thermal loading has not yet been investigated. Henceforward, it is found necessary to survey this problem here for the first time. The graphene sheet is considered to rest on the visco-Pasternak substrate including a linear constant (Winkler coefficient), a nonlinear constant (Pasternak coefficient) and a damping constant. Shear deformation is taken into account using a higher-order two-variable shear deformation plate theory. Moreover, nonlocal strain gradient theory is utilized to consider small-scale effects. Once the nonlocal differential equations are completely derived, they will be solved analytically using an exponential function. The influence of each parameter is precisely explained at the end of the paper.

2. THEORY AND FORMULATION

2.1. Kinematic Relations

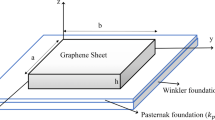
The present section is devoted to the description of the kinematic behavior of graphene sheets. The schematic of an embedded monolayer graphene sheet can be seen in Fig. 1. In order to consider shear deformation effects, a refined higher-order plate theory is utilized. Thus, displacement fields can be written as [16]

$$U(x,y,z) = - z{{\partial {w_{\rm{b}}}} \over {\partial x}} - f(z){{\partial {w_{\rm{s}}}} \over {\partial x}},$$
((1))
$$V(x,y,z) = - z{{\partial {w_{\rm{b}}}} \over {\partial y}} - f(z){{\partial {w_{\rm{s}}}} \over {\partial y}},$$
((2))
$$W(x,y,z) = {w_{\rm{b}}}(x,y) + {w_{\rm{s}}}(x,y),$$
((3))

where wb and ws are the bending and shear deflections in the thickness direction, respectively, and f(z) is the shape function that estimates shear stress and shear strain. In the present theory, a trigonometric function is used as follows:

$$f(z) = z - {h \over \pi }\sin \left( {{{\pi z} \over h}} \right).$$
((4))

Here, h is the plate thickness, and, for shear stress and shear strain estimation, the shape functions are often associated with the deformation of the material within an element. Now, nonzero strains can be written as follows:

((5))

where g(z) can be stated as

$$g(z) = 1 - {{{\rm{d}}f(z)} \over {{\rm{d}}z}}.$$
((6))
Fig. 1.
figure 1

Geometry of a monolayer graphene sheet rested on the viscoelastic medium.

Full size image

Moreover, Hamilton’s principle can be defined as

$$\int\limits_0^t {\delta (U - T + V){\rm{d}}t} = 0,$$
((7))

in which U is the strain energy, T is the kinetic energy, and V is the work done by external loads. The variation of strain energy can be calculated as

$$\delta U = \int\limits_V {{\sigma _{ij}}\delta {\varepsilon _{ij}}{\rm{d}}V} = \int\limits_V {({\sigma _x}\delta {\varepsilon _x} + {\sigma _y}\delta {\varepsilon _y} + {\sigma _{xy}}\delta {\gamma _{xy}} + {\sigma _{yz}}\delta {\gamma _{yz}} + {\sigma _{xz}}\delta {\gamma _{xz}}){\rm{d}}V.} $$
((8))

Substituting Eq. (5) in Eq. (8) gives

$$\delta U = \int\limits_0^a {\int\limits_0^b {\left( { - M_x^{\rm{b}}{{{\partial ^2}\delta {w_{\rm{b}}}} \over {\partial {x^2}}} - M_x^{\rm{s}}{{{\partial ^2}\delta {w_{\rm{s}}}} \over {\partial {x^2}}} - M_y^{\rm{b}}{{{\partial ^2}\delta {w_{\rm{b}}}} \over {\partial {y^2}}} - M_y^{\rm{s}}{{{\partial ^2}\delta {w_{\rm{s}}}} \over {\partial {y^2}}}} \right.} } $$
$$\left. { - 2M_{xy}^{\rm{b}}{{{\partial ^2}\delta {w_{\rm{b}}}} \over {\partial x\partial y}} - 2M_{xy}^{\rm{s}}{{{\partial ^2}\delta {w_{\rm{s}}}} \over {\partial x\partial y}} + {Q_{xz}}{{\partial \delta {w_{\rm{s}}}} \over {\partial x}} + {Q_{yz}}{{\partial \delta {w_{\rm{s}}}} \over {\partial y}}} \right){\rm{d}}y{\rm{d}}x.$$
((9))

In Eq. (9), the unknown parameters can be defined in the following form:

$$(M_i^{\rm{b}},M_i^{\rm{s}}) = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {(z,f){\sigma _i}{\rm{d}}z} ,\;i = (x,y,xy),\;{Q_i} = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {g{\sigma _i}{\rm{d}}z} ,\;i = (xz,yz).$$
((10))

Furthermore, the variation in work done by external forces can be shown as follows:

$$\delta V = \int\limits_0^a {\int\limits_0^b {\left( {N_x^0{{\partial ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial x}}{{\partial \delta ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial x}} + N_y^0{{\partial ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial y}}{{\partial \delta ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial y}} + 2\delta N_{xy}^0{{\partial ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial x}}{{\partial ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial y}}} \right.} } $$
$$\left. { - {k_{\rm{W}}}\delta ({w_{\rm{b}}} + {w_{\rm{s}}}) - {C_{\rm{d}}}\delta {{\partial ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial t}} + {k_{\rm{P}}}\left( {{{\partial ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial x}}{{\partial \delta ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial x}} + {{\partial ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial y}}{{\partial \delta ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial y}}} \right)} \right){\rm{d}}y{\rm{d}}x,$$
((11))

where Nx0, Ny0, Nxy0 are the in-plane applied loads, kW is the Winkler coefficient, kP is the Pasternak coefficient, and Cd is the damping coefficient. The variation in kinetic energy should be written as

$$\delta K = \int\limits_0^a {\int\limits_0^b {\left( {{I_0}{{\partial ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial t}}{{\partial \delta ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial t}} + {I_2}\left( {{{\partial {w_{\rm{b}}}} \over {\partial x\partial t}}{{\partial \delta {w_{\rm{b}}}} \over {\partial x\partial t}} + {{\partial {w_{\rm{b}}}} \over {\partial y\partial t}}{{\partial \delta {w_{\rm{b}}}} \over {\partial y\partial t}}} \right) + {K_2}\left( {{{\partial {w_{\rm{s}}}} \over {\partial x\partial t}}{{\partial \delta {w_{\rm{s}}}} \over {\partial x\partial t}} + {{\partial {w_{\rm{s}}}} \over {\partial y\partial t}}{{\partial \delta {w_{\rm{s}}}} \over {\partial y\partial t}}} \right)} \right.} } $$
$$\left. { + {J_2}\left( {{{\partial {w_{\rm{b}}}} \over {\partial x\partial t}}{{\partial \delta {w_{\rm{s}}}} \over {\partial x\partial t}} + {{\partial {w_{\rm{s}}}} \over {\partial x\partial t}}{{\partial \delta {w_{\rm{b}}}} \over {\partial x\partial t}} + {{\partial {w_{\rm{b}}}} \over {\partial y\partial t}}{{\partial \delta {w_{\rm{s}}}} \over {\partial y\partial t}} + {{\partial {w_{\rm{s}}}} \over {\partial y\partial t}}{{\partial \delta {w_{\rm{b}}}} \over {\partial y\partial t}}} \right)} \right){\rm{d}}y{\rm{d}}x,$$
((12))

in which

$$({I_0},{I_2},{J_2},{K_2}) = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {(1,\;{z^2},\;zf,\;{f^2})\rho {\rm{d}}z} .$$
((13))

By substituting Eqs. (9), (11), and (12) in Eq. (7) and setting the coefficients δwb and δws to zero, the Euler–Lagrange equations of graphene sheets can be rewritten as

$${{{\partial ^2}M_x^{\rm{b}}} \over {\partial {x^2}}} + 2{{{\partial ^2}M_{xy}^{\rm{b}}} \over {\partial x\partial y}} + {{{\partial ^2}M_y^{\rm{b}}} \over {\partial {y^2}}} + ({k_{\rm{P}}} - {N^T}){\nabla ^2}({w_{\rm{b}}} + {w_{\rm{s}}}) - {k_{\rm{W}}}({w_{\rm{b}}} + {w_{\rm{s}}})$$
$$ - {C_{\rm{d}}}{{\partial ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial t}} - {I_0}{{{\partial ^2}({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial {t^2}}} + {I_2}{\nabla ^2}\left( {{{{\partial ^2}{w_{\rm{b}}}} \over {\partial {t^2}}}} \right) + {J_2}{\nabla ^2}\left( {{{{\partial ^2}{w_{\rm{s}}}} \over {\partial {t^2}}}} \right) = 0,$$
((14))
$${{{\partial ^2}M_x^{\rm{s}}} \over {\partial {x^2}}} + 2{{{\partial ^2}M_{xy}^{\rm{s}}} \over {\partial x\partial y}} + {{{\partial ^2}M_y^{\rm{s}}} \over {\partial {y^2}}} + {{\partial {Q_{xz}}} \over {\partial x}} + {{\partial {Q_{yz}}} \over {\partial y}} + ({k_{\rm{P}}} - {N^T}){\nabla ^2}({w_{\rm{b}}} + {w_{\rm{s}}}) - {k_{\rm{W}}}({w_{\rm{b}}} + {w_{\rm{s}}})$$
$$ - {C_{\rm{d}}}{{\partial ({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial t}} - {I_0}{{{\partial ^2}({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial {t^2}}} + {J_2}{\nabla ^2}\left( {{{{\partial ^2}{w_{\rm{b}}}} \over {\partial {t^2}}}} \right) + {K_2}{\nabla ^2}\left( {{{{\partial ^2}{w_{\rm{s}}}} \over {\partial {t^2}}}} \right) = 0,$$
((15))

where Nx0 = Ny0 = NT, Nxy0 = 0, and thermal loading can be formulated as

$${N^T} = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {{E \over {1 - \nu }}\alpha \Delta T} {\rm{d}}z,$$
((16))

where E, ν, α, and ΔT are Young’s modulus, Poisson’s ratio, thermal expansion coefficient, and temperature gradient, respectively.

2.2. Nonlocal Strain Gradient Elasticity

According to nonlocal strain gradient theory, the stress field takes into account the effects of the nonlocal elastic stress field, along with the strain gradient stress field. Therefore, for elastic solids, the theory can be expressed as follows [18]:

$${\sigma _{ij}} = \sigma _{ij}^{(0)} - {{{\rm{d}}\sigma _{ij}^{(1)}} \over {{\rm{d}}x}}.$$
((17))

Here, stresses σxx(0) (classical stress) and σxx(1) (higher-order stress) correspond to strain εxx and strain gradient εxx,x, respectively, as follows:

((18))

where Cijkl is the elastic coefficient, e0a and e1a are introduced to take account of nonlocal effects, and l takes account of strain gradient effects. Once the nonlocal kernel functions α0(x, x′, e0a) and α1(x, x′, e1a) satisfy the developed conditions, the constitutive relation of nonlocal strain gradient theory can be expressed as

$$(1 - {({e_1}a)^2}{\nabla ^2})(1 - {({e_0}a)^2}{\nabla ^2}){\sigma _{ij}} = {C_{ijkl}}(1 - {({e_1}a)^2}{\nabla ^2}){\varepsilon _{kl}} - {C_{ijkl}}{l^2}(1 - {({e_0}a)^2}{\nabla ^2}){\nabla ^2}{\varepsilon _{kl}},$$
((19))

where \({\nabla ^2}\) is the Laplacian operator. If e1 = e0 = e, the general constitutive relation in Eq. (19) becomes

$$(1 - {(ea)^2}{\nabla ^2}){\sigma _{ij}} = {C_{ijkl}}(1 - {l^2}{\nabla ^2}){\varepsilon _{kl}}.$$
((20))

Finally, the simplified constitutive relation can be written as follows:

((21))

In the above equation,

$${Q_{11}} = {Q_{22}} = {E \over {1 - {\nu ^2}}},\;{Q_{12}} = \nu {Q_{11}},\;{Q_{44}} = {Q_{55}} = {Q_{66}} = {E \over {2(1 + \nu )}},$$
((22))

where μ = e0a and η = l. Substituting Eq. (10) in Eq. (21) and considering the Kelvin–Voigt viscoelastic model gives

((23))
((24))
((25))

In Eqs. (23) to (25), the cross-sectional rigidities can be formulated as follows:

((26))
$$A_{44}^{\rm{s}} = A_{55}^{\rm{s}} = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {{g^2}{E \over {2(1 + \nu )}}{\rm{d}}z} .$$
((27))

By substituting Eqs. (23) to (25) in Eqs. (14) and (15), the nonlocal governing equations of monolayer graphene sheets can be directly derived in terms of displacements as follows:

$$\left( {1 + g{\partial \over {\partial t}}} \right)(1 - {\eta ^2}{\nabla ^2})$$
$$ \times \left( { - {D_{11}}{{{\partial ^4}{w_{\rm{b}}}} \over {\partial {x^4}}} - 2({D_{12}} + 2{D_{66}}){{{\partial ^4}{w_{\rm{b}}}} \over {\partial {x^2}\partial {y^2}}} - {D_{22}}{{{\partial ^4}{w_{\rm{b}}}} \over {\partial {y^4}}} - D_{11}^s{{{\partial ^4}{w_{\rm{s}}}} \over {\partial {x^4}}} - 2(D_{12}^{\rm{s}} + 2D_{66}^{\rm{s}}){{{\partial ^4}{w_{\rm{s}}}} \over {\partial {x^2}\partial {y^2}}} - D_{22}^{\rm{s}}{{{\partial ^4}{w_{\rm{s}}}} \over {\partial {y^4}}}} \right)$$
$$ + (1 - {\mu ^2}{\nabla ^2})\left( { - {I_0}{{{\partial ^2}({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial {t^2}}}} \right. + {I_2}\left( {{{{\partial ^4}{w_{\rm{b}}}} \over {\partial {x^2}\partial {t^2}}} + {{{\partial ^4}{w_{\rm{b}}}} \over {\partial {y^2}\partial {t^2}}}} \right) + {J_2}\left( {{{{\partial ^4}{w_{\rm{s}}}} \over {\partial {x^2}\partial {t^2}}} + {{{\partial ^4}{w_{\rm{s}}}} \over {\partial {y^2}\partial {t^2}}}} \right)$$
$$\left. { + ({k_{\rm{P}}} - {N^T})\left( {{{{\partial ^2}({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial {x^2}}} + {{{\partial ^2}({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial {y^2}}}} \right) - \left( {{k_{\rm{W}}} + {\partial \over {\partial t}}{C_{\rm{d}}}} \right)({w_{\rm{b}}} + {w_{\rm{s}}})} \right) = 0,$$
((28))
$$\left( {1 + g{\partial \over {\partial t}}} \right)(1 - {\eta ^2}{\nabla ^2})\left( { - D_{11}^{\rm{s}}{{{\partial ^4}{w_{\rm{b}}}} \over {\partial {x^4}}} - 2(D_{12}^{\rm{s}} + 2D_{66}^{\rm{s}}){{{\partial ^4}{w_{\rm{b}}}} \over {\partial {x^2}\partial {y^2}}} - D_{22}^{\rm{s}}{{{\partial ^4}{w_{\rm{b}}}} \over {\partial {y^4}}}} \right.$$
$$\left. { - H_{11}^{\rm{s}}{{{\partial ^4}{w_{\rm{s}}}} \over {\partial {x^4}}} - 2(H_{12}^{\rm{s}} + 2H_{66}^{\rm{s}}){{{\partial ^4}{w_{\rm{s}}}} \over {\partial {x^2}\partial {y^2}}} - H_{22}^{\rm{s}}{{{\partial ^4}{w_{\rm{s}}}} \over {\partial {y^4}}} + A_{44}^{\rm{s}}{{{\partial ^2}{w_{\rm{s}}}} \over {\partial {x^2}}} + A_{55}^{\rm{s}}{{{\partial ^2}{w_{\rm{s}}}} \over {\partial {y^2}}}} \right)$$
$$ + (1 - {\mu ^2}{\nabla ^2})\left( { - {I_0}{{{\partial ^2}({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial {t^2}}} + {J_2}\left( {{{{\partial ^4}{w_{\rm{b}}}} \over {\partial {x^2}\partial {t^2}}} + {{{\partial ^4}{w_{\rm{b}}}} \over {\partial {y^2}\partial {t^2}}}} \right) + {K_2}\left( {{{{\partial ^4}{w_{\rm{s}}}} \over {\partial {x^2}\partial {t^2}}} + {{{\partial ^4}{w_{\rm{s}}}} \over {\partial {y^2}\partial {t^2}}}} \right)} \right.$$
$$\left. { + ({k_{\rm{P}}} - {N^T})\left( {{{{\partial ^2}({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial {x^2}}} + {{{\partial ^2}({w_{\rm{b}}} + {w_{\rm{s}}})} \over {\partial {y^2}}}} \right) - \left( {{k_{\rm{W}}} + {\partial \over {\partial t}}{C_{\rm{d}}}} \right)({w_{\rm{b}}} + {w_{\rm{s}}})} \right) = 0.$$
((29))

3. SOLUTION PROCEDURE

In this section, the derived nonlocal governing equations will be solved analytically. The displacement fields are assumed to be exponential and can be defined as follows:

((30))

where Wb and Ws are the unknown coefficients, β1 and β2 are the wave numbers of wave propagation along the x and y directions, respectively, and is the angular frequency of a wave. Substituting Eq. (30) in Eqs. (28) and (29) yields

$$({[K]_{2 \times 2}} - {\omega ^2}{[M]_{2 \times 2}})\{ \Delta \} = \{ 0\} ,$$
((31))

where the corresponding kij and mij are defined in Appendix A. The unknown parameters of Eq. (31) can be noted as follows:

$$\{ \Delta \} = {\{ {W_{\rm{b}}},\;{W_{\rm{s}}}\} ^T}.$$
((32))

In order to derive the angular frequency, the determinant of the left-hand side of Eq. (32) should be set to zero:

$$\left| {{{[K]}_{2 \times 2}} - {\omega ^2}{{[M]}_{2 \times 2}}} \right| = 0.$$
((33))

In the above equation, by setting β1 = β2 = β and solving the obtained equation for ω, the angular frequency of a wave in the embedded monolayer graphene sheet can be calculated.

4. RESULTS AND DISCUSSION

Here, the wave propagation responses of monolayer graphene sheets are supposed to be changed depending on various parameters. The thermomechanical properties of graphene sheets are E = 1 TPa, ν = 0.19, ρ = 2300 kg/m3, and α = 1.6 × 10–6 1/K. The thickness is presumed to be h = 0.34 nm. In the diagrams, wave frequencies are calculated by dividing the angular frequency of a wave by 2π (f = ω/(2π)). Figure 2 is plotted to describe the small-scale effects while changing the wave frequency. It is seen that at a lower nonlocal parameter the slope of the curve is steeper, which means that at the constant wave number the wave frequency grows easier when the nonlocal parameter is smaller. Indeed, this phenomenon suggests a softening impact which is attributed to the nonlocal parameter introduced by Eringen. Conversely, the length scale parameter operates in a manner that increases the wave frequency. To put it differently, elevating the length scale parameter evidently leads to higher wave frequencies. In essence, the length scale parameter accommodates the stiffness-hardening effect observed in nanoscale structures, which is not taken into account by the nonlocal parameter.

Fig. 2.
figure 2

Wave frequency versus wave number for various length scale parameters at μ = 1 (a) and 3 nm (b). kW = kP = 0, Cd = 0, g = 0, and ΔT = 0.

Full size image

The damping effect becomes more powerful with increasing structural damping coefficient. Even though the curve shape is similar for all nonzero structural damping coefficients, the wave number at which the wave frequency is maximum is not equal for various values of this coefficient. In other words, the peak of the curve moves to the left as the structural damping coefficient increases. On the other hand, Fig. 3 is plotted to magnify the combined influence of the small size and damping coefficient. From the given figures it is obvious that there are two size-dependent ways for increasing the wave frequency of graphene sheets. The first approach is to use smaller nonlocal parameters, and the second one is to choose higher values for the length scale parameter. Judging from the diagrams, the wave frequency shows a damping behavior. As a matter of fact, the wave frequency can be smaller whatever the damping coefficient value is. It should be also noted that, at the final damping coefficient which is about 12 in this case, the wave frequency reaches a unit value which is exactly zero. Now, we turn to the investigation of the effect of the Winkler and Pasternak coefficients by plotting the wave frequency versus damping coefficients in Fig. 4. It is clearly seen that both the Winkler (linear) and Pasternak (nonlinear) coefficients have enough potential to amplify wave frequency values. Moreover, the strongest change in the wave frequency response can be observed when the Winkler coefficient varies from kW = 0 to kW = 2.5. In other words, the initial shift in the Winkler or Pasternak coefficient from zero to their first nonzero value has the most significant impact on the wave frequency. Next we analyze the variation in the wave frequency by plotting the wave frequency against the Pasternak and Winkler coefficients at various temperature gradients in Fig. 5. It becomes apparent that higher temperature gradients result in lower wave frequencies. Furthermore, comparison shows that the Winkler foundation model yields higher wave frequency values.

Fig. 3.
figure 3

Wave frequency versus damping coefficient for different length scale parameters at μ = 1 (a) and 3 nm (b). kW = kP = 0, ΔT = 0, q = 0, and β = 0.15 × 109 m.

Full size image
Fig. 4.
figure 4

Wave frequency versus damping coefficient for different Winkler (kP = 0) (a) and Pasternak coefficients (kW = 0) (b). μ = η = 1 nm, g = 1, ΔT = 0, and β = 0.1 × 109 m.

Full size image
Fig. 5.
figure 5

Wave frequency versus Pasternak (a) and Winkler coefficients (b) for different temperature gradients. μ = η = 1 nm, Cd = 0, g = 1, and β = 0.3 × 109 m.

Full size image

5. CONCLUSIONS

The present work was devoted to the investigation of the thermally affected wave propagation behavior of monolayer isotropic graphene sheets embedded on the viscoelastic substrate. The small-scale effects were estimated by using nonlocal strain gradient theory. Final governing equations were derived within the Hamiltonian approach, and the obtained eigen-value equation was solved by means of an exponential function to determine wave frequency values. The performed calculations reveal that

(i) adding the length scale parameter increases wave frequency;

(ii) reducing the nonlocal parameter may result in the wave frequency increase;

(iii) amplifying the temperature gradient reduces wave frequency values.

These results may be useful in the design of thermoviscoelastic structural components of nanoelectromechanical systems (NEMS) operating in different environments, and the derived numerical results may serve as benchmarks for future damping analysis of structures containing graphene sheets.

APPENDIX A

In Eq. (31), kij and mij (i, j = 1, 2) are defined as follows:

$${k_{11}} = - \left( {1 + g{\partial \over {\partial t}}} \right)(1 + {\eta ^2}(\beta _1^2 + \beta _2^2))({D_{11}}\beta _1^4 + 2({D_{12}} + 2{D_{66}})\beta _1^2\beta _2^2 + {D_{22}}\beta _2^4)$$
$$ + (1 + {\mu ^2}(\beta _1^2 + \beta _2^2))(({N^T} - {k_{\rm{P}}})(\beta _1^2 + \beta _2^2) - {k_{\rm{W}}} - i\omega {C_{\rm{d}}}),$$
$${k_{12}} = - \left( {1 + g{\partial \over {\partial t}}} \right)(1 + {\eta ^2}(\beta _1^2 + \beta _2^2))(D_{11}^s\beta _1^4 + 2(D_{12}^s + 2D_{66}^s)\beta _1^2\beta _2^2 + D_{22}^s\beta _2^4)$$
$$ + (1 + {\mu ^2}(\beta _1^2 + \beta _2^2))(({N^T} - {k_{\rm{P}}})(\beta _1^2 + \beta _2^2) - {k_{\rm{W}}} - i\omega {C_{\rm{d}}}),$$
((A1))
$${k_{21}} = - \left( {1 + g{\partial \over {\partial t}}} \right)(1 + {\eta ^2}(\beta _1^2 + \beta _2^2))(D_{11}^s\beta _1^4 + 2(D_{12}^s + 2D_{66}^s)\beta _1^2\beta _2^2 + D_{22}^s\beta _2^4)$$
$$ + (1 + {\mu ^2}(\beta _1^2 + \beta _2^2))(({N^T} - {k_{\rm{P}}})(\beta _1^2 + \beta _2^2) - {k_{\rm{W}}} - i\omega {C_{\rm{d}}}),$$
$${k_{22}} = - \left( {1 + g{\partial \over {\partial t}}} \right)(1 + {\eta ^2}(\beta _1^2 + \beta _2^2))(H_{11}^{\rm{s}}\beta _1^4 + 2(H_{12}^{\rm{s}} + 2H_{66}^{\rm{s}})\beta _1^2\beta _2^2 + H_{22}^{\rm{s}}\beta _2^4$$
$$ + A_{55}^{\rm{s}}\beta _1^2 + A_{44}^{\rm{s}}\beta _2^2) + (1 + {\mu ^2}(\beta _1^2 + \beta _2^2))(({N^T} - {k_{\rm{P}}})(\beta _1^2 + \beta _2^2) - {k_{\rm{W}}} - i\omega {C_{\rm{d}}}),$$
$${m_{11}} = - (1 + {\mu ^2}(\beta _1^2 + \beta _2^2))({I_0} + {I_2}(\beta _1^2 + \beta _2^2)),$$
$${m_{12}} = {m_{21}} = - (1 + {\mu ^2}(\beta _1^2 + \beta _2^2))({I_0} + {J_2}(\beta _1^2 + \beta _2^2)),$$
((A2))
$${m_{22}} = - (1 + {\mu ^2}(\beta _1^2 + \beta _2^2))({I_0} + {K_2}(\beta _1^2 + \beta _2^2)).$$