INTRODUCTION

Finding the coefficients of diffusion permeability of membranes with the matrix that contains a fixed charge is an important part of characterization of new composite and hybrid ion-exchange materials obtained by modifying their properties with the use of various organic or inorganic dopants. In [1–3], we have theoretically explained and quantitatively described the asymmetry of diffusion permeability with a change in the orientation of a bilayer membrane in a measuring cell in different symmetric 1 : 1 electrolytes and the proposed model has been successfully verified using reverse-osmosis, bipolar, composite bilayer, and modified ion-exchange membranes with a polystyrene or a perfluorinated matrix and perfluorinated membranes MF-4SK surface-modified with polyaniline. In a study [4] devoted to layered sulfonated hydrophobic fluoroplastic 4SF (F-4SF) films modified with polyaniline, it was shown that the theoretical approach developed in [1] also makes it possible to explain the observed symmetry of diffusion permeability of the resulting composite membranes. A new model of an ion-exchange membrane charged linearly along thickness was developed in [5], and asymmetry of the diffusion permeability of such a membrane was observed. It was found that the “bilayer model” of ion-exchange membrane works well for surface-modified membranes, and the “linear model” is the most suitable in the case of a gradient distribution of the fixed-charge density of a bulk-modified membrane. We also developed a procedure for determining the main physicochemical parameters of bulk-modified ion-exchange membranes (diffusion coefficients and the equilibrium ion distribution in the membrane), which was successfully implemented using perfluorinated monolayer MF-4SK membranes, modified throughout the bulk with silica nanoparticles [6] and platinum nanoparticles-encapsulated halloysite nanotubes [7–9]. Recently, this technique has been used to describe the effects of asymmetry in the transport properties of hybrid nanocomposites based on MF-4SK having a halloysite-modified layer [10]. An additional tool that provides information on the physicochemical properties of the membrane is studying its diffusion permeability for nonsymmetric electrolytes. The corresponding theory and model were also developed and successfully verified in our recent work [11] using the cation-exchange membrane of MK-40 and various asymmetric electrolytes. Explicit analytical solutions of the corresponding boundary value problems are obtained in the case of 1 : 2 and 2 : 1 electrolytes, which made it possible to determine the conditions under which the concentration dependence curves of the integral diffusional permeability of membranes reach a maximum.

However, when studying the transport properties of membranes, the question arises as whether the experimental measurement of diffusion membrane permeability has been made in a correct manner. This question can be answered from the standpoint of thermodynamics of nonequilibrium processes [12] by applying the well-known Onsager approach, which linearly relates thermodynamic forces (independent parameters of the process) to the fluxes caused by these forces (dependent thermodynamic parameters).

FORMULATION OF THE PROBLEM

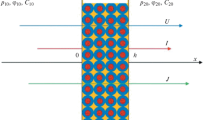
To study nonequilibrium isothermal processes, let us select as thermodynamic forces the pressure, electric potential, and concentration gradients \({{{{\Phi }_{1}} = \nabla p \approx \left( {{{p}_{{20}}} - {{p}_{{10}}}} \right)} \mathord{\left/ {\vphantom {{{{\Phi }_{1}} = \nabla p \approx \left( {{{p}_{{20}}} - {{p}_{{10}}}} \right)} h}} \right. \kern-0em} h}\), \({{{{\Phi }_{2}} = \nabla {\varphi\text{}} \approx \left( {{{{\varphi\text{}}}_{{20}}} - {{{\varphi\text{}}}_{{10}}}} \right)} \mathord{\left/ {\vphantom {{{{\Phi }_{2}} = \nabla {\varphi\text{}} \approx \left( {{{{\varphi\text{}}}_{{20}}} - {{{\varphi\text{}}}_{{10}}}} \right)} h}} \right. \kern-0em} h},\) and \({{{{\Phi }_{3}} = \nabla C \approx \left( {{{C}_{{20}}} - {{C}_{{10}}}} \right)} \mathord{\left/ {\vphantom {{{{\Phi }_{3}} = \nabla C \approx \left( {{{C}_{{20}}} - {{C}_{{10}}}} \right)} h}} \right. \kern-0em} h}.\) Here, h is the membrane thickness and subscripts 1 and 2 refer to the left and right sides of the membrane in the measuring cell filled with an electrolyte solution (Fig. 1).

Fig. 1.
figure 1

Schematic of the two-compartment cell for measuring diffusion flux: (1) membrane, (2) stirrer, (3) compartment with a feed electrolyte solution of a high concentration, (4) compartment with a solution of low concentration, (5) platinum electrodes, and (6) resistance meter.

Full size image

The thermodynamic forces can be independently and appropriately set in an experiment. As dependent thermodynamic parameters determined in the experiment, we choose the fluxes of solvent I1 = U, mobile charges (electric current density) I2 = I, and solute (electrolyte diffusion flux) I3 = J. Then the phenomenological transport equations can be written in one of the following forms:

$$\begin{gathered} {{I}_{i}} = - \sum\limits_{k = 1}^3 {{{L}_{{ik}}}{{\Phi }_{k}}} ,\,\,\,\,i = 1,2,3, \\ \left\{ \begin{gathered} U = - \left( {{{L}_{{11}}}\nabla p + {{L}_{{12}}}\nabla {\varphi\text{}} + {{L}_{{13}}}\nabla C} \right), \hfill \\ I = - \left( {{{L}_{{21}}}\nabla p + {{L}_{{22}}}\nabla {\varphi\text{}} + {{L}_{{23}}}\nabla C} \right), \hfill \\ J = - \left( {{{L}_{{31}}}\nabla p + {{L}_{{32}}}\nabla {\varphi\text{}} + {{L}_{{33}}}\nabla C} \right). \hfill \\ \end{gathered} \right. \\ \end{gathered} $$
((1))

Kinetic coefficients Lik can be determined using the aforementioned differential homogeneous model of the fine porous membrane or the heterogeneous cell model which takes into account the heterogeneous membrane structure [13]. In accordance with Onsager’s reciprocity theorem, the matrix of kinetic coefficients is symmetric: Lik = Lki. In this paper we will discuss only the calculation of the integral coefficient of membrane diffusion permeability, the “true” value of which, L33, can be found from the equation following from relations (1):

$${{L}_{{33}}} = - {{\left. {\frac{J}{{\nabla C}}} \right|}_{{\nabla p = 0,\nabla {\varphi\text{}} = 0}}}.$$
((2))

Equation (2) means that correct measurement of L33 is possible only in the absence of pressure and electric potential drops across the membrane and with a preset constant concentration difference \({{C}_{{20}}} - {{C}_{{10}}} \approx h\nabla C = {\text{const}}{\text{.}}\)

But how the diffusion flux through the membrane is actually measured and the integral coefficient of diffusion permeability is calculated? Many Russian membrane research groups use the technique that has been developed at the Physical Chemistry Department of the Kuban State University and is detailed, for example, in [14]. When this technique is applied, the electric potential difference is not monitored during the experiment, but the total current is absent in the system, meaning violation of the conditions under which Eq. (2) holds. Accordingly, the electric potential difference (diffusional in nature) due to the appearance of the electromigration component of the local electrolyte flow (with different ion diffusion coefficients) arises across the membrane. Formally, in accordance with the Onsager theory, in order to find the “pure” or “true” diffusion permeability (without electromigration), it is necessary to keep the electric potential difference across the membrane at zero. In this case, the diffusion current will present in the system and the “true” diffusion permeability of the ions will differ; i.e., there will be an additional problem: how to determine the membrane diffusion permeability for a given electrolyte. Thus, we deal with a historically formed ambiguity in the name of the coefficient of integral diffusion permeability. The fact is that by integrated diffusion transport in membrane electrochemistry, ion transport is traditionally meant at a given constant external difference of electrolyte concentration on the membrane system in the absence of electric current (see Eq. (5.27) in the monograph [15]). If this case is considered in terms of Onsager’s approach, it is easy to obtain from the system of Eqs. (1) the following expression for the integral diffusion permeability coefficient determined by the conventional method [14]:

$$P = {{\left. {\left( {{{L}_{{33}}} - \frac{{L_{{23}}^{2}}}{{{{L}_{{22}}}}}} \right)} \right|}_{{\nabla p = 0,I = 0}}}.$$
((3))

As can be seen from Eq. (3), the integral coefficient P also depends on the specific electrical conductivity of the membrane L22 and the cross kinetic coefficient L23, which determines the diffusion potential in the system. Since all direct kinetic coefficients must be positive, the experimentally measured values of P are always underestimated as compared to the “true” diffusion membrane permeability L33. It is another matter that due to the weakness of the cross kinetic effects, the magnitude of negative correction \( - \frac{{L_{{23}}^{2}}}{{{{L}_{{22}}}}}\) in Eq. (3) can be insignificant. Thus, following the logic, it would be more correct to call the coefficient P electrodiffusion permeability coefficient. Perhaps, it is for this reason that the diffusion permeability coefficient P, introduced about 30 years ago, was called integral. Below, we follow the recognized terminology in the statement of the problem, since the established and widely used method of conducting diffusion experiments [14] is based on it.

PROBLEM STATEMENT AND ANALYSIS OF SOLUTION

Using the Nernst–Planck transport equations, the quasi-stationary boundary-value problem of diffusion of an aqueous 1 : 1 electrolyte solution with an equivalent concentration C10 through a cation-exchange membrane into a compartment with a low equivalent concentration of the electrolyte solution C20 = C10/k (Fig. 2) was posed and solved in our previous study [7] for the case of electroneutrality, absence of current, and standard boundary conditions for the ion concentration jumps and electric potential differences at the x = 0 and x = h boundaries of the membrane. In that case, the following implicit formula was obtained for the integral diffusion permeability coefficient \(P = \frac{{{{J}_{ \pm }}h}}{{{{C}_{{10}}}}} \equiv \frac{{Jh}}{{{{C}_{{10}}}}}{\text{:}}\)

$$\begin{gathered} \frac{{2P}}{{\sigma {{{\bar {D}}}_{m}}}} = \sqrt {1 + \frac{4}{{{{\gamma }^{2}}{{\sigma }^{2}}}}{{{\left( {1 - \frac{P}{{\bar {D}}}\Delta } \right)}}^{2}}} \\ - \,\,\sqrt {1 + \frac{4}{{{{\gamma }^{2}}{{\sigma }^{2}}}}{{{\left( {\frac{1}{k} + \frac{P}{{\bar {D}}}\Delta } \right)}}^{2}}} \\ + \,\,\nu \ln \frac{{\sqrt {1 + \frac{4}{{{{\gamma }^{2}}{{\sigma }^{2}}}}{{{\left( {1 - \frac{P}{{\bar {D}}}\Delta } \right)}}^{2}}} - \nu }}{{\sqrt {1 + \frac{4}{{{{\gamma }^{2}}{{\sigma }^{2}}}}{{{\left( {\frac{1}{k} + \frac{P}{{\bar {D}}}\Delta } \right)}}^{2}}} - \nu }}, \\ \end{gathered} $$
((4))

where \({{\nu }_{0}} = \frac{{{{D}_{ - }}}}{{{{D}_{ + }}}}\), \({{\nu }_{m}} = \frac{{{{D}_{{m - }}}}}{{{{D}_{{m + }}}}}\), \(\nu = \frac{{{{\nu }_{m}} - 1}}{{{{\nu }_{m}} + 1}}\), \(\sigma = \frac{\rho }{{{{C}_{{10}}}}},\) and \(\Delta = \frac{\delta }{h}.\) Here \(k \equiv {{{{C}_{{10}}}} \mathord{\left/ {\vphantom {{{{C}_{{10}}}} {{{C}_{{20}}}}}} \right. \kern-0em} {{{C}_{{20}}}}} \gg 1\) is the dilution factor; \(J = {{J}_{ + }} = \,{{J}_{ - }}\) are the ion fluxes equal to one another because of the absence of current in the system; D+ and D− are the diffusion coefficients of ions in the electrolyte solution at infinite dilution; δ is the diffusion layer thickness (Fig. 2); and \(\bar {D} = \frac{{2{{D}_{ - }}{{D}_{ + }}}}{{{{D}_{ - }} + {{D}_{ + }}}}\) and \({{\bar {D}}_{m}} = \frac{{2{{D}_{{m - }}}{{D}_{m}}_{ + }}}{{{{D}_{{m - }}} + {{D}_{m}}_{ + }}}\) are the diffusion coefficients of electrolyte molecules in dilute solution and the bulk membrane, respectively. Note that the standard measurement of diffusion permeability [14] suggests that water is on the right to the membrane; so k = ∞ in that case.

Fig. 2.
figure 2

Scheme of electrolyte diffusion through the membrane.

Full size image

The case of an anion-exchange membrane is treated in a similar manner. The membrane is characterized by thickness h; coefficients of diffusion Dm+, Dm− and equilibrium distribution γ+, γ− of cations and anions, respectively, in the membrane matrix; and the concentration of fixed groups (exchange capacity) (−ρ), ρ > 0 that is constant over the membrane thickness. Recall that \({{\gamma }_{ \pm }} = \exp \left( {{{\Phi }_{ \pm }}} \right)\) reflects the degree of interaction of ions with the walls of membrane pores (\({{\Phi }_{ \pm }}\) denotes the dimensionless potentials of the interaction of ions with the walls of membrane pores in kBT units, where kB is the Boltzmann constant, and T is the absolute temperature). Let us introduce the following notation: \(\gamma = \sqrt {{{\gamma }_{ + }}{{\gamma }_{ - }}} ,\) the equilibrium distribution coefficient of the ion pair in the membrane and φ, the dimensionless electric potential in F/RT units (F is the Faraday constant, R is the gas constant). If we neglect both diffusion layers, δ = 0 (Δ = 0), then Eq. (4) becomes explicit:

$$\begin{gathered} P = \frac{{\sigma {{{\bar {D}}}_{m}}}}{2}\left( {\sqrt {1 + \frac{4}{{{{{\left( {\sigma \gamma } \right)}}^{2}}}}} - \sqrt {1 + \frac{4}{{{{{\left( {\sigma \gamma k} \right)}}^{2}}}}} } \right. \\ \left. { + \,\,\nu \ln \frac{{\sqrt {1 + \frac{4}{{{{{\left( {\sigma \gamma } \right)}}^{2}}}}} - \nu }}{{\sqrt {1 + \frac{4}{{{{{\left( {\sigma \gamma k} \right)}}^{2}}}}} - \nu }}} \right) \\ \end{gathered} $$
((5))

and is commonly used in preliminary calculations.

No expression for the transmembrane electric potential Δφ was given in [7]; meanwhile, as shown above, it is of decisive importance for the correct measurement of diffusion permeability. Therefore, here we fill this gap:

$$\begin{gathered} \Delta \varphi \equiv \varphi \left( {h + \delta } \right) = \nu \ln \frac{{\sqrt {1 + {{{\left( {{2 \mathord{\left/ {\vphantom {2 {\sigma \gamma }}} \right. \kern-0em} {\sigma \gamma }}} \right)}}^{2}}{{{\left( {\frac{1}{k} + \frac{P}{{\bar {D}}}\frac{\delta }{h}} \right)}}^{2}}} - \nu }}{{\sqrt {1 + {{{\left( {{2 \mathord{\left/ {\vphantom {2 {\sigma \gamma }}} \right. \kern-0em} {\sigma \gamma }}} \right)}}^{2}}{{{\left( {1 - \frac{P}{{\bar {D}}}\frac{\delta }{h}} \right)}}^{2}}} - \nu }} \\ + \,\,\ln \frac{{\sqrt {1 + {{{\left( {{2 \mathord{\left/ {\vphantom {2 {\sigma \gamma }}} \right. \kern-0em} {\sigma \gamma }}} \right)}}^{2}}{{{\left( {\frac{1}{k} + \frac{P}{{\bar {D}}}\frac{\delta }{h}} \right)}}^{2}}} + 1}}{{\sqrt {1 + {{{\left( {{2 \mathord{\left/ {\vphantom {2 {\sigma \gamma }}} \right. \kern-0em} {\sigma \gamma }}} \right)}}^{2}}{{{\left( {1 - \frac{P}{{\bar {D}}}\frac{\delta }{h}} \right)}}^{2}}} + 1}} \\ - \,\,\frac{{2{{\nu }_{0}}}}{{\left( {1 + {{\nu }_{0}}} \right)}}\ln \frac{{\frac{1}{k} + \frac{P}{{\bar {D}}}\frac{\delta }{h}}}{{1 - \frac{P}{{\bar {D}}}\frac{\delta }{h}}} - \frac{{{{\nu }_{0}} - 1}}{{{{\nu }_{0}} + 1}}\ln k. \\ \end{gathered} $$
((6))

Table 1 lists values of the integral coefficient P calculated by exact equation (4) for k = 100 and C0 = 0.4 mol-eq/L; they show a very weak dependence of the diffusion permeability of the MK-40 membrane for the NaCl electrolyte on the thickness of the diffusion layer over a very wide range of its variation from 0 to 1000 μm (membrane thickness is h = 520 μm, the experimental value of permeability is P = 13.0 μm2/s, and the value calculated according to approximate equation (5) is Р = 13.61 μm2/s). As can be seen from Table 1, the spread of diffusion permeability values does not exceed 2%, which completely fits the experimental error (5%). It follows from the structure of Eq. (4) that for large values of k (which is actually the case in experiments), diffusion permeability P depends little on this parameter. Table 2 shows values for the function P(k) at C0 = 0.1 mol/L, as calculated using exact Eq. (4) and approximate Eq. (5). By Eq. (4), we obtain P = 9.759 μm2/s for infinitely large values of k (i.e., when there is pure water in the compartment to the right of the membrane).

Table 1.   Dependence of the coefficient P on the diffusion layer thickness according to Eq. (4)
Full size table
Table 2.   Dependence of the coefficient P on the dilution k of NaCl solution on the right side of the MK-40 membrane (C0 = 0.1 mol-eq/L), δ = 100 μm
Full size table

Table 2 shows that at k ≥ 100, the results obtained using each of the equations individually are almost indistinguishable and differ by less than 0.5%. Actually, under the experimental conditions, the parameter k is a weakly increasing function of time; i.e., the system under consideration is quasi-stationary. No electric current flows through the system, since the electric circuit is not closed; therefore, the condition J+ = J− is supposed to be fulfilled in the mathematical formulation.

The electric field (diffusion membrane potential) arises as a consequence of the primary reason, setting a constant concentration difference in the system and the difference in mobility between the ions. This electric field varies little with time. In any case, over the characteristic time of establishment of quasi-equilibrium in the system, the change in the electric potential did not exceed 5% in the experiments described below. Therefore, it can be stated that the electric field is controllable. From Eq. (6), in particular, it follows that the electric potential drop at k → ∞ very slowly (logarithmically) tends to infinity as well because of the presence of the last term. If the diffusion coefficients of the ions in the diffusion layer are equal, the last term disappears and the potential drop remains finite at k → ∞. If δ → 0, it follows from Eq. (6) that

$$\begin{gathered} {{\left. {\Delta \varphi } \right|}_{{\delta = 0}}} = \varphi \left( {h + 0} \right) = \nu \ln \frac{{\sqrt {1 + {4 \mathord{\left/ {\vphantom {4 {{{{\left( {k\sigma \gamma } \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {k\sigma \gamma } \right)}}^{2}}}}} - \nu }}{{\sqrt {1 + {4 \mathord{\left/ {\vphantom {4 {{{{\left( {\sigma \gamma } \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {\sigma \gamma } \right)}}^{2}}}}} - \nu }} \\ + \,\,\ln \frac{{\sqrt {1 + {4 \mathord{\left/ {\vphantom {4 {{{{\left( {k\sigma \gamma } \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {k\sigma \gamma } \right)}}^{2}}}}} + 1}}{{\sqrt {1 + {4 \mathord{\left/ {\vphantom {4 {{{{\left( {\sigma \gamma } \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {\sigma \gamma } \right)}}^{2}}}}} + 1}} + \ln k, \\ \end{gathered} $$
((7))

and the last logarithm also becomes infinite at k → ∞. The value of the electric potential on the right-hand side of the interface x = h is given by the expression:

$$\begin{gathered} \varphi \left( {h + 0} \right) = \ln \frac{{1 + \sqrt {1 + {{{\left( {{2 \mathord{\left/ {\vphantom {2 {\sigma \gamma }}} \right. \kern-0em} {\sigma \gamma }}} \right)}}^{2}}{{{\left( {\frac{1}{k} + \frac{P}{{\bar {D}}}\frac{\delta }{h}} \right)}}^{2}}} }}{{1 + \sqrt {1 + {{{\left( {{2 \mathord{\left/ {\vphantom {2 {\sigma \gamma }}} \right. \kern-0em} {\sigma \gamma }}} \right)}}^{2}}{{{\left( {1 - \frac{P}{{\bar {D}}}\frac{\delta }{h}} \right)}}^{2}}} }} \\ + \,\,\frac{{2{{\nu }_{0}}}}{{1 + {{\nu }_{0}}}}\ln \left( {1 - \frac{P}{{\bar {D}}}\frac{\delta }{h}} \right) \\ + \,\,\nu \ln \frac{{\sqrt {1 + {{{\left( {{2 \mathord{\left/ {\vphantom {2 {\sigma \gamma }}} \right. \kern-0em} {\sigma \gamma }}} \right)}}^{2}}{{{\left( {\frac{1}{k} + \frac{P}{{\bar {D}}}\frac{\delta }{h}} \right)}}^{2}}} - \nu }}{{\sqrt {1 + {{{\left( {{2 \mathord{\left/ {\vphantom {2 {\sigma \gamma }}} \right. \kern-0em} {\sigma \gamma }}} \right)}}^{2}}{{{\left( {1 - \frac{P}{{\bar {D}}}\frac{\delta }{h}} \right)}}^{2}}} - \nu }} - \ln \left( {\frac{1}{k} + \frac{P}{{\bar {D}}}\frac{\delta }{h}} \right). \\ \end{gathered} $$
((8))

As can be seen, it remains finite if the diffusion layers are present, δ ≠ 0, even in the case of k → ∞. In the region of the right-hand diffusion layer, the electric potential varies continuously from the value given by Eq. (8) to that defined by Eq. (6) at the outer boundary of this layer. In the absence of diffusion layers, δ = 0, expression (8) coincides with Eq. (7). Thus, the existence of the infinite potential drop is associated exclusively with the assumption of zero concentration of the electrolyte solution on the right-hand side of the membrane. In a practical situation, this concentration is never zero, and the transmembrane electric potential at the initial point of time may be large, but finite. When calculating the integral coefficient P, we did not use the overall electric potential difference in the system, so the purely mathematical effect associated with the infinite discontinuity almost does not affect the analysis of the integral coefficient of diffusion permeability.

EXPERIMENT AND COMPARISON WITH THEORY

Figure 3 shows the fitting of the theoretical curve according to Eq. (5) to experimental values of coefficient P determined by the standard method [14] in the diffusion cell (Fig. 1) using distilled water in the right compartment. In this case, numerical values of the parameters \({{\bar {D}}_{m}}\) = 1.544 μm2/s, νm = 2.696, and γ = 0.115 were found using the deviation minimization procedure written for Mathematica 11 [11]. The measured exchange capacity of the MK-40 membrane turned out to be ρ = 1.52 mol-eq/L, ν0 = 1.504. Note that the NaCl diffusion coefficient of \(\bar {D}\) = 1622 μm2/s in the dilute solution is three orders of magnitude higher than its value in the MK-40 membrane. As can be seen in Fig. 3, there is good agreement between the theory and the experiment. The same values of these parameters were used to calculate the electrical potential difference on the membrane system.

Fig. 3.
figure 3

Experimental (symbols) and theoretical (curve calculated by Eq. (5)) values of the integral diffusion permeability, as a function of electrolyte concentration in the left compartment (the right compartment contains water).

Full size image

In addition, we measured the electrical potential that arises on both sides of the MK-40 membrane during the diffusion of the NaCl electrolyte from the half-cell with a higher concentration into the half-cell with a lower concentration (Fig. 1). After measuring the diffusion permeability of the membrane, the magnetic stirrers were removed, silver/silver chloride electrodes were immersed into the cell instead of them, and the potential difference was determined. The results of the experiment are summarized in Table 3, where k ≡ C10/C20 is the dilution factor of the solution in the right compartment. The error in measuring the potential was no more than 5%. Each column of the table contains three or two numbers: the first number is the measured potential difference, the second was calculated from approximate Eq. (7) without taking into account the diffusion layers, and the third was calculated by exact Eq. (6) with δ = 200 μm. In particular, at electrolyte concentrations of C10 = 0.1 and 0.2 mol-eq/L to the left and C20 = 0.001 and 0.002 mol-eq/L to the right of the membrane, the measured potentials and those calculated by simplified Eq. (7) differ by approximately 5–10%. However, the discrepancy is much higher for other concentrations and increases with the growth in concentration. Note that only one measurement of the potential corresponding to a concentration of C10 = 1 mol-eq/L was made at k = 1000. It is also noteworthy that there are opposite trends in the variation of the theoretical (Eq. (7)) and the experimental dependence of the diffusion potential difference across the membrane. The measured potential is positive, weakly fluctuates, and increases with the electrolyte concentration, thereby suggesting a significant experimental error due to the non-steady-state character of the change in the potential. The potential calculated using both exact Eq. (6) and approximate Eq. (7) shows a steady fall with increasing concentration in the left compartment and growth with an increase in the dilution factor k. The latter effect is explained above and takes place for both the theoretical and experimental relationships. The allowance for the diffusion layer in the considered case of the MK-40 membrane and a sodium chloride solution leads to a decrease in the potential difference. The calculations revealed that the electric potential difference on the membrane changes its sign with a decrease in dilution factor k (which can happen with time in a long-term experiment); i.e., the electromigration component of the flux changes the direction. In our case, for example, for a concentration of 1 mol-eq/L in the left compartment, this occurs at k = 21 (as calculated by approximate Eq. (7)) or somewhat earlier at k = 23 (calculation using exact Eq. (6)).

Table 3.   Values of diffusion potential difference Δφ, mV, as measured/calculated by approximate Eq. (7)/calculated by exact Eq. (6) for δ = 200 μm
Full size table

CONCLUSIONS

The issue of correctness of the experimental determination of the integral coefficient of diffusion permeability of an ion-exchange membrane has been addressed. The Onsager approach based on the thermodynamics of nonequilibrium processes, the well-known fine porous membrane model, and experimental data on the diffusion of sodium chloride through the cation-exchange membrane MK-40 into water and into a more dilute solution have been used for this purpose. It has been revealed that the true values of the integral coefficient of diffusion permeability, determined through the Onsager kinetic coefficients, are larger than the values experimentally measured by the conventional method. It has been shown that the true value of the integral diffusion permeability of a membrane can be experimentally found only under the conditions of absence of pressure and electric potential differences and a constant drop in the electrolyte concentration.