INTRODUCTION

The study of equilibrium orientations of a system of bodies moving in a central Newtonian field on a circular orbit is of considerable practical interest as applied to the development of composite schemes of gravitational orientation systems for satellites that can sustain operations in their orbit for a long time without consumption of power and (or) working mass. The operation principle of gravitational orientation systems is based on the fact that, in a central Newtonian field, a satellite with different principal central moments of inertia moving in a circular orbit has 24 equilibrium positions, of which four are stable (see [1–3]). The dynamics of composite schemes of various types for gravitational orientation systems was considered in detail in [4].

This paper is devoted to the investigation of stationary motions of a system of two bodies (satellite–stabilizer) connected by a spherical hinge that move in a circular orbit. The scheme for a gravitational orientation system according to which the second body (stabilizer), which plays the role of a damping device, is hinge-connected to the satellite was proposed by D.E. Okhotsimskii in 1956. The general ideas of Okhotsimskii’s gravitational system of satellite orientation with use of a composite satellite–stabilizer scheme having triaxial suspension were described in [4, 5]. The theory of the dynamics of a satellite–stabilizer gravitational system was studied in a series of works (see [6–13]). In [6], general nonlinear equations of motion of a satellite–stabilizer system were derived, necessary and sufficient conditions for the asymptotic stability of the trivial solution of the system in the case of a circular orbit were obtained, the amplitudes of eccentricity oscillations of the two-body system caused by the ellipticity of the orbit were determined, and transient processes were studied. The dynamics of a satellite–stabilizer system with a simplified one-degree-of-freedom suspension scheme was analyzed in [7]. The dynamics of two bodies connected by a hinge that move in the plane of a circular orbit was investigated in [8–11]. The problem of finding all spatial equilibrium positions of two bodies connected by a spherical hinge moving in a circular orbit has not been solved in the general form. For a system of two axisymmetric bodies, the problem of spatial equilibria was studied in detail in [12]. In [14], a broad class of equilibrium spatial solutions for a system of two bodies connected by a spherical hinge moving in a circular orbit was obtained by applying a combination of computer and linear algebra methods under certain constraints imposed on the parameters of the problem.

In this investigation, primary attention is given to equilibrium orientations of a two-body system in the special cases when one of the principal axes of inertia of both the first and second body coincides with the normal to the orbital plane, the radius vector, or the tangent to the orbit. To determine the equilibrium orientations of the two-body system, the set of stationary algebraic equations of motion is decomposed into nine subsystems. The system of algebraic equations is solved by applying algorithms for constructing Gröbner bases. The equilibrium positions are determined by numerically analyzing the roots of the algebraic equations from the constructed Gröbner basis.

1. EQUATIONS OF MOTION

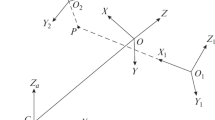
We consider the problem of two bodies connected by a spherical hinge that move in a circular orbit. To write the equations of motion of the satellite–stabilizer system, we introduce the following right-handed coordinate systems (Fig. 1): \(OXYZ\) is an orbital coordinate system, the \(OZ\) axis is directed along the radius vector connecting the Earth’s center of mass C and the center of mass O of the two-body system, the \(OX\) axis is directed along the linear velocity vector of the center of mass \(O\), and the \(OY\) axis coincides with the normal to the orbital plane. The axes of coordinate systems \({{O}_{1}}{{x}_{1}}{{y}_{1}}{{z}_{1}}\) and \({{O}_{2}}{{x}_{2}}{{y}_{2}}{{z}_{2}}\) are directed along the principal central axes of inertia of the satellite and the stabilizer, respectively (Fig. 1). The orientation of the coordinate system \({{O}_{i}}{{x}_{i}}{{y}_{i}}{{z}_{i}}\) with respect to the orbital coordinate system is determined by the aircraft angles \({{\alpha }_{i}}\) (pitch), \({{\beta }_{i}}\) (yaw), and \({{\gamma }_{i}}\) (roll) (see [4]) in the form

$$\begin{gathered} a_{{11}}^{{(i)}} = \cos {{\alpha }_{i}}\cos {{\beta }_{i}}, \\ a_{{12}}^{{(i)}} = \sin {{\alpha }_{i}}\sin {{\gamma }_{i}} - \cos {{\alpha }_{i}}\sin {{\beta }_{i}}\cos {{\gamma }_{i}}, \\ a_{{13}}^{{(i)}} = \sin {{\alpha }_{i}}\cos {{\gamma }_{i}} + \cos {{\alpha }_{i}}\sin {{\beta }_{i}}\sin {{\gamma }_{i}}, \\ \end{gathered} $$
$$\begin{gathered} a_{{21}}^{{(i)}} = \sin {{\beta }_{i}}, \\ a_{{22}}^{{(i)}} = \cos {{\beta }_{i}}\cos {{\gamma }_{i}}, \\ a_{{23}}^{{(i)}} = - \cos {{\beta }_{i}}\sin {{\gamma }_{i}}, \\ \end{gathered} $$
(1.1)
$$\begin{gathered} a_{{31}}^{{(i)}} = - \sin {{\alpha }_{i}}\cos {{\beta }_{i}}, \\ a_{{32}}^{{(i)}} = \cos {{\alpha }_{i}}\sin {{\gamma }_{i}} + \sin {{\alpha }_{i}}\sin {{\beta }_{i}}\cos {{\gamma }_{i}}, \\ a_{{33}}^{{(i)}} = \cos {{\alpha }_{i}}\cos {{\gamma }_{i}} - \sin {{\alpha }_{i}}\sin {{\beta }_{i}}\sin {{\gamma }_{i}}. \\ \end{gathered} $$
Fig. 1.
figure 1

Basic coordinate systems.

Full size image

The indices \(i = 1\) and \(i = 2\) refer to body 1 (satellite) and body 2 (stabilizer), respectively. Consider the case when the hinge is located at the intersection point of the \(O{{x}_{1}}\) and \(O{{x}_{2}}\) axes. Then the coordinates of the spherical hinge in the coordinate systems connected to body 1 and body 2 are \(({{a}_{1}},\;0,\;0)\) and \(({{a}_{2}},\;0,\;0)\). In this case, the kinetic energy and the force function of the two-body system are expressed as follows (see [4]):

$$\begin{gathered} T = \frac{1}{2}[{{A}_{1}}p_{1}^{2} + ({{B}_{1}} + Ma_{1}^{2})q_{1}^{2} + ({{C}_{1}} + Ma_{1}^{2})r_{1}^{2}] + \frac{1}{2}[{{A}_{2}}p_{2}^{2} + ({{B}_{2}} + Ma_{2}^{2})q_{2}^{2} + ({{C}_{2}} + Ma_{2}^{2})r_{2}^{2}] \\ - \;M{{a}_{1}}{{a}_{2}}[({{r}_{1}}{{a}_{{12}}} - {{q}_{1}}{{a}_{{13}}})({{r}_{2}}{{b}_{{12}}} - {{q}_{2}}{{b}_{{13}}}) + ({{r}_{1}}{{a}_{{22}}} - {{q}_{1}}{{a}_{{23}}})({{r}_{2}}{{b}_{{22}}} - {{q}_{2}}{{b}_{{23}}}) + ({{r}_{1}}{{a}_{{32}}} - {{q}_{1}}{{a}_{{33}}})({{r}_{2}}{{b}_{{32}}} - {{q}_{2}}{{b}_{{33}}})], \\ \end{gathered} $$
(1.2)
$$\begin{gathered} U = \frac{3}{2}\omega _{0}^{2}[({{C}_{1}} - {{A}_{1}} + Ma_{1}^{2})a_{{31}}^{2} + ({{C}_{1}} - {{B}_{1}})a_{{32}}^{2}] + \frac{3}{2}\omega _{0}^{2}[({{C}_{2}} - {{A}_{2}} + Ma_{2}^{2})b_{{31}}^{2} + ({{C}_{2}} - {{B}_{2}})b_{{32}}^{2}] \\ \, + M{{a}_{1}}{{a}_{2}}\omega _{0}^{2}({{a}_{{11}}}{{b}_{{11}}} + {{a}_{{21}}}{{b}_{{21}}} - 2{{a}_{{31}}}{{b}_{{31}}}). \\ \end{gathered} $$
(1.3)

By using the kinetic energy expression (1.2) and expression (1.3) for the force function, which determines the action of the Earth’s gravitational field on the two-body system, and applying symbolical differentiation in Maple [16], the equations of motion of this system can be written as Lagrange equations of the second kind in the form

$$\begin{gathered} {{A}_{1}}{{{\dot {p}}}_{1}} + ({{C}_{1}} - {{B}_{1}}){{q}_{1}}{{r}_{1}} = 3\omega _{0}^{2}({{C}_{1}} - {{B}_{1}})a_{{32}}^{{}}a_{{33}}^{{}}, \\ ({{B}_{1}} + Ma_{1}^{2}){{{\dot {q}}}_{1}} - M{{a}_{1}}{{a}_{2}}({{a}_{{13}}}{{b}_{{13}}} + {{a}_{{23}}}{{b}_{{23}}} + {{a}_{{33}}}{{b}_{{33}}}){{{\dot {q}}}_{2}} + M{{a}_{1}}{{a}_{2}}({{a}_{{13}}}{{b}_{{12}}} + {{a}_{{23}}}{{b}_{{22}}} + {{a}_{{33}}}{{b}_{{32}}}){{{\dot {r}}}_{2}} \\ + \;M{{a}_{1}}{{a}_{2}}\{ {{a}_{{13}}}[{{r}_{2}}({{p}_{2}}{{b}_{{13}}} - {{r}_{2}}{{b}_{{11}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{11}}} - {{p}_{2}}{{b}_{{12}}})] + {{a}_{{23}}}[{{r}_{2}}({{p}_{2}}{{b}_{{23}}} - {{r}_{2}}{{b}_{{21}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{21}}} - {{p}_{2}}{{b}_{{22}}})] \\ + \;{{a}_{{33}}}[{{r}_{2}}({{p}_{2}}{{b}_{{33}}} - {{r}_{2}}{{b}_{{31}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{31}}} - {{p}_{2}}{{b}_{{32}}})]\} + [({{A}_{1}} - {{C}_{1}}) - Ma_{1}^{2})]{{r}_{1}}{{p}_{1}} = 3\omega _{0}^{2}({{A}_{1}} - {{C}_{1}}){{a}_{{33}}}{{a}_{{31}}} \\ \, - M{{a}_{1}}\omega _{0}^{2}[{{a}_{2}}({{a}_{{13}}}{{b}_{{11}}} + {{a}_{{23}}}{{b}_{{21}}} + {{a}_{{33}}}{{b}_{{31}}}) + 3{{a}_{{33}}}({{a}_{1}}{{a}_{{31}}} - {{a}_{2}}{{b}_{{31}}})], \\ \end{gathered} $$
$$\begin{gathered} ({{C}_{1}} + Ma_{1}^{2}){{{\dot {r}}}_{1}} + M{{a}_{1}}{{a}_{2}}[({{a}_{{12}}}{{b}_{{13}}} + {{a}_{{22}}}{{b}_{{23}}} + {{a}_{{32}}}{{b}_{{33}}}){{{\dot {q}}}_{2}} - ({{a}_{{12}}}{{b}_{{12}}} + {{a}_{{22}}}{{b}_{{22}}} + {{a}_{{32}}}{{b}_{{32}}})]{{{\dot {r}}}_{2}} \\ - \;M{{a}_{1}}{{a}_{2}}\{ {{a}_{{12}}}[{{r}_{2}}({{p}_{2}}{{b}_{{13}}} - {{r}_{2}}{{b}_{{11}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{11}}} - {{p}_{2}}{{b}_{{12}}})] + {{a}_{{22}}}[{{r}_{2}}({{p}_{2}}{{b}_{{23}}} - {{r}_{2}}{{b}_{{21}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{21}}} - {{p}_{2}}{{b}_{{22}}})] \\ + \;{{a}_{{32}}}[{{r}_{2}}({{p}_{2}}{{b}_{{33}}} - {{r}_{2}}{{b}_{{31}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{31}}} - {{p}_{2}}{{b}_{{32}}})]\} + [({{B}_{1}} - {{A}_{1}}) + Ma_{1}^{2})]{{p}_{1}}{{q}_{1}} = 3\omega _{0}^{2}({{B}_{1}} - {{A}_{1}}){{a}_{{31}}}{{a}_{{32}}} \\ \, + M{{a}_{1}}\omega _{0}^{2}[{{a}_{2}}({{a}_{{12}}}{{b}_{{11}}} + {{a}_{{22}}}{{b}_{{21}}} + {{a}_{{32}}}{{b}_{{31}}}) + 3{{a}_{{32}}}({{a}_{1}}{{a}_{{31}}} - {{a}_{2}}{{b}_{{31}}})], \\ \end{gathered} $$
$${{A}_{2}}{{\dot {p}}_{2}} + ({{C}_{2}} - {{B}_{2}}){{q}_{2}}{{r}_{2}} = 3\omega _{0}^{2}({{C}_{2}} - {{B}_{2}}){{b}_{{32}}}{{b}_{{33}}},$$
(1.4)
$$\begin{gathered} ({{B}_{2}} + Ma_{2}^{2}){{{\dot {q}}}_{2}} - M{{a}_{1}}{{a}_{2}}[({{a}_{{13}}}{{b}_{{13}}} + {{a}_{{23}}}{{b}_{{23}}} + {{a}_{{33}}}{{b}_{{33}}}){{{\dot {q}}}_{1}} - ({{a}_{{12}}}{{b}_{{13}}} + {{a}_{{22}}}{{b}_{{23}}} + {{a}_{{32}}}{{b}_{{33}}}){{{\dot {r}}}_{1}}] \\ + \;M{{a}_{1}}{{a}_{2}}\{ {{b}_{{13}}}[{{r}_{1}}({{p}_{1}}{{a}_{{13}}} - {{r}_{1}}{{a}_{{11}}}) - {{q}_{1}}({{q}_{1}}{{a}_{{11}}} - {{p}_{1}}{{a}_{{12}}})] + {{b}_{{23}}}[{{r}_{1}}({{p}_{1}}{{a}_{{23}}} - {{r}_{1}}{{a}_{{21}}}) - {{q}_{1}}({{q}_{1}}{{a}_{{21}}} - {{p}_{1}}{{a}_{{22}}})] \\ + \;{{b}_{{33}}}[{{r}_{1}}({{p}_{1}}{{a}_{{33}}} - {{r}_{1}}{{a}_{{31}}}) - {{q}_{1}}({{q}_{1}}{{a}_{{31}}} - {{p}_{1}}{{a}_{{32}}})]\} + [({{A}_{2}} - {{C}_{2}}) - Ma_{2}^{2}]{{r}_{2}}{{p}_{2}} \\ = 3\omega _{0}^{2}({{A}_{2}} - {{C}_{2}}){{b}_{{33}}}{{b}_{{31}}} - M\omega _{0}^{2}{{a}_{2}}[{{a}_{1}}({{a}_{{11}}}{{b}_{{13}}} + {{a}_{{21}}}{{b}_{{23}}} + {{a}_{{31}}}{{b}_{{33}}}) + 3{{b}_{{33}}}({{a}_{2}}{{b}_{{31}}} - {{a}_{1}}{{a}_{{31}}})], \\ \end{gathered} $$
$$\begin{gathered} ({{C}_{2}} + Ma_{2}^{2}){{{\dot {r}}}_{2}} + M{{a}_{1}}{{a}_{2}}[({{a}_{{13}}}{{b}_{{12}}} + {{a}_{{23}}}{{b}_{{22}}} + {{a}_{{33}}}{{b}_{{32}}}){{{\dot {q}}}_{1}} - ({{a}_{{12}}}{{b}_{{12}}} + {{a}_{{22}}}{{b}_{{22}}} + {{a}_{{32}}}{{b}_{{32}}}){{{\dot {r}}}_{1}}] \\ + \;[({{B}_{2}} - {{A}_{2}}) + Ma_{2}^{2}]{{p}_{2}}{{q}_{2}} - M{{a}_{1}}{{a}_{2}}\{ {{b}_{{12}}}[{{r}_{1}}({{p}_{1}}{{a}_{{13}}} - {{r}_{1}}{{a}_{{11}}}) - {{q}_{1}}({{q}_{1}}{{a}_{{11}}} - {{p}_{1}}{{a}_{{12}}})] + {{b}_{{22}}}[{{r}_{1}}({{p}_{1}}{{a}_{{23}}} - {{r}_{1}}{{a}_{{21}}}) \\ - \;{{q}_{1}}({{q}_{1}}{{a}_{{21}}} - {{p}_{1}}{{a}_{{22}}})] + {{b}_{{32}}}[{{r}_{1}}({{p}_{1}}{{a}_{{33}}} - {{r}_{1}}{{a}_{{31}}}) - {{q}_{1}}({{q}_{1}}{{a}_{{31}}} - {{p}_{1}}{{a}_{{32}}})]\} = 3\omega _{0}^{2}({{B}_{2}} - {{A}_{2}}){{b}_{{31}}}{{b}_{{32}}} \\ + \;M\omega _{0}^{2}{{a}_{2}}[{{a}_{1}}({{a}_{{11}}}{{b}_{{12}}} + {{a}_{{21}}}{{b}_{{22}}} + {{a}_{{31}}}{{b}_{{32}}}) + 3{{b}_{{32}}}({{a}_{2}}{{b}_{{31}}} - {{a}_{1}}{{a}_{{31}}})]. \\ \end{gathered} $$

Here,

$$\begin{gathered} {{p}_{1}} = ({{{\dot {\alpha }}}_{1}} + {{\omega }_{0}})a_{{21}}^{{}} + {{{\dot {\gamma }}}_{1}}, \\ {{q}_{1}} = ({{{\dot {\alpha }}}_{1}} + {{\omega }_{0}})a_{{22}}^{{}} + {{{\dot {\beta }}}_{1}}\sin {{\gamma }_{1}}, \\ \end{gathered} $$
$$\begin{gathered} {{r}_{1}} = ({{{\dot {\alpha }}}_{1}} + {{\omega }_{0}})a_{{23}}^{{}} + \dot {\beta }\cos {{\gamma }_{1}}, \\ {{p}_{2}} = ({{{\dot {\alpha }}}_{2}} + {{\omega }_{0}})b_{{21}}^{{}} + {{{\dot {\gamma }}}_{2}}, \\ \end{gathered} $$
(1.5)
$$\begin{gathered} {{q}_{2}} = ({{{\dot {\alpha }}}_{2}} + {{\omega }_{0}})b_{{22}}^{{}} + {{{\dot {\beta }}}_{2}}\sin {{\gamma }_{2}}, \\ {{r}_{2}} = ({{{\dot {\alpha }}}_{2}} + {{\omega }_{0}})b_{{23}}^{{}} + {{{\dot {\beta }}}_{2}}\cos {{\gamma }_{2}}. \\ \end{gathered} $$

In (1.2)–(1.5), \({{M}_{i}}\) are the masses of the bodies; \(M = {{{{M}_{1}}{{M}_{2}}} \mathord{\left/ {\vphantom {{{{M}_{1}}{{M}_{2}}} {({{M}_{1}} + {{M}_{2}}}}} \right. \kern-0em} {({{M}_{1}} + {{M}_{2}}}})\); \({{A}_{i}},\;{{B}_{i}},\;{{C}_{i}}\) are the principal central moments of inertia of the bodies; \(({{a}_{i}},\;0,\;0)\) are the coordinates of the hinge in the coordinate system \({{O}_{i}}{{x}_{i}}{{y}_{i}}{{z}_{i}}\) (Fig. 1); \(p{}_{i},\;{{q}_{i}},\;{{r}_{i}}\) are the projections of the absolute angular velocity of the ith body onto the coordinate axes \(O{{x}_{i}},\;O{{y}_{i}},\;O{{z}_{i}}\); \({{a}_{{ij}}},\;{{b}_{{ij}}}\) are the direction cosines determining the orientation of the first and second body, respectively, in the orbital coordinate system; and \({{\omega }_{0}}\) is the angular velocity of the center of mass of the two-body system in a circular orbit. Dotted letters denote derivatives with respect to time \(t\).

2. EQUILIBRIUM POSITIONS

We introduce the following notation:

$${{m}_{1}} = {{M{{a}_{1}}{{a}_{2}}} \mathord{\left/ {\vphantom {{M{{a}_{1}}{{a}_{2}}} {[({{A}_{1}} - {{C}_{1}}) - Ma_{1}^{2}]}}} \right. \kern-0em} {[({{A}_{1}} - {{C}_{1}}) - Ma_{1}^{2}]}},\quad {{m}_{2}}\; = {{M{{a}_{1}}{{a}_{2}}} \mathord{\left/ {\vphantom {{M{{a}_{1}}{{a}_{2}}} {[({{A}_{2}} - {{C}_{2}}) - Ma_{2}^{2}]}}} \right. \kern-0em} {[({{A}_{2}} - {{C}_{2}}) - Ma_{2}^{2}]}},$$
$${{n}_{1}} = {{M{{a}_{1}}{{a}_{2}}} \mathord{\left/ {\vphantom {{M{{a}_{1}}{{a}_{2}}} {[({{B}_{1}} - {{A}_{1}}) + Ma_{1}^{2}]}}} \right. \kern-0em} {[({{B}_{1}} - {{A}_{1}}) + Ma_{1}^{2}]}},\quad {{n}_{2}} = {{M{{a}_{1}}{{a}_{2}}} \mathord{\left/ {\vphantom {{M{{a}_{1}}{{a}_{2}}} {[({{B}_{2}} - {{A}_{2}}) + Ma_{2}^{2}]}}} \right. \kern-0em} {[({{B}_{2}} - {{A}_{2}}) + Ma_{2}^{2}]}}.$$

Setting \({{\alpha }_{i}} = {{\alpha }_{{i0}}} = {\text{const}}\), \({{\beta }_{i}} = {{\beta }_{{i0}}} = {\text{const}}\), and \({{\gamma }_{i}} = {{\gamma }_{{i0}}} = {\text{const}}\) in (1.4) and (1.5) and using the notation introduced above, we obtain the equations

$$\begin{gathered} {{a}_{{22}}}{{a}_{{23}}} - 3{{a}_{{32}}}{{a}_{{33}}} = 0,\quad ({{a}_{{23}}}{{a}_{{21}}} - 3{{a}_{{33}}}{{a}_{{31}}}) + {{m}_{1}}({{b}_{{21}}}{{a}_{{23}}} - 3{{b}_{{31}}}{{a}_{{33}}}) = 0, \\ ({{a}_{{21}}}{{a}_{{22}}} - 3{{a}_{{31}}}{{a}_{{32}}}) - {{n}_{1}}({{b}_{{21}}}{{a}_{{22}}} - 3{{b}_{{31}}}{{a}_{{32}}}) = 0, \\ {{b}_{{22}}}{{b}_{{23}}} - 3{{b}_{{32}}}{{b}_{{33}}} = 0,\quad ({{b}_{{23}}}{{b}_{{21}}} - 3{{b}_{{33}}}{{b}_{{31}}}) + {{m}_{2}}({{a}_{{21}}}{{b}_{{23}}} - 3{{a}_{{31}}}{{b}_{{33}}}) = 0, \\ ({{b}_{{21}}}{{b}_{{22}}} - 3{{b}_{{31}}}{{b}_{{32}}}) - {{n}_{2}}({{a}_{{21}}}{{b}_{{22}}} - 3{{a}_{{31}}}{{b}_{{32}}}) = 0, \\ \end{gathered} $$
(2.1)

from which we can determine the equilibrium positions of the satellite–stabilizer system in the orbital coordinate system. In view of (1.1), system (2.1) can be treated as a system of six equations with unknowns \({{\alpha }_{{i0}}},\;{{\beta }_{{i0}}},\;{{\gamma }_{{i0}}}\)\((i = 1,\;2)\).

Another method for closing Eqs. (2.1), which is more convenient for our study, consists of adding six conditions for the orthogonality of the direction cosines:

$$\begin{gathered} a_{{21}}^{2} + a_{{22}}^{2} + a_{{23}}^{2} = 1,\quad b_{{21}}^{2} + b_{{22}}^{2} + b_{{23}}^{2} = 1, \\ a_{{31}}^{2} + a_{{32}}^{2} + a_{{33}}^{2} = 1,\quad b_{{31}}^{2} + b_{{32}}^{2} + b_{{33}}^{2} = 1, \\ {{a}_{{21}}}{{a}_{{31}}} + {{a}_{{22}}}{{a}_{{32}}} + {{a}_{{23}}}{{a}_{{33}}} = 0,\quad {{b}_{{21}}}{{b}_{{31}}} + {{b}_{{22}}}{{b}_{{32}}} + {{b}_{{23}}}{{b}_{{33}}} = 0. \\ \end{gathered} $$
(2.2)

Equations (2.1) and (2.2) form a closed algebraic system of equations for 12 direction cosines determining the equilibrium positions of the two-body system. The following problem is set up for this system of equations: given \({{m}_{1}},\;{{m}_{2}},\;{{n}_{1}},\;{{n}_{2}}\), determine all 12 direction cosines, i.e., all equilibrium positions of the two-body system in the orbital coordinate system. After finding the direction cosines \({{a}_{{21}}},\;{{a}_{{22}}},\;{{a}_{{23}}},\;{{a}_{{31}}},\;{{a}_{{32}}},\;{{a}_{{33}}}\) and \({{b}_{{21}}},\;{{b}_{{22}}},\;{{b}_{{23}}}\), \({{b}_{{31}}},\;{{b}_{{32}}},\;{{b}_{{33}}}\), the remaining direction cosines \({{a}_{{11}}},\;{{a}_{{12}}},\;{{a}_{{13}}},\;{{b}_{{11}}},\;{{b}_{{12}}},\;{{b}_{{13}}}\) can be obtained from the orthogonality conditions.

In [14] system (2.1), (2.2) was decomposed into homogeneous subsystems, whose solutions were found using algorithms for constructing Gröbner bases [15]. Solving the system of 12 algebraic equations (2.1) and (2.2) with coefficients depending on four parameters by applying methods for constructing Gröbner bases is a very complicated algorithmic problem. Experiments on the construction of a Gröbner basis for the system of polynomials (2.1), (2.2) by applying the Groebner[Basis] package implemented in Maple [16] were performed on a personal computer with 8 GB random-access memory and a 2.4 GHz Intel Core i7 processor. The computation of a Gröbner basis with the lexicographic ordering option took more than 10 h of CPU time, after which the run was terminated because of exceeding the admissible memory size available in Maple. A Gröbner basis for the system of polynomials (2.1), (2.2) was constructed only in the simplest special cases when \({{m}_{1}} = m\), \({{m}_{2}} = {{n}_{2}} = {{n}_{1}} = 1\) and when all parameters were identical: \({{m}_{1}} = {{m}_{2}} = {{n}_{2}} = {{n}_{1}} = m\). In the first case, the computation of a Gröbner basis required more than 4 h of CPU time on a personal computer, while, in the second case, the computation of a Gröbner basis required more than 24 h of CPU time on a server with 16 Intel Xeon processors with the use of Maple 18. In the general case, we failed to construct a Gröbner basis for this system.

3. INVESTIGATION OF EQUILIBRIUM POSITIONS

The solutions of the system of algebraic equations (2.1), (2.2) were examined in detail for nine special cases when one of the principal axes of inertia of both the first and second body coincides with the normal to the orbital plane, the radius vector, or the tangent to the orbit.

Case 1:\(a_{{22}}^{2} = 1\), \(b_{{22}}^{2} = 1\). Then system (2.1), (2.2) with \(a_{{22}}^{{}} = \pm 1\), \({{a}_{{12}}} = {{a}_{{32}}} = {{a}_{{21}}} = {{a}_{{23}}} = 0\) and \(b_{{22}}^{{}} = \pm 1\), \({{b}_{{12}}} = {{b}_{{32}}} = {{b}_{{21}}} = {{b}_{{23}}} = 0\) becomes

$$\begin{gathered} {{a}_{{33}}}({{a}_{{31}}} + {{m}_{1}}{{b}_{{31}}}) = 0,\quad {{b}_{{33}}}({{b}_{{31}}} + {{m}_{2}}{{a}_{{31}}}) = 0, \\ a_{{31}}^{2} + a_{{33}}^{2} - 1 = 0,\quad b_{{31}}^{2} + b_{{33}}^{2} - 1 = 0. \\ \end{gathered} $$
(3.1)

Equations (3.1) determine the equilibrium orientations of the system of two connected bodies in the orbital plane. System (3.1) has solutions of the following four types:

$$\begin{gathered} 1.1.\quad {{a}_{{33}}} = 0,\quad {{a}_{{31}}} = \pm 1,\quad {{a}_{{22}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{23}}} = \;0,\quad {{a}_{{11}}} = {{a}_{{12}}} = {{a}_{{32}}} = 0, \\ {{b}_{{33}}} = 0,\quad {{b}_{{31}}} = \pm 1;\quad {{b}_{{22}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{23}}} = \;0,\quad {{b}_{{11}}} = {{b}_{{12}}} = {{b}_{{32}}} = 0; \\ \end{gathered} $$
$$\begin{gathered} 1.2.\quad {{a}_{{33}}} = 0,\quad {{a}_{{31}}} = \pm 1,\quad {{a}_{{22}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{23}}} = 0,\quad {{a}_{{11}}} = {{a}_{{12}}} = {{a}_{{32}}} = 0, \\ {{b}_{{31}}} = \mp {{m}_{2}},\quad {{b}_{{33}}} = \pm \sqrt {1 - m_{2}^{2}} ,\quad {{b}_{{22}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{23}}} = 0,\quad {{b}_{{12}}} = {{b}_{{32}}} = 0, \\ \end{gathered} $$
$$\begin{gathered} {{b}_{{11}}} = {{b}_{{22}}}{{b}_{{33}}},\quad {{b}_{{13}}} = - {{b}_{{22}}}{{b}_{{31}}},\quad {\text{|}}{{m}_{2}}{\text{|}} < 1; \\ 1.3.\quad {{a}_{{31}}} = \mp {{m}_{1}},\quad {{a}_{{33}}} = \pm \sqrt {1 - m_{1}^{2}} ,\quad {{a}_{{22}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{23}}} = 0,\quad {{a}_{{12}}} = {{a}_{{32}}} = 0, \\ \end{gathered} $$
(3.2)
$$\begin{gathered} {{a}_{{11}}} = {{a}_{{22}}}{{a}_{{33}}},\quad {{a}_{{13}}} = - {{a}_{{22}}}{{a}_{{31}}},\quad {\text{|}}{{m}_{1}}{\text{|}} < 1, \\ {{b}_{{33}}} = 0,\quad {{b}_{{31}}} = \pm 1,\quad {{b}_{{22}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{23}}} = 0,\quad {{b}_{{11}}} = {{b}_{{12}}} = {{b}_{{32}}} = 0; \\ \end{gathered} $$
$$\begin{gathered} 1.4.\quad {{a}_{{31}}} = {{a}_{{32}}} = 0,\quad {{a}_{{33}}} = \pm 1,\quad {{a}_{{22}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{23}}} = 0,\quad {{a}_{{11}}} = {{a}_{{12}}} = 0, \\ {{b}_{{31}}} = {{b}_{{32}}} = 0,\quad {{b}_{{33}}} = \pm 1,\quad {{b}_{{22}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{23}}} = 0,\quad {{b}_{{11}}} = {{b}_{{12}}} = 0,\quad {{m}_{1}}{{m}_{2}} \ne 1. \\ \end{gathered} $$

Depending on the signs of the parameters, these solutions (3.2) with \({\text{|}}{{m}_{1}}{\text{|}} < 1,\)\({\text{|}}{{m}_{2}}{\text{|}} < 1\), \({{m}_{1}}{{m}_{2}} \ne 1\) determine 16 different equilibrium positions of the two-body system in each case. All equilibrium positions determined by Eqs. (3.1) in aircraft angles (1.1) were determined in [8]. Sufficient conditions for the stability of the equilibrium positions were obtained with the energy integral used as a Lyapunov function. The possibility of ensuring the asymptotic stability of the equilibrium positions was explored in the case of dissipation.

Case 2:\(a_{{23}}^{2} = 1\), \(b_{{23}}^{2} = 1\). In this case, the \(O{{z}_{1}}\) axis of the satellite and the \(O{{z}_{2}}\) axis of the stabilizer coincide with the normal to the orbital plane. System (2.1), (2.2) with \(a_{{23}}^{2} = 1\), \({{a}_{{13}}} = {{a}_{{33}}} = {{a}_{{21}}} = {{a}_{{22}}} = 0\) and \(b_{{23}}^{2} = 1\), \({{b}_{{13}}} = {{b}_{{33}}} = {{b}_{{21}}} = {{b}_{{22}}} = 0\) becomes

$$\begin{gathered} {{a}_{{32}}}({{a}_{{31}}} - {{n}_{1}}{{b}_{{31}}}) = 0,\quad {{b}_{{32}}}({{b}_{{31}}} - {{n}_{2}}{{a}_{{31}}}) = 0, \\ a_{{31}}^{2} + a_{{32}}^{2} - 1 = 0,\quad b_{{31}}^{2} + b_{{32}}^{2} - 1 = 0. \\ \end{gathered} $$
(3.3)

The solutions of system (3.3) in Case 2 have the form

$$\begin{gathered} 2.1.\quad {{a}_{{32}}} = 0,\quad {{a}_{{31}}} = \pm 1,\quad {{a}_{{23}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{22}}} = 0,\quad {{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{33}}} = 0, \\ {{b}_{{32}}} = 0,\quad {{b}_{{31}}} = \pm 1,\quad {{b}_{{23}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{22}}} = 0,\quad {{b}_{{11}}} = {{b}_{{13}}} = {{b}_{{33}}} = 0; \\ \end{gathered} $$
$$\begin{gathered} 2.2.\quad {{a}_{{32}}} = 0,\quad {{a}_{{31}}} = \pm 1,\quad {{a}_{{23}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{22}}} = 0,\quad {{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{33}}} = 0, \\ {{b}_{{31}}} = \pm {{n}_{2}},\quad {{b}_{{32}}} = \pm \sqrt {1 - n_{2}^{2}} ,\quad {{b}_{{23}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{22}}} = 0,\quad {{b}_{{13}}} = {{b}_{{33}}} = 0, \\ \end{gathered} $$
$$\begin{gathered} {{b}_{{11}}} = - {{b}_{{23}}}{{b}_{{32}}},\quad {{b}_{{12}}} = {{b}_{{23}}}{{b}_{{31}}},\quad {\text{|}}{{n}_{2}}{\text{|}} < 1; \\ 2.3.\quad {{a}_{{31}}} = \pm {{n}_{1}},\quad {{a}_{{32}}} = \pm \sqrt {1 - n_{1}^{2}} ,\quad {{a}_{{23}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{22}}} = 0,\quad {{a}_{{13}}} = {{a}_{{33}}} = 0, \\ \end{gathered} $$
(3.4)
$$\begin{gathered} {{a}_{{11}}} = - {{a}_{{23}}}{{a}_{{32}}},\quad {{a}_{{12}}} = {{a}_{{23}}}{{a}_{{31}}},\quad {\text{|}}{{n}_{1}}{\text{|}} < 1, \\ {{b}_{{32}}} = 0,\quad {{b}_{{31}}} = \pm 1,\quad {{b}_{{23}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{22}}} = 0,\quad {{b}_{{11}}} = {{b}_{{13}}} = {{b}_{{33}}} = 0; \\ \end{gathered} $$
$$\begin{gathered} 2.4.\quad {{a}_{{31}}} = {{a}_{{33}}} = 0,\quad {{a}_{{32}}} = \pm 1,\quad {{a}_{{23}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{22}}} = 0,\quad {{a}_{{12}}} = {{a}_{{13}}} = 0, \\ {{b}_{{31}}} = {{b}_{{33}}} = 0,\quad {{b}_{{32}}} = \pm 1,\quad {{b}_{{23}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{22}}} = 0,\quad {{b}_{{12}}} = {{b}_{{13}}} = 0,\quad {{n}_{1}}{{n}_{2}} \ne 1. \\ \end{gathered} $$

Depending on the signs of the parameters, solutions (3.4) with \({\text{|}}{{n}_{1}}{\text{|}} < 1\), \({\text{|}}{{n}_{2}}{\text{|}} < 1\), \({{n}_{1}}{{n}_{2}} \ne 1\) determine 16 different equilibrium positions of the system of two connected bodies in each case.

Case 3:\(a_{{32}}^{2} = 1\), \(b_{{32}}^{2} = 1\) and Case 4:\(a_{{33}}^{2} = 1\), \(b_{{33}}^{2} = 1\) are similar to Cases 1 and 2.

Consider the following case in detail.

Case 5:\(a_{{12}}^{2} = 1\), \(b_{{12}}^{2} = 1\). Then system (2.1), (2.2) with \(a_{{12}}^{2} = 1\), \({{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{22}}} = {{a}_{{32}}} = 0\) and \(b_{{12}}^{2} = 1\), \({{b}_{{11}}} = {{b}_{{13}}} = {{b}_{{22}}} = {{b}_{{32}}} = 0\) when \({{a}_{{12}}} = {{b}_{{12}}} = \;1\) or \({{a}_{{12}}} = {{b}_{{12}}} = \; - 1\) becomes

$$\begin{gathered} 4{{a}_{{21}}}{{a}_{{23}}} + {{m}_{1}}({{a}_{{23}}}{{b}_{{21}}} + 3{{b}_{{23}}}{{a}_{{21}}}) = 0,\quad 4{{b}_{{21}}}{{b}_{{23}}} + {{m}_{2}}({{a}_{{21}}}{{b}_{{23}}} + 3{{a}_{{23}}}{{b}_{{21}}}) = 0, \\ a_{{21}}^{2} + a_{{23}}^{2} - 1 = 0,\quad b_{{21}}^{2} + b_{{23}}^{2} - 1 = 0. \\ \end{gathered} $$
(3.5)

The solutions of system (3.5) are obtained using the algorithm for constructing a Gröbner basis [15]. A Gröbner basis of the system of polynomials representing the left-hand sides of Eqs. (3.5) was computed by applying the Groebner[Basis] package with the lexicographic ordering option for the plex variables implemented in Maple 18 (see [16]). The resulting Gröbner basis contained nine polynomials. In the Gröbner basis constructed for system (3.5), we consider a polynomial depending on only one variable \({{a}_{{23}}}\); it is written as

$${{P}_{1}}({{a}_{{23}}}){{P}_{2}}({{m}_{1}},{{m}_{2}},{{a}_{{23}}}) = 0,$$
(3.6)

where

$$\begin{gathered} {{P}_{1}}({{a}_{{23}}}) = {{a}_{{23}}}(a_{{23}}^{2} - 1),\quad {{P}_{2}}({{m}_{1}},{{m}_{2}},{{a}_{{23}}}) = {{p}_{0}}a_{{23}}^{4} + {{p}_{1}}a_{{33}}^{2} + {{p}_{2}}, \\ {{p}_{0}} = 64({{m}_{1}}{{m}_{2}} - 4)({{m}_{1}}{{m}_{2}} - 1),\quad {{p}_{1}} = - 32(m_{1}^{2} + 2)({{m}_{1}}{{m}_{2}} - 4)({{m}_{1}}{{m}_{2}} - 1), \\ {{p}_{2}} = 9m_{1}^{2}({{(2{{m}_{1}}{{m}_{2}} - 4)}^{2}} - {{({{m}_{1}} + {{m}_{2}})}^{2}}). \\ \end{gathered} $$
(3.7)

To determine equilibrium solutions, the following three cases have to be considered separately:

$${{a}_{{23}}} = 0,\quad a_{{23}}^{2} = 1,\quad {\text{and}}\quad {{P}_{2}}({{m}_{1}},{{m}_{2}},{{a}_{{23}}}) = 0.$$

In the case \({{a}_{{23}}} = 0\), system (3.5) has the solutions

$$\begin{gathered} a_{{12}}^{2} = 1,\quad a_{{21}}^{2} = 1,\quad a_{{33}}^{2} = 1,\quad {{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{22}}} = {{a}_{{31}}} = {{a}_{{32}}} = 0, \\ b_{{12}}^{2} = 1,\quad b_{{21}}^{2} = 1,\quad b_{{33}}^{2} = 1,\quad {{b}_{{11}}} = {{b}_{{13}}} = {{b}_{{22}}} = {{b}_{{23}}} = {{b}_{{31}}} = {{b}_{{32}}} = 0. \\ \end{gathered} $$

In the case \(a_{{23}}^{2} = 1\), we obtain the solutions

$$\begin{gathered} a_{{12}}^{2} = 1,\quad a_{{23}}^{2} = 1,\quad a_{{31}}^{2} = 1,\quad {{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{21}}} = {{a}_{{22}}} = {{a}_{{32}}} = {{a}_{{33}}} = 0, \\ b_{{12}}^{2} = 1,\quad b_{{23}}^{2} = 1,\quad b_{{31}}^{2} = 1,\quad {{b}_{{11}}} = {{b}_{{13}}} = {{b}_{{21}}} = {{b}_{{22}}} = {{b}_{{32}}} = {{b}_{{33}}} = 0. \\ \end{gathered} $$

Consider the third case, when the equilibria of the satellite are determined by the real roots of the biquadratic equation \({{P}_{2}}({{m}_{1}},{{m}_{2}},{{a}_{{23}}}) = 0\). The number of real roots of this equation is even and at most four. For each solution \({{a}_{{23}}}\), from the third equation in (3.5), we can obtain two values of \({{a}_{{21}}}\) and, next, \({{b}_{{21}}},\;{{b}_{{23}}}\).

For each set of values \({{a}_{{21}}}\), \({{a}_{{23}}}\), \({{b}_{{21}}},\;\;{{b}_{{23}}}\), the corresponding values of the direction cosines \({{a}_{{31}}},\;{{a}_{{33}}}\) and \({{b}_{{31}}},\;{{b}_{{33}}}\) are uniquely determined by the original system (2.1), (2.2). Thus, each real root of the biquadratic equation from (3.6) is associated with two sets of values \({{a}_{{ij}}}\), \({{b}_{{ij}}}\) (two equilibrium orientations). Since the number of real roots of the biquadratic equation from (3.6) is at most four, the number of equilibrium positions of the satellite–stabilizer system in the third case in Case 5 is at most eight. The solutions of the biquadratic equation from (3.6)

$$a_{{23}}^{2} = \frac{{m_{1}^{2} + 2}}{4} \pm \frac{{(2m_{1}^{3}{{m}_{2}} - 5{{m}_{1}}({{m}_{1}} + {{m}_{2}}) + 8)\sqrt {({{m}_{1}}{{m}_{2}} - 1)({{m}_{1}}{{m}_{2}} - 4)} }}{{8({{m}_{1}}{{m}_{2}} - 1)({{m}_{1}}{{m}_{2}} - 4)}}$$
(3.8)

exist if \({{m}_{1}}{{m}_{2}} < 1\), \({{m}_{1}}{{m}_{2}} > 4\) and if the right-hand side of (3.8) is nonnegative and does not exceed 1.

The solutions \(a_{{13}}^{2} = 1\), \(b_{{13}}^{2} = 1\) in Case 6 are similar to Case 5 if the parameters \({{m}_{1}},\;{{m}_{2}}\) in the latter case are replaced by the parameters \({{n}_{1}},\;{{n}_{2}}\).

In Case7:\((a_{{11}}^{2} = 1,\;b_{{11}}^{2} = 1)\), from system (2.1), (2.2) we obtain simple equations independent of the parameters of the two-body system:

$$\begin{gathered} {{a}_{{22}}}{{a}_{{23}}} = 0,\quad {{b}_{{22}}}{{b}_{{23}}} = 0, \\ a_{{22}}^{2} + a_{{23}}^{2} = 1,\quad b_{{22}}^{2} + b_{{23}}^{2} = 1. \\ \end{gathered} $$
(3.9)

Case8: (\(a_{{21}}^{2} = 1\), \(b_{{21}}^{2} = 1\)) and Case 9: (\(a_{{31}}^{2} = 1\), \(b_{{31}}^{2} = 1\)) are considered in a similar manner to Case 7.

CONCLUSIONS

The motion of a system of two bodies connected by a spherical hinge that move in a circular orbit under the action of a gravitational torque was investigated.

Primary attention was given to the equilibrium orientations of the two-body system. An algebraic method (based on the construction of a Gröbner basis) for determining the equilibrium positions of the two-body system in the orbital coordinate system with given parameter values was proposed in the special cases when one of the principal axes of inertia of both the first and second body coincides with the normal to the orbital plane, the radius vector, or the tangent to the orbit.

The results obtained in this paper can be used at the stage of preliminary design of gravitational orientation control systems for artificial satellites orbiting the Earth.