INTRODUCTION

In the first part of the author’s article [1], two problems were formulated that need to be solved in the theory of the formation of supermassive black hole (SMBH) nuclei in the early Universe using the mechanism of scalar-gravitational instability of the cosmological medium of scalarly charged fermions, in order to lead it in accordance with the observed picture:

1. According to the results presented, the process of increasing the SMBH mass does not stop when the required mass (1) is reached (see [2, 3]),

$$m_{\rm smbh}\sim 10^{4}{-}10^{6}M_{\odot}\approx 10^{42}{-}10^{44}\,m_{\mathrm{pl}},$$
(1)

but continues endlessly. Now we need to find a mechanism to stop this process.

2. What does the large-scale structure of the Universe become after the completion of this process, what is the fate of the matter that fell into the sphere of influence of a SMBH?

The first question was partly answered in the second part of the article [4]—the process of evolution of spherical scalar-gravitational disturbances ends quite quickly automatically precisely due to the geometric factor of spherical symmetry. As shown in this paper, the process of SMBH formation is determined by the fundamental parameters of the cosmological model,

$$\mathbf{P}=[[\alpha,m_{s},e,\pi_{0}],\Lambda],$$

where \(\alpha\) is the self-interaction constant of the Higgs potential, \(m_{s}\) is the mass of scalar bosons, \(e\) is the scalar charge of fermions, \(\pi_{0}\) is their initial Fermi momentum, \(\Lambda\) is the cosmological constant, and on the initial conditions, which in the simplest case (if the initial values of the derivatives of functions are equal to zero) can be written with three quantities:

$$I=[\Phi_{0},m_{0},q_{0}],$$

where \(\Phi_{0}\), \(m_{0}\), and \(q_{0}\) are the initial values of the scalar potential, the central singular mass, and the perturbation charge, respectively. In this paper, we, firstly, specify the dependence of the evolution parameters of BHs in the early Universe on the parameters of the field-theoretical model of interactions; secondly, we study the large-scale geometric factors that stop the process of growth of the BH mass; and thirdly, we consider a possible large-scale picture of the Universe at the end of the SMBH formation process.

1 FORMATION AND EVOLUTION OF BLACK HOLES IN VARIOUS FIELD-THEORETICAL MODELS

In [4], three similar process models are considered:

The basic model corresponding to the Planck interaction scalesFootnote 1 ,

$$\mathbf{P_{0}}=\bigl{[}\bigl{[}1,1,1,0.1\bigr{]},3\times 10^{-6}\bigr{]};$$
(2)

the field-theoretical model SU(5), resulting from the base model with the similarity coefficient \(k=10^{-5}\):

$$\mathbf{P_{SU(5)}}=\bigl{[}\bigl{[}10^{-10},10^{-5},\sqrt{10}\times 10^{-3},\sqrt{10}\times 10^{-4}\bigr{]},$$
$$3\times 10^{-16}\bigr{]}\quad(k=10^{-5}),$$
(3)

and the standard field-theoretical model SM—with the similarity coefficient \(k=10^{-15}\):

$$\mathbf{P_{SM}}=\bigl{[}\bigl{[}10^{-30},10^{-15},\sqrt{10}\times 10^{-8},\sqrt{10}\times 10^{-9}\bigr{]},$$
$$3\times 10^{-36}\bigr{]}\quad(k=10^{-15}).$$
(4)

In this case, as shown in [4], the final parameters of the process significantly depend on the initial conditions only by the factor of the location of the initial state of the system in relation to the unstable state in this model, which corresponds to the value of the scalar potential \(\Phi_{+}=1\) in the models under consideration. Namely, we will denote the process models as those with an initial state “above” the stable one, \(\Phi(0)>\Phi_{+}\), by the upper symbol \({}^{+}\), and models with an initial state “below” the stable one, \(\Phi(0)<\Phi_{+}\), with the upper symbol \({}^{-}\): \(M^{+}_{0},M^{-}_{0}\), etc.

Taking into account the properties of the similarity transformation (see [4]), we present the approximate results of numerical simulation of the evolution of the BH mass for three similar cosmological models.

Table 1 The maximum mass of a black hole
Full size table

Explanations for Table 1: \(t_{\textrm{max}}\) is the time at which the maximum BH mass \(m_{\textrm{max}}\) is reached for the model (2), \(t_{su(5)}\)—for the model \(\mathbf{P_{SU(5)}}\), and \(t_{sm}\)—for the model \(\mathbf{P_{SM}}\); \(m^{\odot}_{\textrm{max}}\) is the value of this mass in solar mass units; the numbers in parentheses indicate order.

Let us note, firstly, that in all cases the initial singular mass in the spherical perturbation was assumed to be equal to \(m(0)=m_{\rm Pl}\) (!). When the initial mass increases by a factor of \(p\), it is necessary to increase the maximum mass by the same factor. From Table 1, secondly, one can see that models of the \(\mathbf{M^{-}}\) type lead to maximum masses of formed BHs that are approximately 25(!) orders of magnitude smaller than the \(\mathbf{Mtype^{+}}\) models. Thirdly, the smaller are the fundamental constants \(\mathbf{P}\), the longer is the BH formation time. Fourth, and finally, the maximum masses of formed BHs in all \(\mathbf{M^{+}}\) type models that suit us, even in the \(\mathbf{M^{+}_{0}}\) model, are many orders of magnitude higher than the required SMBH masses (1). Therefore, although the problem with limiting the mass of SMBHs was fundamentally resolved in [4], the answer to the question of why the SMBH masses are limited precisely by the value (1) was not obtained in that work.

In this paper we will try, firstly, to answer this question as well as the second question, which turns out to be closely related to the first one.

Figure 1
figure 1

Cosmological evolution of the scalar field potential \(\Phi(t)\) in the \(\mathbf{SM^{+}}\) model (4).

Full size image
Figure 2
figure 2

Dependence of the number of e-folds \(N=\ln{a(t)}\) on cosmological time \(t\) (dashed line) and the Hubble parameter (solid line) in the \(\mathbf{SM^{+}}\) model (4).

Full size image

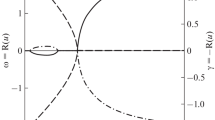
In what follows, we will consider the standard interaction model \(\mathbf{SM}\) (4) as the base model. Figures 1 and 2 present an example for the standard model of the evolution of cosmological parameters.

From these plots it is clear, firstly, that at the time instant (\(t\sim 10^{16}\)) there is a sharp transition of the cosmological system from a state with a scalar potential \(\Phi_{+}\approx 1\) to a state with \(\Phi_{\infty}\to 0\), accompanied by microscopic oscillations of this scalar potential (Fig. 2). Secondly, this transition is accompanied by an equally rapid decrease in the Hubble parameter: from \(H_{1}\approx 2.8888\times 10^{-16}\) to \(H_{2}\approx 1.8300\times 10^{-17}\), while the inflationary expansion rate decreases by approximately a factor of 16, which corresponds to a decrease in the effective cosmological constant \(\Lambda\) by approximately a factor of 250(!) (Fig. 3). As shown in the previous parts of the work, these transitions arise due to the instability of the cosmological system in state 1, as a result of which the cosmological system passes into a stable state 2, characterized by a lower inflation rate. Thirdly, according to the results of the previous paper [4], it is precisely during this transition that there begins a rapid growth of the BH mass.

Figure 3 shows the results of a numerical simulation of the cosmological evolution of the BH mass under spherical perturbations, in comparison with the expression for the mass in the \(n\)th harmonic of a plane perturbation, based on qualitative considerations (see [1]),

$$m(n,t)=\frac{4\pi}{n^{3}}H^{2}_{0}\mathrm{e}^{3H_{0}t}.$$
(5)

The results of numerical modeling confirm the approximate results of Table 1: a noticeable increase in mass begins immediately after the transition of the cosmological system to a stable state (see Fig. 2) at time \(t\backsimeq 4\times 10^{16}\), and the mass reaches its maximum value \(m_{\textrm{max}}\approx 10^{52}\) at time \(t_{\textrm{max}}\approx 4\times 10^{17}\). After reaching this maximum, the mass begins to fall and reaches a constant limit of \(m_{\infty}\approx 10^{42}\). Let us immediately note that the drop in the BH mass is a shortcoming of the linear approximation of the perturbation theory used. The mass of a macroscopic black hole, as is known, can only increase its mass with time. In the linear approximation of perturbation theory, the geometric properties of the BH horizon do not manifest themselves. In this regard, the maximum mass of the BH obtained within the framework of linear perturbation theory should be taken as the final mass of the formed BH.

Figure 3
figure 3

Cosmological evolution of the BH mass in the model of spherical perturbations (solid line) and according to the qualitative formula (dashed line) in the interaction model \(\mathbf{SM^{+}}\) (4).

Full size image

Comment 1 (On the estimates). Next, comparing the results of numerical modeling with those obtained on the basis of the qualitative formula (5), we see that the latter gives the BH mass values achieved by \(t_{\textrm{max}}\) is 10 orders of magnitude smaller than the precise results of numerical simulation. Or, in other words, the value \(m_{\textrm{max}}\) is achieved based on the qualitative relation (5) at times 2 orders of magnitude later than \(t_{\textrm{max}}\). This must be kept in mind in the future when assessing the cosmological process of SMBH formation.

2 END OF THE SMBH FORMATION PROCESS

In the previous parts of the article, we considered the evolution of a single local spherical disturbance in the Friedmann Universe,

$$ds^{2}=dt^{2}-a^{2}(t)(dx^{2}+dy^{2}+dz^{2}),$$
(6)

with \(dx^{2}+dy^{2}+dz^{2}\equiv d\mathbf{r}^{2}\). In fact, such disturbances are formed, albeit randomly, taking into account the macroscopic homogeneity and isotropy of the Universe, on the average, uniformly. Of course, the initial parameters of these disturbances are largely random, but nevertheless, to simplify the model, we will assume them to be the same. Let \(\tau_{g}\) be the time instant of BH birth in scalar-gravitational disturbances. At the inflation stage (where \(H_{0}=H_{1}\) or \(H_{0}=H_{2}\), depending on the stage of evolution),

$$a(t)=\mathrm{e}^{H_{0}t},$$
(7)

and according to [1], this time instant is

$$\tau_{g}\backsimeq\frac{1}{H_{0}}\ln\biggl{(}\frac{n}{\sqrt{8\pi}H_{0}}\biggr{)},$$
(8)

where \(n\equiv|\mathbf{n}|\) is the wave number of the perturbation mode \(\exp(i\mathbf{nr})\). The mass \(m_{g}\) of a new-born BH at the inflation stage does not depend on the wave number \(n\) [1],

$$m_{g}\backsimeq\frac{1}{4\sqrt{2\pi}}\frac{1}{H_{0}}.$$
(9)

Let us take into account that the disturbance wavelength \(\lambda(t)\) is related to the wave number \(n\) by [5]

$$\lambda(t)=\frac{a(t)}{n}\ \Rightarrow\ n=\frac{a(t)}{\lambda(t)}\equiv\frac{a(\tau_{g})}{\lambda(\tau_{g})},$$
(10)

and

$$\lambda(\tau_{g})\gtrsim 2m_{g}\ \Rightarrow\ \backsimeq\sqrt{8\pi}H_{0}.$$
(11)

Then we obtain an estimate for the time of BH birth in unstable disturbance modes:

$$\tau_{g}\gtrsim\frac{1}{H_{0}}\ln 2.$$
(12)

Thus we get, for example, in Fig. 3:

$$\mathbf{1{:}}\quad\tau_{g}\backsimeq 2.4\times 10^{15};\quad m_{g}{:}\quad{\backsimeq}3.5\times 10^{14},$$
(13)
$$\mathbf{2{:}}\quad\tau_{g}\backsimeq 3.7\times 10^{17};\quad m_{g}{:}\quad{\backsimeq}5.3\times 10^{15}.$$
(14)

Let further \(\nu(t)\) be the average number density of identical BHs formed at \(t>\tau_{g}\) with horizon radius \(R_{m}=2m(t)\), so that \(m(\tau_{g})=m_{g}\), \(\nu(\tau_{g})=\nu_{g}\). Then the average distance between the BHs is (see Fig. 1)

$$R_{N}(t)=\left(\frac{3}{4\pi\nu(t)}\right)^{1/3}.$$
(15)

Assuming that starting from this moment \(\tau_{g}\) the number of BHs does not change, we obtain:

$$\nu(t)=\nu_{g}\left(\frac{a(\tau_{g})}{a(t)}\right)^{3}\quad(=\nu_{g}e^{-3H_{0}(t-\tau_{g})}).$$
(16)

Thus from (15) (see Fig. 4) we find

$$R_{N}(t)=\frac{a(t)}{a(\tau_{g})}\left(\frac{3}{4\pi\nu_{g}}\right)^{1/3}\equiv\frac{a(t)}{a(\tau_{g})}R_{N}(\tau_{g}).$$
(17)
Figure 4
figure 4

The SMBH number density and their radii.

Full size image

Next, to estimate the radius of the BH horizon at the inflation stage, we use the qualitative relation from [1] (5):

$$R_{M}(t)=2m(t)\backsimeq 8\pi H_{0}^{2}\frac{a^{3}(t)}{n^{3}}$$
$${}\backsimeq\frac{1}{\sqrt{8\pi}H_{0}}\mathrm{e}^{3H_{0}(t-\tau_{g})}.$$
(18)

When the horizon radii of two BHs come into contact, the process of their mass increase must be stopped, at least before the possible BH merger. According to (17) and (18), this point in time, \(\tau_{\textrm{max}}\), is determined by the relation

$$\frac{a(t)}{a(\tau_{g})}\gtrsim\sqrt{\delta}\ \Rightarrow\ \tau_{\textrm{max}}\backsimeq\frac{1}{2H_{0}}\ln(\delta+4),$$
(19)

where

$$\delta\equiv\frac{R_{N}(\tau_{g})}{R_{M}(\tau_{g})}=\sqrt{8\pi}H_{0}R_{N}(\tau_{g})>1$$

is the ratio of the average distance between the BHs to the BH horizon radius at the moment of their formation. The BH density introduced above at the moment of their birth, \(\nu_{g}\), is related to the dimensionless parameter \(\delta>1\) by

$$\nu_{g}=6\sqrt{8\pi}\left(\frac{H_{0}}{\delta}\right)^{3}.$$
(20)

From (18) and (19) we obtain an estimate for the maximum mass of SMBHs,

$$M_{\textrm{max}}\gtrsim\frac{\delta^{3/2}}{\sqrt{8\pi}H_{0}}\equiv\sqrt{\frac{3}{8\pi\Lambda}}\delta^{3/2}.$$
(21)

Thus, firstly, the maximum mass of a BH is determined by only two parameters—the cosmological constant and the number density of the number of newborn black holes (20), and, secondly, it increases with a decrease in the cosmological constant. For example, the minimum SMBH mass threshold (1) \(m=10^{44}\) in the case of \(\delta=10^{8}\) is achieved at a value of the cosmological constant \(\Lambda\backsimeq 10^{-65}\). Note, firstly, that according to (19), the time to reach the maximum mass (21) is greater than or of the order of the cosmological time \(\tau_{0}\backsimeq H^{-1}_{0}\) at this stage of expansion. The values of the Hubble constant in the early stages of expansion should be greater than its modern value. Secondly, as we noted, the estimating formula (18) gives a greatly underestimated growth rate of the BH mass (see footnote 1), so we must make appropriate corrections to Eq. (21).

Summarizing the results of this section, we note that the macroscopic geometric factor is, apparently, the main one in determining the maximum parameters of SMBHs formed in the process of cosmological evolution.

3 THE COSMOLOGICAL CONSTANT AFTER SMBH FORMATION

3.1 Scalar Field in the Neighborhood of SMBH

So since, as a result of the scalar-gravitational instability of the cosmological medium of scalarly charged fermions, scalarly charged BHs are apparently formed, it is necessary, firstly, to consider the question on such isolated static BHs. For the first time, the spherically symmetric solution in the case of a massless canonical scalar field was found by I.Z. Fisher (1948) [6]. In Ref. [7] (see also the reviews [8, 9]), the question of the geometry of a scalarly charged BHs with a massless scalar field (\(V(\Phi)\equiv 0\)) was studied in detail in the absence of ordinary matter. In the classical work [10], the “no-hair” theorem was proved on the absence of scalar hair in BHs. According to this theorem, outside a black hole horizon, the scalar field can only be constant: \(\Phi=\textrm{const}\). It should be noted that the conditions for the validity of the theorem are, firstly, the Minkowski nature of the metric at infinity, and, secondly, the presence of the event horizon itself.

Let us consider a static spherically symmetric metric in curvature coordinates (see, e.g., [5])

$$ds^{2}=\mathrm{e}^{\nu(r)}dt^{2}-\mathrm{e}^{\lambda(r)}dr^{2}-r^{2}d\Omega^{2},$$
(22)

which the equation for the scalar Higgs field \(\Phi(r)\) has the form

$$\frac{1}{r^{2}}\frac{d}{dr}\left(r^{2}\mathrm{e}^{(\nu-\lambda)/2}\frac{d}{dr}\Phi\right)$$
$${}-\mathrm{e}^{(\nu-\lambda)2}\Phi(m^{2}_{s}-\alpha\Phi^{2})=0.$$
(23)

In [11], Eq. (23) was solved in the spatially flat metric \(\nu=\lambda=0\) for the central point scalar charge \(e\). For the self-interaction constant \(\alpha=0\), Eq. (23) reduces to the well-known Yukawa equation

$$\frac{1}{r^{2}}\frac{d}{dr}\left(r^{2}\frac{d}{dr}\Phi\right)-m_{s}^{2}\Phi=0$$
(24)

and has as its solution the well-known Yukawa potential

$$\Phi=\displaystyle{\frac{2G}{r}\mathrm{e}^{-m_{s}r}},$$
(25)

where \(G\) is a scalar charge.

The self-interaction constant factor \(\alpha\not\equiv 0\) fundamentally changes the nature of solutions to Eq. (23). Now this equation has no stable solutions with zero asymptotics at infinity,

$$\Phi(r)\Big{|}_{r\to\infty}\to 0.$$
(26)

Stable solutions of Eq. (23) in a spatially flat metric are solutions with nonzero asymptotic behavior at infinity corresponding to special stable points of the dynamical system,

$$\Phi(r)\Big{|}_{r\to\infty}\to\Phi_{\pm}=\pm\frac{m_{s}}{\sqrt{\alpha}}.$$
(27)

For solutions close to stable, assuming

$$\Phi(r)=\Phi_{\pm}+\phi(r)\quad(\phi\ll 1),$$
(28)

in the linear approximation we obtain the equation, instead of (24),

$$\frac{1}{r^{2}}\frac{d}{dr}\biggl{(}r^{2}\frac{d\phi}{dr}\biggr{)}+2m_{s}^{2}\phi=0.$$
(29)

Let us pay attention to the change in the sign of the massive term as compared to the Yukawa equation (24), due to which the stable solution of the equation for the Higgs field will be [11]

$$\Phi(r)=\pm\frac{m_{s}}{\sqrt{\alpha}}+\frac{2G}{r}\cos(\sqrt{2}m_{s}r).$$
(30)

The presence of a fundamental scalar field with the Higgs potential fundamentally changes the physical picture. Now the vacuum state corresponds to one of the stable points of the Higgs potential (27), which, in turn, corresponds to the zero potential energy of the scalar field,

$$V(\Phi_{\pm})=0.$$
(31)

Taking into account the above, we study the solution to the complete problem of a self-gravitating scalar Higgs field. Nontrivial combinations of Einstein’s equations with a cosmological constant in the metric (22)Footnote 2 can be reduced to the form

$$2r\Phi^{\prime 2}+(\lambda+\nu)^{\prime}=0,$$
(32)
$$\mathrm{e}^{\lambda}-1-r\nu^{\prime}=r^{2}\mathrm{e}^{\lambda}\bigg{[}\Lambda-\frac{\alpha}{2}\left(\Phi^{2}-\frac{m^{2}_{s}}{\alpha}\right)^{2}\bigg{]}.$$
(33)

We will seek solutions to the set of equations (23), (32), (33) that are close to being stable, assuming (28). Then, in the zeroth approximation, due to the smallness of \(\phi(r)\), Eq. (23) becomes an identity, and Eq. (32) gives

$$\lambda=-\nu.$$
(34)

As a result, Eq. (33) is reduced to the closed equation for \(\nu\) (or \(\lambda\))

$$r\nu^{\prime}+1+\mathrm{e}^{-\nu}(1-\Lambda r^{2})=0,$$
(35)

solving which, we find in the zeroth approximation:

$$\nu_{0}=-\lambda_{0}=\ln\left(1-\frac{2m}{r}-\frac{\Lambda r^{2}}{3}\right),$$
(36)

where \(m\) is an integration constant. Thus in the zeroth approximation we obtain the well-known Schwarzschild–de Sitter solution [12]

$$ds^{2}=\left(1-\frac{2m}{r}-\frac{\Lambda r^{2}}{3}\right)dt^{2}$$
$${}-\frac{dr^{2}}{1-\dfrac{2m}{r}-\dfrac{\Lambda r^{2}}{3}}-r^{2}d\Omega^{2}.$$
(37)

Due to (32), in the first approximation in the smallness of \(\phi\), the relation (34) is preserved, and therefore Eq. (35) is also preserved. It follows that the metric (37) is preserved in the approximation linear in \(\phi\) . Therefore, in a linear approximation, the field equation (23) can be considered against the background of the Schwarzschild–de Sitter solution (37):

$$\frac{1}{r^{2}}\frac{d}{dr}\left(r^{2}\mathrm{e}^{\nu_{0}}\frac{d}{dr}\phi\right)+2m^{2}_{s}\mathrm{e}^{\nu_{0}}\phi=0.$$
(38)

Without posing, in this article, the problem of finding solutions to Eq. (38) and studying their behavior near the horizons of the metric (37), we only note that, in general, the solution is in the form (28) with \(\Phi(\infty)=\Phi_{\pm}=\textrm{const}\), (27), does not contradict the theorem on the absence of scalar hair in BHs. At the same time, the Higgs potential is implicitly included in the solution of field equations, firstly, through the vacuum value of the scalar potential (27), and secondly, through renormalization of the bare cosmological constant \(\Lambda_{0}\) (see, e.g., [1]), decreasing its value:

$$\Lambda=\Lambda_{0}-\frac{1}{4}\frac{m_{s}^{4}}{\alpha}.$$
(39)

3.2 The Cosmological Factor

One should remember, however, that the properties of a scalarly charged BH discussed above refer to an isolated static system. In fact, the process of BH formation occurs in a cosmological environment, which determines its evolution. In this regard, let us again turn to Figs. 1, 2, illustrating the evolution of the cosmological medium during the BH formation for the standard model \(\mathbf{SM}\) (4).

In this regard, the question arises of how to combine the model of an isolated static scalarly charged BH with the model of a BH in a cosmological environment. In particular, what can happen to the quasi-vacuum state of this BH, corresponding in this case to the value of the scalar potential \(\Phi_{\pm}=1\), which in the cosmological environment after the transition should tend to zero, thereby violating the quasi-vacuum nature of the state and causing instability of the scalar field. This rather serious issue requires an additional research, which we hope to conduct in the future.

For now, we will explore the essence of this issue from the point of view of the qualitative theory of ordinary differential equations (see, e.g, [13]). To do that, consider the equation of the scalar field \(\Phi(x,t)\) with the potential energy \(V(\Phi)\) in flat space-time

$$\ddot{\Phi}-\Phi^{\prime\prime}+V^{\prime}_{\Phi}(\Phi)=0,$$
(40)

where, as usual, the dot denotes derivatives with respect to \(t\), and the prime with respect to \(x\). Let us consider two fundamentally different situations: the case where \(\Phi=\Phi(t)\), and the case where \(\Phi=\Phi(x)\). We will call the first situation the T-situation, and the second the X-situation. The corresponding field equations are obtained from (40):

$$\mathbf{T}:\quad\ddot{\Phi}+V^{\prime}_{\Phi}(\Phi)=0,$$
(41)
$$\mathbf{X}:\quad\Phi^{\prime\prime}-V^{\prime}_{\Phi}(\Phi)=0.$$
(42)

According to the qualitative theory of differential equations, in both situations the singular points \(\Phi_{i}\) of the corresponding normal system of differential equations are determined by the equations

$$V^{\prime}_{\Phi}(\Phi_{i})=0,$$

and the eigenvalues of the characteristic matrix of the system \(\lambda_{s}\) are, in turn, determined through these singular points:

$$\mathbf{T}:\quad\lambda_{i}=\pm\sqrt{-V^{\prime\prime}_{\Phi\Phi}(\Phi_{i})}=0,$$
$$\mathbf{X}:\quad\lambda_{i}=\pm\sqrt{V^{\prime\prime}_{\Phi\Phi}(\Phi_{i})}=0.$$

In the case of the Higgs potential

$$V(\Phi)=-\frac{\alpha}{4}\left(\Phi^{2}-\frac{m^{2}_{s}}{\alpha}\right)^{2},$$

there are singular points of the system

$$\Phi_{0}=0,\quad\Phi_{\pm}=\pm\frac{m_{s}}{\sqrt{\alpha}}.$$

So, we get for the eigenvalues:

$$\mathbf{T}:\quad\lambda_{0}=\pm im_{s};\quad\lambda_{\pm}=\pm\sqrt{2}m_{s};$$
$$\mathbf{X}:\quad\lambda_{0}=\pm m_{s};\quad\lambda_{\pm}=\pm i\sqrt{2}m_{s}=0.$$

Thus, according to the qualitative theory of differential equations in the T-situation, the zero singular point \(\Phi_{0}=0\) is an attracting focus (cycle), and the singular points \(\Phi_{\pm}\) are saddle points, i.e., unstable points of the system. In the case of the X-situation, on the contrary, the zero singular point \(\Phi_{0}=0\) is a saddle point, i.e., it is unstable, and the singular points \(\Phi_{\pm}\) are attracting foci (cycles). This explains why in the static case the scalar potential tends to a quasi-vacuum solution at infinity (27) (X-situation), which is unstable for the cosmological T-situation, while in the cosmological situation at \(t\to\infty\) the stable solution is zero. The collision of these systems, which are opposite from the point of view of differential equations, is a problem that we have to solve in the future.

One can, of course, object to this conclusion. Indeed, in the standard model of a scalar field with a parabolic potential, the zero singular point is preserved, as are the eigenvalues of the characteristic matrix at this point. But then it turns out that the solution \(\Phi=C_{1}\exp(-m_{s}x)\) at this point \(\Phi\to 0\) as \(x\to\infty\) is not stable for a static field, just like the Yukawa solution. Yes, indeed, these solutions, strictly speaking, are not stable since they do not have a growing branch as compared to general solutions. The damped (only as \(x\to+\infty\)!) solution corresponds to the particular initial conditions

$$\Phi(0)=\Phi_{0},\quad\Phi^{\prime}(0)=-\frac{\Phi_{0}}{m_{s}}.$$

With a slight variation of these conditions, a second branch appears in the solution, diverging exponentially quickly at positive infinity, which corresponds to a classical Lyapunov instability. A completely similar situation arises with the Yukawa potential in the case of spherical symmetry. In the case of a parabolic potential of a scalar field, this contradiction can be quite simply eliminated using the fact that there is only one singular point of the X- and T-systems. If there are several singular points with different characteristics, this contradiction cannot be easily eliminated. Nevertheless, even in this case there is a way out, as long as the cosmological system is, in though an unstable but rather a long inflationary phase, as in Figs. 2, 3. In this case, the cosmologically unstable state (T-situation) with \(\Phi=1\) is at the same time stable for the X-situation, i.e., for a scalarly charged BH.

If we assume that the general cosmological trend in the course of evolution nevertheless turns out to be dominant, then we must accept as a fact that the scalar field in the outer regions close to the BH horizons should completely disappear in the course of cosmological evolution. Thus there should be a strong drop in the value of the cosmological constant, possibly even to zero, in accordance with Eq. (39). In this case, under the horizon, the scalar field can remain in a state close to a stable one, \(\Phi=\Phi_{\pm}\) (27).

3.3 Macroscopic Picture of the Universe with Black Holes

Let us find out the possible outcome of the situation when the Universe is filled with supermassive scalarly charged BHs surrounded by fermionic matter in the absence of a scalar field or when it is weak. In the author’s early papers [14–16], foundations of a statistical theory of relativistic classical systems with gravitational interaction were formulated. In the papers [17, 18], based on this theory, a kinetic equation for massless particles in the macroscopic Friedmann world was derived, taking into account the gravitational interaction with microscopic spherically symmetric local fluctuations of the metric generated by point sources of mass. In this case, the cosmological evolution of spherical local fluctuations generated by point masses was taken into account, studied in [19] for the ultrarelativistic equation of state of matter in the Universe, and in [20] and other papers for the equation of state of a perfect fluid with an arbitrary constant barotropic coefficient. Finally, in [21] these results were applied to obtain an effective energy-momentum correlation tensor for quadratic fluctuations of the gravitational field of BHs arising due to the an overlap of their gravitational attraction regions in the macroscopically spatially flat Friedmann Universe. The resulting expression for the energy-momentum tensor components at the nonrelativistic stage of evolution of the material component of the cosmological environment, adapted to our notation, has the form

$$\delta T^{i}_{k}=-\frac{1}{8\pi}\delta\overline{G^{(2)}\!\ {}^{i}_{k}}$$
$${}=3\pi\nu_{s}r_{s}\left(\frac{2m(t)}{r_{s}}\right)^{2}\delta^{i}_{k}\equiv\langle\varepsilon_{g}\rangle\delta^{i}_{k},$$
(43)

where \(\langle\varepsilon_{g}\rangle\) is the average correlation energy density, \(\nu_{s}=\nu(r_{s})\) is the average BH density per accompanying volume, \(\mu(t)=m(t)/a(t)\) is the reduced BH mass, \(r_{s}\) is the sound horizon at the moment of transition to the total nonrelativistic state of cosmological matter. Assuming that after completion of the process of exponentially rapid mass growth, the matter becomes nonrelativistic, and the SMBH mass remains practically unchanged (only due to slow gas accretion), we obtain

$$\langle\varepsilon_{g}\rangle\sim 12\pi\frac{\nu_{s}m^{2}_{\rm smbh}}{r_{s}}=\textrm{const}.$$
(44)

Thus, at the nonrelativistic stage of expansion after completion of the SMBH formation, the Universe can be described by a cosmological model with the effective cosmological constant

$$\Lambda_{eff}=\langle\varepsilon_{g}\rangle,$$

generated by quadratic correlations of local gravitational fields of SMBHs.

4 CONCLUSION

Note that the BH number density \(\nu(t)\) appears in Section 2, therefore the formulas for the effective constant (44) and the maximum achievable mass of the BH (21) are quite strictly related to each other. Thus, to clarify the correctness of the estimate (44) of the modern value of the cosmological constant, one can use the observational data on the maximum mass of SMBHs \(m_{\textrm{max}}\), their average density \(\nu(t)\) and the radius of the sound horizon of matter at the nonrelativistic stage.