Earth-Like Models of the Internal Structure of Venus

Abstract—

Based on the PREM Earth model, more than a thousand models of the internal structure of Venus have been built, differing in the radius and density of the core, the density of the mantle, the viscosity distribution and rheology. The core radius varies from 2800 to 3600 km, and the density in the mantle and core varies within a few percent of the PREM model values. When calculating tidal Love numbers, Andrade rheology is used to take into account the inelasticity of the mantle. Specifically the values of the Andrade rheological model parameters that best describe the tidal deformation of the Earth are used. This significantly reduces the error when calculating Love numbers. It has been shown that Venus can have an internal solid core only if the composition of the planet is very different from that of Earth. Comparison of the observed values of the moment of inertia and tidal Love number k₂ with model values allowed us to conclude that the radius of the core of Venus is with a high probability in the range of 3288 ± 167 km.

INTRODUCTION

Venus was once called Earth’s twin planet due to the similarity of these planets in mass and radius. However, a number of features were discovered in Venus due to which the planet lost this title, for example, the absence of its own magnetic field, the absence of plate tectonics, and the presence of a dense atmosphere of volcanic origin (Smrekar et al., 2018). All these differences between the Earth and Venus are closely related to the conditions and processes in their interiors and, therefore, the study of the internal structure of Venus is an important task in the field of planetary geophysics.

The first steps in studying the internal structure of Venus were made in the 1980s in the papers (Zharkov and Zasurskii, 1982; Kozlovskaya, 1982), where the equation of state of the Earth from the PEM (Preliminary Earth model) (Dziewonski et al., 1975) was used as the equation of state of Venus, and it was noted that the convenience of such a choice lies in the automatic consideration of the influence of temperature on the equation of state. The radius of the core of Earth-like Venus was approximately 3200 km, and the thickness of the crust was taken to be 70 km (Zharkov and Zasurskii, 1982).

In the paper (Aitta, 2012), a model was constructed, whose mantle is also based on the PREM (Preliminary reference Earth model) (Dziewonski and Anderson, 1981), but with a changed composition of the core. The thickness of the crust is taken to be 30 km. In such a model, the radius of the core is 3228 km, and the moment of inertia is 0.3380 (higher than the Earth’s moment of inertia, 0.3307). The pressure at the center of Venus is 275 GPa, which is much less than the pressure at the boundary of the Earth’s inner core (approximately 330 GPa according to (Dziewonski and Anderson, 1981)). For this reason, the paper (Aitta, 2012) states that the core of Venus is in a completely molten state.

On Earth, the formation and growth of the solid inner core is closely related to the generation of magnetic field (Zhou et al., 2022). According to (Aitta, 2012), the absence of an internal core in Venus may explain the absence of its own magnetic field. The paper (Aitta, 2012) also estimates the intensity of convection in the mantle of Venus, which turned out to be almost half that of Earth, which, in turn, can explain the absence of plate tectonics on Venus.

In the paper (Dumoulin et al., 2017), various models of the internal structure of Venus were constructed with chemical compositions both similar and very different from those on Earth. In some models, the core is partially or even completely solid. This is only possible because the equation of state of pure iron at high pressures is used as the equation of state of the inner core (Dorogokupets et al., 2017). The cores of terrestrial planets must contain admixtures of light elements, which, in turn, reduce the melting point. For this reason, models with a pure iron core are less likely.

For some models in (Dumoulin et al., 2017), the tidal Love number k₂ was calculated for different values of viscosity in the mantle. Inelasticity in the interior was taken into account using Andrade rheology. Comparison of model k₂ values with measured ones (Konopliv and Yoder, 1996) allowed the authors of (Dumoulin et al., 2017) to determine the likelihood of the constructed models.

A set of Earth-like models of the internal structure of Venus and corrections due to the influence of the inelasticity of the planet’s interior on the value of the model Love number k₂ were calculated in (Gudkova and Zharkov, 2020). In the paper (Amorim and Gudkova, 2023), dozens of models of the internal structure of Venus were constructed with compositions close to, but not identical to, those on Earth. Love numbers were calculated for various values of mantle viscosity and parameters of the Andrade rheological model. A comparison of model and measured values of the moment of inertia (Konopliv and Yoder, 1996; Margot et al., 2021) gave an estimate of the radius of the core of Venus in the range of 3100–3500 km.

One of the main problems that arises when calculating Love numbers is the uncertainty in the rheological model of the planet. The Andrade model is actively used in problems of planetary geophysics, since it has been experimentally confirmed for various minerals (Efroimsky, 2012). However, it is unknown whether it is applicable under mantle conditions (at very high pressures and temperatures) and, if applicable, what values of the two parameters on which it depends are suitable for describing the inelasticity of the planetary interior. The uncertainty of the Andrade parameters causes a significant scatter in the values of the model Love numbers, and this prevented a more accurate determination of the internal structure of Venus in the paper (Amorim and Gudkova, 2023).

In order to resolve this problem, the authors “calibrated” Andrade rheological model on Earth (Amorim and Gudkova, 2024). The values of the Andrade parameters α and ζ were determined, which give a good description of the inelasticity and tidal deformation of the Earth at the frequency of the semidiurnal lunar tide M2, and it is these values that should be used in models of the internal structure of the terrestrial planets.

This work is a continuation of the paper (Amorim and Gudkova, 2023). Here we significantly increased the variety of models compared to (Amorim and Gudkova, 2023) and applied a refined rheological model based on the results of (Amorim and Gudkova, 2024).

This article first examines models of the internal structure of Venus. Then the algorithm for calculating tidal deformation is modernized to take into account the influence of the dense atmosphere of Venus on the Love numbers. The rheological model used and the viscosity distribution are discussed next. Models are selected based on the Love number k₂, and the most probable models are assessed based on a joint analysis of the moment of inertia and k₂. Finally, the contribution to the task of studying the interior of Venus that the VERITAS (Cascioli et al., 2021) and EnVision (Rosenblatt et al., 2021) missions can make is discussed.

MODELS OF THE INTERNAL STRUCTURE OF VENUS

Observational data used in constructing models of the internal structure of Venus are given in Table 1: planet mass M₀ (without atmosphere), average radius R, dimensionless moment of inertia I/M₀R², tidal Love number k₂, pressure P_s and atmospheric density ρ_S on the surface.

Table 1.  Observational data for Venus

Mass, radius and surface pressure are constraints that each model must satisfy. The moment of inertia and Love number k₂ are criteria that are used to assess the likelihood of models, and atmospheric density is used in calculating Love numbers.

Calculation of models of the internal structure of planets is based on the use of the equation for mass and the equation of hydrostatic equilibrium:

$$\begin{gathered} \frac{{dM(r)}}{{dr}} = 4\pi {{r}^{2}}\rho (P), \\ \frac{{dP}}{{dr}} = - g(r)\rho (P) = - \frac{{GM(r)}}{{{{r}^{2}}}}\rho (P). \\ \end{gathered} $$

(1)

The boundary conditions when solving the equations have the form:

$$M\left( R \right) = {{M}_{0}},~\,\,\,M\left( 0 \right) = 0,~\,\,\,P\left( R \right) = {{P}_{{\text{s}}}}.$$

(2)

The error in measuring the mass of Venus is less than 0.01%, and for our purposes it is meaningless to take it into account. As М₀, we take a fixed value М₀ = 4.8673 × 10²⁴ kg for all models (Saliby et al., 2023). The mass of the atmosphere has already been subtracted from this value.

System (1) contains the equation of state of matter ρ = ρ(P), which is unknown for Venus. We take the equation of state from the PREM Earth model (Dziewonski and Anderson, 1981) as the basis for our models. We will vary the density distribution on Venus relative to the density on Earth using two parameters, A and B, similar to the paper (Amorim and Gudkova, 2023).

Equations of state in the mantle ρ_m(P) and in the core ρ_c(P) of Venus is defined as:

$${{\rho }_{{\text{m}}}}(P) = A\rho _{{\text{m}}}^{{{\text{PREM}}}}(P),\,\,\,\,{{\rho }_{{\text{c}}}}(P) = B\rho _{{\text{c}}}^{{{\text{PREM}}}}(P).$$

(3)

Models with A > 1 correspond to a planet with a mantle denser than the Earth’s. Models with A < 1 correspond to a planet with a mantle lighter than the Earth’s. Similarly, in the case of the core for parameter B. The difference in the equation of state of matter on Venus compared to Earth may be due to differences in composition and temperature distribution. If, for example, Venus’ mantle is lighter than the Earth’s, this could indicate a composition containing less iron, a higher temperature, or a combination of these two factors.

Based on various papers on the topography and gravimetry of Venus, we assume a crustal thickness of 25 km and a constant density of 2900 kg/m³ (James et al., 2013; Jiménez-Díaz et al., 2015; Yang et al., 2016).

In addition to parameters A and B, each of our models of the internal structure of Venus is characterized by the value of the core radius R_c. The planet model must have a fixed mass and therefore A, B and R_c cannot be changed independently. For each combination of two of these values, the third can take only one specific value. We take R_c and B as the two main parameters, and the value of A is selected so that the mass of the model planet coincides with М₀.

So, when constructing the model, we set the values of R_c and B. As an initial approximation, we assume that A = 1 and integrate system (1) from the surface to the center of the planet. Next, using Newton’s method (an iterative method for finding the root of a given function), we look for the value of parameter A at which the second condition from (2) is exactly satisfied. Integration of the system of differential equations (1) and search for A are performed using Scipy library functions (Virtanen et al., 2020).

In models of Venus with a large core, the transition from the silicate mantle to the iron core occurs at lower pressures than the pressure at the Earth’s core mantle boundary (hereinafter CMB). In such cases, we approximate the equation of state of the Earth’s outer core by a 4th order polynomial and extrapolate it to the pressure region $P < P_{{{\text{CMB}}}}^{{{\text{PREM}}}}$. In models with a small core, the mantle core boundary occurs at higher pressures than $P_{{{\text{CMB}}}}^{{{\text{PREM}}}}$, and, similarly, we extrapolate the equation of state of the Earth’s mantle to the region with $P > P_{{{\text{CMB}}}}^{{{\text{PREM}}}}$.

Once A has been successfully determined, the density, pressure, mass and gravitational acceleration profiles for the given model are calculated. The profiles of the compression modulus K and the shear modulus μ are obtained based on the distributions K(ρ) and μ(ρ) from the PREM model. The value of the core radius R_c varies from 2800 to 3600 km, and the value of B from 0.98 to 1.02 (i.e., the density of the core of Venus is within ±2% of the density of the Earth’s core). With this combination of parameters, a total of 51 models of the internal structure of Venus were obtained.

Figure 1 shows the dependences ρ(l), ρ(P), μ(l) and K(l) for three models, where l is the depth. One of them (with R_c = 3200 and B = 1) can be considered Earth-like, and the rest differ markedly from the Earth model according to the equations of state of the mantle and core. The model with a very large and dense core (R_c = 3600 and B = 1.02) has a light mantle, and the model with a small and light core (R_c = 2800 and B = 0.98) has an extensive and heavy mantle. These two models are extreme, and all others fall in between. For comparison, Fig. 1 also shows dependences for the PREM Earth model.

Fig. 1.

For three models of Venus, the following dependences are given: (a) density versus depth; (b) density versus pressure; (c) shear modulus versus depth; (d) compression modulus versus depth. The following models of Venus are considered: with an Earth-like structure (R_c = 3200 km, B = 1), with a small and light core (R_c = 2800 km, B = 0.98), with a large and dense core (R_c = 3600 km, B = 1.02).

Figure 2 shows the values of parameter A for all models. The dashed lines highlight the “most Earth-like” models, for which А ∈ [0.98, 1.02]. The remaining models have mantles either significantly heavier or significantly lighter than the Earth’s.

Fig. 2.

Values of parameter A for a set of models of the internal structure of Venus. Dashed lines highlight Earth-like models with A in the range from 0.98 to 1.02. Models with A = 1 correspond to a planet with a mantle density similar to PREM.

Figure 3 for all models shows the pressure values at the center of the planet. Even in a model with a very large and heavy core (R_c = 3600 km, B = 1.02) the pressure at the very center of Venus is about 8 GPa less than the pressure at the boundary of the Earth’s inner core. Lower pressure values are associated with the reduced mass of Venus compared to Earth.

Fig. 3.

Pressure values at the center of Venus for a set of internal structure models. The dashed line shows the pressure value at the boundary of the Earth’s inner core (EIC boundary).

From the analysis of Figs. 2 and 3, we can conclude that the presence of a solid inner core of Venus is possible only in three cases: (1) the proportion of admixtures of light elements in the Venusian core is significantly less than that of the Earth; (2) temperatures in the core of Venus are noticeably lower than in the core of the Earth; (3) a combination of these two factors.

It is, however, often discussed in the literature that Venus’ lack of plate tectonics and high surface temperatures may prevent efficient convection in the mantle, and therefore the temperature in the interior of Venus may be quite high (see, for example, Smrekar et al., 2018; O’Neil, 2021). In such a case, a solid inner core can only exist when it contains very few traces of light elements compared to the Earth’s inner core. All our models have a completely liquid core.

The moment of inertia of Venus was measured very recently (Margot et al., 2021) and is 0.337 ± 0.024. The uncertainty is still too high to determine the internal structure of the planet with the desired accuracy, but, nevertheless, this observed value can be used to assess the likelihood of the models.

The values of the moment of inertia of all constructed models are shown in Fig. 4. The dashed lines highlight the interval 0.337 ± 0.024, and the blue solid line, for comparison, shows the Earth’s moment of inertia. It can be noted that all models fall within the ±1σ interval with a margin. Models with a large core are furthest from the mean value of 0.337, and those closest to it are those with core radii ranging from 3000  to 3250 km.

Fig. 4.

Values of the moment of inertia for the constructed models of the internal structure of Venus. The dashed lines highlight the interval 0.337 ± 0.024 (Margot et al., 2021), the blue solid line is the Earth’s moment of inertia.

Due to the large error in the measured value of the moment of inertia of Venus, we will use another observed value to continue our study of the internal structure of the planet. This is the tidal Love number k₂. In the following sections, we will discuss the method for calculating tidal deformation, the Andrade rheological model, and the viscosity distribution on Venus.

CALCULATION OF LOVE NUMBERS AND INFLUENCE OF THE ATMOSPHERE

The method for calculating Love numbers in this paper is similar to the method for calculating Love numbers for Earth, and the method described in detail in (Amorim and Gudkova, 2024), but with two differences.

(1) In the constructed models of Venus there is no internal core, and the integration of tidal deformation begins from the boundary of the liquid core with the initial conditions from the paper (Saito, 1974).

(2) The influence of the dense atmosphere of Venus on the Love numbers is taken into account.

We will use the same notation as in (Amorim and Gudkova, 2024). Tidal deformation is expressed in terms of six quantities: y₁ and y₃ have the meaning of radial and tangential displacements that arise due to tidal deformation; y₂ and y₄, are radial and tangential stress components, y₅ is the change in gravitational potential, and y₆ depends on y₅, y₁ and on the density of the medium. More detailed information about these quantities and the integration of tidal deformation over the planet can be found in the papers (Alterman et al., 1959; Saito, 1974; Michel and Boy, 2022; Amorim and Gudkova, 2024).

When calculating the Love numbers of a planet without an atmosphere (or with a rarefied atmosphere, which has virtually no effect on tidal deformation), the following boundary conditions on the surface are often used:

$$\begin{gathered} y_{2}^{{\text{S}}} = 0,\,\,\,\,y_{4}^{{\text{S}}} = 0, \\ y_{6}^{{\text{S}}} = \left( {2n + 1} \right)g_{0}^{{\text{S}}} - \left( {n + 1} \right){{y_{5}^{{\text{S}}}} \mathord{\left/ {\vphantom {{y_{5}^{{\text{S}}}} R}} \right. \kern-0em} R}, \\ \end{gathered} $$

(4)

where R is the radius of the planet, and $g_{0}^{{\text{S}}}$ denotes gravitational acceleration on an undisplaced surface. Here and below, the superscript S denotes the value of the quantity on the surface.

The first two inequalities mean that there is no stress on the surface. If there is an atmosphere above the surface, the condition on y₄ will not change in any way, since this quantity is proportional to the shear modulus of the medium (see Amorim and Gudkova, 2024), and in gases it is equal to zero. How the remaining two conditions change will be discussed below.

The new condition on y₂ is obtained from the same considerations as the condition during the transition from the Earth’s inner core to the outer core (Amorim and Gudkova, 2024). In liquid and gaseous media, the following relationship holds (Saito, 1974):

$${{y}_{2}} = {{\rho }_{0}}\left( {{{g}_{0}}{{y}_{1}} - {{y}_{5}}} \right).$$

(5)

Therefore, from the condition of continuity of y₁, y₂ and y₅ we obtain a new condition on y₂:

$$y_{2}^{{\text{S}}}~\,\, = {{\rho }_{{\text{A}}}}\left( {g_{0}^{{\text{S}}}y_{1}^{{\text{S}}} - y_{5}^{{\text{S}}}} \right),$$

(6)

where ρ_A denotes the density of the atmosphere directly above the planet’s surface.

The third condition in (4) is obtained from the properties of the potentials and the jump in the derivative of the potential of y₅ due to the jump in density during the transition from the crust to vacuum. If we do not neglect the fact that there is a medium with nonzero density above the surface, an additional term should appear in the third condition (4):

$$y_{6}^{{\text{S}}} = \left( {2n + 1} \right)g_{0}^{{\text{S}}} - \left( {n + 1} \right){{y_{5}^{{\text{S}}}} \mathord{\left/ {\vphantom {{y_{5}^{{\text{S}}}} R}} \right. \kern-0em} R} - 4{{\pi }}G{{{{\rho }}}_{{\text{A}}}}y_{1}^{{\text{S}}}.$$

(7)

The new term, in the case of Venus, is approximately 0.3–0.5% of the rest. There should be one more term in (7), which depends on the change in atmospheric potential due to tidal deformation. Its value, however, is unknown and can only be calculated by integrating the differential equations from the paper (Saito, 1974) over the atmosphere.

Even on Venus, the mass of the entire atmosphere is only 0.01% of the mass of the planet. Since the change in atmospheric potential is proportional to the mass of the atmosphere itself, we believe that its contribution to (7) is small and can be neglected. Thus, the system is closed at the surface without the need to integrate atmospheric deformation.

The new boundary conditions on the surface then take the form:

$$\begin{gathered} y_{2}^{{\text{S}}}~\,\, = {{\rho }_{A}}\left( {g_{0}^{{\text{S}}}y_{1}^{{\text{S}}} - y_{5}^{{\text{S}}}} \right),\,\,\,\,y_{4}^{S} = 0, \\ y_{6}^{{\text{S}}} = \left( {2n + 1} \right)g_{0}^{{\text{S}}} - \left( {n + 1} \right){{y_{5}^{{\text{S}}}} \mathord{\left/ {\vphantom {{y_{5}^{{\text{S}}}} R}} \right. \kern-0em} R} - 4{{\pi }}G{{{{\rho }}}_{{\text{A}}}}y_{1}^{{\text{S}}}. \\ \end{gathered} $$

(8)

Our calculations show that these “atmosphere” corrections reduce the Love numbers by approximately 3%, which is comparable to the ratio of the atmospheric density ρ_A to the density of the planet’s crust. In the paper (Dumoulin et al., 2017), the atmosphere is taken into account by integrating its deformation without the approximation that we made; as a result, the atmosphere reduces the Love numbers by 3–4%, which is very close to our results.

In the paper (Saliby et al., 2023), the atmosphere is also taken into account when calculating Love numbers, but it is stated that its influence is 7–8%, which is twice as much as in the paper (Dumoulin et al., 2017) and in this article. The explanation for this is most likely the following: in (Saliby et al., 2023), the atmosphere is approximated as a layer with a constant density of 36.5 kg/m³ and a thickness of 100 km, and the mass of such an atmosphere is approximately 3.5 times greater than the real mass of the atmosphere of Venus, 4.77 × 10²⁰ kg (Taylor, 1985).

Thus, we believe that our approximation allows us to take into account the influence of the atmosphere when calculating Love numbers with good accuracy and in a very simple way, simply by changing the boundary conditions on the surface without additional integration.

RHEOLOGICAL MODEL AND VISCOSITY

At long periods, characteristic of tides, inelasticity plays an important role in deformations and must be taken into account when calculating Love numbers (Castillo-Rogez et al., 2011; Efroimsky, 2012). In the case of Venus, the solar tide period is very long compared to tides on Earth, 58.4 days, which necessitates the need to account for inelasticity in internal structure models using a suitable rheological model.

Experiments at different temperatures and pressures have shown that the Andrade model gives a good description of the inelasticity and shear frequency dependence of the shear modulus in various minerals (Jackson et al., 2002; Castillo-Rogez et al., 2011; Efroimsky, 2012). In addition, the Andrade model is parsimonious compared to other more complex models and depends on only two empirical parameters: α and ζ. It is for these reasons that Andrade rheology is actively used in models of the internal structure of Venus and other bodies of the Solar System (Castillo-Rogez et al., 2011; Efroimsky, 2012; Dumoulin et al., 2017; Xiao et al., 2021; Petricca et al., 2022; Saliby et al., 2023; Amorim and Gudkova, 2024).

Andrade rheology parameters have been measured for a variety of minerals (see, for example, Jackson et al., 2002). However, the laboratory conditions under which they were obtained are very different from mantle conditions (very high temperatures and pressures), and the periods of shear deformations in the experiments are much shorter than the characteristic periods of tides in the Solar System. For these reasons, two important problems arise: whether Andrade rheology is applicable in the conditions of the mantles of planets and satellites, and, even if applicable, the values of its parameters that should be used in models are unknown.

In order to solve these problems, the rheology of the Earth’s interior was studied in the paper (Amorim and Gudkova, 2024). Since the internal structure of the Earth is known much better than that of any other planet, and its Love numbers are measured with fairly good accuracy, our planet is a good candidate for “calibrating” the rheological equation.

The paper (Amorim and Gudkova, 2024) used the PREM model, measurements of the Earth’s Love numbers at the frequency of the semidiurnal lunar tide M2, and modern estimates of viscosity in its interior. Tidal deformation has been calculated for thousands of different combinations of parameters α and ζ. Comparing the model values with the observed values allowed us to verify that the Andrade model does indeed successfully describe the inelasticity of the Earth’s mantle, and also to determine which parameter values fit best.

Andrade rheology gives the dependence of the shear modulus μ on the deformation frequency χ. It depends on the elastic value of the shear modulus μ₀, on the viscosity of the medium η, and on two dimensionless parameters α and ζ. The law for converting the elastic shear modulus into a complex one has the form

$$\mu \left( \chi \right)~\,\, = \,\,~{{\mu }_{0}}{{[1 + {{\left( {i\chi {{\tau }_{{\text{M}}}}\zeta } \right)}^{{ - \alpha }}}\Gamma \left( {1 + \alpha } \right) - i{{\left( {\chi {{\tau }_{{\text{M}}}}} \right)}^{{ - 1}}}]}^{{ - 1}}},$$

(9)

where τ_M = η/μ₀ is the Maxwell time, and Г is the gamma function.

In the paper (Amorim and Gudkova, 2024), we obtained intervals of values α and ζ that successfully describe the inelasticity of the Earth at the frequency M2. The parameter ζ varied from 1 to 10⁵, and for each value of ζ, a certain range of acceptable values α $~ \in$ [α_min, α_max] can be identified. They are given in Table 2, and these combinations are used in our Venus models. This approach makes it possible to reduce the uncertainty in the model Love numbers of Venus compared to the results of the paper (Amorim and Gudkova, 2023).

Table 2.  Used values of Andrade rheology parameters α and ζ

Andrade rheology (9) also depends on viscosity, the values of which are unknown for the interior of Venus. In this regard, we have constructed two limiting model viscosity distributions for Venus, and the real viscosity profile most likely lies between them. Let us denote the viscosity distributions in the interior of Venus as an LVM (low viscosity model) and an HVM (high viscosity model); they are given in Table 3. These values are based on the distribution of viscosity in the Earth’s interior, which is used in the paper (Amorim and Gudkova, 2024), but with some modifications to take into account possible differences in temperatures in the interior of these two planets.

Table 3.  Limiting model viscosity distributions on Venus (in Pa s)

For each viscosity model and for each combination of rheological parameters α and ζ, a new shear modulus profile is calculated using formula (9), and this profile is used in the calculation of tidal deformation. Since the shear modulus μ is a complex quantity, the resulting Love numbers are also complex.

SELECTION OF MODELS BY LOVE NUMBER k ₂

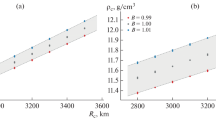
For each of the 51 models of the internal structure of Venus, Love numbers were calculated for two viscosity distributions and 12 combinations of rheological parameters. A total of 1224 inelastic models of Venus were calculated. For a fixed core radius R_c, we have a certain range of k₂ values due to the variation of B, α, ζ and η. Figure 5 shows the values of the real part of k₂ for the LVM and HVM separately, and Fig. 6 for both viscosity distributions.

Fig. 5.

Values of the real part of the tidal Love number k₂ for Venus models depending on the core radius for limiting viscosity models: (a) LVM; (b) HVM. Dashed lines highlight the interval of the observed value 0.295 ± 0.066 (2σ) from (Konopliv and Yoder, 1996). The colored triangles represent k₂ values for some models with specific combinations of B, ζ, and α.

Fig. 6.

Values of the real part of the tidal Love number k₂ of the constructed models of Venus depending on the radius of the core. For each R_c value, there is an interval of k₂, which is obtained by varying the viscosity, B, α and ζ within the limits discussed in the text. Dashed lines highlight the interval of the observed value 0.295 ± 0.066 (2σ) from (Konopliv and Yoder, 1996). The colored dots indicate the k₂ values of specific models.

From Fig. 5, we can draw the following conclusion: for the LVM, models with R_c = 3300 km are closest to the central value 0.295 of the observed value of the Love number k₂, and for the HVM with R_c = 3350 km. It can also be noted that with the same values of B, α and ζ, the values of k₂ for the HVM are smaller than for the LVM. Indeed, with increasing viscosity, α or ζ, the Love number k₂ tends to its elastic value. For each value of R_c we have an interval of k₂, which is obtained by varying the viscosity, B, α and ζ within the limits discussed above. From Fig. 6 it can be seen that models with a core radius of 3300 km have k₂ values closest to the central value of 0.295, and models with R_c ≤ 2950 km or R_c ≥ 3600 km can be confidently excluded.

ANALYSIS OF MODELS PROBABILITY

Based on the measured values of the moment of inertia (Margot et al., 2021) and the values of the Love number k₂ (Konopliv and Yoder, 1996), the probability of a particular model can be estimated using the following formula:

$$p({{k}_{2}},I) = \exp \left( { - \frac{{{{{({{k}_{2}} - {{\mu }_{1}})}}^{2}}}}{{2\sigma _{1}^{2}}} - \frac{{{{{(I - {{\mu }_{2}})}}^{2}}}}{{2\sigma _{2}^{2}}}} \right),$$

(10)

where p is the probability, k₂ and I the Love number and dimensionless moment of inertia of a given model, μ₁ = 0.295, σ₁ = 0.033, μ₂ = 0.337, and σ₂ = 0.024.

Figure 7 shows all calculated models on the plane I × k₂. Colored level lines highlight areas on this plane with certain probability values calculated using formula (10). Each value of the moment of inertia in Fig. 7 corresponds to one of 51 models of the internal structure of Venus with a certain combination of R_c and B, and for each of them the Love number can be calculated for two viscosity distributions and 12 combinations of Andrade rheology parameters. From Fig. 7 it can be seen that the value of the Love number k₂ plays a more important role in determining the probability of the model. This is because all models are within 1σ of the observed value of the moment of inertia, but not all models fall within 1σ of the observed value of k₂.

Fig. 7.

All calculated models of the internal structure of Venus on the plane I × k₂. The intersection of the dashed lines indicates the central values of I = 0.337 and k₂ = 0.295. The colored lines are the level lines of the probability function according to formula (10).

In Fig. 8, only models with R_c = 3100, 3300 and 3500 km are shown on the plane I × k₂. For each value of R_c, we have three groups of models corresponding to B = 0.98, 1.00, 1.02, and for each of them we have a certain interval of k₂ due to varying viscosity and rheology parameters.

Fig. 8.

Models with specific values of the core radius on the plane I × k₂. The intersection of the dashed lines indicates the central values of I = 0.337 and k₂ = 0.295. The level lines of the probability function are shown, as in Fig. 7.

Models corresponding to one value of R_c can be outlined by a certain rectangle, and the probability that the radius of the core of Venus is exactly this can be estimated by averaging the probability function (10) over this rectangle:

$$P({{R}_{{\text{c}}}}) = \frac{1}{{\Delta {{k}_{2}} \times \Delta I}}\int\limits_{k_{2}^{{\min }}}^{k_{2}^{{\max }}} {\int\limits_{{{I}^{{\min }}}}^{{{I}^{{\max }}}} {p({{k}_{{2,}}}I)d{{k}_{2}}dI} } ,$$

(11)

where $k_{2}^{{{\text{min}}}}$, $k_{2}^{{{\text{max}}}}$, ${{I}^{{{\text{min}}}}}$ and ${{I}^{{{\text{max}}}}}$ are the minimum and maximum values of k₂ and I of models with the specific R_c value considered,$~~~~~~~~{{\Delta }}{{k}_{2}} = k_{2}^{{{\text{max}}}} - k_{2}^{{{\text{min}}}}{\text{\;}}$ and ${{\Delta }}I = {{I}^{{{\text{max}}}}} - {{I}^{{{\text{min}}}}}$.

Figure 9 shows the probabilities estimated using formula (11) for all considered R_c values. The models with R_c = 3300 km have the highest probability. Indeed, one can see from Fig. 8 that these particular models almost completely fall into the region with p > 0.9.

Fig. 9.

Probability of each value of the radius of the Venus core. The models with R_c = 3300 km have the highest probability. If we approximate points with P > 0.3 with a normal distribution (dashed line), R_c = 3288 ± 167 km.

Distribution in Fig. 9 is not symmetrical with respect to R_c = 3300 km. This is because the peak of the probability based only on the moment of inertia is located around R_c = 3150 km (see Fig. 4). As R_c decreases from 3300 to 3150 km, the probability for k₂ decreases, but the probability for I increases. As R_c increases from 3300 km, the probabilities according to the two criteria decrease simultaneously.

We approximated points with a probability higher than 0.3 using a normal distribution and obtained the following estimate for the radius of the core of Venus: R_c = 3288 ± 167 km.

PROSPECTS FOR REFINING MODELS

The moment of inertia and tidal Love number k₂ of Venus have so far been measured with large errors, which do not allow us to determine the internal structure of the planet with the desired accuracy. In order to refine these geophysical parameters, the VERITAS (Cascioli et al., 2021) and EnVision (Rosenblatt et al., 2021) missions are planned.

The paper (Cascioli et al., 2021) notes that the VERITAS mission will determine the moment of inertia and k₂ with an accuracy of about 0.3 and 0.2%. The EnVision mission should measure k₂ with an accuracy of 0.3% and moment of inertia with an accuracy of 1.4% (Rosenblatt et al., 2021).

Another geophysical parameter that can provide valuable information is the tidal phase lag ε. It depends on the imaginary part of k₂, and is determined by the formula:

$$\varepsilon = - \frac{{\operatorname{Im} ({{k}_{2}})}}{{2\left| {{{k}_{2}}} \right|}}.$$

(12)

The tidal phase lag of Venus has not yet been measured, but the VERITAS and EnVision missions plan to determine it with an error of no more than 0.1°. Therefore, we have computed its values for all the calculated models and, when this parameter is measured, comparison of the model results with the observed value will provide important information about the viscosity in the interior of Venus.

Figure 10 shows the values of ε for all models. If the tidal phase shift turns out to be above 0.5°, then this definitely means that the viscosity in the mantle of Venus is quite low and, accordingly, the temperatures are high compared to the Earth. At ε < 0.5° the situation is ambiguous and conclusions about viscosity will depend on the values of the Love number k₂ and the moment of inertia I.

Fig. 10.

Values of the tidal phase shift ε for all calculated models. Models with low viscosity have large phase shift values, and models with high viscosity have small ε.

The VERITAS mission should also determine the Love number h₂ with an accuracy of about 20–33% (Cascioli et al., 2021). Measuring this parameter, even with such precision, will provide important information about the interior of Venus. Its values for all considered models are shown in Fig. 11.

Fig. 11.

Values of the tidal Love number h₂ for all calculated models.

CONCLUSIONS

Studying the internal structure of Venus is the key to understanding the evolution of this planet. In this regard, we built more than a thousand models of its interior, and assessed their probability based on the measured values of the tidal number k₂ and the moment of inertia I.

The basis of models of any planet is its internal structure, i.e., density and pressure profiles. Our models are described by two main parameters: the core radius R_c and the coefficient B, which reflects the ratio of the density in the core of Venus to the density in the Earth’s core. We vary R_c from 2800 to 3600 km, and the coefficient B from 0.98 to 1.02. A total of 51 models of the internal structure of Venus were built.

The results show that even with a very large and dense core, the pressure at the very center of Venus does not reach the pressure at the boundary of Earth’s inner core. This means that if the composition of Venus is close to that of Earth, then it cannot have an internal solid core. This, in turn, may be related to Venus’ lack of its own magnetic field and says a lot about the planet’s thermal evolution.

In this paper, an approximation was proposed that allows us to take into account the influence of the dense atmosphere of Venus on its tidal deformation in a very simple way. Our results show that the atmosphere reduces k₂ by about 3%. This value is quite significant and, in the future, the influence of the atmosphere should not be neglected.

To take into account the inelasticity of the subsurface when calculating Love numbers, Andrade rheology is used. Uncertainty in the values of the parameters of this rheological model in the interiors of planets gives rise to significant errors in the final results when solving various problems of planetary geophysics. In order to reduce these errors, in the paper (Amorim and Gudkova, 2024), we “calibrated” Andrade rheology on Earth and obtained the values of the parameters α and ζ that best describe the tidal deformation of the Earth. These are the values used in our Venus models. Thanks to this, we were able to significantly reduce the uncertainty in the model values of k₂ compared to the results of the paper (Amorim and Gudkova, 2023).

The moment of inertia was calculated for all constructed models (51 models). Love numbers were calculated for them for two viscosity distributions and 12 combinations of rheological parameters. Comparison of model values of k₂ and moment of inertia with observed values (Konopliv and Yoder, 1996; Margot et al., 2021) made it possible to assess the likelihood of the constructed models. It was found that the most probable models are those with a core radius in the range of 3288 ± 167 km.

The VERITAS (Cascioli et al., 2021) and EnVision (Rosenblatt et al., 2021) missions plan to obtain more accurate values of k₂ and the moment of inertia and measure two still uncertain geophysical parameters— tidal phase shift and Love number h₂. Comparing the results of these missions with the models of Venus presented in the paper will make it possible to clarify the internal structure of Venus, study its evolution in more detail and understand why the development paths of Earth and its twin diverged so much.