Models of the Internal Structure of the Earth-like Venus

Abstract

A working model of the Venusian interior (radial distribution of the density, pressure, gravitational acceleration, and velocities of compressional and shear seismic waves) has been constructed based on observational data and general experience of geophysics. Corrections for the influence of the planetary interior anelasticity on the value of the model Love number k₂ were calculated. The equilibrium figure parameters of Venus were determined.

INTRODUCTION

Unlike the atmosphere and the surface of Venus, which have been intensively studied by space probes, the interior structure of the planet has not been sufficiently studied because of large error ranges in the observational data. Seismic data could serve as a proper tool for determining the internal structure of the planet. Due to harsh conditions on the surface of Venus (temperature 740 K, pressure 9.3 MPa), a seismic experiment has not yet been carried out. Currently, a joint mission of the Russian Space Agency (ROSCOSMOS) and the National Aeronautics and Space Administration (NASA), which contains a launch of the Venera-D spacecraft with a lander, is under design. The lander (carrying a seismometer as one of the onboard instruments) is to operate on the surface of the planet for approximately two months. The European Space Agency is developing the EnVision mission (Ghail et al., 2018), the objective of which is to refine the data on the gravitational field of Venus. The Venus Emissivity, Radio Science, InSAR, Topography, and Spectroscopy (VERITAS) mission has been proposed to improve the accuracy of the gravitational field of Venus to 3 mGal with a spatial resolution of 145 km (Smrekar et al., 2016).

Due to the planned experiments, there is a growing interest in studies of the Venusian interior; among these studies, there are papers on the thermal history and rheology of Venus and the estimation of the crust thickness and lithosphere structure from the data on the gravitational field and topography of Venus (Li et al., 2015; Jimenez-Diaz et al., 2015; Yang et al., 2016; Karimi and Dombard, 2016; Dumoulin et al., 2017).

Usually, when constructing a model of the internal structure of a planet, developers use data based on the gravitational field and topography: the mass, mean radius, moment of inertia, and the Love tidal number k₂, which is a functional of the distribution of elastic parameters in the planetary interior. As distinct from the Earth and Mars, there are no observational data that allow the moment of inertia of Venus to be calculated (only two decimal places are available in the estimates, and the value of the dimensionless moment of inertia I/MR² varies from 0.327 to 0.342). The moment of inertia is one of the main restrictions on the interior model. The polar and equatorial moments of inertia—C and A ≈ B, respectively—contained in the precession constant H = (C − A)/C are unknown for Venus; and it is not clear whether H will be determined in the foreseeable future. Zharkov and Gudkova (2019) obtained the model value for the inertia moment and the prognostic value of the precession constant by taking into account the data on the gravitational field. The model value of H is very small, approximately 2 × 10⁻⁵. Consequently, there is apparently no way to estimate the inertia moment of Venus in the immediate future.

A single restriction obtained from the Magellan and Pioneer Venus Orbiter data is the Love number k₂ for Venus; however, it was measured with a low accuracy. Due to the insufficient accuracy in estimating a range of the Love tidal number k₂ (k₂ = 0.295 ± 0.066) (Konopliv and Yoder, 1996), which was determined from the solar tide on Venus (its period is 58.4 days), and the absence of the data on anelastic properties of the Venusian interior, the problem of whether the planetary core is in a liquid or a solid state and whether there is any inner solid core is still under discussion (Dumoulin et al., 2017). Acceptable values for the core radius are within a range of 2800 to 3500 km.

The evaluation of k₂ meets certain difficulties, since a clear understanding of the Venusian interior anelasticity is required. The value of k₂ depends on the interior anelasticity under the tidal wave period. Since the elastic value of k₂ is calculated when constructing a model of the internal structure, it is necessary to introduce the correction for anelasticity, which takes into account the fact that tidal deformations under large periods occur in the unsteady creep regime. This problem will be considered in the present paper.

In its mechanical parameters—mass, mean radius, and mean density—Venus is considered as a twin planet of the Earth. The Earth-like models of the Venusian interior are calculated with the equations of state of the terrestrial material determined from dynamical and static experimental data.

Some models of the Venusian interior (Zharkov et al., 1981; Zharkov and Zasurskii, 1982; Kozlovskaya, 1982; Yoder, 1995; Mocquet et al., 2011; Aitta, 2012) were constructed based on a parametric model of the Earth (Dziewonski et al., 1975). In the papers by Kozlovskaya (1982) and Zharkov (1983), a large number of Venus models were constructed and the radial distribution of density, pressure, and gravitational acceleration were obtained to determine the differences between the composition of Venus and the mean composition of the Earth. Zharkov and Zasurskii (1982) thoroughly analyzed the models of the Venusian interior on the basis of models of the Earth and other data and created a physical model of Venus (distribution of thermal capacity, thermal expansion coefficient, adiabatic temperature, and effective viscosity). It was assumed that the depth of the Venusian lithosphere is 200 km, and the temperature at this depth is ~1200°C. Further, by assuming the temperature distribution in the mantle to be a smooth continuous function of depth like that of the Earth, the authors estimated the temperature in the phase transition zone (approximately 1500°C) and found that the temperature in the convective lower mantle is adiabatically distributed and is ~3500 K on the boundary between the core and the mantle. The temperatures in the core are assumed to be adiabatic. As a result, the temperature at the center of Venus was determined to be ~4670 K. The studies revealed important differences between the Earth and Venus rather than only the similarity and showed that each of the planets has its own unique characteristics.

Since no seismic data are available for Venus, the depths of the phase transitions, which allow the reference points in the temperature distribution to be determined from the phase diagrams, are unknown. It is clear that the Venusian interior is under high temperatures; however, in spite of the importance of this problem, uncertainties in the actual temperature distribution still remain, which is seen from the comparison of the calculated theoretical profiles presented by Steinberger et al. (2010) and Armann and Tackley (2012). Due to the uncertainties in the temperature distribution in the Venusian interior, the question of whether the core of Venus is liquid or solid remains open (Dumoulin et al., 2017).

Until now, the crust of Venus has been considered to be thick. The crust thickness was assumed to be 60−70 km, which was justified by the fact that the basalt-eclogite phase transition should take place in basalts at this depth. In plate tectonics, there is a mechanism for the crust sinking down into the mantle; for Venus, such a mechanism has not been proposed, and the crust accumulates (see, e.g., Zharkov, 1992). The thermal evolution models of the planet and the interpretations of data on the topography and gravitational field yield estimates of the crust thickness varying from 15 to 35 km (Breuer and Moore, 2007; Wieczorek, 2007). In some recent papers (Jimenez-Diaz et al., 2015; O’Rourke and Korenaga, 2015; Yang et al., 2016), the estimate of the crust thickness was revised downwards; moreover, it was noted that the mean thickness of the crust may be substantially smaller, about 25−30 km, while the regional values of the crust thickness vary from 12 to 65 km (Yang et al., 2016). Dumoulin et al. (2017) continue to assume the crust thickness at 60 km. The analysis of rock samples lead to density estimates in a range of 2700−2900 kg/m³, which corresponds to the composition of basalt (Grimm and Hess, 1997).

Hereafter, we present the Earth-like models of the internal structure of Venus that satisfy the available data regardless of whether the crust is thick or thin. We also estimate the changes in the Love number k₂ due to anelasticity and calculate the equilibrium figure parameters of the planet for the model density distribution.

EARTH-LIKE MODELS OF THE VENUSIAN INTERIOR

The observational data used for constructing the model of the internal structure of Venus are gathered in Table 1: the mass M, mean R and equatorial R_e radii, mean density ρ, dimensionless moment of inertia I/MR², and Love number k₂. Table 1 also contains the rotation period τ and the small parameter m of the figure theory.

Table 1.   Data of observations of Venus

To calculate models of the internal structure of planets, the hydrostatic equilibrium equation and the equation of conservation of mass are used and the equation of state is specified. The density profile should satisfy the moment of inertia of the planet and the Love number k₂. Venus is close to the Earth in mass and size (Table 1), and this circumstance is taken into account as a basis of our approach for constructing the Venusian interior model. We assume the equation of state of the Earth as the initial one. An additional convenience of this choice is that the effect of temperature on the equation of state is automatically accounted for, since the temperature distributions in both planets at a depth exceeding ~200 km are apparently close.

The simple parametric Venus model (PVM) (Zharkov and Zasurskii, 1982) will be assumed as a basic one (see Table 2). In this model the distribution of the density ρ(x) and the velocities of the compressional and shear waves—V_p(x) and V_s(x), respectively—are specified by piecewise continuous analytic functions of the radius x (x = r/R is the dimensionless radius, and R = 6050 km is the mean radius of Venus). The continuous sections of the distributions are described by polynomials of x with degrees not exceeding three.

Table 2.   The simple parametric model of Venus (PVM) (Zharkov and Zasurskii, 1982)

A major problem in constructing the Venusian interior model is parametrization (crust thickness, depth of the phase transitions for silicates, and the core radius). In view of the present uncertainties, the variable model parameters are the core radius R_c (from 2800 to 3500 km), the crust thickness h_cr (from 30 to 100 km), and the mantle density ρ_m (see Table 3).

Table 3.   Parameters of the Venus model

The crust density is assumed to be 2800 kg/m³. The mantle density as a function of pressure is specified by introducing the coefficient A: ρ_m(P) = ρ(P) × A, where ρ(P) is the equation of state for the basic PVM. In this way, the curves ρ_m(P) are built by shifting the basic PVM up or down the density axis. Table 3 includes the models with both “lightened” and “weighted” silicate mantle as compared to the basic PVM. The density deviates from the basic model by less than 6%. If the coefficient A is less than unity, the iron content in the mantle silicates is lower than that assumed in the basic model. The mantle composition changes due to the change in the Fe molar fraction relative to magnesium Mg (Fe/(Mg + Fe)). As was shown by Zharkov (1992), the 1% decrease of the density corresponds to the 1.4% decrease of iron in the mantle silicates.

According to the data of cosmochemistry, the iron content in the mantle silicates should systematically decrease when passing from Mars to Mercury. If the coefficient A is less than unity, the models of Venus exhibit the iron deficit in the mantle silicates.

Several models of the Venusian interior are presented in Table 3. If the density distribution in the Venus model is known, a seismic model of Venus can be constructed. For this, the V_p and V_s functions for the Parametric Earth Model (PEM) should be used (Dziewonski and Anderson, 1981).

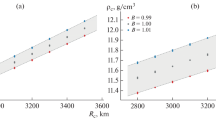
Figure 1 shows the distribution of the density ρ, the gravity g, and the velocities of compressional and shear waves, V_p and V_s, for the V_5 trial model of Venus. The model of Venus includes three layers: the crust, the mantle, and the core. The value of the moment of inertia for the models (see Table 3) is within a range of 0.326−0.344. For each of the models, the Love number k₂ was calculated. Figure 2 shows the dependence of the elastic part of the model Love number $k_{2}^{S}$ on the dimensionless moment of inertia I/MR² for a wide range of the crust and mantle composition and the core radius. It is seen from Fig. 1 and Table 3 that the Love number k₂ exhibits the strongest correlation with the core size. However, the dispersion in acceptable values of the Love number does not allow us to impose restrictions on the planetary core radius. As will be shown below, in applications to elastic models, the boundaries of the acceptable observed values should be moved at least 0.02−0.03 down due to the anelasticity effect.

Fig. 1.

The radial distributions of the density ρ, the gravity g, and the velocities of compressional and shear waves, V_p(x) and V_s(x), for the V_5 model, the parameters of which are listed in Table 3.

Fig. 2.

The elastic part of the Love number $k_{2}^{s}$ depending on the dimensionless moment of inertia I/MR² for several models of Venus presented in Table 3 (black circles, white circles, and black triangles correspond to the crust 70, 50, and 30 km thick, respectively). The horizontal solid line corresponds to the observed value of k₂. The horizontal dashed lines show a band of the acceptable observed values of k₂.

ANELASTIC EFFECTS

The interior models of Venus are elastic (the shear modulus is assumed to be independent of frequency), while the value of k₂ contains both the elastic and anelastic parts. To use k₂ as a limit for constructing the models for the Venusian interior, the estimate of k₂ should be reduced due to the interior anelasticity effect. The problem of partitioning the Love number k₂ into elastic and anelastic components was examined in detail for Mars by Zharkov and Gudkova (2005).

In this paper, to determine the correction for anelasticity, we take into account the similarity of the Earth and Venus in mechanical parameters (the mass, radius, and density) and assume the distribution Q_μ(l) inside a silicate layer of Venus to be that of the Earth. The four-layer piecewise constant distribution from the Earth model QML9 (Lawrence and Wysession, 2006) is assumed to be the initial one (Table 4): Q_μ = 600, 80, 143, and 276 for the depths in ranges of 0−80, 80−220, 220−400, and 400−670 km.

Table 4.   Values of the dissipative factor Q_μ(l) and changes in the shear modulus in four layers of the silicate layer of Venus in transition from the 1-second period to a period of 1 hour and 58.4 days, which correspond to the frequencies σ₁, σ₂, and σ₃, under values of n = 0.15 and 0.2 in formulas (1) and (2)

In a dissipative medium, like the Venusian interior, the dissipative function Q_μ(l), the shear modulus μ(l), and the tidal Love number of the planet k₂ depend on frequency.

The frequency dependence of the dissipative factor Q_i of the terrestrial interior is determined on the basis of the seismic and laboratory data (Zharkov, 2012). A review of recent studies of dissipative properties of the terrestrial interior can be found in the paper by Zharkov et al. (2017).

In the standard model of the Earth PREM, the value of Q_μ is constant in the interval of periods from ~1 s to ~1 h (3.6 × 10³ s), which corresponds to terrestrial seismology. This case is described by the creep logarithmic function (the Lomnitz model) (Zharkov, 2012), while the ratio of the shear moduli μ₀(σ) at two frequencies σ₁ and σ₂ is specified by the following formula (Akopyan et al., 1977)

$$\frac{{{{\mu }_{0}}({{\sigma }_{2}})}}{{{{\mu }_{0}}({{\sigma }_{1}})}} = 1 - \frac{2}{{\pi {{Q}_{{\mu }}}}}\ln \frac{{{{\sigma }_{1}}}}{{{{\sigma }_{2}}}}.$$

(1)

For lower frequencies, Q_μ weakly depends on frequency; this dependence is connected with the unsteady creep stage (Zharkov and Molodensky, 1979; Molodensky and Zharkov, 1982; Anderson and Minster, 1979; Smith and Dahlen, 1981; Zharkov et al., 1996) and described by the following formulas (Akopyan et al., 1977; Zharkov, 2012)

$$\frac{{{{\mu }_{0}}({{\sigma }_{2}})}}{{{{\mu }_{0}}({{\sigma }_{1}})}} = 1 - \frac{1}{{{{Q}_{{\mu }}}({{\sigma }_{1}})}}\left[ {{{{\left( {\frac{{{{\sigma }_{1}}}}{{{{\sigma }_{2}}}}} \right)}}^{n}} - 1} \right]{\text{cot}}\frac{{n\pi }}{2},$$

(2)

$${{Q}_{{\mu }}}({{\sigma }_{2}}) = {{Q}_{{\mu }}}({{\sigma }_{1}}){{\left( {\frac{{{{\sigma }_{2}}}}{{{{\sigma }_{1}}}}} \right)}^{n}}.$$

(3)

In Eqs. (2) and (3) the index n is within an interval of approximately 0.1−0.2.

In this paper, we will use the Lomnitz formula and Eq. (1) for the ratio of the shear moduli μ₀(σ) for the periods between 1 s and 1 h. In a range of periods between 1 h and 58.4 d, formula (2) is used. Let σ₁ be the frequency corresponding to a period of 1 s, while σ₂ will correspond to a period of 1 h = 3.6 × 10³ s. The frequency of the solar tidal wave on Venus, corresponding to a period of ~58.4 d ≈ 5 × 10⁶ s, will be denoted as σ₃. Formulas (1) and (2) allow the decrease in the shear modulus in transition from σ₁ to σ₃ to be estimated (see Table 4).

Table 4 presents the results of calculations for transformation of the initial distribution Q_μ(l) in the seismic band of periods (~1 s) to that in periods of 1 h and 58.4 d, the corresponding changes of the shear modulus in four layers of the silicate envelope of Venus, and the total change of the shear modulus. The value of n within an interval of approximately 0.15−0.2 was chosen according to the laboratory data and the experience of studying this problem for the Earth.

Due to anelasticity, the values of μ are smaller at 5 × 10⁶ s than those at 1 s by 5, 35, 23, and 11% in four layers, respectively. Since the number k₂ is roughly in inverse proportion to the shear modulus, the anelasticity effect of the interior leads to the increase of the Love number k₂ as compared to the k₂^s value for the elastic model.

The calculations showed that the use of the power index n within an interval of 0.15−0.2 yields the 8−12% increase of k₂. Thus, according to this estimate, the difference between the values of k₂ for 5 × 10⁶ and 1 s is 0.02−0.03, which is within the measurement error of the Love number.

The values of the Love number k₂ for the models of Venus with a liquid and a solid core noticeably differ. For the models with a solid core, k₂^s is approximately 0.17 (Yoder, 1995). Dumoulin et al. (2017) conclude that, due to the anelasticity effect, we cannot assert whether the core of Venus is in a liquid or a solid state.

Estimates of the anelasticity-induced changes in the value of k₂ depend on a choice of the dissipative factor of the planetary interior and the value of n in the creep function. If n is chosen to be 0.25−0.3, the presence of a solid core cannot be excluded. A step forward in solution of this problem can be reduction of the measurement errors, which will also allow the core radius and the iron content in the mantle to be determined more accurately.

THE EQUILIBRIUM FIGURE PARAMETERS OF VENUS

To construct an equilibrium figure, the equation of a standard spheroid (the figure of a planet) is sought in the following form (Zharkov and Trubitsyn, 1980; Zharkov and Gudkova, 2005)

$$r(s,\theta ) = s\{ 1 + {{s}_{0}}(s) + {{s}_{2}}(s){{P}_{2}}(t) + {{s}_{4}}(s){{P}_{4}}(t) + ...\} ,$$

(4)

where s is the mean radius (the radius of the equivalent-volume sphere), P₂(t) and P₄(t) are two first even Legendre polynomials that depend on even degrees of t = cosθ. The second-order value s₀(s) is connected with s₂(s) by the relationship

$$ - {{s}_{0}} = \frac{1}{5}s_{2}^{2}.$$

(5)

The external gravitational potential V(r, t) of an equilibrium planet also contains only even harmonics

$$\begin{gathered} V(r,t) = \frac{{GM}}{r} \\ \times \,\,\left\{ {1 - {{{\left( {\frac{{{{R}_{{\text{e}}}}}}{r}} \right)}}^{2}}J_{2}^{0}{{P}_{2}}(t) - {{{\left( {\frac{{{{R}_{e}}}}{r}} \right)}}^{4}}J_{4}^{0}{{P}_{4}}(t) - ...} \right\}, \\ \end{gathered} $$

(6)

where r is the distance to the center of a planet, R_e is the equatorial radius (the normalizing radius in V(r, t)), M is the mass of a planet, and G is the gravitational constant.

The figure theory is constructed by successive approximations. A small parameter of the figure theory is the dimensionless square of the angular rotational velocity of a planet

$$m = \frac{{{{\omega }^{2}}{{R}^{3}}}}{{GM}} = \frac{{3\pi }}{{G{{\rho }_{0}}{{\tau }^{2}}}},$$

(7)

where ω, τ, and ρ₀ are the angular velocity, the rotation period, and the mean velocity of a planet, respectively.

In the first-approximation figure theory, the function s₂(s) and the moment $J_{{\text{2}}}^{0},$ which are small values of the mth order, are kept in formulas (4) and (6), respectively. In this case, the reference surfaces are ellipsoids of revolution. In the second-approximation figure theory—the Darwin−De Sitter theory—the function s₄(s) and the moment $J_{{\text{4}}}^{0}$ are kept in (4) and (6), respectively, while the reference surfaces in the second approximation deviate from ellipsoids of revolution and the both functions s₄(s) and $J_{{\text{4}}}^{0}$ are of the order of m².

Venus is the most nonequilibrium planet in the Solar System. This fact is apparently not accidental, and it is connected with severe deceleration of the rotation of Venus by tidal friction in the past. In an earlier epoch, a young Venus rotated much faster, with a period of ~10 h (Zharkov and Trubitsyn, 1980). For an effectively equilibrium Venus, Zharkov and Gudkova (2005) assumed J₂/m to be 0.3 (i.e., almost the same value as that for the Earth) and noted that, due to cooling, the Venusian interior became very solid (or very viscous) and the figure of the planet was “fixed” in the state it was in the distant epoch. Consequently, this figure is not consistent with the current value of the angular rotational velocity of the planet. The ratio J₂/m = 0.312, which is assumed for an effectively equilibrium Venus, yields the value of the small parameter m = 0.15 × 10⁻⁶. This value is preserved from the epoch when the equilibrium figure of the planet was fixed; at that time, the rotational paleoperiod of Venus was ~15.7 days. In further calculations, the value of the small parameter was taken as that for an effectively equilibrium Venus.

For the model distribution of the density ρ(s), the equations of the figure theory in the second approximation make it possible to calculate the figure parameters ${{s}_{2}}(R) = s_{2}^{0}$ and ${{s}_{4}}(R) = s_{4}^{0}.$ The parameters of the figure theory are connected with the gravitational moments by algebraic relationships (Zharkov and Trubitsyn, 1980)

$$\begin{gathered} - J_{2}^{0} = s_{2}^{0} + \frac{m}{3} + \frac{1}{7}\left( {11s_{2}^{0} + m} \right)s_{2}^{0}, \\ - J_{4}^{0} = s_{4}^{0} + \frac{6}{7}\left( {\frac{6}{5}s_{2}^{0} + m} \right)s_{2}^{0}. \\ \end{gathered} $$

(8)

The dynamical flattening e_d⁰ of an equilibrium planet is the flattening of an external reference surface under s = R; with an accuracy to the terms with m², it is

$$e_{{\text{d}}}^{0} = \frac{1}{2}\left( {3J_{2}^{0} + m} \right)\left( {1 + \frac{3}{2}J_{2}^{0}} \right) + \frac{5}{8}J_{4}^{0}.$$

(9)

The functions s₂, s₄, and $e_{{\text{d}}}^{{ - 1}}$ are shown in Fig. 3 depending on the mean radius of the planet.

Fig. 3.

The functions s₂, s₄, and $e_{{\text{d}}}^{{ - 1}}$ depending on the mean radius of the planet s.

CONCLUSIONS

The available data of observations do not impose severe constrains on the crust thickness and the core radius of Venus. The Earth-like models of Venus were developed after the first successful Russian missions to Venus (Venera-9, -10, -15, and -16), and some of their features have remained in the current models.

In this paper we considered the models with a wide range of values for the core size, crust thickness, and mantle density. It has been found that the anelasticity effects should be taken into account in selection between the models by the Love number k₂. The estimates have shown that the anelasticity of the Venusian mantle makes k₂ larger by more than 10%. The observationally determined number k₂ for a solar tide on Venus, the period of which is 58.4 days, should be diminished at least by 0.02−0.03, which is still within the limits of measurement errors for the number k₂.

The Venusian interior is close to spherical symmetry. Consequently, spherically symmetric models of Venus are used. To determine the small parameter in the Earth-like model of Venus, it was proposed to assume the value of this parameter as that for an effectively equilibrium planet. The equilibrium figure parameters of Venus were also calculated; for the chosen trial model V_5, they are J₂⁰ = 4.77 × 10⁻⁶, J₄⁰ = −5.79 × 10⁻¹¹, and e_d⁻¹ = 0.9 × 10⁻⁶ (the dynamical flattening).