Metastable Equilibrium between Cubic and Tetragonal Ferrites in Fe–C Alloys with Excluded Carbide Formation

Abstract

Metastable equilibrium of the α- and α'-phases comprising solid solutions of carbon in iron with cubic and tetragonal lattices, respectively, has been analyzed using the Zener–Khachaturyan theory of tetragonality of martensite of Fe–C alloys. The condition of the absence of carbide precipitates was imposed, as in the case of very low tempering or the formation of non-carbide bainite. A phase equilibrium diagram has been plotted in the region of low temperatures between 300–600 K. The violation of the linear dependence of the degree of tetragonality c/a on the carbon concentration in the concentration range 0.17–0.61 wt % C, established by Academician G.V. Kurdyumov for higher carbon concentrations, is explained.

1 INTRODUCTION

In [1], we analyzed the equilibrium of a conventional α-ferrite with a bcc lattice or tetragonal bainitic ferrite (α') with austenite under the conditions in which the precipitation of ε-carbide or cementite cannot take place. It is assumed that the phases under consideration can rapidly exchange diffusing carbon atoms. Such a situation can be seen in the formation of carbide-free bainite or in the tempering of martensite near room temperature [2], for example. It was somewhat surprising that the limiting carbon concentration in the α'-phase is hundreds of times higher than that in cubic ferrite. The first region in the diagram of the phase metastable equilibrium of Fe–C plotted at low temperatures in [1] on the basis on our calculations was the region of α'-solutions. However, since iron itself has a bcc lattice, the first single-phase region in this diagram must reflect the solid solution of carbon in α-iron. According to Gibbs [3], the number of degrees of freedom in the Fe–C system at a constant pressure is

$$f = k + 1 - {\Phi}{\text{,}}$$

((1))

where k is the number of components in Fe–C (k = 2) and Ф is the number of phases in equilibrium. For the first region of the diagram, Φ = 1; then, f = 2; i.e., at a fixed temperature, there is a range of carbon concentrations in which the solution of carbon in α-iron exists. Further on, an equilibrium of the α- and α'‑phases with a mutual exchange of components is possible. Since Φ = 2, at a constant temperature, f = 0; i.e., both phases have fixed compositions. An interval of the biphase equilibrium α = α' therefore appears. Then a concentration region of the existence of the α'‑phase, which comprises a solid solution of carbon in tetragonal iron, and, finally, a region of two-phase equilibrium α' = γ, which we previously studied in [1], must appear.

The aim of this work is a thermodynamic analysis of the α = α' equilibrium of solid solutions of carbon in iron with bcc and bct lattices, the determination of the boundary carbon concentrations for both phases, and plotting a metastable phase equilibrium diagram for temperatures at which redistribution of carbon in martensite or bainite steels between the phases without carbide precipitation is possible.

2 THERMODYNAMIC ANALYSIS

For the thermodynamic description of the disordered carbon solution in α-iron, we used the results of [4–6] obtained in the Hillert–Staffanson model [7], which underlies the thermodynamic analysis of equilibrium using the “CALPHAD” method. This model and the method of description are detailed in the works [4, 8] by famous Russian scientist V.V. Popov and others. In [4, 6, 8], the following expressions for the chemical potentials of the components of the α‑Fe–C system are given:

$$\mu _{{{\text{Fe}}}}^{\alpha } = {}^{0}G_{{{\text{Fe}}}}^{{{\text{bcc}}}} + 3RT\ln (1 - y_{{\text{C}}}^{\alpha }) + {}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}{{(y_{{\text{C}}}^{\alpha })}^{2}}{\text{;}}$$

((2a))

$$\begin{gathered} \mu _{{\text{C}}}^{\alpha } = \frac{1}{3}\left( {{}^{0}G_{{{\text{Fe}}:{\text{C}}}}^{{h\,{\text{bcc}}}} - {}^{0}G_{{{\text{Fe}}}}^{{h\,{\text{bcc}}}}} \right) + \,\,RT\ln \frac{{y_{{\text{C}}}^{\alpha }}}{{1 - y_{{\text{C}}}^{\alpha }}} \\ + \,\,\frac{1}{3}(1 - 2y_{{\text{C}}}^{\alpha }){}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}} \\ = \frac{1}{3}\left( {{}^{0}G_{{{\text{Fe}}:{\text{C}}}}^{{h\,{\text{bcc}}}} - {}^{0}G_{{{\text{Fe}}}}^{{h\,{\text{bcc}}}} + {}^{0}L_{{{\text{Fe}}:{\text{Va}}{\text{,C}}}}^{{{\text{bcc}}}}} \right) \\ + \,\,RT\ln \frac{{x_{C}^{\alpha }}}{{3 - 4x_{{\text{C}}}^{\alpha }}} - \frac{2}{9}\left( {\frac{{x_{{\text{C}}}^{\alpha }}}{{1 - x_{{\text{C}}}^{\alpha }}}} \right){}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}, \\ \end{gathered} $$

((2b))

where ${}^{0}G_{{{\text{Fe}}}}^{{{\text{bcc}}}}$ is the free energy of α-iron with a bcc lattice; the superscript h denotes the nonmagnetic component; and $y_{{\text{C}}}^{\alpha } = \frac{1}{3}\left( {\frac{{x_{{\text{C}}}^{\alpha }}}{{1 - x_{{\text{C}}}^{\alpha }}}} \right)$ is the fraction of interstices occupied by carbon atoms in the interstitial sublattice, where $x_{{\text{C}}}^{\alpha }$ is the atomic fraction of carbon in the α-phase. In this model, the excess mixing energy of components, including carbon and vacancies, is calculated using the Redlich–Kister polynomial model and ${}^{i}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}$ is the coefficient of the ith degree term. According to Gustafson [5], who found the numerical values of many quantities in expressions (2a) and (2b), only the zeroth term of the polynomial is nonzero, for which Gustafson adopted the value

$${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}} = - 190T,\,\,{{\text{J}} \mathord{\left/ {\vphantom {{\text{J}} {{\text{mol}}}}} \right. \kern-0em} {{\text{mol}}}}.$$

((3a))

The quantity ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}$ in the Hillert–Staffonson model [7] is equivalent to the mixing energy of carbon atoms and octahedral pores, $\Delta {{E}_{{{\text{C-C}}}}}$ = $Z{{N}_{0}}\left( {\frac{{{{\varepsilon }_{{{\text{C-C}}}}}}}{2} + \frac{{{{\varepsilon }_{{{\text{O-O}}}}}}}{2} - {{\varepsilon }_{{{\text{C-O}}}}}} \right)$, in the theory of regular interstitial solutions [9], where the interaction energy of octahedral interstices, ${{\varepsilon }_{{{\text{O-O}}}}}$, is zero and the carbon–pore interaction is either weak or absent. In fact, the term $\Delta {{E}_{\text{C-C}}}$ reflects the interaction of pairs of carbon atoms. It enters into the equation of the chemical potential of carbon [9] in an α-solid solution as the term $\frac{2}{3}\left( {\frac{{x_{{\text{C}}}^{\alpha }}}{{1 - x_{{\text{C}}}^{\alpha }}}} \right)\Delta E_{{{\text{C}} - {\text{C}}}}^{\alpha }.$ In formula (2b), the quantity ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}$ has the same concentration-dependent factor but the numerical coefficient $- \frac{2}{9}$ differs in the absolute value and sign. Hence,

$${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}} = - 3\Delta E_{{{\text{C-C}}}}^{\alpha }.$$

((3b))

In expression (2b), ${}^{0}G_{{{\text{Fe:C}}}}^{{h\,{\text{bcc}}}}$ is the standard value of the Gibbs energy of a hypothetical alloy in which the iron atoms are surrounded only by carbon atoms. In contrast, ${}^{0}G_{{{\text{Fe:Va}}}}^{{h\,{\text{bcc}}}}$ is the energy of an alloy in which the iron atoms are surrounded by unoccupied interstices. It therefore comprises the free energy of pure nonmagnetic bcc iron. The complementary quantity ${{G}_{m}}$ is the magnetic component of the free energy of α-Fe. Below, we will use the equality [4]

$$\begin{gathered} {}^{0}G_{{{\text{Fe:C}}}}^{{h\,{\text{bcc}}}} = {}^{0}G_{{{\text{Fe:Va}}}}^{{h\,{\text{bcc}}}} + 3{}^{0}G_{{\text{C}}}^{{{\text{bcc}}}} \\ + \,\,322{\kern 1pt} {\kern 1pt} 050 + 75.667T,\,\,{{\text{J}} \mathord{\left/ {\vphantom {{\text{J}} {{\text{mol}}}}} \right. \kern-0em} {{\text{mol}}}} \\ \end{gathered} $$

and transform formula (2b) to

$$\begin{gathered} \mu _{{\text{C}}}^{\alpha } = \left( {{}^{0}G_{{\text{C}}}^{{{\text{bcc}}}} + 107\,350 - 38.110T} \right) \\ + \,\,RT\ln \frac{{x_{{\text{C}}}^{\alpha }}}{{3 - 4x_{{\text{C}}}^{\alpha }}} - \frac{{2x_{{\text{C}}}^{\alpha }}}{{9(1 - x_{{\text{C}}}^{\alpha })}}{}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}. \\ \end{gathered} $$

((4a))

Henceforth, the quantity in the parentheses will be denoted by ${}^{0}{{\mu }_{{\text{C}}}}{\text{:}}$

$${}^{0}\mu _{{\text{C}}}^{\alpha } = {}^{0}G_{{\text{C}}}^{{{\text{bcc}}}} + 107\,{\kern 1pt} 350 - 38.110T,\,\,{{\text{J}} \mathord{\left/ {\vphantom {{\text{J}} {{\text{mol}}}}} \right. \kern-0em} {{\text{mol}}}}.$$

((4b))

It represents the free energy of the standard state of carbon in a solution with bcc iron. Its value is close to the result obtained by Agren [10]: ${}^{0}G_{{\text{C}}}^{{{\text{bcc}}}}$ + 108 299 – 39.603T, J/mol, but, according to Agren, ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{h\,{\text{bcc}}}} = 0.$ Expression (2a) for the chemical potential of the second component, iron, after obvious transformations takes the form:

$$\begin{gathered} \mu _{{{\text{Fe}}}}^{\alpha } = {}^{0}G_{{{\text{Fe}}}}^{{{\text{bcc}}}} + 3RT\ln \frac{{3 - 4x_{{\text{C}}}^{\alpha }}}{{3(1 - x_{{\text{C}}}^{\alpha })}} \\ + \,\,\frac{1}{9}{{\left( {\frac{{x_{{\text{C}}}^{\alpha }}}{{1 - x_{{\text{C}}}^{\alpha }}}} \right)}^{2}}{}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}. \\ \end{gathered} $$

((4c))

The tetragonality of martensite and likely bainite is caused by two circumstances. Firstly, an octahedron of 6 iron atoms forming at the center of a pore possibly containing a carbon atom is irregular. Of the three diagonals along the axes ox, oy, or oz, one is always $\sqrt 2$ times shorter than the other two. The pores and, accordingly, the sublattices in which they are found, are denoted according to the orientation of the short diagonal: a z-pore or the z-sublattice of pores, an x‑pore, etc. A carbon atom placed in a z-pore will move apart iron atoms along the axis oz. Secondly, carbon atoms initially found, e.g., in the z-sublattice create a collective deformation field along the axis oz, which forces other carbon atoms to fill z-pores. This leads to the preferential arrangement of the carbon atoms in the z-sublattice and to the tetragonality. The theory of this phenomenon was developed by K. Zener [11] and A. G. Khachaturyan [12]. Khachaturyan obtained the following expression for the variation in the molar free energy in the course of such ordering:

$$\begin{gathered} G(c,T,\eta ) = G(c,T,0) - \frac{1}{3}N{{c}^{2}}{{\lambda }_{0}}{{\eta }^{2}} \\ + \,\,\frac{{{{k}_{{\text{B}}}}T{{n}_{{\text{C}}}}}}{3}\left[ {2(1 - \eta )ln(1 - \eta ) + (1 + 2\eta )ln(1 + 2\eta )} \right], \\ \end{gathered} $$

((5))

where

$$\eta = \frac{{n_{{\text{C}}}^{z} - \frac{1}{3}{{n}_{{\text{C}}}}}}{{\frac{2}{3}{{n}_{{\text{C}}}}}}$$

((6))

is an order parameter reflecting the excess of carbon atoms in z-octahedral pores as compared to the variant of the uniform occupation of all pores by carbon atoms $\left( {n_{{\text{C}}}^{x} = n_{{\text{C}}}^{y} = n_{{\text{C}}}^{z} = \frac{{{{n}_{{\text{C}}}}}}{3}} \right).$ Here, $N$ and ${{n}_{{\text{C}}}}$ are the numbers of iron and carbon atoms, respectively; ${{\lambda }_{0}}$ is the parameter of deformation interaction; c = $\frac{{{{n}_{{\text{C}}}}}}{N} = \frac{{{{x}_{{\text{C}}}}}}{{1 - {{x}_{{\text{C}}}}}},$ where ${{x}_{{\text{C}}}}$ is the fraction of carbon atoms in the solution; $T$ is the absolute temperature; ${{k}_{{\text{B}}}}$ is the Boltzmann constant; and $G(c,T,0)$ is the free energy of the solution at $\eta = 0,$ i.e., in the disordered state. We should note that the energy of the deformation interaction is negative; therefore, we assume that ${{\lambda }_{0}}$ is a positive quantity and place the minus sign before the second term in (5). In the equilibrium state, $\frac{{\partial G(c,T,\eta )}}{{\partial \eta }} = 0.$ Solving this equation, we determine the temperature and concentration dependence of the order parameter:

$$\frac{{{{k}_{{\text{B}}}}T(1 - {{x}_{{\text{C}}}})}}{{{{\lambda }_{0}}{{x}_{{\text{C}}}}}} = \frac{\eta }{{\ln \left( {\frac{{1 + 2\eta }}{{1 - \eta }}} \right)}}.$$

((7))

A detailed analysis of the stability of the ordering process [12] has shown that this dependence holds in the interval $0.5 < \eta \leqslant 1.$ The value of $\eta = 0.5$ is critical. At a temperature ${{T}_{{\text{C}}}}$ corresponding to this value,

$${{T}_{{\text{C}}}} = 0.361\frac{{{{\lambda }_{0}}}}{{{{k}_{{\text{B}}}}}}\frac{{{{x}_{{\text{C}}}}}}{{1 - {{x}_{{\text{C}}}}}}$$

((8))

the parameter $\eta$ decreases abruptly to zero. We calculated the chemical potentials of the components of the tetragonal α'-solution in [1]. For clear distinction, the index α' was replaced by “T”:

$$\begin{gathered} \mu _{{\text{C}}}^{{\text{T}}} = {}^{0}G_{{\text{C}}}^{{bcc}} + 107{\kern 1pt} 350 - 38.110T + \,\,RT\ln \left( {\frac{{x_{{\text{C}}}^{{\text{T}}}}}{{3 - 4x_{{\text{C}}}^{{\text{T}}}}}} \right) \\ - \,\,\frac{2}{3}\frac{{x_{{\text{C}}}^{{\text{T}}}}}{{1 - x_{{\text{C}}}^{{\text{T}}}}}\left( {{{N}_{0}}{{\lambda }_{0}}{{\eta }^{2}} + \frac{1}{3}{}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}} \right) \\ + \,\,\frac{{RT}}{3}\left[ {2\left( {1 - \eta } \right)\ln \left( {1 - \eta } \right) + \left( {1 + 2\eta } \right)\ln \left( {1 + 2\eta } \right)} \right]; \\ \end{gathered} $$

((9a))

$$\begin{gathered} \mu _{{{\text{Fe}}}}^{{\text{T}}} = {}^{0}G_{{{\text{Fe}}}}^{{{\text{bcc}}}} + 3RT\ln \left( {\frac{{3 - 4x_{{\text{C}}}^{{\text{T}}}}}{{3\left( {1 - x_{{\text{C}}}^{{\text{T}}}} \right)}}} \right) \\ + \,\,\frac{1}{3}{{\left( {\frac{{x_{{\text{C}}}^{{\text{T}}}}}{{1 - x_{{\text{C}}}^{{\text{T}}}}}} \right)}^{2}}\left( {{{N}_{0}}{{\lambda }_{0}}{{\eta }^{2}} + \frac{1}{3}{}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}} \right). \\ \end{gathered} $$

((9b))

Since the molar free energy of the alloy and the chemical potentials of the components are related by a simple formula $G_{{\text{m}}}^{{\text{T}}} = x_{{\text{C}}}^{{\text{T}}}\mu _{{\text{C}}}^{{\text{T}}} + (1 - x_{{\text{C}}}^{{\text{T}}})\mu _{{{\text{Fe}}}}^{{\text{T}}}$ [9], for $G_{{\text{m}}}^{{\text{T}}}$, we have

$$\begin{gathered} G_{{\text{m}}}^{{\text{T}}} = {}^{0}\mu _{{\text{C}}}^{\alpha }x_{{\text{C}}}^{{\text{T}}} + x_{{\text{C}}}^{{\text{T}}}RT\ln \left( {\frac{{x_{{\text{C}}}^{{\text{T}}}}}{{3 - 4x_{{\text{C}}}^{{\text{T}}}}}} \right) \\ + \,\,{}^{0}G_{{{\text{Fe}}}}^{{{\text{bcc}}}}\left( {1 - x_{{\text{C}}}^{{\text{T}}}} \right) + 3RT(1 - x_{{\text{C}}}^{{\text{T}}})\ln \left( {\frac{{3 - 4x_{{\text{C}}}^{{\text{T}}}}}{{3\left( {1 - x_{{\text{C}}}^{{\text{T}}}} \right)}}} \right) \\ - \,\,\frac{1}{3}\frac{{{{{\left( {x_{{\text{C}}}^{{\text{T}}}} \right)}}^{2}}}}{{1 - x_{{\text{C}}}^{{\text{m}}}}}\left( {{{N}_{0}}\lambda {{\eta }^{2}} + \frac{1}{3}{}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}} \right) \\ + \,\,\frac{{RTx_{{\text{C}}}^{{\text{T}}}}}{3}\left[ {2\left( {1 - \eta } \right)\ln (1 - \eta ) + (1 + 2\eta )ln(1 + 2\eta )} \right]. \\ \end{gathered} $$

((10a))

In a similar manner, we obtain for $G_{{\text{m}}}^{\alpha }$ the expression

$$\begin{gathered} G_{{\text{m}}}^{\alpha } = \left( {{}^{{\text{0}}}G_{{\text{C}}}^{{bcc}} + 107\,350 - 38.110T} \right)x_{{\text{C}}}^{\alpha } \\ + \,\,x_{{\text{C}}}^{\alpha }RT\ln \left( {\frac{{x_{{\text{C}}}^{\alpha }}}{{3 - 4x_{{\text{C}}}^{\alpha }}}} \right) + {}^{0}G_{{{\text{Fe}}}}^{{{\text{bcc}}}}\left( {1 - x_{{\text{C}}}^{\alpha }} \right) \\ + \,\,3\left( {1 - x_{{\text{C}}}^{\alpha }} \right)RT\ln \left( {\frac{{3 - 4x_{{\text{C}}}^{\alpha }}}{{3\left( {1 - x_{{\text{C}}}^{\alpha }} \right)}}} \right) - \frac{1}{9}\frac{{{{{(x_{{\text{C}}}^{\alpha })}}^{2}}}}{{(1 - x_{{\text{C}}}^{\alpha })}}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}. \\ \end{gathered} $$

((10b))

The diffusionless equilibrium of the cubic and tetragonal phases must be seen at a temperature ${{T}_{0}}$ at which the free energies of these phases of the same composition are equal. Obviously, in this case, the concentrations of each element in both phases will be the same: $x_{{\text{C}}}^{{\text{T}}} = x_{{\text{C}}}^{\alpha } = x_{{\text{C}}}^{0}.$ Then:

$$\begin{gathered} G_{{\text{m}}}^{{\text{T}}} - G_{{\text{m}}}^{\alpha } = - \frac{1}{3}{{N}_{0}}{{\lambda }_{0}}\frac{{{{{\left( {x_{{\text{C}}}^{0}} \right)}}^{2}}}}{{1 - x_{{\text{C}}}^{0}}}{{\eta }^{2}} \\ + \,\,\frac{{RTx_{{\text{C}}}^{0}}}{3}\left[ {2(1 - \eta )ln(1 - \eta ) + (1 + 2\eta )\ln (1 + 2\eta )} \right] = 0. \\ \end{gathered} $$

((11))

Hence, at a fixed temperature, the carbon concentration $x_{{\text{C}}}^{0}$ for an equilibrium point is given by the equation

$$\begin{gathered} \frac{{x_{{\text{C}}}^{0}}}{{1 - x_{{\text{C}}}^{0}}} \\ = \frac{{RT\left[ {2(1 - \eta )ln(1 - \eta ) + (1 + 2\eta )\ln (1 + 2\eta )} \right]}}{{{{N}_{0}}{{\lambda }_{0}}{{\eta }^{2}}}}. \\ \end{gathered} $$

Let us take into account that, according to the Zener–Khachaturyan theory, the loss of tetragonality and the transition to a cubic structure occur spasmodically on reaching η = 0.5. To estimate x₀, we take $T = 300\,\,{\text{K}}$ and λ₀ = 5.5 eV/atom. Then,

$$\frac{{x_{{\text{C}}}^{0}}}{{1 - x_{{\text{C}}}^{0}}} = \frac{{8.314 \times 300 \times 0.693}}{{\frac{1}{4} \times 96{\kern 1pt} 500 \times 5.5}} = 0.013.$$

Therefore, at 300 K, the diffusionless bct → bcc transition must occur in steel containing 0.013  atomic fractions, or 0.28 wt %, of carbon. Now, let us consider a situation in which the phases can exchange carbon atoms. The boundary concentrations of the cubic and tetragonal phases that appeared under the conditions of diffusion equilibrium can be determined graphically by drawing a common tangent to the graphs of the molar free energies [9]. In this case, the concentration $x_{{\text{C}}}^{0}$ must lie within the biphase α + α'-region. In the analytical calculation of these concentrations, we use the phase equilibrium equations

$$\mu _{{\text{C}}}^{{\text{T}}} = \mu _{{\text{C}}}^{\alpha };\,\;\mu _{{{\text{Fe}}}}^{{\text{T}}} = \mu _{{{\text{Fe}}}}^{\alpha }.$$

((12))

After substituting expressions (4a) and (4c) and also (9a) and (9b) into Eqs. (12), we obtain a system of equations for the chemical equilibrium of the tetragonal and cubic phases:

$$\begin{gathered} RT\left( {\ln \left( {\frac{{x_{{\text{C}}}^{{\text{T}}}}}{{3 - 4x_{{\text{C}}}^{{\text{T}}}}}} \right) - \ln \left( {\frac{{x_{{\text{C}}}^{\alpha }}}{{3 - 4x_{{\text{C}}}^{\alpha }}}} \right)} \right) \\ - \,\,\frac{2}{3}\frac{{x_{{\text{C}}}^{{\text{T}}}}}{{1 - x_{{\text{C}}}^{{\text{T}}}}}\left( {{{N}_{0}}{{\lambda }_{0}}{{\eta }^{2}} + \frac{1}{3}{}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}} \right) \\ + \,\,\frac{2}{9}\left( {\frac{{x_{{\text{C}}}^{\alpha }}}{{1 - x_{{\text{C}}}^{\alpha }}}} \right){}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}} \\ + \,\,\frac{{RT}}{3}\left[ {2(1 - \eta )\ln (1 - \eta ) + (1 + 2\eta )\ln (1 + 2\eta )} \right] = 0, \\ \end{gathered} $$

((13a))

$$\begin{gathered} 3RT\left( {\ln \left( {\frac{{3 - 4x_{{\text{C}}}^{{\text{T}}}}}{{3(1 - x_{{\text{C}}}^{{\text{T}}})}}} \right) - \ln \left( {\frac{{3 - 4x_{{\text{C}}}^{\alpha }}}{{3(1 - x_{{\text{C}}}^{\alpha })}}} \right)} \right) \\ + \frac{1}{3}{{\left( {\frac{{x_{{\text{C}}}^{{\text{T}}}}}{{1 - x_{{\text{C}}}^{{\text{T}}}}}} \right)}^{2}}\left( {{{N}_{0}}{{\lambda }_{0}}{{\eta }^{2}} + \frac{1}{3}{}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}} \right) \\ - \frac{1}{9}{{\left( {\frac{{x_{{\text{C}}}^{\alpha }}}{{1 - x_{{\text{C}}}^{\alpha }}}} \right)}^{2}}{}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}} = 0. \\ \end{gathered} $$

((13b))

The dependence of the order parameter $\eta$ on the temperature and the carbon concentration, required for calculations, is determined by Eq. (7). It should be noted that the sought-for solution for the concentrations—besides the temperature $a_{{\text{C}}}^{\alpha }$ and composition of the steel—is determined by two energy parameters: the interaction energy of carbon atoms in ferrite $\left( {{}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}} \right)$ and the deformation interaction parameter of carbon in the tetragonal martensite, λ₀. If ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}} > 0,$ then the system of equations (13a) and (13b) has no roots; for ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}} = 0$, the roots are also absent but are ready to appear. For negative values of ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}$, as in (3a), the roots exist. We solved the systems of equations (13a) and (13b) using the MathCad software package. However, there is some doubt about the accuracy of formula (3a), which, according to Agren [14], was proposed by Gustafson to eliminate the emergence of another zone of stability of the bcc phase in the liquid state region. It would be reasonable to calculate the interaction energy of the carbon atoms in α-iron, $\Delta E_{{{\text{C}} - {\text{C}}}}^{\alpha }$ directly, on the basis of the data on the activity of carbon, ${{a}_{{\text{C}}}}$, and thermodynamic relations, as it was made by McLellan and Dunn [15] for austenite. Shiflet et al. [16] derived similar equations $a_{{\text{C}}}^{\alpha }$ but, when using the numerical coefficients from [15], did not take into account the change in the coordination number from 8 for fcc to 4 for bcc in the intersticial sublattices and obtained an incorrect result with $\Delta E_{{{\text{C}} - {\text{C}}}}^{\alpha } < 0.$ The same mistake was made in [17], which was first pointed out by McLellan [18]. In both cases, the energy of the C–C bonds turned out to be negative. Rigorous calculations were later made by Bhadeshia [19, 20]. His first result was +(105.4–112.1) kJ/mol, and, after refining the quasi-chemical theory of activity, he found $\Delta E_{{{\text{C}} - {\text{C}}}}^{\alpha }$ = 150 kJ/mol, or 1.54 eV per pair of nearest neighbors of С–С. There is a confirmation of these results by Bhadeshia [21, 22]. First-principle calculations of the energy of pair interaction of neighboring carbon atoms in the α-phase gave 1.8 eV/atom in the first work and 2.0 eV/atom in the second. The authors of both studies emphasize the existence of an exceptionally strong repulsion of the nearest carbon atoms. Since the cell volume in [22] was significantly higher than in [21], the results of [22] are more accurate. Taking into account that the coordination number of the interstitial lattice is $Z_{\alpha }^{{\text{C}}} = 4,$ we find that $\Delta E_{{{\text{C}} - {\text{C}}}}^{\alpha }$ = 430 kJ/mol and ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}$ = –1300 kJ/mol. The further calculations of the boundary concentrations were carried out with this value.

3 RESULTS AND DISCUSSION

The calculated temperature dependences of the carbon boundary concentrations in α- and α'-solid solutions in a biphase equilibrium for λ₀ = 5.5 eV/atom, established in [1], and ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}$ = –1300 kJ/mol are shown in Fig. 1a. With an increasing temperature, both concentrations sharply increase, as a result of which the region of the biphase equilibrium of α + α' also expands and shifts to the right.

Fig. 1.

Calculated equilibrium carbon concentrations in cubic (α) and tetragonal (α') martensite or bainitic ferrite for (a) ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}} = - 1300\,\,{{{\text{kJ}}} \mathord{\left/ {\vphantom {{{\text{kJ}}} {{\text{mol}}}}} \right. \kern-0em} {{\text{mol}}}}$ and λ₀ = 5.5 eV/atom; (b) ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}} = - 1300\,\,{{{\text{kJ}}} \mathord{\left/ {\vphantom {{{\text{kJ}}} {{\text{mol}}}}} \right. \kern-0em} {{\text{mol}}}}$ and λ₀ = 2.73 eV/atom; and (c) ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}} = - 1500\,\,{{{\text{kJ}}} \mathord{\left/ {\vphantom {{{\text{kJ}}} {{\text{mol}}}}} \right. \kern-0em} {{\text{mol}}}}$ and λ₀ = 5.5 eV/atom.

Figure 1b presents the results of calculations in which ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}$ have the same value as in the calculations for Fig. 1a and the value of λ₀ is reduced to 2.73 eV, which was recommended by Khachaturyan [12], but they did not confirm the results of our simulation [13]. The reduction in λ₀ led to a strong increase in both boundary concentrations. In the calculations of $x_{{\text{C}}}^{\alpha }$ and $x_{{\text{C}}}^{{\text{T}}},$ the results of which are shown in Fig. 1c, it was found that the reduction in ${}^{0}L_{{{\text{Fe:Va}}{\text{,C}}}}^{{{\text{bcc}}}}$ has almost no effect on the position of the boundary line α/α' but, in comparison with Fig. 1a, causes a shift to lower concentrations of the line ${{x_{{\text{C}}}^{{\text{T}}}} \mathord{\left/ {\vphantom {{x_{{\text{C}}}^{{\text{T}}}} {x_{{\text{C}}}^{\alpha }}}} \right. \kern-0em} {x_{{\text{C}}}^{\alpha }}}.$

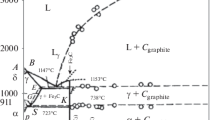
Our calculations show that, at relatively low carbon concentrations, there is a diffusion-controlled equilibrium between martensite or bainitic ferrite with the α'‑phase and an α-solution of carbon in iron. Thermodynamically, it is due to the possibility of drawing a common tangent to the curves of the molar free energy of the α- and α'-phases. The nature of this equilibrium is somewhat different than in the spinodal decomposition of martensite. Let us consider a metastable equilibrium diagram of the Fe–C phases (Fig. 2) more detailed than the diagram we presented in [1]. In this diagram, a single-phase region of α-solid solutions appears again. It is much wider than for the classical equilibrium diagram, since its boundary is determined by the equilibrium of the cubic ferrite with tetragonal ferrite rather than with cementite. As already noted, the α + α' biphase region then follows. According to our calculations, at room temperature, for ${{\lambda }_{0}}$ = 5.5 eV/atom, it extends from 0.24 to 0.57 wt % C. This is exactly the range of concentrations in which, according to [22], the linear dependence (Fig. 3) of the degree of tetragonality с/a of the martensite lattice on the carbon content, established by G.V. Kurdyumov [23], is interrupted. The X-ray diffraction analysis of quenched steels of this composition does not reveal a distinct martensitic doublet. There is an asymmetrically broadened maximum. This fact was explained by M.A. Shtremel’ and L.M. Kaputkina [24] by diffraction on a mixture of cubic and tetragonal martensites in accordance with our theory and diagram. Single-phase tetragonal martensite emerges for a substantially narrower range of concentrations from 0.57 to 1.58 wt % C. Then the α' + γ region appears. The field of single-phase stable austenite must be observed at concentrations exceeding 7.8 wt % C. In this form, the metastable equilibrium diagram seems to be rather realistic.

Fig. 2.

Low-temperature metastable phase equilibrium diagram of Fe–C (calculated under the assumption of suppressed carbide precipitates).

Fig. 3.

Lattice parameter ratio c/a of carbon martensite vs. carbon content [23, 24].

CONCLUSIONS

(1) The chemical potentials of carbon and iron calculated in [1] for Fe–C alloys with a bct lattice allowed us to consider metastable equilibrium of α- and α'‑solutions with cubic and tetragonal lattices.

(2) The existence of a α ↔ α' biphase equilibrium region between 0.24 and 0.57 wt % C (according to our calculations) was established. The reaction of martensite decomposition during tempering or self-tempering likely causes the violation in this area of the equation of Kurdyumov’s linearity of the ratio с/a as a function of the carbon content [23]. Here, α' is martensite enriched with carbon.

(3) A complete diagram of the metastable equilibrium of the α-, α'-, and γ-phases of the Fe–C system at low temperatures, valid in the absence of carbide precipitation, as, e.g., in the formation of carbideless bainite is obtained.