1 INTRODUCTION

As we know [1], applied problems require maximization of the minimum (fundamental) vibration mode to expand the resonanceless frequency range of the structure in order to increase its operational characteristics. For shells of revolution, as structural elements with a variety of technical applications, an increase in the lower vibration frequency along with the choice of suitable boundary conditions, geometric dimensions, variable stiffness, initial stresses, reinforcement angles and others [2–6] can also be achieved by specifying a varied wall thickness [7]. For truncated conical shells, which are the focus of this work, the effect of thickness varying along the length in some way on the frequency spectrum was also estimated in [8–26]. These works present the results of studying the effect of various parameters on the free vibrations of isotropic, orthotropic, composite, layered and reinforced shells, the wall thickness of which changes according to power, exponential or harmonic laws, based on numerical and numerical-analytical methods (collocations, wavelet analysis, Rayleigh–Ritz method, power series expansions, finite elements, or discrete orthonormalization). But among these publications, only in [17–19, 21] the focus is on maximizing the lower vibration frequency relative to the reference, which is taken as the frequency of a shell with a constant thickness and equivalent mass. In addition, the research is limited only to the case of a linear change in thickness. A similar discussion of cylindrical shells in [27, 28] was carried out for a larger number of thickness variations. At the same time, it is noted that the variation of the wall thickness according to the quadratic law most significantly affects the increase of the fundamental frequency. The purpose of this work is to perform a similar analysis for conical shells, involving more varied laws of thickness variation along the length than those presented in literature.

2 PROBLEM SETUP

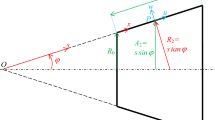
Let us consider a truncated conical shell (Fig. 1) with a minimum radius \({{R}_{1}}\), apex angle \(\alpha \) and generatrix length \(l\). The shell wall thickness \(h = h(s)\) varies along the length of the generatrix and is mathematically described as \(h = {{h}_{e}}g(s)\). Here \({{h}_{e}}\) is the equivalent thickness calculated relative to the reference thickness \({{h}_{0}}\), and \(g(s)\) is the function of the meridian coordinate \(s\), determining the law of thickness variation.

Fig. 1.
figure 1

Computational model.

Full size image

Figure 2 presents the variants of shell wall thicknesses, which correspond to the function \(g(s)\) of the form:

V1:

\(g(s) = 1 + k\left| {\xi - 1} \right|\);

V2:

\(g(s) = 1 + k\left| {2\xi - 1} \right|\);

V3:

\(g(s) = 1 + k{{\left( {\xi - 1} \right)}^{2}}\);

V4:

\(g(s) = 1 + k{{\left( {2\xi - 1} \right)}^{2}}\);

V5:

\(g(s) = 1 + k\sin \left( {\pi \xi } \right)\);

V6:

\(g(s) = 1 + k\left[ {1 - \sin \left( {\pi \xi } \right)} \right]\),

Fig. 2.
figure 2

Longitudinal section of the shell walls with different versions of changing the thickness: V1—linear asymmetric; V2—linear symmetric; V3—quadratic asymmetric; V4—quadratic symmetric; V5—harmonic convex; V6—harmonic concave.

Full size image

where \(\xi = {s \mathord{\left/ {\vphantom {s l}} \right. \kern-0em} l}\) and \(k\) is the thickness variability coefficient. The value of \({{h}_{e}}\) is calculated from the condition of mass equivalence with the reference shell according to the following formulas:

V1, V2:

\({{h}_{e}} = \frac{{2{{h}_{0}}}}{{2 + k}}\);

V5:

\({{h}_{e}} = \frac{{\pi {{h}_{0}}}}{{2k + \pi }}\);

V3, V4:

\({{h}_{e}} = \frac{{3{{h}_{0}}}}{{3 + k}}\);

V6:

\({{h}_{e}} = \frac{{\pi {{h}_{0}}}}{{\pi k + \pi - 2k}}\).

As can be seen from the formulas, at \(k = 0\) the shell thickness is constant and equal to \(h = {{h}_{0}}\).

Thus, the problem is to study the effect of the thickness, described by different laws, on the frequency spectrum of the truncated conical shell both for its different linear size and for kinematic boundary conditions set at the edges based on the condition of mass equivalence for a specific cone angle.

3 FUNDAMENTAL RELATIONS

Within the classical shell theory based on the Kirchhoff–Love hypotheses, the components of the deformation vector \({{{\text{E}}}_{{ij}}}\) in a curvilinear coordinate system \(\{ s,\theta ,z\} \) can be represented as [29]:

$${{{\rm E}}_{{11}}} = {{\varepsilon }_{{11}}} + z{{\kappa }_{{11}}},\quad {{{\rm E}}_{{22}}} = {{\varepsilon }_{{22}}} + z{{\kappa }_{{22}}},\quad {{{\rm E}}_{{12}}} = {{\varepsilon }_{{12}}} + 2z{{\kappa }_{{12}}},$$

where

$$\begin{gathered} {{\varepsilon }_{{11}}} = u{\kern 1pt} {{'}} + {{r}_{1}}w,\quad {{\varepsilon }_{{22}}} = {{v}^{ \bullet }} + \psi u + {{r}_{2}}w,\quad {{\varepsilon }_{{12}}} = v{\kern 1pt} {{'}} + {{u}^{ \bullet }} - \psi v, \\ {{\kappa }_{{11}}} = \theta _{1}^{'},\quad {{\kappa }_{{22}}} = \theta _{2}^{ \bullet } + \psi {{\theta }_{1}},\quad {{\kappa }_{{12}}} = \theta _{1}^{ \bullet } - \psi {{\theta }_{2}} + {{r}_{2}}v{\kern 1pt} {{'}},\quad {{\theta }_{1}} = - w{\kern 1pt} {{'}} + {{r}_{1}}u,\quad {{\theta }_{2}} = - {{w}^{ \bullet }} + {{r}_{2}}v, \\ \left( \cdots \right){\kern 1pt} {{'}} = \frac{1}{{{{A}_{1}}}}\frac{{\partial \left( \cdots \right)}}{{\partial s}},\quad {{\left( \cdots \right)}^{ \bullet }} = \frac{1}{{{{A}_{2}}}}\frac{{\partial \left( \cdots \right)}}{{\partial \theta }},\quad \psi = \frac{1}{{{{A}_{2}}}}{{{A'}}_{2}}. \\ \end{gathered} $$
(1)

Here, \({{A}_{1}},\;{{A}_{2}}\) are Lamé coefficients; \({{r}_{1}},\;{{r}_{2}}\) are curvatures; u, \(v\), w are meridian, circumferential and normal components of the shell displacement vector; and \({{\theta }_{1}},\;{{\theta }_{2}}\) are rotation angles of the nondeformable normal.

The physical relations establishing the relationship between the vector of forces and moments \({\mathbf{T}} = {{\left\{ {{{T}_{{11}}},{{T}_{{22}}},S,{{M}_{{11}}},{{M}_{{22}}},H} \right\}}^{{\text{T}}}}\) and the vector of generalized deformations \(\varepsilon = {{\left\{ {{{\varepsilon }_{{11}}},{{\varepsilon }_{{22}}},{{\varepsilon }_{{12}}},{{\kappa }_{{11}}},{{\kappa }_{{22}}},2{{\kappa }_{{12}}}} \right\}}^{{\text{T}}}}\), are written in matrix form as

$${\mathbf{T}} = {\mathbf{D}}\varepsilon = \left[ {\begin{array}{*{20}{c}} {{\mathbf{\bar {A}}}}&{{\mathbf{\bar {B}}}} \\ {{\mathbf{\bar {B}}}}&{{\mathbf{\bar {C}}}} \end{array}} \right]\varepsilon {\text{.}}$$
(2)

Here, the quantities making up the stiffness matrix D are functions of the meridian coordinate \(s\) and are calculated by the formulas:

$${{\bar {a}}_{{ij}}}(s) = \int\limits_{h(s)} {{{{\bar {Q}}}_{{ij}}}dz} ,\quad {{\bar {b}}_{{ij}}}(s) = \int\limits_{h(s)} {z{{{\bar {Q}}}_{{ij}}}dz,} \quad {{\bar {c}}_{{ij}}}(s) = \int\limits_{h(s)} {{{z}^{2}}{{{\bar {Q}}}_{{ij}}}dz} \quad (i,j = 1,2,3),$$
(3)

where the coefficients \({{\bar {Q}}_{{ij}}}\) are determined in a known manner [29] with respect to the elastic moduli (\({{E}_{{11}}},\;{{E}_{{22}}}\)), Poisson’s ratio (\({{\nu }_{{12}}}\)) and shear modulus (\({{G}_{{12}}}\)) of the shell material.

The equations of motion for the shell are:

$$T_{{11}}^{'} + \psi ({{T}_{{11}}} - {{T}_{{22}}}) + {{S}^{ \bullet }} + {{r}_{1}}({{Q}_{{11}}} - {{H}^{ \bullet }}) - {{\rho }_{0}}\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} = 0,$$
$$S{\kern 1pt} {{'}} + 2\psi (S + {{r}_{1}}H) + T_{{22}}^{ \bullet } + {{r}_{2}}({{Q}_{{22}}} + H{\kern 1pt} {{'}}) - {{\rho }_{0}}\frac{{{{\partial }^{2}}v}}{{\partial {{t}^{2}}}} = 0,$$
$$Q_{{11}}^{'} + \psi {{Q}_{{11}}} + Q_{{22}}^{ \bullet } - {{r}_{1}}{{T}_{{11}}} - {{r}_{2}}{{T}_{{22}}} - {{\rho }_{0}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = 0,$$
(4)
$$M_{{11}}^{'} + \psi ({{M}_{{11}}} - {{M}_{{22}}}) + {{H}^{ \bullet }} - {{Q}_{{11}}} = 0,$$
$$H{\kern 1pt} {{'}} + 2\psi H + M_{{22}}^{ \bullet } - {{Q}_{{22}}} = 0,$$

where \({{Q}_{{ii}}}\) are shear forces and \({{\rho }_{0}}(s) = \int_{h\left( s \right)} {\rho dz} \), \(\rho \) is the density of the material.

Expanding all the parameters describing the behavior of the truncated conical shell in Fourier series in the circumferential coordinate θ

$$\begin{gathered} X(s,\theta ) = \sum\limits_{j = 0} {{{X}_{j}}(s)\cos (j\theta )} ,\quad Y(s,\theta ) = \sum\limits_{j = 0} {{{Y}_{j}}(s)\sin (j\theta )} , \\ X = \left\{ {u,w,{{\theta }_{1}},{{E}_{{11}}},{{E}_{{22}}},{{K}_{{11}}},{{K}_{{22}}},{{T}_{{11}}},{{T}_{{22}}},{{M}_{{11}}},{{M}_{{22}}},{{Q}_{{11}}}} \right\},\quad Y = \left\{ {v,{{\theta }_{2}},{{E}_{{12}}},{{K}_{{12}}},S,H,{{Q}_{{22}}}} \right\}, \\ \end{gathered} $$

we reduce the geometric (1) and physical (2) relations, as well as the equations of motion (4) to a system of eight ordinary differential equations of the first order in new variables [29]:

$$\begin{gathered} {{y}_{1}} = {{T}_{{11}}},\quad {{y}_{2}} = S + 2{{r}_{2}}H,\quad {{y}_{3}} = {{M}_{{11}}},\quad {{y}_{4}} = {{Q}_{{11}}} + \bar {j}H, \\ {{y}_{5}} = u,\quad {{y}_{6}} = v,\quad {{y}_{7}} = w,\quad {{y}_{8}} = {{\theta }_{1}}. \\ \end{gathered} $$

Here, \(\bar {j} = {j \mathord{\left/ {\vphantom {j {{{A}_{2}}}}} \right. \kern-0em} {{{A}_{2}}}}\), where j is the harmonic order in Fourier series expansion. Taking this into account and seeking a solution in the form \({\mathbf{y}}\left( t \right) = {\mathbf{y}}\exp \left( {{\text{i}}\omega t} \right)\), we write the desired system as follows:

$${\mathbf{y}}{\kern 1pt} ' = {\mathbf{f}}(j,\omega ,{\mathbf{y}}),$$
(5)

where

$$\begin{gathered} {{f}_{1}} = \bar {j}(2{{r}_{2}}H - {{y}_{2}}) - \psi ({{y}_{1}} - {{T}_{{22}}}) - {{r}_{1}}{{y}_{4}} - {{\omega }^{2}}{{\rho }_{0}}{{y}_{5}},\quad {{f}_{2}} = \bar {j}{{T}_{{22}}} - 2\psi {{y}_{2}} - {{r}_{2}}{{Q}_{{22}}} - {{\omega }^{2}}{{\rho }_{0}}{{y}_{6}}, \\ {{f}_{3}} = {{y}_{4}} - \psi ({{y}_{3}} - {{M}_{{22}}}) - 2\bar {j}H,\quad {{f}_{4}} = {{r}_{1}}{{y}_{1}} - \psi {{y}_{4}} + {{r}_{2}}{{T}_{{22}}} - \bar {j}({{Q}_{{22}}} + 2\psi H) - {{\omega }^{2}}{{\rho }_{0}}{{y}_{7}}, \\ {{f}_{5}} = {{\varepsilon }_{{11}}} - {{r}_{1}}{{y}_{7}},\quad {{f}_{6}} = {{\varepsilon }_{{12}}} + \psi {{y}_{6}} + \bar {j}{{y}_{5}},\quad {{f}_{7}} = - {{y}_{8}} + {{r}_{1}}{{y}_{5}},\quad {{f}_{8}} = {{\kappa }_{{11}}}; \\ \end{gathered} $$
(6)

ω is the vibration frequency, \({{{\text{i}}}^{2}} = - 1\). The quantities included in expressions (6), taking into account (1) and (2), are calculated by the formulas:

$${{\varepsilon }_{{22}}} = \bar {j}{{y}_{6}} + {{r}_{2}}{{y}_{7}} + \psi {{y}_{5}},\quad {{\kappa }_{{22}}} = \bar {j}{{\theta }_{2}} + \psi {{y}_{8}},\quad {{\theta }_{2}} = {{r}_{2}}{{y}_{6}} + \bar {j}{{y}_{7}},\quad H = {{\bar {b}}_{{33}}}{{\varepsilon }_{{12}}} + 2{{\bar {c}}_{{33}}}{{\kappa }_{{12}}},$$
$${{Q}_{{22}}} = - \bar {j}{{M}_{{22}}},\quad {{\kappa }_{{11}}} = {{\left[ {{{{\bar {a}}}_{{11}}}({{y}_{3}} - {{{\bar {b}}}_{{12}}}{{\varepsilon }_{{22}}} - {{{\bar {c}}}_{{12}}}{{\kappa }_{{22}}}) - } \right.\left. {{{{\bar {b}}}_{{11}}}({{y}_{1}} - {{{\bar {a}}}_{{12}}}{{\varepsilon }_{{22}}} - {{{\bar {b}}}_{{12}}}{{\kappa }_{{22}}})} \right]} \mathord{\left/ {\vphantom {{\left[ {{{{\bar {a}}}_{{11}}}({{y}_{3}} - {{{\bar {b}}}_{{12}}}{{\varepsilon }_{{22}}} - {{{\bar {c}}}_{{12}}}{{\kappa }_{{22}}}) - } \right.\left. {{{{\bar {b}}}_{{11}}}({{y}_{1}} - {{{\bar {a}}}_{{12}}}{{\varepsilon }_{{22}}} - {{{\bar {b}}}_{{12}}}{{\kappa }_{{22}}})} \right]} {({{{\bar {a}}}_{{11}}}{{{\bar {c}}}_{{11}}} - \bar {b}_{{11}}^{2})}}} \right. \kern-0em} {({{{\bar {a}}}_{{11}}}{{{\bar {c}}}_{{11}}} - \bar {b}_{{11}}^{2})}},$$
$${{\varepsilon }_{{11}}} = {{({{y}_{1}} - {{{\bar {a}}}_{{12}}}{{\varepsilon }_{{22}}} - {{{\bar {b}}}_{{11}}}{{\kappa }_{{11}}} - {{{\bar {b}}}_{{12}}}{{\kappa }_{{22}}})} \mathord{\left/ {\vphantom {{({{y}_{1}} - {{{\bar {a}}}_{{12}}}{{\varepsilon }_{{22}}} - {{{\bar {b}}}_{{11}}}{{\kappa }_{{11}}} - {{{\bar {b}}}_{{12}}}{{\kappa }_{{22}}})} {{{{\bar {a}}}_{{11}}}}}} \right. \kern-0em} {{{{\bar {a}}}_{{11}}}}},\quad {{\kappa }_{{12}}} = {{r}_{2}}({{\varepsilon }_{{12}}} + \bar {j}{{y}_{5}}) - \bar {j}({{y}_{8}} + \psi {{y}_{7}}),$$
$${{T}_{{22}}} = {{\bar {a}}_{{12}}}{{\varepsilon }_{{11}}} + {{\bar {a}}_{{22}}}{{\varepsilon }_{{22}}} + {{\bar {b}}_{{12}}}{{\kappa }_{{11}}} + {{\bar {b}}_{{22}}}{{\kappa }_{{22}}},\quad {{M}_{{22}}} = {{\bar {b}}_{{12}}}{{\varepsilon }_{{11}}} + {{\bar {b}}_{{22}}}{{\varepsilon }_{{22}}} + {{\bar {c}}_{{12}}}{{\kappa }_{{11}}} + {{\bar {c}}_{{22}}}{{\kappa }_{{22}}},$$
$${{\varepsilon }_{{12}}} = {{\left[ {{{y}_{2}} - 2({{{\bar {b}}}_{{33}}} + 2{{r}_{2}}{{{\bar {c}}}_{{33}}})\bar {j}({{r}_{2}}{{y}_{5}} - {{y}_{8}} - \psi {{y}_{7}})} \right]} \mathord{\left/ {\vphantom {{\left[ {{{y}_{2}} - 2({{{\bar {b}}}_{{33}}} + 2{{r}_{2}}{{{\bar {c}}}_{{33}}})\bar {j}({{r}_{2}}{{y}_{5}} - {{y}_{8}} - \psi {{y}_{7}})} \right]} {\left[ {{{{\bar {a}}}_{{33}}} + 4{{r}_{2}}({{{\bar {b}}}_{{33}}} + {{r}_{2}}{{{\bar {c}}}_{{33}}})} \right]}}} \right. \kern-0em} {\left[ {{{{\bar {a}}}_{{33}}} + 4{{r}_{2}}({{{\bar {b}}}_{{33}}} + {{r}_{2}}{{{\bar {c}}}_{{33}}})} \right]}}.$$

Let us set homogeneous boundary conditions at the edges of the shell:

$${{\left. {{{y}_{i}}} \right|}_{{s = 0}}}{{\delta }_{i}} + {{\left. {{{y}_{{i + 4}}}} \right|}_{{s = 0}}}(1 - {{\delta }_{i}}) = 0\quad (i = 1,\; \ldots ,\;4),$$
(7)
$${{\left. {{{y}_{i}}} \right|}_{{s = L}}}{{\delta }_{{i + 4}}} + {{\left. {{{y}_{{i + 4}}}} \right|}_{{s = L}}}(1 - {{\delta }_{{i + 4}}}) = 0\quad (i = 1,\; \ldots ,\;4),$$
(8)

where for known kinematic and static boundary conditions \({{\delta }_{i}} = 0\) and \({{\delta }_{i}} = 1\), respectively.

Let us now solve system (5) with boundary conditions (7) and (8) using the Godunov orthogonal sweep method [30] with numerical integration of differential equations by the Runge–Kutta fourth order method. To do this, we represent its general solution in the form:

$${\mathbf{y}} = \sum\limits_{j = 1}^4 {{{C}_{j}}{{{\mathbf{y}}}_{j}}} ,$$

where \({{C}_{j}}\) are certain constants and \({{{\mathbf{y}}}_{j}}\) is the set of linearly independent solutions satisfying the boundary conditions (7). As a result of integration over a given interval and satisfaction of boundary conditions (8) we obtain the following algebraic system to determine the constants \({{C}_{j}}\):

$$\sum\limits_{j = 1}^4 {{{C}_{j}}{{f}_{{ij}}}} = 0\quad (i = 1,\; \ldots ,\;4).$$
(9)

Thus, the problem is reduced to calculating the values of \(\omega \), for which there is a nontrivial solution to system (9). A necessary condition is the equality to zero of the determinant of the matrix \(\left| {{{f}_{{ij}}}(\omega )} \right| = 0\). For this purpose, let us use a combination of the step method and the bisection method. Using the former we calculate such values of \(\omega \), at which the determinant of \(\left| {{{f}_{{ij}}}(\omega )} \right|\) changes sign, and using the latter we specify \(\omega \) in the obtained range of their values.

4 NUMERICAL RESULTS

The given numerical examples consider a conical shell (\({{R}_{1}} = 0.1,\;\nu = 0.3\)), either simply supported at the edges (\(v = w = {{T}_{{11}}} = {{M}_{{11}}} = 0\), symbol SS), or rigidly clamped (\(u = v = w = {{\theta }_{1}} = 0\), CC), or has a cantilevered support (\({{T}_{{11}}} = 0,\;S + 2{{r}_{2}}H = 0,\;{{M}_{{11}}} = 0,\;{{Q}_{{11}}} + \bar {j}H = 0\), CF). To represent the results, we use the dimensionless frequency \(\lambda = \omega l{{\left[ {{{\rho (1 - \nu _{{12}}^{2})} \mathord{\left/ {\vphantom {{\rho (1 - \nu _{{12}}^{2})} {{{E}_{{11}}}}}} \right. \kern-0em} {{{E}_{{11}}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\) or the frequency ratio \({\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}\), where \({{\omega }_{0}}\) corresponds to the minimum vibration frequency of a shell of constant thickness at the same cone angle. The variability of the thickness is set using the parameter \(\beta = k - 1 = {{{{h}_{{\max }}}} \mathord{\left/ {\vphantom {{{{h}_{{\max }}}} {{{h}_{{\min }}}}}} \right. \kern-0em} {{{h}_{{\min }}}}}\), where \({{h}_{{\max }}}\) and \({{h}_{{\min }}}\) are maximum and minimum wall thickness. Figure 3 shows the profile examples of shells with a mass equivalent to the reference mass for different values of the parameter β and different laws of thickness variation.

Fig. 3.
figure 3

Longitudinal sections of the shell walls with different versions of changing the thickness and equivalent masses at the values of the parameter \(\beta \): 2 (a); 5 (b).

Full size image

To verify the algorithm described above, we compared the results obtained by it with the data for a conical shell of constant thickness from [31–33] at \(\alpha = 45^\circ \), \({{\nu }_{{12}}} = 0.3\), \({h \mathord{\left/ {\vphantom {h {{{R}_{1}}}}} \right. \kern-0em} {{{R}_{1}}}} = 0.01\). Table 1 shows the values of the dimensionless minimum frequencies \(\lambda \) corresponding to the first nine circumferential vibration modes \(j\) for shells with different boundary conditions. In the case of shells of variable thickness, a comparison was made with the solution from [18], which was obtained by the finite element method. Minimum vibration frequencies \(\omega \) (Hz) and their respective harmonic orders \(j\), calculated in the present work for a rigidly clamped (CC) conical shell at \({{E}_{{11}}} = 181\) GPa, \({{E}_{{22}}} = 10.5\) GPa, \({{G}_{{12}}} = 7.17\) GPa, \({{\nu }_{{12}}} = 0.28\), \(\rho = 1600\) kg/m3, \({h \mathord{\left/ {\vphantom {h {{{R}_{1}}}}} \right. \kern-0em} {{{R}_{1}}}} = 0.01\), \({{R}_{1}} = 0.1\) m and thickness varying according to symmetric linear law (version V2), are presented in Table 2 for various cone angles \(\alpha \), linear size \({{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} l}} \right. \kern-0em} l}\) and different values of the thickness variability parameter \(\beta \). The data in Tables 1 and 2 shows that the results are in good agreement with the previously published results of numerical-analytical and numerical solutions.

Table 1.   Comparison of the dimensionless lower vibration frequencies \(\lambda \) of a conical shell (\(\alpha = 45^\circ \)) of constant thickness under various boundary conditions
Full size table
Table 2.   Comparison of the minimum vibration frequencies \(\omega \) (Hz) of a rigidly clamped (CC) conical shell of variable thickness (V2) at different values of the cone angles \(\alpha \), linear size \({{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} l}} \right. \kern-0em} l}\) and thickness variability parameter \(\beta \)
Full size table

Figures 4a, 5a, and 6a present dependences of dimensionless frequencies \(\lambda \) on the cone angle \(\alpha \), calculated for different values of the circumferential harmonic \(j\) for different combinations of boundary conditions set at the edges of a conical shell of constant thickness (\({{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} l}} \right. \kern-0em} l} = 2\), \(\beta = 1\)). These data demonstrate a significant dependence of the circumferential vibration mode with the minimum frequency on the cone angle α, especially in the case of symmetric (SS and CC) boundary conditions. For the same boundary conditions, increasing the cone angle to a certain value leads to a noticeable increase in the minimum vibration frequency, which in itself can serve as an obvious design solution aimed at maximizing the frequency spectrum.

Fig. 4.
figure 4

Dependences of dimensionless \(\lambda \) (a) and normalized \({\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}\) (b–d) frequencies on the cone angle \(\alpha \) of a simply supported shell with values of the thickness variability parameter \(\beta \): 1 (a), 2 (b), 5 (c), 8 (d).

Full size image
Fig. 5.
figure 5

Dependences of dimensionless \(\lambda \) (a) and normalized \({\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}\) (b–d) frequencies on the cone angle \(\alpha \) of a rigidly clamped shell with values of the thickness variability parameter \(\beta \): 1 (a), 2 (b), 5 (c), 8 (d).

Full size image
Fig. 6.
figure 6

Dependences of dimensionless \(\lambda \) (a) and normalized \({\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}\) (b–d) frequencies on the cone angle \(\alpha \) of a cantilevered shell with values of the thickness variability parameter \(\beta \): 1 (a), 2 (b), 5 (c), 8 (d).

Full size image

The rest of the graphs in Figs. 4–6 reflect the effect of the cone angle \(\alpha \) on the frequency ratio \({\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}\), obtained with different laws of thickness variation and different values of the variability parameter \(\beta \). Here, ω is the smallest value in the frequency spectrum corresponding to several circumferential harmonics. The nonmonotonic nature of the curves is largely due to the change in the circumferential harmonic with a minimum vibration frequency. Such a transformation can occur both for shells with constant (as reflected in all curves) and variable profiles. The demonstrated dependences clearly illustrate the advantages or disadvantages of a variable profile in comparison with a constant one for shells with different combinations of boundary conditions and the same weight at a specific value of the cone angle.

Summarizing the data shown in Figs. 4–6, we can conclude:

1) There is no universal law of thickness variation suitable for various boundary conditions; every law behaves in a specific way for a particular configuration.

2) For some laws of thickness variation that are most suitable for certain boundary conditions, an increase in the variability parameter \(\beta \) leads to an increase in the minimum vibration frequency.

3) For the same laws, an increase in the cone angle \(\alpha \) and the associated increment of the lateral surface of the shell lead to a significant increase in the minimum vibration frequency, especially in the case of cantilever support.

The most complex picture appears in the case of simply supported shells (Figs. 4b–4d). Here, in certain ranges of cone angles, it is preferable to use either asymmetrical or any of the symmetrical profiles. Under the same boundary conditions, the convex harmonic profile (version V5) shows its advantages over other configurations uniquely at \(\beta = 2\) and for a narrow range of \(\alpha \). For a counter case, one can reference [34], which shows that for a cylindrical shell loaded with a uniform axial force, this law of thickness variation with rigid edge restraint provides the most effective stability parameters.

Based on the data obtained, it can be concluded that the applicability of symmetric and asymmetric profiles is uniquely determined by the specified boundary conditions. In the case of two-sided rigid clamped (see Figs. 5b–5d) each of the symmetrical profiles has an advantage at any cone angle, guaranteeing an increase in the minimum frequency even in comparison with a cylindrical shell of constant thickness. On the contrary, examples with a cantilever boundary condition (see Figs. 6b–6d, the shell is supported along the edge with the maximum thickness), demonstrate a clear superiority of asymmetric thickness variation in comparison with symmetrical. The only exception is the version with \(\beta = 5\), where the V4 profile with a small cone angle is more effective.

Note also that, with rare exceptions under such boundary conditions the variable wall thickness provides higher frequency values, in comparison with the uniform distribution of mass along the meridian coordinate.

The results obtained for other geometrical sizes and summarized in Table 3 demonstrate that both for very short (\({{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} l}} \right. \kern-0em} l} = 0.5\)) and for longer shells (\({{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} l}} \right. \kern-0em} l} > 5\)) the above dependences are not observed only under the free support condition. But, while for these boundary conditions the asymmetric profiles V1 and V3 are inferior to the symmetric in the case of short shells at large cone angles, for longer shells they conversely guarantee an increase in the vibration frequency in the entire variation range of cone angle. Moreover, the use of long shells with a symmetrical profile becomes unreasonable due to the deterioration of characteristics in comparison with shells of constant thickness. Quantitative differences in the minimum vibration frequencies of shells with variable and constant thicknesses depend both on the geometric size and on the specified boundary conditions. For simply supported shells the frequency ration \({\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}\) reaches maximum for a short shell: at \({{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} l}} \right. \kern-0em} l} = 2\), for rigidly clamped shells, at \({{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} l}} \right. \kern-0em} l} = 0.5\), and for cantilevered support the value of \({\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}\) increases with the increase in the \({{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} l}} \right. \kern-0em} l}\) ratio.

Table 3.   Normalized frequencies \({\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}\) of a shell of variable thickness under different boundary conditions
Full size table

5 CONCLUSIONS

We present the results of numerical study of the frequency spectrum of truncated circular conical shells, the wall thickness of which varies along the meridian coordinate according to the power law or harmonic law. We analyzed the influence of boundary conditions, geometric size, thickness variability parameter, and cone angle on the natural vibration frequencies of the structure. The frequencies obtained for shells with constant and variable thicknesses are compared, under the condition that their masses are equivalent. For shells, the thickness of which is a function of the meridian coordinate, we obtained combinations of boundary conditions, the law of thickness variation with a symmetric/asymmetric wall profile or positive/negative curvature of the lateral surface, linear size, etc., at which there is a significant increase in the minimum frequencies compared to a shell of constant thickness. It is shown that for specific boundary conditions, by selecting a number of parameters, one can significantly maximize the minimum vibration frequency while keeping the shell mass (at a certain cone angle) unchanged.